T-이중성
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
T-이중성은 물리학, 특히 끈 이론에서 나타나는 이중성의 한 형태이다. 끈 이론에서 끈이 축소된 차원에 따라 감길 수 있는데, T-이중성은 끈이 반지름 R인 원에서 전파되는 이론과 반지름 1/R인 원에서 전파되는 이론이 동일하다는 것을 의미한다. 이러한 이중성은 IIA와 IIB 끈 이론, 그리고 두 종류의 잡종 끈 이론을 서로 연결하며, 초끈 이론의 저에너지 극한인 초중력에서도 나타난다. T-이중성은 2차원 등각 장론, 위상 T-이중성, 거울 대칭과도 관련이 있으며, 1980년대에 깃카와 게이지, 야마사키 마사미, 사카이 노리스케, 센다 이쿠오 등에 의해 초기적인 형태로 도입되었고, 부셔, 로체크, 페를린더에 의해 개량 및 확장되었다.
더 읽어볼만한 페이지
- 끈 이론 - 중력자
중력자는 중력 상호작용을 매개하는 가상의 기본 입자로 여겨지지만, 양자화된 일반 상대성 이론의 문제로 인해 완전한 이론이 확립되지 않았으며, 중력파의 존재가 간접적으로 뒷받침하지만 직접적인 검출은 현재 불가능하고 질량에 대한 상한선이 제시되고 있으며 초대칭 파트너인 그라비티노의 존재가 예측된다. - 끈 이론 - 잡종 끈 이론
잡종 끈 이론은 닫힌 끈의 왼쪽 진동 모드는 보손 끈, 오른쪽 진동 모드는 초끈으로 전개하며, 10차원 시공간에서 E8×E8 또는 SO(32) 게이지 군을 갖는 끈 이론이다. - 양자장론 - 페르미-디랙 통계
페르미-디랙 통계는 파울리 배타 원리를 따르는 페르미 입자의 통계적 분포를 설명하는 양자 통계로, 금속 내 전자 현상 등을 이해하는 데 기여하며 페르미 입자가 특정 에너지 준위를 점유할 확률을 나타낸다. - 양자장론 - 양자 색역학
양자 색역학은 색 전하를 국소 대칭으로 정의한 SU(3) 게이지 군의 비아벨 게이지 이론으로, 쿼크와 글루온을 기본 입자로 하여 쿼크 사이의 강한 상호작용을 매개하며, 점근적 자유성과 색 가둠의 특징을 가지는 이론이다.
2. 정의
T-이중성은 물리학, 특히 끈 이론에서 나타나는 이중성의 한 형태이다. 겉보기에 서로 다른 두 개의 물리계가 실제로는 동일한 현상을 다르게 설명하는 경우가 있는데, 이를 이중성이라고 한다. T-이중성은 이러한 이중성의 특정한 예시이다.[3]
이론 물리학에서 T-이중성은 끈 이론에서 발견되었다. 끈 이론에서는 입자를 0차원의 점이 아니라 1차원의 끈으로 본다. 끈 이론은 우리가 일상적으로 경험하는 3차원 공간(위/아래, 좌/우, 앞/뒤) 외에도, 콤팩트 차원이라고 불리는, 원처럼 말려 있는 추가적인 차원을 포함할 수 있다.[4]
이러한 추가 차원을 이해하기 위해 정원 호스를 생각해 볼 수 있다. 멀리서 보면 호스는 1차원, 즉 길이만 있는 것처럼 보인다. 하지만 가까이 다가가면 둘레라는 두 번째 차원이 존재함을 알 수 있다. 마찬가지로, 끈 이론에서도 추가적인 차원이 존재할 수 있으며, T-이중성은 반지름 인 원에서 전파되는 끈 이론과 반지름 인 원에서 전파되는 끈 이론을 연결한다.[4]
2. 1. 끈과 이중성
끈 이론에서, T-이중성은 서로 다른 콤팩트화 차원을 가진 두 이론이 물리적으로 동등함을 의미한다. 이는 끈이 콤팩트 차원에서 감길 수 있다는 점과, 운동량이 양자화된다는 점을 통해 설명된다.원기둥에 축소화한 닫힌 보손 끈을 생각하자. 축소 차원의 크기가 이라고 하자. 그렇다면 축소 차원에서의 운동량은 의 단위로 양자화된다.
:,
끈은 또한 축소 차원에 따라 (점입자와 달리) 감길 수 있다. 닫힌 끈의 경우, 축소 차원에 따라 감긴 수를 '''감음수'''(winding number영어) 라고 부른다.
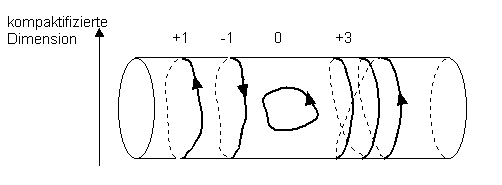
그렇다면 끈의 질량은 다음과 같다.
:
여기서 은 끈의 총 진동 모드의 수다. (로 놓자.) 따라서
:
와 같이 바꾸면 끈의 질량 스펙트럼이 같은 것을 알 수 있다. 또한 마찬가지로 끈의 상호 작용도 같다는 사실을 보일 수 있다.
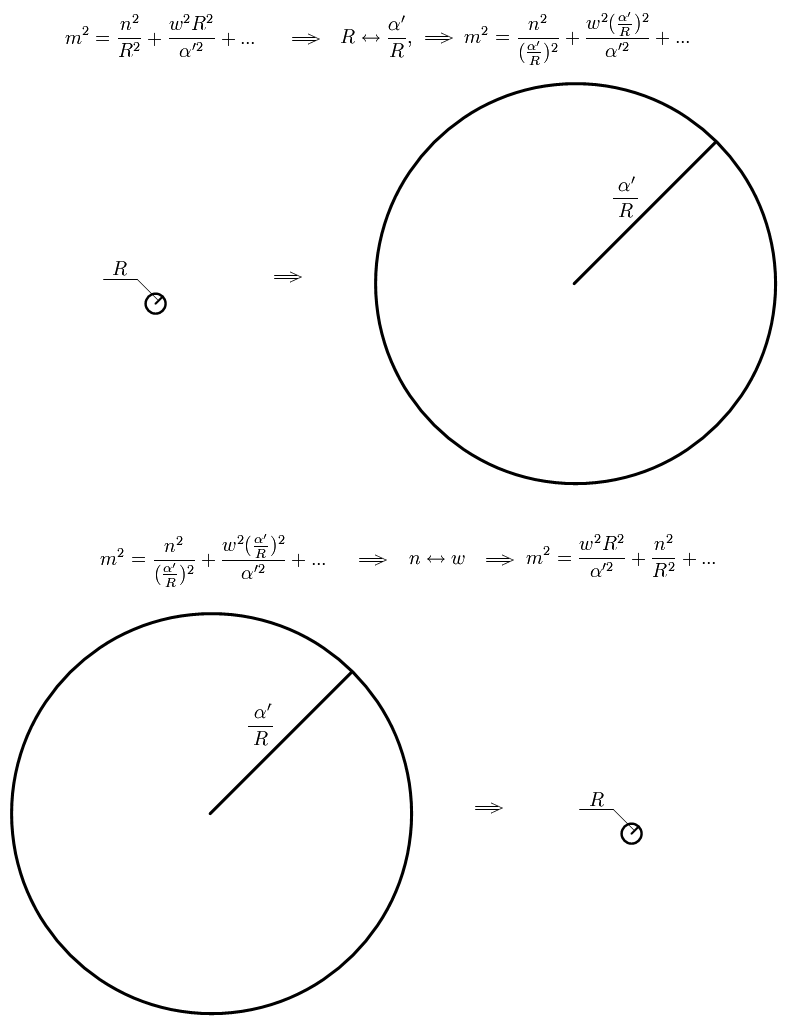
T-이중성은 물리학에서 일반적인 이중성의 특정한 예시이다. "이중성"은 겉보기에 서로 다른 두 개의 물리계가 비자명한 방식으로 동일하게 나타나는 상황을 지칭한다. 두 이론이 이중성에 의해 관련되어 있다면, 하나의 이론이 어떤 방식으로 변환되어 다른 이론과 똑같이 보이게 될 수 있다는 것을 의미한다. 그러면 두 이론은 그 변환 하에서 서로 "이중적"이라고 한다. 다르게 말하면, 두 이론은 동일한 현상에 대한 수학적으로 다른 설명이다.
이론 물리학에서 연구되는 많은 이중성과 마찬가지로, T-이중성은 끈 이론의 맥락에서 발견되었다.[3] 끈 이론에서 입자는 0차원 점이 아니라 끈이라고 불리는 1차원 확장 객체로 모델링된다. 끈의 물리학은 다양한 차원에서 연구될 수 있다. 일상적인 경험에서 친숙한 세 차원(위/아래, 좌/우, 앞/뒤) 외에도, 끈 이론은 하나 이상의 콤팩트 차원을 포함할 수 있으며, 이는 원으로 말려 있다.
이에 대한 표준적인 비유는 정원 호스와 같은 다차원 객체를 고려하는 것이다.[4] 호스를 충분한 거리에서 보면, 그것은 단지 하나의 차원, 즉 길이를 갖는 것처럼 보인다. 그러나 호스에 접근할수록, 그것은 두 번째 차원, 즉 둘레를 포함한다는 것을 알게 된다. 따라서, 그 안을 기어가는 개미는 두 차원에서 움직일 것이다. 이러한 추가 차원은 T-이중성에서 중요한데, 이는 끈이 반지름 의 원에서 전파되는 이론을 끈이 반지름 의 원에서 전파되는 이론과 관련시킨다.
끈 이론은 일반적인 공간 차원 3개와 시간 차원 1개 외에 여분의 차원을 예측한다. 이러한 여분의 차원의 서로 다른 크기나 모양은 4차원의 저에너지 물리학에 나타나는 서로 다른 힘이나 서로 다른 입자가 되므로, 서로 다른 모양의 우주는 서로 다른 물리학을 가질 것이다. 그러나, 이러한 많은 기하학이 동일한 물리학의 결과를 낳고, 이것이 T-이중성의 기초가 된다.
예를 들어, 차원 중 하나가 반지름 인 원인 경우를 생각해 보자. 이 방향으로 입자나 끈은 운동량을 가지므로, 그러한 상태를 '''칼루자-클라인 모드'''라고 부른다. 이 방향의 운동량은 다음을 만족함으로써 양자화된다.
:
반지름 을 작게 하면, 모드 중 하나를 여기시키는 데 더 많은 에너지가 필요하게 된다. 한편, 이 커지면, 칼루자-클라인 상태 사이의 간격이 작아지고, 반지름이 무한대인 극한에서 운동량은 더 이상 양자화되지 않는다.
입자와 달리, 닫힌 끈은 또한 여분의 차원에 감길 수도 있다. 그러한 상태를 '''감김 모드'''라고 한다. 감김 모드를 여기시키는 에너지는 반지름 에 비례하여 양자화되어 있으므로, 반지름이 작아짐에 따라 감김 모드가 작아지므로, 반지름이 0이 되는 극한에서는 더 이상 양자화되지 않는다. 한편, 반지름이 커지면 감김 모드를 여기시키는 데 사용하는 에너지는 커진다. 이 칼루자-클라인 모드의 거동은 반대이며, 감김 모드와 칼루자-클라인 모드를 교환하면, 반지름이 작을 때와 클 때 닫힌 끈의 거동은 동일해진다. 반지름 에서의 물리학과 반지름 에서의 물리학이 동일해진다. 이 관계가 T-이중성의 예이다.
T-이중성의 아이디어를 설명하기 위해, 반지름 인 원으로 콤팩트화된 보존 끈 이론을 생각해 보자. 끈은 순수한 운동량 를 콤팩트화된 차원 내에서도 가지고 있다. 이 입자의 경우에는, 운동량은 의 단위로 양자화되어야 한다.
:
여기서 은 정수이다.
그러나 입자의 경우와는 달리, 닫힌 끈은 콤팩트화된 차원을 감싸고 있을 수 있다. 그 차원을 감은 횟수를 감김수 라고 한다. 따라서 닫힌 끈의 질량은 다음과 같다.
:
여기서 과 는 닫힌 끈의 좌(left-) 및 우(right-) 이동의 여기 상태이며, 는 기울기 매개변수(slope parameter)이다. 이 스펙트럼은 다음 변환 아래에서 불변이다.
:
즉, 닫힌 끈의 스펙트럼은 반지름 의 배경을 가진 닫힌 끈의 스펙트럼과 동일한 스펙트럼을 갖는다. 닫힌 끈의 상호 작용도 이 변환 아래에서 불변임을 보일 수 있다. 이는 반지름 로 콤팩트화된 닫힌 보존 끈은 반지름 인 이론과 등가임을 의미한다.
2. 2. 감음수
원기둥에 축소화한 닫힌 보손 끈을 생각할 때, 닫힌 끈이 축소 차원에 따라 감기는 횟수를 '''감음수'''(winding number영어)라고 부른다.[3] 끈은 점입자와 달리 축소 차원에 따라 감길 수 있다. 감음수는 끈이 시계 방향으로 감기면 음수, 시계 반대 방향으로 감기면 양수로 정의한다.수학에서 주어진 점을 중심으로 평면 위 곡선의 회전수는 곡선이 점을 반시계 방향으로 도는 총 횟수를 나타내는 정수이다.[3] 회전수는 T-이중성의 수학적 설명에서 콤팩트 여분 차원 주위의 끈의 감김을 측정하는 데 사용된다.
총 회전수를 계산할 때 반시계 방향 회전은 양수, 시계 방향 회전은 음수로 계산한다. 예를 들어 곡선이 먼저 원점을 반시계 방향으로 네 번 돌고, 시계 방향으로 한 번 돌면 총 회전수는 3이다. 점을 전혀 돌지 않는 곡선은 회전수가 0이고, 시계 방향으로 도는 곡선은 음수 회전수를 갖는다. 다음 표는 회전수에 따른 곡선의 예시를 보여준다.
2. 3. 운동량 양자화
원기둥에 축소화한 닫힌 보손 끈을 생각하면, 축소 차원의 크기가 일 때, 축소 차원에서의 운동량은 단위로 양자화된다.[3]:,
끈은 점입자와 달리 축소 차원에 따라 감길 수 있다. 닫힌 끈이 축소 차원에 감긴 수를 '''감음수'''(winding number|와인딩 수영어) 라고 부른다.[3]
닫힌 끈의 질량은 다음과 같다.
:
여기서 은 끈의 총 진동 모드의 수이다. (로 놓자.)
따라서
:
와 같이 바꾸면 끈의 질량 스펙트럼이 같다는 것을 알 수 있다.
이는 T-이중성이 끈의 운동량과 감음수를 서로 교환하는 변환임을 보여준다.
3. 보손 끈 이론에서의 T-이중성
보손 끈 이론에서 T-이중성은 반지름 을 가진 원에서 전파되는 끈 이론과 반지름 을 가진 원에서 전파되는 끈 이론이 서로 동등하다는 것을 의미한다. 여기서 는 끈의 장력을 나타내는 기울기 매개변수이다.
끈 이론에서는 입자를 0차원 점이 아닌 1차원의 끈으로 모델링한다. 우리가 일상적으로 경험하는 3차원 공간 외에도, 끈 이론에서는 원처럼 말려 있는 콤팩트 차원이 존재할 수 있다. 정원 호스를 멀리서 보면 1차원 선처럼 보이지만, 가까이 다가가면 2차원 둘레를 가지는 것처럼, 콤팩트 차원도 마찬가지이다.
반지름 인 원으로 콤팩트화된 보존 끈 이론에서, 끈은 콤팩트 차원 내에서 운동량 를 가질 수 있으며, 이 운동량은 단위로 양자화된다. 즉,
:
(여기서 은 정수)이다.
또한 닫힌 끈은 콤팩트 차원을 감을 수 있는데, 감은 횟수를 감음수 라고 한다. 닫힌 끈의 질량은 다음과 같이 표현된다.
:
여기서 과 은 닫힌 끈의 좌, 우 이동 여기 상태이다.
이 식은 다음 변환에 대해 불변이다.
:
즉, 반지름 인 경우와 인 경우, 운동량과 감음수를 서로 바꾸면 닫힌 끈의 질량 스펙트럼은 동일하게 유지된다. 닫힌 끈의 상호작용 또한 이 변환에서 불변이다. 따라서 반지름 로 콤팩트화된 닫힌 보존 끈 이론은 반지름 로 콤팩트화된 이론과 동등하다.
3. 1. 닫힌 끈의 T-이중성
원기둥에 축소화한 닫힌 보손 끈을 생각해보자. 축소 차원의 크기가 이라고 할 때, 축소 차원에서의 운동량은 단위로 양자화된다.[3]:,
끈은 점입자와 달리 축소 차원에 따라 감길 수 있다. 닫힌 끈의 경우, 축소 차원에 따라 감긴 수를 '''감음수'''(winding number|와인딩 수영어) 라고 부른다.[3]
이때 끈의 질량은 다음과 같다.
:
여기서 은 끈의 총 진동 모드의 수다. (로 놓자.) 따라서
:
와 같이 바꾸면 끈의 질량 스펙트럼이 같다는 것을 알 수 있다. 마찬가지로 끈의 상호 작용도 같다는 것을 보일 수 있다.[3]
이는 반지름 로 콤팩트화된 닫힌 보존 끈은 반지름 인 이론과 등가임을 의미한다. 즉, 작은 반지름을 가진 이론과 큰 반지름을 가진 두 이론이 동등하다는 것이다.
3. 2. 열린 끈과 D-막의 T-이중성
열린 끈의 경우, 노이만 경계 조건이 디리클레 경계 조건에 대응된다. 따라서 이론에 디리클레 경계 조건과 D-막을 포함하여야 한다. 이에 따라, Dp-막은 (축소화하는 방향에 따라서) Dp-막 또는 D(p-1)-막에 대응된다. T-이중성은 D-브레인에 작용하여 그 차원을 +1 하거나 -1 하도록 작용한다.3. 3. 등각 장론의 관점
2차원 등각 장론의 관점에서 T-이중성은 이미 나타난다. 가장 간단하게, 스칼라 장:
을 생각할 수 있다. 이 경우, 그 분배 함수는 다음과 같은 형태를 가진다.[20]
: (
4. 초끈 이론에서의 T-이중성
초끈 이론에서 T-이중성은 ⅡA와 ⅡB종 이론, HE와 HO 이론을 각각 서로 연관짓는다. T-이중성은 끈 이론에서 나타나는 일반적인 이중성의 한 예시이다. 이중성이란 겉보기에는 서로 다른 두 이론이 실제로는 동일한 현상을 설명하는 다른 방식임을 의미한다.
끈 이론에서는 입자를 0차원의 점이 아닌 1차원의 끈으로 모델링한다. 끈 이론은 우리가 일상적으로 경험하는 3차원 공간 외에도, 원처럼 말려 있는 콤팩트 차원을 추가로 포함할 수 있다. 예를 들어, 멀리서 보면 1차원으로 보이는 정원 호스도 가까이서 보면 둘레라는 두 번째 차원을 갖는 것과 같다. T-이중성은 끈이 반지름
1990년대 중반까지 물리학자들은 제1종, 제2A종, 제2B종, 그리고 두 가지 종류의 잡종 끈 이론(SO(32)와 E8×E8)과 같이 다섯 가지 종류의 끈 이론이 있다고 믿었다. 그러나 이후 T-이중성을 통해 이 이론들이 서로 연결되어 있음이 밝혀졌다. 1995년 에드워드 위튼은 이 다섯 가지 이론이 모두 M-이론이라는 하나의 이론의 서로 다른 극한이라는 제안을 했고,[5] 이는 제2차 초끈 혁명으로 이어졌다.
4. 1. IIA와 IIB 이론의 관계
IIA 끈 이론을 원 위에 축소화하면 IIB 끈 이론을 얻고, 그 반대도 성립한다. 이는 M-이론의 관점에서 설명될 수 있다.[5] 예를 들어, 문제의 방향으로 한 번 감긴 IIA형 끈은 T-이중성에 의해 해당 방향으로 운동량을 가진 IIB형 끈으로 변환된다. 감김수 2를 가진 IIA형 끈은 운동량 단위 2를 가진 IIB형 끈으로 변환되는 등 다른 경우도 마찬가지이다.1990년대 중반까지 끈 이론 연구자들은 끈 이론에 제1종, 제2A종, 제2B종, 그리고 두 가지 종류의 이종 끈 이론 (SO(32)와 E8×E8)의 다섯 가지 버전이 있다고 믿었다. 그러나 1990년대 중반에 물리학자들은 이 다섯 가지 끈 이론이 T-이중성과 같은 이중성에 의해 서로 관련되어 있다는 것을 알아냈다. 예를 들어, 제2A종 끈 이론은 T-이중성을 통해 제2B종 끈 이론과 동일하며, 두 가지 버전의 이종 끈 이론도 T-이중성에 의해 관련되어 있다.
초끈 이론에서 T-이중성은 ⅡA와 ⅡB종 이론을 서로 연관시킨다. 축소화 관계는 다음과 같다.
:
D=11 & \mathrm{M} \\
& \downarrow \\
D=10 & \mathrm{IIA} & & \mathrm{IIB} & \mathrm{H}\operatorname E_8\times\operatorname E_8 & & \mathrm H\operatorname{SO}(32) \\
& \downarrow & \swarrow & & \downarrow & \swarrow \\
D=9 & \mathcal N=2 & & & \mathcal N=1
\end{matrix}
4. 2. 잡종 끈 이론의 관계
HE와 HO 이론은 T-이중성에 의해 서로 연결된다.[18] 예를 들어, 문제의 방향으로 한 번 감긴 IIA형 끈으로 시작하면, T-이중성은 해당 방향으로 운동량을 가진 IIB형 끈으로 변환한다. 감김수 2를 가진 IIA형 끈은 운동량 단위 2를 가진 IIB형 끈으로 변환되는 등 다른 경우도 마찬가지이다.4. 3. I'종 이론 (IA종 이론)
I′종 끈 이론(IA종 이론)은 T-이중성 변환을 통해 I종 끈 이론에서 유도된다. I′종 이론은 D-막에 의해 10차원 푸앵카레 대칭이 깨지는 특징을 갖는다.[18][21] 이 이론은 IIA종 끈 이론에 오리엔티폴드 사영을 가한 것으로 볼 수 있다. IIA종 끈 이론에서는 오른쪽 및 왼쪽 모드의 손지기(Chirality)가 서로 반대이므로, 사영을 위해서는 향의 반전4. 4. 부셔 규칙
T-이중성 아래, NS-NS 배경장:
:
:
:
:
:
여기서
5. 초중력의 T-이중성
초끈 이론의 저에너지 극한인 초중력에서도 T-이중성이 나타난다. 10차원 ⅡA 초중력과 ⅡB 초중력을 각각 원 위에 축소화하면 9차원에서는 동일한
9차원으로 축소화하면 9차원 보손 장들의 종류와 개수가 같아진다. ⅡB 라몽-라몽 4차 형식의 장세기는 자기 쌍대(self-dual영어)이므로, 축소화하면 4차 형식을 남기지 않는다.
5. 1. IIA와 IIB 초중력의 관계
초끈 이론의 저에너지 극한은 초중력이다. ⅡA 초끈 이론의 저에너지 극한은 10차원 ⅡA 초중력이고, ⅡB 초끈 이론의 저에너지 극한은 10차원 ⅡB 초중력이다. 이 경우, T-이중성에 의하여 10차원 ⅡA 초중력을 원 위에 축소화하여 얻는 9차원그 자세한 대응성은 다음과 같다. 10차원 ⅡA 초중력의 보손 장과 10차원 중 한 차원을 축소화하여 얻는 9차원 장들은 다음과 같다.
ⅡB 초중력의 보손 장과 이를 축소화하여 얻는 장들은 다음과 같다.
(ⅡB 라몽-라몽 4차 형식의 장세기는 자기 쌍대(self-dual영어)이므로, 축소화하면 4차 형식을 남기지 않는다.)
따라서 9차원으로 축소화하면 9차원 보손 장들의 종류와 개수가 같아지는 것을 알 수 있다.
6. 위상 T-이중성
T-이중성은 원과의 곱공간 대신 원을 올로 하는 올다발에 대하여 적용될 수 있다. 이 경우 T-이중성은 서로 위상 동형이지 않을 수 있는 올다발 사이의 쌍대성을 정의한다.
7. 거울 대칭과의 관계
현대 끈 이론과 대수기하학에서 "거울 대칭"은 칼라비-야우 다양체와 관련된 현상을 의미한다. 이러한 다양체는 끈이 전파될 수 있는 흥미로운 기하학을 제공하며, 그 결과 이론은 입자 물리학에 적용될 수 있다.[6] 1980년대 후반, 이 칼라비-야우 다양체가 이론의 물리학을 고유하게 결정하지 않는다는 사실이 밝혀졌다. 대신, 동일한 물리학을 발생시키는 두 개의 칼라비-야우 다양체가 존재하며, 이들을 서로 "거울"이라고 부른다.[7] 거울 이중성은 끈 이론에서 중요한 계산 도구이며, 수학자들이 열거 기하학의 어려운 문제를 해결하는 데 도움을 주었다.[8]
7. 1. SYZ 추측
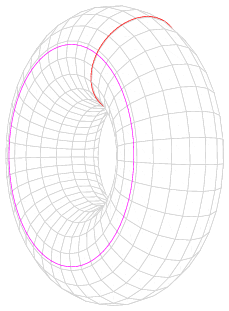
앤드루 스트로민저, 싱퉁 야우, Eric Zaslow|에릭 자슬로영어는 거울 대칭이 칼라비-야우 다양체의 3차원 토로이드 파이버 공간에 적용된 T-이중성으로 이해될 수 있음을 보였다.[9] SYZ 추측에 따르면, 거울 대칭은 복잡한 칼라비-야우 다양체를 더 단순한 조각으로 나누고 이러한 조각에 대한 T-이중성의 영향을 고려하여 이해할 수 있다.[10]칼라비-야우 다양체의 가장 간단한 예는 토러스(도넛 모양의 표면)이다. 이러한 표면은 두 원의 데카르트 곱으로 볼 수 있다. 이것은 토러스를 세로 원(이미지의 빨간색 원과 같은) 모음의 합집합으로 볼 수 있음을 의미한다. 이러한 원들이 어떻게 구성되는지를 알려주는 보조 공간이 있으며, 이 공간 자체는 원(분홍색 원)이다. 이 공간은 토러스의 세로 원을 "매개변수화"한다고 한다. 이 경우, 거울 대칭은 세로 원에 작용하는 T-이중성과 동일하며, 그 반지름을
SYZ 추측은 이 아이디어를 6차원 칼라비-야우 다양체의 더 복잡한 경우로 일반화한다. 토러스의 경우처럼, 6차원 칼라비-야우 다양체를 더 단순한 조각으로 나눌 수 있는데, 이 경우 3-토러스(토러스 개념을 일반화한 3차원 객체)는 3-구(구의 3차원 일반화)에 의해 매개변수화된다.[11] T-이중성은 원에서 이 분해에 나타나는 3차원 토러스로 확장될 수 있으며, SYZ 추측은 거울 대칭이 이러한 3차원 토러스에 대한 T-이중성의 동시 적용과 동일하다고 명시한다.[12] 이러한 방식으로, SYZ 추측은 거울 대칭이 칼라비-야우 다양체에 어떻게 작용하는지에 대한 기하학적 그림을 제공한다.
8. 역사
오사카 대학의 깃카와 게이지(吉川 圭二|きっかわ けいじ일본어)와 야마사키 마사미(山崎 眞見|やまさき まさみ일본어)가 1984년에[22], 도쿄 공업대학의 사카이 노리스케(坂井 典佑|さかい のりすけ일본어)와 센다 이쿠오(仙田 郁夫|せんだ いくお일본어)가 1986년에[23] 초기적인 형태로 도입하였다. 토머스 헨리 부셔(Thomas Henry Buscher영어)[24][25][26]와 마르틴 로체크(Martin Ročekcs), 에리크 페터르 페를린더(Erik Peter Verlindenl)[27]가 이를 개량하고 확장하였다.
오늘날에는 이와 같은 가환(Abelian) T-이중성 말고도, 이를 일반화한 비가환 T-이중성[28]과 페르미온 T-이중성[29][30]이 알려져 있다. 또한, 거울 대칭도 T-이중성을 일반화한 것으로 볼 수 있다.[31]
참조
[1]
논문
Sathiapalan 1987
[2]
논문
Seiberg 2006
[3]
논문
Sathiapalan 1987
[4]
논문
Greene 2000
[5]
논문
Witten 1995
[6]
논문
Candelas et al. 1985
[7]
논문
Dixon 1988; Lerche, Vafa, and Warner 1989
[8]
논문
Zaslow 2008
[9]
논문
Strominger, Yau, and Zaslow 1996
[10]
논문
Yau and Nadis 2010
[11]
논문
Yau and Nadis 2010
[12]
논문
Yau and Nadis 2010
[13]
웹사이트
T-duality in nlab
http://ncatlab.org/n[...]
[14]
웹사이트
Generalised complex geometry and T-duality
http://www.staff.sci[...]
2013-10-29
[15]
웹사이트
Looking for extra dimensions
http://www.superstri[...]
[16]
저널
Target space duality in string theory
[17]
저널
An introduction to T-duality in string theory
1995-04
[18]
서적
String Theory and M-Theory: A Modern Introduction
Cambridge University Press
2006-12
[19]
서적
String Theory, Volume 1: An introduction to the bosonic string
Cambridge University Press
[20]
서적
Introduction to conformal field theory with applications to string theory
Springer-Verlag
[21]
서적
The many faces of the superworld: Yuri Golfand memorial volume
World Scientific
2010-07
[22]
저널
Casimir effects in superstring theories
1984-12-20
[23]
저널
Vacuum energies of string compactified on torus
[24]
저널
Quantum corrections and extended supersymmetry in new σ-models
1985-09-19
[25]
저널
A symmetry of the string background field equations
1987-07-30
[26]
저널
Path-integral derivation of quantum duality in nonlinear sigma-models
1988-02-18
[27]
저널
Duality, quotients and currents
1992-04-13
[28]
저널
Recent developments in non-Abelian T-duality in string theory
2011-11
[29]
저널
Dual superconformal symmetry, and the amplitude/Wilson loop connection
2008-09-11
[30]
저널
Fermionic T-duality: a snapshot review
2012-11-20
[31]
저널
Mirror symmetry is ''T''-duality
1996-11-11
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com
