나눗셈
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
나눗셈은 주어진 수를 다른 수로 등분하는 연산으로, 몫과 나머지를 결과로 얻는다. 나눗셈은 몫과 분할의 관점에서 이해할 수 있으며, 자연수를 나눌 때 나머지가 생길 수 있다. 나눗셈은 교환 법칙과 결합 법칙이 성립하지 않으며, 덧셈과 뺄셈에 대해서는 오른쪽 분배 법칙이 성립한다. 나눗셈 표기법은 콜론(:), 분수, 슬래시(/) 등을 사용하며, 나눗셈 기호(÷)는 초등 산술에서 주로 사용된다. 나눗셈은 정수, 유리수, 실수, 복소수, 다항식, 행렬 등 다양한 수학적 대상에 대해 정의되며, 0으로 나누는 것은 일반적으로 정의되지 않는다. 나눗셈은 손으로 계산하거나, 주판, 로그 표, 계산기, 컴퓨터 등을 이용하여 계산할 수 있으며, 한국에서는 주판을 이용한 나눗셈 방법이 변화해왔다.
더 읽어볼만한 페이지
- 나눗셈 - 약수
약수는 정수 b=ac를 만족하는 정수 c가 존재할 때 a를 b의 약수라고 정의하며, 모든 정수는 1, -1, 자기 자신, 반수를 약수로 가지고, 이외 약수를 고유 약수, 자연수에서는 자기 자신을 제외한 양의 약수를 진약수라고 부른다. - 나눗셈 - 나머지
나머지는 정수 나눗셈에서 나누어 떨어지지 않고 남는 값으로, 최소 양의 나머지 및 최소 절대 나머지로 구분되며, 모듈러 연산, 다항식 나눗셈, 프로그래밍 언어, 암호화 기술 등 다양한 분야에서 활용된다. - 이항연산 - 뺄셈
뺄셈은 두 수의 관계를 나타내는 연산으로, 덧셈의 역연산이며, 피감수에서 감수를 빼는 연산으로 차를 구하고, 반교환법칙과 결합 법칙은 성립하지 않으며, 다양한 계산 방법과 함께 여러 분야에서 활용된다. - 이항연산 - 거듭제곱
거듭제곱은 같은 수를 여러 번 곱하는 연산을 간결하게 나타내는 방법으로, 지수가 자연수일 때는 밑을 지수만큼 반복하여 곱하고, 유리수 지수는 거듭제곱근, 실수 지수는 유리수 제곱의 근사나 지수·로그 함수, 복소수 지수는 다가 함수로 정의된다.
2. 나눗셈의 기본
나눗셈은 주어진 수를 다른 수로 등분하는 연산으로, 몫과 나머지를 결과로 얻는다.[4] 10 ÷ 2 = 5에서 10은 나누어지는 수, 2는 나누는 수, 5는 몫이다.
나눗셈을 이해하는 방법은 몫과 분할의 관점에서 살펴볼 수 있다. 몫의 관점에서는 20을 얻기 위해 5를 몇 번 더해야 하는지를, 분할의 관점에서는 크기가 20인 집합을 5개의 부분으로 나눌 때 각 부분의 크기를 의미한다. 예를 들어, 20개의 사과를 4개씩 5개의 그룹으로 나누면 "20 나누기 5는 4와 같다"는 것을 의미하며, 이는 20 / 5 = 4 로 표시된다.[4]
자연수를 나눌 때, 나누어 떨어지지 않고 나머지가 생기는 경우가 있다. 예를 들어 10 / 3은 나머지가 1이다.[5] 때로는 이 나머지를 몫에 소수 부분으로 추가하여 나타내기도 하지만, 정수 나눗셈에서는 나머지를 별도로 유지하거나 버리기도 한다. 나머지를 분수로 유지하면 유리수가 된다.
곱셈, 덧셈과 달리 나눗셈은 교환 법칙이 성립하지 않는다. 즉, ''a'' / ''b''는 항상 ''b'' / ''a''와 같지 않다.[6] 또한, 나눗셈은 일반적으로 결합 법칙도 성립하지 않는다.[7] 여러 번 나눌 때 순서에 따라 결과가 달라질 수 있다. 예를 들어 (24 / 6) / 2 = 2이지만, 24 / (6 / 2) = 8이다.
나눗셈은 전통적으로 왼쪽 결합으로 간주되어, 여러 개의 나눗셈이 연속으로 있을 때 왼쪽에서 오른쪽으로 계산한다.[8][9]
: a / b / c = (a / b) / c = a / (b × c) ≠ a / (b / c) = (a × c) / b.
나눗셈은 덧셈과 뺄셈에 대해 오른쪽 분배 법칙이 성립한다. 즉,
: (a ± b) / c = (a / c) ± (b / c).
그러나 나눗셈은 왼쪽 분배 법칙이 성립하지 않는다.
2. 1. 용어
2. 2. 표기법
고트프리트 빌헬름 라이프니츠는 1684년 ''Acta eruditorum''에서 나눗셈 표기법으로 콜론(:)을 도입했다.[10] 라이프니츠는 비율과 나눗셈에 대해 별도의 기호를 사용하는 것을 싫어했다. 그러나 영어에서는 콜론이 관련 개념인 비율을 표현하는 데만 제한적으로 사용된다. 일부 영어권이 아닌 국가에서는 콜론을 사용하여 나눗셈을 나타낸다.[12] (예: 10 : 2 = 5) 독일이나 프랑스에서는 나눗셈 기호로 콜론(:)이 사용된다.[17]나눗셈은 종종 대수학과 과학에서 피제수를 제수 위에 놓고 그 사이에 수평선(분수선이라고도 함)을 그어 표시한다. 예를 들어, 'b로 a를 나누기'는 $\frac ab$ 로 쓸 수 있다. 이는 "b로 a를 나누기" 또는 "a 분의 b"로 읽을 수도 있다. 한 줄에 나눗셈을 표현하는 방법은 피제수(또는 분자)를 쓴 다음 슬래시를 쓰고, 그 다음 제수(또는 분모)를 쓰는 것이다.(예: 10 / 2 = 5) 이는 대부분의 컴퓨터 프로그래밍 언어에서 나눗셈을 지정하는 일반적인 방법이다. 간단한 ASCII 문자열로 쉽게 입력할 수 있기 때문이다. MATLAB 및 GNU 옥타브와 같은 일부 수학 소프트웨어에서는 나눗셈 연산자로 역슬래시를 사용하여 피연산자를 역순으로 쓸 수 있다. 세계적으로는 나눗셈 기호로 슬래시(/)가 우세하며, 컴퓨터 프로그래밍에서도 반각의 '/'를 사용하는 것이 일반적이다.[17]
분수형태: 10/2 또는 $\frac{10}{2}$
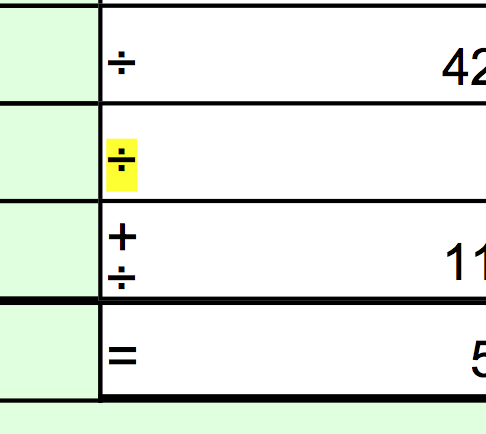
산술에서 일반적인 나눗셈 기호(÷, 오벨루스라고도 하지만 이 용어에는 추가적인 의미가 있음)를 사용한다.(예: 10 ÷ 2 = 5) 이 형태는 초등 산술을 제외하고는 드물다. ISO 80000-2-9.6에서는 이를 사용하지 말아야 한다고 명시하고 있다. 나눗셈 기호는 계산기의 키에 레이블처럼 나눗셈 연산 자체를 나타내는 데도 사용된다. 오벨루스는 스위스 수학자 요한 라인이 1659년 ''Teutsche Algebra''에서 소개했다.[10] ÷ 기호는 일부 유럽 국가에서는 뺄셈을 나타내는 데 사용되므로 잘못 이해될 수 있다.[11] 대한민국에서는 나눗셈 기호로 「÷」가 널리 사용되지만, 대한민국 외에 「÷」를 널리 사용하는 국가는 미국, 영국, 대한민국, 중국, 태국 등 제한적인 국가에 불과하다.[17]
19세기 이후 미국 교과서에서는 특히 장 나눗셈을 논의할 때 b로 a를 나누기를 나타내는 데 $b)a$ 또는 $b \overline{)a}$를 사용했다. 이 표기법의 역사는 시간이 지남에 따라 진화했기 때문에 완전히 명확하지 않다.[13]
3. 나눗셈의 성질
나눗셈 연산은 분수의 성질을 갖는다.
:
:
:
나눗셈은 몫과 나머지 성질을 갖는다.
4. 정수의 나눗셈
나눗셈 연산에서는 피제수와 제수의 관계에 따라 몫과 나머지가 생성된다. 나머지 값이 0인 경우에는 생략할 수 있다.[18]
이처럼 나눗셈 연산은 나머지에 대한 중요한 성질을 가지며, 나머지를 결과값으로 하는 나눗셈 연산을 나머지 연산이라고 하고, mod 기호를 사용한다. 예시는 다음과 같다.
:9 mod 3 = 0 , 10 mod 3 = 1
유클리드 호제법의 기초가 되는 ''유클리드 나눗셈''은 정수의 나눗셈 과정의 결과를 수학적으로 공식화한 것이다. 0이 아닌 두 정수 ''a''(피제수)와 ''b''(제수)가 주어지면, ''a'' = ''bq'' + ''r'' 이고 0 ≤ ''r'' < |''b''|을 만족하는 유일한 정수 ''q''(몫)과 ''r'' (나머지)가 존재한다. 여기서 |''b''|는 ''b''의 절댓값을 나타낸다.[18]
다른 나머지에 대한 제한 방법으로, 나머지의 절댓값이 최소가 되도록 몫을 정하는 방법이 있다. 이 경우,
:
:- / 2 < ''r'' ≤ / 2}}
또는
:- / 2 ≤ ''r'' < / 2}}
의 범위에 나머지 ''r''이 포함된다. 유클리드 나눗셈과 달리 ''r''은 음수 값을 가질 수 있다. 이렇게 정해지는 나머지를 '''절댓값 최소 나머지'''(절대적 최소 나머지라고도 함)라고 부른다.[18]
절댓값 최소 나머지를 사용하는 경우의 계산 예시는 다음과 같다. (제수: 4, -4, 피제수: 22, -22)
- / 2 < ''r'' ≤ / 2}}
::몫 5, 나머지 2
::몫 -5, 나머지 2
::몫 -6, 나머지 2
::몫 6, 나머지 2
- / 2 ≤ ''r'' < / 2}}
::몫 6, 나머지 -2
::몫 -6, 나머지 -2
::몫 -5, 나머지 -2
::몫 5, 나머지 -2
어느 방법을 사용하든, 제수 ''n''이 0이면 나머지 ''r''은 0이어야 하며, 피제수 ''m''이 어떤 수이든 몫 ''q''를 유일하게 정할 수 없다.
'''절댓값 최소 나머지'''와 유클리드 나눗셈에 의해 정해지는 '''최소 양의 나머지''' 중 어느 것을 사용할지는 자유이며, 주어지는 나머지가 그 중 어느 것인지는 미리 정해진 규약을 따른다. 이 규약은 계산하는 대상이나 컴퓨터의 기종, 또는 프로그래밍 언어에 따라 다르다.[18]
4. 1. 유클리드 나눗셈
나눗셈 연산에서는 피제수와 제수의 관계에 따라 몫과 나머지가 생성된다. 나머지 값이 0인 경우에는 생략할 수 있다.[18]이처럼 나눗셈 연산은 나머지에 대한 중요한 성질을 가지며, 나머지를 결과값으로 하는 나눗셈 연산을 나머지 연산이라고 하고, 기호를 사용한다. 예시는 다음과 같다.
:
유클리드 나눗셈은 정수의 나눗셈 과정의 결과를 수학적으로 공식화한 것이다. 0이 아닌 두 정수 ''a''(피제수)와 ''b''(제수)가 주어지면, ''a'' = ''bq'' + ''r'' 이고 0 ≤ ''r'' < |''b''|을 만족하는 유일한 정수 ''q''(몫)과 ''r'' (나머지)가 존재한다. 여기서 |''b''|는 ''b''의 절댓값을 나타낸다.[18]
다른 나머지에 대한 제한 방법으로, 나머지의 절댓값이 최소가 되도록 몫을 정하는 방법이 있다. 이 경우,
:$- \frac