모노드로미

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
- 2.1. 위상 공간에서의 정의
- 2.2. 대수적 정의 (갈루아 이론)
3. 예시
- 3.1. 복소해석학에서의 예시
- 3.2. 리만 기하학에서의 예시 (홀로노미)
4. 복소 미분 방정식
5. 위상적 및 기하학적 측면
- 5.1. 잎층 구조와 모노드로미
참조

1. 개요

모노드로미는 위상 공간, 대수 기하학, 복소 해석학 등 다양한 분야에서 나타나는 개념으로, 피복 공간과 기본군 사이의 관계를 설명한다. 구체적으로, 연결 국소 연결 공간 X의 피복 공간 p:X̃ → X와 X의 폐곡선 γ를 고려할 때, γ를 피복 공간으로 올린 곡선이 정의하는 기본군의 작용을 모노드로미 작용이라고 한다. 이 작용의 상을 모노드로미 군이라고 부른다. 모노드로미는 복소 로그 함수의 해석적 연속과 같은 복소해석학적 예시를 가지며, 복소 미분 방정식 및 잎상 구조와도 관련이 있다.

더 읽어볼만한 페이지

복소해석학 - 선적분
선적분은 스칼라장이나 벡터장의 곡선에 대한 적분으로, 함수의 종류와 곡선의 표현 방식에 따라 다양하게 정의되며, 물리학과 공학 등에서 활용된다.
복소해석학 - 테일러 급수
테일러 급수는 매끄러운 함수를 무한 멱급수로 나타내는 방법으로, 함수의 미분 계수를 사용하여 함수를 근사하며, a=0일 때의 테일러 급수를 매클로린 급수라고 한다.
호모토피 이론 - 베유 대수
베유 대수는 체 K 위의 리 대수 g에 대하여 정의되는 미분 등급 대수이며, g의 쌍대 공간과 그 등급 이동으로 생성되는 외대수와 대칭 대수의 텐서곱으로 표현되고, 리 군의 분류 공간의 주다발의 무한소 형태를 나타내는 완전열과 관련이 있다.
호모토피 이론 - 변형 수축
변형 수축은 위상 공간의 부분 공간에 대하여 전체 공간에서 부분 공간으로의 연속 함수가 특정한 조건을 만족시키는 경우를 말하며, 약한 변형 수축과 강한 변형 수축으로 나뉘고 호모토피 동치 및 축약 가능 공간과 관련이 있으며 카롤 보르수크가 도입하였다.
대수적 위상수학 - 매시 곱
매시 곱은 미분 등급 대수 원소에 대한 연산으로 코호몰로지 곱으로 파악하기 어려운 위상수학적 불변량을 측정하며, 2항 곱과 3항 곱을 일반화한 형태로 불확정성을 가지지만, 브루니안 링크, 보로메오 고리 연구 및 꼬인 K-이론 등 다양한 분야에 응용된다.
대수적 위상수학 - 톰 공간
톰 공간은 파라콤팩트 공간 위의 벡터 다발을 이용하여 구성되며, 르네 톰에 의해 도입되었고, 톰 동형을 통해 기저 공간의 코호몰로지와 관계를 가지며 특성류 이론 등에서 중요한 역할을 한다.

모노드로미
모노드로미
개요
분야	수학
연구 분야	미분기하학 대수기하학 복소해석학 미분 방정식 위상수학
역사 및 개념
어원	그리스어 "μονόδρομος" (단일 순환)
최초 연구	베른하르트 리만 (대수 함수 연구)
개념 확장	앙리 푸앵카레 (미분 방정식 연구)
현대적 관점	경로 공간 및 기본군 활용
응용 분야	미분기하학 대수기하학 복소해석학 미분 방정식 위상수학 끈 이론
모노드로미 군
정의	주어진 공간의 기본군에서 자기 동형 사상 군으로의 군 준동형 사상
표현 방식	행렬 치환
성질	기본군의 표현에 대한 정보 제공
예시
복소 평면에서의 함수	제곱근 함수, 로그 함수
미분 방정식	2계 선형 미분 방정식 (푸크스 방정식)
응용
대수적 함수의 해석적 연속	리만 곡면 구성
미분 방정식의 해 연구	특이점에서의 해의 행동 분석
위상수학	덮개 공간 분류
끈 이론	거울 대칭성 연구
관련 개념
기본군	기본군
덮개 공간	덮개 공간
리만 곡면	리만 곡면
푸크스 방정식	푸크스 방정식
거울 대칭성	거울 대칭성

2. 정의

모노드로미는 어떤 공간의 기본군이 그 공간의 피복 공간의 올(fiber)에 어떻게 작용하는지를 설명하는 개념이다.

구체적으로, 밑점 $x$ 를 가진 연결이고 국소 연결인 위상 공간 $X$ 와 그 피복 공간 $p\colon\tilde X\to X$ 를 생각하자. 밑점 $x$ 에서의 폐곡선 $\gamma$ (즉, $\gamma(0)=\gamma(1)=x$ 인 경로)는 피복 공간 $\tilde X$ 의 올 $F_x = p^{-1}(x)$ 위의 점들을 움직이게 한다. 즉, 폐곡선 $\gamma$ 를 따라 올 위의 한 점 $\tilde x \in F_x$ 에서 시작하여 경로를 올리면(lift|리프트^영어) $\tilde\gamma$ 가 되는데, 이 올린 경로의 끝점 $\tilde\gamma(1)$ 은 일반적으로 시작점 $\tilde x$ 와 다르다.

이 과정은 기본군 $\pi_1(X, x)$ (폐곡선들의 호모토피 동치류 집합)이 올 $F_x$ 에 작용하는 것으로 해석할 수 있다. 이 군의 작용을 모노드로미 작용(monodromy action|모노드로미 액션^영어)이라고 부른다.

이 작용은 기본군 $\pi_1(X, x)$ 에서 올 $F_x$ 의 자기동형군 $\operatorname{Aut}(F_x)$ 으로 가는 군 준동형을 정의하며, 이 준동형의 상을 모노드로미 군(monodromy group|모노드로미 그룹^영어)이라고 한다. 모노드로미 군은 기본군이 올의 점들을 어떻게 섞는지(permute)를 나타내는 군이다.

2. 1. 위상 공간에서의 정의

X

가 연결 공간이고 국소 연결 공간인 위상 공간이라고 하자.

p\colon\tilde X\to X

가

X

의 피복 공간이고,

x\in X

를 밑점이라고 하자. 밑점

x

의 올(fiber^영어)을

F_x = p^{-1}(x)

라고 정의한다.

밑점

x

에서 시작하고 끝나는 폐곡선

\gamma\colon[0,1]\to X

(즉,

\gamma(0)=\gamma(1)=x

)를 생각하자. 이 폐곡선

\gamma

를 피복 공간

\tilde X

로 올림(lift^영어)할 수 있다. 올림된 경로

\tilde\gamma\colon[0,1]\to\tilde X

는 일반적으로 폐곡선이 아니다.

\tilde\gamma

가 올

F_x

의 한 점

\tilde x = \tilde\gamma(0)

에서 시작한다고 할 때, 그 끝점은

\tilde\gamma(1)

이 된다. 이 끝점은 시작점

\tilde x

와 일반적으로 다르며, 폐곡선

\gamma

의 호모토피 동치류

[\gamma] \in \pi_1(X, x)

에만 의존한다. 이 끝점을

\tilde x \cdot [\gamma] := \tilde\gamma(1)

로 표기한다.

이 대응 관계는 기본군

\pi_1(X,x)

의 올

F_x

에 대한 군 작용

:

F_x \times \pi_1(X, x) \to F_x

:

(\tilde x, [\gamma]) \mapsto \tilde x \cdot [\gamma]

으로 잘 정의된다(well-defined^영어). 이 작용을 '''모노드로미 작용'''(monodromy action^영어)이라고 부른다.

이 모노드로미 작용에 해당하는 군 준동형

:

\rho\colon \pi_1(X, x) \to \operatorname{Aut}(F_x)

을 '''모노드로미 (표현)'''(monodromy (representation)^영어)이라고 하며, 이 준동형의 상

\operatorname{Im}(\rho) \subseteq \operatorname{Aut}(F_x)

을 '''모노드로미 군'''(monodromy group^영어)이라고 한다. 모노드로미 군은 올

F_x

의 자기동형군

\operatorname{Aut}(F_x)

의 부분군이다.

참고로, 올의 한 점

\tilde x \in F_x

의 안정자군은

p_*(\pi_1(\tilde{X},\tilde{x}))

와 일치한다. 즉, 기본군의 원소

[\gamma]

가

F_x

의 점

\tilde x

를 고정시키는 것(즉,

\tilde x \cdot [\gamma] = \tilde x

)은

[\gamma]

가 피복 공간

\tilde X

에서

\tilde x

를 기점으로 하는 폐곡선의 상으로 표현될 수 있다는 것과 동치이다.

2. 2. 대수적 정의 (갈루아 이론)

'''F'''(''x'')를 변수 ''x''에 대한 유리 함수의 체, 즉 다항식환 '''F'''[''x'']의 분수체라고 한다. '''F'''(''x'')의 원소 ''y'' = ''f''(''x'')는 유한 체 확대 ['''F'''(''x'') : '''F'''(''y'')]를 결정한다.

이 확대는 일반적으로 갈루아 확대가 아니지만, 갈루아 폐포 ''L''(''f'')를 가진다. 체 확대 [''L''(''f'') : '''F'''(''y'')]에 관련된 갈루아 군을 ''f''의 모노드로미 군이라고 부른다.

'''F''' = '''C'''인 경우에는, 리만 곡면 이론을 통해 앞서 언급된 기하학적 해석이 성립한다. 만약 체 확대 ['''C'''(''x'') : '''C'''(''y'')]가 이미 갈루아 확대라면, 관련된 모노드로미 군은 덮개 변환 군(deck transformation group)이라고도 불린다.

이는 피복 공간의 갈루아 이론과 관련되어 있으며, 리만 존재 정리를 이끌어낸다.

3. 예시

모노드로미의 대표적인 예시는 복소해석학에서 찾아볼 수 있다. 예를 들어, 복소 로그 함수 $\log(z)$ 를 원점을 중심으로 하는 닫힌 경로를 따라 해석적 연속을 통해 값을 추적하면, 출발점으로 돌아왔을 때 원래 값에 $2\pi i$ 가 더해지는 현상이 나타난다. 이는 복소 로그 함수가 여러 값을 가질 수 있는 다가 함수(multi-valued function)임을 보여주는 대표적인 사례이다.

또한 미분기하학, 특히 리만 기하학에서 중요한 개념인 홀로노미(holonomy)도 모노드로미의 한 유형으로 볼 수 있다. 이는 곡면이나 고차원 다양체 위에서 벡터를 닫힌 경로를 따라 평행 이동시켰을 때 처음 벡터와 달라지는 현상과 관련된다.

3. 1. 복소해석학에서의 예시

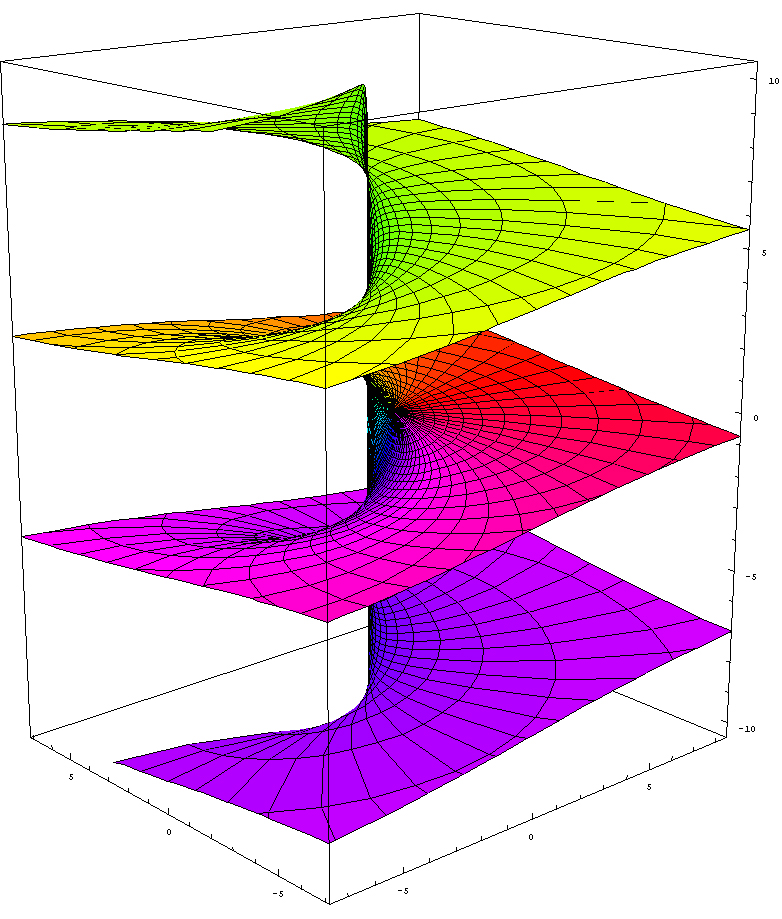
모노드로미 개념은 복소해석학 연구에서 중요하게 다뤄진다. 복소 로그 함수

\log(z)

를 예로 들어보자. 원점을 제외한 복소 평면

\mathbb{C} \setminus \{0\}

의 어떤 영역, 예를 들어

E = \{z\in \mathbb{C} \mid \operatorname{Re}(z)>0\}

(실수부가 양수인 영역)에서 정의된 로그 함수

F(z) = \log(z)

를 생각할 수 있다.

이 함수를 원점을 포함하는 폐곡선, 가령 단위 원

|z| = 1

이나

|z| = 0.5

인 원을 따라 해석적 연속을 통해 한 바퀴 돌려 원래 위치로 돌아오면, 함수의 값은 처음의

F(z)

가 아니라

F(z) + 2\pi i

가 된다. 즉, 폐곡선을 따라 한 바퀴 돌 때마다

2\pi i

만큼의 차이가 발생하는 것이다.

이 현상을 피복 공간의 관점에서 이해할 수 있다. 복소 로그 함수는

\mathbb{C}

에서

\mathbb{C}\setminus\{0\}

으로 가는 일종의 피복 사상

p\colon\mathbb C\to\mathbb C\setminus\{0\}

으로 볼 수 있다. 이때 양의 실수

x\in\mathbb R^+

에 대응하는 점들의 집합인 올(fiber)은

F=\{\log(x)+2\pi ni \mid n\in\mathbb Z\}

로 주어진다. 여기서

n

은 정수이다.

원점을 제외한 복소 평면

\mathbb C\setminus\{0\}

의 기본군은 폐곡선이 원점을 감는 횟수(감음수)로 결정되며, 정수 집합

\mathbb Z

와 동형이다 (

\pi_1(\mathbb C\setminus\{0\})=\mathbb Z

). 기본군의 원소

n \in \mathbb Z

는 피복 공간의 올에 작용하는데, 이 작용이 바로 모노드로미 작용이다. 로그 함수의 경우, 이 작용은

n\colon\log(x)\mapsto\log(x)+2\pi ni

로 나타낼 수 있다. 이는 원점을

n

번 감는 경로를 따라 해석적 연속을 했을 때 로그 값이

2\pi ni

만큼 변하는 것을 의미한다.

따라서 복소 로그 함수의 모노드로미 군은 이러한 작용들의 집합으로, 정수 덧셈군

\mathbb Z

와 동형인 무한 순환군이다. 이 피복 공간은 3차원 공간에서 나선면(helicoid)의 형태로 시각화될 수 있으며, 피복 사상은 이 나선면을

z

축 방향으로 수직 투영하여 구멍 뚫린 복소 평면

\mathbb{C}\setminus\{0\}

을 얻는 과정에 해당한다.

3. 2. 리만 기하학에서의 예시 (홀로노미)

리만 기하학의 홀로노미는 모노드로미의 한 예시로 볼 수 있다.

미분기하학에서는 평행 이동(parallel transport)이 비슷한 역할을 수행한다. 매끄러운 다양체 M 위의 주다발 B에 접속이 주어지면, 이는 다양체 M 위의 한 점 m에서의 올(fiber)에서 인접한 점의 올로 벡터나 텐서 등을 "수평적으로" 옮기는 방법을 제공한다. 점 m에서 시작하여 다시 m으로 돌아오는 닫힌 경로(루프)를 따라 평행 이동을 적용했을 때, 시작점의 올과 끝점의 올 사이에 발생하는 변환들의 군을 홀로노미 군(holonomy group)이라고 정의한다. 만약 주다발 B의 구조군이 G라면, 홀로노미 군은 G의 부분군이 된다. 이 홀로노미 군은 해당 주다발 B가 곱다발 M × G와 얼마나 다른지를 나타내는 중요한 정보를 담고 있다.

4. 복소 미분 방정식

미분 방정식 분야에서 중요한 응용 중 하나는, 하나의 해를 해석적 연속을 통해 선형적으로 독립인 다른 해들을 얻는 경우이다. 해석적 연속이란 어떤 영역에서 정의된 해석 함수를 그 정의 영역 밖으로 확장하는 과정을 말한다. 복소 평면의 열린 연결 집합 S에서 정의된 선형 미분 방정식은 모노드로미 군(monodromy group)을 가진다. 이 군은 S의 기본군의 선형 표현으로, S 안의 닫힌 경로(루프)를 따라 해를 해석적 연속할 때 해가 어떻게 변하는지를 나타낸다.

주어진 모노드로미 표현을 갖는 미분 방정식을 찾는 역 문제를 리만-힐베르트 문제라고 하며, 특히 정칙 특이점(regular singularity)을 갖는 방정식을 구성하는 것이 중요하다. 정칙 특이점을 갖는 선형 시스템, 특히 푸크스형 시스템(Fuchsian system)의 경우, 모노드로미 군의 생성자로는 보통 시스템의 특이점 각각을 반시계 방향으로 한 바퀴 도는 경로에 대응하는 선형 변환(연산자) ''M_j''를 선택한다. 특이점들을 적절한 순서(예: 기점을 기준으로 시계 반대 방향)로 번호 ''j'' = 1, ..., ''p'' + 1을 매기면, 이 생성자들 사이에는 $M_1 \cdots M_{p+1} = \operatorname{id}$ (항등 변환)라는 유일한 관계식이 성립한다.

들리뉴-심슨 문제(Deligne–Simpson problem)는 다음과 같은 실현 문제이다: GL(''n'', '''C''') (복소수 성분을 갖는 ''n'' × ''n'' 가역 행렬의 군)의 주어진 켤레류(conjugacy classes)들에 속하면서 위의 관계식을 만족하는 기약(irreducible) 행렬들의 튜플(tuple) ''M_j''가 존재하는가? 이 문제는 피에르 들리뉴(Pierre Deligne)에 의해 공식화되었고, 카를로스 심슨(Carlos Simpson)이 해결을 위한 첫 결과를 얻었다. 푸크스형 시스템의 잉여(residue)에 대한 문제의 덧셈적 형태(additive version)는 블라디미르 코스토프(Vladimir Kostov)에 의해 공식화되고 연구되었다. 이 문제는 GL(''n'', '''C''') 외의 다른 행렬 군에 대해서도 여러 수학자에 의해 연구되었다.^[2]^[5]

5. 위상적 및 기하학적 측면

피복 사상은 올뭉치의 특별한 경우로 볼 수 있다. 호모토피 올림 성질에 따라, 밑공간 ''X''(편의상 경로 연결되어 있다고 가정) 위의 경로를 피복 공간 ''C''로 들어 올릴 수 있다. ''X''의 한 점 ''x''에서 시작하고 끝나는 닫힌 경로(루프)를 생각해보자. 이 루프를 ''x'' 위에 있는 점 ''c''에서 시작하도록 ''C''로 들어 올리면, 그 끝점은 일반적으로 시작점 ''c''와 다른 ''x'' 위의 점 ''c*''가 될 수 있다( $c \neq c^*$ ). 이러한 경로 올림의 결과로 발생하는 ''x'' 위 점들의 변화는 기본군 $\pi_1(X, x)$ 의 작용으로 설명할 수 있다. 즉, 기본군의 각 원소는 ''x'' 위에 있는 점들의 집합(올) 위에 순열로 작용하며, 이 작용을 나타내는 순열군을 '''모노드로미 군'''이라고 부른다.

미분기하학에서는 평행 이동이 모노드로미와 유사한 역할을 한다. 매끄러운 다양체 ''M'' 위의 주다발 ''B''에 접속이 주어지면, 다양체 위의 경로를 따라 올(fiber) 사이를 "수평으로" 이동하는 방법이 정의된다. ''M'' 위의 한 점 ''m''에서 시작하고 끝나는 루프를 따라 평행 이동을 수행하면, ''m'' 위의 올에 있는 벡터나 점들이 변환된다. 이러한 변환들의 집합은 군을 이루며, 이를 '''홀로노미 군'''이라고 한다. 만약 주다발 ''B''의 구조군이 ''G''라면, 홀로노미 군은 ''G''의 부분군이 되며, 이는 주다발 ''B''가 자명한 곱다발 $M \times G$ 와 얼마나 다른지를 측정하는 지표가 된다.

5. 1. 잎층 구조와 모노드로미

밑공간의 경로는 전체 공간에서 이를 들어올리는 경로를 갖는다. 이러한 경로를 따라 이동하면 기본 군에서 모노드로미 작용이 생성된다.

기본군의 개념을 확장하여, 기준점을 고정하지 않고 경로의 호모토피 클래스를 다루는 준군(groupoid) 구조를 생각할 수 있다. 이는 피복 공간

p:\tilde X\to X

의 밑공간 ''X''에서 경로의 리프트를 고려하는 방식으로 정의되며, ''X''가 연결 공간이 아니어도 적용 가능하다는 장점이 있다.

이러한 모노드로미 개념은 잎층(foliation) 구조로 일반화될 수 있다.

(M,\mathcal{F})

를 다양체 ''M'' 위의 (특이점을 가질 수 있는) 잎층 구조라고 하자.

\mathcal{F}

의 각 잎(leaf) 안의 경로를 따라 이동하는 것을 생각할 수 있다. 이 경로의 끝점을 지나는 국소적인 횡단 절단면(transversal section)을 고려하면, 경로를 따라 이동하는 과정에서 횡단 절단면 위의 점들이 어떻게 변환되는지를 나타내는 미분동형사상이 유도된다.

만약 경로가 포함된 영역이 단일 연결된 좌표 조각(chart) 안에 있다면, 이 미분동형사상은 경로의 구체적인 모양보다는 양 끝점에만 의존하게 된다. 특히, 끝점 주변에서의 변환만을 고려하는 싹(germ)의 개념을 사용하면, 서로 다른 횡단 절단면 사이에서도 이 변환은 표준적(canonical)으로 정의된다. 결과적으로, 단일 연결된 영역 내에서는 잎 안의 경로에 대한 모노드로미가 경로의 호모토피에 대해 불변인 성질을 갖게 된다.

참조

_[1] 서적 Karl Weierstraß (1815–1897): Aspekte seines Lebens und Werkes – Aspects of his Life and Work https://books.google[...] Springer-Verlag 2015
_[2] 간행물 The Deligne–Simpson problem — a survey
_[3] 웹사이트 http://cpu.icu.ac.jp[...]
_[4] 서적 The Words of Mathematics: An Etymological Dictionary of Mathematical Terms Used in English https://google books[...] Mathematical Association of America
_[5] 간행물 The Deligne–Simpson problem — a survey

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com