베타 붕괴
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
베타 붕괴는 원자핵이 불안정해져 중성자가 양성자로, 또는 그 반대로 변환되면서 전자나 양전자, 중성미자 등을 방출하는 방사성 붕괴의 한 유형이다. 베타 붕괴는 음의 베타 붕괴(β⁻), 양의 베타 붕괴(β⁺), 전자 포획 세 가지 유형으로 나뉜다. β⁻ 붕괴는 중성자가 양성자로 변환되며 전자와 반전자 중성미자를 방출하고, β⁺ 붕괴는 양성자가 중성자로 변환되며 양전자와 전자 중성미자를 방출한다. 전자 포획은 핵 내의 양성자가 전자를 포획하여 중성자로 변환되며 전자 중성미자를 방출한다. 베타 붕괴는 핵 변환을 일으켜 원자 번호를 변화시키며, 에너지 스펙트럼은 연속적이고 약한 상호작용에 의해 일어난다. 이중 베타 붕괴는 핵의 전하가 두 단위 변하는 드문 경우이며, 중성미자 없는 이중 베타 붕괴는 아직 관측되지 않았다. 베타 붕괴는 바리온 수와 렙톤 수를 보존하며, 각운동량 보존 법칙을 따른다.
더 읽어볼만한 페이지
- 방사능 - 방사성 탄소 연대 측정
방사성 탄소 연대 측정은 윌러드 리비가 1949년에 발견한 유기 물질 연대 측정 방법으로, 탄소-14의 방사성 붕괴를 이용하여 최대 6만 년까지의 연대를 측정하며, 고고학 유물 연대 측정에 주로 사용된다. - 방사능 - 핵분열
핵분열은 원자핵이 중성자와 충돌하여 두 개 이상의 조각으로 분열되는 현상으로, 막대한 에너지를 방출하며 원자력 발전과 핵무기에 응용되지만 방사성 폐기물 처리 등의 문제점을 가지고 있다. - 핵물리학 - 핵분열
핵분열은 원자핵이 중성자와 충돌하여 두 개 이상의 조각으로 분열되는 현상으로, 막대한 에너지를 방출하며 원자력 발전과 핵무기에 응용되지만 방사성 폐기물 처리 등의 문제점을 가지고 있다. - 핵물리학 - 알파 붕괴
알파 붕괴는 원자핵이 헬륨-4 원자핵인 알파 입자를 방출하여 원자 번호와 질량수가 감소하는 방사성 붕괴의 한 형태로, 무거운 원자핵에서 주로 발생하며 양자 터널링 효과로 설명되고 연기 감지기 등에 활용되지만 인체에 유해할 수도 있다. - 입자물리학 - 전자볼트
전자볼트는 전자가 1볼트의 전위차를 통과할 때 얻거나 잃는 에너지 단위로, 1.602 × 10⁻¹⁹ 줄과 같으며, 다양한 물리학 분야와 공학에서 에너지, 질량, 운동량, 온도, 거리 등을 표현하는 데 널리 활용된다. - 입자물리학 - 알파 붕괴
알파 붕괴는 원자핵이 헬륨-4 원자핵인 알파 입자를 방출하여 원자 번호와 질량수가 감소하는 방사성 붕괴의 한 형태로, 무거운 원자핵에서 주로 발생하며 양자 터널링 효과로 설명되고 연기 감지기 등에 활용되지만 인체에 유해할 수도 있다.
2. 베타 붕괴의 종류
베타 붕괴는 크게 음의 베타 붕괴(β⁻), 양의 베타 붕괴(β⁺), 그리고 전자 포획으로 나눌 수 있다.
; β− 붕괴와 전자 포획
염소 36 (반감기 30만 1000년)
:
:
이리듐 192 (반감기 73.83일)
:
:
;β+붕괴와 전자 포획
알루미늄 26 (반감기 71만 7000년)
:
:
;망가니즈 52 (반감기 5.59일)
:
:
; β− 붕괴와 β+ 붕괴, 그리고 전자 포획
칼륨-40(반감기 12억 7700만 년)
:
:
:
아이오딘-126(반감기 13일)
:
:
:
== 음의 베타 붕괴 (β⁻) ==
음의 베타 붕괴(β⁻ 붕괴)에서는 약한 상호작용에 의해 중성자가 양성자로 변환되면서 전자와 전자 반중성미자를 방출한다.[28] 이 과정에서 중성자 내의 아래 쿼크가 위 쿼크로 바뀌면서 W⁻ 보손을 방출하고, 이 W⁻ 보손은 곧 붕괴하여 전자와 반중성미자가 된다.[28]
일반적인 붕괴식은 다음과 같이 나타낼 수 있다.[28]
:.
β⁻ 붕괴가 일어나면 원자핵의 원자 번호가 1 증가하고, 질량수는 변하지 않는다.[28] 붕괴 후 운동에너지 스펙트럼은 연속적인데, 이는 방출되는 반중성미자가 운동에너지의 일부를 임의로 가지기 때문이다.
β⁻ 붕괴는 Q 값이 양수일 때만 반응이 진행되는데, 이는 원자 질량이 원자의 질량보다 클 때 β⁻ 붕괴가 발생할 수 있다는 것을 나타낸다. 방출되는 총 에너지는 초기 핵의 질량 에너지에서 최종 핵, 전자 및 반뉴트리노의 질량 에너지를 뺀 값이며, 이 에너지는 전자와 반중성미자의 운동 에너지로 방출된다.
일반적으로, '''중성자 과잉 핵종''', 즉 안정 동위원소보다 중성자가 많은 핵종에서 β⁻ 붕괴가 발생한다.
예를 들어, 아르곤 42는 β⁻ 붕괴를 통해 칼륨 42 (반감기 32.9년)로 변환된다.
:
칼륨-40(반감기 12억 7700만 년)은 β⁻ 붕괴, β⁺ 붕괴, 전자 포획의 세가지 붕괴 모드를 모두 갖는 핵종의 예시이다.
:
:
:
== 양의 베타 붕괴 (β⁺) ==
양의 베타 붕괴(β+ 붕괴)에서는 양성자가 에너지를 흡수하여 중성자로 바뀌면서 양전자(e+)와 전자 중성미자()를 방출한다.[28] 이 과정은 양성자 내의 위 쿼크가 W+ 보손을 방출하고 아래 쿼크로 바뀌는 과정으로 볼 수 있으며, 방출된 W+ 보손은 곧 양전자와 중성미자로 붕괴한다.
일반적인 붕괴식은 다음과 같다.
:
이때,
베타 붕괴는 에너지를 필요로 하므로, 고립된 양성자에게서 스스로 일어날 수 없다. (중성자의 질량이 양성자보다 크다.) 따라서, 베타 붕괴는 결합 에너지의 절댓값이 부모 원자핵보다 자식 원자핵에서 더 큰 경우에만 핵 내부에서 일어날 수 있다. 이 두 결합 에너지의 차이만큼이 양성자를 중성자, 양전자, 중성미자로 변환하는 데에 쓰이고, 남는 에너지는 생성물의 운동 에너지로 전환된다.[28]
β+ 붕괴가 일어나려면, 원자
β+ 붕괴는 양성자 과잉 핵, 즉 안정 동위원소보다 중성자가 적은 핵종에서 주로 발생한다.[48] 붕괴가 일어나면 원자 번호가 하나 작은 원소로 변환된다. 예를 들어, 네오디뮴(Nd) 132는 프라세오디뮴(Pr) 132로 붕괴한다. (
핵종에 따라 두 가지 이상의 붕괴 모드를 갖는 경우가 있으며, 특유의 확률로 붕괴한다. 일반적으로 양성자수와 중성자수가 모두 짝수인 쪽이 안정적이며, 안정적인 딸핵종이 여러 개 존재하는 경우에 그러한 일이 일어나기 쉽다. 예를 들어 칼륨-40은 β− 붕괴, β+ 붕괴, 전자 포획을 모두 할 수 있다.
== 전자 포획 (ε 또는 EC) ==
전자 포획(ε 또는 EC)은 중성자보다 양성자가 더 많은 방사성 핵종에서 일어나는 붕괴 현상이다. 핵 내의 양성자가 원자 내부의 전자껍질에 있는 전자를 포획하여 중성자로 변환되면서 전자 중성미자를 방출한다.[24] 이 과정은 다음과 같이 표현된다.
:
포획된 전자의 빈자리는 더 높은 에너지 준위의 전자가 채우면서 고유 X선을 방출한다. 전자 포획 후 방출되는 중성미자는 일정한 운동 에너지를 가지므로, 운동 에너지 스펙트럼은 불연속적이다.[24]
전자 포획은 양성자가 더 많을 때 일어나는 β+ 붕괴와 경쟁적으로 일어난다. 결합 에너지 차이가 충분하여 β+ 붕괴를 일으킬 수 있다면 전자 포획도 가능하다. 하지만 부모 핵과 자식 핵의 에너지 차이가 크지 않은 경우에는 전자 포획만이 유일한 붕괴 방법이 된다.[24]
포획된 전자가 원자의 가장 안쪽 껍질인 K-껍질에서 나올 경우 K-포획, L-껍질에서 나올 경우 L-포획이라고 한다.[23]
전자 포획의 예로는 크립톤-81이 브롬-81로 붕괴되는 과정이 있다.
: + → + }}
일반적으로 양성자 수와 중성자 수가 모두 짝수인 쪽이 안정적이며, 안정적인 딸핵종이 여러 개 존재하는 경우 다양한 붕괴 모드를 가질 수 있다. 예를 들어 칼륨-40은 β− 붕괴, β+ 붕괴, 전자 포획을 모두 겪는다.
:
:
:
2. 1. 음의 베타 붕괴 (β-)
음의 베타 붕괴(β⁻ 붕괴)에서는 약한 상호작용에 의해 중성자가 양성자로 변환되면서 전자와 전자 반중성미자를 방출한다.[28] 이 과정에서 중성자 내의 아래 쿼크가 위 쿼크로 바뀌면서 W⁻ 보손을 방출하고, 이 W⁻ 보손은 곧 붕괴하여 전자와 반중성미자가 된다.[28] 쿼크 수준에서의 β⁻ 붕괴는 오른쪽 그림과 같다.일반적인 붕괴식은 다음과 같이 나타낼 수 있다.[28]
:.
β⁻ 붕괴가 일어나면 원자핵의 원자 번호가 1 증가하고, 질량수는 변하지 않는다.[28] 붕괴 후 운동에너지 스펙트럼은 연속적인데, 이는 방출되는 반중성미자가 운동에너지의 일부를 임의로 가지기 때문이다.
β⁻ 붕괴는 Q 값이 양수일 때만 반응이 진행되는데, 이는 원자 질량이 원자의 질량보다 클 때 β⁻ 붕괴가 발생할 수 있다는 것을 나타낸다. 방출되는 총 에너지는 초기 핵의 질량 에너지에서 최종 핵, 전자 및 반뉴트리노의 질량 에너지를 뺀 값이며, 이 에너지는 전자와 반중성미자의 운동 에너지로 방출된다.
일반적으로, '''중성자 과잉 핵종''', 즉 안정 동위원소보다 중성자가 많은 핵종에서 β⁻ 붕괴가 발생한다.
예를 들어, 아르곤 42는 β⁻ 붕괴를 통해 칼륨 42 (반감기 32.9년)로 변환된다.
:
칼륨-40(반감기 12억 7700만 년)은 β⁻ 붕괴, β⁺ 붕괴, 전자 포획의 세가지 붕괴 모드를 모두 갖는 핵종의 예시이다.
:
:
:
2. 2. 양의 베타 붕괴 (β+)
양의 베타 붕괴(β+ 붕괴)에서는 양성자가 에너지를 흡수하여 중성자로 바뀌면서 양전자(e+)와 전자 중성미자()를 방출한다.[28] 이 과정은 양성자 내의 위 쿼크가 W+ 보손을 방출하고 아래 쿼크로 바뀌는 과정으로 볼 수 있으며, 방출된 W+ 보손은 곧 양전자와 중성미자로 붕괴한다.일반적인 붕괴식은 다음과 같다.
:
이때,
베타 붕괴는 에너지를 필요로 하므로, 고립된 양성자에게서 스스로 일어날 수 없다. (중성자의 질량이 양성자보다 크다.) 따라서, 베타 붕괴는 결합 에너지의 절댓값이 부모 원자핵보다 자식 원자핵에서 더 큰 경우에만 핵 내부에서 일어날 수 있다. 이 두 결합 에너지의 차이만큼이 양성자를 중성자, 양전자, 중성미자로 변환하는 데에 쓰이고, 남는 에너지는 생성물의 운동 에너지로 전환된다.[28]
β+ 붕괴가 일어나려면, 원자
β+ 붕괴는 양성자 과잉 핵, 즉 안정 동위원소보다 중성자가 적은 핵종에서 주로 발생한다.[48] 붕괴가 일어나면 원자 번호가 하나 작은 원소로 변환된다. 예를 들어, 네오디뮴(Nd) 132는 프라세오디뮴(Pr) 132로 붕괴한다. (
핵종에 따라 두 가지 이상의 붕괴 모드를 갖는 경우가 있으며, 특유의 확률로 붕괴한다. 일반적으로 양성자수와 중성자수가 모두 짝수인 쪽이 안정적이며, 안정적인 딸핵종이 여러 개 존재하는 경우에 그러한 일이 일어나기 쉽다. 예를 들어 칼륨-40은 β− 붕괴, β+ 붕괴, 전자 포획을 모두 할 수 있다.
2. 3. 전자 포획 (ε 또는 EC)
전자 포획(ε 또는 EC)은 중성자보다 양성자가 더 많은 방사성 핵종에서 일어나는 붕괴 현상이다. 핵 내의 양성자가 원자 내부의 전자껍질에 있는 전자를 포획하여 중성자로 변환되면서 전자 중성미자를 방출한다.[24] 이 과정은 다음과 같이 표현된다.:
포획된 전자의 빈자리는 더 높은 에너지 준위의 전자가 채우면서 고유 X선을 방출한다. 전자 포획 후 방출되는 중성미자는 일정한 운동 에너지를 가지므로, 운동 에너지 스펙트럼은 불연속적이다.[24]
전자 포획은 양성자가 더 많을 때 일어나는 β+ 붕괴와 경쟁적으로 일어난다. 결합 에너지 차이가 충분하여 β+ 붕괴를 일으킬 수 있다면 전자 포획도 가능하다. 하지만 부모 핵과 자식 핵의 에너지 차이가 크지 않은 경우에는 전자 포획만이 유일한 붕괴 방법이 된다.[24]
포획된 전자가 원자의 가장 안쪽 껍질인 K-껍질에서 나올 경우 K-포획, L-껍질에서 나올 경우 L-포획이라고 한다.[23]
전자 포획의 예로는 크립톤-81이 브롬-81로 붕괴되는 과정이 있다.
: + → + }}
일반적으로 양성자 수와 중성자 수가 모두 짝수인 쪽이 안정적이며, 안정적인 딸핵종이 여러 개 존재하는 경우 다양한 붕괴 모드를 가질 수 있다. 예를 들어 칼륨-40은 β− 붕괴, β+ 붕괴, 전자 포획을 모두 겪는다.
:
:
:
3. 베타 붕괴의 이론
베타 붕괴는 양자역학의 섭동 이론으로 해석될 수 있으며, 페르미 황금률을 따른다.
== 에너지 스펙트럼 ==
베타 붕괴에서 방출되는 전자의 에너지 스펙트럼은 연속적이다.[1] 이는 전자와 반중성미자(또는 중성미자)가 붕괴 에너지(Q값)를 나누어 갖기 때문이다. Q값은 주어진 핵붕괴에서 방출되는 총 에너지로, 베타 붕괴에서는 방출된 베타 입자, 중성미자, 그리고 반동 핵의 운동 에너지의 합이다. 하지만 핵의 질량이 매우 크기 때문에 반동 핵의 운동 에너지는 무시할 수 있다. 따라서 베타 입자는 0부터 Q값까지의 범위의 어떤 운동 에너지로든 방출될 수 있다.[1] 전형적인 Q값은 약 1 MeV이지만, 몇 keV부터 수십 MeV까지 다양하다. 전자의 정지 질량이 511 keV이므로, 가장 에너지가 높은 베타 입자는 극한 상대론적이며, 속도는 광속에 매우 가깝다.
베타 붕괴는 섭동으로 간주될 수 있으며, 페르미의 황금률을 적용할 수 있다. 방출된 베타 입자의 운동 에너지 스펙트럼 ''N''(''T'')는 다음과 같이 주어진다.[29]
:''N(T) = CL(T) F(Z,T) p E (Q-T)2''
여기서 ''T''는 운동 에너지, ''CL''은 붕괴의 금지 정도에 따라 달라지는 형태 함수(허용 붕괴의 경우 상수), ''F''(''Z'', ''T'')는 페르미 함수(''Z''는 최종 상태 핵의 전하), ''E'' = ''T'' + ''mc''2는 총 에너지, ''p'' = √(E/c)2 - (mc)2는 운동량, Q는 붕괴의 Q값이다. 방출된 중성미자의 운동 에너지는 Q에서 베타 입자의 운동 에너지를 뺀 값으로 근사할 수 있다.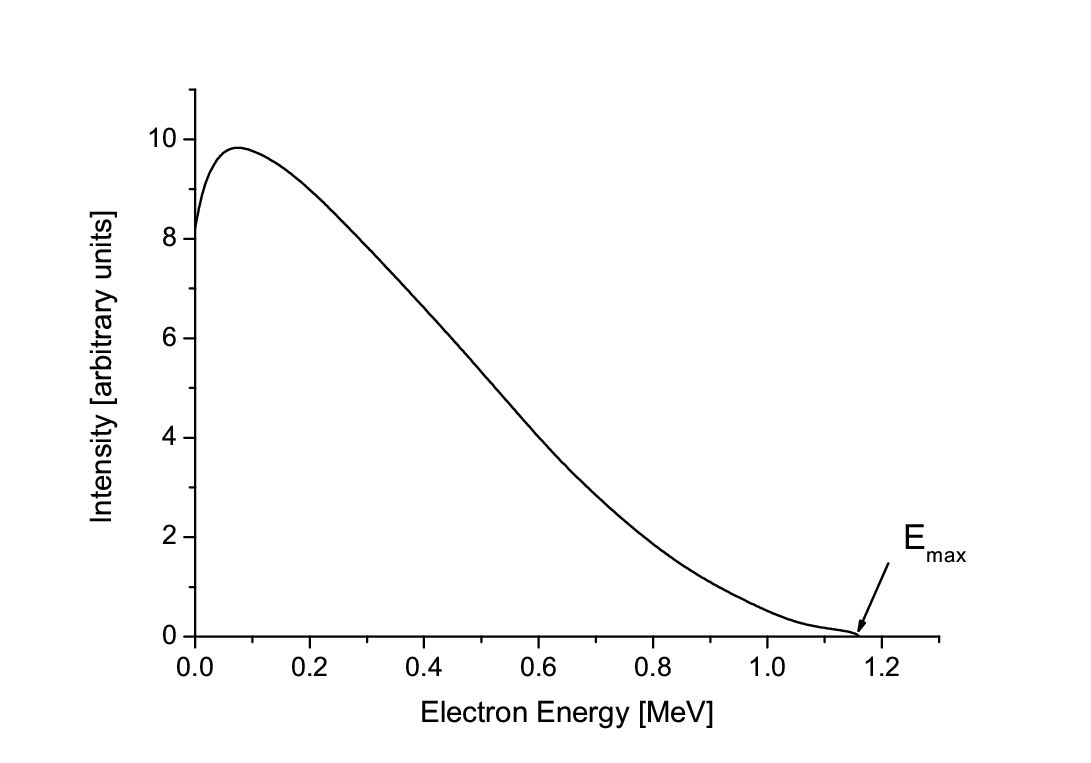
오른쪽 그림은 210Bi(RaE)의 베타 붕괴 스펙트럼을 보여준다.
프란츠 N. D. 쿠리가 개발한 커리 도표(또는 페르미-커리 도표)는 베타 붕괴 연구에 사용되는 그래프이다. 특정 좁은 범위 내에 운동량을 가진 베타 입자의 수의 제곱근을 페르미 함수로 나눈 값을 베타 입자 에너지에 대해 그래프로 나타낸 것이다.[34][35] 페르미 베타 붕괴 이론에 따라 허용 전이와 일부 금지 전이에 대해 직선을 이룬다. 쿠리 도표의 x축 절편은 붕괴의 Q값에 해당하며, 이를 통해 중성미자의 유효 질량에 대한 한계를 찾을 수 있다.[36]
== 페르미 상호작용 ==
엔리코 페르미는 베타 붕괴를 설명하기 위해 페르미 상호작용 모델을 제시했다. 이 모델은 중성미자의 존재를 예측하고, 베타 붕괴의 연속 스펙트럼을 설명하는 데 성공했다. 볼프강 파울리는 새로운 입자의 존재를 가정하면 베타 붕괴의 연속 에너지 분포를 설명할 수 있다는 것을 지적했다. 닐스 보어는 에너지 보존 법칙이 엄밀하게 성립할 필요는 없다는 가설을 제시했으나, 실험 및 이론 양면에서 모순이 지적되어 파울리의 중성미자 가설이 우세하게 되었다.
1911년 리제 마이트너와 오토 한은 베타 붕괴에서 발생하는 전자 에너지의 스펙트럼이 연속적인 스펙트럼이 됨을 실험으로 보였다. 1920년에서 1927년 사이에, 찰스 엘리스(Charles D. Ellis)는 제임스 채드윅 등과 수행한 공동 연구에서 베타 붕괴의 스펙트럼이 정말로 연속이라는 것을 논쟁의 여지가 없이 보여주었다.
== 약한 상호작용 ==
현대 물리학에서는 베타 붕괴가 약한 상호작용에 의해 일어나는 것으로 이해된다.[49] 약한 상호작용은 W 및 Z 보손을 매개로 하며, 쿼크의 맛깔을 바꿀 수 있다. 볼프강 파울리는 새로운 입자의 존재를 가정하면 베타 붕괴의 연속 에너지 분포를 설명할 수 있다는 것을 지적했다. 즉, 베타 붕괴에서는 전자와 함께, 일반적인 방법으로는 관측할 수 없는 미지의 입자가 하나 더 방출되고 있으며, 베타 붕괴 전후의 원자핵 에너지 차이는 전자와 이 새로운 입자 사이에 나뉘어져 있기 때문에, 베타선(전자)의 에너지는 0부터 어떤 일정 값까지의 연속적인 임의의 값을 취하는 것이 아닌가 했다.[49] 이에 대해 닐스 보어는 1934년에 베타 붕괴와 같은 원자핵 내부의 현상은 원자 스펙트럼 등과는 달리, 더 높은 수준의 본질적으로 새로운 물리학의 범위에 속하기 때문에, 반드시 에너지 보존 법칙이 엄밀하게 성립할 필요는 없다는 가설을 제시하며 파울리의 새로운 입자설에 반대했다(에너지 비보존 가설).[49] 그러나 이후 보어의 에너지 비보존 가설은 실험 및 이론 양면에서 그 모순이 지적되어, 결국 파울리의 새로운 입자설이 우세하게 되었다. 파울리의 새로운 입자는 뉴트리노(중성미자)라고 명명되었고, 베타 붕괴 이론(약한 상호작용 이론) 건설의 시발점이 되었다.
3. 1. 에너지 스펙트럼
베타 붕괴에서 방출되는 전자의 에너지 스펙트럼은 연속적이다.[1] 이는 전자와 반중성미자(또는 중성미자)가 붕괴 에너지(Q값)를 나누어 갖기 때문이다. Q값은 주어진 핵붕괴에서 방출되는 총 에너지로, 베타 붕괴에서는 방출된 베타 입자, 중성미자, 그리고 반동 핵의 운동 에너지의 합이다. 하지만 핵의 질량이 매우 크기 때문에 반동 핵의 운동 에너지는 무시할 수 있다. 따라서 베타 입자는 0부터 Q값까지의 범위의 어떤 운동 에너지로든 방출될 수 있다.[1] 전형적인 Q값은 약 1 MeV이지만, 몇 keV부터 수십 MeV까지 다양하다. 전자의 정지 질량이 511 keV이므로, 가장 에너지가 높은 베타 입자는 극한 상대론적이며, 속도는 광속에 매우 가깝다.베타 붕괴는 섭동으로 간주될 수 있으며, 페르미의 황금률을 적용할 수 있다. 방출된 베타 입자의 운동 에너지 스펙트럼 ''N''(''T'')는 다음과 같이 주어진다.[29]
:''N(T) = CL(T) F(Z,T) p E (Q-T)2''
여기서 ''T''는 운동 에너지, ''CL''은 붕괴의 금지 정도에 따라 달라지는 형태 함수(허용 붕괴의 경우 상수), ''F''(''Z'', ''T'')는 페르미 함수(''Z''는 최종 상태 핵의 전하), ''E'' = ''T'' + ''mc''2는 총 에너지, ''p'' = √(E/c)2 - (mc)2는 운동량, Q는 붕괴의 Q값이다. 방출된 중성미자의 운동 에너지는 Q에서 베타 입자의 운동 에너지를 뺀 값으로 근사할 수 있다.
오른쪽 그림은 210Bi(RaE)의 베타 붕괴 스펙트럼을 보여준다.
커리 도표(또는 페르미-커리 도표)는 베타 붕괴 연구에 사용되는 그래프로, 프란츠 N. D. 쿠리가 개발하였다. 특정 좁은 범위 내에 운동량을 가진 베타 입자의 수의 제곱근을 페르미 함수로 나눈 값을 베타 입자 에너지에 대해 그래프로 나타낸 것이다.[34][35] 페르미 베타 붕괴 이론에 따라 허용 전이와 일부 금지 전이에 대해 직선을 이룬다. 쿠리 도표의 x축 절편은 붕괴의 Q값에 해당하며, 이를 통해 중성미자의 유효 질량에 대한 한계를 찾을 수 있다.[36]
3. 2. 페르미 상호작용
엔리코 페르미는 베타 붕괴를 설명하기 위해 페르미 상호작용 모델을 제시했다. 이 모델은 중성미자의 존재를 예측하고, 베타 붕괴의 연속 스펙트럼을 설명하는 데 성공했다. 볼프강 파울리는 새로운 입자의 존재를 가정하면 베타 붕괴의 연속 에너지 분포를 설명할 수 있다는 것을 지적했다. 닐스 보어는 에너지 보존 법칙이 엄밀하게 성립할 필요는 없다는 가설을 제시했으나, 실험 및 이론 양면에서 모순이 지적되어 파울리의 중성미자 가설이 우세하게 되었다.1911년 리제 마이트너와 오토 한은 베타 붕괴에서 발생하는 전자 에너지의 스펙트럼이 연속적인 스펙트럼이 됨을 실험으로 보였다. 1920년에서 1927년 사이에, 찰스 엘리스(Charles D. Ellis)는 제임스 채드윅 등과 수행한 공동 연구에서 베타 붕괴의 스펙트럼이 정말로 연속이라는 것을 논쟁의 여지가 없이 보여주었다.
3. 3. 약한 상호작용
현대 물리학에서는 베타 붕괴가 약한 상호작용에 의해 일어나는 것으로 이해된다.[49] 약한 상호작용은 W 및 Z 보손을 매개로 하며, 쿼크의 맛깔을 바꿀 수 있다. 볼프강 파울리는 새로운 입자의 존재를 가정하면 베타 붕괴의 연속 에너지 분포를 설명할 수 있다는 것을 지적했다. 즉, 베타 붕괴에서는 전자와 함께, 일반적인 방법으로는 관측할 수 없는 미지의 입자가 하나 더 방출되고 있으며, 베타 붕괴 전후의 원자핵 에너지 차이는 전자와 이 새로운 입자 사이에 나뉘어져 있기 때문에, 베타선(전자)의 에너지는 0부터 어떤 일정 값까지의 연속적인 임의의 값을 취하는 것이 아닌가 했다.[49] 이에 대해 닐스 보어는 1934년에 베타 붕괴와 같은 원자핵 내부의 현상은 원자 스펙트럼 등과는 달리, 더 높은 수준의 본질적으로 새로운 물리학의 범위에 속하기 때문에, 반드시 에너지 보존 법칙이 엄밀하게 성립할 필요는 없다는 가설을 제시하며 파울리의 새로운 입자설에 반대했다(에너지 비보존 가설).[49] 그러나 이후 보어의 에너지 비보존 가설은 실험 및 이론 양면에서 그 모순이 지적되어, 결국 파울리의 새로운 입자설이 우세하게 되었다. 파울리의 새로운 입자는 뉴트리노(중성미자)라고 명명되었고, 베타 붕괴 이론(약한 상호작용 이론) 건설의 시발점이 되었다.4. 이중 베타 붕괴
어떤 핵은 이중 베타 붕괴(ββ 붕괴)를 일으키기도 하는데, 이때 핵의 전하는 2 단위만큼 변한다. 대부분 이중 베타 붕괴가 실제로 의미있는 경우는 단일 베타 붕괴가 에너지 측면에서 불가능할 경우이다. 왜냐하면, 만약 단일/이중 베타 붕괴가 모두 가능한 경우엔 대부분 단일 베타 붕괴의 확률이 훨씬 커서, 이중 베타 붕괴를 관측하기가 거의 불가능하기 때문이다. 이런 이유로, 이중 베타 붕괴를 연구할 때에는 보통 (단일) 베타 붕괴에 안정한 핵을 대상으로 하게 된다. 이중 베타 붕괴 역시 단일 베타 붕괴와 마찬가지로 핵자의 개수 ''A''를 바꾸지 않으므로, 주어진 ''A''의 값을 갖는 핵 중 단일/이중 베타 붕괴 모두에 안정적인 핵이 최소한 하나는 존재해야 한다.
일부 원자핵은 이중 베타 붕괴(ββ 붕괴)를 통해 원자핵의 전하가 두 단위만큼 변할 수 있다. 이중 베타 붕괴는 반감기가 극도로 길기 때문에 연구하기 어렵다. β 붕괴와 ββ 붕괴가 모두 가능한 원자핵의 경우, 더 드문 ββ 붕괴 과정은 관측이 사실상 불가능하다. 그러나 β 붕괴는 금지되지만 ββ 붕괴는 허용되는 원자핵에서는 이 과정을 관찰하고 반감기를 측정할 수 있다.[46] 따라서 ββ 붕괴는 일반적으로 베타 안정 핵종에 대해서만 연구된다.
"일반적인" 이중 베타 붕괴는 두 개의 전자와 두 개의 반중성미자를 방출하는 결과를 초래한다. 중성미자가 마요라나 입자(즉, 자신의 반입자)인 경우 중성미자 없는 이중 베타 붕괴라고 알려진 붕괴가 발생한다. 대부분의 중성미자 물리학자들은 중성미자 없는 이중 베타 붕괴가 관측된 적이 없다고 믿는다.[46]
베타 붕괴가 거의 동시에 두 번 일어나는 현상이다. 한 번의 베타 붕괴는 원자핵의 질량이 증가하는 변화이기 때문에 일어나지 않고, 베타 붕괴가 두 번 일어나면 질량이 감소하는 원자핵에서 일어난다. 매우 드물게 일어나는 현상이기 때문에 반감기는 매우 길다.
4. 1. 중성미자를 방출하는 이중 베타 붕괴
일부 원자핵은 이중 베타 붕괴(ββ 붕괴)를 통해 원자핵의 전하가 두 단위만큼 변할 수 있다. 이 과정에서 두 개의 중성자가 두 개의 양성자로 변환되면서 두 개의 전자와 두 개의 반중성미자를 방출한다.[46] 이중 베타 붕괴는 반감기가 극도로 길기 때문에 연구하기 어렵다. 단일 베타 붕괴와 이중 베타 붕괴가 모두 가능한 원자핵의 경우, 더 드문 ββ 붕괴 과정은 관측이 사실상 불가능하다. 그러나 단일 베타 붕괴는 금지되지만 ββ 붕괴는 허용되는 원자핵에서는 이 과정을 관찰하고 반감기를 측정할 수 있다.[46] 따라서 ββ 붕괴는 일반적으로 베타 안정 핵종에 대해서만 연구된다. 단일 베타 붕괴와 마찬가지로 이중 베타 붕괴는 핵자수(질량수) 를 변화시키지 않는다. 따라서 주어진 를 갖는 핵종 중 적어도 하나는 단일 및 이중 베타 붕괴 모두에 대해 안정적이어야 한다.4. 2. 중성미자를 방출하지 않는 이중 베타 붕괴
일부 원자핵에서는 전하가 두 단위만큼 변하는 이중 베타 붕괴(ββ 붕괴)가 일어날 수 있다. 이중 베타 붕괴는 반감기가 매우 길어 연구하기 어렵지만, 베타 붕괴가 금지되고 ββ 붕괴가 허용되는 원자핵에서는 이 과정을 관찰하고 반감기를 측정할 수 있다.[46]일반적인 이중 베타 붕괴는 두 개의 전자와 두 개의 반중성미자를 방출한다. 그러나 중성미자가 자신의 반입자인 마요라나 입자일 경우, 중성미자를 방출하지 않는 이중 베타 붕괴가 발생할 수 있다. 대부분의 중성미자 물리학자들은 이러한 현상이 아직 관측된 적이 없다고 믿는다.[46]
중성미자 없는 이중 베타 붕괴는 표준 모형에서는 예측되지 않는 현상이다. 이 붕괴가 관측된다면 중성미자의 질량과 스핀에 대한 중요한 정보를 얻을 수 있기에 연구가 진행 중이다. 마요라나 입자 외에도 초대칭성 등이 관련된 발생 가능성도 제시되고 있다.
만약 중성미자가 마요라나 입자라면, 다음과 같은 과정을 통해 중성미자 없는 이중 베타 붕괴가 일어날 수 있다.
:
:
:
결과적으로 전체 반응은 다음과 같으며, 중성미자는 방출되지 않는다.
:
5. 핵변환
베타 붕괴는 핵 내 핵자 수는 유지하면서 원자 번호를 변화시켜, 하나의 원소를 다른 원소로 변환시키는 핵 변환 과정이다.[25] 예를 들어, 다음과 같은 반응이 일어날 수 있다.
베타 붕괴가 일어나면 핵 내부 핵자의 개수(''A'')는 그대로이지만 전하(''Z'')가 바뀐다.[25] 음의 베타 붕괴에서는 ''Z''가 하나 증가하고, 양의 베타 붕괴에서는 하나 감소한다. 따라서 ''A''가 같은 핵종을 통틀어 하나의 집합으로 생각할 수 있는데, 이를 동중핵 원소(isobaric element)라 부른다. 이들 중 최소한 하나는 "베타 붕괴에 대해 안정적"(beta stable)이다. 예를 들어, , , 그리고 는 모두 베타 안정적이다. 하지만 베타 붕괴에 안정적인 원소라도 알파 붕괴 등 다른 방법으로 붕괴할 수도 있다.[25]
지구상에 존재하는 대부분의 자연 발생 핵종은 베타 안정적이다. 베타 안정적이지 않은 핵종은 반감기가 1초 미만부터 우주의 나이보다 훨씬 긴 시간까지 다양하다. 장수 동위원소의 일반적인 예로는 홀수 양성자 홀수 중성자 핵종인 이 있는데, 이는 세 가지 유형의 베타 붕괴(베타-, 베타+, 그리고 전자 포획)를 거치며 반감기는 1.277×109 년이다.[27]
베타 붕괴 후의 원자핵이 불안정한 경우, 추가적인 붕괴를 거치게 되어, 여러 동중원소를 거치는 붕괴 계열을 형성한다. 특히 핵분열에 의해 생성된 핵분열 생성물은 양성자 수와 중성자 수의 균형이 부족하여, 양자의 균형을 유지하는 곳(베타 안정선)까지 베타 붕괴를 반복한다. r-과정은 마법수를 가진 중성자 과잉핵이 이와 같은 현상을 일으킴으로써 핵종 분포의 봉우리를 만든다는 가설에 의해 추정되고 있다.
산소 20에서 플루오린 20, 그리고 네온 20으로의 핵변환은 다음과 같다.
:
6. 역사
1896년 앙리 베크렐이 우라늄에서 방사능을 발견하고,[5] 이후 마리 퀴리와 피에르 퀴리가 토륨과 새로운 원소인 폴로늄과 라듐에서 방사능을 관찰하면서 베타 붕괴 연구가 시작되었다.[5] 1899년 어니스트 러더퍼드는 방사선 방출을 물체 투과력과 이온화 능력에 따라 알파선과 베타선(현재는 베타 마이너스)의 두 가지 유형으로 분류하였다.[5] 1900년, 폴 빌라르는 더욱 투과력이 강한 방사선을 확인하였고, 러더퍼드는 1903년 이것이 근본적으로 새로운 유형의 방사선임을 밝히고 감마선이라고 명명하였다.[5]
1911년 리제 마이트너와 오토 한은 베타 붕괴에서 발생하는 전자 에너지의 스펙트럼이 선 스펙트럼이 아닌 연속적인 스펙트럼이 됨을 실험으로 보였다.[6] 이는 에너지 보존 법칙이 깨지는 것처럼 보였다.[6] 1914년 제임스 채드윅은 한스 가이거의 계수기 중 하나를 사용하여 자기 분광계를 이용하여 더 정확한 측정을 수행했는데, 그 결과 스펙트럼이 연속적이라는 것을 보여주었다.[6][7] 1920년부터 1927년까지 찰스 드럼몬드 엘리스는 (채드윅과 동료들과 함께)는 베타 붕괴 스펙트럼이 연속적이라는 것을 더욱 확립했다. 1933년 엘리스와 네빌 모트는 베타 스펙트럼이 에너지에 대한 효과적인 상한선을 갖는다는 강력한 증거를 얻었다.[8]
또 다른 문제는 질소-14 (14N) 원자핵의 스핀이 1이라는 것이었는데, 어니스트 러더퍼드가 제안한 원자 모델에 따르면 질소-14 원자핵의 스핀은 1/2이어야 했다.
1930년 볼프강 파울리는 유명한 편지에서, 원자핵 속에는 전자와 양성자 말고도 전하를 띠지 않은 지극히 가벼운 입자가 존재할 것이라고 예측하고, 이를 "중성자(neutron)"라고 불렀다. 그는 이 "중성자"가 베타 붕괴에서도 방출되는데 단지 아직 검출되지 않았을 뿐이라고 제안하였다. 1931년 엔리코 페르미는 파울리가 제안한 "중성자"를 "중성미자(neutrino)"로 이름을 바꾸었고, 1934년에 페르미의 상호작용 모델을 고안하여 베타 붕괴를 성공적으로 설명하였다.
1934년, 프레데리크 졸리오퀴리와 이렌 졸리오퀴리 부부는 알파 입자를 알루미늄에 충돌시켜 ⁴He + ²⁷Al → ³⁰P + ¹n 의 핵반응을 일으켰고, 생성된 동위원소 ³⁰P가 양전자를 방출하는 것을 관찰했다. 이것이 β⁺ 붕괴영어(양전자 방출)의 첫 번째 예였는데, 이 발견으로 1935년 노벨 화학상을 수상했다.[10]
전자 포획 이론은 1934년 지안-카를로 위크(Gian-Carlo Wick)의 논문에서 처음 논의되었고, 이후 유카와 히데키 등에 의해 발전되었다. K-전자 포획은 1937년 루이스 알바레즈가 ⁴⁸V 핵종에서 처음 관찰했다.[11][12][13]
1956년 리정다오와 양첸닝은 약한 상호작용에서 파리티가 보존된다는 증거가 없다는 점에 주목하여, 약한 힘에 의해 이 대칭성이 보존되지 않을 수 있다고 가정했다.[16] 같은 해 후반, 우젠슝과 동료들은 우 실험을 수행하여 저온에서 의 비대칭 베타 붕괴를 보여주었고, 이는 베타 붕괴에서 파리티가 보존되지 않음을 증명했다.[17][18]
7. 보존 법칙
7. 1. 바리온 수 보존
바리온 수는 다음 공식으로 정의된다.:
여기서
- 는 구성 쿼크의 수이고,
- 는 구성 반쿼크의 수이다.
베타 붕괴는 중성자를 양성자로, 또는 양전자 방출(전자 포획)의 경우 양성자를 중성자로 변환시키지만, 개별 쿼크의 수는 변하지 않는다. 변하는 것은 아이소스핀으로 표시되는 바리온의 종류(flavor)이다.
업 쿼크와 다운 쿼크는 총 아이소스핀 과 아이소스핀 투영
:
을 갖는다. 다른 모든 쿼크는 ''I'' = 0이다.
일반적으로
:
7. 2. 렙톤 수 보존
렙톤 수()는 모든 렙톤에는 +1, 반렙톤에는 −1, 비렙톤 입자에는 0의 값이 할당된다. 예를 들어 중성자(n)가 양성자(p), 전자(), 반전자 중성미자()로 붕괴하는 베타 붕괴()에서 렙톤 수는 보존된다.()7. 3. 각운동량 보존
허용 붕괴의 경우, 총 궤도 각운동량은 0이므로 스핀 양자수만 고려된다. 전자와 반중성미자는 페르미온이며 스핀이 1/2인 입자이므로, 총 (평행) 또는 (반평행)으로 결합할 수 있다. 금지 붕괴의 경우에는 궤도 각운동량도 고려해야 한다.참조
[1]
서적
Nuclear and Radio-chemistry
Elsevier
[2]
논문
Valence and sea quarks in the nucleon
[3]
서적
An introduction to nuclear physics
https://archive.org/[...]
Cambridge University Press
[4]
서적
Fundamentals in Nuclear Physics: From Nuclear Structure to Cosmology
Springer
[5]
서적
Handbook of Radioactivity Analysis
https://books.google[...]
Elsevier Inc.
2017-10-04
[6]
서적
Controversy and Consensus: Nuclear Beta Decay 1911-1934
https://www.springer[...]
Birkhäuser Verlag
[7]
논문
Intensitätsverteilung im magnetischen Spektren der β-Strahlen von Radium B + C
[8]
논문
The idea of the neutrino
[9]
논문
Detection of the Free Neutrino: a Confirmation
[10]
웹사이트
The Nobel Prize in Chemistry 1935
https://www.nobelpri[...]
2018-04-25
[11]
서적
Discovering Alvarez: Selected Works of Luis W. Alvarez
https://archive.org/[...]
University of Chicago Press
[12]
웹사이트
The Nobel Prize in Physics 1968: Luis Alvarez
http://nobelprize.or[...]
The Nobel Foundation
2009-10-07
[13]
논문
Nuclear K Electron Capture
[14]
논문
Electron Capture and Internal Conversion in Gallium 67
[15]
논문
The Capture of Orbital Electrons by Nuclei
[16]
논문
Question of Parity Conservation in Weak Interactions
[17]
논문
Experimental Test of Parity Conservation in Beta Decay
[18]
웹사이트
Channeling Ada Lovelace: Chien-Shiung Wu, Courageous Hero of Physics
http://blogs.scienti[...]
[19]
웹사이트
The Nobel Prize in Physics 1957
https://www.nobelpri[...]
The Nobel Foundation
2015-03-24
[20]
논문
Precision theoretical analysis of neutron radiative beta decay to order O ( α 2 / π 2 )
2017-06-26
[21]
논문
Gauge properties of hadronic structure of nucleon in neutron radiative beta decay to order O(α/π) in standard ''V – A'' effective theory with QED and linear sigma model of strong low-energy interactions
2018-11-30
[22]
서적
Modern Nuclear Chemistry
https://books.google[...]
Wiley
[23]
서적
Nuclear Principles in Engineering
https://books.google[...]
Springer Science + Business Media
[24]
서적
Neutrino Physics
CRC Press
[25]
웹사이트
Interactive Chart of Nuclides
http://www.nndc.bnl.[...]
National Nuclear Data Center, Brookhaven National Laboratory
2014-09-18
[26]
웹사이트
WWW Table of Radioactive Isotopes, Copper 64
http://ie.lbl.gov/to[...]
Lawrence Berkeley National Laboratory
2014-09-18
[27]
웹사이트
WWW Table of Radioactive Isotopes, Potassium 40
http://ie.lbl.gov/to[...]
Lawrence Berkeley National Laboratory
2014-09-18
[28]
서적
Introductory Nuclear Physics
https://books.google[...]
Wiley
1987-11-05
[29]
웹사이트
Energy and Momentum Spectra for Beta Decay
http://hyperphysics.[...]
2013-03-09
[30]
논문
Versuch einer Theorie der β-Strahlen. I
[31]
서적
The Theory of Atomic Collisions
Clarendon Press
[32]
논문
A simple relation for the Fermi function
[33]
논문
A simple approximation of the fermi function in nuclear beta decay
[34]
논문
The Radiations Emitted from Artificially Produced Radioactive Substances. I. The Upper Limits and Shapes of the β-Ray Spectra from Several Elements
[35]
논문
On the Use of the Kurie Plot
[36]
논문
Neutrinoless double beta decay and neutrino physics
[37]
논문
Parity and the Polarization of Electrons fromCo60
[38]
서적
Alpha-, Beta- and Gamma-Ray Spectroscopy
North-Holland Publishing Company
[39]
웹사이트
An Overview Of Neutron Decay
http://www.physi.uni[...]
[40]
논문
Sur la possibilité d'existence d'un type particulier de radioactivité phénomène de création e
https://hal.archives[...]
[41]
논문
First observation of bound-state β− decay
[42]
웹사이트
Bound-state beta decay of highly ionized atoms
http://www.ca.infn.i[...]
2013-06-09
[43]
논문
Bound-State Beta Decay of 205Tl81+ Ions and the LOREX Project
https://link.aps.org[...]
American Physical Society
2024-12-02
[44]
논문
Re-Os ages of group IIA, IIIA, IVA, and IVB iron meteorites
[45]
논문
Observation of bound-state beta minus decay of fully ionized 187Re: 187Re–187Os Cosmochronometry
[46]
논문
Neutrinoless double beta-decay
[47]
서적
富永, 佐野 (2018)
[48]
서적
基礎原子力工学
電気学会
1982-05-20
[49]
서적
岩波講座 現代物理学
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com

