비 해석적 매끄러운 함수

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 함수의 예시
3. 매끄러운 전이 함수
4. 어떤 점도 해석적이지 않은 매끄러운 함수
5. 테일러 급수의 적용
6. 고 차원으로 적용
7. 복소해석학적 관점
참조

1. 개요

비 해석적 매끄러운 함수는 모든 차수의 도함수를 갖지만, 테일러 급수가 원래 함수와 일치하지 않아 해석적이지 않은 함수를 의미한다. 이러한 함수의 예시로, 실수 x에 대해 정의된 함수 f(x) = exp(-1/x) (x > 0일 때), f(x) = 0 (x ≤ 0일 때)가 있다. 이 함수는 매끄럽지만, 원점에서 해석적이지 않다. 매끄러운 전이 함수와 테일러 급수의 적용을 통해 다양한 형태의 비 해석적 매끄러운 함수를 구성할 수 있으며, 푸리에 급수를 이용해 모든 점에서 매끄럽지만 해석적이지 않은 함수를 만들 수도 있다. 이러한 현상은 복소해석학에서는 발생하지 않으며, 실수 변수 분석과 복소 변수 분석의 중요한 차이점을 보여준다.

더 읽어볼만한 페이지

매끄러운 함수 - 분포 (해석학)
해석학에서 분포는 시험 함수 공간의 연속 쌍대 공간의 원소로 정의되며, 로랑 슈바르츠에 의해 정립되어 편미분 방정식의 해를 다루는 데 유용하고 미분 불가능하거나 특이점을 갖는 함수를 포함한 다양한 함수를 다루는 데 효과적인 일반적인 함수의 개념을 확장한 것이다.
매끄러운 함수 - 모스 이론
모스 이론은 미분다양체 위의 함수의 임계점과 지표를 이용하여 다양체의 위상수학적 성질을 연구하는 이론으로, 함수값에 따른 부분공간 변화를 관찰하여 다양체의 호몰로지를 계산하고 위상수학적 성질을 밝히는 데 응용된다.

비 해석적 매끄러운 함수
개요
이름	비 해석적 매끄러운 함수
설명	해석 함수가 아니지만 매끄러운 함수
예시
함수	exp(-1/x²) (x ≠ 0), 0 (x = 0)
설명	모든 점에서 무한 번 미분 가능하지만, 0에서의 테일러 급수는 0이므로 0 근방에서 원래 함수와 일치하지 않음.
관련 개념
관련 개념	매끄러운 함수, 해석 함수

2. 함수의 예시

(내용 없음)

2. 1. 함수의 정의

다음 함수를 고려해 보자.

:

f(x)=\begin{cases}e^{-\frac{1}{x}}&\text{if }x>0,\\ 0&\text{if }x\le0,\end{cases}

이는 모든 실수 ''x''에 대해 정의된다.

2. 2. 이 함수는 매끄럽다

함수 ''f''는 실선의 모든 점 ''x''에서 모든 차수의 연속적인 미분이 존재한다.^[1]

:

f^{(n)}(x) = \begin{cases}\displaystyle\frac{p_n(x)}{x^{2n}}\,f(x) & \text{if }x>0, \\ 0 &\text{if }x \le 0,\end{cases}

여기서 ''p_n''(''x'')는 ''p''₁(''x'') = 1과 다음 식에서 재귀적으로 주어진 ''n'' - 1차 다항식이다.

:

p_{n+1}(x)=x^2p_n'(x)-(2nx-1)p_n(x),\qquad n\in\mathbb{N}.

^[1]

위 공식에서 도함수가 0에서 연속적인지 바로 알 수 없지만, 다음의 일방 극한을 통해 확인할 수 있다.

:

\lim_{x\searrow 0} \frac{e^{-\frac{1}{x}}}{x^m} = 0

(단, ''m''은 음이 아닌 정수)^[1]

따라서, 함수 ''f''는 모든 차수의 연속적인 도함수를 가지는 매끄러운 함수이다.

2. 2. 1. 증명의 개요

증명은 음이 아닌 정수 ''m''에 대한 다음의 극한값으로부터 시작한다.

:

\lim_{x\searrow0} \frac{e^{-1/x}}{x^m} = 0.

이 극한은 모든 ''f''^(''n'')이 연속이고 ''x'' = 0에서 미분가능하다는 것을 보여주는 데 사용된다.

:

\lim_{x\searrow0} \frac{f^{(n)}(x) - f^{(n)}(0)}{x-0} = \lim_{x\searrow0} \frac{p_n(x)}{x^{2n+1}}\,e^{-1/x} = 0.

함수 ''f''는 실수선의 모든 점 ''x''에서 모든 차수에 대해 연속적인 도함수를 가진다. 이러한 도함수에 대한 공식은 다음과 같다.

:

f^{(n)}(x) = \begin{cases}\displaystyle\frac{p_n(x)}{x^{2n}}\,f(x) & \text{if }x>0, \\ 0 &\text{if }x \le 0,\end{cases}

여기서 ''p_n''(''x'')는 재귀적으로 주어지는 다항식이며, ''p''₁(''x'') = 1이고,

:

p_{n+1}(x)=x^2p_n'(x)-(2nx-1)p_n(x)

이다. 모든 양의 정수 ''n''에 대해, 이 공식은 도함수가 0에서 연속임을 보여준다.

:

\lim_{x\searrow 0} \frac{e^{-\frac{1}{x}}}{x^m} = 0

2. 2. 2. 상세 증명

지수 함수의 멱급수 표현에 의해, 0을 포함한 모든 자연수 ''m''에 대하여 다음 식이 성립한다.

:

\frac{1}{x^m} = x \Bigl( \frac{1}{x} \Bigr)^{m+1} \le (m+1)! x \sum_{n=0}^\infty \frac{1}{n!} \Bigl( \frac{1}{x} \Bigr)^n = (m+1)! x \exp \Bigl( \frac{1}{x} \Bigr), \qquad x > 0.

이는 ''n'' ≠ ''m'' + 1인 모든 양의 항들이 더해지기 때문이다. 따라서 지수 함수의 함수식을 이용하면 다음과 같다.

:

\lim_{x \searrow 0} \frac{e^{-1/x}}{x^m} \le (m+1)! \lim_{x \searrow 0} x = 0.

이제 수학적 귀납법으로 ''f''의 ''n''차 도함수에 대한 공식을 증명한다. 연쇄 법칙과 역함수의 미분 법칙, 지수 함수의 도함수가 다시 도함수인 성질을 이용해서 ''x'' > 0이고, ''p''₁(''x'')가 0차 다항식일 때 ''f''의 일계도함수의 식이 성립함을 보일 수 있다. 당연히 ''f''의 일계도함수는 ''x'' < 0에서 0이다. ''x'' = 0에서 ''f''의 우측 편미분이 0인 것을 보이면 된다. 위의 극한을 사용하면 다음을 알 수 있다.

:

f'(0) = \lim_{x \searrow 0} \frac{f(x) - f(0)}{x - 0} = \lim_{x \searrow 0} \frac{e^{-1/x}}{x} = 0.

''n''에서 ''n'' + 1로 가는 과정은 유사하다. ''x'' > 0일 때 우리는 다음 도함수를 얻을 수 있다.

:

\begin{align}f^{(n+1)}(x) &= \biggl( \frac{p'_n(x)}{x^{2n}} - 2n \frac{p_n(x)}{x^{2n+1}} + \frac{p_n(x)}{x^{2n+2}} \biggr) f(x) \\&= \frac{x^2 p'_n(x) - (2nx - 1) p_n(x)}{x^{2n+2}} f(x) \\&= \frac{p_{n+1}(x)}{x^{2(n+1)}} f(x).\end{align}

여기서 ''p''_''n''+1(''x'')은 ''n'' = (''n'' + 1) - 1차 다항식이다. 물론 ''x'' < 0일 때, ''f''의 (''n'' + 1)계도함수는 0이다. ''x'' = 0일 때 ''f''^(''n'')의 우미분계수는 다음과 같다.

:

\lim_{x \searrow 0} \frac{f^{(n)}(x) - f^{(n)}(0)}{x - 0} = \lim_{x \searrow 0} \frac{p_n(x)}{x^{2n+1}} e^{-1/x} = 0.

함수 ''f''는 실수선의 모든 점 ''x''에서 모든 차수에 대해 연속적인 도함수를 가진다. 이러한 도함수에 대한 공식은 다음과 같다.

:

f^{(n)}(x) = \begin{cases}\displaystyle \frac{p_n(x)}{x^{2n}} f(x) & \text{if } x > 0, \\0 & \text{if } x \le 0,\end{cases}

여기서 ''p_n''(''x'')는 다항식의 차수가 ''n'' - 1인 재귀적으로 주어진 다항식이며, ''p''₁(''x'') = 1이고,

:

p_{n+1}(x) = x^2 p'_n(x) - (2nx - 1) p_n(x)

모든 양의 정수 ''n''에 대해 성립한다.

2. 3. 이 함수는 비 해석적이다

앞에서 봤듯이 함수 ''f''는 매끄럽고 원점에서 모든 미분계수는 0이다. 따라서 원점에서 ''f''의 테일러 급수는 항상 0이다.

:

\sum_{n=0}^\infty \frac{f^{(n)}(0)}{n!}x^n=\sum_{n=0}^\infty \frac{0}{n!}x^n = 0,\qquad x\in\mathbb{R},

그리고 테일러 급수는 x > 0에서 ''f''(''x'')와 같지 않다. 따라서 ''f''는 원점에서 해석적이지 않다.

3. 매끄러운 전이 함수

:

g(x)=\frac{f(x)}{f(x)+f(1-x)},\qquad x\in\mathbb{R},

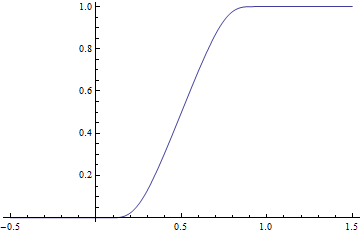
이 함수는 실수 전체에서 양수이기 때문에 ''g''는 매끄럽다. 게다가 x ≤ 0에서 ''g''(''x'') = 0이고 x ≥ 1에서 ''g''(''x'') = 1이다. 따라서 이 함수는 단위 구간 [0, 1]에서 0에서 1까지 매끄러운 전이를 제공한다. ''a'' < ''b''인 실수 구간 [''a'',''b'']에서 매끄러운 전이를 갖기 위해서는 다음 함수를 고려한다.

:

\mathbb{R}\ni x\mapsto g\Bigl(\frac{x-a}{b-a}\Bigr).

실수 ''a'' < ''b'' < ''c'' < ''d''에서, 다음의 매끄러운 함수

:

\mathbb{R}\ni x\mapsto g\Bigl(\frac{x-a}{b-a}\Bigr)\,g\Bigl(\frac{d-x}{d-c}\Bigr)

는 닫힌 구간 [''b'',''c'']에서 1이며 구간 (''a'',''d'') 외부에서 0이 된다.

4. 어떤 점도 해석적이지 않은 매끄러운 함수

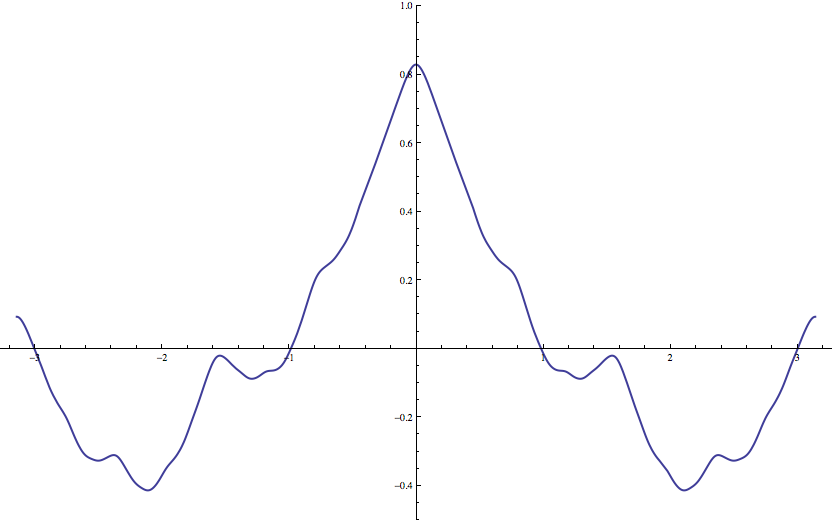
무한히 미분 가능하지만 어떤 점에서도 해석적이지 않은 함수는 푸리에 급수를 이용하여 만들 수 있다. ''A'' := { 2^''n'' : ''n'' ∈ '''N''' }를 2의 모든 거듭제곱의 집합이라고 하고, 모든 ''x'' ∈ '''R'''에서 다음과 같이 정의한다.

:

F(x):=\sum_{k\in A} e^{-\sqrt{k}}\cos(kx)\ .

여기서 급수

\sum_{k\in A} e^{-\sqrt{k}}k^n

는 모든 ''n'' ∈ '''N'''에서 수렴하며, 바이어슈트라스 M-판정법을 이용해 각 급수의 도함수가 균등수렴함을 증명할 수 있다. 따라서 이 함수는 C^∞의 원소, 즉 무한히 미분 가능한 함수이다.

π의 어떠한 이진 유리수배에 대해서, 즉 p ∈ '''N'''이고 ''q'' ∈ A이며, n ≥ 4 이고 n > q인 모든 n ∈ A 차수의 도함수에서, 모든 ''x'' := π·''^p/_q''에서 다음을 얻을 수 있다.

:

F^{(n)}(x):=\sum_{k\in A} e^{-\sqrt{k}} k^n\cos(kx)  = \sum_{k\in A\atop k>q} e^{-\sqrt{k}} k^n+\sum_{k\in A\atop k\le q} e^{-\sqrt{k}} k^n\cos(kx) \ge  e^{-\sqrt{n}} n^n  + O(q^n)\quad  (\mathrm{as}\; n\to \infty)

여기서 모든 ''k'' > ''q''에서 cos(kx) = 1이라는 사실을 사용했다. 결과적으로 그러한 어떤 ''x'' ∈ '''R'''에서

:

\limsup_{n\to\infty} \left(\frac

{n!}\right)^{1/n}=+\infty\, ,

코시-아다마르 정리에 의해서 x에서 ''F''의 수렴반경은 0이 된다. 함수의 해석성은 열린집합이고 이진 유리수는 밀도가 높기 때문에 ''F''는 '''R'''의 어떠한 점에서도 해석적이지 않다는 결론을 내릴 수 있다.

5. 테일러 급수의 적용

실수 또는 복소수의 모든 수열 α₀, α₁, α₂, ... 에 대해서, 이 수들을 수직선의 원점에서 미분계수로 가지는 매끄러운 함수 ''F''가 존재한다.^[3] 특히 모든 수열의 숫자는 매끄러운 함수의 테일러 급수의 계수로 나타날 수 있다. 이 결과는 에밀 보렐 이후 보렐의 보조정리로 알려져 있다.

위에서 정의한 매끄러운 전이 함수 ''g''를 사용하여 다음을 정의한다:

: $h(x)=g(2+x)g(2-x),\qquad x\in\mathbb{R}.$

이 함수 ''h''역시 매끄럽다. 이 함수는 닫힌 구간 [−1,1]에서는 1이고 열린 구간 (−2,2)의 외부에서는 사라진다. ''h''를 사용하여 0을 포함한 모든 자연수에 대하여 매끄러운 함수를 정의한다:

: $\psi_n(x)=x^n h(x),\qquad x\in\mathbb{R},$

이는 구간 [−1,1]에서 단항식 ''xⁿ''과 일치하고 구간 (−2,2) 외부에서는 사라진다. 따라서 원점에서 ''ψ_n''의 ''k''차 미분계수는 다음을 만족한다

: $\psi_n^{(k)}(0)=\begin{cases}n!&\text{if }k=n,\\0&\text{otherwise,}\end{cases}\quad k,n\in\mathbb{N}_0,$

그리고 최대 최소 정리는 ''ψ_n''과 ''ψ_n''의 모든 도함수들이 유계함수라는 것을 내포한다. 따라서 상수

: $\lambda_n=\max\bigl\{1,|\alpha_n|,\|\psi_n\|_\infty,\|\psi_n^{(1)}\|_\infty,\ldots,\|\psi_n^{(n)}\|_\infty\bigr\},\qquad n\in\mathbb{N}_0,$

''ψ_n''의 균등 수렴 위상과 그것의 첫번째 ''n'' 도함수를 포함해서 잘 정의된 실수이다. 크기를 조절한 함수를 정의한다:

: $f_n(x)=\frac{\alpha_n}{n!\,\lambda_n^n}\psi_n(\lambda_n x),\qquad n\in\mathbb{N}_0,\;x\in\mathbb{R}.$

연쇄 법칙을 반복적으로 적용한다

: $f_n^{(k)}(x)=\frac{\alpha_n}{n!\,\lambda_n^{n-k}}\psi_n^{(k)}(\lambda_n x),\qquad k,n\in\mathbb{N}_0,\;x\in\mathbb{R},$

이전에 계산한 0에서 ''ψ_n''의 ''k''차 미분계수를 사용하면

: $f_n^{(k)}(0)=\begin{cases}\alpha_n&\text{if }k=n,\\0&\text{otherwise,}\end{cases}\qquad k,n\in\mathbb{N}_0.$

우리가 구하고자 하는 함수는 다음과 같다:

: $F(x)=\sum_{n=0}^\infty f_n(x),\qquad x\in\mathbb{R},$

이것은 잘 정의되어 있고, 순차적으로 무한히 미분할 수 있다.^[4] 이를 위해 모든 ''k''에 대해서 보자

: $\sum_{n=0}^\infty\|f_n^{(k)}\|_\infty\le \sum_{n=0}^{k+1}\frac$

{n!\,\lambda_n^{n-k}}\|\psi_n^{(k)}\|_\infty+\sum_{n=k+2}^\infty\frac1{n!}\underbrace{\frac1{\lambda_n^{n-k-2}}}_{\le\,1}\underbrace{\frac

{\lambda_n}}_{\le\,1}\underbrace{\frac{\|\psi_n^{(k)}\|_\infty}{\lambda_n}}_{\le\,1}<\infty,

남은 무한급수는 비판정법에 의해 수렴한다.

6. 고 차원으로 적용

모든 반지름 ''r'' > 0에 대하여,

:

\mathbb{R}^n\ni x\mapsto \Psi_r(x)=f(r^2-\|x\|^2)

여기서 유클리드 노름 ||''x''||은 ''n''차원 유클리드 공간에서 반지름 ''r''의 구 내에 지지 집합을 가지며

\Psi_r(0)>0

인 매끄러운 함수를 정의한다.

7. 복소해석학적 관점

함수 ''f''는 매끄럽고 원점에서 모든 미분계수는 0이다. 따라서 원점에서 ''f''의 테일러 급수는 항상 0이다.

: $\sum_{n=0}^\infty \frac{f^{(n)}(0)}{n!}x^n=\sum_{n=0}^\infty \frac{0}{n!}x^n = 0,\qquad x\in\mathbb{R},$

그리고 테일러 급수는 x > 0에서 ''f''(''x'')와 같지 않다. 따라서 ''f''는 원점에서 해석적이지 않다. 이 과정은 실수가 아닌 복소수를 변수로 가지는 미분 가능한 복소함수에서는 일어나지 않는다. 사실 모든 정칙함수의 해석성이기 때문에 ''f''가 무한히 미분가능함에도 불구하고 해석적이지 않다는 점은 실해석학과 복소해석학의 가장 큰 차이점을 나타낸다.

함수 ''f''가 실수선 상에서 모든 차수의 도함수를 갖지만, 양의 실수 절반 ''x'' > 0에서부터 복소평면에서 ''f''의 해석적 연속성을 갖는 다음의 함수를 보자.

: $\mathbb{C}\setminus\{0\}\ni z\mapsto \exp(-1/z)\in\mathbb{C},$

이 함수는 본질적 특이점을 가지고 있다. 따라서 연속적이지도 않으며, 덜 해석적이다. 피카르의 정리에 의해서 이것은 원점 주변에서 무한히 자주 0을 제외한 모든 복소수를 얻는다.

참조

_[1] 서적 Real and Complex Analysis McGraw-Hill
_[2] 간행물 Analysis I Birkhäuser Verlag
_[3] 문서 Real and Complex Analysis "//en.wikipedia-mirr[...]
_[4] 문서 See e.g.

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com