전송선로

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

전송 선로는 전기 신호를 전송하는 데 사용되는 구조로, 19세기 제임스 클러크 맥스웰 등의 연구를 통해 이론적 기초가 마련되었다. 초기에는 해저 케이블의 성능 문제를 예측하는 데 기여했으며, 이후 올리버 헤비사이드의 전신 방정식 개발을 통해 이론이 발전했다. 한국에서는 한국전쟁 이후 군사 및 민간 통신망 구축에 핵심적인 역할을 했으며, 최근에는 5G, 6G 등 차세대 통신망 구축에 중요한 기술로 활용되고 있다. 전송 선로는 전압과 전류를 설명하는 편미분 방정식인 전신 방정식을 통해 분석되며, 분산 요소 모델을 사용하여 표현된다. 전송 선로의 종류에는 동축 케이블, 평면 전송 선로, 평형 선로 등이 있으며, 신호 전송, 분산 소자 회로, 펄스 발생 등 다양한 응용 분야에서 사용된다.

더 읽어볼만한 페이지

통신공학 - 무선 통신
무선 통신은 전선 없이 전자기파 등을 이용하여 정보를 전달하는 방식으로, 마르코니의 무선 전신 실험 성공 이후 다양한 형태로 발전해왔으며, 현대 사회에서 필수적인 기술로 자리 잡았다.
통신공학 - FM 방송
FM 방송은 주파수 변조 방식을 사용하여 음질이 좋고 잡음에 강하며 스테레오 방송과 부가 서비스를 제공하는 라디오 방송 기술이다.

전송선로
개요
종류	전선 케이블 평행선 동축 케이블 유전체 도파관 광섬유
상세 정보
특성 임피던스	특성 임피던스
감쇠	감쇠
분산	분산
전파 속도	전파 속도
모드	TEM 모드 TE 모드 TM 모드 HE 모드
응용 분야
통신	라디오 텔레비전 인터넷 전화
전력 전송	전력 전송
신호 전송	신호 전송

2. 역사

전송 선로 이론의 기초는 19세기 제임스 클러크 맥스웰, 제1대 켈빈 남작 윌리엄 톰슨, 올리버 헤비사이드 등의 연구를 통해 확립되었다. 1855년 켈빈 남작은 해저 케이블의 전류 확산 모델을 제시하여 1858년 대서양 횡단 전신 케이블의 성능 문제를 정확히 예측했다. 1885년 헤비사이드는 전신 방정식의 현대적 형태를 제시하며 전송 선로 이론 발전에 기여했다.^[7]^[32]

마쓰마에 시게요시는 1932년에 무장전 케이블을 이용한 장거리 전송 시스템을 제안했다. 비록 마쓰마에 시게요시는 일본인이지만, 무장전 케이블은 한국 통신 기술 발전에 중요한 영향을 미쳤다. 한국전쟁 이후, 전송 선로 기술은 군사 통신 및 민간 통신망 구축에 핵심적인 역할을 수행했다. 최근에는 광통신 기술 발전에 따라 전송 선로의 중요성이 더욱 커지고 있으며, 5G, 6G 등 차세대 통신망 구축에 핵심 기술로 활용되고 있다.

2. 1. 초기 역사

전송 선로의 동작에 대한 수학적 분석은 제임스 클러크 맥스웰, 제1대 켈빈 남작 윌리엄 톰슨, 올리버 헤비사이드를 통해 발전하였다. 1855년 켈빈 남작은 해저 케이블의 전류에 대한 확산 모델을 공식화했다. 이 모델은 1858년 대서양 해저 전신 케이블의 저조한 성능을 정확하게 예측했다. 1885년 헤비사이드는 케이블 내 전파에 대한 분석과 전신 방정식의 현대적 형태를 설명하는 최초의 논문을 발표했다.^[7]^[32] 1887년에는 장전 코일을 추가한 장전 케이블을 제안했다.

1932년에는 마쓰마에 시게요시가 무장전 케이블을 이용한 장거리 전송을 가능하게 하는 시스템(마쓰마에 시게요시#무장전 케이블)을 제안했다.

2. 2. 대한민국의 전송 선로 기술 발전

마쓰마에 시게요시는 1932년에 무장전 케이블을 이용한 장거리 전송 시스템을 제안했다.^[32] 이 기술은 이후 한국 통신 기술 발전에 영향을 주었다.

3. 전송 선로 이론

일반적인 전기 케이블은 교류(AC)와 같은 낮은 주파수의 전원(주전원) 및 오디오 신호를 전달하는 데 사용될 수 있지만, 약 30kHz 이상의 무선 주파수 전류를 전달하는 데는 적합하지 않다.^[1] 이는 에너지가 전파로 케이블에서 방사되어 전력 손실을 유발하고, 무선 주파수 전류가 케이블의 불연속성에서 반사되어 신호 전력이 대상에 도달하는 것을 방해하기 때문이다.^[1]^[2]

전송선은 최소한의 반사 및 전력 손실로 전자기 신호를 전달하기 위해 특수 구조와 임피던스 정합을 사용한다. 대부분의 전송선은 길이를 따라 균일한 단면 치수를 가지므로 균일한 전기 임피던스(특성 임피던스)를 갖는다.^[2]^[3]^[4] 전송선 유형에는 평행선 (래더 라인, 꼬인 쌍), 동축 케이블, 스트립 라인, 마이크로스트립과 같은 평면 전송선이 있다.^[5]^[6] 전송선은 전송된 주파수의 파장이 케이블 길이에 비해 충분히 짧아질 때 필요해진다.

마이크로파 이상의 주파수에서는 전송선 대신 도파관이 사용된다.^[1]^[6]

thumb 전자 기호의 변형]]

Image:Transmission line 4 port.svg

전송선이 길이를 따라 균일하면, 그 동작은 ''특성 임피던스''(Z₀)와 ''신호 전파 지연''(τ_p)로 설명된다. Z₀는 선의 임의 지점에서 주어진 파동의 복소 전압과 전류의 비율이다. Z₀의 일반적인 값은 동축 케이블의 경우 50 또는 75 옴, 연선 쌍의 경우 약 100옴, 비연선 쌍의 경우 약 300옴이다. 전파 지연은 전송선의 길이에 비례하며, 광속으로 나눈 값보다 작을 수 없다.

전송선을 통해 전력을 전송할 때, 부하 임피던스를 Z₀와 같게 하면(''정합'') 전력 반사를 최소화할 수 있다.

전송선에 공급되는 전력의 일부는 저항으로 인해 손실(''옴'' 손실 또는 ''저항'' 손실)된다.^[1] 고주파수에서는 ''유전 손실''이 발생하여 저항 손실을 더한다. 유전 손실은 전송선 내부의 절연 재료가 교류 전기장으로부터 에너지를 흡수하여 열로 변환할 때 발생한다.^[1] 전송선은 저항(R)과 인덕턴스(L)가 직렬로, 커패시턴스(C)와 컨덕턴스(G)가 병렬로 연결된 것으로 모델링할 수 있다.

전송선의 총 전력 손실은 종종 데시벨 미터(dB/m) 단위로 나타내며, 신호 주파수에 따라 달라진다. 3dB 손실은 대략 전력의 절반 감소에 해당한다. 전파 지연은 종종 미터당 나노초 단위로 지정된다.

3. 1. 전신 방정식

올리버 헤비사이드가 개발한 전신 방정식은 거리와 시간에 따른 전송 선로의 전압과 전류를 설명하는 선형 미분 방정식이다. 이 방정식은 맥스웰 방정식을 기반으로 하며, 전송 선로를 무한히 작은 2포트 기본 요소들로 구성된 분산 요소 모델로 나타낸다.^[1]

전송 선로 모델은 다음과 같은 요소들로 구성된다.^[1]

도체의 분산 저항 ''R'' (단위 길이당 옴)
분산 인덕턴스 ''L'' (단위 길이당 헨리)
두 도체 사이의 정전 용량 ''C'' (단위 길이당 패럿)
두 도체를 분리하는 유전 물질의 전기 전도도 ''G'' (단위 길이당 지멘스)

이 요소들을 이용하여 주파수 영역에서 전압 ''V(x)''와 전류 ''I(x)''를 나타내면 다음과 같다.^[1]

:

\frac{\partial V(x)}{\partial x} = -(R + j\,\omega\,L)\,I(x)

:

\frac{\partial I(x)}{\partial x} = -(G + j\,\omega\,C)\,V(x) ~\,.

여기서 ''j''는 허수 단위, ''ω''는 각 주파수이다.

''R''과 ''G''가 매우 작아 무시할 수 있는 무손실 전송 선로의 경우, 전신 방정식은 다음과 같이 단순화된다.^[1]

:

\frac{\partial^2 V(x)}{\partial x^2}+ \omega^2 L\,C\,V(x) = 0

:

\frac{\partial^2 I(x)}{\partial x^2} + \omega^2 L\,C\,I(x) = 0 ~\,.

이 방정식들은 파동 방정식이며, 정방향 및 역방향으로 동일한 전파 속도를 갖는 평면파를 해로 갖는다. 이는 전송 선로를 따라 전자기파가 전파되며, 반사 성분이 존재할 수 있음을 의미한다.^[1]

일반적인 유손실 전송 선로의 경우, 전신 방정식은 다음과 같다.^[1]

:

\frac{\partial^2 V(x)}{\partial x^2} = \gamma^2 V(x)\,

:

\frac{\partial^2 I(x)}{\partial x^2} = \gamma^2 I(x)\,

여기서 ''γ''는 복소수 전파 정수이며, 다음과 같이 표현된다.^[1]

:

\gamma = \sqrt{(R + j\,\omega\,L)(G + j\,\omega\,C)\,}

특성 임피던스 ''Z''₀는 다음과 같다.^[1]

:

Z_0 = \sqrt{\frac{R + j\,\omega\,L}{G + j\,\omega\,C}\,} ~\,.

''V(x)''와 ''I(x)''의 해는 다음과 같이 주어진다.^[1]

:

V(x) = V_{(+)} e^{-\gamma\,x} + V_{(-)} e^{+\gamma\,x} \,

:

I(x) = \frac{1}{Z_0}\,\left( V_{(+)} e^{-\gamma\,x} - V_{(-)} e^{+\gamma\,x} \right) ~\,.

상수

V_{(\pm)}

는 경계 조건에 의해 결정된다. 입력 전압 펄스

V_{\mathrm{in}}(t) \,

가 주어지면, 위치 ''x''에서 전송된 펄스

V_{\mathrm{out}}(x,t) \,

는 푸리에 변환과 역 푸리에 변환을 통해 계산할 수 있다.^[1]

전파 정수 ''γ''의 실수부와 허수부는 복잡한 수식을 통해 계산되거나, 대수적으로 계산될 수 있다. 작은 손실과 높은 주파수에서는 다음과 같이 근사할 수 있다.^[1]

:

\operatorname{Re}(\gamma) = \alpha \approx \tfrac{1}{2}\sqrt{L\,C\,}\,\left( \frac{R}{L} + \frac{G}{C} \right) \,

:

\operatorname{Im}(\gamma) = \beta \approx \omega\,\sqrt{L\,C\,} ~.\,

이를 통해 출력 전압

V_{out}(x,t)

를 근사적으로 계산할 수 있다.^[1]

:

V_{\mathrm{out}}(x,t) \approx V_{\mathrm{in}}(t - \sqrt{L\,C\,}\,x)\,e^{- \tfrac{1}{2}\sqrt{L\,C\,}\,\left( \frac{R}{L} + \frac{G}{C} \right)\,x }. \,

3. 2. 특성 임피던스

전송 선로의 동작은 주로 특성 임피던스(기호 Z₀)와 신호 전파 지연(기호 τ_p)라는 두 가지 매개변수로 설명됩니다.^[2]^[3]^[4] 특성 임피던스는 전송 선로의 임의의 지점에서 전압과 전류의 비율을 나타내는 값입니다. 일반적인 전송 선로의 특성 임피던스 값은 다음과 같습니다.

동축 케이블: 50 또는 75 옴
연선 쌍: 약 100옴
비연선 쌍 (라디오 전송에 사용): 약 300옴

전송 선로를 통해 전력을 효율적으로 전송하려면, 부하 임피던스를 특성 임피던스(Z₀)와 같게 만들어야 합니다. 이를 정합이라고 하며, 이 경우 전송 선로는 정합되었다고 합니다.

전송 선로의 특성 임피던스

Z_0

는 ''단일'' 전압파의 진폭과 전류파의 비율입니다.^[1] 대부분의 전송 선로에는 반사파도 있으므로, 특성 임피던스는 일반적으로 선로에서 측정되는 임피던스가 아닙니다.

부하 임피던스

Z_\mathrm{L}

에서 주어진 거리

\ell

에서 측정된 임피던스는 다음과 같이 표현될 수 있습니다.

:

Z_\mathrm{in}\left(\ell\right)=\frac{V(\ell)}{I(\ell)} = Z_0 \frac{1 + \mathit{\Gamma}_\mathrm{L} e^{-2 \gamma \ell}}{1 - \mathit{\Gamma}_\mathrm{L} e^{-2 \gamma \ell}}

여기서

\gamma

는 전파 상수이고

\mathit{\Gamma}_\mathrm{L} = \frac{\,Z_\mathrm{L} - Z_0\,}{Z_\mathrm{L} + Z_0}

는 전송 선로의 부하단에서 측정된 전압 반사 계수입니다. 또는 위의 수식을 재정렬하여 부하 전압 반사 계수 대신 부하 임피던스 측면에서 입력 임피던스를 표현할 수 있습니다.

:

Z_\mathrm{in}(\ell) = Z_0\,\frac{Z_\mathrm{L} + Z_0 \tanh\left(\gamma \ell\right)}{Z_0 + Z_\mathrm{L}\,\tanh\left(\gamma \ell \right)}

.

무손실 전송 선로의 경우, 전파 정수는 순수 허수이며,

\gamma = j\,\beta

이므로, 위의 공식은 다음과 같이 다시 쓸 수 있습니다.

:

Z_\mathrm{in}(\ell) = Z_0 \frac{Z_\mathrm{L} + j\,Z_0\,\tan(\beta \ell)}{Z_0 + j\,Z_\mathrm{L}\tan(\beta \ell)}

여기서

\beta = \frac{\,2 \pi\,}{\lambda}

는 파수입니다.

\beta

를 계산할 때, 파장은 일반적으로 전송 선로 ''내부''에서 자유 공간에서와 다릅니다. 결과적으로, 이러한 계산을 수행할 때 전송 선로를 구성하는 재료의 속도 계수를 고려해야 합니다.

무손실 전송 선로의 길이 $\ell$ 을 통해 부하를 바라볼 때, 임피던스는 $\ell$ 이 증가함에 따라 변경되며, 이 임피던스 스미스 차트의 파란색 원을 따릅니다. (이 임피던스는 반사 계수로 특징지어지며, 이는 입사 전압으로 나눈 반사 전압입니다.) 차트 내부에 중심을 둔 파란색 원은 때때로 ''SWR 원'' (''정재파비'' 상수'정재파비')이라고도 합니다.

\beta l\approx n\pi

이고, n이 정수(전송 선로가 반파장의 정수배에 가깝다는 것을 나타냄)인 특수한 경우, 모든

l

에 대해 이 식은

Z_{in}=Z_L

이 되도록 부하 임피던스까지 감소합니다. 이것은

n=0

인 경우를 포함하며, 이 경우에는 전송 선로의 길이가 파장의 1/100 이하인 경우입니다. 이것은 전송 선로를 무시할 수 있음(즉, 배선으로 취급할 수 있음)을 나타냅니다.

또 다른 특수한 예로는 부하 임피던스가 전송 선로의 특성 임피던스와 같은 경우(즉, "정합 상태")가 있습니다. 이 경우, 전송 선로의 임피던스는 모든

l

과

\lambda

에 대해

Z_{in}=Z_0

로 감소합니다.

\beta

를 계산할 경우, 전송 선로 내의 파장은 진공 내의 파장과 다르며, 전송 선로 재료의 속도 상수가 계산에 필요합니다.

3. 3. 임피던스 정합

전송 선로를 통해 전력을 전송할 때, 가능한 한 많은 전력이 부하에 흡수되고 가능한 한 적은 전력이 소스로 반사되는 것이 바람직하다. 이를 위해 부하 임피던스를 전송 선로의 특성 임피던스(

Z_0

)와 같게 만드는 것을 임피던스 정합이라고 하며, 이 경우 전송 선로는 '정합'되었다고 한다.

만약 부하 임피던스가 전송 선로의 특성 임피던스와 일치하지 않으면, 전력 반사가 발생하여 전송 효율이 감소하고, 신호 왜곡이 발생할 수 있다.

임피던스 정합의 특수한 경우는 부하 임피던스가 선로의 특성 임피던스와 같을 때이며, 이때 임피던스는 선로의 특성 임피던스로 감소한다.

:

Z_\mathrm{in}=Z_\mathrm{L}=Z_0 \,

이는 모든

\ell

(거리) 및 모든

\lambda

(파장)에 대해 성립한다.

일반적인 전기 회로에서는 소자에 연결되는 배선의 길이를 무시할 수 있지만, 신호의 파장이 배선 길이에 비해 짧아지는 경우에는 배선 길이를 고려해야 하며, 이때 배선을 전송 선로로 취급해야 한다. 경험적으로 케이블이나 배선의 길이가 파장의 1/100을 초과하는 경우 전송 선로로 간주해야 하며, 그렇지 않으면 위상 지연, 반사, 간섭 등으로 인해 시스템 동작을 예측하기 어려워진다.

3. 4. 전력 손실

전송선에 공급되는 전력의 일부는 저항 때문에 손실된다. 이를 ''옴'' 손실 또는 ''저항'' 손실이라고 한다(옴 줄 참조). 고주파에서는 ''유전 손실''이라는 또 다른 효과가 중요해져 저항 손실을 증가시킨다. 유전 손실은 전송선 내부의 절연 재료가 교류 전기장으로부터 에너지를 흡수하여 열로 변환할 때 발생한다(유전 가열 참조). 전송선은 저항(R)과 인덕턴스(L)가 직렬로, 커패시턴스(C)와 컨덕턴스(G)가 병렬로 연결된 것으로 모델링할 수 있다. 저항과 컨덕턴스는 전송선의 손실에 기여한다.

전송선의 총 전력 손실은 종종 데시벨 미터(dB/m) 단위로 나타내며, 일반적으로 신호 주파수에 따라 달라진다. 제조사들은 다양한 주파수에서 dB/m 단위의 손실을 보여주는 차트를 제공하기도 한다. 3dB 손실은 대략 전력의 절반 감소에 해당한다.

4. 전송 선로의 종류

전송 선로는 구조, 사용 주파수, 용도에 따라 다양한 종류가 있다.

'''동축 케이블''': 전자기파를 케이블 내부로 제한하여 전달하며, 텔레비전 신호 전송 등에 사용된다.
'''평면 전송 선로''': 평평한 도체나 유전체 스트립을 사용하며, 마이크로스트립, 스트립라인, 코플래너 도파관 등이 있다.
'''평형 선로''': 접지에 대해 동일한 임피던스를 갖는 두 도체로 구성되며, 꼬임쌍선, 스타 쿼드, 트윈 리드, 레처 선 등이 있다.
'''단일 도선''': 과거 전신 전송에 사용되었으며, 현재는 단선 접지 귀환 방식의 전력 전송에 일부 사용된다.

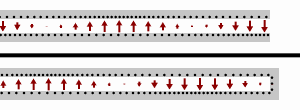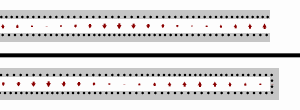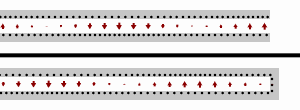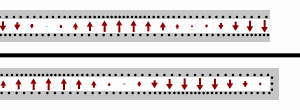
정재파는 개방 회로 부하(위쪽)와 단락 부하(아래쪽)가 있는 전송선로에 표시됩니다. 검은색 점은 전자를 나타내고 화살표는 전기장을 나타냅니다.

전송 선로 ''내부''에서 파장은 자유 공간에서와 다르다. 따라서

\beta

를 계산할 때 전송 선로 재료의 속도 계수를 고려해야 한다. 전송 선로 길이가 반 파장의 정수 배(

\beta\,\ell= n\,\pi

)가 되면 입력 임피던스는 부하 임피던스와 같아진다(

Z_\mathrm{in} = Z_\mathrm{L} \,

). 이는 전송 선로 길이가 파장에 비해 매우 작을 때도 마찬가지이며, 이 경우 전송 선로를 무시할 수 있다.

부하 임피던스가 선로의 특성 임피던스와 같으면, 즉 선로가 ''정합''되면, 임피던스는 선로의 특성 임피던스로 감소한다.

단락 부하 (

Z_\mathrm{L} = 0

)의 경우 입력 임피던스는 다음과 같다.

:

Z_\mathrm{in}(\ell) = j\,Z_0\,\tan(\beta \ell). \,

개방 부하 (

Z_\mathrm{L} = \infty

)의 경우 입력 임피던스는 다음과 같다.

:

Z_\mathrm{in}(\ell) = -j\,Z_0 \cot(\beta \ell). \,

4. 1. 동축 케이블

전자기파를 케이블 내부로 제한하여 전달하는 동축선로(동축 케이블)는 구부리거나 비틀어도 특성 저하가 적고, 도체로 고정해도 불필요한 전류 유도가 발생하지 않는 장점이 있다.

수 기가헤르츠(GHz)까지의 무선 주파수에서는 횡파 전기 및 자기 모드(TEM)로 전파된다. 즉, 전기장은 방사형, 자기장은 원주 방향으로 전파 방향에 수직이다. 그러나 파장이 케이블 원주보다 짧은 고주파에서는 횡전기(TE) 및 횡자기(TM) 도파관 모드가 발생할 수 있다. 케이블 구조의 불규칙성은 전력이 한 모드에서 다른 모드로 전달되게 할 수 있다.

동축 케이블은 주로 텔레비전 및 기타 신호 전송에 사용되며, 대역폭은 수 메가헤르츠(MHz)이다. 20세기 중반에는 장거리 전화 연결에도 사용되었다.^[1] 동축 케이블(동축 선로)은 중심 도체와 차폐 금속으로 구성되어, 케이블 내부로 전자기파를 전달한다. 에너지 전달은 도체 사이의 유전체에서 이루어진다.

수 GHz의 고주파에서는 TEM 모드로 전파된다. 전계와 자계는 모두 진행 방향에 수직이다. 그러나 차단 주파수 이상에서는 도파관으로 기능하며, TE 모드, TM 모드, 혼성 모드 간 특성이 변화한다. 동축 케이블은 마이크로파 영역에서도 사용 가능하지만, 이 용도로 만들어진 도파관만큼 성능이 좋지는 않다.

4. 2. 평면 전송 선로

평면 전송 선로는 평평하고 리본 형태의 전기 도체나 유전체 스트립을 사용하는 전송 선로이다. 마이크로파 주파수에서 작동하는 인쇄 회로 및 집적 회로의 부품을 상호 연결하는 데 사용된다.

대표적인 평면 전송 선로로는 마이크로스트립, 스트립라인, 코플래너 도파관 등이 있다.

'''마이크로스트립'''은 접지면과 평행한 얇고 평평한 도체를 사용하며, 주로 인쇄 회로 기판(PCB) 형태로 제작된다.
'''스트립라인'''은 두 접지면 사이에 평평한 금속 스트립이 있는 구조이다.
'''코플래너 도파관'''은 중심 도체와 양쪽의 외부 도체가 같은 평면에 있는 형태이다.

4. 2. 1. 마이크로스트립

마이크로스트립 선로는 접지면에 평행한 얇고 평평한 유전체(유전 물질)를 사용하는 전송 선로이다. 마이크로스트립 회로는 PCB 등의 기판 한 면에 금속 배선을 만들고, 반대쪽 면 전체를 접지면으로 한다. 배선의 두께, 유전체의 두께와 유전율이 특성 임피던스를 결정한다.^[1]

마이크로스트립은 인쇄 회로 기판 (PCB) 또는 세라믹 기판의 한 쪽에 구리 스트립을 배치하고 반대쪽은 연속적인 접지면으로 구성하여 만들 수 있다. 스트립의 너비, 절연층 (PCB 또는 세라믹)의 두께 및 절연층의 유전율은 특성 임피던스를 결정한다. 마이크로스트립은 개방형 구조인 반면 동축 케이블은 폐쇄형 구조이다.^[1]

4. 2. 2. 스트립라인

스트립라인 회로는 두 개의 평행한 접지면 사이에 끼워진 평평한 금속 스트립을 사용한다. 기판의 절연 재료는 유전체를 형성한다. 스트립의 폭, 기판의 두께 및 기판의 상대 유전율은 전송선인 스트립의 특성 임피던스를 결정한다.^[1]

4. 2. 3. 코플래너 도파관

코플래너 도파관은 중심 스트립과 인접한 두 개의 외부 도체로 구성되며, 이 세 구조 모두 동일한 절연 기판 위에 증착된 평평한 구조이므로 동일 평면("coplanar")에 위치한다. 중심 도체의 너비, 내부 및 외부 도체 사이의 거리, 그리고 기판의 상대 유전율은 코플래너 전송 선로의 특성 임피던스를 결정한다.^[1]

4. 3. 평형 선로

평형 회선은 동일한 유형의 두 개의 도체로 구성되며, 접지 및 다른 회로에 대해 동일한 임피던스를 갖는 전송 선로이다. 평형 회선에는 꼬임쌍선, 스타 쿼드, 트윈 리드, 레처 선 등 다양한 형식이 있다.

4. 3. 1. 꼬임쌍선

꼬임쌍선은 일반적으로 육상 전화 통신에 사용된다. 이러한 케이블에서는 여러 쌍의 전선이 하나의 케이블로 묶여 있으며, 그 수는 두 쌍에서 수천 쌍에 이른다.^[22] 이 형식은 건물 내부의 데이터 네트워크 분배에도 사용되지만, 전송 선로의 매개변수가 엄격하게 제어되기 때문에 케이블의 가격이 더 비싸다.

4. 3. 2. 스타 쿼드

스타 쿼드는 4개의 도체가 케이블 축을 중심으로 꼬여 있는 4도체 케이블이다. 이는 4선식 전화 및 기타 통신 응용 프로그램과 같은 두 개의 회선에 사용되기도 하고, 오디오 응용 프로그램 및 2선식 전화와 같은 단일 평형 회선에 사용되기도 한다. 두 개의 회선에 사용되는 경우, 각 쌍은 인접하지 않은 두 개의 도체를 사용하며, 누화는 두 개의 별도 연선쌍이 있는 케이블에 비해 감소한다. 단일 평형 회선으로 사용되는 경우에는 두 개의 인접하지 않은 도체는 케이블의 양쪽 끝에서 함께 종단되고 다른 두 개의 도체도 함께 종단된다. 이때 케이블에 의해 수집된 자기 간섭은 사실상 완벽한 공통 모드 신호로 도착하며, 이는 결합 변압기를 통해 쉽게 제거할 수 있다.

꼬임, 평형 신호 전송 및 쿼드러플 패턴의 결합된 이점은 특히 마이크 케이블과 같이 신호 레벨이 낮은 응용 프로그램에서 전원 케이블에 매우 가깝게 설치된 경우에도 뛰어난 노이즈 내성을 제공한다.^[23]^[24] 하지만, 스타 쿼드는 두 개의 도체를 결합하여 일반적으로 유사한 2도체 연선 및 차폐 오디오 케이블의 두 배의 정전 용량을 갖는다는 단점이 있다. 높은 정전 용량은 거리가 증가함에 따라 왜곡이 증가하고 고주파수 손실이 커지는 원인이 된다.^[25]^[26]

4. 3. 3. 트윈 리드

트윈 리드는 연속적인 절연체로 서로 떨어져 유지되는 한 쌍의 도체로 구성된다. 도체를 알려진 거리만큼 떨어뜨려 놓음으로써 기하학적 구조가 고정되고 선로 특성이 안정적으로 일관성을 유지한다. 트윈 리드의 특성 임피던스는 동축 케이블보다 일반적으로 더 높기 때문에 감소된 전류로 인해 저항 손실이 줄어들어 동축 케이블보다 손실이 적다. 그러나 간섭에 더 취약하다.^[1]

4. 3. 4. 레처 선

레처 선은 UHF에서 공진 회로를 생성하는 데 사용되는 평행 도체 형태이다. 이는 집중 소자 (HF/VHF에서 사용)와 공진 공동 (UHF/SHF에서 사용) 사이의 간격을 채워주는 편리하고 실용적인 형식이다. 레처 선은 HF부터 VHF 주파수 대역에서 집중 정수 소자를 이용하거나, VHF부터 SHF 주파수 대역에서 기본적인 공동 공진기를 이용할 때 사용된다.

4. 4. 단일 도선

불평형 회선은 과거에 전신 전송에 많이 사용되었지만, 현재는 이러한 형태의 통신은 거의 사용되지 않는다. 연선과 유사하게 케이블은 여러 개의 코어가 같은 케이블에 묶여 있지만, 회로당 하나의 도체만 제공되며 꼬임은 없다. 동일한 경로의 모든 회로는 반환 전류에 대한 공통 경로(어스 리턴)를 사용한다. 많은 지역에서 단선 어스 리턴 방식의 전력 전송이 사용된다.

5. 전송 선로의 응용

전송 선로는 단순히 신호를 전달하는 것 외에 여러 가지 회로 소자로도 활용될 수 있다.

전송 선로를 사용하면 임피던스 정합 회로, 분산 소자 필터, 전력 분배기, 지향성 결합기 등 다양한 회로를 구현할 수 있다. 고주파에서는 집중 소자 모델에서 인덕터와 커패시터에 기생 반응 효과가 발생하여 사용에 제한이 생긴다. 이러한 이유로 리처드 변환을 통해 고주파에서 인덕터와 커패시터의 특성을 전송 선로로 근사화하여 집중 소자 대신 전송 선로를 사용하기도 한다.^[28]^[29]^[30] 전송 선로를 활용한 고급 설계를 위해, 멀티모드 고주파 인덕터 모델링과 같이 더 정확한 방법도 존재한다.^[31]

5. 1. 신호 전송

일반적인 전기 케이블은 낮은 주파수의 교류 전류 및 오디오 신호를 전달하는 데는 충분하지만, 약 30kHz 이상의 무선 주파수 전류를 전달하는 데는 적합하지 않다.^[1] 이는 에너지가 전파 형태로 케이블에서 방사되어 전력 손실을 유발하고, 케이블의 불연속성에서 반사되어 신호가 목적지에 도달하는 것을 방해하기 때문이다.^[1]^[2]

전송 선로는 이러한 문제를 해결하기 위해 특수 구조와 임피던스 정합을 사용하여 최소한의 반사와 전력 손실로 전자기 신호를 전달한다. 대부분의 전송 선로는 길이에 따라 균일한 단면 치수를 가지므로 균일한 전기 임피던스(특성 임피던스)를 갖는다.^[2]^[3]^[4] 전송 선로의 유형에는 평행선 (래더 라인, 꼬인 쌍), 동축 케이블, 스트립 라인, 마이크로스트립과 같은 평면 전송선이 있다.^[5]^[6]

전송 선로는 전송되는 주파수의 파장이 케이블 길이에 비해 충분히 짧아질 때 필요해진다. 마이크로파 이상의 주파수에서는 전송 선로의 전력 손실이 커져 도파관이 대신 사용된다.^[1]^[6]

동축 케이블은 전자기파를 케이블 내부로 제한하여 구부리거나 비틀어도 성능 저하가 적고, 전도성 지지대에 고정할 수 있다. 주로 텔레비전 및 기타 신호 전송에 사용되며, 20세기 중반에는 장거리 전화 연결에도 사용되었다.

꼬임쌍선은 일반적으로 육상 전화 통신에 사용되며, 건물 내부의 데이터 네트워크 분배에도 사용된다.

스타 쿼드 케이블은 4개의 도체가 케이블 축을 중심으로 꼬여 있는 케이블로, 누화 감소 및 노이즈 내성이 뛰어나 마이크 케이블과 같이 신호 레벨이 낮은 응용 프로그램에 유용하다.

전송 선로는 장거리 또는 단거리에서 고주파 신호를 효율적으로 전송하는 데 널리 사용되며, TV 또는 라디오 안테나에서 수신기로 연결되는 다운 리드가 대표적인 예이다.

5. 2. 분산 소자 회로

전송 선로를 사용하면 임피던스 정합 회로, 분산 소자 필터, 전력 분배기, 지향성 결합기 등 다양한 회로를 구현할 수 있다.

고주파에서는 집중 소자 모델에서 인덕터와 커패시터에 기생 반응 효과가 발생하여 사용에 제한이 생긴다.^[28] 이러한 이유로, 리처드 변환을 통해 고주파에서 인덕터와 커패시터의 특성을 전송 선로로 근사화하여 집중 소자 대신 전송 선로를 사용하기도 한다.^[29]^[30]

전송 선로를 활용한 고급 설계를 위해, 멀티모드 고주파 인덕터 모델링과 같이 더 정확한 방법도 존재한다.^[31]

5. 2. 1. 스텝 전송 선로

스텝 전송 선로는 광대역 임피던스 정합에 사용된다. 이는 각각의 개별 요소의 특성 임피던스가

Z_\mathrm{0,i}

인 여러 개의 직렬로 연결된 전송 선로 세그먼트로 간주할 수 있다.^[27] 입력 임피던스는 체인 관계를 반복적으로 적용하여 얻을 수 있다.

:

Z_\mathrm{i+1} = Z_\mathrm{0,i}\,\frac{\,Z_\mathrm{i} + j\,Z_\mathrm{0,i}\,\tan(\beta_\mathrm{i} \ell_\mathrm{i})\,}{Z_\mathrm{0,i} + j\,Z_\mathrm{i}\,\tan(\beta_\mathrm{i} \ell_\mathrm{i})}\,

여기서

\beta_\mathrm{i}

는

\mathrm{i}

번째 전송 선로 세그먼트의 파수이고,

\ell_\mathrm{i}

는 이 세그먼트의 길이이며,

Z_\mathrm{i}

는

\mathrm{i}

번째 세그먼트에 부하가 걸리는 프론트 엔드 임피던스이다.

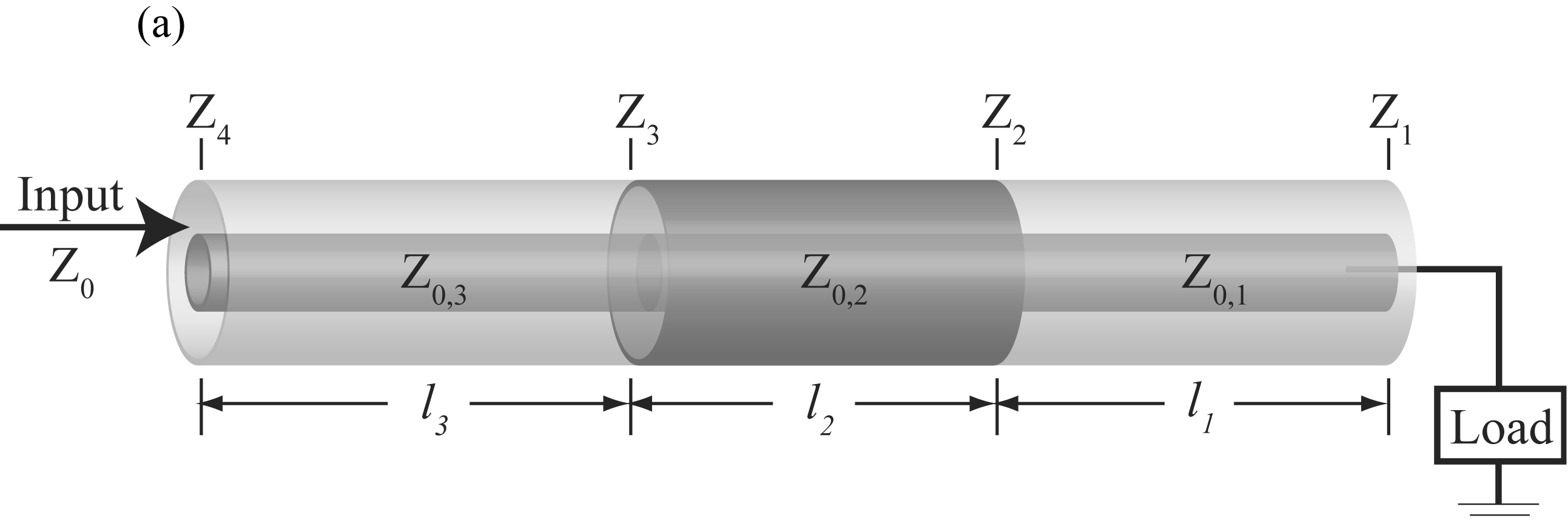
각 전송 선로 세그먼트의 특성 임피던스

Z_\mathrm{0,i}

는 종종 입력 케이블(위 다이어그램의 왼쪽 측면에

Z_0

로 표시된 화살표로만 표시됨)의 임피던스

Z_0

와 다르기 때문에, 임피던스 변환 원은 일반적으로

Z_0

에 대해 정규화된 임피던스 표현을 갖는 스미스 차트의

x

축을 따라 중심에서 벗어나게 된다.

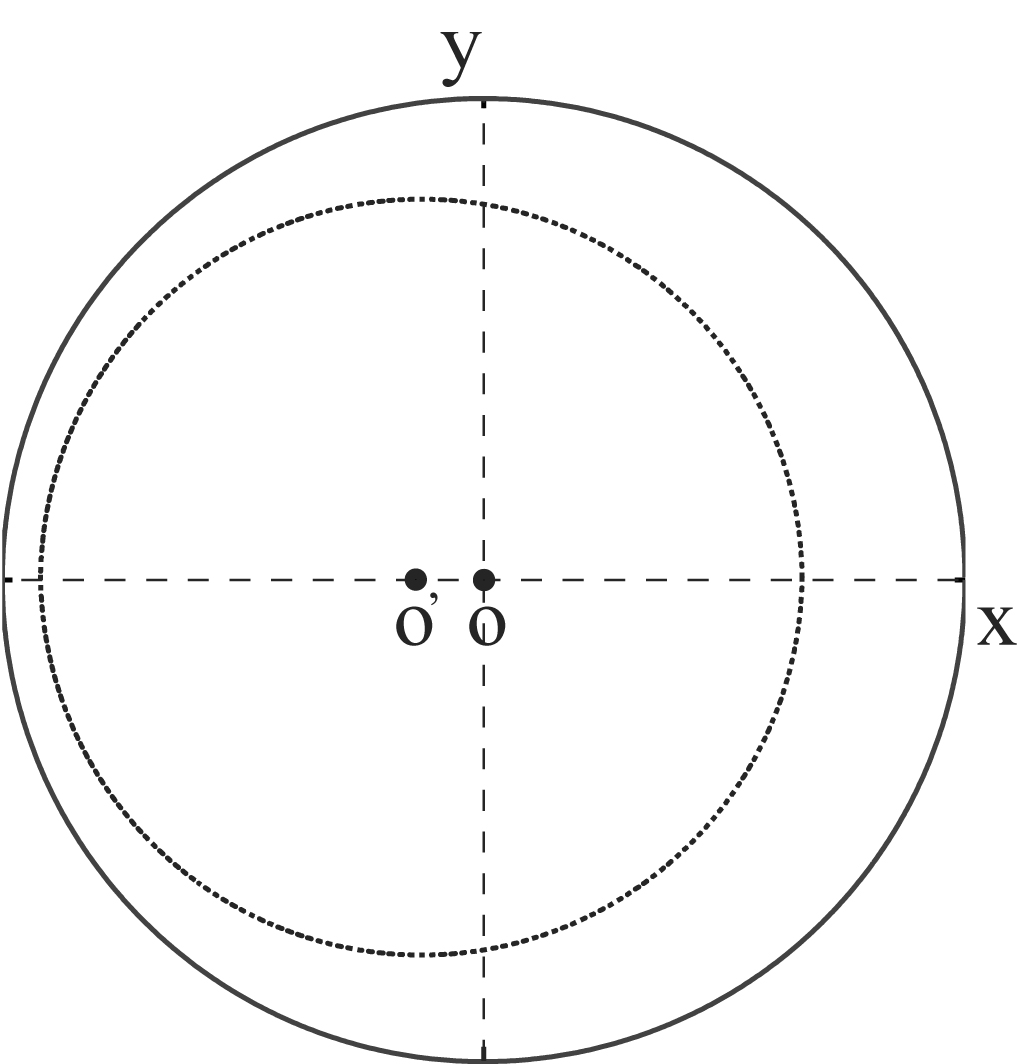
특성 임피던스 $Z_\mathrm{0,i}$ 가 입력 케이블 $Z_0$ 의 임피던스보다 작은 전송 선로를 따라 임피던스 변환 원. 그 결과 임피던스 곡선은 $-x$ 축으로 중심에서 벗어난다. 반대로, $Z_\mathrm{0,i} > Z_0$ 인 경우, 임피던스 곡선은 $+x$ 축으로 중심에서 벗어나야 한다.

5. 2. 2. 스터브 필터

단락 또는 개방 회로 전송 선로가 A 지점에서 B 지점으로 신호를 전송하는 데 사용되는 선로와 병렬로 연결되면 필터 역할을 한다. 스텁을 만드는 방법은 조악한 주파수 측정을 위해 레처 선을 사용하는 방법과 유사하지만 '역방향으로 작동'한다. RSGB의 무선 통신 핸드북에서 권장하는 한 가지 방법은 안테나에서 신호를 전달하는 피더와 병렬로 연결된 개방 회로 전송 선로를 사용하는 것이다. 전송 선로의 자유 단을 절단하여 수신기에서 관찰되는 신호 강도의 최소값을 찾는다. 이 단계에서 스텁 필터는 이 주파수와 홀수 고조파를 거부하지만,^[1] 스텁의 자유 단이 단락되면 스텁은 짝수 고조파를 거부하는 필터가 된다.^[1]

다중 스텁을 사용하여 광대역 필터를 얻을 수 있다. 그러나 이것은 다소 구식 기술이다. 병렬 선 공진기와 같은 다른 방법을 사용하여 훨씬 더 소형 필터를 만들 수 있다.

5. 3. 펄스 발생

전송 선로는 펄스 발생기로 사용된다. 전송 선로를 충전한 다음 저항성 부하로 방전시키면 선로의 전기적 길이의 2배에 해당하는 직사각형 펄스를 얻을 수 있지만, 전압은 절반으로 줄어든다.^[1] 블룸레인 전송 선로는 이러한 제한을 극복하는 관련 펄스 형성 장치이다.^[1] 이것들은 때때로 레이더 송신기 및 기타 장치의 펄스 전력 공급원으로 사용된다.^[1]

6. 음향 전송 선로

음파의 전파 이론은 수학적으로 전자기파의 전파 이론과 매우 유사하므로, 음파를 전달하는 구조물을 구축하기 위해 전송선 이론의 기술을 사용하며, 이를 음향 전송선이라고 한다.

7. 4단자 모델

전송 선로는 2포트 네트워크(4단자 회로망)로 모델링될 수 있다. 가장 간단한 경우, 회로는 선형이며 두 포트는 상호 교환 가능하다. 전송 선로가 균일하면, 그 동작은 특성 임피던스(Z₀)와 전파 지연 ( $\tau_p$ )으로 설명된다. 전력을 부하에 최대한 전달하고 반사를 최소화하려면 부하 임피던스를 Z₀와 같게 해야 하며, 이를 임피던스 정합이라고 한다.

전송 선로의 시뮬레이션에는 어드미턴스 파라미터(Y 행렬), 임피던스 파라미터(Z 행렬), 산란 파라미터(S 행렬)가 활용된다.

어드미턴스 파라미터(Y 행렬): 전송 선로의 한 포트에 전압을 가하고 다른 쪽 끝을 접지시킨 후, 각 포트로 흐르는 전류를 측정하여 어드미턴스를 계산한다.^[8]^[9] 전송 선로는 수동적이고 대칭적인 장치이므로 Y₁₂ = Y₂₁, Y₁₁ = Y₂₂이다.

무손실 및 손실 전송 선로에 대한 Y 파라미터 행렬은 다음과 같다.^[10]^[11]

:

Y_{\text{Lossless}}=\begin{bmatrix}\frac{-jcot(\beta l)}{Z_o} & \frac{jcsc(\beta l)}{Z_o} \\\frac{jcsc(\beta l)}{Z_o}  & \frac{-jcot(\beta l)}{Z_o}\end{bmatrix}\text{    }Y_{\text{Lossy}}=\begin{bmatrix}\frac{coth(\gamma l)}{Z_o} & \frac{-csch(\gamma l)}{Z_o} \\\frac{-csch(\gamma l)}{Z_o} & \frac{coth(\gamma l)}{Z_o}\end{bmatrix}

임피던스 파라미터(Z 행렬): 다른 포트가 개방된 상태에서 전송 선로의 한 포트에 전류를 가하고 각 포트에서 발생하는 전압을 측정한다.^[8]^[9] 전송 선로는 수동적이고 대칭적인 장치이므로 Z₁₂ = Z₂₁, Z₁₁ = Z₂₂이다. Y 행렬과 Z 행렬은 서로 역행렬 관계이다.^[12]

무손실 및 유손실 전송 선로의 경우 Z 파라미터 행렬은 다음과 같다:^[10]^[11]

:

Z_{\text{Lossless}}=\begin{bmatrix}

jZ_ocot(\beta l) & -jZ_ocsc(\beta l) \\
jZ_ocsc(\beta l) & -jZ_ocot(\beta l)

\end{bmatrix}\text{ }Z_{\text{Lossy}}=\begin{bmatrix}Z_ocoth(\gamma l) & Z_ocsch(\gamma l) \\Z_ocsch(\gamma l) & Z_ocoth(\gamma l)\end{bmatrix}

산란 파라미터(S 행렬): 각 종단에서 정합된 부하를 갖는 전송 선로의 전기적 특성을 모델링한다.^[10]

무손실 및 손실 전송 선로에 대한 S 파라미터 행렬은 다음과 같다.^[13]^[14]

:

S_{\text{Lossless}}=\begin{bmatrix}\frac{(Z_o^2-Z_p^2)sin(\beta l)}{(Z_o^2+Z_p^2)sin(\beta l)-j2Z_oZ_pcos(\beta l)}&\frac{2Z_oZ_p}{j(Z_o^2+Z_p^2)sin(\beta l)+2Z_oZ_pcos(\beta l)}\\\frac{2Z_oZ_p}{j(Z_o^2+Z_p^2)sin(\beta l)+2Z_oZ_pcos(\beta l)}&\frac{(Z_o^2-Z_p^2)sin(\beta l)}{(Z_o^2+Z_p^2)sin(\beta l)-j2Z_oZ_pcos(\beta l)}\end{bmatrix}\text{    }S_{\text{Lossy}}=\begin{bmatrix}\frac{(Z_o^2-Z_p^2)sinh(\gamma l)}{(Z_o^2+Z_p^2)sinh(\gamma l)+2Z_oZ_pcosh(\gamma l)}&\frac{2Z_oZ_p}{(Z_o^2+Z_p^2)sinh(\gamma l)+2Z_oZ_pcosh(\gamma l)}\\\frac{2Z_oZ_p}{(Z_o^2+Z_p^2)sinh(\gamma l)+2Z_oZ_pcosh(\gamma l)}&\frac{(Z_o^2-Z_p^2)sinh(\gamma l)}{(Z_o^2+Z_p^2)sinh(\gamma l)+2Z_oZ_pcosh(\gamma l)}\end{bmatrix}

8. 결합 전송 선로

전송 선로는 서로 가까이 있을 때 전기적으로 영향을 주고받을 수 있다. 예를 들어, 두 개의 마이크로스트립 선로가 서로 가까이 있는 경우가 이에 해당한다. 이렇게 서로 연결된 전송 선로를 결합된 전송 선로라고 한다.

결합된 전송 선로는 짝수 모드 및 홀수 모드 분석으로 특징을 알 수 있다. 짝수 모드는 두 도체를 같은 크기와 위상을 가진 신호로 여기는 것이고, 홀수 모드는 크기는 같지만 부호가 반대인 신호로 여기는 것이다. 짝수 모드와 홀수 모드는 각각 고유한 특성 임피던스(Z_oe, Z_oo)와 위상 상수( $\beta_e\text{, }\beta_o$ )를 가진다. 손실이 있는 결합된 전송 선로는 고유한 짝수 모드 및 홀수 모드 감쇠 상수( $\alpha_e\text{, }\alpha_o$ )를 가지며, 이는 짝수 모드 및 홀수 모드 전파 상수( $\gamma_e\text{, }\gamma_o$ )로 이어진다.

결합 전송 선로는 입력 포트 1과 2, 출력 포트 3과 4를 사용하여 앞 문단에서 정의된 짝수 및 홀수 모드 전송 선로 매개변수를 사용하여 모델링할 수 있다.^[21]

$\begin{align}Y &=\begin{bmatrix}y11 & y12 & y13 & y14 \\y21 & y22 & y23 & y24 \\y31 & y32 & y33 & y34 \\y41 & y42 & y43 & y44 \\\end{bmatrix}\\Z &= [Y]^{-1} \\&\\\text{여기서:}& \\\text{무손실 결합 선로의 경우:}& \\y11 &= y22 = y33 = y44 = \frac{-j}{2} \bigg(\frac{cot(\beta_e l)}{Z_{oe}}+\frac{cot(\beta_o l)}{Z_{oo}}\bigg) \\y12 &= y22 = y34 = y43 = \frac{-j}{2} \bigg(\frac{cot(\beta_e l)}{Z_{oe}}-\frac{cot(\beta_o l)}{Z_{oo}}\bigg) \\y13 &= y31 = y24 = y42 = \frac{j}{2} \bigg(\frac{csc(\beta_e l)}{Z_{oe}}+\frac{csc(\beta_o l)}{Z_{oo}}\bigg) \\y14 &= y41 = y23 = y32 = \frac{j}{2} \bigg(\frac{csc(\beta_e l)}{Z_{oe}}-\frac{csc(\beta_o l)}{Z_{oo}}\bigg) \\\text{유손실 결합 선로의 경우:}& \\y11 &= y22 = y33 = y44 = \frac{1}{2} \bigg(\frac{coth(\gamma_e l)}{Z_{oe}}+\frac{coth(\gamma_o l)}{Z_{oo}}\bigg) \\y12 &= y22 = y34 = y43 = \frac{1}{2} \bigg(\frac{coth(\gamma_e l)}{Z_{oe}}-\frac{coth(\gamma_o l)}{Z_{oo}}\bigg) \\y13 &= y31 = y24 = y42 = \frac{-1}{2} \bigg(\frac{csch(\gamma_e l)}{Z_{oe}}+\frac{csch(\gamma_o l)}{Z_{oo}}\bigg) \\y14 &= y41 = y23 = y32 = \frac{-1}{2} \bigg(\frac{csch(\gamma_e l)}{Z_{oe}}-\frac{csch(\gamma_o l)}{Z_{oo}}\bigg) \\\end{align}$

참조

_[1] 서적 CWDP Certified Wireless Design Professional Official Study Guide: Exam PW0-250 https://books.google[...] John Wiley & Sons
_[2] 서적 High-Performance Energy-Efficient Microprocessor Design https://books.google[...] Springer Science & Business Media
_[3] 서적 Electromagnetic Field Theory Fundamentals, 2nd Ed. https://books.google[...] Cambridge Univ. Press
_[4] 서적 Electromagnetics Explained: A Handbook for Wireless/ RF, EMC, and High-Speed Electronics https://archive.org/[...] Newnes
_[5] 서적 Microwave & Wireless Communications Technology https://books.google[...] Newnes
_[6] 서적 Radio Engineering for Wireless Communication and Sensor Applications https://books.google[...] Artech House
_[7] 서적 The Evolution of Electrical Engineering IEEE Press
_[8] 서적 Basic Linear Networks for Electrical and Electronics Engineer https://archive.org/[...] Holt, Rinehart, and Winston 1970
_[9] 서적 Microwave Engineering John Wiley & Sones, Inc. 2013
_[10] 서적 Microwave Filters, Impudence-Matching Networks, and Coupling Structures https://archive.org/[...] Artech House, Inc. 1984
_[11] 웹사이트 Transmission Line https://qucs.sourcef[...] 2013-11-22
_[12] 서적 Microwave Engineering https://archive.org/[...] John Wiley & Sons, Inc. 1998
_[13] 웹사이트 Microsoft Word - dissertation_def_rev.doc - ch_2.pdf http://weewave.mer.u[...] 2015-12-14
_[14] 웹사이트 2.3: Scattering Parameters - Engineering LibreTexts https://eng.libretex[...] 2020-10-21
_[15] 서적 Microwave Engineering https://archive.org/[...] John Wiley and Sons, Inc.
_[16] 서적 Microwave filters, impedance-matching networks, and coupling structures https://archive.org/[...] Artech House Books 1964
_[17] 서적 HF Filter Design and Computer Simulation https://archive.org/[...] McGraw-Hill 1995
_[18] 웹사이트 5.6: Formulas for Impedance of Coupled Microstrip Lines https://eng.libretex[...] 2022-10-21
_[19] 웹사이트 Parallel coupled microstrip lines https://qucs.sourcef[...] 2013-11-22
_[20] 서적 Microstrip Lines and Slotlines https://ieeexplore.i[...] Artech House 2013
_[21] 웹사이트 5.9: Models of Parallel Coupled Lines - Engineering LibreTexts https://eng.libretex[...] 2020-10-21
_[22] 간행물 Design and engineering of intelligent communication systems Springer
_[23] Webarchive Evaluating Microphone Cable Performance & Specifications http://www.canare.co[...] 2016-05-09
_[24] Webarchive How Starquad Works http://www.belden.co[...] 2016-11-12
_[25] 서적 Audio/Video Cable Installer's Pocket Guide McGraw-Hill
_[26] 서적 Eargle's The Microphone Book: From Mono to Stereo to Surround – A Guide to Microphone Design and Application https://archive.org/[...] Focal Press
_[27] 논문 Impedance matching with an adjustable segmented transmission line
_[28] 웹사이트 Microwaves101 {{!}} Parasitics https://www.microwav[...] 2024-04-02
_[29] 웹사이트 2.12: Richards's Transformation - Engineering LibreTexts https://eng.libretex[...] 2021-02-01
_[30] 서적 HF Filter Design and Computer Simulation https://archive.org/[...] McGraw-Hill, Inc. 1995
_[31] 간행물 A Multimode High-Frequency Inductor Model Noble Publishing, Atlanta, Georgia 1997-11-01
_[32] 간행물 The Evolution of Electrical Engineering IEEE Press, Piscataway, New Jersey USA

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com