수심 (기하학)

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
- 2.1. 증명
3. 성질
4. 좌표
- 4.1. 직교 좌표
- 4.2. 무게중심 좌표
참조

1. 개요

수심은 삼각형의 각 꼭짓점에서 대변에 내린 수선이 만나는 점이다. 수심은 삼각형의 종류에 따라 위치가 다르며, 예각삼각형의 내부에, 직각삼각형의 직각 꼭짓점에, 둔각삼각형의 외부에 위치한다. 수심은 무게중심, 외심과 오일러선 위에 있으며, 구점원의 중심과 관련이 있다. 또한, 수심은 수심 삼각형, 방심 삼각형, 테일러 원, 드로츠파르니 직선 등 다양한 기하학적 개념과 연결된다.

더 읽어볼만한 페이지

삼각형의 중심 - 슈피커 중심
슈피커 중심은 삼각형의 중점 삼각형의 내접원 중심으로, 중점 삼각형의 내심이자 세 클리버의 교차점이며, 삼선좌표와 무게중심 좌표로 표현되고, 내심, 무게중심, 나겔 점과 공선 관계에 있으며, 키퍼트 쌍곡선 위에 있다.

수심 (기하학)
정의
정의	삼각형의 세 높이가 교차하는 점이다.
위치	예각삼각형: 삼각형 내부에 위치한다. 직각삼각형: 직각 꼭짓점에 위치한다. 둔각삼각형: 삼각형 외부에 위치한다.
명칭
한국어	수심(垂心)
한자	垂(드리울 수), 心(마음 심)
영어	Orthocenter (오쏘센터)
어원	그리스어 ὀρθός (orthos, "똑바른, 직각의")
성질
오일러 직선	수심은 외심, 무게중심과 함께 오일러 직선 위에 있다.
페르마 점	삼각형의 각 꼭짓점에서 수심까지의 거리가 최소가 되는 점은 페르마 점이다.
수심의 위치	예각삼각형의 수심은 삼각형 내부에 위치한다. 직각삼각형의 수심은 직각 꼭짓점에 위치한다. 둔각삼각형의 수심은 삼각형 외부에 위치한다.
추가 성질	삼각형의 세 꼭짓점과 수심은 정심계를 이룬다. 즉, 각 점은 나머지 세 점으로 만들어진 삼각형의 수심이다.

2. 정의

삼각형 $ABC$ 의 꼭짓점 $A$ , $B$ , $C$ 에서 마주보는 변 $BC$ , $AC$ , $AB$ 에 내린 수선은 한 점에서 만난다. 이 점을 삼각형 $ABC$ 의 '''수심'''( $H$ )이라고 정의한다.

수심의 삼선좌표^[3]는 다음과 같다.

: $\sec A:\sec B:\sec C = \cos A-\sin B\sin C:\cos B-\sin C\sin A:\cos C-\sin A\sin B$

수심의 바리 중심 좌표는 다음과 같다.

: $(a^2+b^2-c^2)(a^2-b^2+c^2):(a^2+b^2-c^2)(-a^2+b^2+c^2):(a^2-b^2+c^2)(-a^2+b^2+c^2) = \tan A:\tan B:\tan C$

바리 중심 좌표는 삼각형 내부의 점에 대해서는 모두 양수이지만, 외부의 점에 대해서는 적어도 하나는 음수이며, 꼭짓점의 경우에는 두 개의 바리 중심 좌표가 0이다. 따라서 수심의 바리 중심 좌표를 통해 수심이 예각삼각형의 내부에, 직각삼각형의 직각 꼭짓점에, 둔각삼각형의 외부에 있음을 알 수 있다.

복소 평면에서 점 $A$ , $B$ , $C$ 가 복소수 $z_A$ , $z_B$ , $z_C$ 를 나타내고, 삼각형 $ABC$ 의 외접원의 중심이 평면의 원점에 위치한다고 가정하면, 복소수

: $z_H = z_A + z_B + z_C$

는 점 $H$ 로 표시되며, 이는 삼각형 $ABC$ 의 수심이다.^[4] 이를 통해, 유클리드 벡터를 이용하여 수심 $H$ 의 다음 특성을 쉽게 설정할 수 있다.

: $\vec{OH} = \sum_{\scriptstyle\rm cyclic} \vec{OA}, \qquad 2 \cdot \vec{HO} = \sum_{\scriptstyle\rm cyclic} \vec{HA}$

위의 벡터 항등식 중 첫 번째는 제임스 조셉 실베스터가 제안한 '실베스터의 문제'로도 알려져 있다.^[5]

2. 1. 증명

삼각형의 세 꼭짓점에서 각 대변에 내린 수선은 한 점에서 만나며, 이 점을 수심이라고 한다. 수심의 존재성에 대한 증명은 다음과 같다.

'''원주각을 통한 증명'''

삼각형

ABC

의 꼭짓점

B

,

C

에서 대변에 내린 수선의 발을 각각

H_B

,

H_C

라 하고, 두 수선

BH_B

,

CH_C

의 교점을

H

라고 하자. 그러면

:

\angle AH_BH=\angle AH_CH=\angle BH_BC=\angle BH_CC=90^\circ

이므로,

H_B

와

H_C

는 선분

AH

를 지름으로 하는 원 위의 점이자 선분

BC

를 지름으로 하는 원 위의 점이다. 따라서 점

A

,

H_B

,

H

,

H_C

는 한 원 위에 있으며, 점

B

,

C

,

H_B

,

H_C

역시 한 원 위에 있다. 원주각의 성질에 따라

:

\angle HAB=\angle HH_BH_C=\angle BCH_C

이다. 따라서

:

\angle HAB+\angle ABC=\angle BCH_C+\angle ABC=\angle AH_CC=90^\circ

이므로,

AH

는

BC

의 수선이다.

'''외심과 무게 중심을 통한 증명'''^[34]

정삼각형의 각 꼭짓점을 지나는 대변의 수선은 대변의 수직 이등분선과 일치하며, 삼각형의 세 변의 수직 이등분선은 외심에서 만나므로, 정삼각형의 각 꼭짓점을 지나는 대변의 수선은 한 점에서 만난다. 정삼각형이 아닌 삼각형

ABC

의 외심을

O

, 무게 중심을

G

, 변

BC

의 중점을

M_A

라고 하자. 그러면

O\ne G

이다. 유향 선분

OG

의 연장선 위에서

GH=2OG

인 점

H

를 잡자. 그러면

G

는 선분

AM_A

위의 점이며

AG=2GM_A

,

\angle AGH=\angle M_AGO

이므로, 삼각형

AGH

와

M_AGO

는 닮음이다. 특히

\angle GAH=\angle GM_AO

이므로

AH

와

OM_A

는 평행하며,

OM_A

는

BC

의 수선이므로

AH

역시 변

BC

의 수선이다. 마찬가지로

BH

,

CH

는 각각 변

AC

,

AB

의 수선이다.

'''근축을 통한 증명'''^[33]

삼각형

ABC

의 꼭짓점

A

,

B

,

C

에서 대변에 내린 수선의 발을 각각

H_A

,

H_B

,

H_C

라고 하자. 그러면 변

AB

,

AC

를 지름으로 하는 두 원은 두 점

A

,

H_A

에서 만나므로 두 원의 근축은 직선

AH_A

이다. 마찬가지로, 변

AB

와

BC

를 지름으로 하는 두 원의 근축은 직선

BH_B

이며, 변

AC

,

BC

를 지름으로 하는 두 원의 근축은 직선

CH_C

이다. 따라서 세 직선

AH_A

,

BH_B

,

CH_C

는 세 원의 근심에서 만난다.

'''체바 정리를 통한 증명'''

삼각형

ABC

의 꼭짓점

A

,

B

,

C

에서 대변에 내린 수선의 발을 각각

H_A

,

H_B

,

H_C

라고 하자. 그러면

:

\frac{AH_C}{H_CB}\cdot\frac{BH_A}{H_AC}\cdot\frac{CH_B}{H_BA}=\frac{b\cos A}{a\cos B}\cdot\frac{c\cos B}{b\cos C}\cdot\frac{a\cos C}{c\cos A}=1

이므로 체바 정리에 따라 직선

AH_A

,

BH_B

,

CH_C

는 한 점에서 만난다.

3. 성질

삼각형 $ABC$ 의 꼭짓점 $A$ , $B$ , $C$ 에서 각 대변 $BC$ , $AC$ , $AB$ 에 내린 수선은 한 점에서 만나는데, 이 점을 '''수심''' $H$ 라고 한다.

수심은 다음과 같은 방법으로 증명할 수 있다.

원주각을 이용
외심과 무게 중심을 이용^[34]
근축을 이용^[33]
체바 정리를 이용

삼각형

ABC

의 수심을

H

, 각 꼭짓점에서 대변에 내린 수선의 발을

H_A

,

H_B

,

H_C

, 외접원의 반지름을

R

이라고 하면, 다음이 성립한다.^[33]

$AH_A=\frac{bc}{2R}=b\sin C=c\sin B$
$BH_B=\frac{ac}{2R}=a\sin C=c\sin A$
$CH_C=\frac{ab}{2R}=a\sin B=b\sin A$

또한, 다음이 성립한다.^[34]^[33]

$AH_A\cdot HH_A=BH_A\cdot CH_A$
$BH_B\cdot HH_B=AH_B\cdot CH_B$
$CH_C\cdot HH_C=AH_C\cdot BH_C$
$AH\cdot HH_A=BH\cdot HH_B=CH\cdot HH_C$

수심은 삼선좌표^[3]와 바리 중심 좌표로 표현할 수 있다. 변수

A

,

B

,

C

는 삼각형의 꼭짓점이자 각도를,

a = \left|\overline{BC}\right|

,

b = \left|\overline{CA}\right|

,

c = \left|\overline{AB}\right|

는 변의 길이를 나타낸다.

삼선좌표: $\cos A-\sin B \sin C:\cos B-\sin C \sin A:\cos C-\sin A\sin B$
바리 중심 좌표: $(a^2+b^2-c^2)(a^2-b^2+c^2) : (a^2+b^2-c^2)(-a^2+b^2+c^2) : (a^2-b^2+c^2)(-a^2+b^2+c^2)$
또는 $\tan A:\tan B:\tan C$

복소 평면에서 점

A

,

B

,

C

가 복소수

z_A

,

z_B

,

z_C

를 나타내고, 삼각형

ABC

의 외접원 중심이 원점에 있다고 가정하면, 복소수

z_H=z_A+z_B+z_C

는 점

H

, 즉 삼각형

ABC

의 수심을 나타낸다.^[4]

유클리드 벡터를 이용하면 수심

H

에 대해 다음이 성립한다.

$\vec{OH}=\sum\limits_{\scriptstyle\rm cyclic}\vec{OA}$
$2\cdot\vec{HO}=\sum\limits_{\scriptstyle\rm cyclic}\vec{HA}$
첫 번째 식은 제임스 조셉 실베스터가 제안한 ''실베스터의 문제''로도 알려져 있다.^[5]

포물선의 준선은 삼각형의 한 변에 외접하고 다른 변의 연장선에 접하며, 수심을 통과한다.^[15]

삼각형의 수심을 지나는 외접 원뿔 곡선은 직교 쌍곡선이다.^[16]

수심의 등각 켤레점은 삼각형의 외심이다.^[10]

수심의 등조 켤레점은 반여삼각형의 심중선 점이다.^[11]

평면상의 네 점 중 하나가 나머지 세 점으로 형성된 삼각형의 수심일 경우, 이 네 점을 수심 사심 또는 수심 사변형이라고 한다.

삼각형의 외접원 반지름을 로 표시하면 다음과 같다.^[12]^[13]

을 삼각형의 내접원 반지름, 를 방접원 반지름, 을 외접원 반지름으로 표시하면, 수심에서 꼭짓점까지의 거리에 관해 다음 관계가 성립한다.^[14]

와 같은 임의의 고도가 외접원과 에서 만나도록 연장되어 가 외접원의 현이 되면, 발 는 선분 를 이등분한다.^[7]

3. 1. 위치

예각 삼각형의 수심은 삼각형의 내부에 속한다. 직각 삼각형의 수심은 직각의 꼭짓점이다. 둔각 삼각형의 수심은 삼각형의 외부에 속한다.

3. 2. 외접원과의 관계

삼각형의 수심과 한 꼭짓점 사이의 거리는 외심과 그 꼭짓점의 대변 사이의 거리의 2배이다.^[34]
삼각형의 수심을 각 변에 대해 반사시킨 점은 외접원 위에 있다.^[34]
삼각형의 외심은 중점 삼각형의 수심이다.
삼각형의 수심과 외심은 등각 켤레점이다.^[34]

3. 3. 오일러 직선과 구점원

삼각형의 수심, 무게 중심, 외심은 한 직선 위에 있으며, 이를 오일러 직선이라고 한다. 삼각형의 세 수선의 발, 세 변의 중점, 각 꼭짓점과 수심을 이은 선분의 중점, 이 아홉 점은 한 원 위에 있으며, 이 원을 구점원이라고 한다.^[17]^[18]

구점원의 중심은 무게 중심과 외심을 잇는 선분의 중점이다. 특히 삼각형이 정삼각형이 아닐 경우 구점원의 중심은 오일러 직선 위의 점이다. 구점원은 수심과 외접원 위의 점을 잇는 선분의 중점의 자취이다.

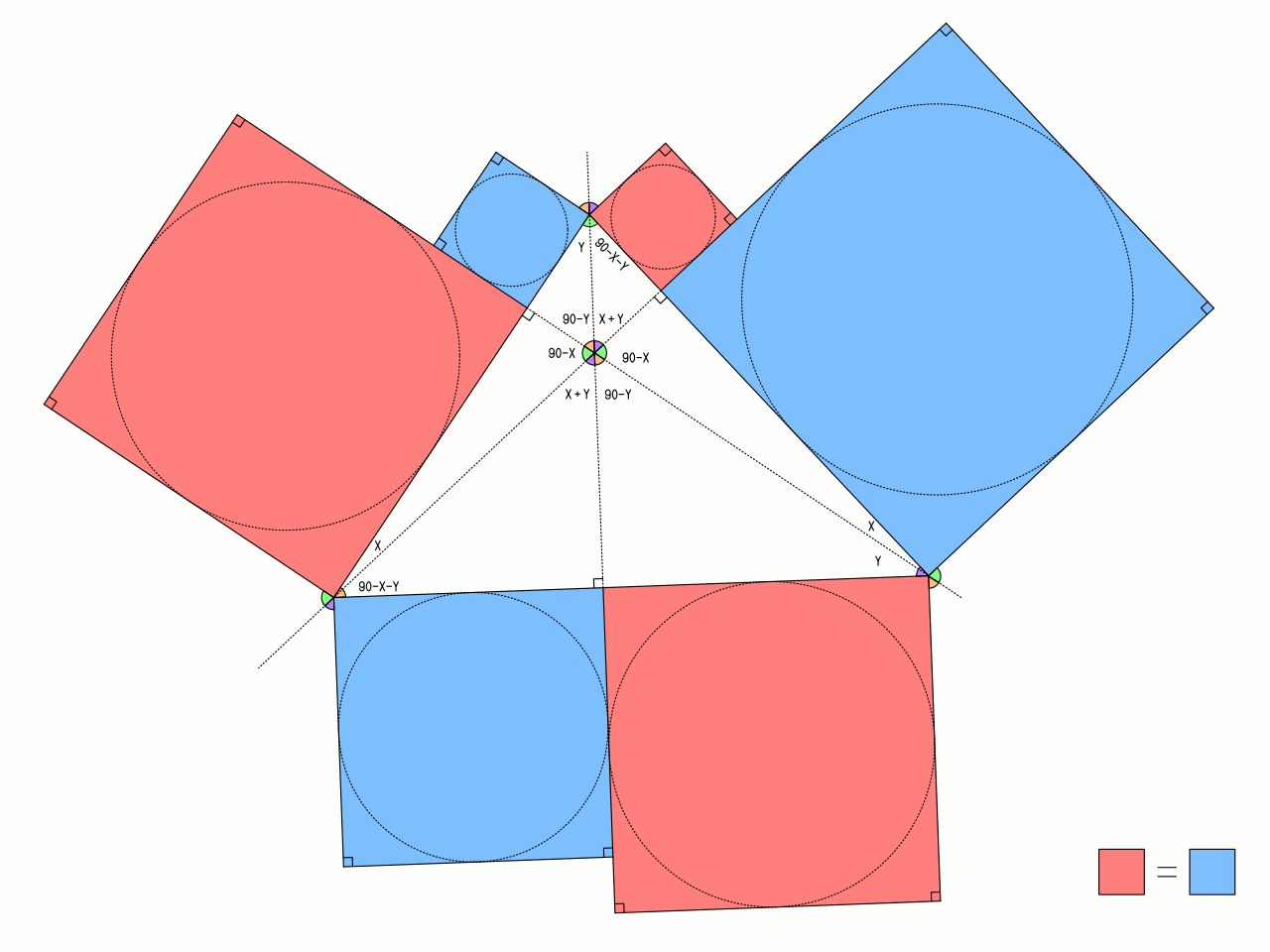
삼각형의 수심에서 만나는 3개의 수선에 의해 만들어지는 6개의 각에는, 그림과 같이 해당 삼각형의 3개의 각이 2개씩 포함된다.

삼각형의 각 변을 수선과의 교점에서 분할하고, 분할 후 각각의 길이의 변을 가진 정방형을 6개 만든다. 그림과 같이 시계 방향으로 빨강·파랑·빨강·파랑·빨강·파랑으로 그룹화하여, 빨강과 파랑의 면적을 구하면, 양쪽 면적은 같아진다. 3개의 꼭짓점을 A, B, C, 수심을 H, 3개의 수선의 발을 H_a, H_b, H_c로 한다.

무게중심·외심과 동일 직선상에 있다. 이 선을 오일러선이라고 한다.
직각삼각형의 수심은, 직각이 되는 꼭짓점이다. 둔각삼각형의 수심은, 그 삼각형의 외부에 있다.
수심은 삼각형 H_aH_bH_c의 내심 또는 방심이 된다.
수심과 외심의 중점은 구점원의 중심이다.
삼각형 ABH의 수심은 C이다.
$\overline{AH} \cdot \overline{HH_{a}}= \overline{BH} \cdot \overline{HH_{b}} = \overline{CH} \cdot \overline{HH_{c}}$
$\frac{a}{\sin \alpha} =\frac{b}{\sin \beta} = \frac{c}{\sin \gamma} = \frac{AH}{\cos \alpha} = \frac{BH}{\cos \beta} = \frac{CH}{\cos \gamma} = 2R$
a, b, c는 3변의 길이. α·β·γ는 3개의 각. R은 외접원의 반지름이다.
P를 외접원상의 점으로 하고, M을 PH의 중점으로 한다.
M은 구점원상에 있다.
P에서의 심슨 선은 M을 통과한다.
각 꼭짓점 ABC를 통과하는 대변에 대한 평행선을 3개 모두 그어, 새로운 삼각형 A'B'C'를 만들면(위의 그림 참조), 삼각형 ABC의 수심과 삼각형 A'B'C'의 외심은 일치한다.

3. 4. 수심 삼각형

직각삼각형이 아닌 삼각형의 각 꼭짓점에서 대변에 내린 수선의 발을 꼭짓점으로 하는 삼각형을 수심 삼각형이라고 한다. 삼각형

ABC

의 꼭짓점

A

,

B

,

C

에서 대변에 내린 수선의 발을 각각

H_A

,

H_B

,

H_C

라 할 때, 삼각형

H_AH_BH_C

가 수심 삼각형이다.

예각삼각형의 수심은 수심 삼각형의 내심이고,^[21] 둔각삼각형의 수심은 수심 삼각형의 방심이다. 수심 삼각형은 방심 삼각형 또는 고도 삼각형이라고도 불린다. 모든 예각 삼각형에서 둘레가 가장 작은 내접 삼각형은 수심 삼각형이며, 이는 파냐노 문제의 해답이다.^[24]^[25]

방심 삼각형의 변은 원래 삼각형의 꼭짓점에서 외접원에 접하는 접선과 평행하고,^[26] 참조 삼각형의 반대쪽 연장된 변과 세 개의 공선점에서 만난다.^[22]^[23]^[21]

방심 삼각형의 꼭지점에 대한 삼선 좌표는 다음과 같다.

꼭짓점	삼선 좌표
$D$	$0:\sec B:\sec C$
$E$	$\sec A:0:\sec C$
$F$	$\sec A:\sec B:0$

3. 4. 1. 파냐노 문제

삼각형

ABC

가 예각 삼각형일 때, 최소 둘레의 내접 삼각형은 세 꼭짓점

A

,

B

,

C

에서 각 대변에 내린 수선의 발

H_A

,

H_B

,

H_C

를 꼭짓점으로 하는 수심 삼각형

H_AH_BH_C

이다. 이를 '''파냐노 문제'''(Pagnano’s problem^영어)라고 한다.^[33]

만약 삼각형

ABC

가 직각삼각형 또는 둔각삼각형이고, 직각 또는 둔각의 꼭짓점이

A

라면, 최소 둘레의 내접삼각형은 퇴화 삼각형

AAH_A

이다. (두 꼭짓점이 같은 삼각형을 허용하지 않을 경우 존재하지 않는다).^[33]

모든 예각 삼각형에서 둘레가 가장 작은 내접 삼각형은 방심 삼각형이다.^[24] 이것은 1775년에 제기된 파냐노 문제의 해답이다.^[25]

3. 4. 2. 수심축

방심 삼각형의 연장된 변은 참조 삼각형의 반대쪽 연장된 변과 세 개의 공선점에서 만난다.^[22]^[23]^[21]

3. 5. 드로츠파르니 직선

삼각형 ABC의 수심 H에서 직교하는 두 직선이 직선 BC와 점 D₁, D₂에서, 직선 AC와 점 E₁, E₂에서, 직선 AB와 점 F₁, F₂에서 만난다고 하자. 그렇다면 선분 D₁D₂, E₁E₂, F₁F₂의 중점 D, E, F는 한 직선 위의 점이다. 이 직선을 삼각형 ABC의 드로츠파르니 직선(Droz-Farny line^영어)이라고 한다.^[38]

3. 6. 테일러 원

삼각형

ABC

의 각 꼭짓점에서 대변에 내린 수선의 발을 각각

H_A

,

H_B

,

H_C

라 하자.

H_A

,

H_B

,

H_C

에서 다른 두 변에 내린 수선의 발 여섯 개를 각각

P

,

Q

,

R

,

S

,

T

,

U

라 하면, 이 여섯 개의 점은 모두 한 원 위에 있다. 이 원을 삼각형

ABC

의 '''테일러 원'''(Taylor circle^영어)이라고 한다.^[34] 테일러 원은 터커 원의 특수한 경우이다.

3. 7. 기타 성질

를 각각 에서 내린 수선의 발이라고 할 때, 다음과 같은 성질이 있다.

수심이 고도를 나누는 선분의 길이의 곱은 세 고도에서 모두 같다.^[6]^[7]
:

수심에서 밑변까지의 거리와 고도의 길이의 비의 합은 1이다.^[9]
:

수심에서 꼭짓점까지의 거리와 고도의 길이의 비의 합은 2이다.^[9]
:

수심의 등각 켤레점은 삼각형의 외심이다.^[10]
수심의 등조 켤레점은 반여삼각형의 심중선 점이다.^[11]
평면상의 네 점 중 하나가 나머지 세 점으로 형성된 삼각형의 수심일 경우, 이 네 점을 수심 사심 또는 수심 사변형이라고 한다.
삼각형의 외접원 반지름을 로 표시하면 다음과 같다.^[12]^[13]
:

을 삼각형의 내접원 반지름, 를 방접원 반지름, 을 외접원 반지름으로 표시하면, 수심에서 꼭짓점까지의 거리에 관해 다음 관계가 성립한다.^[14]
:

와 같은 임의의 고도가 외접원과 에서 만나도록 연장되어 가 외접원의 현이 되면, 발 는 선분 를 이등분한다.^[7]
:

포물선의 준선은 삼각형의 한 변에 외접하고 다른 변의 연장선에 접하며, 수심을 통과한다.^[15]

삼각형의 수심을 지나는 외접 원뿔 곡선은 직교 쌍곡선이다.^[16]

3개의 꼭짓점을 A, B, C, 수심을 H, 3개의 수선의 발을 H_a, H_b, H_c로 할때, 다음과 같은 관계가 성립한다.
무게중심, 외심과 동일 직선상에 있다. 이 선을 오일러선이라고 한다.
직각삼각형의 수심은 직각이 되는 꼭짓점이다. 둔각삼각형의 수심은 그 삼각형의 외부에 있다.
수심은 삼각형 H_aH_bH_c의 내심 또는 방심이 된다.
수심과 외심의 중점은 9점 원의 중심이다.
삼각형 ABH의 수심은 C이다.

: a, b, c는 3변의 길이. α·β·γ는 3개의 각. R은 외접원의 반지름이다.
P를 외접원상의 점으로 하고, M을 PH의 중점으로 하면 M은 9점 원상에 있다.
P에서의 심슨 선은 M을 통과한다.
각 꼭짓점 ABC를 통과하는 대변에 대한 평행선을 3개 모두 그어, 새로운 삼각형 A'B'C'를 만들면, 삼각형 ABC의 수심과 삼각형 A'B'C'의 외심은 일치한다.

4. 좌표

삼각형의 세 꼭짓점 A, B, C의 좌표가 주어졌을 때, 직교좌표 또는 무게중심좌표를 이용하여 수심의 좌표를 나타낼 수 있다. 변수 A, B, C는 삼각형의 꼭짓점이자 각도를 나타내고, $a = \left|\overline{BC}\right|, b = \left|\overline{CA}\right|, c = \left|\overline{AB}\right|$ 는 변의 길이를 나타낸다.

수심은 삼선좌표^[3]로 다음과 같이 표현된다.

: $\begin{align}& \sec A:\sec B:\sec C \\&= \cos A-\sin B \sin C:\cos B-\sin C \sin A:\cos C-\sin A\sin B,\end{align}$

복소 평면에서 점 A, B, C가 복소수 $z_A, z_B, z_C$ 를 나타내고, 삼각형 ABC의 외접원의 중심이 평면의 원점에 위치한다고 가정하면, 복소수

: $z_H=z_A+z_B+z_C$

는 점 H로 표시되며, 이는 삼각형 ABC의 수심이다.^[4] 이를 통해, 유클리드 벡터를 이용하여 수심 H의 다음 특성을 쉽게 설정할 수 있다.

: $\vec{OH}=\sum\limits_{\scriptstyle\rm cyclic}\vec{OA},\qquad2\cdot\vec{HO}=\sum\limits_{\scriptstyle\rm cyclic}\vec{HA}.$

앞의 벡터 항등식 중 첫 번째는 제임스 조셉 실베스터가 제안한 '실베스터의 문제'로도 알려져 있다.^[5]

4. 1. 직교 좌표

좌표 평면에서, 세 꼭짓점의 좌표를 (x_a, y_a), (x_b, y_b), (x_c, y_c)라고 하면, 수심의 좌표는 다음과 같다.

:(''x'' 좌표) =

\frac{\left| \begin{array}{ccc}

x_bx_c - y_a^2 & y_a & 1 \\
x_ax_c - y_b^2 & y_b & 1 \\
x_ax_b - y_c^2 & y_c & 1 \end{array} \right|}

{\left| \begin{array}{ccc}x_a & y_a & 1 \\x_b & y_b & 1 \\x_c & y_c & 1 \end{array} \right|}

:(''y'' 좌표) =

\frac{\left| \begin{array}{ccc}x_a & -x_a^2 - y_by_c & 1 \\x_b & -x_b^2 - y_ay_c & 1 \\x_c & -x_c^2 - y_ay_b & 1 \end{array} \right|}{\left| \begin{array}{ccc}x_a & y_a & 1 \\x_b & y_b & 1 \\x_c & y_c & 1 \end{array} \right|}

세 꼭짓점이 단위 원 위에 있는 경우, 수심은 다음과 같이 간단하게 나타낼 수 있다.

:(x_a+x_b+x_c, y_a+y_b+y_c)

4. 2. 무게중심 좌표

삼각형의 꼭짓점 A, B, C의 각을 α, β, γ라고 할 때, 수심은 무게중심 좌표로 다음과 같이 표현된다.^[3]

:

\tan \alpha:\tan \beta:\tan \gamma

이 좌표는 삼각형 내부의 점에 대해서는 모두 양수이지만, 외부의 점에 대해서는 적어도 하나는 음수이다. 꼭짓점의 경우에는 두 개의 무게중심 좌표가 0이다. 따라서 수심의 무게중심 좌표는 수심이 예각삼각형의 내부에, 직각삼각형의 직각 꼭짓점에, 둔각삼각형의 외부에 있음을 보여준다.

참조

_[1] 간행물
_[2] 간행물
_[3] 웹사이트 Encyclopedia of Triangle Centers http://faculty.evans[...] 2012-04-19
_[4] 서적 Complex numbers from A to...Z Birkhäuser, Boston
_[5] 서적 100 Great Problems of Elementary Mathematics. Their History and Solution Dover Publications, Inc., New York
_[6] 간행물
_[7] 웹사이트 "Orthocenter of a triangle" http://www.pballew.n[...] 2012-05-04
_[8] 간행물
_[9] University Some properties of the orthocenter of a triangle http://jwilson.coe.u[...] University of Georgia
_[10] 간행물
_[11] 웹사이트 Isotomic conjugate http://mathworld.wol[...]
_[12] 웹사이트 Orthocenter http://mathworld.wol[...]
_[13] 간행물
_[14] 간행물 Hansen's right triangle theorem, its converse and a generalization http://forumgeom.fau[...]
_[15] 웹사이트 Kiepert Parabola http://mathworld.wol[...]
_[16] 웹사이트 Jerabek Hyperbola http://mathworld.wol[...]
_[17] 간행물
_[18] 간행물
_[19] 간행물 Distances between the circumcenter of the extouch triangle and the classical centers http://forumgeom.fau[...]
_[20] 간행물 Euler and triangle geometry
_[21] 서적 Continuous symmetry: from Euclid to Klein American Mathematical Society
_[22] 간행물
_[23] 간행물
_[24] 간행물
_[25] 간행물
_[26] 간행물
_[27] 간행물 Triangular Light Routes
_[28] 서적 College Geometry / A Discovery Approach HarperCollins
_[29] 서적 The Mathematical Papers of Isaac Newton Cambridge University Press
_[30] 간행물 Concurrency of the Altitudes of a Triangle https://www.research[...]
_[31] 간행물 XXIV. Geometry and geometers https://zenodo.org/r[...]
_[32] 서적 Solutions peu connues de différens problèmes de Géométrie-pratique Devilly, Metz et Courcier
_[33] 서적 Geometry Revisited Mathematical Association of America 1967
_[34] 서적 Episodes in Nineteenth and Twentieth Century Euclidean Geometry The Mathematical Association of America 1995
_[35] 서적 Geometry for College Students Brooks/Cole 2001
_[36] 서적 Recent Advances in Geometric Inequalities Springer Science+Business Media, B.V. 1989
_[37] 논문 The Conics of Ludwig Kiepert: A Comprehensive Lesson in the Geometry of the Triangle 1994-06
_[38] 논문 A Purely Synthetic Proof of the Droz-Farny Line Theorem http://forumgeom.fau[...] 2020-06-16

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com