조화급수
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
조화 급수는 1/1 + 1/2 + 1/3 + 1/4 + ... 와 같이 각 항이 단위 분수인 무한 급수이다. 이 급수는 14세기에 발산함이 증명되었으며, 건축 도면의 비례에 활용되는 등 역사적으로 다양한 분야에서 사용되었다. 조화 급수는 발산하며, 교대 조화 급수, 리만 제타 함수, p-급수 등 관련 급수들이 존재한다. 조화 급수는 지프 문제, 블록 쌓기 문제, 소수 관련 문제, 쿠폰 수집가 문제, 퀵 정렬 알고리즘 분석 등 다양한 수학적 문제와 응용 분야에서 활용된다.
더 읽어볼만한 페이지
2. 역사
조화 급수가 발산한다는 사실은 14세기 니콜 오렘에 의해 처음 증명되었으나, 이 발견은 세상에서 잊혀졌다. 이후 17세기 피에트로 멩골리, 요한 베르누이, 야코프 베르누이에 의해 다시 증명되었다.[58]
조화급수는 다음과 같은 무한 급수이다.
조화 급수는 각 항이 0으로 수렴함에도 불구하고 그 합은 무한대로 발산한다. 발산 속도는 매우 느려서 ln(n)에 가깝다. 오일러-마스케로니 상수는 조화수열과 자연로그의 오차의 극한을 나타내는 상수이다. 조화 급수는 최초 개의 항을 더해도 100을 넘지 않기 때문에, 수열의 항의 극한값이 0임에도 급수의 값은 수렴하지 않는 예로 자주 등장한다.[51]
역사적으로 조화 급수는 건축가들에게 특히 인기 있었다. 이러한 경향은 바로크 시대에 특히 강해서, 건축가들은 교회와 궁전을 건축할 때 평면도 및 입면도상의 비례와 건물 내·외부간의 건축 디테일의 조화를 위해 조화 급수를 사용하였다.[46]
3. 정의
:
이 급수의 항들은 모두 양의 단위 분수들이다. 이 급수는 발산하는 급수이다. 급수의 더 많은 항들이 급수의 부분합에 포함될수록, 이 부분합의 값은 임의로 커져서 어떤 유한한 극한을 넘어선다. 발산하는 급수이기 때문에, 수치 값으로 평가될 수 있는 것이라기보다는 단위 분수를 결합한 추상적인 수학적 표현인 형식적인 합으로 해석해야 한다. 조화 급수의 발산에 대한 여러 가지 증명이 있다.[45][46]
4. 발산성
조화 급수는 다음과 같은 무한 급수이다.
:
이 급수의 항들은 모두 양의 단위 분수들이며, 발산하는 급수이다.
조화 급수가 발산하기 때문에 발생하는 몇 가지 역설과 직관에 반하는 결과가 알려져 있다. 대표적인 예로 블록 쌓기 문제와 고무 밧줄 위의 개미 문제가 있다. 블록 쌓기 문제는 똑같은 도미노를 테이블 가장자리에 쌓을 때 도미노가 충분하다면 얼마든지 원하는 만큼 내밀 수 있다는 직관적이지 않은 결과를 보여준다.[47][50][48][49] 고무줄 위의 애벌레 문제는 1미터 길이의 고무줄 위를 매분 1센티미터씩 기어가는 애벌레가 고무줄이 1분마다 1미터씩 늘어나는 상황에서 결국 끝에 도달할 수 있다는 역설적인 결과를 보여준다.
조화 급수의 발산은 매우 느리다. 부분합이 로그 증가를 보이기 때문이다. 특히 다음 식이 성립한다.
:
여기서 는 오일러-마스케로니 상수이며, 는 가 무한대로 갈 때 0에 접근한다. 이 결과는 레온하르트 오일러가 증명하였다.
4. 1. 비교 판정법
니콜 오렘은 개씩 항을 묶어 더 작은 값의 수열의 합이 발산함을 보임으로써, 더 큰 값의 수열(조화 급수)도 발산함을 증명하는 방법을 제시했다.
:
조화 급수보다 작은 급수가 발산하므로, 비교 판정법에 의해 조화 급수도 발산한다.
발산을 증명하는 또 다른 방법은 각 분모를 다음으로 가장 큰 2의 거듭제곱으로 대체하여 비교하는 것이다.
:
같은 항을 묶으면 두 번째 급수가 발산한다는 것을 알 수 있다.
:
조화 급수의 각 항이 두 번째 급수의 해당 항보다 크거나 같고, 모든 항이 양수이므로, 두 번째 급수가 발산하면 비교 판정법에 의해 조화 급수도 발산한다.
이 증명은 니콜 오렘이 1350년경에 제시했으며, 코시 응축 판정법은 이 논증을 일반화한 것이다.
4. 2. 적분 판정법
적분 판정법으로 조화 급수가 발산함을 보일 수 있다. 조화 급수는 오른쪽 그림에서 색칠한 사각형들의 넓이를 모두 더한 것이다. 곡선 아래쪽 넓이가 무한대로 발산하면, 조화 급수도 발산한다. 곡선 아래쪽의 넓이는 다음과 같이 적분으로 계산한다.
조화 급수의 최초 항까지 더한 값()과 1부터 까지의 구간을 적분한 값()은 적분판정법에 의하여 동시에 발산한다. 그런데
:이다.
따라서 적분 판정법에 의해 조화 급수도 동시에 발산한다.
5. 성질
조화 급수는 리만 제타 함수에 1을 대입했을 때 얻어지는 수열이다. 부호가 번갈아 나타나는 교대 조화 급수는 수렴하며, 그 값은 이다. 교대 조화 급수는 절대 수렴하지 않는다.[51] 따라서 항을 재배치하여 원하는 어떤 실수 값이든 만들어낼 수 있다.
다음과 같은 급수는 '''교대 조화 급수''' alternating harmonic series영어로 알려져 있다.
:
이 급수의 수렴성은 라이프니츠 판정법에서 알 수 있다. 특히 이 급수의 합은 2의 자연로그와 같다. 즉,
:
가 성립한다. 이 식은 자연로그 함수의 테일러 급수인 메르카토르 급수의 특수한 경우이다.
역탄젠트 함수의 테일러 급수에서 유도되는 관련 급수로 다음과 같은 식이 있다.
:
이것은 라이프니츠의 π 공식으로 알려져 있다.
5. 1. 부분합 (조화수)
조화 급수의 처음 개의 항을 더하면 부분합이 생성되며, 이를 조화수라고 하며 으로 표기한다.:
이 수들은 로그 성장으로 매우 느리게 증가한다. 더 정확하게는, 오일러-매클로린 공식에 의해,
:
여기서 는 오일러-마스케로니 상수이며 이고, 이 무한대로 갈 때 0에 접근한다.
조화급수의 발산은 매우 느려서, 예를 들어 처음 1043개의 항의 합은 100보다 작다.[51]。 이것은 부분합이 로그 증가이기 때문이다. 특히,
:
가 성립한다. 여기서 는 오일러-마스케로니 상수이며, 는 의 극한에서 0에 접근한다. 이 결과는 레온하르트 오일러에 의한 것이다.
발산하는 조화 급수의 제 부분합
:
는 제 '''조화수'''라고 불린다. 이것은 다음의 성질을 가진다[52]。
- 번째 조화수 와 의 차이는 오일러-마스케로니 상수 로 수렴한다.
- 서로 다른 번호의 조화수끼리의 차이는 결코 정수가 되지 않는다.
- 을 제외하고 어떤 조화수도 정수가 아니다.
5. 2. 정수 조화수
Harmonic number영어 중 정수인 것은 뿐이다.[52] 이 정수가 아님을 증명하는 한 가지 방법은 1부터 까지의 범위에서 가장 높은 2의 거듭제곱인 을 고려하는 것이다. 이 1부터 까지의 숫자들의 최소공배수라고 하면, 는 다음과 같이 동일한 분모를 가진 분수의 합으로 다시 쓸 수 있다.:
여기서 분자 중 만 홀수이고 나머지는 짝수이며, (일 때) 자체는 짝수이다. 따라서 결과는 홀수 분자와 짝수 분모를 가진 분수이며, 이는 정수가 될 수 없다. 더 일반적으로, 연속된 정수 시퀀스는 다른 시퀀스 구성원보다 더 큰 2의 거듭제곱으로 나누어지는 고유한 구성원을 가지며, 같은 논증에 의해 두 개의 조화수가 정수로 차이가 나지 않는다.[52]
조화수가 정수가 아니라는 또 다른 증명은 의 분모가 보다 크고 보다 작거나 같은 모든 소수로 나누어져야 한다는 것을 관찰하고, 베르트랑의 공준을 사용하여 이러한 소수 집합이 비어 있지 않음을 증명한다. 같은 논증은 , 및 를 제외하고, 조화수는 유한 소수 표현을 가질 수 없다는 것을 더욱 강력하게 의미한다.[52]
6. 응용
조화 급수와 그 부분합은 여러 수학 문제의 해와 관련이 있다.[1]
- '''사막 횡단 문제(지프 문제)'''는 알쿠인의 9세기 문제집인 ''청년을 날카롭게 하기 위한 제안''에 나오는 문제로, 지프(원래는 낙타)가 사막을 횡단하며 연료를 저장해 가면서 얼마나 멀리 갈 수 있는지를 묻는다. 조화급수의 발산은 충분한 연료가 있다면 어떤 거리라도 횡단 가능하다는 것을 보여준다.[2]
- '''블록 쌓기 문제'''는 동일한 직사각형 블록들을 테이블에서 떨어지지 않게 쌓아 가장 멀리 튀어나오게 하는 문제이다. 블록들은 조화 급수에 따라 튀어나오도록 배치되며, 조화 급수의 발산은 블록 스택이 테이블 밖으로 얼마나 멀리 튀어나올 수 있는지에 제한이 없음을 의미한다.[47]
- 1737년 레온하르트 오일러는 조화 급수가 각 항이 소수에서 나오는 오일러 곱과 같다는 것을 발견하고, 소수 역수의 합이 발산한다는 것을 증명하여 소수가 무한히 많다는 결론을 내렸다. 이는 메르텐스 정리로 확인되었고, 소수 정리의 전조로 여겨진다.
- 정수론에서 조화 급수는 1부터 까지의 수의 평균 약수의 수와 관련이 있다. 페터 구스타프 르줜 디리클레는 평균 약수의 수가 임을 보였다. (빅 오 표기법으로 표현).[1]
- '''쿠폰 수집가 문제'''는 모든 항목이 선택될 때까지 항목 집합에서 무작위 선택을 반복하는 문제로, 모든 항목을 수집하는 데 필요한 예상 시도 횟수는 ''nH''''n''이다. 여기서 ''H''''n''은 ''n''번째 조화수이다.[4]
- 퀵 정렬 알고리즘은 조화수를 사용하여 분석할 수 있다. 평균 시간 복잡도 또는 기대 시간 분석에서, 모든 항목은 피벗으로 선택될 가능성이 동일하며, 재귀 과정에서 두 항목이 서로 비교될 확률은 최종 정렬 순서에서 두 항목을 구분하는 다른 항목의 수의 함수로 계산할 수 있다.
6. 1. 사막 횡단 문제 (지프 문제)
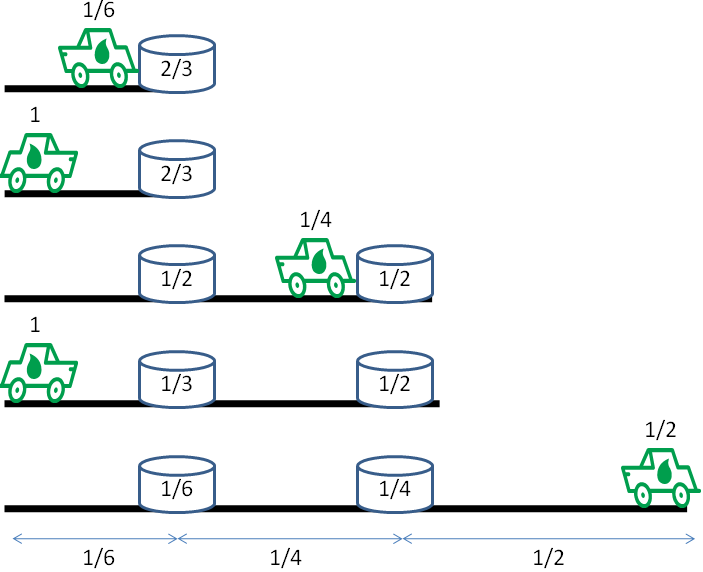
지프 문제는 알쿠인의 9세기 문제집인 ''청년을 날카롭게 하기 위한 제안''에 포함되어 있지만(지프 대신 낙타를 사용), 잘못된 해결책을 제시하고 있다.[1] 이 문제는 지프가 사막으로 얼마나 멀리 가서 기지로 돌아올 수 있는지를 묻는다. 기지에는 n개의 연료 적재물이 있고, 연료를 사막으로 운반하여 저장소에 남겨두는 방식으로 진행된다. 최적의 해결책은 저장소를 시작 지점으로부터 r|영어/2n, r|영어/2(n-1), r|영어/2(n-2), … 만큼 떨어진 거리에 배치하는 것이다. 여기서 r은 지프가 한 번의 연료 적재로 이동할 수 있는 거리이다. 기지에서 왕복하는 각 여정에서 지프는 저장소를 하나 더 설치하고, 가는 길에 다른 저장소에서 연료를 보급하며, 이전 저장소와 기지로 돌아갈 연료를 남겨두면서 새롭게 설치된 저장소에 최대한 많은 연료를 배치한다. 따라서 n번째 여정에서 도달하는 총 거리는 다음과 같다.
:r|영어/2n + r|영어/2(n-1) + r|영어/2(n-2) + … = r|영어/2 Hn
여기서 Hn은 n번째 조화수이다. 조화급수의 발산은 충분한 연료가 있다면 어떤 거리라도 횡단이 가능하다는 것을 의미한다.[2]
예를 들어, 알쿠인의 문제 버전에서 r=30이다. 낙타는 30개의 곡물 량을 운반할 수 있고, 곡물 1개를 먹으면서 1 레우카(leuca)를 이동할 수 있다. 여기서 레우카는 대략 2.3km에 해당하는 거리 단위이다. 이 문제에는 n=3이 있다. 즉, 90개의 곡물 량이 있어 세 번의 여행을 공급하기에 충분하다. 사막 횡단 문제의 표준 공식에 따르면, 낙타는 30/2 (1/3 + 1/2 + 1/1) = 27.5 레우카를 이동하여 돌아올 수 있다. 첫 번째 여정에서 기지로부터 5 레우카 떨어진 곳에 곡물 저장소를 설치하고, 두 번째 여정에서 기지로부터 12.5 레우카 떨어진 곳에 설치함으로써 가능하다. 그러나 알쿠인은 대신 약간 다른 질문을 한다. 즉, 마지막 귀환 여정 없이 30 레우카 거리를 얼마나 많은 곡물을 운송할 수 있는가에 대한 질문으로, 사막에 낙타를 남겨두거나 낙타가 왕복 여행에서 소비하는 곡물량을 계산하지 못한다.[1]
6. 2. 블록 쌓기 문제

블록 쌓기 문제는 개의 동일한 직사각형 블록을 테이블에서 떨어지지 않으면서 가장 멀리 튀어나오도록 층별로 하나씩 쌓는 문제이다. 맨 위 블록은 길이의 만큼 아래 블록보다 더 튀어나오도록 놓을 수 있다. 그 다음 블록은 위 두 블록의 질량 중심이 지지되어 넘어지지 않도록 길이의 만큼만 아래 블록보다 더 튀어나오도록 놓아야 한다. 세 번째 블록은 길이의 만큼만 아래 블록보다 더 튀어나오도록 놓아야 하며, 이와 같은 방식으로 개의 블록을 쌓아 테이블에서 길이만큼 더 튀어나오도록 할 수 있다. 여기서 은 번째 조화수이다. 조화 급수의 발산은 블록 스택이 테이블 밖으로 얼마나 멀리 튀어나올 수 있는지에 제한이 없음을 의미한다.[47] 층당 하나의 블록이 있는 스택은 더 나은 해결책이 없지만, 층당 여러 개의 블록이 있는 스택을 사용하면 훨씬 더 많은 오버행을 달성할 수 있다.
6. 3. 소수와 약수
1737년, 레온하르트 오일러는 조화 급수가 각 항이 소수에서 나오는 오일러 곱과 같다는 것을 관찰했다. 이는 소수 역수의 합이 발산한다는 것을 보여주며, 소수는 무한히 많다는 결론으로 이어진다. 오일러의 결론은 메르텐스 정리 중 하나로 후대 수학자들에 의해 확인되었으며, 소수 정리의 전조로 볼 수 있다.정수론에서 조화 급수와 관련된 문제는 1부터 까지의 수의 평균 약수의 수에 관한 것이다. 이는 약수 함수의 평균 차수로 공식화된다. 조화 급수의 각 항을 의 다음으로 작은 정수 배수로 반올림하는 연산은 이 평균이 조화수와 작은 상수로 다르도록 한다. 페터 구스타프 르줜 디리클레는 평균 약수의 수가 임을 보였다(빅 오 표기법으로 표현). 최종 오차항을 더 정확하게 경계 짓는 것은 디리클레의 약수 문제로 알려진 미해결 문제로 남아 있다.[1]
6. 4. 쿠폰 수집가 문제

일부 흔한 게임이나 오락은 가능한 모든 선택이 선택될 때까지 항목 집합에서 무작위 선택을 반복하는 것을 포함한다. 여기에는 트레이딩 카드 수집과 일련의 달리기 행사에서 시간의 모든 60가지 가능한 초를 얻는 것을 목표로 하는 파크런 빙고 완성이 포함된다.[1] 이 문제의 더 심각한 응용 분야에는 품질 관리를 위해 제조된 제품의 모든 변형을 샘플링하는 것과 랜덤 그래프의 연결성이 있다.[2][3] 이러한 형태의 상황에서, 총 ''n''개의 똑같이 가능한 항목 중에서 수집해야 할 항목이 ''k''개 남았을 때, 단일 무작위 선택에서 새로운 항목을 수집할 확률은 ''k/n''이고, 새로운 항목을 수집하는 데 필요한 예상 무작위 선택 횟수는 ''n/k''이다. ''n''에서 1까지 모든 ''k'' 값에 대해 합하면 모든 항목을 수집하는 데 필요한 총 예상 무작위 선택 횟수가 ''nH''''n''이 되고, 여기서 ''H''''n''은 ''n''번째 조화수이다.[4]
6. 5. 퀵 정렬 알고리즘 분석
퀵 정렬 알고리즘은 조화수를 사용하여 분석할 수 있다. 이 알고리즘은 하나의 항목을 "피벗"으로 선택하고, 다른 모든 항목과 비교하여, 비교 결과에 따라 피벗 앞과 뒤에 놓이는 두 개의 항목 하위 집합을 재귀적으로 정렬하는 방식으로 작동한다. 평균 시간 복잡도(모든 입력 순열이 동일하게 발생할 가능성이 있다는 가정 하에) 또는 무작위로 선택된 피벗을 사용하는 최악의 경우 입력에 대한 기대 시간 분석에서, 모든 항목은 피벗으로 선택될 가능성이 동일하다. 이러한 경우, 재귀 과정에서 두 항목이 서로 비교될 확률은 최종 정렬 순서에서 두 항목을 구분하는 다른 항목의 수의 함수로 계산할 수 있다. 항목 와 가 개의 다른 항목으로 구분되는 경우, 이 알고리즘은 재귀가 진행됨에 따라 또는 를 그 사이에 있는 다른 개 항목보다 먼저 피벗으로 선택하는 경우에만 와 를 비교한다. 이 개의 각 항목이 먼저 선택될 가능성이 동일하기 때문에, 이는 확률 로 발생한다. 알고리즘의 총 실행 시간을 제어하는 총 기대 비교 횟수는 모든 쌍에 대해 이러한 확률을 합산하여 계산할 수 있으며, 그 식은 다음과 같다.7. 관련 급수
'''일반 조화 급수'''(general harmonic series영어)는 , 를 실수로 하고, 인 형태로 나타나는 급수이다. 비교 판정법에 의해, 임의의 일반 조화 급수가 발산한다는 것을 알 수 있다.[53]
켐프너 급수(en:Kempner series)는 조화 급수의 항 중에서 분모의 십진 표기 각 자리 숫자 중 9가 나타나는 모든 항을 제거하여 얻어지는 급수이다. 열화 조화 급수는 수렴하며, 그 값은 22.92067...가 된다.[57]
7. 1. 교대 조화 급수
부호가 번갈아 나타나는 조화 급수로, 조건 수렴한다.다음 급수
:
는 '''교대 조화 급수'''(alternating harmonic series영어)로 알려져 있다. 이 급수는 라이프니츠 판정법에 따라 수렴하지만, 절대 수렴하지는 않는다. 그 합은 2의 자연 로그와 같다. 즉,
:
가 성립한다. 이 식은 자연로그 함수의 테일러 급수인 메르카토르 급수의 특수한 경우이다.
역탄젠트 함수의 테일러 급수에서 유도되는 관련 급수로 라이프니츠의 π 공식이 있다.
:
7. 2. 리만 제타 함수
리만 제타 함수는 실수 에 대해 다음과 같은 수렴하는 급수로 정의된다.일 경우 이는 조화 급수가 된다. 이는 해석적 연속을 통해 을 제외한 모든 복소수에 대한 정칙 함수로 확장될 수 있으며, 확장된 함수는 해당 지점에서 단순 극점을 갖는다. 제타 함수의 다른 중요한 값으로는 바젤 문제의 해인 , 아페리 상수 가 있으며, 이는 로제 아페리에 의해 무리수임이 증명되었고, 리만 가설에 의해 이 함수가 0이 될 수 있는 유일한 값(음의 정수 제외)으로 추정되는 실수부가 인 복소수의 "임계선"이 있다.
리만 제타 함수는 p-급수(''p''-series영어)라고 불리는 일반화된 형태로, 양의 실수 p를 사용하여
의 형태로 나타낸다. p=1일 때의 p-급수는 일반적인 조화급수이며, 발산한다. 적분 판정법이나 코시 판정법을 사용하면, p>1일 때 p-급수는 반드시 수렴한다는 것을 알 수 있다(이 때의 p-급수는, 우조화급수(over-harmonic series영어)라고도 불린다). 반대로, p≤1일 때는 발산한다. p>1일 때, p-급수의 합의 값은 리만 제타 함수의 p에서의 값 와 같다.
7. 3. 확률 조화 급수
확률 조화 급수(random harmonic series영어)는 다음과 같다.:
여기서 은 +1과 -1 값을 각각 1/2의 동일한 확률로 가지는 독립 동일 분포 확률 변수열이다. 이 확률 변수의 합이 확률 1로 수렴한다는 것은 콜모고로프 3-계열 정리 등을 이용하여 나타낼 수 있다.[55]
앨버타 대학교의 바이런 슘랜드(Byron Schmuland)는 확률 조화 급수의 성질에 대해 연구했다.[54][55] 슘랜드는 그 극한이 몇 가지 흥미로운 성질을 가진 확률 변수가 됨을 보였다. 특히, 그 확률 변수의 확률 밀도 함수 ±2에서의 값은
: 0.124 999 999 999 999 999 999 999 999 999 999 999 999 764…
이며, 이는 1/8(=0.125)보다 10-42 정도 작다. 슘랜드의 논문에는 이 확률이 1/8에 가깝지만 일치하지 않는다는 설명이 제시되어 있다. 이 확률의 엄밀한 값은
:
로 주어진다.[55]
7. 4. 열화 조화 급수 (켐프너 급수)
켐프너 급수(en:Kempner series)는 조화 급수의 항 중에서 분모의 십진 표기 각 자리 숫자 중 9가 나타나는 모든 항을 제거하여 얻어지는 급수이다. 열화 조화 급수는 수렴하며, 그 값은 22.92067...가 된다.[57] 조화 급수에서 분모에 숫자 9가 어디에든 포함된 항을 모두 제거한 고갈된 조화 급수는 22.92067...로 수렴한다. 실제로, 특정 문자열의 숫자(어떤 진법에서든)를 포함하는 모든 항을 제거하면 급수가 수렴한다.[57]참조
[1]
논문
A family of shifted harmonic sums
[2]
논문
Problems to sharpen the young: An annotated translation of ''Propositiones ad acuendos juvenes''
1992-03
[3]
논문
Sums of reciprocals of integers missing a given digit
1979-05
[4]
논문
Small values of signed harmonic sums
[5]
논문
Partial sums of the harmonic series
[6]
논문
The classical theory of zeta and -functions
[7]
서적
A Radical Approach to Real Analysis
https://books.google[...]
Mathematical Association of America
[8]
서적
Introduction to Algorithms
[9]
서적
Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics
Joseph Henry Press
[10]
논문
The Bernoullis and the harmonic series
1987-01
[11]
논문
Variae observationes circa series infinitas
https://scholarlycom[...]
[12]
논문
On Riemann's rearrangement theorem for the alternating harmonic series
http://eprints.gla.a[...]
[13]
서적
Introduction to Random Graphs
Cambridge University Press, Cambridge
[14]
논문
The jeep once more or jeeper by the dozen
1970-05
[15]
논문
How much is it going to cost me to complete a collection of football trading cards?
2013-04
[16]
서적
Concrete Mathematics
Addison-Wesley
[17]
서적
Gamma: Exploring Euler's Constant
Princeton University Press
[18]
서적
Architecture and Geometry in the Age of the Baroque
University of Chicago Press
[19]
서적
The Pleasures of Probability
Springer-Verlag
[20]
서적
Propositiones arithmeticae de seriebus infinitis earumque summa finita
J. Conrad
1689
[21]
서적
Ars conjectandi, opus posthumum. Accedit Tractatus de seriebus infinitis
https://books.google[...]
Thurneysen
1713
[22]
서적
Opera Omnia
Marc-Michel Bousquet & Co.
1742
[23]
논문
The harmonic series diverges again and again
https://stevekifowit[...]
American Mathematical Association of Two-Year Colleges
2006
[24]
서적
The Art of Computer Programming, Volume I: Fundamental Algorithms
Addison-Wesley
[25]
논문
What's harmonic about the harmonic series?
2001-05
[26]
논문
The "coupon collector's problem" and quality control
2009-03
[27]
논문
A problem in cartophily
1938-10
[28]
서적
Novae quadraturae arithmeticae, seu De additione fractionum
Giacomo Monti
1650
[29]
서적
Quaestiones super Geometriam Euclidis
1360
[30]
논문
96.53 Partial sums of series that cannot be an integer
2012-11
[31]
논문
Maximum overhang
[32]
웹사이트
The coupon collector's problem (with Geoff Marshall)
https://www.youtube.[...]
YouTube
2022-02-12
[33]
논문
Euler and the partial sums of the prime harmonic series
[34]
서적
Mathematical Time Capsules: Historical Modules for the Mathematics Classroom
Mathematical Association of America
[35]
논문
The psi function
[36]
논문
Review of ''A Radical Approach to Real Analysis'' by David M. Bressoud
2007-12
[37]
논문
Could Euler have conjectured the prime number theorem?
[38]
논문
On the -adic valuation of harmonic numbers
[39]
논문
Summing a curious, slowly convergent series
2008-06
[40]
논문
Random harmonic series
http://www.stat.ualb[...]
2003-05
[41]
논문
Problem 52: Overhanging dominoes
https://www.pme-math[...]
[42]
논문
The three infinite harmonic series and their sums (with topical reference to the Newton and Leibniz series for )
[43]
서적
Mathematics and its History
Springer
[44]
논문
Recent progress on the Dirichlet divisor problem and the mean square of the Riemann zeta-function
[45]
서적
Quaestiones super Geometriam Euclidis
c. 1360
[46]
문서
Architecture and Geometry in the Age of the Baroque
[47]
간행물
Problem 52: Overhanging dominoes
[48]
웹사이트
ORメモランダム 古典的オーヴァーハングパズルをLPで解く
https://orsj.org/wp-[...]
日本オペレーションズ・リサーチ学会
2024-07-22
[49]
서적
モデリング: 広い視野を求めて (シリーズ:最適化モデリング 1) 第15章「双対問題の教えてくれるコト
近代科学社
2015-03-20
[50]
서적
Concrete Mathematics
Addison-Wesley
[51]
웹사이트
Sequence A082912 in the On-Line Encyclopedia of Integer Sequences
[52]
url
http://mathworld.wol[...]
[53]
웹사이트
General Harmonic Series
http://www.artofprob[...]
Art of Problem Solving
[54]
간행물
Random Harmonic Series
2003-05
[55]
url
Schmuland's preprint of Random Harmonic Series
http://www.stat.ualb[...]
[56]
웹사이트
Infinite Cosine Product Integral
http://mathworld.wol[...]
2014-11-09
[57]
웹사이트
Nick's Mathematical Puzzles: Solution 72
http://www.qbyte.org[...]
[58]
서적
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com

