게이지 이론 (수학)
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
게이지 이론은 맥스웰 방정식에서 시작되어 양자역학 및 입자물리학 표준 모형의 기초가 되는 수학 및 물리학의 중요한 연구 분야이다. 게이지 이론은 벡터 다발과 주다발, 그리고 그 위에 정의된 접속을 연구하며, 특히 4차원 리만 다양체에서 자기 쌍대성 및 반자기 쌍대성 방정식을 통해 연구가 활발히 진행되었다. 사이먼 도널드슨은 4차원 다양체의 불변량을 구성하여 필즈상을 수상했으며, 에드워드 위튼은 천-사이먼스 이론을 매듭 불변량과 연결하여 위상 양자장론 연구에 기여했다. 3차원 및 2차원 게이지 이론, 특히 양-밀스 이론은 자기 홀극, 힉스 다발, 그리고 천-사이먼스 이론과 같은 다양한 수학적 구조와 연결된다. 4차원에서는 위상 양자장론과 밀접한 관련이 있으며, 도널드슨 불변량, 자이베르그-위튼 불변량과 같은 개념을 통해 4차원 다양체의 미분 구조를 연구하는 데 중요한 역할을 한다. 더 높은 차원에서는 에르미트 양-밀스 방정식 연구가 진행되며, 초끈 이론과 같은 현대 물리학 모델에서도 중요한 역할을 한다.
더 읽어볼만한 페이지
- 수리물리학 - 라플라스 변환
라플라스 변환은 함수 f(t)를 복소수 s를 사용하여 적분을 통해 다른 함수 F(s)로 변환하는 적분 변환이며, 선형성을 가지고 미분방정식 풀이 등 공학 분야에서 널리 사용된다. - 수리물리학 - 불확정성 원리
불확정성 원리는 1927년 베르너 하이젠베르크가 발표한 양자역학의 기본 원리로, 입자의 위치와 운동량 등 짝을 이루는 물리량들을 동시에 정확하게 측정하는 것이 불가능하며, 두 물리량의 불확정성은 플랑크 상수에 의해 제한된다. - 미분기하학 - 가우스 곡률
가우스 곡률은 3차원 유클리드 공간에 놓인 곡면의 두 주곡률의 곱으로, 곡면의 형태를 나타내는 지표이며 곡면 자체의 길이 측정만으로 결정되는 내재적인 값이다. - 미분기하학 - 가우스의 빼어난 정리
가우스의 빼어난 정리는 곡면의 가우스 곡률이 외부 공간이 아닌 곡면 자체의 리만 계량만으로 결정된다는 정리로, 곡면의 변형 시 가우스 곡률이 보존됨을 의미하며, 지도 제작의 불가능성 증명과 고차원 리만 다양체 일반화에 응용되어 미분기하학과 일반 상대성 이론의 기초가 된다.
| 게이지 이론 (수학) | |
|---|---|
| 개요 | |
| 분야 | 수학 |
| 하위 분야 | 미분기하학, 대수적 위상수학, 수리물리학 |
| 주제 | |
| 주요 개념 | 주다발 벡터 다발 접속 곡률 특성류 |
| 관련 이론 | 미분기하학 대수적 위상수학 수리물리학 끈 이론 양자장론 |
| 역사 | |
| 주요 인물 | 천싱선 마이클 아티야 라울 보트 사이먼 도널드슨 알랭 콘 |
| 응용 | |
| 물리학 | 양-밀스 이론 표준 모형 끈 이론 |
| 수학 | 매끄러운 다양체의 불변량 4차원 다양체의 분류 |
2. 역사
게이지 이론은 고전 전자기학을 설명하는 맥스웰 방정식의 공식화에서 시작되었으며, 이는 구조군이 원군인 게이지 이론으로 표현될 수 있다.[1] 폴 디랙의 자기 단극과 상대론적 양자역학에 대한 연구는 다발과 연결이 양자역학의 많은 문제를 표현하는 올바른 방법이라는 아이디어를 촉진시켰다. 수학 물리학의 게이지 이론은 로버트 밀스와 천-닝 양의 양-밀스 게이지 이론에 대한 연구로 중요한 연구 분야로 부상했으며, 이는 현재 입자물리학의 표준 모형의 기초가 되는 기본 모델이다.
게이지 이론에서 중심적으로 연구하는 대상은 주다발과 벡터 다발이다.[54]
수학적 게이지 이론의 연구는 4차원 리만 다양체에서 자기 이중성 방정식을 연구한 마이클 아티야, 이자도어 싱어, 나이젤 히친의 연구에서 시작되었다.[2][3] 이들은 유클리드 공간에서 자기 이중 연결(인스턴턴)의 모듈라이 공간을 연구했으며, 그 차원이 양의 정수 에 대해 임을 보였다. 이는 물리학자들이 인 4차원 양-밀스 방정식의 진공 해인 BPST 인스턴턴을 발견한 것과 연결되었다. 이러한 인스턴턴은 중심 및 규모 를 선택하여 정의되며, 이는 차원 모듈라이 공간에 해당한다.
이와 동시에, 마이클 아티야와 리처드 워드는 자기 이중성 방정식의 해와 복소 투영 공간 에 대한 대수 다발 사이의 연결을 발견했다.[4] 또 다른 중요한 초기 발견은 마이클 아티야, 블라디미르 드린펠트, 나이젤 히친, 유리 마닌에 의한 ADHM 작도의 개발이었다.[5] 이 구성은 순전히 선형 대수 데이터를 사용하여 유클리드 공간 에서 반자기 이중성 방정식의 해를 구할 수 있게 했다.
1980년대 초는 수학적 게이지 이론의 발전에 중요한 돌파구가 된 시기였다. 이 시기에 마이클 아티야와 라울 보트는 리만 곡면에서 양-밀스 방정식에 대한 중요한 연구를 통해 게이지 이론 문제가 흥미로운 기하학적 구조를 생성할 수 있음을 보여주었다. 이는 무한 차원 모멘트 사상, 등변 모스 이론, 게이지 이론과 대수 기하학 간의 관계 발전을 촉진했다.[6] 카렌 울렌벡은 기하학적 해석학의 중요한 분석 도구를 개발했는데, 그는 연결과 곡률의 분석적 특성을 연구하고 중요한 컴팩트성 결과를 증명했다.[7] 이 분야에서 가장 중요한 발전은 사이먼 도널드슨과 에드워드 위튼의 연구에서 비롯되었다.
사이먼 도널드슨은 대수 기하학과 기하학적 해석학 기술을 조합하여 4차원 다양체의 새로운 불변량인 도널드슨 불변량을 구성했다.[8][9] 이러한 불변량은 매끄러운 구조가 없는 위상적 다양체의 존재 또는 유클리드 공간 에 많은 별개의 매끄러운 구조의 존재와 같은 새로운 결과를 증명하는 데 사용되었다. 이 연구로 사이먼 도널드슨은 1986년에 필즈상을 수상했다.
에드워드 위튼은 3차원에서 천-시몬스 이론에서 발생하는 양을 매듭의 불변량인 존스 다항식과 관련시켜 게이지 이론이 위상 불변량을 설명하는 강력함을 관찰했다.[10] 이 연구와 사이먼 도널드슨의 불변량 발견, 그리고 안드레아스 플로어의 플로어 호몰로지에 대한 새로운 연구는 위상 양자장론 연구에 영감을 주었다.
게이지 이론이 다양체의 불변량을 정의하는 강력함을 발견한 후, 수학적 게이지 이론 분야는 인기를 얻었다. 자이베르그-위튼 불변량 및 바파-위튼 불변량과 같은 추가 불변량이 발견되었다.[11][12] 고바야시-히친 대응에 대한 사이먼 도널드슨, 카렌 울렌벡, 싱퉁 야우의 연구를 통해 양-밀스 연결이 안정적 벡터 다발과 관련되어 대수 기하학과의 강력한 연결이 실현되었다.[13][14] 힉스 다발에 대한 나이젤 히친과 카를로스 심슨의 연구는 게이지 이론에서 발생하는 모듈라이 공간이 초켈러 다양체와 같은 이국적인 기하학적 구조를 가질 수 있으며, 히친 시스템을 통해 적분 가능 시스템과 연결될 수 있음을 보여주었다.[15][16] 끈 이론 및 거울 대칭과의 연결이 실현되었으며, 여기서 게이지 이론은 호몰로지 거울 대칭 추측 및 AdS/CFT 대응을 표현하는 데 필수적이다.
3. 기본 연구 대상
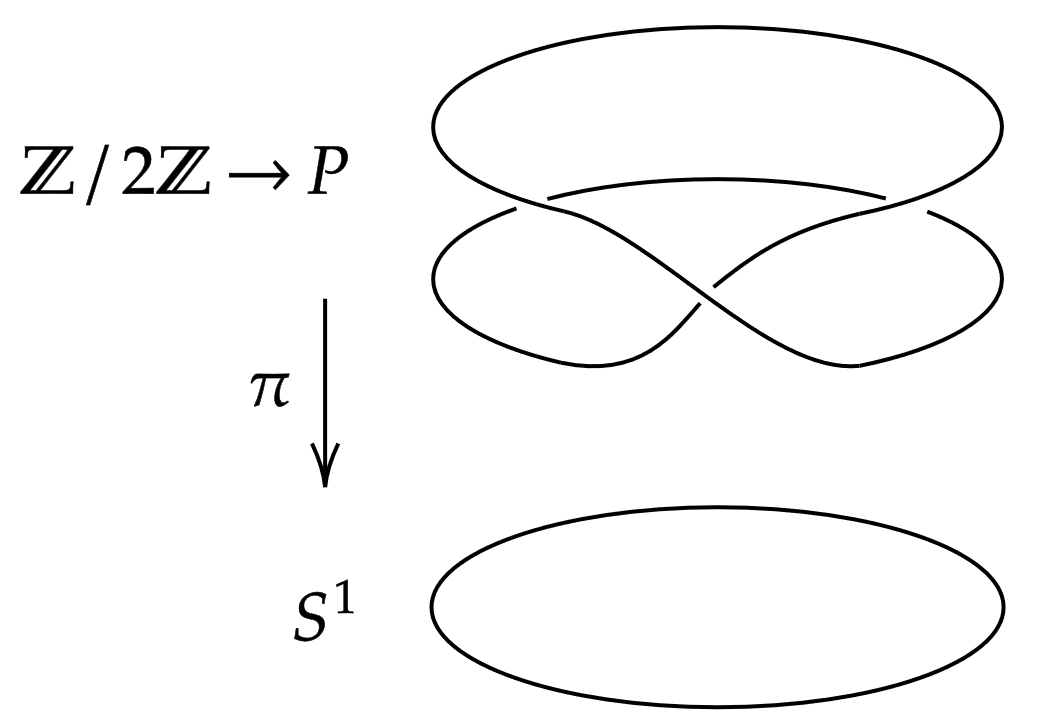
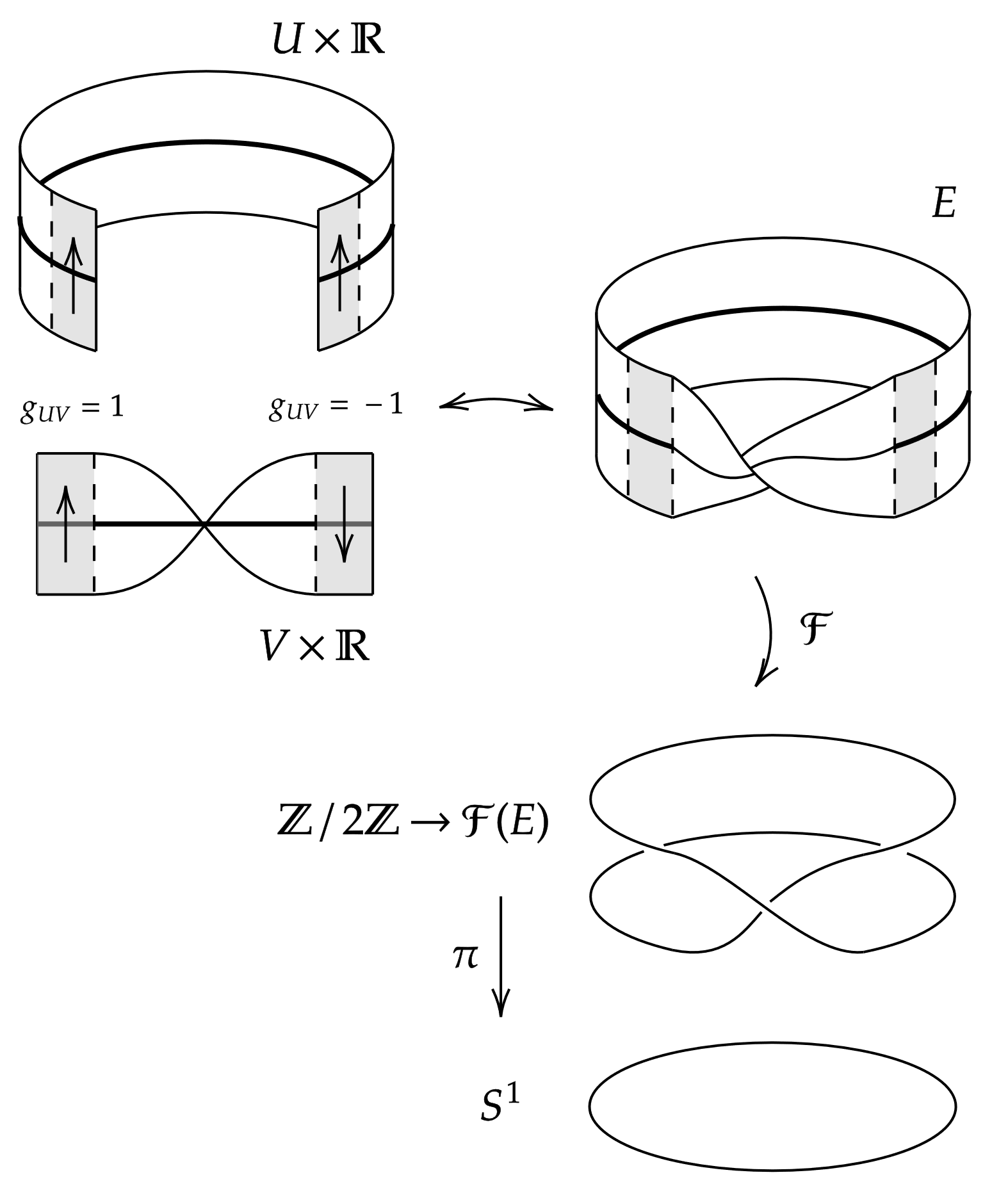
'''구조 군 '''를 가진 '''주다발''' 는 다음 요소들로 구성된다.
각 에 대한 오른쪽 군 작용과 임의로 선택한 에 대해 사상 는 위의 올과 매끄러운 다양체로서 리 군 사이의 미분동형사상 을 정의한다.
주다발의 가장 간단한 예는 구조군 가 원 군 일 때이다. 이 경우 이면 주다발의 차원 이다. 또 다른 예는 가 다양체 의 접다발의 틀다발이거나, 의 선형 다발의 틀다발인 경우다. 이때 의 올은 일반선형군 이다.
주다발은 올다발이므로 국소적으로 곱공간 구조를 갖는다. 따라서 의 열린 덮개 와 미분동형사상 가 존재한다. 는 사영 , 와 가환이며 모든 에서 코사이클 조건
:
이 성립하는 로 정의되는 추이 사상 를 가진다. 주다발을 정의하려면 특정한 추이 사상들을 선택하는 것으로 충분하다. 그런 다음 다발은 에서 추이 사상을 가지고 자명한 다발 들을 붙여서 정의한다. 코사이클 조건 때문에, 이는 분리 합집합 에 대한 동치 관계가 된다. 따라서 몫 공간 은 잘 정의되어 있다. 위 내용은 ''올다발 구성 정리''로 알려져 있으며, 주다발이나 선형 다발뿐만 아니라 추이 사상으로 설명되는 모든 올다발에 대해 동일한 방법이 적용된다.
이 성립하는 ''국소 단면'' 을 선택하는 것은 국소 자명화 사상을 지정하는 것과 동일한 방법이다. 즉, 를 정의할 수 있다. 여기서 는 를 만족하는 유일한 군의 원소이다.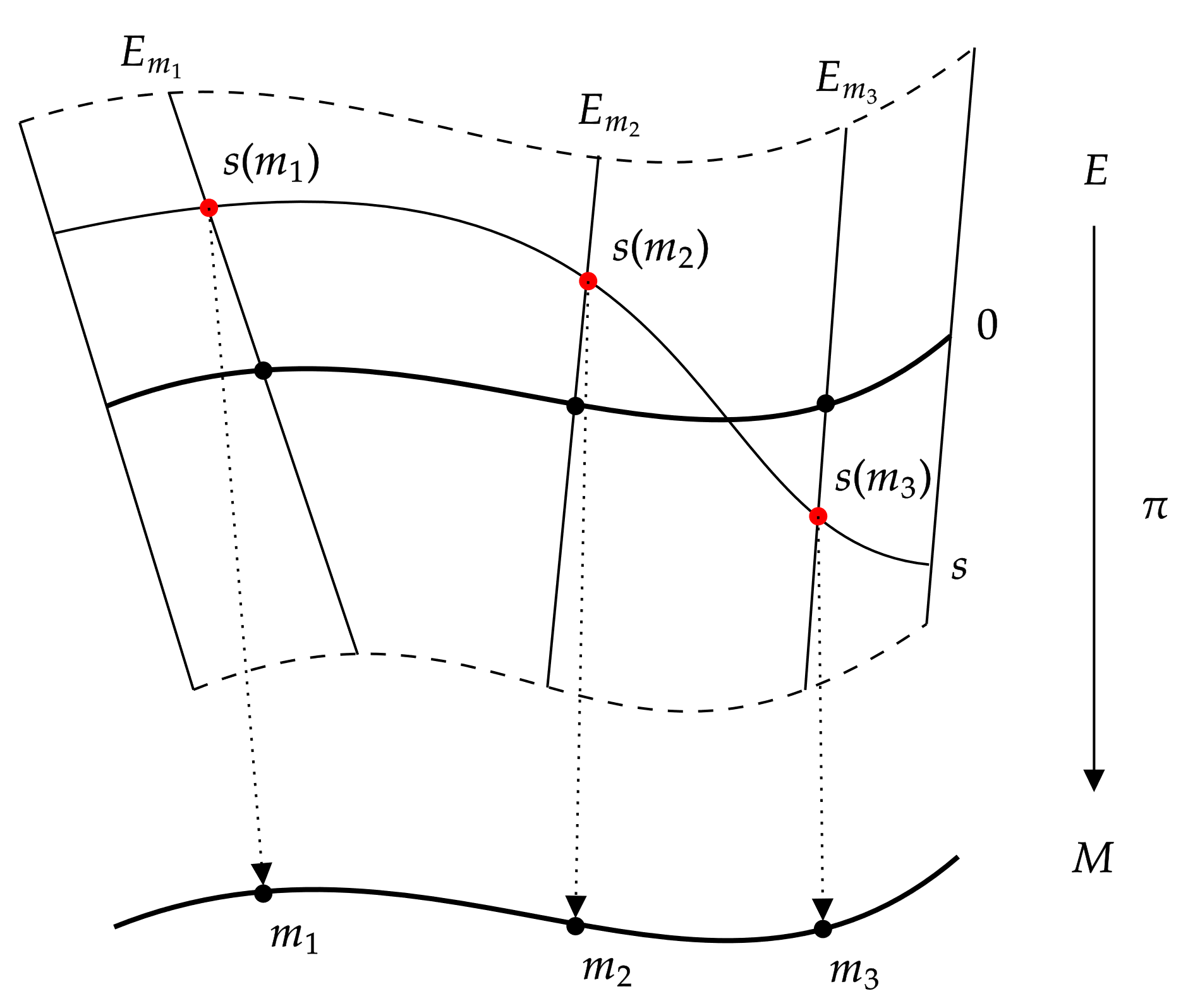
'''선형 다발''' 은 올이 선형 공간 인 올다발 이다. 여기서 이다. 선형 다발은 자명화하는 열린 덮개 를 통해 국소적으로 묘사할 수 있다. 동형사상
:
에 대해, 선형 공간 의 기저 벡터 에 해당하는 의 서로 다른 국소 단면 를 얻는다. 이들은 다음 방정식으로 정의된다.
:
따라서 자명화를 특정하는 것은, 모든 곳에서 선형 독립인 개의 국소 단면들의 모임을 주고 이 표현을 사용하여 해당 동형을 정의하는 것과 같다. 이러한 국소 단면들의 모임을 ''틀''이라고 한다.
주다발과 유사하게, 선형 다발에 대해, 다음과 같이 정의된 추이 사상 을 얻는다.
:
이 추이 사상을 가지고 구조 군 과 동형인 올을 가진 주다발에 대한 국소 자명화를 구성하는 경우, -주다발 의 틀다발을 얻는다.
주어진 -주다발 와 선형 공간 위에서 의 표현 에 대해, 선형 공간 를 올로 가지는 '''연관된 선형 다발''' 을 구성할 수 있다. 이 선형 다발을 정의하기 위해, 곱공간 에 대한 로 정의되는 오른쪽 군 작용을 고려한다. 그리고 를 이 작용에 대한 몫 공간으로 정의한다.
추이 사상 관점에서 연관된 다발을 더 간단하게 이해할 수 있다. 주다발 가 국소 자명화 에 대한 추이 사상 을 가지고 있으면, 을 사용하여 관련 선형 다발을 구성할 수 있다.
연관된 다발 구성은 군 동형 사상 이 주어진 선형 공간뿐만 아니라 모든 올 공간 에 대해 수행할 수 있다. 한 가지 주요 예는 로 정의된 군 동형 사상 를 이용하여 구성된 올을 가진 ''대문자 A 인접 다발'' 이다. 올 를 가졌음에도 불구하고, 이 인접 다발은 주다발도 아니고 올다발처럼 자신과 동형이 아니다. 예를 들어 군 가 가환이면 켤레 작용이 자명하고, 도 가 자명하든 그렇지 않든 상관 없이, 위의 자명한 -올다발이 된다. 또 다른 주요 예는 의 리 대수 에 대해, 딸림표현 을 사용하여 구성된 ''소문자 인접 다발'' 이다.
4. 표기법
게이지 이론에서 사용되는 다양한 표기법은 다음과 같이 정리할 수 있다.
- '''A''': 선형 다발이나 주다발에서 정의된 접속을 나타낼 때 가장 일반적으로 사용되는 기호이다. 이는 다음 두 가지 이유 때문이다.
- 모든 접속들 중에서 한 접속 를 고르면, 다른 모든 접속들은 어떤 1-형식 에 대해 로 표현 가능.
- 선형 다발의 접속의 국소 형식을 로 나타내며, 이는 전자기학에서 전자기 포텐셜을 나타내는 기호 A와 동일.
- 때로는 기호 가 접속 형식을 나타낼 때 쓰이기도 하지만, 이 경우 대역적 접속 1-형식 를 뜻하며, 수학에서는 잘 사용하지 않는다.
- '''∇''': 미분 연산자로서 선형 다발 위의 접속을 나타내거나, 공변 도함수 를 나타낼 때 쓰인다.
- 는 공변 도함수가 A에 따라 달라짐을 강조.
- '''dA''': 접속 A의 공변 외미분을 나타낼 때 가장 많이 쓰인다. 0차 공변 외미분은 공변 도함수와 같기 때문에, 접속 또는 공변 도함수를 대신 로 나타내기도 한다.
- '''FA''' 또는 '''F∇''': 접속의 곡률을 나타낸다. 접속이 로 표기되는 경우 곡률은 로 표기한다.
- '''H''': 주다발 접속 또는 에레스만 접속이 수평 분포 위에 위치함을 강조.
- '''ad(P)''': 리 대수 수반 다발.
- '''Ad(P)''': 리 군 수반 다발.
수학적 표기법과 물리학적 표기법 사이의 대응 관계는 다음 표와 같다.[55][17][19]
| 수학 | 물리학 |
|---|---|
| 주다발 | 인스턴톤 섹터 또는 차지 섹터 |
| 구조군 | 게이지 군 또는 국소 게이지 군 |
| 게이지 군 | 대역적 게이지 변환 군 또는 대역적 게이지 군 |
| 게이지 변환 | 게이지 변환 또는 게이지 대칭 |
| 국소 자명화의 변화 | 국소 게이지 변환 |
| 국소 자명화 | 게이지 |
| 국소 자명화를 선택한다 | 게이지를 고정한다 |
| 접속 공간에 정의된 함수 | 게이지 이론의 라그랑지언 |
| 게이지 변환에 대해 대상이 바뀌지 않는다. | 게이지 불변성 |
| 접속에 대해 공변적으로 일정한 게이지 변환 | 대역적 게이지 대칭성 |
| 접속에 대해 공변적으로 일정하지 않은 게이지 변환 | 국소적 게이지 대칭성 |
| 접속 | 게이지 장 또는 게이지 포텐셜 |
| 곡률 | 게이지 장의 세기 또는 장의 세기 |
| 연관된 다발 위에서 유도된 접속/공변 도함수 | 최소 결합 |
| 연관된 선형 다발의 단면 | 물질장 |
| 여러 다른 양을 포함하는 라그랑주 함수의 항 | 상호 작용 |
| 실 또는 복소(보통 자명한) 선다발의 단면 | (실수 또는 복소수) 스칼라장 |
5. 양-밀스 이론
미분 기하학에서 게이지 이론은 마이클 아티야, 이저도어 싱어 및 나이절 히친의 4차원 리만 다양체에 대한 자기 쌍대 방정식 연구에서 시작되었다.[39][40] 이들은 유클리드 공간에서 자기 쌍대 접속(순간자)의 모듈라이 공간을 연구했고, 이 공간이 양의 정수 에 대해 차원임을 보였다. 이는 물리학자들의 BPST 순간자 발견과 일 때 4차원 양-밀스 방정식에 대한 진공 해와 관련이 있다.
양-밀스 이론은 수학적 게이지 이론에서 중요한 이론이다. 양-밀스 이론에서는 '''양-밀스 범함수'''를 이용해 정의되는 접속을 연구한다. 양-밀스 범함수는 다음과 같이 정의된다.
:
여기서 는 부피 형식 와 인접 다발 에 대한 -norm인 가 주어진 향을 줄 수 있는 리만 다양체이다. 이 범함수는 접속 의 곡률의 -norm의 제곱이므로, 이 범함수의 임계점인 접속은 곡률이 최소인 접속이다.
이러한 임계점들은 연관된 오일러-라그랑주 방정식에 해당하는 '''양-밀스 방정식'''의 해로 특징지어진다.
:
여기서 는 위에서 정의된 의 유도된 공변 외미분이고, 는 호지 별 연산자이다. 이러한 해를 '''양-밀스 접속'''이라고 하며, 기하학적으로 중요하다.
비앙키 항등식에 따라 모든 접속에 대해 이다. 미분 형식과 비슷하게, 조화 형식 는 으로 특징지어진다. 따라서 으로 조화 접속을 정의하면, 양-밀스 접속 연구는 조화 형식 연구와 본질적으로 비슷하다. 호지 이론에서 모든 드람 코호몰로지류 의 유일한 조화 대표원을 얻는다. 코호몰로지류를 게이지 궤도 로 대체하면, 양-밀스 접속 연구는 몫 공간 에서 각 궤도에 대한 고유한 대표원을 찾는 것으로 볼 수 있다.
5. 1. 자기 쌍대성 및 반 자기 쌍대성 방정식
4차원에서 호지 별 연산자 는 2-형식을 2-형식으로 보내며 (), 제곱하면 항등원이 된다(). 따라서 2-형식에 작용하는 호지 별은 고윳값 을 갖는다. 방향을 줄 수 있는 4차원 리만 다양체에서 정의된 2-형식은 다음과 같이 분해된다.:
이는 호지 별 연산자의 과 고윳값에 대응하는 '''자기 쌍대''' 및 '''반 자기 쌍대''' 2-형식으로 분해한 것이다. 즉, 가 이면 자기 쌍대이고, 이면 반 자기 쌍대이다. 모든 2-형식은 처럼 자기 쌍대 및 반 자기 쌍대 부분으로 분해할 수 있다.
4차원 다양체를 밑공간으로 하는 주다발의 접속 의 곡률이 자기 쌍대 또는 반 자기 쌍대이면, 비앙키 항등식에 의해 이므로, 이 접속은 자동적으로 양-밀스 방정식의 해가 된다. 방정식
:
는 접속 에 대한 1차 편미분 방정식이므로, 2차 양-밀스 방정식보다 연구하기 쉽다. 는 '''자기 쌍대 방정식''', 는 '''반 자기 쌍대 방정식'''이라 부른다. 이 방정식의 해는 각각 '''자기 쌍대 접속'''과 '''반 자기 쌍대 접속'''이다.[75]
5. 2. 차원 축소
차원 축소는 양-밀스 방정식을 더 낮은 차원에서 연구하기 위해 사용되는 기법이다. 이 과정을 통해 원래 방정식의 해가 특정 대칭성을 갖도록 제한함으로써, 더 단순하고 다루기 쉬운 새로운 방정식들을 얻을 수 있다.차원 축소의 대표적인 예로는 보고몰니 방정식, 남 방정식, 히친 방정식 등이 있다. 이들은 각각 4차원 양-밀스 방정식을 3차원, 1차원, 2차원으로 축소하여 얻어진다.
- 보고몰니 방정식: 4차원 유클리드 공간에서 정의된 양-밀스 방정식의 해가 한 방향으로의 평행 이동에 대해 불변이라는 조건을 추가하여 얻어진다. 이 방정식은 3차원 공간에서 자기 홀극을 기술하는 데 사용된다.[59]
- 남 방정식: 4차원 양-밀스 방정식의 해가 세 방향으로의 평행 이동에 대해 불변이라는 조건을 추가하여 얻어진다. 이 방정식은 1차원, 즉 실수 구간에서 정의되며, 다음과 같은 연립 미분 방정식으로 표현된다.[59]
:
여기서 는 실수 구간 에서 정의된 행렬 값 함수이다. 남 방정식의 해는 보고몰니 방정식의 해와 밀접하게 관련되어 있으며,[60] 복소 사영 직선에서 자기 자신으로의 유리 사상과도 대응된다.[61]
- 히친 방정식: 4차원 양-밀스 방정식의 해가 두 방향으로의 평행 이동에 대해 불변이라는 조건을 추가하여 얻어진다. 이 방정식은 2차원, 즉 리만 곡면에서 정의되며, 다음과 같은 연립 방정식으로 표현된다.[62]
:
여기서 는 접속 형식, 는 힉스라고 불리는 복소수 값 함수이다. 히친 방정식의 해는 힉스 다발과 밀접하게 관련되어 있으며,[52][53] 비가환 호지 정리를 통해 고차원 켈러 다양체로 일반화될 수 있다.[63][64][65][66][67]
이처럼 차원 축소를 통해 얻어진 방정식들은 원래의 양-밀스 방정식보다 더 단순하지만, 여전히 풍부한 기하학적, 위상수학적 정보를 담고 있다. 이 방정식들의 해를 연구함으로써, 원래 양-밀스 이론의 다양한 측면을 이해할 수 있을 뿐만 아니라, 새로운 수학적 구조를 발견할 수 있다.
6. 1차원 및 2차원 게이지 이론
기저 다양체 가 낮은 차원일 때 양-밀스 방정식은 1차원에서는 2-형식이 없고, 2차원에서는 2-형식에 대한 호지 별 연산자가 로 작용하기 때문에 단순화된다.
2차원 다양체에서는 양-밀스 방정식을 직접 연구할 수 있다. 마이클 아티야와 라울 보트는 기저 다양체가 콤팩트 리만 곡면일 때 양-밀스 방정식을 연구하였다.[56] 이 경우 복소 선형 다발 에 대한 양-밀스 접속의 모듈라이 공간은 다양하고 풍부하게 해석되며, 더 높은 차원의 방정식을 이해하는 가장 간단한 경우가 된다. 양-밀스 방정식은 에 따라 다른 위상 수학적 상수 에 대해 다음과 같다.
:
이러한 접속을 ''사영적으로 평평하다''고 하며, 선형 다발이 위상학적으로 자명한 경우() 평탄 접속이 된다.
선형 다발의 랭크와 차수가 서로소인 경우, 양-밀스 접속의 모듈라이 공간 은 매끄러우며, 심플렉틱 다양체 구조를 가진다. 아티야와 보트는 이 공간이 리만 곡면의 기본 군의 사영 유니타리 표현의 모듈라이 공간인 character variety과 동등하다고 설명했다. 나라심한-세샤드리 정리는 와 동형인 안정한 정칙 선형 다발의 모듈라이 공간으로서 이 표현들의 공간에 대한 대안적인 설명을 제공한다.[57] 이 동형사상을 통해 양-밀스 접속의 모듈라이 공간은 아티야 및 보트의 심플렉틱 구조와 상호 작용하여 콤팩트 켈러 다양체를 만드는 복소 구조를 얻는다.
사이먼 도널드슨은 양-밀스 접속에서 안정적 정칙 구조로 직접 전달된 나라심한과 세샤드리 정리의 대안적인 증명을 제시했다.[58] 아티야와 보트는 게이지 군 의 작용에 대한 무한 차원 운동량 사상으로서 극단적인 양-밀스 접속과 선형 다발의 안정성 사이의 관계를 밝혔다.
워너 남이 도입한 남 방정식은 세 방향의 병진 불변성을 이용해 4차원에서 반 자기 쌍대성을 1차원으로 차원 축소해서 얻어진다.[59] 접속 형식 이 좌표에 대해 불변이 되도록 조건을 주면, 구간 위에서 네 가지 행렬들 에 대한 연립 방정식인 남 방정식은 다음 연립 방정식을 만족한다.
:
남은 이 방정식의 해가 의 자기 홀극을 묘사하는 보고몰니 방정식의 해를 구성하는데 쓰일 수 있음을 보였다. 나이절 히친은 두 문제의 해가 동치임을 보였다.[60] 도널드슨은 남 방정식의 해들이 복소 사영 직선 에서 자신으로 가는 차 유리형 사상과 동치임을 보였다.[61] 남 방정식에 대한 해의 모듈라이 공간은 초켈러 다양체 구조를 가진다.
나이절 히친이 도입한 히친 방정식은 4차원의 자기 쌍대 방정식을 두 방향으로 병진 불변성을 부과하여 2차원으로 차원 축소하여 얻어진다.[62] 두 개의 추가 접속 형식 성분 들은 단일 복소수 값 자기 사상 으로 결합될 수 있다. 방정식은 공형 불변이 되므로 보다는 콤팩트 리만 곡면 위에서 하는 것이 자연스럽다. 히친 방정식은 인 복소 선형 다발 위의 쌍 에 대해 다음과 같다.
:
여기서 는 의 -성분이다. 히친 방정식의 해를 '''히친 쌍'''이라고 한다.
히친은 히친 방정식에 대한 해가 곡면 군의 사영 복소수 표현에 해당함을 보여주었다. 히친 쌍의 모듈라이 공간은 자연스럽게 켈러 다양체의 구조를 갖는다. 히친은 히친 쌍이 이른바 안정적인 힉스 다발에 해당함을 보여주었다. 여기서 힉스 다발은 쌍 이며, 는 홀로모픽 선형 다발이고 는 리만 곡면 의 표준 선다발 값을 가지는 의 정칙 자기 사상이다. 힉스 다발의 모듈라이 공간 에서 두 개의 복소 구조로 이어진다. 이들은 결합하여 이 모듈라이 공간을 초켈러 다양체로 만드는 세 번째 요소를 제공한다.
히친의 작업은 카를로스 심슨에 의해 일반화되었으며, 히친 방정식의 해와 임의의 켈러 다양체에 대한 힉스 다발 사이의 대응 관계는 비가환 호지 정리로 알려져 있다.[63][64][65][66][67]
7. 3차원 게이지 이론
한 방향으로의 병진 불변성을 이용해 양-밀스 방정식을 3차원으로 차원 축소하면, 가 행렬족인[68] 쌍 에 대한 보고몰니 방정식이 유도된다. 이 방정식은 다음과 같다.
:
구조군이 원군 인 주다발 에서, 보고몰니 방정식의 해는 고전 전자기학의 자기 홀극을 설명하는 디랙 홀극을 모형으로 한다. 남과 히친의 연구에 따르면, 구조군이 특수 유니터리 군 일 때 자기 홀극 방정식의 해는 남 방정식의 해에 해당한다. 도날드슨의 연구에 의해, 이는 자기 홀극의 전하가 일 때 에서 자신으로 가는 차 유리 사상에 대응한다는 것이 밝혀졌다. 이 전하는 다음 식으로 정의된다.
:
이는 안의 구 위에서 쌍 적분의 반지름 이 무한대로 갈 때의 극한값이다.
3차원 천-사이먼스 이론은 천-사이먼스 형식의 적분에 비례하는 작용 범함수를 갖는 위상 양자장론이다. 천-사이먼스 형식은 다음과 같이 정의된다.
:
닫힌 3차원 다양체 에서 천-사이먼스 범함수의 오일러-라그랑주 방정식의 고전적 해는 구조군 를 갖는 주다발 의 평탄 접속에 해당한다. 그러나 의 경계가 있으면 상황은 더 복잡해진다. 에드워드 위튼은 매듭 불변량인 존스 다항식을 위에서 천-사이먼스 이론 안의 윌슨 고리의 진공 기댓값으로 표현했다.[69] 이는 위상수학에 대한 새로운 통찰력을 제공하는 게이지 이론 문제의 힘을 보여주는 사례였으며, 위상 양자장론의 초기 사례 중 하나였다.
고전적인 천-사이먼스 이론을 양자화하면, 3차원 다양체 안의 곡면 으로 제한된 주 다발에서 유도된 평면 또는 사영적 평탄 접속을 연구하게 된다. 각 곡면에 해당하는 고전적 상태 공간은 아티야와 보트가 연구한 양-밀스 방정식의 모듈라이 공간과 정확히 일치한다.[70] 이 공간들의 기하학적 양자화는 나이절 히친과 Axelrod-Della Pietra-위튼에 의해 독립적으로 이루어졌으며, 구조군이 복소적인 경우 구성 공간은 힉스 다발의 모듈라이 공간이 된다. 이 양자화는 위튼에 의해 수행되었다.[71][72][73]
안드레아스 플로어는 유한 차원에서 모스 호몰로지와 비슷하게 정의된 3차원 다양체에 대한 호몰로지 유형을 도입했다.[74] 이 호몰로지 이론에서 모스 함수는 구조군 를 가지는 3차원 다양체 위의 주다발의 접속들의 공간에서 정의된 천-사이먼스 범함수이다. 임계점은 평탄 접속이며, 흐름선은 두 경계 요소의 임계 평탄 접속으로 제한된 위의 양-밀스 순간자로 정의된다. 이는 '''순간자 플뢰어 호몰로지'''로 이어진다. 아티야-플뢰어 추측은 순간자 플뢰어 호몰로지가 의 히가드 분할을 정의하는 곡면 의 평탄 접속의 모듈라이 공간의 라그랑주 교차 플뢰어 호몰로지와 일치한다고 주장한다. 이는 아티야와 보트의 관찰로 인해 심플렉틱이다.
순간자 플뢰어 호몰로지와 비슷하게, 순간자가 자이베르그-위튼 방정식의 해로 대체되는 자이베르그-위튼 플뢰어 호몰로지를 정의할 수 있다. 클리포드 타우베스의 업적에 의해 이것은 매장된 접촉 호몰로지와, 후속적으로 히가드 플뢰어 호몰로지에 대해 동형인 것으로 알려져 있다.
8. 4차원 게이지 이론
4차원 게이지 이론은 입자 물리학의 표준 모형이 4차원 시공간에서 양자장론으로 생각할 수 있기 때문에 물리학적 게이지 이론과 상당히 겹치며, 자연스럽게 위상 양자장론으로 이어진다. 위상 양자장론은 배경이 되는 4차원 리만 다양체에 주어진 리만 계량의 변화에 민감하지 않은 물리학적 게이지 이론이므로, 다양체의 미분 위상 수학적 불변량을 정의하는 데 사용될 수 있다.[75]
4차원에서 양-밀스 방정식은 향을 줄 수 있는 4차원 리만 다양체 를 기저 다양체로 하는 주다발 의 접속 에 대한 1차 반자기 쌍대 방정식 으로 단순화된다.[75] 이 방정식의 해는 양-밀스 범함수의 절대 최소값을 나타내며, 더 높은 임계점은 반자기 쌍대 접속에서 발생하지 ''않는'' 해 에 해당한다. 반자기 쌍대 방정식에 대한 해의 모듈라이 공간 에서 배경 4차원 다양체에 대한 유용한 불변량을 도출할 수 있다.
이 이론은 가 단일 연결 공간인 경우에 가장 효과적이다. 예를 들어, 이 경우 도널드슨 정리는 4차원 다양체가 음의 정부호 교차 형식 (4차원 다양체)를 갖고 주 다발이 구조 군 을 갖고 천 특성류 을 가진다면, 모듈라이 공간 은 5차원이며 자신과 들 개 분리 합집합 사이에 보충 경계를 제공한다(방향이 반대인 경우). 이는 이러한 4차원 다양체의 교차 형식이 대각화 가능함을 의미한다. E8 다양체와 같이 대각화 불가능한 교차 형식을 갖는 단순 연결 위상 4차원 다양체의 예가 있으므로, 도널드슨 정리는 미분 구조를 부여할 수 없는 4차원 위상 다양체의 존재를 암시한다. 이는 위상 구조와 매끄러운 구조가 동등한 2차원 또는 3차원 다양체의 경우와 극명한 대조를 이룬다. 3보다 작거나 같은 차원의 모든 위상 다양체는 유일한 미분 구조를 갖는다.
클리포드 토브스와 도널드슨은 비슷한 방법을 사용하여 유클리드 공간 이 비가산 무한 가지의 서로 다른 미분 구조들을 허용함을 보여주었다. 이는 4차원이 아닌 모든 유클리드 공간이 유일한 미분 구조를 가지고 있다는 사실과 극명한 대조를 이룬다.
이러한 아이디어의 확장은 도날드슨 이론으로 이어지며, 이는 접속들의 모듈라이 공간에서 매끄러운 4차원 다양체의 추가적 불변량을 구성한다. 이러한 불변량들은 카렌 울렌벡, 토브스 및 도널드슨이 모듈라이 공간의 향을 줄 수 있음과 콤팩트성을 보여주는 해석학적 작업으로 인해 존재하는 기본류에 대해 모듈 공간의 코호몰로지 류를 계산하여 얻는다.
4차원 다양체가 켈러 다양체 또는 대수 곡면이고 주다발이 소멸하는 첫 번째 천 특성류를 가질 때, 반자기 쌍대 방정식은 복소 다양체 의 에르미트 양-밀스 방정식과 동일하다. 도널드슨과 일반적으로 울렌벡 및 야우싱퉁에 의해 대수 곡면에 대해 입증된 고바야시-히친 대응은 HYM 방정식에 대한 해가 안정적인 정칙 선형 다발에 해당한다고 주장한다. 이 작업은 모듈라이 공간과 그 콤팩트화에 대한 대안적인 대수적 설명을 제공했는데, 이는 복소 다양체에 대한 '준안정' 정칙 선형 다발의 모듈라이 공간이 사영 다형체이고, 따라서 콤팩트하기 때문이다. 이것은 연결의 모듈라이 공간을 콤팩트화하는 한 가지 방법이 소위 '준 해밀턴 양-밀스 접속'이라고 하는 준안정 선형 다발에 해당하는 접속을 추가하는 것임을 나타낸다.
4차원 공간에서 초대칭을 연구하는 동안, 에드워드 위튼과 나탄 자이베르그는 현재 자이베르그-위튼 방정식이라고 하는 접속 와 스피너 장 에 대한 연립 방정식을 발견했다.[76] 이 경우 4차원 다양체는 디터미넌트 선 다발 과 연관된 스피너 다발 에 대한 스핀C 주다발 를 정의하는 스핀C 구조를 허용해야 한다. 여기서 접속 는 의 접속이고, 스피너 장 는 이다. 자이베르그-위튼 방정식은 다음과 같다:
:
자이베르그-위튼 방정식의 해를 자기 홀극이라고 한다. 자이베르그-위튼 방정식에 대한 해의 모듈라이 공간 (여기서 는 스핀 구조의 선택을 나타낸다.)은 자이베르그-위튼 불변량을 유도하는 데 사용된다. 자이베르그-위튼 방정식은 방정식 자체가 해의 모듈라이 공간에 더 나은 특성을 제공하기 위해 약간 섭동될 수 있다는 점에서 반자기 쌍대 방정식보다 이점이 있다. 이를 위해 임의의 자기 쌍대 제2형식을 첫 번째 방정식에 추가한다. 배경 4차원 다양체에서 계량 의 일반적인 선택과 섭동 제2형식의 선택에 대해, 해의 모듈라이 공간은 매끄러운 콤팩트 다양체이다. 적당한 조건에서(즉, 다양체 가 '단순 유형'일 때), 이 모듈라이 공간은 0차원이다. 즉, 유한한 수의 점들의 집합이다. 이 경우 자이베르그-위튼 불변량은 단순히 모듈라이 공간의 점들의 수이다. 자이베르그-위튼 불변량은 도널드슨 불변량과 동일한 결과를 증명하는 데 사용할 수 있지만 더 일반적으로 적용되는 더 쉬운 증명을 사용하는 경우가 많다.
9. 더 높은 차원의 게이지 이론
켈러 다양체 또는 에르미트 다양체 위에서 양-밀스 접속의 특정 부류에 대한 연구가 가능하다. 에르미트-양-밀스 방정식은 4차원 양-밀스 이론에서 나타나는 자기 반쌍대성을 에르미트 복소 다양체 위의 정칙 벡터 다발로 일반화한 것이다.
콤팩트 켈러 다양체 위에 정의된 정칙 벡터 다발 와, 에르미트 계량 에 대한 위의 에르미트 접속 가 주어졌을 때, 에르미트-양-밀스 방정식은 다음과 같이 표현된다.
:
여기서 는 에 의존하는 위상 상수이다. 이 방정식은 에르미트 접속 에 대한 방정식으로 볼 수도 있고, 연관된 천 접속 를 갖는 해당 에르미트 계량 에 대한 방정식으로 볼 수도 있다. 4차원에서 HYM 방정식은 ASD 방정식과 동일하며, 2차원에서는 아티야와 보트가 고려한 양-밀스 방정식에 해당한다.
고바야시-히친 대응은 HYM 방정식의 해가 반안정 정칙 벡터 다발과 대응된다고 명시한다. 콤팩트 리만 곡면의 경우, 이는 도널드슨이 증명한 나라시만-세샤드리 정리와 같다. 대수 곡면의 경우에는 도널드슨이 증명했고, 일반적인 경우에는 카렌 울렌벡과 싱퉁 야우가 증명했다.[13][14] 이 정리는 심슨에 의해 비가환 호지 정리로 일반화되었으며, 이는 힉스 다발 에서 힉스 장을 0으로 설정한 특수한 경우이다.[26]
양-밀스 방정식의 해가 4차원 다양체의 불변량을 정의하는 데 효과적이라는 사실은, 7차원 G2 다양체 및 8차원 Spin(7) 다양체와 같은 예외적인 홀로노미 다양체와 칼라비-야우 6-다양체, 근접 켈러 다양체와 같은 관련 구조를 구별하는 데 도움이 될 수 있다는 관심을 불러일으켰다.[36][37]
초끈 이론 모델에서는 새로운 게이지 이론 문제가 발생한다. 이 모델에서 우주는 4차원 일반 시공간과 6차원 칼라비-야우 다양체로 구성된 10차원으로 표현된다. 이 이론에서 끈에 작용하는 장은 고차원 공간 위의 다발에 존재하며, 이와 관련된 게이지 이론 문제가 중요하다. 예를 들어, 초끈 이론에서 끈 반경이 0으로 수렴할 때 (''큰 부피 극한'') 칼라비-야우 6차원에서의 자연 장 이론 극한은 이 다양체에 대한 에르미트-양-밀스 방정식으로 주어진다. 큰 부피 극한에서 벗어나면, 초끈 이론의 B-모델에서 D-브레인의 운동 방정식을 설명하는 변형된 에르미트-양-밀스 방정식을 얻게 된다. 거울 대칭은 이러한 방정식의 해가 거울 쌍대 칼라비-야우 다양체의 특수 라그랑지안 부분다양체에 대응되어야 한다고 예측한다.[38]
참조
[1]
논문
Conservation of isotopic spin and isotopic gauge invariance
Physical review
1954
[2]
논문
Deformations of instantons
Proceedings of the National Academy of Sciences
1977
[3]
논문
Self-duality in four-dimensional Riemannian geometry
Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences
1978
[4]
논문
Instantons and algebraic geometry
Communications in Mathematical Physics
1977
[5]
논문
Construction of instantons
Physics Letters A
1978
[6]
논문
The yang-mills equations over riemann surfaces
Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences
1983
[7]
논문
Connections with Lp bounds on curvature
Communications in Mathematical Physics
1982
[8]
논문
An application of gauge theory to four-dimensional topology
Journal of Differential Geometry
1983
[9]
논문
Polynomial invariants for smooth four-manifolds
Topology
1990
[10]
논문
Quantum field theory and the Jones polynomial
Communications in Mathematical Physics
1989
[11]
논문
Monopoles and four-manifolds.
https://arxiv.org/ab[...]
Mathematical Research Letters
1994
[12]
논문
A strong coupling test of S-duality
arXiv preprint
1994
[13]
논문
Anti self-dual Yang-Mills connections over complex algebraic surfaces and stable vector bundles
Proceedings of the London Mathematical Society
1985
[14]
논문
On the existence of Hermitian–Yang-Mills connections in stable vector bundles.Frontiers of the mathematical sciences: 1985 (New York, 1985)
Communications on Pure and Applied
[15]
논문
The self-duality equations on a Riemann surface
Proceedings of the London Mathematical Society
1987
[16]
논문
Higgs bundles and local systems
http://www.numdam.or[...]
Publications Mathématiques de l'IHÉS
1992
[17]
서적
The geometry of four-manifolds
Oxford University Press
1990
[18]
서적
Gauge theory and variational principles
Courier Corporation
2005
[19]
서적
An introduction to quantum field theory
Westview Press
1995
[20]
논문
Stable and unitary vector bundles on a compact Riemann surface
Annals of Mathematics
1965
[21]
논문
A new proof of a theorem of Narasimhan and Seshadri
Journal of Differential Geometry
1983
[22]
논문
All self-dual multimonopoles for arbitrary gauge groups
Springer, Boston, MA
1983
[23]
논문
On the construction of monopoles
Communications in Mathematical Physics
1983
[24]
논문
Nahm's equations and the classification of monopoles
Communications in mathematical physics
1984
[25]
논문
The self‐duality equations on a Riemann surface
Proceedings of the London Mathematical Society
1987
[26]
논문
Constructing variations of Hodge structure using Yang-Mills theory and applications to uniformization
Journal of the American Mathematical Society
1988
[27]
논문
Higgs bundles and local systems
Publications Mathématiques de l'IHÉS
1992
[28]
논문
Moduli of representations of the fundamental group of a smooth projective variety I
Publications Mathématiques de l'IHÉS
1994
[29]
논문
Moduli of representations of the fundamental group of a smooth projective variety. II
https://doi.org/10.1[...]
Publications Mathématiques de L’Institut des Hautes Scientifiques
1994
[30]
논문
The Hodge filtration on nonabelian cohomology
arXiv preprint
1996
[31]
서적
The geometry and dynamics of magnetic monopoles
Princeton University Press
1988
[32]
논문
Flat connections and geometric quantization
Communications in mathematical physics
1990
[33]
논문
Geometric quantization of Chern–Simons gauge theory
representations
1991
[34]
논문
Quantization of Chern-Simons gauge theory with complex gauge group
Communications in Mathematical Physics
1991
[35]
논문
An instanton-invariant for 3-manifolds
Communications in mathematical physics
1988
[36]
서적
Gauge theory in higher dimensions
Oxford Univ. Press
[37]
서적
Gauge theory in higher dimensions, II
Int. Press
[38]
논문
From special lagrangian to hermitian-Yang-Mills via Fourier-Mukai transform
[39]
논문
Deformations of instantons
[40]
논문
Self-duality in four-dimensional Riemannian geometry
[41]
논문
Instantons and algebraic geometry
[42]
논문
Construction of instantons
[43]
논문
The yang-mills equations over riemann surfaces
[44]
논문
Connections withL p bounds on curvature
[45]
논문
An application of gauge theory to four-dimensional topology
[46]
논문
Polynomial invariants for smooth four-manifolds
[47]
논문
Quantum field theory and the Jones polynomial
[48]
논문
Monopoles and four-manifolds.
https://doi.org/10.4[...]
[49]
논문
A strong coupling test of S-duality
[50]
논문
Anti self-dual Yang-Mills connections over complex algebraic surfaces and stable vector bundles
[51]
논문
On the existence of Hermitian–Yang-Mills connections in stable vector bundles.Frontiers of the mathematical sciences: 1985 (New York, 1985). Communications on Pure and Applied
[52]
논문
The self-duality equations on a Riemann surface
[53]
논문
Higgs bundles and local systems
http://www.numdam.or[...]
[54]
서적
The geometry of four-manifolds
Oxford University Press
[55]
서적
An introduction to quantum field theory
Westview Press
[56]
논문
The yang-mills equations over riemann surfaces
[57]
논문
Stable and unitary vector bundles on a compact Riemann surface
[58]
논문
A new proof of a theorem of Narasimhan and Seshadri
[59]
서적
All self-dual multimonopoles for arbitrary gauge groups
Springer, Boston, MA
[60]
논문
On the construction of monopoles
[61]
논문
Nahm's equations and the classification of monopoles
[62]
논문
The self‐duality equations on a Riemann surface
[63]
논문
Constructing variations of Hodge structure using Yang-Mills theory and applications to uniformization
[64]
논문
Higgs bundles and local systems
[65]
논문
Moduli of representations of the fundamental group of a smooth projective variety I
[66]
논문
Moduli of representations of the fundamental group of a smooth projective variety. II
https://doi.org/10.1[...]
[67]
논문
The Hodge filtration on nonabelian cohomology
[68]
서적
The geometry and dynamics of magnetic monopoles
Princeton University Press
[69]
논문
Quantum field theory and the Jones polynomial
[70]
논문
The yang-mills equations over riemann surfaces
[71]
논문
Flat connections and geometric quantization
1990
[72]
논문
Geometric quantization of Chern–Simons gauge theory
1991
[73]
논문
Quantization of Chern-Simons gauge theory with complex gauge group
1991
[74]
논문
An instanton-invariant for 3-manifolds
1988
[75]
서적
The geometry of four-manifolds
Oxford University Press
1990
[76]
논문
Monopoles and four-manifolds.
https://arxiv.org/ab[...]
1994
[77]
논문
Anti self-dual Yang-Mills connections over complex algebraic surfaces and stable vector bundles
1985
[78]
논문
On the existence of Hermitian–Yang-Mills connections in stable vector bundles
Frontiers of the mathematical sciences: 1985 (New York, 1985)
[79]
논문
Gauge theory in higher dimensions
Oxford Univ. Press,Oxford
1998
[80]
논문
Gauge theory in higher dimensions, II
Int. Press,Somerville, MA
2011
[81]
논문
From special lagrangian to hermitian-Yang-Mills via Fourier-Mukai transform
https://arxiv.org/ab[...]
2000
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com