네트워크 이론
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
네트워크 이론은 복잡한 데이터를 분석하는 데 사용되는 이론으로, 1736년 레온하르트 오일러의 '쾨니히스베르크의 일곱 다리' 문제 연구에서 시작되었다. 그래프 이론을 기반으로 발전하여 사회 연결망 분석, 생물학적 네트워크 분석, 텍스트 분석 등 다양한 분야에 적용되며, 네트워크의 속성과 최적화, 다양한 네트워크 모델 연구가 이루어진다. 네트워크의 성능을 향상시키기 위한 최적화 문제와 재귀 네트워크, 네트워크 확산, 다층 네트워크 등 다양한 주제를 다룬다.
더 읽어볼만한 페이지
- 네트워크 이론 - 사회 연결망
사회 연결망 분석은 개인이나 집단 간의 관계를 분석하여 사회적 구조와 행동을 이해하는 학제 간 연구 방법론으로, 다양한 이론적 틀을 활용하여 네트워크 내 위치와 정보 접근의 중요성을 분석하며 여러 분야에서 활용된다. - 네트워크 이론 - 중심성
중심성은 그래프 이론에서 네트워크 내 노드의 중요성을 평가하기 위한 지표로, 차수 중심성, 근접 중심성 등 다양한 종류가 있으며 네트워크 흐름, 워크 구조 등 다양한 특징에 따라 분류된다. - 응용수학 - 확률
확률은 사건의 가능성을 수치화한 개념으로, 도박에서 시작되어 수학적으로 발전했으며, 다양한 해석과 요소, 응용 분야를 가지며 양자역학, 사회 현상 등에도 적용된다. - 응용수학 - 수리사회학
수리사회학은 수학적 모델과 방법론을 활용하여 사회 현상을 분석하는 사회학 분야로, 사회 네트워크 분석을 통해 사회 구조를 규명하고 빅데이터 분석 및 예측에 기여하며 그 중요성이 인정받고 있다. - 그래프 이론 - 다이어그램
다이어그램은 2차원 기하학적 기호를 사용하여 정보를 시각적으로 표현하는 기술로, 과학, 공학, IT, 비즈니스 등 다양한 분야에서 활용되며 정보를 간략하게 나타내고 시각적 사고를 돕는다. - 그래프 이론 - 쾨니히스베르크의 다리 문제
쾨니히스베르크의 다리 문제는 프레겔 강에 놓인 7개의 다리를 한 번씩만 건너 출발점으로 되돌아올 수 있는지 묻는 문제로, 오일러에 의해 그래프 이론적으로 분석되어 해결되었으며 그래프 이론의 탄생에 기여했다.
2. 역사적 배경
네트워크 이론은 복잡한 데이터를 분석하는 수단으로서 다양한 분야에서 언급된다.
1930년대 게슈탈트 학파의 심리학자 야코프 모레노는 소시오그램을 발표했다.
1998년 데이비드 크라크하트(David Krackhardt)와 캐서린 칼리(Kathleen Carley)는 PCANS 모델을 이용한 메타 네트워크의 개념을 발표했으며, 모든 조직은 개인, 태스크, 리소스라는 세 개의 도메인으로 구성된다고 했다. 해당 논문에 따르면 네트워크는 여러 도메인에 걸쳐 발생하며, 서로 관련되어 있다. 이 분야는 다이내믹 네트워크 분석이라는 분야로 발전했다.
최근에는 네트워크 이론을 사용하여 위상 기하학을 수학적으로 표현하려는 시도가 주목받고 있다.
2. 1. 쾨니히스베르크 다리 문제와 그래프 이론의 탄생
1736년 레온하르트 오일러는 쾨니히스베르크의 일곱 다리 문제에 대한 논문을 발표했다. 정점과 변을 이용한 오일러의 수학적 증명은 그래프 이론의 기초가 되었으며, 이는 훗날 화학에도 응용되었다[41]。2. 2. 사회 연결망 분석의 등장
1930년대 게슈탈트 학파의 심리학자 야코프 모레노는 미국에서 사회학을 발전시켜, 1933년 4월에 소시오그램을 의료학자 모임에서 발표했다. 모레노는 "소시오그램의 출현 이전에는 어떤 그룹에서의 대인관계 구조가 정확히 어떤 것인지 아무도 알 수 없었습니다."라고 발표했다[42]。 소시오그램은 많은 용도를 찾아내어 사회 연결망 분석이라는 분야로 발전하고 있다.초등학교 1학년의 사회적 구조를 나타낸 소시오그램을 보면, 남학생과 여학생은 각각 동성이 친구였지만, 예외로 한 남학생이 여학생을 좋아한다고 말했지만, 상호적인 관계가 아님을 알 수 있다.
2. 3. 확률론적 네트워크 모형과 복잡계 네트워크 이론
폴 에르되시와 알프레드 레니의 랜덤 그래프에 관한 8개의 그래프 이론 논문에서 네트워크 이론의 확률론이 파생되었다. 사회적 네트워크의 경우 지수 랜덤 그래프 모델(p*)이 네트워크에서 발생하는 관계의 확률 공간을 나타내는 데 사용된다. 네트워크 확률론에 대한 또 다른 접근 방식은 확률 행렬인데, 이는 네트워크의 샘플에서 나타나는 에지의 과거 유무에 기초하여 네트워크 전체에서 발생하는 에지의 확률을 모델링한다.[41]1998년 던컨 와츠는 수학적 표현을 가진 네트워크에서 실험 데이터를 사용하여 스몰 월드 현상을 발표했다. 알베르트-라슬로 바라바시와 레카 알베르트는 스케일 프리 네트워크를 구현했다. 이는 다수의 연결을 가진 허브 정점을 포함하는 광의의 네트워크 토폴로지이며, 다른 모든 노드와의 연결 수의 비율이 일정하게 유지되도록 성장한다. 인터넷 등 많은 네트워크는 이러한 측면을 유지하는 것처럼 보이지만, 다른 네트워크에서는 이 비율이 노드의 긴 꼬리 분포에 근사한다.
3. 네트워크의 속성
많은 네트워크는 그 특성을 분석하는 데 사용되는 속성을 가지고 있다. 이러한 속성은 대부분 네트워크 모델을 정의하여 특정 모델과의 비교 분석에 사용된다. 네트워크 과학에서 사용되는 용어 정의의 상당수는 그래프 이론에서도 사용된다.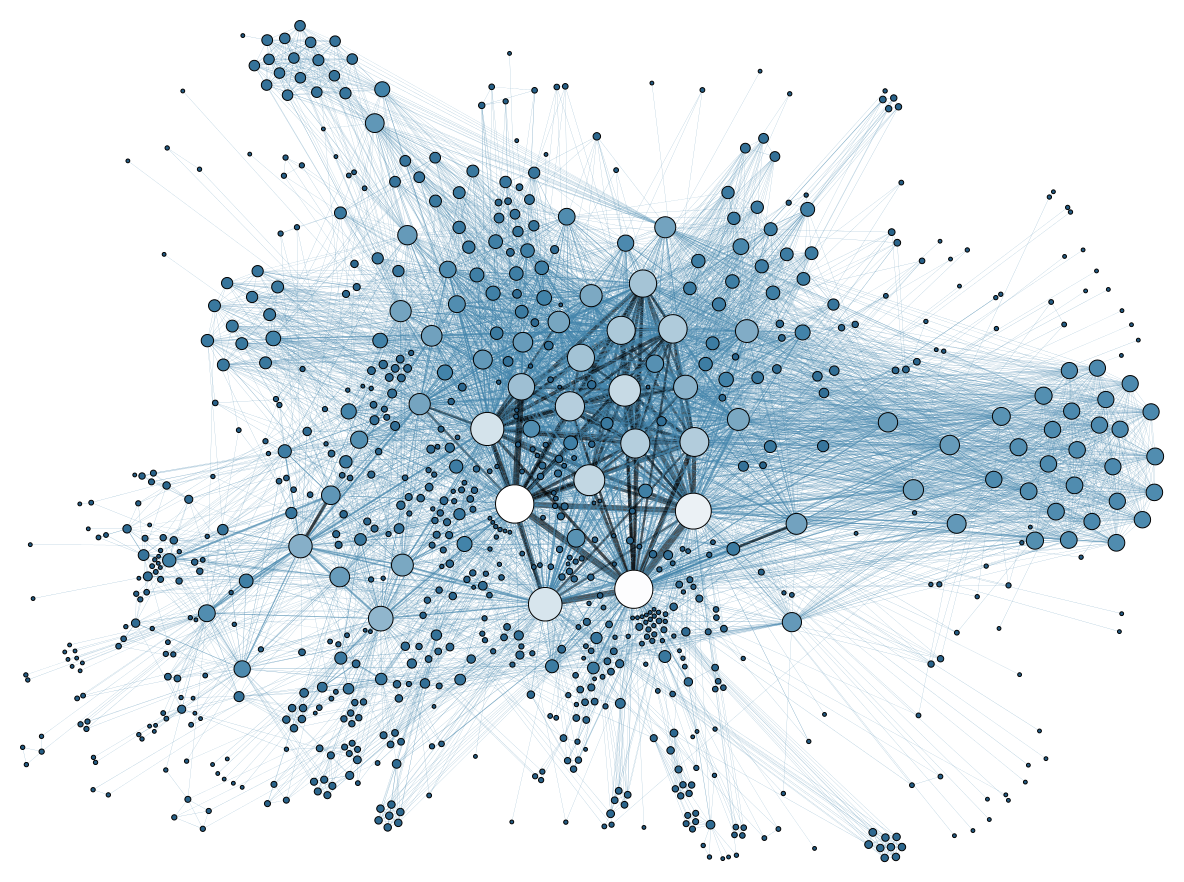
3. 1. 기본 속성
많은 네트워크는 해당 특성을 분석하는 데 사용되는 속성을 가지고 있다. 이러한 속성은 대부분 네트워크 모델을 정의하여 특정 모델과의 비교 분석에 사용된다. 네트워크 과학에서 사용되는 용어 정의의 상당수는 그래프 이론에서도 사용된다.- 노드(Node): 네트워크를 구성하는 기본 단위이다.
- 엣지(Edge): 노드 간의 연결을 의미한다.
- 차수(Degree): 한 노드에 연결된 엣지의 수이다.
- 평균 차수: 네트워크 내 모든 노드의 차수 평균값으로, 로 계산된다.
- 평균 경로 길이(Average path length): 네트워크 내 임의의 두 노드 사이의 최단 거리 평균값이다.
- 지름(Diameter): 네트워크 내에서 가장 멀리 떨어진 두 노드 사이의 최단 거리이다.
네트워크의 크기는 노드 의 수 또는 (일반적이지 않지만) 엣지 의 수로 나타낸다. 엣지 의 수는 (트리)부터 (완전 그래프)까지 다양하다.
3. 2. 밀도와 연결성
네트워크의 밀도는 노드 간 연결 정도를 나타내는 지표이며, 연결성은 네트워크가 얼마나 잘 연결되어 있는지를 나타낸다. 네트워크 과학에서 사용되는 용어 정의의 상당수는 그래프 이론에서도 사용된다.네트워크가 어떻게 연결되어 있는지, 즉 노드 사이에 에지를 따라가는 경로가 있는지는 네트워크와 그 부분 그래프의 중요한 특징 중 하나이다. 연결성에 따라 다음과 같은 네트워크 및 부분 그래프의 종류가 있다.
- 완전 그래프 · 클리크: 모든 노드가 다른 모든 노드와 링크로 직접 연결된 네트워크를 완전 그래프라고 하며, 네트워크에 포함된, 완전 그래프를 이루는 부분 그래프를 클리크라고 한다.
- 거대 연결 성분: 네트워크의 일정 비율을 차지하는 연결 성분. 엄밀히는 크기가 네트워크 전체 크기에 비례하는 연결 성분을 가리킨다. 랜덤 그래프에서는 거대 연결 성분이 기껏해야 1개만 존재한다는 것이 알려져 있다.
- 약 연결 성분: 유향 네트워크에서 에지의 방향을 무시했을 때, 어느 노드에서든 다른 노드로의 경로가 존재하는 연결 성분.
- 강 연결 성분: 유향 네트워크에서 에지의 방향을 고려했을 때, 어느 노드에서든 다른 노드로의 경로가 존재하는 연결 성분.
3. 3. 군집성
많은 네트워크는 해당 특성을 분석하는 데 사용되는 속성을 가지고 있다. 이러한 속성은 대부분 네트워크 모델을 정의하여 특정 모델과의 비교 분석에 사용된다. 네트워크 과학에서 사용되는 용어 정의의 상당수는 그래프 이론에서도 사용된다.군집 계수란, "모든 친구가 서로를 알고 있다"는 특성을 나타낸다. "친구의 친구는 친구이다"라고도 표현된다. 노드의 군집 계수는, 노드가 인접한 노드와 실제로 서로 연결되어 있는 링크와, 가능한 링크의 최대 개수의 비율이다. 네트워크 전체의 군집 계수는, 모든 노드의 군집 계수의 평균이다. 네트워크의 군집 계수가 높다는 것은, 스몰 월드라는 것을 나타내는 지표이기도 하다. 번째 노드의 군집 계수는 로 나타낸다. 여기서, 는 번째 노드의 이웃의 수이며, 는 이 이웃들 사이의 링크의 수이다. 이웃 간의 가능한 링크의 최대 개수는 다음과 같이 나타낸다:
3. 4. 중심성 척도
사회학 등 여러 분야에서 널리 사용되는 중심성 척도를 통해 그래프 내 노드와 엣지의 상대적 중요성에 대한 정보를 얻을 수 있다. 예를 들어, 고유 벡터 중심성은 네트워크에 해당하는 인접 행렬의 고유 벡터를 사용하여 자주 방문되는 노드를 결정한다. 공식적으로 확립된 중심성 척도는 차수 중심성, 근접 중심성, 매개 중심성, 고유 벡터 중심성, 부분 그래프 중심성, Katz 중심성이 있다. 분석 목적이나 목표에 따라 일반적으로 사용될 중심성 척도의 유형이 결정된다. 예를 들어, 네트워크 역학이나 노드/링크 제거에 대한 네트워크 견고성에 관심이 있는 경우, 종종 노드의 동적 중요성[32]이 가장 관련 있는 중심성 척도이다.중심성 지수는 네트워크 모델에서 가장 중요한 노드를 식별하는 데 사용된다. 중심성 지수로 파악되는 "중요도"는 네트워크에 따라 의미가 다르다. 예를 들어, 매개 중심성은 다른 많은 노드 사이에 다리(bridge)를 형성하는 노드를 매우 중요하게 간주한다. 또한, 고유값 중심성은 다른 많은 중요한 노드가 연결되어 있는 경우 중요하게 간주된다. 이처럼 중요도의 정의는 수많은 문헌에서 언급되고 있다. 중심성 지수는 가장 중요한 노드를 식별하기 위해서만 적용이 가능하며, 다른 노드 부분에서는 무의미한 경우가 대부분이다. 예를 들어, 두 개의 별개 커뮤니티가 있고, 서로의 연결은 각 커뮤니티의 가장 어린 구성원들끼리만 있다고 가정해 보자. 그러면 하나의 커뮤니티에서 다른 커뮤니티로 이동하려면 반드시 이 링크를 거쳐야 하므로, 두 어린 구성원은 높은 매개 중심성을 갖게 된다. 하지만 그들은 어리기 때문에, 아마도 커뮤니티 내 중요 노드와 연결이 적어 고유값 중심성은 매우 낮을 것이다. 정적 네트워크에서의 중심성 개념은, 경험적 및 이론적 연구를 바탕으로, 시간적 네트워크에서의 동적 중심성으로 확장되었다.
중심성 지수의 단점을 극복하기 위해 보다 일반적인 척도로 개발된 것이 접근성(네트워크의 나머지 부분에 특정 노드로부터 얼마나 접근 가능한지를 측정하기 위해, 임의 보행의 다양성을 사용한다)[49]와 영향력(노드의 감염력 기대치로부터 산출된다)이다. 이러한 측정값은 네트워크의 구조만으로 계산할 수 있다[44]。
3. 5. 동류 연결과 이류 연결
네트워크에서 허브 노드는 많은 링크를 가진 노드를 의미하며, 이러한 허브 노드의 연결 선호도에 따라 네트워크의 특성을 파악할 수 있다. 허브 노드가 다른 허브 노드에 연결되는 경향을 동류 연결(Assortative Mixing)이라고 한다. 반면, 허브 노드가 다른 허브 노드와의 연결을 피하고 연결성이 낮은 노드에 연결되는 경향을 이류 연결(Disassortative Mixing)이라고 한다. 만약 허브 노드가 무작위 확률로 연결을 가진다면, 이는 중립적인 연결이라고 한다.[33]4. 네트워크 분석
네트워크 분석은 사회, 생물학, 통신 등 다양한 분야에서 활용된다.
사회 네트워크 분석은 개인, 집단, 조직, 국가, 웹사이트 등 사회적 실체 간의 관계 구조를 연구한다. 1970년대 이후 사회 과학의 핵심적인 역할을 해왔으며, 혁신의 확산, 뉴스 및 소문, 질병 및 건강 관련 행동의 확산, 시장 연구, 정치 운동 및 사회 조직 연구, 학문적 불일치 및 명성 개념화 등 다양한 분야에 활용된다.
생물학적 네트워크 분석은 분자 네트워크 분석에 중점을 두며, 네트워크 모티프, 활동 모티프 등을 통해 생물학적 시스템의 패턴을 분석한다. 푸드 웹과 같은 시스템에서 종 간 상호 작용을 시각화하고, 질병 관련 네트워크 분석을 통해 네트워크 의학 분야 발전을 이끌었다. 세포 주기 및 발달 과정 이해에도 활용된다.
내러티브 네트워크 분석은 텍스트 코퍼스를 자동 구문 분석하여 행위자와 관계 네트워크를 추출한다. 이를 통해 주요 행위자, 커뮤니티, 네트워크의 견고성 등을 파악한다.
링크 분석은 객체 간 연관성을 탐구하는 네트워크 분석의 하위 집합이다. 경찰 수사, 사기 탐지, 통신 사업자에서 통신 네트워크 분석, 의료 부문에서 역학 및 약리학, 법 집행 수사, 검색 엔진에서 관련성 평가 등 다양한 분야에서 활용된다.
웹 검색 랭킹 알고리즘에는 구글의 PageRank, 클라인버그의 HITS 알고리즘 등 링크 기반 중심성 지표가 사용된다. 링크 분석은 정보 과학 및 커뮤니케이션 과학에서 웹 페이지 구조를 이해하고 정보를 추출하는 데에도 사용된다.
전력 시스템 분석은 네트워크 이론을 통해 추상적인 관점과 가중치 그래프 관점에서 수행될 수 있다. 추상적인 관점에서는 송전선 임피던스 등을 고려하지 않고 전력망의 취약성을 평가하고, 가중치 그래프 관점에서는 복잡한 네트워크 이론과 전력 시스템 속성을 결합하여 분석한다.
4. 1. 사회 네트워크 분석
'''소셜 네트워크 분석'''은 사회적 실체 간의 관계 구조를 연구한다.[13] 이러한 실체는 흔히 개인이지만, 집단, 조직, 국가, 웹사이트, 또는 학술 출판물일 수도 있다.
1970년대 이후 네트워크에 대한 실증적 연구는 사회 과학에서 핵심적인 역할을 해왔으며, 네트워크 연구에 사용되는 많은 수학 및 통계학 도구는 처음 사회학에서 개발되었다.[14] 소셜 네트워크 분석은 혁신의 확산, 뉴스 및 소문을 이해하는 데 사용되었다.[15] 마찬가지로, 질병과 건강 관련 행동의 확산을 조사하는 데 사용되었다.[16] 또한 시장 연구에도 적용되어, 사회 교환에서 신뢰의 역할과 가격 결정에 있어서 사회적 메커니즘의 역할을 조사하는 데 사용되었다.[17] 정치 운동, 무장 단체 및 기타 사회 조직으로의 모집을 연구하는 데 사용되었다.[18] 또한 학문적 불일치[19]와 학문적 명성을 개념화하는 데 사용되었다.[20] 더 최근에는 네트워크 분석(그리고 이와 밀접한 관련이 있는 트래픽 분석)이 군사 정보에서 중요한 사용례를 얻었으며, 계층적 및 무지도자 저항 성격의 반군 네트워크를 밝히는 데 사용된다.
4. 2. 생물학적 네트워크 분석
최근 공개적으로 이용 가능한 고처리량 생물학적 데이터의 폭발적인 증가와 함께 분자 네트워크 분석이 상당한 관심을 받고 있다.[22] 이 맥락에서의 분석 유형은 사회 네트워크 분석과 밀접하게 관련되어 있지만, 종종 네트워크의 지역적 패턴에 초점을 맞춘다. 예를 들어, 네트워크 모티프는 네트워크에서 과다하게 표현되는 작은 하위 그래프이다. 마찬가지로, 활동 모티프는 네트워크 구조를 고려할 때 과다하게 표현되는 네트워크의 노드 및 엣지 속성의 패턴이다. 푸드 웹과 같은 생물학적 시스템의 패턴을 분석하기 위해 네트워크를 사용하면 종 간의 상호 작용의 본질과 강도를 시각화할 수 있다. 질병과 관련한 생물학적 네트워크 분석은 네트워크 의학 분야의 발전을 이끌었다.[23] 생물학에서 네트워크 이론을 적용한 최근 사례로는 세포 주기 이해[24]뿐만 아니라 발달 과정을 위한 정량적 프레임워크가 있다.[25]4. 3. 내러티브 네트워크 분석
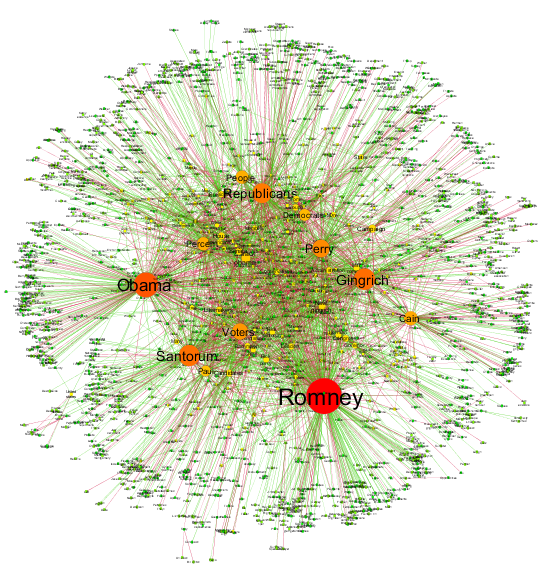
''텍스트 코퍼스''의 자동 구문 분석은 방대한 규모의 행위자와 그 관계 네트워크를 추출할 수 있게 했다. 결과적으로 수천 개의 노드를 포함할 수 있는 내러티브 네트워크는 네트워크 이론의 도구를 사용하여 주요 행위자, 주요 커뮤니티 또는 파티, 전반적인 네트워크의 견고성 또는 구조적 안정성과 같은 일반적인 속성 또는 특정 노드의 중심성을 식별하여 분석한다.[27] 이는 주어-동사-목적어 삼중항을 식별하여 행위자 쌍을 동작으로 연결하거나 행위자-객체로 형성하는 정량적 내러티브 분석에 의해 도입된 접근 방식을 자동화한다.[28][26]
4. 4. 링크 분석
링크 분석은 네트워크 분석의 하위 집합으로, 객체 간의 연관성을 탐구한다. 예를 들어, 경찰 수사에서 용의자와 피해자의 주소, 전화 번호, 금융 거래, 가족 관계 등을 조사할 수 있다. 링크 분석은 개별 정보로는 파악하기 어려운 다양한 객체 간의 관계와 연관성을 제공한다. 컴퓨터 기반 링크 분석은 은행과 보험 회사에서 사기 탐지에, 통신 사업자에서 통신 네트워크 분석에, 의료 부문에서 역학 및 약리학에, 법 집행 수사에, 검색 엔진에서 관련성 평가에 (그리고 반대로 스팸 발송자는 스팸덱싱에, 사업주는 검색 엔진 최적화에) 활용된다. 또한, 두 노드 간 시간 동작의 유사성으로부터 링크가 파생되기도 한다. 예를 들어, 기후 네트워크에서 두 위치 간 링크는 강수량 또는 온도 변동의 유사성에 의해 결정된다.웹 검색 랭킹 알고리즘에는 구글의 PageRank, 클라인버그의 HITS 알고리즘, CheiRank, TrustRank 알고리즘 등 링크 기반 중심성 지표를 사용하는 경우가 많다. 링크 분석은 정보 과학 및 커뮤니케이션 과학에서 웹 페이지 모음 구조에서 정보를 이해하고 추출하는 데에도 사용된다. 예를 들어, 정치인 웹사이트 또는 블로그 간의 상호 연결을 분석할 수 있다. 다른 페이지에서 언급된 내용에 따라 페이지를 분류하는 데에도 활용된다.[31]
4. 5. 전력망 분석
전력 시스템의 분석은 네트워크 이론을 사용하여 다음 두 가지 관점에서 수행할 수 있다.# 추상적인 관점(즉, 노드와 엣지로 구성된 그래프)으로, 송전선 임피던스 등 전력 측면은 고려하지 않는다. 이러한 연구는 대부분 노드 차수 분포 및 중간 중심성 분포를 사용하여 전력망의 추상적 구조에만 초점을 맞추며, 이는 전력망의 취약성 평가에 대한 상당한 통찰력을 제공한다. 이러한 유형의 연구를 통해 복잡한 네트워크 관점에서 전력망 구조의 범주(예: 단일 규모, 무척도)를 식별할 수 있다. 이러한 분류는 인프라를 업그레이드(예: 새로운 송전선 추가)하거나 계획 단계에서 전력 시스템 엔지니어가 전송 시스템에서 적절한 중복 수준을 유지하는 데 도움이 될 수 있다.
# 복잡한 네트워크 이론과 전력 시스템 속성에 대한 추상적인 이해를 혼합한 가중치 그래프.
5. 네트워크 모형
네트워크 모델은 현실 세계의 복잡한 네트워크에서 발생하는 상호작용을 이해하고, 랜덤 그래프에서 생성된 네트워크 구조 모델을 실제 복잡 네트워크와 비교하는 데 사용된다.
- 에르되시-레니 무작위 그래프 모형: 폴 에르되시와 앨프레드 레니의 이름을 딴 모형으로, 노드 사이에 동일한 확률로 에지(연결)가 설정된 랜덤 그래프를 생성한다. 확률론적 방법을 사용하여 그래프의 속성을 증명하거나 정의하는 데 사용된다.
- 왓츠-스트로가츠 스몰 월드 네트워크 모형: 스몰 월드 네트워크의 특징인 높은 군집 계수(노드들이 서로 연결된 정도)와 짧은 평균 거리(두 노드 사이의 평균 거리)를 갖는 네트워크를 생성한다. 격자 구조에서 시작하여, 각 에지를 일정 확률로 무작위로 재배선하는 방식으로 만들어진다.
- 바라바시-알버트 척도 없는 네트워크 모형: 선호적 연결(preferential attachment) 또는 "부익부" 현상을 보여주는 랜덤 네트워크 모델이다. 연결이 많은 노드(허브)가 새로운 연결을 얻을 가능성이 더 높다. 이 모델의 차수 분포는 멱법칙을 따르며, 허브 노드는 짧은 경로를 가능하게 하여 네트워크의 평균 거리를 짧게 만든다.
- 피트니스 모형: 각 노드의 적합도(fitness)가 중요하게 고려되는 모델이다. 두 노드 사이의 연결 확률은 적합도 함수에 의해 결정되며, 적합도가 멱법칙으로 분포하면 노드 차수도 멱법칙을 따르게 된다. 이 모델은 국가 간 무역을 설명하는 데 사용되기도 한다.[54][55]
- 중개 기반 연결 (MDA) 모형: 새로운 노드가 기존 노드를 무작위로 선택하고, 선택된 노드뿐만 아니라 그 이웃 노드에도 무작위로 연결되는 모델이다. 이 모델은 "부익부" 현상을 설명하며, 특정 조건에서 한 노드가 대부분의 연결을 독점하는 현상이 나타나기도 한다.[51]
5. 1. 에르되시-레니 무작위 그래프 모형
에르되시-레니 모형(Erdős-Rényi model)은 폴 에르되시와 앨프레드 레니의 이름을 딴 것으로, 에지가 동일한 확률로 노드 사이에 설정된 랜덤 그래프를 생성한다. 확률론적 방법을 사용하여 다양한 속성을 만족하는 그래프의 존재를 증명하거나, 많은 그래프에 대해 어떤 속성이 갖는 중요성을 엄밀하게 정의할 수 있다.에르되시-레니 모형을 생성하려면 두 개의 매개변수가 필요하다. 하나는 생성된 그래프 내의 노드 수 N과, 두 노드 사이에 링크 p를 형성할 확률이다. E를 에지 수의 기댓값이라고 하면, 식 2 · ''E'' / ''N'' = ''p'' · (''N'' - 1)를 사용하여 상수 k를 도출할 수 있다.
에르되시-레니 모형은 다른 그래프에 비해 몇 가지 흥미로운 특징을 가지고 있다. 이 모형은 특정 노드에 바이어스를 가하지 않고 생성되므로, 차수 분포는 다음과 같은 이항식으로 나타난다.
:
또한 평균 차수 k가 일정하고, 노드 수 N이 증가함에 따라, 클러스터 계수가 0으로 작아진다. 이 모형에서는 k > 1에서 거대한 연결 요소가 존재한다(이 현상을 "퍼콜레이션"이라고 부른다). 또한 이 모형에서는 평균 거리가 비교적 짧고, log ''N''에 가까워진다.
5. 2. 왓츠-스트로가츠 스몰 월드 네트워크 모형
스몰 월드 네트워크의 특징인 높은 군집 계수와 짧은 평균 거리를 갖는 네트워크를 생성하는 모형이다. 이 모형을 만들기 위해서는 우선 격자 구조가 필요하다. 네트워크의 각 노드는 처음에 개의 인접 노드에 연결된다. 각 엣지(edge)는 다른 매개변수인 재배선 확률 에 따라 무작위 엣지로 재배선된다. 이 모델에서 재배선되는 링크의 기대값은 이다.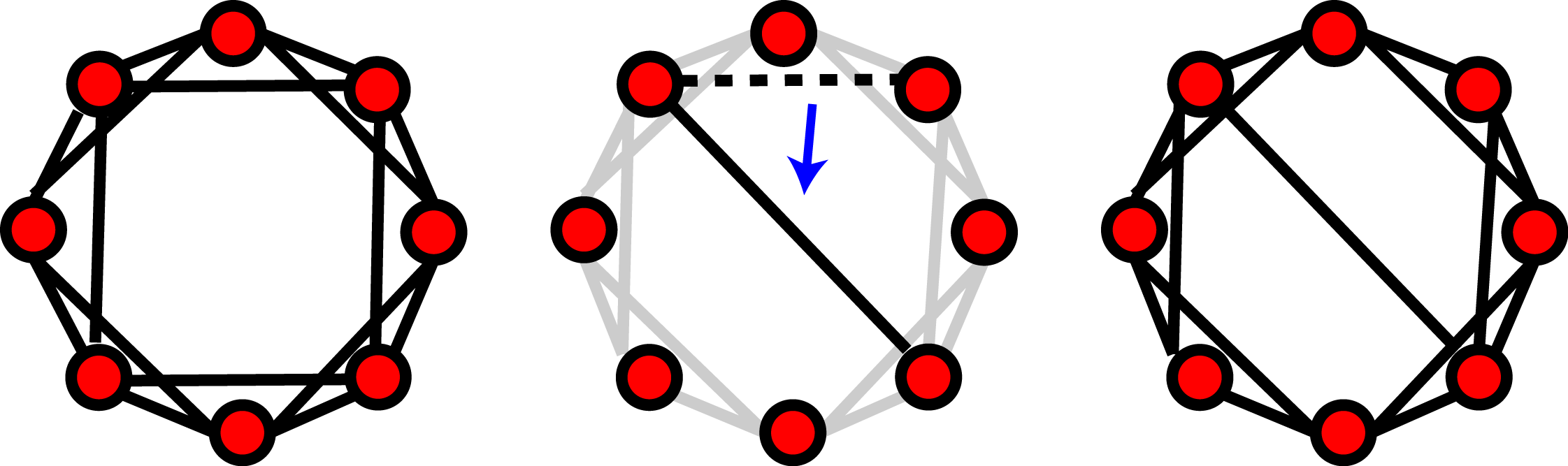
이 모델은 초기에는 비무작위 격자 구조이므로 평균 거리가 높고 클러스터 계수가 매우 높다. 재배선 확률이 높아짐에 따라 클러스터 계수는 평균 거리보다 느리게 감소한다. 이러한 특징은 클러스터 계수의 감소를 억제하면서 네트워크의 평균 거리가 크게 감소하는 것을 가능하게 한다. 확률 의 값이 높을수록 더 많은 엣지가 재배선되어 와츠-스트로가츠 모델은 실질적으로 무작위 네트워크가 된다.
5. 3. 바라바시-알버트 척도 없는 네트워크 모형
BA 모델은 선호적 연결(preferential attachment) 또는 "부익부" 현상을 실증할 수 있는 랜덤 네트워크 모델이다. 이 모델에서는 엣지가 더 높은 차수의 노드에 연결될 가능성이 높다.[50] 네트워크는 처음에 ''m''0 개의 노드를 가지며, ''m''0 ≥ 2이고 네트워크의 각 노드의 차수는 1 이상이어야 한다. 그렇지 않으면 네트워크의 나머지 부분에서 항상 고립된 상태가 된다.BA 모델에서는 새로운 노드가 하나씩 네트워크에 추가된다. 각 새로운 노드는 기존 노드가 이미 가진 링크의 수에 비례하는 확률로 기존 노드 개에 연결된다. 요약하면, 새로운 노드가 노드 에 연결될 확률 는 다음과 같다. 는 노드 의 차수이다.
:
여기서, 많은 링크를 가진 노드(허브라고 불림)는 더 많은 링크를 축적하는 경향이 있지만, 소수의 링크만 가진 노드는 새로운 링크의 대상으로 선택될 가능성이 낮다. 즉, 새로운 노드는 이미 많은 링크가 연결된 노드에 연결되는 경향이 있다.
BA 모델에서 얻어지는 차수 분포는 스케일 프리이며, 멱법칙으로 표시된다.
:
허브가 되는 많은 링크를 가진 노드는 노드 간의 짧은 경로 (Path)의 존재를 가능하게 하는 높은 중간 중심성을 나타낸다. 결과적으로 BA 모델은 평균 거리가 매우 짧아지는 경향이 있다. 이 모델의 클러스터 계수도 0이 되는 경향이 있다. 에르되시-레니 모델과 스몰 월드 네트워크를 포함한 많은 모델의 지름 D는 log N에 비례하지만, BA 모델은 D~loglogN이 된다. 이 때 평균 거리는 N을 지름으로 하는 척도임에 주의해야 한다.
5. 4. 피트니스 모형
스몰 월드 현상의 네트워크 모델도 참고하라.네트워크 모델은 복잡 네트워크 내에서 일어나는 상호 작용을 이해하는 데 도움이 된다. 또한, 랜덤 그래프에서 생성된 네트워크 구조 모델은 실제 복잡 네트워크와 비교하여 사용된다.
Caldarelli 등이 도입한 피트니스 모델에서는 정점의 성질이 중시된다.[52] 이 모델에서는 두 정점 사이의 링크가 함수 에 의해 산출되는 확률을 가진다. 정점 의 차수는 다음과 같이 나타낼 수 있다.[53]
:
가 에 역수를 가지며 증가하는 함수인 경우, 확률 분포 는 다음과 같다.
:
결과적으로, 가 멱함수 법칙으로 분배되는 경우, 노드 차수도 마찬가지가 된다. 빠른 붕괴 확률 분포에서는 링크 함수와 함께, 와 가 된다.
헤비사이드 함수의 상수와 를 사용하면, 스케일 없는 네트워크가 된다.
이 모델은 다양한 노드 에 대한 피트니스에 GDP를 사용함으로써 국가 간의 무역을 기술하는 데 성공했다.[54][55]
:
5. 5. 중개 기반 연결 (MDA) 모형
중개 주도형 연결(MDA, Mediation-Driven Attachment) 모델에서는 m개의 에지를 가진 새로운 노드가 이미 링크된 노드를 무작위로 선택하고, 해당 노드뿐만 아니라 그 이웃 노드 m개에 무작위로 링크한다. 기존 노드 i가 새로운 노드로 선택될 확률 Π(i)는 다음과 같다.:
이 식의 두 번째 인수는 조화 평균(IHM)의 역수이다. 노드 i의 ki 근방의 차수 (IHM)를 계산한다. 대규모의 수치 연구에 따르면 m>14인 경우, 큰 한도 N에서의 조화 평균은 상수가 되며, 이는 Π(i)∝ki로 나타낼 수 있다. 이는 노드가 가진 링크(차수)가 높을수록 더 많은 링크를 얻는 경향을 의미하며, "부유층이 더 부유해지는" 현상을 설명한다. 따라서 MDA 네트워크는 PA의 법칙에 암묵적으로 따른다.[51]
m=1인 경우 "1명이 모든 것을 얻는" 메커니즘이 나타난다. 여기에서는 노드의 거의 99%가 차수 1을 가지며, 1명이 초부유층이 된다. "부유층이 더 부유해지는" 현상은 m>14부터 나타난다.
6. 네트워크 최적화
조합 최적화를 통해 네트워크에서 최적의 방법을 찾는 연구가 이루어진다. 예시로는 네트워크 흐름, 최단 경로 문제, 수송 문제, 환적 문제, 입지 문제, 매칭 문제, 할당 문제, 패킹 문제, 라우팅 문제, 임계 경로 분석, 프로그램 평가 및 검토 기법 등이 있다.
7. 추가 주제
네트워크 이론에는 재귀 네트워크, 네트워크 확산 등 여러 추가 주제가 있다.
7. 1. 재귀 네트워크
재귀 플롯의 재귀 행렬은 무방향, 가중치가 없는 네트워크의 인접행렬로 간주될 수 있다. 이를 통해 네트워크 측정 방법을 통해 시계열을 분석할 수 있다. 응용 분야는 정권 변화 감지에서 역학 특성 규명, 동기화 분석에 이르기까지 다양하다.[34][35][36]7. 2. 네트워크 확산
복잡한 네트워크에서 콘텐츠는 보존적 확산과 비보존적 확산, 이 두 가지 주요 방법으로 확산될 수 있다.[38]보존적 확산에서는 복잡한 네트워크에 들어가는 총 콘텐츠 양이 네트워크를 통과하면서 일정하게 유지된다. 이 모델은 일정량의 물이 튜브로 연결된 일련의 깔때기에 부어지는 물병으로 가장 잘 표현될 수 있다. 여기서 물병은 원래 소스를, 물은 확산되는 콘텐츠를 나타낸다. 깔때기와 연결 튜브는 각각 노드와 노드 간의 연결을 나타낸다. 물이 한 깔때기에서 다른 깔때기로 흐르면서, 이전에 물에 노출되었던 깔때기에서는 즉시 물이 사라진다.
비보존적 확산에서는 콘텐츠의 양이 복잡한 네트워크에 들어가고 통과하면서 변한다. 이 모델은 튜브로 연결된 일련의 깔때기를 통해 계속 흐르는 수도꼭지로 가장 잘 표현될 수 있다. 여기서 원래 소스의 물의 양은 무한하다. 또한 물에 노출된 깔때기는 물이 연속적인 깔때기로 흘러가도 계속해서 물을 경험한다. 비보존적 모델은 대부분의 전염병, 신경 흥분, 정보 및 소문 등의 전송을 설명하는 데 가장 적합하다.
참조
[1]
논문
Quantitative analysis of intracellular communication and signaling errors in signaling networks
2014-08
[2]
서적
Networks and nodal points: the emergence of towns in early Viking Age Scandinavia - Antiquity 81(311)
Cambridge University Press
[3]
논문
Selected poster presentations from the American Association of Applied Linguistics conference, Denver, USA, March 2020: Out-of-class peer interactions matter for second language acquisition during short-term overseas sojourns: The contributions of Social Network Analysis
2021
[4]
서적
Language, Mobility and Study Abroad in the Contemporary European Context
Routledge
[5]
논문
How output outweighs input and interlocutors matter for study-abroad SLA: Computational Social Network Analysis of learner interactions
https://www.reposito[...]
2022
[6]
논문
Forty years of secondhand smoke research: the gap between discovery and delivery
2009-06
[7]
논문
Social Network Methodology in the Study of Disasters: Issues and Insights Prompted by Post-Katrina Research
2009
[8]
논문
Care and support networks of community-dwelling frail individuals in North West London: a comparison of patient and healthcare workers' perceptions
2022-12
[9]
서적
Social Movements 2e: An Introduction
Wiley-Blackwell
[10]
논문
The predictors of L2 grit and their complex interactions in online foreign language learning: Motivation, self-directed learning, autonomy, curiosity, and language mindsets
[11]
논문
Network neuroscience
2017-02
[12]
논문
La connaissance est un réseau
http://www.cairn.inf[...]
2014-10-15
[13]
문서
Wasserman, Stanley and Katherine Faust. 1994. Social Network Analysis: Methods and Applications. Cambridge: Cambridge University Press. Rainie, Lee and Barry Wellman, Networked: The New Social Operating System. Cambridge, MA: MIT Press, 2012.
[14]
문서
Newman, M.E.J. Networks: An Introduction. Oxford University Press. 2010
[15]
서적
Python for Graph and Network Analysis
2017
[16]
논문
Network analysis in public health: history, methods, and applications
2007-04
[17]
논문
Markets as Governance Environments for Organizations at the Edge of Illegality: Insights From Social Network Analysis
2017-10
[18]
논문
Networks of Conflict and Cooperation
2021-05-11
[19]
논문
A network analysis of the propagation of evidence regarding the effectiveness of fat-controlled diets in the secondary prevention of coronary heart disease (CHD): Selective citation in reviews
2018-05-24
[20]
논문
The Academic Caste System: Prestige Hierarchies in PhD Exchange Networks
https://journals.sag[...]
2021-09-22
[21]
논문
Strategies for Combating Dark Networks
https://www.cmu.edu/[...]
2021-09-22
[22]
논문
Advanced fault diagnosis methods in molecular networks
2014-10-07
[23]
논문
Network medicine: a network-based approach to human disease
2011-01
[24]
논문
Delineation of key regulatory elements identifies points of vulnerability in the mitogen-activated signaling network
2011-12
[25]
논문
Network-based approaches to quantify multicellular development
2017-10
[26]
논문
Automated analysis of the US presidential elections using Big Data and network analysis
http://journals.sage[...]
2015
[27]
간행물
Network analysis of narrative content in large corpora
http://orcp.hustoj.c[...]
S Sudhahar, G De Fazio, R Franzosi, N Cristianini
2013
[28]
문서
Quantitative Narrative Analysis
Roberto Franzosi
2010
[29]
논문
What Do Networks Have to Do with Climate?
[30]
논문
Prediction of extreme floods in the eastern Central Andes based on a complex networks approach
2014-10
[31]
논문
Categorization by Context
http://www.jucs.org/[...]
[32]
논문
Characterizing the dynamical importance of network nodes and links
2006-09
[33]
논문
Mixing patterns in networks
2003
[34]
논문
Complex network approach for recurrence analysis of time series
[35]
논문
The Geometry of Chaotic Dynamics – A Complex Network Perspective
[36]
논문
Geometric signature of complex synchronisation scenarios
[37]
논문
Routing of multipoint connections
1988
[38]
서적
The Structure and Dynamics of Networks.
Princeton University Press
2006
[39]
논문
Network robustness and fragility: percolation on random graphs
2000-12
[40]
간행물
Network Science
http://www.nap.edu/c[...]
National Research Council
2006
[41]
문서
シルベスター
1878
[42]
문서
モレノ
1953
[43]
논문
Understanding the spreading power of all nodes in a network
http://www.nature.co[...]
2015-03
[44]
논문
Understanding the spreading power of all nodes in a network
http://www.nature.co[...]
2015-03
[45]
논문
Centrality and Network Flow
Elsevier
2005
[46]
논문
From Centrality to Temporary Fame: Dynamic Centrality in Complex Networks
2006
[47]
논문
Dynamic Model of Time-Dependent Complex Networks
2010
[48]
서적
Temporal Networks.
Springer
2013
[49]
논문
Accessibility in complex networks
2008
[50]
논문
Statistical mechanics of complex networks
http://www.nd.edu/~n[...]
2002
[51]
논문
Degree distribution, rank-size distribution, and leadership persistence in mediation-driven attachment networks
2017
[52]
논문
2002
[53]
논문
2004
[54]
논문
2004
[55]
논문
2015
[56]
문서
복잡계 네트워크에 대한 최근 연구 동향
http://www.kps.or.kr[...]
2007
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com
