맨위로가기

구점원

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

구점원은 삼각형의 9개의 특정 점, 즉 세 변의 중점, 세 수선의 발, 수심과 세 꼭짓점의 중점을 지나는 원을 의미한다. 이 원은 오일러선 상의 수심과 외심의 중점을 중심으로 하며, 외접원 반지름의 절반 길이를 갖는다. 구점원은 삼각형의 세 변의 중점, 세 수선의 발, 그리고 각 꼭짓점과 수심을 잇는 선분의 중점을 지난다. 1822년 카를 포이어바흐는 구점원이 삼각형의 내접원과 세 방접원에 접한다는 것을 발견했고, 이는 포이어바흐 정리로 알려져 있다. 구점원은 오일러선 상에서 무게중심, 수심, 외심과 관련이 있으며, 한국 수학 교육 과정에서는 심화 학습이나 경시대회 등에서 다루어진다. 구점원은 일반화되어 9점 원뿔 곡선의 특수한 경우로도 나타난다.

더 읽어볼만한 페이지

  • 평면기하학 정리 - 베주 정리
    베주 정리는 대수적으로 닫힌 체 위에서 정의된 사영 공간 또는 아핀 공간 내 초곡면들의 교차점을 다루는 대수기하학의 중요한 정리이며, 교차점의 개수는 각 초곡면의 차수의 곱과 같다는 내용을 담고 있고, 오류 정정 부호 설계, 타원 곡선 암호 등 다양한 분야에 응용된다.
  • 평면기하학 정리 - 탈레스 정리 (평행)
    탈레스 정리(평행)는 평면 위의 세 평행선과 두 직선이 만날 때 생기는 선분들 사이의 비례 관계를 설명하는 기하학 정리로, 닮음 삼각형의 성질과 관련되어 다양한 분야에 응용되며 다차원 아핀 공간으로 일반화되어 활용된다.
  • 원 (기하학) - 대원
    구면기하학에서 대원은 구의 중심을 지나는 평면과 구의 교선으로, 유클리드 공간의 직선에 대응하며, 서로 대극점이 아닌 두 점을 잇는 최단 거리인 대원 거리를 정의하고, 자오선이나 적도처럼 항해, 천문학 등 다양한 분야에서 응용된다.
  • 원 (기하학) - 반지름
    반지름은 원의 중심에서 원 위의 점까지의 거리로, 원의 지름과 둘레, 넓이 계산에 사용될 뿐 아니라 정다각형 외접원, 그래프 이론, 극좌표계 등 다양한 분야에서 활용되며, 여러 도형의 반지름을 구하는 공식이 존재하고 한국의 교육, 건축, 디자인 분야에서도 널리 쓰인다.
  • 삼각 기하학 - 피타고라스 삼조
    피타고라스 삼조는 a² + b² = c²을 만족하는 양의 정수 세 쌍 (a, b, c)이며, 특히 서로소인 세 정수로 이루어진 경우를 원시 피타고라스 삼조라고 한다.
  • 삼각 기하학 - 페르마 점
    페르마 점은 삼각형 세 꼭짓점까지의 거리 합이 최소가 되는 점으로, 120도 이상의 각이 없는 삼각형에서는 내부에 존재하며 ∠AFB=∠BFC=∠CFA=120도를 만족하고, 120도 이상의 각이 있는 삼각형에서는 가장 큰 각의 꼭짓점이 되며, 작도를 통해 찾을 수 있고 기하중앙값, 슈타이너 나무 문제 등과 관련된다.
구점원
개요
정의삼각형의 특정 점들을 지나는 원
별칭오일러 원
포이어바흐 원
영어 이름Nine-point circle
다른 영어 이름Euler's circle
Feuerbach circle
일본어 이름九点円 (Kyūten'en)
로마자 표기Kyūten'en
특징
원의 중심구점원 중심
지나는 점각 변의 중점
각 꼭짓점에서 대변에 내린 수선의 발
수심과 각 꼭짓점 사이의 선분의 중점
관련 인물레온하르트 오일러

2. 정의

구점원은 삼각형 ABC에서 다음 9개의 점을 지난다.


  • 세 변의 중점 (D, E, F)
  • 세 꼭짓점에서 대변에 내린 수선의 발 (G, H, I)
  • 수심과 세 꼭짓점 사이의 선분의 중점 (J, K, L)

3. 성질



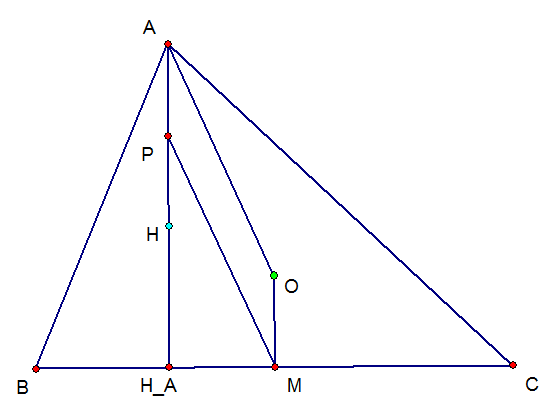
삼각형 ABC에서, 수심을 H, 외심을 O, A에서 BC에 내린 수선의 발을 HA, BC의 중점을 M, AH의 중점을 P라 하자.

  • PM은 구점원의 지름이다.


: 구점원은 P, HA, M을 지나며 \angle{PH_AM}=90^\circ이므로 PM은 구점원의 지름이다.

  • AO와 PM은 평행하다.


: AH=2OM(세르보어의 정리 참고)이므로 AP=OM이고, AP와 OM은 BC와 수직하므로 평행하다.

: 따라서 APMO는 평행사변형이므로 AO와 PM은 평행하다.

  • 구점원은 해당 삼각형의 수심에서 외접원의 임의의 점으로 가는 선분을 이등분한다.
  • -|]]|]]

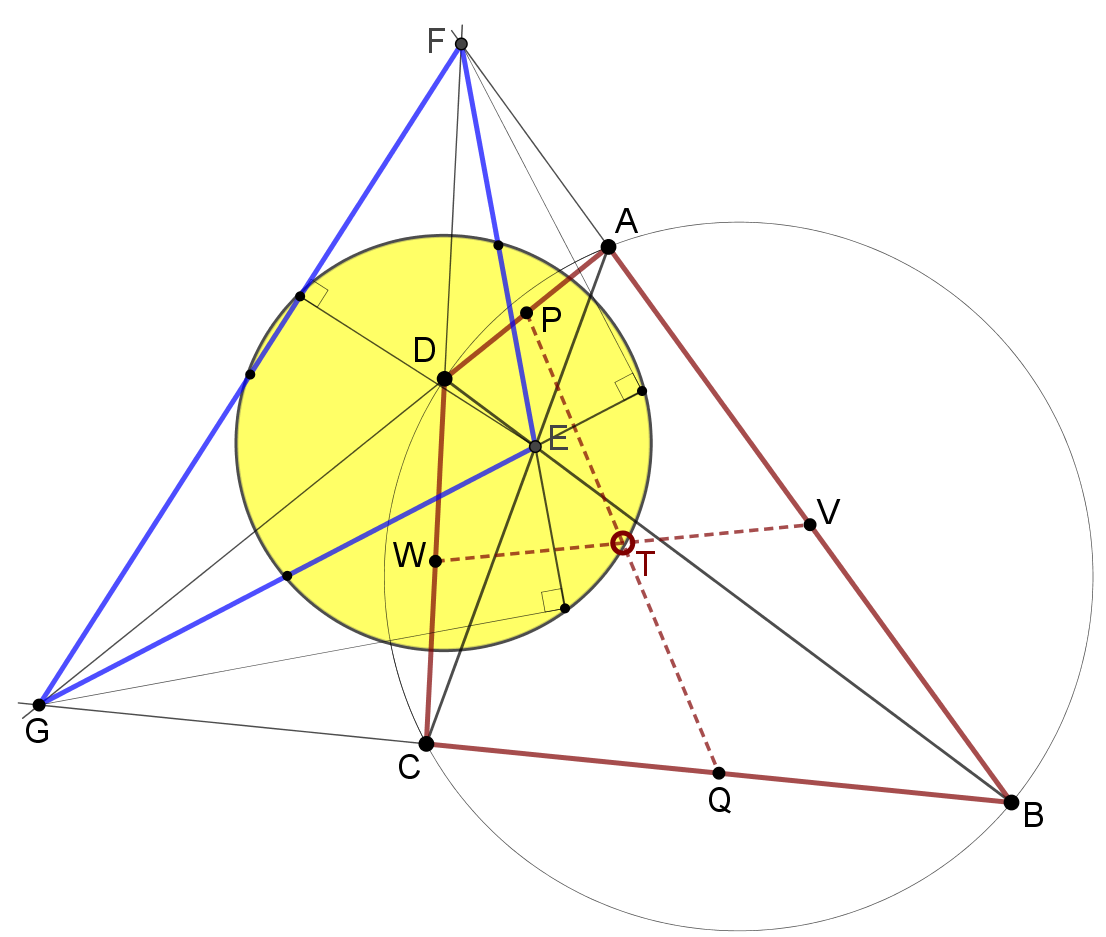
  • 원내접 사각형의 대각선 삼각형의 구점원을 ω라 하자. 원내접 사각형의 이중선분의 교점은 구점원에 속한다.[6][7]

ABCD는 원내접 사각형이다. △''EFG''는 ABCD의 대각선 삼각형이다. ABCD의 이중선분의 교점 T는 △''EFG''의 구점원에 속한다.

  • 기준 삼각형의 구점원은 기준 삼각형의 중점 삼각형(기준 삼각형의 변의 중점에 꼭짓점을 둠)과 수족 삼각형(기준 삼각형의 높이의 발에 꼭짓점을 둠) 모두의 외접원이다.[5]
  • 삼각형의 꼭짓점을 지나는 모든 직교 쌍곡선의 중심은 구점원 위에 있다. 예로는 키퍼트 쌍곡선, 예르자벡 쌍곡선, 포이어바흐의 직교 쌍곡선이 있다. 이 사실을 포이어바흐 원뿔 곡선 정리라고 한다.


구점원과 수심계를 이루는 16개의 접원

  • 네 점 A, B, C, H의 수심계가 주어지면, 해당 시스템의 세 개의 서로 다른 점의 임의의 조합으로 형성된 네 개의 삼각형은 모두 동일한 구점원을 공유한다. 이는 대칭성의 결과이다.
  • 결과적으로, 이 네 개의 삼각형은 동일한 반지름을 가진 외접원을 갖는다. N이 공통 구점의 중심을 나타내고 P가 수심계의 평면의 임의의 점이라고 하자. 그러면


::\overline{NA}^2 + \overline{NB}^2 + \overline{NC}^2 + \overline{NH}^2 = 3R^2

: 여기서 R은 공통 외접반지름이고, 만약

::\overline{PA}^2 + \overline{PB}^2 + \overline{PC}^2 + \overline{PH}^2 = K^2,

: 여기서 K가 상수이면, P의 자취는 반지름이 \tfrac{1}{2} \sqrt{K^2-3R^2}.인 N을 중심으로 하는 원이다. P가 N에 접근함에 따라, 해당 상수 K에 대한 P의 자취는 구점의 중심 N으로 축소된다. 또한, 구점원은 다음을 만족하는 P의 자취이다.

::\overline{PA}^2 + \overline{PB}^2 + \overline{PC}^2 + \overline{PH}^2 = 4R^2.

  • 삼각형의 내심과 방심의 중심은 수심계를 형성한다. 해당 수심계에 대해 생성된 구점원은 원래 삼각형의 외접원이다. 수심계의 높이의 발은 원래 삼각형의 꼭짓점이다.
  • 네 개의 임의의 점 A, B, C, D가 수심계를 형성하지 않으면, △''ABC'', △''BCD'', △''CDA'', △''DAB''의 구점원은 퐁슬레 점인 점 A, B, C, D에서 만난다. 이 구점원의 나머지 여섯 개의 교점은 각각 네 개의 삼각형의 중점과 공통적으로 만난다.
  • 네 점 A, B, C, D가 원내접 사각형을 형성하면, △''ABC'', △''BCD'', △''CDA'', △''DAB''의 구점원은 원내접 사각형의 반중심에서 만난다. 구점원은 모두 원내접 사각형의 외접원 반지름의 절반과 동일한 반지름을 갖는다. 구점원은 네 개의 존슨 원 세트를 형성한다. 결과적으로, 네 개의 구점 중심은 순환적이며, 원내접 사각형의 반중심을 중심으로 하는 네 개의 구점원과 동일한 원 위에 놓인다. 또한, 네 개의 구점 중심으로부터 형성된 원내접 사각형은 비율이 –1/2이고 호모테틱 중심 N이 외심 O에서 반중심 M을 연결하는 선 위에 놓이는 참조 원내접 사각형 ABCD에 호모테틱이다. 여기서


::\overline{ON} = 2\overline{NM}.

  • 외심을 통과하는 선의 수심점은 구점원 위에 있다.
  • 삼각형의 외접원, 구점원, 극원, 접선 삼각형의 외접원[8]은 공축원이다.[9]
  • 삼선좌표는 키퍼트 쌍곡선의 중심에 대해


::\frac{(b^2 -c^2)^2}{a} : \frac{(c^2-a^2)^2}{b} : \frac{(a^2-b^2)^2}{c}

: 이고, 예르자벡 쌍곡선의 중심에 대한 삼선좌표는

::\cos(A)\sin^2(B-C) : \cos(B)\sin^2(C-A) : \cos(C)\sin^2(A-B)

: 이다.

  • x : y : z를 삼선좌표의 변수 점으로 두면, 구점원에 대한 방정식은


::x^2\sin 2A + y^2\sin 2B + z^2\sin 2C-2(yz\sin A + zx\sin B + xy\sin C) = 0.

구점원은 삼각형 ABC의 다음 9개의 점을 통과한다.

  • 3변의 중점 (D, E, F)
  • 3개의 꼭짓점에서 대변에 내린 수선의 발 (G, H, I)
  • 수심과 3개의 꼭짓점의 중점 (J, K, L)


구점원의 중심 N은 오일러선 상의 수심과 외심의 중점이며, 반지름은 외접원의 반지름 R의 절반(1/2)이다.

포이어바흐의 정리에 따르면 구점원은 내접원에 내접하고 방접원에 외접한다. 구점원과 내접원의 접점을 포이어바흐 점이라고 부른다.

이외에도 다음과 같은 특징이 있다.

  • 삼각형의 세 꼭짓점과 수심의 네 점 중 어떤 세 점을 선택하더라도 해당 삼각형에 대한 구점원은 동일하다.
  • 외접원의 대척점에 있는 두 점에서 유도되는 두 개의 심슨선은 구점원에서 직교한다.
  • 수심과 외접원 위의 임의의 점의 중점은 구점원 위에 있다.
  • 삼각형의 내심 I와 방심 IA, IB, IC의 중점, 방심 IA, IB, IC끼리의 중점은 모두 외접원 위에 있다. 이는 트릴리움의 정리를 포함한다.


3. 1. 기본 성질

구점원


구점원은 삼각형의 세 변의 중점, 세 꼭짓점에서 마주보는 변에 내린 수선의 발, 각 꼭짓점과 수심을 이은 선분의 중점, 이렇게 9개의 점을 지나는 원이다.[5]

  • 삼각형의 외접원 반지름은 그 삼각형의 구점원의 반지름의 두 배이다.[5]
  • 구점원의 중심은 오일러선 상에서 외심과 수심의 중점이다.[5]

  • -|]]

3. 2. 포이어바흐 정리

삼각형의 구점원은 삼각형의 내접원과 세 방접원에 접한다. 이때 내접원과 구점원의 접점을 포이어바흐 점이라고 한다.

구점원은 내접원과 방접원에 접한다.


1822년, 카를 포이어바흐(Karl Feuerbach)는 모든 삼각형의 구점원이 세 방접원에 외접하고 내접원에 내접한다는 사실을 발견했으며, 이 결과는 포이어바흐 정리로 알려져 있다. 그는 다음과 같이 증명했다.

> ... 삼각형의 높이의 발을 지나는 원은 차례로 삼각형의 세 변에 접하는 네 개의 모든 원에 접한다...

내접원과 구점원이 만나는 삼각형의 중심을 포이어바흐 점이라고 부른다.

이 정리는 포이어바흐의 정리라고 불리며, 구점원에 관한 가장 유명한 정리 중 하나이다.

이 정리는 로저스의 정리, 하트의 정리, 폰트네의 정리 등으로 일반화되었다.

3. 3. 오일러 직선

오일러 직선 문서에서 발췌하면, 구점원의 중심은 수심, 외심, 무게중심과 한 직선 위에 있으며, 이 직선을 오일러 직선이라고 한다.

  • 구점원의 중심 은 수심 에서 외심 까지의 선분을 이등분한다.[5]


::\overline{ON} = \overline{NH}.

  • 구점의 중심 은 오일러 직선 상에서 무게중심 에서 수심 까지의 거리의 1/4 지점에 있다.[5]


::\overline{HN} = 3\overline{NG}.

구점원의 중심 N은 오일러 직선 상의 수심과 외심의 중점이다.

3. 4. 기타 성질

정삼각형의 내접원과 구점원은 일치한다. 따라서 정삼각형은 외심, 내심, 무게중심, 수심, 구점원의 중심이 모두 한 점이다.[5]

삼각형의 세 꼭짓점과 수심 네 점 중 어떤 세 점을 선택하여 만든 삼각형의 구점원은 모두 같다.

삼각형의 외접원 위의 한 점에서 각 변에 내린 수선은 모두 한 점에서 만나며, 이 점은 구점원 위에 있다. (심슨 정리)

4. 역사

오일러는 1765년에 삼각형 위의 6개의 점(세 변의 중점, 세 수선의 발)을 지나는 원이 존재함을 증명했다.[10] 1821년, 샤를 브리앙숑과 장 빅토르 퐁슬레는 오일러가 발견한 여섯 점 외에 세 점(수심과 각 꼭짓점을 이은 선분의 중점)도 같은 원 위에 있음을 증명하였다.

1822년, 카를 포이어바흐는 이 원이 삼각형의 내접원과 방접원에 접한다는 것을 증명하는 논문을 발표했다. 오를리 테르케므는 1842년에 포이어바흐의 정리에 대한 해석적 증명을 제시하고 이 원을 le cercle des neuf points|구점원프랑스어(nine-point circle|나인 포인트 서클영어)이라고 명명했다. 이 원은 한때 육점원이라고도 불렸지만, 현재 육점원은 다른 원을 가리킨다.

5. 한국 수학 교육과 구점원

한국의 중학교 수학 교육과정에서는 삼각형의 오심(외심, 내심, 무게중심, 수심, 방심)을 학습하며, 이와 관련된 오일러 직선, 심슨 정리 등을 배운다. 구점원은 직접적으로 교육과정에 명시되어 있지는 않지만, 심화 학습이나 수학 경시대회, 영재 교육 등에서 자주 다루어지는 주제이다.

구점원의 여러 성질은 작도, 증명, 문제 해결 등 다양한 수학적 활동을 통해 학생들의 기하적 사고력 및 문제 해결 능력을 향상시키는 데 기여할 수 있다. 특히, 포이어바흐 정리는 내접원, 방접원, 외접원 등 다양한 원과 관련된 기하 문제 해결에 중요한 통찰력을 제공한다.

6. 일반화

구점원은 원뿔 곡선의 한 예시이며, 일반적인 9점 원뿔 곡선의 특수한 경우이다. 일반적인 9점 원뿔 곡선은 삼각형 $ABC$와 네 번째 점 $P$에 의해 결정된다. 9점원은 $P$가 $ABC$의 수심일 때의 경우이다.[1]

삼각형의 꼭짓점과 $P$는 완전 사변형을 결정하고, 이 사변형의 반대쪽 변이 교차하는 세 개의 "대각선 점"을 결정한다. 사변형에는 6개의 "측선"이 있는데, 9점 원뿔 곡선은 이들의 중점과 대각선 점을 지난다. $P$가 $ABC$의 내부에 있거나 삼각형과 맞꼭지각을 공유하는 영역에 있을 때, 9점 원뿔 곡선은 타원이 된다. 반면 $P$가 세 개의 인접 영역 중 하나에 있을 때는 9점 쌍곡선이 되며, 이 쌍곡선은 $P$가 $ABC$의 외접원 위에 놓일 때 직사각형이 된다.[1]

참조

[1] 논문
[2] 논문
[3] 간행물 Disentangling a Triangle http://www.maa.org/p[...]
[4] 서적 Nine-Point Circle Theorem, in A Sequel to the First Six Books of Euclid http://babel.hathitr[...] Longmans, Green, & Co
[5] 서적 The Secrets of Triangles Prometheus Books
[6] 간행물 New points that belong to the nine-point circle 2019-07
[7] 간행물 New applications of method of complex numbers in the geometry of cyclic quadrilaterals https://ijgeometry.c[...] 2018
[8] 논문
[9] 논문
[10] 웹사이트 Nine-Point Circle https://mathworld.wo[...] 2024-10-02


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com