사원수와 회전

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

사원수는 복소수를 확장한 수 체계로, 3차원 회전을 표현하는 데 널리 사용된다. 사원수는 1, i, j, k의 네 가지 기본 요소로 구성되며, i² = j² = k² = ijk = -1의 규칙을 따른다. 사원수의 곱셈은 비가환적이며, 3차원 회전의 합성과 유사한 특성을 갖는다. 사원수는 4개의 실수로 축-각도 표현을 인코딩하여 3차원 공간에서 회전을 표현하고, 회전 행렬보다 간결하고 효율적이며 짐벌락 현상을 피할 수 있다는 장점이 있다. 사원수는 컴퓨터 그래픽스, 로봇 공학, 항공우주 공학 등 다양한 분야에서 활용되며, 4차원 공간의 회전을 표현하는 데에도 사용된다.

더 읽어볼만한 페이지

강체역학 - 고체역학
고체역학은 고체 재료와 구조물의 응력, 변형, 파괴를 연구하는 학문으로, 구조물의 안정성, 동역학계, 열역학, 생체역학 등 다양한 분야를 포괄하며 사회 기반 시설 설계에 필수적으로 활용된다.
강체역학 - 피로 (재료)
피로(재료)는 반복적인 응력으로 인해 재료가 파괴되는 현상으로, 초기 균열 형성, 균열 성장, 최종 파괴 단계를 거치며 환경 요인의 영향을 받아 설계 단계 고려, 검사, 부재 교체, 재료 변경 등의 방법으로 대처할 수 있다.
사원수 - 사원수 벡터 공간
사원수 벡터 공간은 환론의 가군, 복소수 벡터 공간 위의 사원수 구조, 실수 벡터 공간 위의 사원수 구조를 통해 정의되며, 이 세 가지 정의는 서로 동치이다.
사원수 - 초켈러 다양체
초켈러 다양체는 리만 다양체 위에 정의된 초켈러 구조를 가지며, 세 개의 복소구조가 사원수 관계식을 만족시키고 켈러 구조의 모듈라이 공간을 이루는 짝수 차원의 다양체로서, 칼라비-야우 다양체와 사원수 켈러 다양체의 일종이며 물리학 분야에서도 중요한 역할을 한다.
3차원 회전 - 방향
방향은 2차원, 3차원 공간에서 방향 벡터로 표현되며, 단위 벡터, 각도(편각), 방향각, 방위각, 방향 코사인 등으로 나타낼 수 있고, 언어적으로는 가로세로, 상하, 전후, 좌우와 같은 상대적인 표현이 사용되기도 한다.
3차원 회전 - 오일러 각
오일러 각은 레온하르트 오일러가 소개한 3차원 공간 좌표계의 회전으로 강체의 방향을 나타내는 세 개의 각도이며, 로봇 제어 등 기기 제어 분야에서 널리 쓰이고, 회전축 순서에 따라 정오일러 각과 테이트-브라이언 각으로 나뉜다.

사원수와 회전
개요
주제	3차원 공간에서의 회전
관련 항목	사원수 회전 회전군 SO(3) 회전 표현 로드리고 방정식
추가 정보
참고 문헌	Shoemake, Ken (1985). "Animating Rotation with Quaternion Curves". Computer Graphics. 19 (3): 245–254. doi:10.1145/325165.325242. ISBN 978-1575240169. S2CID 206784347. Hanson, Andrew J. (2006). Visualizing Quaternions. Morgan Kaufmann. ISBN 978-0-12-088441-3. Kuipers, Jack B. (1999). Quaternions and Rotation Sequences: A Primer with Applications to Orbits, Aerospace and Virtual Reality. Princeton University Press. ISBN 978-0-691-10298-6. Kunze, Karsten; Schaeben, Helmut (November 2004). "The Bingham Distribution of Quaternions and Its Spherical Radon Transform in Texture Analysis". Mathematical Geology. 36 (8): 917–943. doi:10.1023/B:MATG.0000048799.56445.59. S2CID 55009081.

2. 사원수의 정의 및 성질

복소수가 실수에 허수 단위 $\mathbf{i}$ ( $\mathbf{i}^2 = -1$ )를 추가하여 정의되는 것처럼, 사원수는 실수에 세 개의 허수 단위 $\mathbf{i}$ , $\mathbf{j}$ , $\mathbf{k}$ 를 추가하여 정의된다. 이 허수 단위들은 다음과 같은 기본 규칙을 만족한다.

: $\mathbf{i}^2 = \mathbf{j}^2 = \mathbf{k}^2 = \mathbf{i}\mathbf{j}\mathbf{k} = -1$

이 규칙들과 일반적인 대수학 규칙(단, 곱셈의 교환 법칙은 제외)으로부터 사원수의 모든 연산 규칙이 유도된다. 사원수는 일반적으로 $a + b\mathbf{i} + c\mathbf{j} + d\mathbf{k}$ 형태로 표현되며, 여기서 ''a'', ''b'', ''c'', ''d''는 실수이다. ''a''는 스칼라 부분, $b\mathbf{i} + c\mathbf{j} + d\mathbf{k}$ 는 벡터 부분으로 간주될 수 있다.

복소수와 달리 사원수의 곱셈은 교환 법칙이 성립하지 않는 중요한 특징을 가진다. 예를 들어, $\mathbf{i}\mathbf{j} = \mathbf{k}$ 이지만 $\mathbf{j}\mathbf{i} = -\mathbf{k}$ 이다. 이러한 비가환성은 행렬 곱셈에서도 볼 수 있는 성질이다.

사원수의 벡터 부분은 3차원 벡터 공간의 벡터와 자연스럽게 대응되며, 사원수 곱셈은 벡터의 내적 및 외적 연산과 깊은 관련이 있다.^[14] 또한, 사원수에는 켤레, 노름, 그리고 0이 아닌 사원수에 대한 곱셈 역원이 정의되어 나눗셈 연산도 가능하다. 이러한 대수적 구조와 성질 덕분에 사원수는 특히 3차원 공간에서의 회전을 표현하고 계산하는 데 효과적으로 사용된다.

2. 1. 기본 정의

복소수는 일반적인 대수학 규칙과 함께 '''i'''² = −1 이라는 추가 규칙을 만족하는 추상 기호 '''i'''를 도입하여 정의할 수 있다. 이 규칙만으로 복소수 연산의 모든 규칙을 유도할 수 있다. 예를 들어, 두 복소수의 곱셈은 다음과 같이 계산된다.

:

(a+b\mathbf{i})(c+d\mathbf{i}) = ac + ad\mathbf{i} + b\mathbf{i}c + b\mathbf{i}d\mathbf{i} = ac + ad\mathbf{i} + bc\mathbf{i} + bd\mathbf{i}^2 = (ac - bd) + (bc + ad) \mathbf{i}.

마찬가지로, 사원수는 일반적인 대수 규칙(곱셈의 교환 법칙은 제외)과 함께 '''i'''² = '''j'''² = '''k'''² = '''i j k''' = −1 이라는 규칙을 만족하는 추상 기호 '''i''', '''j''', '''k'''를 도입하여 정의할 수 있다. 곱셈이 비가환적이라는 점이 복소수와의 중요한 차이점이며, 이는 행렬 곱셈과 유사하다. 이 기본 규칙들로부터 사원수 기저 요소의 곱셈 규칙을 포함한 사원수 연산의 모든 규칙이 파생된다. 예를 들어, 두 사원수의 곱셈은 다음과 같다.

:

\begin{align}&(a + b\mathbf{i} + c\mathbf{j} + d\mathbf{k}) (e + f\mathbf{i} + g\mathbf{j} + h\mathbf{k}) = \\&(ae - bf - cg - dh) + (af + be + ch - dg) \mathbf{i} + (ag - bh + ce + df) \mathbf{j} + (ah + bg - cf + de) \mathbf{k}.\end{align}

사원수

a + b\mathbf{i} + c\mathbf{j} + d\mathbf{k}

에서 실수 부분 ''a''는 스칼라처럼 취급되고, 허수 부분

b\mathbf{i} + c\mathbf{j} + d\mathbf{k}

는 3차원 벡터 공간의 벡터

\vec{v} = (b,c,d)

처럼 다룰 수 있다. 따라서 기하학적 응용에서는 사원수를 스칼라와 벡터의 합으로 표현하는 것이 편리하다.

:

q = a + \vec{v} = a + b\mathbf{i} + c\mathbf{j} + d\mathbf{k}.

이는 단순히 사원수의 실수부와 허수부를 나타내는 표기법으로 이해할 수 있다. 즉, 벡터 부분이 0인 사원수

(s, \vec{0})

와 스칼라 부분이 0인 사원수

(0, \vec{v})

의 합으로 생각할 수 있다.

:

q_1 = s + \vec{v} = \left(s, \vec{0}\right) + \left(0, \vec{v}\right).

사원수 곱셈은 현대 벡터 연산인 내적과 외적을 사용하여 표현할 수 있다(실제로 내적과 외적 개념은 사원수 연구에서 비롯되었다^[14]). 두 벡터(순수 허수 사원수)

\vec{v}

와

\vec{w}

의 곱셈은 다음과 같이 정의된다.

:

\vec{v} \vec{w} = - \vec{v} \cdot \vec{w} + \vec{v} \times \vec{w},

여기서

\vec{v} \cdot \vec{w}

는 벡터 내적(스칼라)이고,

\vec{v} \times \vec{w}

는 벡터 외적(벡터)이다.

벡터 외적은 반가환성을 가지므로(

\vec{v} \times \vec{w} = - \vec{w} \times \vec{v}

), 사원수 곱셈 역시 일반적으로 비가환적이다. 이를 이용하여 두 일반 사원수

q_1 = s + \vec{v}

와

q_2 = t + \vec{w}

의 곱셈은 다음과 같이 표현된다(사원수와 3차원 기하학 참조).

:

q_1 q_2 = \left(s + \vec{v}\right) \left(t + \vec{w}\right) = \left(s t - \vec{v} \cdot \vec{w}\right) + \left(s \vec{w} + t \vec{v} + \vec{v} \times \vec{w}\right).

0이 아닌 사원수

q = s + \vec{v}

의 곱셈 역원 또는 역수는 켤레

q^* = s - \vec{v}

와 노름

\lVert q \rVert^2 = s^2 + \lVert \vec{v} \rVert^2 = s^2 + b^2 + c^2 + d^2

을 이용하여 다음과 같이 계산된다(자세한 내용 참조).

:

q^{-1} = \left(s + \vec{v}\right)^{-1} = \frac{q^*}{\lVert q \rVert^2} = \frac{s - \vec{v}}{s^2 + \lVert \vec{v} \rVert^2}.

이는 복소수의 곱셈 역수 계산과 유사하다.

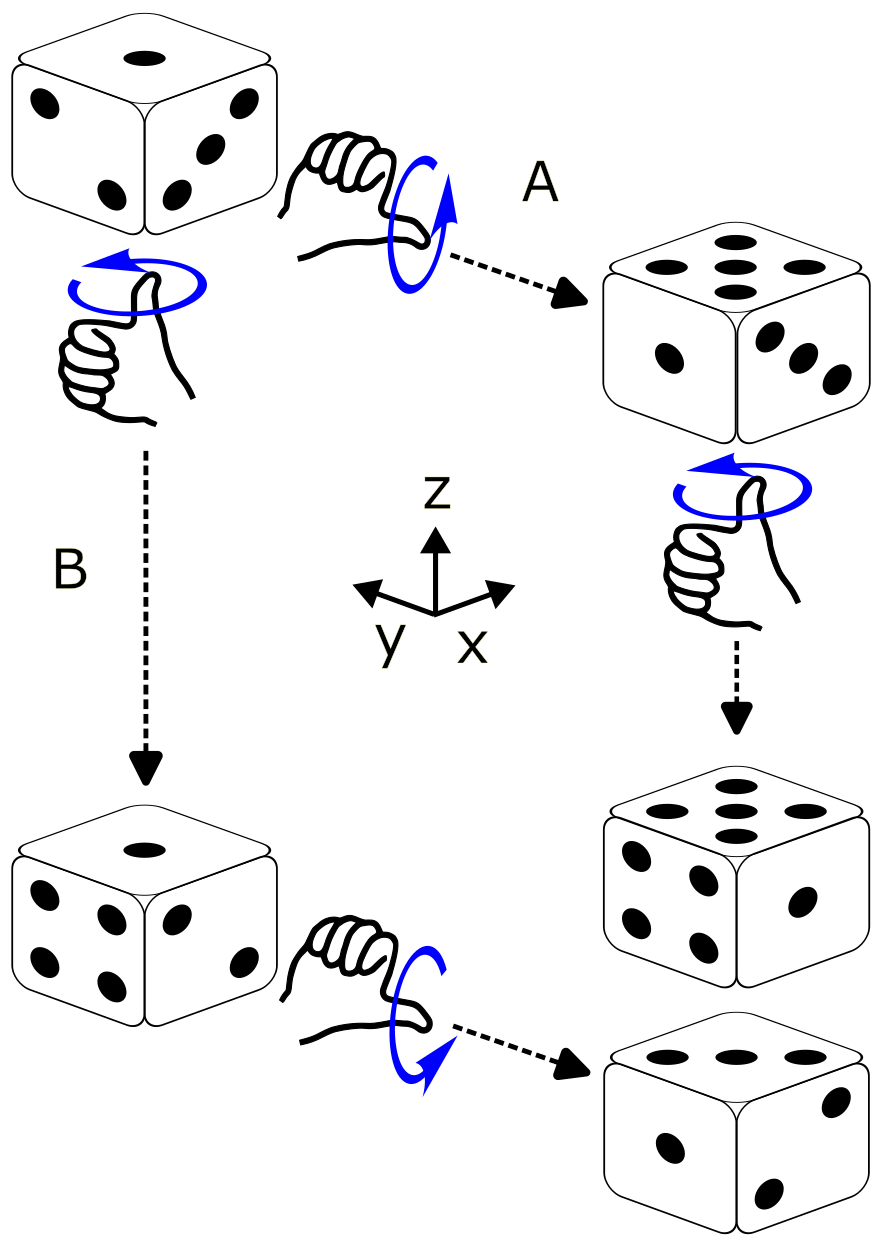
주사위의 비가환 회전. 사원수 곱셈은 비가환적이므로 회전 순서에 따라 결과가 달라진다.

사원수의 곱셈이 비가환적이라는 성질은 3차원 회전을 표현할 때 중요하다. 단위 사원수를 이용한 회전 변환 공식

p \mapsto q p q^{-1}

이 작동하는 방식과 관련 있으며, 3차원 공간에서의 회전 자체가 일반적으로 교환 가능하지 않다는 사실을 반영한다. 예를 들어, 주사위를 서로 다른 축으로 두 번 회전시킬 때, 회전 순서를 바꾸면 최종 결과가 달라지는 것을 통해 비가환성을 직관적으로 확인할 수 있다. 오른쪽 그림은 ''-y'' 축과 ''+z'' 축을 중심으로 90도 회전을 서로 다른 순서로 적용했을 때 주사위 윗면의 숫자가 달라지는 것을 보여준다.

2. 2. 켤레, 노름, 역원

사원수

q = s + \vec{v} = s + b\mathbf{i} + c\mathbf{j} + d\mathbf{k}

(여기서

s

는 스칼라 부분,

\vec{v} = b\mathbf{i} + c\mathbf{j} + d\mathbf{k}

는 벡터(허수) 부분)에 대해 켤레, 노름, 역원을 정의할 수 있다.

사원수

q

의 '''켤레'''(conjugate)는

q^*

또는

\bar{q}

로 표기하며, 벡터(허수) 부분의 부호를 바꾸어 정의한다.

:

q^* = (s + \vec{v})^* = s - \vec{v} = s - b\mathbf{i} - c\mathbf{j} - d\mathbf{k}

이는 복소수의 켤레 복소수 개념을 확장한 것이다.

사원수

q

의 '''노름'''(norm) 또는 크기는

\lVert q \rVert

로 표기하며, 각 성분의 제곱의 합의 제곱근으로 정의된다.

:

\lVert q \rVert = \sqrt{q q^*} = \sqrt{q^* q} = \sqrt{s^2 + b^2 + c^2 + d^2} = \sqrt{s^2 + \lVert \vec{v} \rVert^2}

노름의 제곱은

\lVert q \rVert^2 = s^2 + \lVert \vec{v} \rVert^2

이다. 노름은 항상 음이 아닌 실수 값을 가진다.

0이 아닌 사원수

q

의 (좌우) 곱셈 역원

q^{-1}

은 켤레와 노름의 제곱을 이용하여 다음과 같이 정의된다.

:

q^{-1} = (s + \vec{v})^{-1} = \frac{(s + \vec{v})^*}{\lVert s + \vec{v} \rVert^2} = \frac{s - \vec{v}}{s^2 + \lVert \vec{v} \rVert^2}

이는

q q^{-1} = q^{-1} q = 1

을 만족하며, 직접 계산을 통해 확인할 수 있다. 이 공식은 복소수의 곱셈 역원을 구하는 방식과 유사하다.

2. 3. 사원수와 벡터

사원수는 실수 부분과 허수 부분으로 구성되며, 허수 부분은 3차원 벡터 공간의 벡터로 간주될 수 있다. 즉, 사원수

q = a + b\mathbf{i} + c\mathbf{j} + d\mathbf{k}

에서 허수 부분

b\mathbf{i} + c\mathbf{j} + d\mathbf{k}

는 3차원 벡터

\vec{v} = (b,c,d)

에 해당하고, 실수 부분

a

는 스칼라로 볼 수 있다. 이러한 관점에서 사원수는 스칼라 더하기 벡터 형태로 편리하게 표현된다.

:

q = a + \vec{v}

여기서

a

는 스칼라 부분이고

\vec{v} = b\mathbf{i} + c\mathbf{j} + d\mathbf{k}

는 벡터 부분이다. 이는 표기상의 편의를 위한 것으로, 실제로는 스칼라

a

를

(a, \vec{0})

형태의 사원수로, 벡터

\vec{v}

를

(0, \vec{v})

형태의 사원수로 간주하여 더하는 것과 같다.

:

q = s + \vec{v} = \left(s, \vec{0}\right) + \left(0, \vec{v}\right)

두 벡터(즉, 실수부가 0인 순수 허수 사원수)의 곱셈은 현대적인 벡터 내적과 외적 연산을 사용하여 표현할 수 있다.^[14] 벡터

\vec{v}

와

\vec{w}

를 각각 실수부가 0인 사원수로 간주할 때, 그 곱은 다음과 같이 정의된다.

:

\vec{v} \vec{w} = - (\vec{v} \cdot \vec{w}) + (\vec{v} \times \vec{w})

여기서

\vec{v} \cdot \vec{w}

는 두 벡터의 내적(결과는 스칼라)이고,

\vec{v} \times \vec{w}

는 두 벡터의 외적(결과는 벡터)이다. 이 곱셈 결과는 일반적으로 스칼라 부분(

-\vec{v} \cdot \vec{w}

)과 벡터 부분(

\vec{v} \times \vec{w}

)을 모두 가지는 사원수가 된다.

벡터 외적은 반가환성(

\vec{v} \times \vec{w} = - \vec{w} \times \vec{v}

)을 가지므로, 순수 벡터 사원수 간의 곱셈은 교환적이지 않다. 이는 일반적인 사원수 곱셈이 비가환적인 중요한 이유 중 하나이다.

두 일반적인 사원수

q_1 = s + \vec{v}

와

q_2 = t + \vec{w}

의 곱셈은 분배 법칙과 위의 벡터 곱셈 규칙을 이용하여 다음과 같이 계산할 수 있다.

:

q_1 q_2 = \left(s + \vec{v}\right) \left(t + \vec{w}\right)

:

\qquad = st + s\vec{w} + t\vec{v} + \vec{v}\vec{w}

:

\qquad = st + s\vec{w} + t\vec{v} + (-\vec{v} \cdot \vec{w} + \vec{v} \times \vec{w})

:

\qquad = \left(st - \vec{v} \cdot \vec{w}\right) + \left(s \vec{w} + t \vec{v} + \vec{v} \times \vec{w}\right)

결과적으로 얻어지는 사원수의 스칼라 부분은

st - \vec{v} \cdot \vec{w}

이고, 벡터 부분은

s \vec{w} + t \vec{v} + \vec{v} \times \vec{w}

이다.

3. 사원수를 이용한 3차원 회전 표현

사원수는 3차원 공간에서의 회전을 표현하고 계산하는 데 유용한 수학적 도구이다. 오일러의 회전 정리에 따르면 모든 3차원 회전은 특정 축을 중심으로 특정 각도만큼 회전하는 것으로 나타낼 수 있는데, 사원수는 이러한 축-각 표현을 네 개의 실수를 이용하여 간결하게 나타낸다.

사원수를 이용하면 벡터를 회전시키는 연산을 켤레 연산이라는 대수적 방법으로 수행할 수 있다. 또한, 여러 번의 회전을 연속적으로 적용하는 경우, 각 회전에 해당하는 사원수들을 곱하여 하나의 합성된 사원수로 표현할 수 있어 계산을 효율적으로 처리할 수 있다. 주어진 회전 사원수로부터 원래의 회전축과 회전 각도를 다시 추출하는 방법도 존재한다.

사원수를 이용한 구체적인 회전 표현 방식, 회전 연산 방법, 그리고 회전축과 각도를 복원하는 방법에 대한 자세한 내용은 아래 하위 섹션에서 다룬다.

3. 1. 회전의 사원수 표현

3차원 공간에서 오일러의 회전 정리에 따르면, 고정된 점을 중심으로 하는 강체 또는 좌표계의 모든 회전은 그 고정점을 통과하는 고정된 축(오일러 축)을 중심으로 특정 각도

\theta

만큼 회전하는 것과 같다.^[6] 이 오일러 축은 보통 단위 벡터

\vec{u}

(그림에서는

\hat{e}

)로 나타낸다. 따라서 3차원 공간의 모든 회전은 벡터

\vec{u}

와 각도

\theta

의 조합, 즉 축-각 표현으로 나타낼 수 있다.^[7]

사원수는 이 축-각 표현을 4개의 실수로 간단하게 나타내는 방법을 제공한다. 이를 이용하면 원점을 기준으로 하는 점의 위치 벡터

(x,y,z)

에 회전을 적용하는 계산을 수행할 수 있으며, 이는

\mathbb{R}^3

에서 점을 나타낸다.

유클리드 벡터

(x, y, z)

는 사원수의 연산을 위해 스칼라 부분이 0인 '순수 사원수'

x\mathbf{i} + y\mathbf{j} + z\mathbf{k}

로 표현할 수 있다. 여기서

\mathbf{i}, \mathbf{j}, \mathbf{k}

는 데카르트 좌표계의 세 축(

x, y, z

)을 나타내는 단위 벡터이자 기본적인 사원수 단위이다.

단위 벡터로 주어진 회전축

\mathbf{u} = (u_x, u_y, u_z) = u_x\mathbf{i} + u_y\mathbf{j} + u_z\mathbf{k}

를 중심으로 각도

\theta

만큼 회전하는 것은 다음과 같은 단위 사원수

\mathbf{q}

로 표현할 수 있다. 이 공식은 오일러 공식을 사원수로 확장한 결과이다.

\mathbf{q} = e^{\frac{\theta}{2}{(u_x\mathbf{i} + u_y\mathbf{j} + u_z\mathbf{k})}} = \cos \frac{\theta}{2} + (u_x\mathbf{i} + u_y\mathbf{j} + u_z\mathbf{k}) \sin \frac{\theta}{2} = \cos \frac{\theta}{2} + \mathbf{u} \sin \frac{\theta}{2}

벡터

\mathbf{p} = (p_x, p_y, p_z)

(순수 사원수

\mathbf{p'} = p_x\mathbf{i} + p_y\mathbf{j} + p_z\mathbf{k}

로 표현)를 이 사원수

\mathbf{q}

를 이용해 회전시키는 연산은 켤레 연산으로 수행된다.^[8] 회전된 벡터

\mathbf{r}

은 다음과 같이 계산된 사원수의 벡터 부분이다.

L(\mathbf{p'}) := \mathbf{q} \mathbf{p'} \mathbf{q}^{-1} = (0, \mathbf{r})

여기서

\mathbf{q}^{-1}

는

\mathbf{q}

의 곱셈의 역원으로, 단위 사원수의 경우 켤레 사원수와 같다.

\mathbf{q}^{-1} = \cos \frac{\theta}{2} - \mathbf{u} \sin \frac{\theta}{2}

회전된 벡터

\mathbf{r}

은 해밀턴 곱을 사용하여 다음과 같이 계산된다.

\mathbf{r} = (\cos^2\frac{\theta}{2}-\sin^2\frac{\theta}{2}||\mathbf u||^2)\mathbf p + 2\sin^2\frac{\theta}{2} (\mathbf u \cdot \mathbf p)\mathbf u + 2\cos\frac{\theta}{2}\sin\frac{\theta}{2}(\mathbf u \times \mathbf p)

이 켤레 연산은 다음과 같이 더 적은 연산으로 표현할 수도 있다.

\mathbf{r} = \mathbf{p} + 2\cos\frac{\theta}{2}\sin\frac{\theta}{2}(\mathbf u \times \mathbf p) + 2 \sin^2\frac{\theta}{2} \mathbf u \times (\mathbf u \times \mathbf p)

이 연산

L

은 사원수 공간에서의 선형 변환이며,

\mathbf{q}

가 단위 사원수이므로 등거리 변환이기도 하다.^[9] 이 변환은 벡터

\mathbf{p}

를 회전축

\mathbf{u}

를 중심으로 각도

\theta

만큼 회전시키는 것과 동일하며, 이는 로드리게스 회전 공식과 같다.

\vec{v}' = \vec{v}_{\|} + \left(\vec{u} \times \vec{v}\right) \sin \theta + \vec{v}_\bot \cos \theta

(여기서

\vec{v}_{\|}

와

\vec{v}_{\bot}

는 각각

\vec{v}

의

\vec{u}

에 평행한 성분과 수직한 성분이다.)

기하학적으로, 회전축

\vec{u}

를 중심으로 각도

\theta

만큼 회전하는 것과 반대 방향의 축

-\vec{u}

를 중심으로 각도

2\pi-\theta

만큼 회전하는 것은 동일한 최종 방향을 나타낸다. 사원수 표현에서는 각각

\mathbf{q} = \cos \frac{\theta}{2} + \mathbf{u} \sin \frac{\theta}{2}

와

-\mathbf{q} = \cos \frac{2\pi-\theta}{2} + (-\mathbf{u}) \sin \frac{2\pi-\theta}{2} = -\cos \frac{\theta}{2} - \mathbf{u} \sin \frac{\theta}{2}

에 해당한다. 즉, 사원수

\mathbf{q}

와

-\mathbf{q}

는 동일한 3차원 회전을 나타낸다. 이는 켤레 연산

\mathbf{q} \mathbf{p'} \mathbf{q}^{-1}

에서

\mathbf{q}

의 부호가 제곱되어 사라지기 때문에 대수적으로도 확인된다. 이는 회전군 SO(3)과 스핀 군 SU(2) 사이의 2:1 대응 관계와 관련이 있다.

두 번의 회전을 연속으로 적용하는 것은 해당하는 두 회전 사원수의 곱으로 표현된다. 회전

\mathbf{q}_1

을 먼저 적용하고 그 다음 회전

\mathbf{q}_2

를 적용하는 것은 다음과 같은 합성된 사원수

\mathbf{q}'

에 의한 한 번의 회전과 같다.

\mathbf{q}' = \mathbf{q}_2 \mathbf{q}_1

이를 통해 여러 회전을 하나의 사원수로 결합하여 한 번에 적용할 수 있다.

사원수

\mathbf{q}

에 의한 회전을

n

번 반복하는 것은

\mathbf{q}^n

에 의한 회전과 같으며, 이는 동일한 축을 중심으로 각도

n\theta

만큼 회전하는 것에 해당한다. 이 성질은 실수

n

에 대해서도 확장될 수 있어, 공간상의 두 방향 사이를 부드럽게 보간하는 Slerp(구면 선형 보간) 등에 활용된다.

사원수의 곱셈은 비가환적이다. 즉, 일반적으로

\mathbf{q}_1 \mathbf{q}_2 \neq \mathbf{q}_2 \mathbf{q}_1

이다. 이는 3차원 회전의 합성이 일반적으로 가환적이지 않다는 사실과 일치한다. 예를 들어, 물체를

x

축으로 90도 회전시킨 후

y

축으로 90도 회전시킨 결과는,

y

축으로 90도 회전시킨 후

x

축으로 90도 회전시킨 결과와 다르다. 오른쪽 그림의 주사위 예시는 이를 잘 보여준다. 경로 A(y축 회전 후 z축 회전)와 경로 B(z축 회전 후 y축 회전)는 다른 최종 상태를 만든다.

사원수 회전 표현에서 공간의 방향성은 사원수 곱셈 순서와 관련이 있다. 벡터 외적

\mathbf{a} \times \mathbf{b} = \mathbf{c}

는 오른손 법칙(또는 왼손 법칙)에 따라 공간의 방향을 정의하는데, 이는 사원수 단위의 곱셈 규칙

\mathbf{ij} = \mathbf{k}

,

\mathbf{ji} = -\mathbf{k}

에 반영되어 있다. 만약 공간의 방향을 반대로 정의하면(예: 왼손 좌표계 사용), 이는 회전 사원수

\mathbf{q}

를 그 켤레

\mathbf{q}^{-1}

로 바꾸는 것과 같으며, 회전 연산은

\mathbf{p'} \mapsto \mathbf{q}^{-1} \mathbf{p'} \mathbf{q}

가 된다.

3. 2. 사원수를 이용한 회전 연산

3차원 공간에서, 오일러의 회전 정리에 따르면 고정된 점을 중심으로 하는 강체 또는 좌표계의 회전이나 일련의 회전은 고정된 점을 통과하는 고정된 축(이를 '오일러 축'이라고 부름)을 중심으로 주어진 각도 θ만큼 회전하는 것과 동일하다.^[6] 오일러 축은 일반적으로 단위 벡터 '''u'''(그림에서는 '''ê''')로 표시된다. 따라서 3차원에서의 모든 회전은 벡터 '''u'''와 각도 θ를 통해 표현될 수 있다.

사원수는 4개의 실수로 이^[7] 축-각도 표현을 인코딩하는 간단한 방법을 제공하며, 위치 벡터 (x,y,z)에 해당 회전을 적용(계산)하는 데 사용할 수 있다. 이는 '''R'''³에서 원점을 기준으로 하는 점을 나타낸다.

(2, 3, 4) 또는 (''a_x'', ''a_y'', ''a_z'')와 같은 유클리드 벡터는 2'''i''' + 3'''j''' + 4'''k''' 또는 ''a_x'''''i''' + ''a_y'''''j''' + ''a_z'''''k'''로 다시 쓸 수 있다. 여기서 '''i''', '''j''', '''k'''는 세 개의 데카르트 축 (전통적으로 ''x'', ''y'', ''z'')을 나타내는 단위 벡터이다. 또한 유클리드 벡터 (''a_x'', ''a_y'', ''a_z'')를 실수부가 0인 순수 사원수 (0, ''a_x'', ''a_y'', ''a_z'')로 해석하여 기본 사원수 단위의 곱셈 규칙을 따르게 할 수 있다.

단위 벡터로 정의된 축 '''u''' = (u_x, u_y, u_z) = u_x'''i''' + u_y'''j''' + u_z'''k'''를 중심으로 각도 θ 회전하는 것은 단위 사원수 '''q'''를 이용한 켤레 연산으로 표현할 수 있다. 이 사원수 '''q'''는 오일러 공식과 유사한 형태로 다음과 같이 주어진다. 이는 사원수 곱 (0 + u_x'''i''' + u_y'''j''' + u_z'''k''')(0 - u_x'''i''' - u_y'''j''' - u_z'''k''') = u_x² + u_y² + u_z² = 1 이 성립하기 때문에 테일러 급수를 이용한 지수 함수 e^{('''u''' θ)/2}로 표현할 수 있다.

: '''q''' = e^{(θ/2)(u_x'''i''' + u_y'''j''' + u_z'''k''')} = cos(θ/2) + (u_x'''i''' + u_y'''j''' + u_z'''k''') sin(θ/2) = cos(θ/2) + '''u''' sin(θ/2)

벡터 '''p''' = (p_x, p_y, p_z) = p_x'''i''' + p_y'''j''' + p_z'''k'''를 순수 사원수 '''p'''' = (0, p_x, p_y, p_z)로 간주하고, 이 벡터에 회전을 적용하는 것은 사원수 '''q'''를 이용한 켤레 연산으로 계산할 수 있다.^[8] 즉, 회전된 벡터 '''r'''은 다음과 같이 순수 사원수 L('''p''')의 벡터 부분으로 얻어진다.

: L('''p''') := '''q''' '''p'''' '''q'''^-1 = (0, '''r'''),

: '''r''' = (cos²(θ/2) - sin²(θ/2)||'''u'''||²)'''p''' + 2sin²(θ/2) ('''u''' ⋅ '''p''')'''u''' + 2cos(θ/2)sin(θ/2)('''u''' × '''p'''),

여기서 계산은 해밀턴 곱을 사용한다. 프로그래밍 방식으로 구현할 때는 벡터 '''p'''를 벡터 부분으로 하는 순수 사원수를 구성한 다음, 사원수 '''q'''와 그 역원 '''q'''^-1를 곱하여 켤레 연산을 수행한다. 결과로 얻어지는 순수 사원수의 벡터 부분이 원하는 회전된 벡터 '''r'''이다.

수학적으로, 이 연산 L은 사원수 공간에서 선형 변환을 정의한다.^[9] '''q'''가 단위 사원수이므로 노름(norm)이 보존되어 이 변환은 등거리 변환이다. 또한 L('''q''') = '''q'''이므로, L은 회전축 '''u''' 방향의 벡터(즉, '''q'''의 벡터 부분에 평행한 벡터)를 불변으로 유지한다. 벡터 '''p'''를 '''u'''에 평행한 성분과 수직인 성분으로 분해하면, L은 수직 성분만을 회전시킨다는 것을 보일 수 있다. '''n'''을 '''p'''의 '''u'''에 수직인 성분이라 하고 '''n'''_T = '''n''' × '''u'''라고 하면, L(0, '''n''')의 벡터 부분은 다음과 같다.

:(cos²(θ/2) - sin²(θ/2)) '''n''' + 2(cos(θ/2)sin(θ/2))'''n'''_T = cos(θ) '''n''' + sin(θ) '''n'''_T

이는 '''n'''을 '''u''' 축을 중심으로 각도 θ만큼 회전시킨 결과이다.

'''p''''에 대한 '''q'''의 켤레 연산은 다음과 같이 더 적은 연산으로 표현할 수도 있다.

: '''r''' = '''p''' + 2cos(θ/2)sin(θ/2)('''u''' × '''p''') + 2 sin²(θ/2) '''u''' × ('''u''' × '''p''') .

기하학적으로, 물리적인 회전과 이를 나타내는 사원수 사이에는 2:1 대응 관계가 존재한다. 즉, 사원수 '''q'''와 -'''q'''는 동일한 회전을 나타낸다. 예를 들어, 축 '''u'''를 중심으로 각도 θ만큼 회전하는 것(0 ≤ θ ≤ 2π)과 축 -'''u'''를 중심으로 각도 2π-θ만큼 회전하는 것은 동일한 최종 방향을 가지지만, 중간 경로는 다르다. 위 공식에 이 값들을 대입하면, 첫 번째 회전을 '''q'''가 나타낸다면 두 번째 회전은 -'''q'''가 나타냄을 알 수 있다. 켤레 연산 '''q''' '''p'''' '''q'''^-1는 '''q'''에 대해 이차식이므로, (-'''q''') '''p'''' (-'''q''')^-1 = (-'''q''') '''p'''' (-'''q'''^-1) = '''q''' '''p'''' '''q'''^-1가 되어 부호가 상쇄되므로 '''q'''와 -'''q'''는 같은 회전을 정의한다. (SO(3)과 SU(2) 사이의 2:1 매핑 참조)

회전에 사용되는 사원수 '''q'''는 단위 사원수이며, 그 곱셈 역원 '''q'''^-1은 켤레 사원수 '''q'''^*와 같다.

: '''q'''^-1 = '''q'''^* = cos(θ/2) - '''u''' sin(θ/2) = cos(θ/2) - (u_x'''i''' + u_y'''j''' + u_z'''k''') sin(θ/2) .

두 회전의 합성은 사원수의 곱으로 표현된다. 만약 '''p'''와 '''q'''가 각각 회전을 나타내는 단위 사원수라면, 먼저 '''q'''에 의한 회전을 적용하고 그 다음 '''p'''에 의한 회전을 적용하는 것은 합성 사원수 '''pq'''에 의한 켤레 연산과 같다.

:('''pq''') '''v''' ('''pq''')^-1 = '''p''' '''q''' '''v''' '''q'''^-1 '''p'''^-1 = '''p''' ('''q''' '''v''' '''q'''^-1) '''p'''^-1

이는 벡터 '''v'''를 먼저 '''q'''로 회전시킨 후, 그 결과를 다시 '''p'''로 회전시키는 것과 동일하다.

회전의 사원수 역원 '''q'''^-1은 반대 방향으로의 회전을 나타낸다. '''q'''^-1 ('''q''' '''v''' '''q'''^-1) '''q''' = '''v'''이므로, 역회전을 적용하면 원래 벡터로 돌아온다. 사원수 '''q'''에 의한 회전을 두 번 적용하는 것, 즉 '''q'''²에 의한 켤레 연산은 동일한 축을 중심으로 각도 2θ만큼 회전하는 것과 같다. 더 일반적으로, '''q'''^''n''은 '''q'''와 동일한 축을 중심으로 각도의 ''n''배만큼 회전하는 것을 나타낸다. 이는 임의의 실수 ''n''에 대해서도 성립하므로, 공간상의 두 방향 사이를 부드럽게 보간하는 데 사용될 수 있다. (Slerp 참조)

두 회전 사원수 '''q'''₁과 '''q'''₂가 있을 때, 회전 '''q'''₁을 먼저 적용하고 그 다음에 회전 '''q'''₂를 적용하는 합성 회전은 새로운 사원수 '''q''''로 표현된다.

: '''q'''' = '''q'''₂ '''q'''₁

이를 통해 여러 회전을 순차적으로 적용하는 대신, 모든 회전을 나타내는 사원수들을 곱하여 하나의 합성 사원수를 구한 뒤, 이 합성 사원수를 이용해 한 번의 연산으로 최종 회전을 적용할 수 있다. 단, 사원수 곱셈은 교환 법칙이 성립하지 않으므로 곱하는 순서에 유의해야 한다.

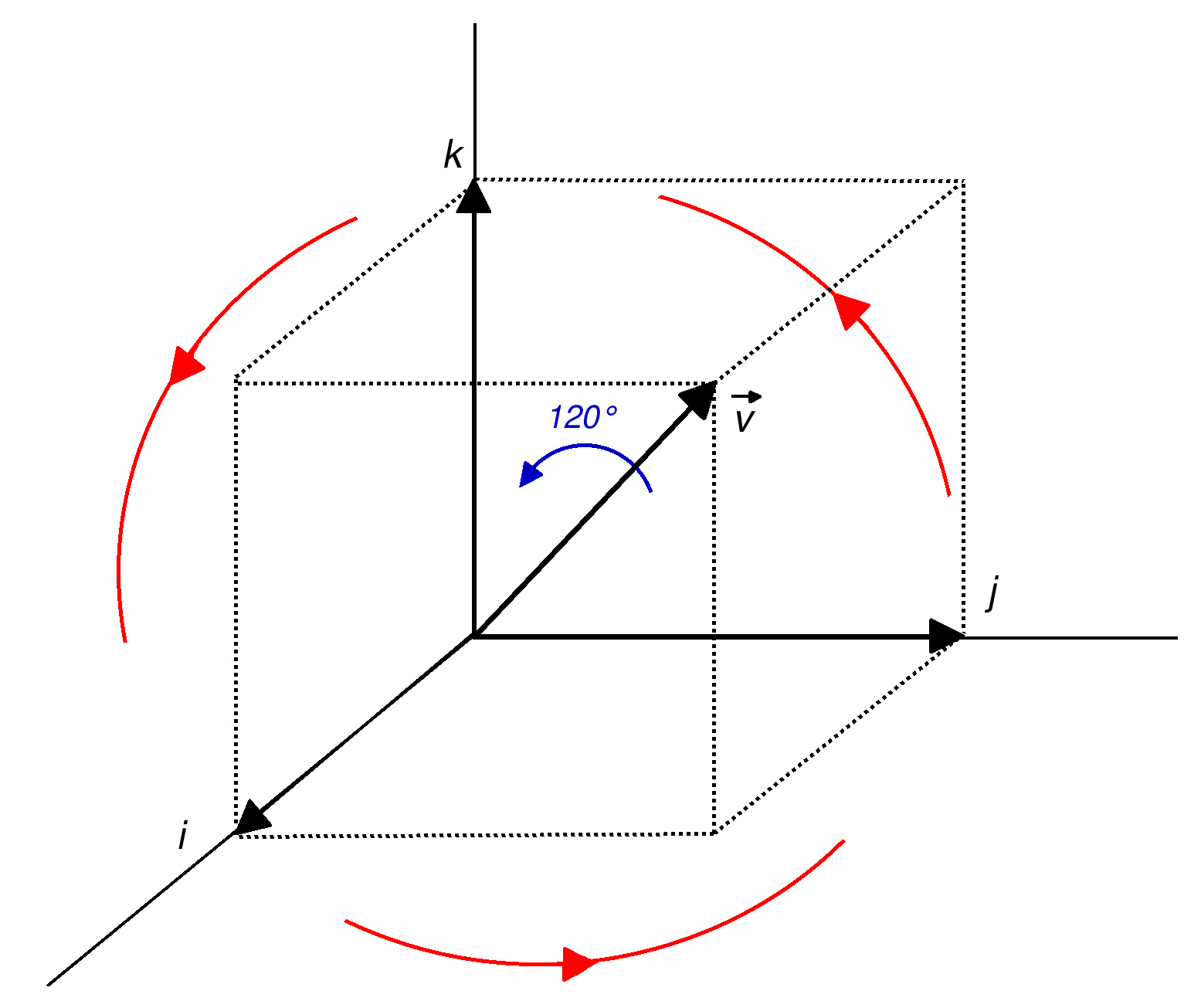
첫 번째 대각선을 중심으로 120° 회전하면 '''i''', '''j''', '''k'''가 순환적으로 순열된다.

'''예시: 대각선 축 중심 회전'''

벡터 '''v''' = '''i''' + '''j''' + '''k'''를 회전축으로 하여 120° (α = 2π/3 라디안) 회전하는 경우를 생각해보자.

회전축 벡터 '''v'''의 크기는 ||'''v'''|| = √(1²+1²+1²) = √3이다. 회전각의 절반은 α/2 = π/3 (60°)이다. 이때 코사인 값은 cos(π/3) = 1/2이고, 사인 값은 sin(π/3) = √3/2이다. 따라서 이 회전을 나타내는 단위 사원수 ''u''는 다음과 같다.

:''u'' = cos(α/2) + sin(α/2) ⋅ (1/||'''v'''||)'''v'''

:''u'' = cos(π/3) + sin(π/3) ⋅ (1/√3)'''v'''

:''u'' = 1/2 + (√3/2) ⋅ (1/√3)'''v'''

:''u'' = 1/2 + (√3/2) ⋅ ('''i'''+'''j'''+'''k''')/√3

:''u'' = (1 + '''i''' + '''j''' + '''k''')/2

회전 함수 ''f''는 다음과 같이 정의된다.

:''f''(a'''i''' + b'''j''' + c'''k''') = ''u'' (a'''i''' + b'''j''' + c'''k''') ''u''^-1

단위 사원수의 역원은 허수 성분의 부호만 바꾼 것과 같으므로,

:''u''^-1 = (1 - '''i''' - '''j''' - '''k''')/2

이고,

:''f''(a'''i''' + b'''j''' + c'''k''') = [(1 + '''i''' + '''j''' + '''k''')/2] (a'''i''' + b'''j''' + c'''k''') [(1 - '''i''' - '''j''' - '''k''')/2]

이를 사원수 연산 규칙에 따라 계산하면 다음과 같이 단순화된다.

:''f''(a'''i''' + b'''j''' + c'''k''') = c'''i''' + a'''j''' + b'''k'''

결과적으로 이 회전은 점 (a, b, c)를 (c, a, b)로 이동시킨다. 이는 원점을 지나는 대각선 (1, 1, 1)을 축으로 120° 회전하는 것에 해당하며, 세 좌표축이 순환적으로 바뀌는 것을 확인할 수 있다. 이는 한 점에 고정된 정육면체를 해당 점을 통과하는 긴 대각선을 중심으로 120° 회전시키는 것과 같다.

사원수 회전 '''p'''' = '''q''' '''p''' '''q'''^-1 (여기서 '''p'''는 순수 사원수, '''q''' = q_r + q_i'''i''' + q_j'''j''' + q_k'''k''')는 행렬 회전 '''p'''' = '''R p'''로 변환될 수 있으며, 여기서 '''R'''은 다음과 같은 회전 행렬이다:^[10]

: '''R''' = --

여기서 s = ||'''q'''||^-2이며, 만약 ''q''가 단위 사원수이면, s = 1^-2 = 1이다.

이 행렬은 '''p'''와 '''q'''를 스칼라 및 벡터 부분으로 표현하고, 방정식 '''p'''' = '''q''' '''p''' '''q'''^-1에서 곱셈 연산 공식을 사용하여 벡터 미적분학과 선형대수학을 통해 유도할 수 있다. '''p'''를 (0, '''p''')로, '''p''''를 (0, '''p''''')로, 그리고 '''q'''를 (q_r, '''v''')로 쓰면 (여기서 '''v''' = (q_i, q_j, q_k)), 방정식은 (0, '''p''''') = (q_r, '''v''') (0, '''p''') s(q_r, -'''v''')가 된다. 스칼라와 벡터 부분으로 표현된 두 사원수의 곱셈 공식:

:(r₁, '''v'''₁) (r₂, '''v'''₂) = (r₁r₂ - '''v'''₁ ⋅ '''v'''₂, r₁'''v'''₂ + r₂'''v'''₁ + '''v'''₁×'''v'''₂),

을 이용하면 이 방정식은 다음과 같이 전개될 수 있다.

:(0, '''p''''') = s('''v''' ⊗ '''v''' + q_r²'''I''' + 2 q_r['''v''']_× + ['''v''']_×²) '''p'''

여기서 ⊗는 외적, '''I'''는 단위 행렬, ['''v''']_×는 벡터 '''u'''와 곱해질 때 벡터곱 '''v''' × '''u'''를 제공하는 변환 행렬이다.

'''p'''' = '''R''' '''p'''이므로, '''R''' = s('''v''' ⊗ '''v''' + q_r²'''I''' + 2 q_r['''v''']_× + ['''v''']_×²)로 식별할 수 있으며, 이를 확장하면 위에 행렬 형태로 작성된 표현식이 생성된다.

두 회전 ''R''_B와 ''R''_A의 합성을 사원수로 계산하는 것의 이점은 합성 회전 ''R''_C = ''R''_B''R''_A의 회전축과 각도를 직접 얻을 수 있다는 점이다.

공간 회전 ''R''에 대응하는 사원수를 해당 회전축 '''S'''와 이 축을 중심으로 하는 회전각 φ로부터 구성한다고 가정하자. 관련된 사원수는 다음과 같다.

: S = cos(φ/2) + '''S'''sin(φ/2).

그러면 회전 ''R''_B와 ''R''_A의 합성은 사원수의 곱으로 정의되는 회전축과 각도를 가진 회전 ''R''_C = ''R''_B''R''_A이다.

: A = cos(α/2) + '''A'''sin(α/2) and B = cos(β/2) + '''B'''sin(β/2),

즉,

: C = cos(γ/2) + '''C'''sin(γ/2) = (cos(β/2) + '''B''' sin(β/2)) (cos(α/2) + '''A'''sin(α/2)).

이 곱을 전개하면 다음과 같다.

: cos(γ/2) + '''C'''sin(γ/2) = (cos(β/2) cos(α/2) - '''B''' ⋅ '''A''' sin(β/2) sin(α/2)) + ('''B''' sin(β/2) cos(α/2) + '''A''' sin(α/2) cos(β/2) + '''B''' × '''A''' sin(β/2) sin(α/2)).

이 방정식의 양변을 스칼라 부분으로 나누면 합성 회전의 축 '''C'''와 각 γ/2의 탄젠트 값을 얻을 수 있다. 스칼라 부분은 구면 코사인 법칙에 해당하는 항등식이다.

: cos(γ/2) = cos(β/2) cos(α/2) - '''B''' ⋅ '''A''' sin(β/2) sin(α/2).

벡터 부분으로부터 다음을 계산할 수 있다.

: '''C''' tan(γ/2) = ('''B''' tan(β/2) + '''A''' tan(α/2) + '''B''' × '''A''' tan(β/2)tan(α/2)) / (1 - '''B''' ⋅ '''A''' tan(β/2)tan(α/2)).

이것은 두 회전의 축과 각도를 기준으로 합성 회전의 축과 각도를 구하는 로드리게스 공식이다. 그는 1840년에 이 공식을 유도했다.

세 개의 회전축 '''A''', '''B''', '''C'''는 구면 삼각형을 형성하고, 이 삼각형의 변으로 형성된 평면 사이의 이면각은 회전각으로 정의된다. 해밀턴은^[12] 사원수 곱이 두 개의 주어진 꼭짓점과 그와 관련된 호의 길이를 사용하여 구면 삼각형의 세 번째 꼭짓점을 계산하는 이러한 방정식의 구성 요소 형태를 제시했으며, 이는 또한 타원 기하학의 점에 대한 대수를 정의한다.

합성 회전의 각 γ와 (정규화되지 않은) 축 벡터 '''D'''는 다음과 같이 계산할 수 있다.

: γ = 2cos^-1(cos(β/2) cos(α/2) - '''B''' ⋅ '''A''' sin(β/2) sin(α/2))

: '''D''' = '''B''' sin(β/2) cos(α/2) + '''A''' sin(α/2) cos(β/2) + '''B''' × '''A''' sin(β/2) sin(α/2)

마지막으로 회전축을 정규화한다: '''C''' = '''D''' / ||'''D'''||. (단, γ가 0 또는 2π의 정수배에 가까울 경우, 즉 회전이 항등 변환에 가까울 때는 '''D'''가 0에 가까워지므로 정규화에 주의해야 한다.)

'''로드리게스 회전 공식과의 관계'''

'''u'''를 단위 벡터(회전축)로 하고 q = cos(α/2) + '''u''' sin(α/2)라고 하자. 목표는 다음 식이 축 '''u'''를 중심으로 α만큼 회전된 벡터 '''v'''를 생성하는 것을 보이는 것이다.

:'''v'''' = q '''v''' q^-1 = ( cos(α/2) + '''u''' sin(α/2) ) '''v''' ( cos(α/2) - '''u''' sin(α/2) )

사원수 곱셈 규칙('''uv''' = '''u''' × '''v''' - '''u''' ⋅ '''v''' 등)을 사용하여 전개하면,

:'''v'''' = '''v''' cos²(α/2) + ('''uv''' - '''vu''') sin(α/2) cos(α/2) - '''uvu''' sin²(α/2)

: = '''v''' cos²(α/2) + 2 ('''u''' × '''v''') sin(α/2) cos(α/2) - (('''u''' × '''v''') - ('''u''' ⋅ '''v'''))'''u''' sin²(α/2)

: = '''v''' cos²(α/2) + 2 ('''u''' × '''v''') sin(α/2) cos(α/2) - (('''u''' × '''v''')'''u''' - ('''u''' ⋅ '''v''')'''u''') sin²(α/2)

: = '''v''' cos²(α/2) + 2 ('''u''' × '''v''') sin(α/2) cos(α/2) - ((('''u''' × '''v''') × '''u''' - ('''u''' × '''v''') ⋅ '''u''') - ('''u''' ⋅ '''v''')'''u''') sin²(α/2)

: = '''v''' cos²(α/2) + 2 ('''u''' × '''v''') sin(α/2) cos(α/2) - (('''v''' - ('''u''' ⋅ '''v''')'''u''') - 0 - ('''u''' ⋅ '''v''')'''u''') sin²(α/2)

: = '''v''' cos²(α/2) + 2 ('''u''' × '''v''') sin(α/2) cos(α/2) - ('''v''' - 2 '''u''' ('''u''' ⋅ '''v''')) sin²(α/2)

: = '''v''' cos²(α/2) + 2 ('''u''' × '''v''') sin(α/2) cos(α/2) + (2 '''u''' ('''u''' ⋅ '''v''') - '''v''') sin²(α/2)

'''v'''_⊥과 '''v'''_∥를 각각 '''v'''의 '''u'''에 수직 및 평행한 성분이라고 하면, '''v''' = '''v'''_⊥ + '''v'''_∥이고 '''u'''('''u''' ⋅ '''v''') = '''v'''_∥이므로,

:'''v'''' = ('''v'''_∥ + '''v'''_⊥) cos²(α/2) + 2 ('''u''' × '''v''') sin(α/2) cos(α/2) + ('''v'''_∥ - '''v'''_⊥) sin²(α/2)

: = '''v'''_∥ (cos²(α/2) + sin²(α/2)) + ('''u''' × '''v''') (2 sin(α/2) cos(α/2)) + '''v'''_⊥ (cos²(α/2) - sin²(α/2))

삼각함수 항등식(피타고라스 정리와 배각 공식)을 사용하면 다음을 얻는다.

:'''v'''' = '''v'''_∥ + ('''u''' × '''v''') sin(α) + '''v'''_⊥ cos(α)

이것은 '''u''' 축을 중심으로 α만큼 회전하는 로드리게스 회전 공식이다.

사원수의 곱셈은 비가환적(non-commutative)이다. 이는 단위 사원수의 곱셈이 3차원 회전의 합성에 해당하므로, 3차원 회전이 일반적으로 가환적이지 않다는 사실로부터 직관적으로 이해할 수 있다.

오른쪽 그림은 주사위를 사용하여 이를 보여준다. 오른손을 사용하여 90도의 회전을 두 번 수행한다. 두 주사위 모두 처음에 왼쪽 상단 모서리에 표시된 대로 구성되어 있다(윗면에 점 1개).

경로 A: ''-y'' 축을 중심으로 회전(오른손 법칙 사용)한 다음 ''+z'' 축을 중심으로 회전하면 왼쪽 하단 모서리에 표시된 구성(윗면에 점 5개)을 생성한다.
경로 B: 연산 순서를 반대로 하여 ''+z'' 축 중심으로 먼저 회전하고 ''-y'' 축 중심으로 회전하면 위에 점 3개가 나오도록 한다.

두 경로의 최종 결과가 다르므로 회전 순서가 중요하며, 이는 사원수 곱셈의 비가환성과 일치한다.

3. 3. 축-각 표현 복원

주어진 사원수

\mathbf{q} = q_r + q_i \mathbf{i} + q_j \mathbf{j} + q_k \mathbf{k}

로부터 회전축 벡터

\mathbf{a}

와 회전각

\theta

는 다음 공식을 통해 복원할 수 있다.

회전축 벡터

\mathbf{a} = (a_x, a_y, a_z)

는 사원수의 벡터 성분

(q_i, q_j, q_k)

를 그 크기로 나누어 구한다.

:

(a_x, a_y, a_z) = \frac{(q_i, q_j, q_k)}{\sqrt{q_i^2 + q_j^2 + q_k^2}}

회전각

\theta

는 두 인수 아크탄젠트 함수를 이용하여 다음과 같이 계산할 수 있다.

:

\theta = 2 \operatorname{atan2} \left(\sqrt{q_i^2 + q_j^2 + q_k^2},\, q_r \right)

회전각은

\theta = 2 \operatorname{acos} (q_r)

공식을 사용할 수도 있지만, 이 공식은

q_r = \pm1

(즉, 회전각이 0 또는

2\pi

에 가까운 경우) 근처에서 부동소수점 연산 시 수치적으로 불안정하여 부정확한 결과를 낼 수 있다. 반면, `atan2` 함수를 사용하는 공식은 이러한 경우에도 비교적 안정적인 결과를 제공한다.

사원수가 스칼라 값(즉,

q_i = q_j = q_k = 0

)에 가까워지는 경우 주의가 필요하다. 이는 항등 회전에 해당하며, 항등 회전의 축은 퇴화되어 명확하게 정의되지 않기 때문이다.

4. 회전 공간의 시각화

3차원 공간에서의 회전은 추상적인 개념이지만, 기하학적인 방법을 통해 시각적으로 이해하는 것이 가능하다. 모든 3차원 회전은 특정 축을 중심으로 특정 각도만큼 돌리는 것으로 표현될 수 있다. 이러한 회전들의 전체 집합이 이루는 공간의 구조를 파악하려는 시도는 회전을 더 깊이 이해하는 데 도움을 준다.

회전 공간의 구조를 시각화하는 한 가지 방법은 회전을 특정 공간 위의 점으로 대응시키는 것이다. 예를 들어, 간단한 경우로 회전축이 특정 평면(예: ''xy'' 평면)에 제한될 때, 회전은 3차원 구면 위의 점으로 나타낼 수 있다. 더 나아가 일반적인 3차원 회전 전체의 공간은 4차원 공간의 초구면(3-sphere)과 위상적으로 동일하다는 것이 알려져 있다. 이러한 기하학적 구조는 사원수, 특히 단위 사원수를 통해 대수적으로 명확하게 표현될 수 있으며, 이는 회전을 다루는 데 매우 유용한 도구를 제공한다. 회전 공간의 구체적인 구조와 사원수와의 관계는 하위 섹션에서 더 자세히 다룬다.

4. 1. 회전 공간의 구조

단위 사원수는 3차원 유클리드 군의 회전을 매우 직접적인 방식으로 나타낸다. 회전과 사원수 간의 관계는 회전 공간 자체를 시각화함으로써 더 깊이 이해할 수 있다.

회전 공간에서 각도와 축이 모두 다른 두 개의 개별 회전. 여기서 각 축 벡터의 길이는 해당 축을 중심으로 한 회전의 크기에 상대적이다.

회전 공간을 시각화하기 위해 먼저 간단한 경우를 생각해보자. 3차원의 모든 회전은 특정 축을 중심으로 특정 각도만큼 회전하는 것으로 설명될 수 있다. 편의상, 회전축을 나타내는 벡터를 사용하여 각도에 대한 좌표계를 설정할 수 있다. 회전축이 ''xy'' 평면에 놓이는 특별한 경우를 생각해보면, 이러한 회전의 축은 원 위의 한 점으로 지정할 수 있으며, 원의 반지름을 통해 회전각을 나타낼 수 있다.

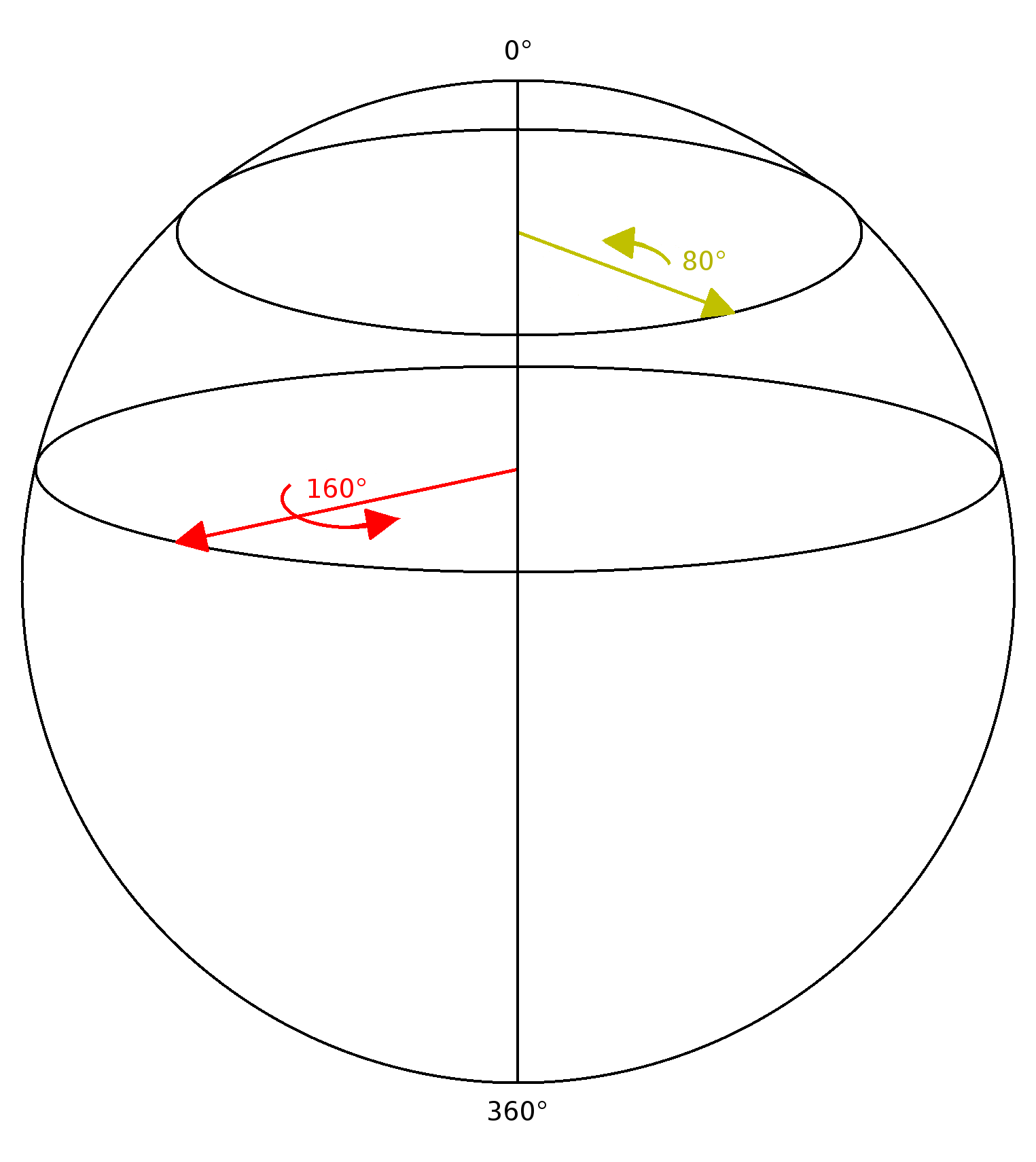
비슷하게, 축이 ''xy'' 평면에 있는 회전은 3차원 공간에서 고정된 반지름을 가진 구면 위의 점으로 나타낼 수 있다. 구의 북극에서 시작하여, 이 점을 항등 회전(0도 회전)으로 정의한다. 항등 회전의 경우 회전축은 정의되지 않고 회전각(0)은 의미가 없다. 매우 작은 각도의 회전은 북극에 매우 가까우면서 ''xy'' 평면에 평행한 단면으로 만들어지는 작은 원 위의 점으로 나타낼 수 있다. 이 원의 작은 크기는 회전각이 작다는 것을 의미한다. 회전각이 커짐에 따라, 단면은 음의 ''z'' 방향으로 이동하고 원은 점점 커져 적도에 도달하면 회전각이 180도가 된다. 남쪽으로 계속 이동하면 원의 반지름은 다시 작아지며(회전각의 절댓값에 해당, 부호는 반대 방향을 의미할 수 있음), 최종적으로 남극에 도달하면 다시 항등 회전으로 수렴하며 점으로 표현된다.

이 시각화를 통해 회전 공간의 몇 가지 중요한 특징을 파악할 수 있다:

연속성: 회전 공간은 연속적이다. 즉, 모든 회전은 자신과 거의 동일한 다른 회전들로 둘러싸여 있으며, 이 주변 영역은 점점 작아질수록 평평한 공간처럼 보인다.
대칭성 (이중 덮개): 각 회전은 실제로는 구의 중심을 기준으로 서로 반대편에 있는 두 점(대척점)으로 표현된다. 이는 어떤 회전이 특정 축 $\mathbf{v}$ 를 중심으로 각도 $\theta$ 만큼 회전하는 것과, 반대 방향 축 $-\mathbf{v}$ 를 중심으로 각도 $-\theta$ (또는 $360^\circ - \theta$ )만큼 회전하는 것이 동일한 결과를 낳는다는 사실을 반영한다. 이를 이중 덮개라고 한다.
위도와 회전각: 구면 위 점의 "위도"는 해당 회전각의 절반에 해당한다. 점이 북극(0도 회전)에서 남극(360도 회전, 즉 다시 0도 회전과 동일)으로 이동함에 따라 위도는 0도에서 180도까지 변하지만, 실제 회전각은 0도에서 360도까지 변하기 때문이다. 점의 "경도"는 특정 회전축을 나타낸다.
한계점: 이 구면 모델은 축이 ''xy'' 평면에 있는 회전만을 나타낸다. 중요한 점은, 이러한 회전들의 집합은 회전의 합성에 대해 닫혀 있지 않다는 것이다. 즉, ''xy'' 평면의 축을 가진 두 회전을 연속적으로 수행한다고 해서 그 결과가 반드시 ''xy'' 평면의 축을 가진 회전이 되는 것은 아니므로, 항상 구 위의 점으로 표현될 수는 없다. 이는 일반적인 3차원 회전과는 다른 점이다. 일반적인 3차원 회전의 집합은 합성에 대해 닫혀 있다.

이 시각화는 3차원 공간의 일반적인 회전으로 확장될 수 있다. 항등 회전은 여전히 하나의 점으로 표현된다. 어떤 축을 중심으로 작은 각도만큼 회전하는 것은 작은 반지름을 가진 구 위의 점으로 나타낼 수 있다. 회전각이 커짐에 따라 이 구는 점점 커지다가, 회전각이 180도에 도달하면 최대 크기가 된다. 그 후 회전각이 360도(또는 음의 방향에서 0도)에 가까워짐에 따라 구는 다시 수축하여 점으로 돌아온다. 이렇게 확장하고 수축하는 구들의 집합은 4차원 공간의 초구 (3-sphere)를 형성한다.

앞서 살펴본 더 간단한 구면 모델과 마찬가지로, 초구 위의 점으로 표현되는 각 회전은 그 대척점(초구의 중심을 기준으로 정반대 위치에 있는 점)과 짝을 이룬다. 초구의 "위도"는 해당 회전각의 절반에 해당하며, 초구 위의 어떤 점 주변의 작은 영역은 그 영역이 작아질수록 점점 "평평해져" 3차원 유클리드 공간처럼 보이게 된다.

이러한 초구의 동작은 단위 사원수의 집합과 정확히 일치한다. 일반적인 사원수는 4차원 공간의 점으로 생각할 수 있는데, 크기가 1인 단위 사원수만을 고려하면 이는 4차원 공간 내의 단위 반지름을 가진 초구 표면, 즉 3-구와 동일한 3차원 공간을 형성한다.

단위 사원수의 크기는 1이며, 이는 단위 반지름의 초구에 해당한다.
단위 사원수의 벡터 부분은 회전축 방향을 나타내는 3차원 벡터이며, 그 크기는 회전각 절반의 사인 값( $\sin(\theta/2)$ )과 같다. (스칼라 부분은 $\cos(\theta/2)$ ).
각 회전은 부호가 서로 반대인 두 개의 단위 사원수( $q$ 와 $-q$ )로 표현된다. 이는 초구에서의 대척점 표현과 일치한다.
두 단위 사원수의 곱 또한 단위 사원수가 되므로, 회전의 합성에 해당하며 집합은 닫혀 있다.
단위 사원수 공간 역시 국소적으로 "평평하다". 즉, 어떤 단위 사원수 주변의 작은 영역은 3차원 유클리드 공간으로 근사할 수 있다.

구면의 표면은 위도와 경도라는 두 개의 좌표로 나타낼 수 있지만, 북극과 남극에서는 위도/경도 좌표계가 제대로 작동하지 않는 퇴화 현상이 발생한다(털 뭉치 정리). 이는 극점이 본질적으로 다른 점들과 다르기 때문이 아니라 좌표계 자체의 문제이다. 극점(위도 +90° 및 -90°)에서는 경도가 무의미해진다. 이러한 퇴화를 피할 수 있는 두 개의 매개변수만 사용하는 좌표계는 존재하지 않는다는 것이 증명되어 있다.

이 문제를 피하기 위해 구를 3차원 공간에 포함된 것으로 보고, 세 개의 데카르트 좌표

(w, x, y)

로 매개변수화할 수 있다. 이때

w^2 + x^2 + y^2 = 1

이라는 제약 조건을 만족해야 한다. 예를 들어 북극을

(1, 0, 0)

, 남극을

(-1, 0, 0)

, 적도를

w = 0, x^2 + y^2 = 1

로 설정할 수 있다. 구면 위의 점은 세 좌표로 표현되지만, 제약 조건 때문에 여전히 두 개의 자유도만 가진다. 구면 위의 한 점

(w, x, y)

는 수평축(벡터

(x, y, 0)

방향)을 중심으로 각도

\alpha = 2 \arccos w = 2 \arcsin \sqrt{x^2+y^2}

만큼 회전하는 것을 나타낼 수 있다.

마찬가지로, 3차원 회전을 나타내는 초구면 공간(3-구)은 세 개의 각도(오일러 각)로 매개변수화될 수 있지만, 이러한 방식은 특정 지점에서 퇴화되어 짐벌락 문제를 일으킨다. 이를 피하기 위해 네 개의 유클리드 좌표

w, x, y, z

를 사용하며,

w^2 + x^2 + y^2 + z^2 = 1

이라는 제약 조건을 만족한다. 초구면 위의 한 점

(w, x, y, z)

는 벡터

(x, y, z)

방향의 축을 중심으로 각도

\alpha = 2 \arccos w = 2 \arcsin \sqrt{x^2+y^2+z^2}

만큼 회전하는 것을 나타낸다. 이는 단위 사원수의 표현과 직접적으로 연결된다.

4. 2. 초구면 공간과의 관계

단위 사원수는 유클리드 군의 회전을 3차원에서 매우 직접적인 방식으로 나타낸다. 회전과 사원수 간의 대응 관계는 먼저 회전 공간 자체를 시각화하여 이해할 수 있다.

회전 공간을 시각화하기 위해, 3차원의 모든 회전은 특정 각도와 특정 축으로 설명될 수 있다는 점을 이용한다. 회전축을 나타내는 벡터를 사용하여 각도에 대한 좌표계를 설정할 수 있다. 예를 들어, 회전축이 ''xy'' 평면에 놓인 경우를 생각해보자. 이 회전의 축은 원 위의 점으로 나타낼 수 있고, 원의 반지름을 통해 회전각을 표현할 수 있다.

이 아이디어를 확장하여, ''xy'' 평면의 축을 가진 회전은 3차원 공간에서 고정된 반지름을 가진 구면 위의 점으로 설명할 수 있다. 구의 북극은 항등 회전(0도 회전)을 나타낸다고 가정한다. 항등 회전은 축이 정의되지 않고 회전각도 0이므로 의미가 없다. 아주 작은 각도의 회전은 북극 근처의 작은 원 위의 점으로 표현될 수 있으며, 이 원의 작은 크기는 작은 회전각에 해당한다. 회전각이 커짐에 따라 해당 점은 구면을 따라 남쪽으로 이동하고, 점이 지나는 원의 크기는 커져서 적도에 도달하면 180도 회전에 해당한다. 계속 남쪽으로 이동하면 원의 반지름은 다시 작아지며, 남극에 도달하면 다시 항등 회전(360도 회전)을 나타낸다.

이 시각화를 통해 몇 가지 회전의 특징을 알 수 있다.

회전 공간은 연속적이다. 즉, 모든 회전은 자신과 아주 약간 다른 회전들로 둘러싸여 있다.
각 회전은 구면 위에서 서로 정반대에 위치한 두 점으로 표현된다. 이는 어떤 축 $\mathbf{v}$ 에 대한 회전 $\theta$ 가 반대 축 $-\mathbf{v}$ 에 대한 회전 $-\theta$ (또는 $360^\circ - \theta$ )와 동일하다는 사실을 반영한다. 이를 이중 덮개라고 한다.
구면 위 점의 "위도"는 실제 회전각의 절반에 해당한다. 점이 북극(0도 회전)에서 남극(360도 회전)까지 이동할 때 위도는 0도에서 180도까지 변한다. 점의 "경도"는 회전축의 방향을 나타낸다.

그러나 이 방식(xy 평면 축 회전만 고려)으로는 회전의 합성을 완벽히 설명할 수 없다. xy 평면에 축을 둔 두 회전을 합성한다고 해서 결과 회전의 축이 반드시 xy 평면에 놓이지는 않기 때문이다. 즉, 이 구면 모델만으로는 모든 3차원 회전의 합성에 대해 닫혀 있지 않다.

이 시각화는 일반적인 3차원 회전으로 확장될 수 있다. 항등 회전은 한 점으로 표현된다. 작은 각도의 회전은 작은 구 위의 점으로 표현된다. 회전각이 커짐에 따라 이 구의 반지름은 커져서 180도 회전에서 최대가 되고, 다시 작아져 360도(0도) 회전에서 다시 한 점으로 축소된다. 이렇게 커졌다 작아지는 구들의 집합은 4차원 공간의 초구 (3-구)의 표면을 형성한다.

3차원 회전 공간을 나타내는 이 초구는 단위 사원수 집합과 밀접한 관련이 있다. 일반적인 사원수는 4차원 공간의 점으로 볼 수 있는데, 크기가 1인 단위 사원수만을 고려하면 이는 반지름이 1인 4차원 초구면 위의 점들과 같다.

단위 사원수 $q = w + x\mathbf{i} + y\mathbf{j} + z\mathbf{k}$ 에서 스칼라 부분 ''w''는 회전각 $\alpha$ 와 $w = \cos(\alpha/2)$ 관계를 가진다.
벡터 부분 $(x, y, z)$ 는 회전축의 방향을 나타내며, 그 크기 $\sqrt{x^2+y^2+z^2}$ 는 $\sin(\alpha/2)$ 와 같다.
각 회전은 두 개의 단위 사원수 $q$ 와 $-q$ 로 표현된다 (초구 위의 반대쪽 점). 이는 앞서 설명한 이중 덮개 특성과 일치한다.
두 단위 사원수의 곱은 항상 다른 단위 사원수가 되므로, 회전의 합성에 대해 닫혀 있다.

구면(2-구)의 표면은 위도와 경도 두 좌표로 나타낼 수 있지만, 북극과 남극에서는 경도가 무의미해지는 문제가 발생한다(퇴화). 이는 털 뭉치 정리와 관련 있으며, 구면 위의 모든 점에서 잘 정의되는 두 개의 좌표계는 존재하지 않는다. 이 문제를 피하기 위해 구면을 3차원 공간에 포함시켜 세 개의 데카르트 좌표 ''(w, x, y)'' (단, ''w''² + ''x''² + ''y''² = 1)로 나타낼 수 있다. 북극을 ''(w, x, y) = (1, 0, 0)'', 남극을 ''(w, x, y) = (-1, 0, 0)'', 적도를 ''w'' = 0, ''x''² + ''y''² = 1에 위치시킨다. 구면의 점은 제약 조건 ''w''² + ''x''² + ''y''² = 1을 만족하므로 세 개의 좌표가 있지만 여전히 두 개의 자유도가 있다. 구면의 한 점 ''(w, x, y)''는 벡터 ''(x, y, 0)''에 의해 향하는 수평축을 중심으로 각도

\alpha= 2 \cos^{-1} w = 2 \sin^{-1} \sqrt{x^2+y^2}

만큼의 일반 공간에서의 회전을 나타낸다.

마찬가지로 3D 회전의 초구면 공간은 세 개의 각도 (오일러 각)로 매개변수화될 수 있지만, 이러한 매개변수화는 초구면의 일부 지점에서 퇴화되어 짐벌락 문제를 야기한다. ''w''² + ''x''² + ''y''² + ''z''² = 1인 네 개의 유클리드 좌표 ''w'', ''x'', ''y'', ''z''를 사용하여 이를 피할 수 있다. 점 ''(w, x, y, z)''는 벡터 ''(x, y, z)''에 의해 향하는 축을 중심으로 각도

\alpha = 2 \cos^{-1} w = 2 \sin^{-1} \sqrt{x^2+y^2+z^2}

만큼의 회전을 나타낸다. 이 4차원 표현 방식은 짐벌락 문제를 피할 수 있게 해준다.

5. 다른 회전 표현과의 비교

3차원 공간에서의 회전을 나타내는 방법에는 여러 가지가 있으며, 대표적으로 회전 행렬, 오일러 각, 그리고 사원수가 사용된다. 각 방식은 고유한 특징과 장단점을 가진다.

회전 행렬은 선형대수학의 표준적인 도구로, 3x3 행렬을 사용하여 회전을 표현하고 벡터에 직접 행렬 곱셈을 적용하여 변환을 수행한다. 반면, 오일러 각은 세 개의 각도를 사용하여 회전을 표현하여 직관적일 수 있지만, 특정 각도에서 짐벌 락이라는 문제가 발생하여 회전의 자유도를 잃는 심각한 단점이 있다.^[1]^[3]

사원수는 4개의 실수( $w, x, y, z$ , 단 $w^2 + x^2 + y^2 + z^2 = 1$ )를 사용하여 회전을 표현한다. 이는 9개의 숫자를 사용하는 회전 행렬보다 간결하며,^[2] 오일러 각과 달리 짐벌 락 문제가 발생하지 않는다는 중요한 장점이 있다.^[2]^[3] 또한 사원수는 회전 합성과 보간 등에서 유용하게 사용된다.^[2]

사원수를 이용한 회전 표현의 또 다른 중요한 특징은 비가환성(non-commutativity)이다. 즉, 두 사원수 $\mathbf{q}_1, \mathbf{q}_2$ 에 대해 일반적으로 $\mathbf{q}_1 \mathbf{q}_2 \neq \mathbf{q}_2 \mathbf{q}_1$ 이다. 이는 3차원 공간에서의 회전 순서가 결과에 영향을 미치는 현실과 일치한다. 예를 들어, 물체를 x축 기준으로 90도 회전시킨 후 y축 기준으로 90도 회전시키는 것과, y축 기준으로 먼저 회전시킨 후 x축 기준으로 회전시키는 것은 다른 결과를 낳는다. 오른쪽 그림의 주사위 예시는 이러한 회전의 비가환성을 잘 보여준다.

각 표현 방식 간의 더 자세한 비교, 상호 변환 방법, 연산 성능 분석 등은 하위 섹션에서 구체적으로 다룬다.

5. 1. 회전 행렬과의 비교

사원수를 이용한 회전 표현

\mathbf{p'} = \mathbf{q} \mathbf{p} \mathbf{q}^{-1}

는 회전 행렬을 이용한 표현

\mathbf{p'} = \mathbf{R p}

와 동일한 결과를 나타낸다. 여기서

\mathbf{q}

는 회전을 나타내는 사원수이고,

\mathbf{R}

은 해당 회전을 나타내는 회전 행렬이다.

=== 사원수에서 회전 행렬로 변환 ===

단위 사원수

\mathbf{q} = q_r + q_i \mathbf{i} + q_j \mathbf{j} + q_k \mathbf{k}

(또는

\mathbf{q} = a + b\mathbf{i} + c\mathbf{j} + d\mathbf{k}

로 표기)가 주어졌을 때, 이에 해당하는 3x3 회전 행렬

\mathbf{R}

은 다음과 같이 계산한다.^[10]

\mathbf{R} = \begin{bmatrix}1 - 2(q_j^2 + q_k^2) &2 (q_i q_j - q_k q_r) &2 (q_i q_k + q_j q_r) \\2 (q_i q_j + q_k q_r) &1 - 2(q_i^2 + q_k^2) &2 (q_j q_k - q_i q_r) \\2 (q_i q_k - q_j q_r) &2 (q_j q_k + q_i q_r) &1 - 2(q_i^2 + q_j^2)\end{bmatrix}

또는

\mathbf{q} = a + b\mathbf{i} + c\mathbf{j} + d\mathbf{k}

(단,

a^2+b^2+c^2+d^2=1

)를 사용하면 다음과 같다.

R = \begin{pmatrix}a^2 + b^2 - c^2 - d^2 & 2bc - 2ad             & 2bd + 2ac           \\2bc + 2ad             & a^2 - b^2 + c^2 - d^2 & 2cd - 2ab           \\2bd - 2ac             & 2cd+2ab               & a^2 -b^2 -c^2 + d^2 \\\end{pmatrix}.

이 회전 행렬

\mathbf{R}

은 벡터

\mathbf{p}

에 대해

\mathbf{p'} = \mathbf{R} \mathbf{p}

와 같이 행렬 곱셈을 통해 회전된 벡터

\mathbf{p'}

를 계산하는 데 사용된다.

사원수를 단위 정규화할 필요 없이 회전 행렬을 계산하는 더 효율적인 방법도 존재한다.^[19]

=== 회전 행렬에서 사원수로 변환 ===

반대로 회전 행렬

\mathbf{R}

로부터 해당하는 사원수

\mathbf{q}

를 계산할 수도 있다. 하지만 이 변환 과정에서는 주의가 필요한데, 일부 간단한 변환 방법들은 회전 행렬의 대각합(trace, 대각선 원소의 합)이 0에 가까울 때 불안정한 결과를 낼 수 있다. 회전 행렬#사원수 항목에서 안정적인 변환 방법을 찾아볼 수 있다.

만약 주어진 행렬

\mathbf{Q}

가 반올림 오차 등으로 인해 완벽한 직교 행렬이 아닐 경우, 이 행렬에 가장 가까운 회전을 나타내는 사원수를 찾는 방법도 있다. 이는 다음과 같은 대칭 4x4 행렬

\mathbf{K}

를 구성하고,

K = \frac{1}{3}\begin{bmatrix}Q_{xx}-Q_{yy}-Q_{zz} & Q_{yx}+Q_{xy}        & Q_{zx}+Q_{xz}        & Q_{zy}-Q_{yz}        \\Q_{yx}+Q_{xy}        & Q_{yy}-Q_{xx}-Q_{zz} & Q_{zy}+Q_{yz}        & Q_{xz}-Q_{zx}        \\Q_{zx}+Q_{xz}        & Q_{zy}+Q_{yz}        & Q_{zz}-Q_{xx}-Q_{yy} & Q_{yx}-Q_{xy}        \\Q_{zy}-Q_{yz}        & Q_{xz}-Q_{zx}        & Q_{yx}-Q_{xy}        & Q_{xx}+Q_{yy}+Q_{zz}\end{bmatrix}

이 행렬

\mathbf{K}

의 가장 큰 고유값에 해당하는 고유 벡터

(x, y, z, w)

를 찾는 방식으로 수행한다. 이렇게 얻어진 사원수

\mathbf{q} = w + x\mathbf{i} + y\mathbf{j} + z\mathbf{k}

는 주어진 행렬

\mathbf{Q}

가 나타내는 변환과 가장 유사한 회전을 나타낸다.

=== 장단점 비교 ===

사원수와 회전 행렬은 각각 3차원 회전을 표현하는 데 다음과 같은 장단점을 가진다.

특징	사원수	회전 행렬
표현 간결성	4개의 실수로 표현되어 더 간결하다.	9개의 실수(3x3 행렬)로 표현되어 더 복잡하다.
축-각도 변환	주어진 축과 각도로 사원수를 구성하거나, 사원수에서 축과 각도를 추출하기 쉽다.	축과 각도로부터 행렬을 구성하거나, 행렬에서 축과 각도를 추출하는 것이 상대적으로 복잡하다.
회전 보간	Slerp(구면 선형 보간) 등을 사용하여 두 회전 사이를 부드럽게 보간하기 용이하다. 이는 비디오 게임 등에서 자연스러운 움직임을 표현하는 데 유리하다.	회전 행렬 사이의 직접적인 보간은 구현이 더 복잡하고 직관적이지 않다.
연산 효율성 (합성)	사원수 곱셈(16번 곱셈, 12번 덧셈/뺄셈)으로 회전 합성이 가능하다.	행렬 곱셈(27번 곱셈, 18번 덧셈/뺄셈)으로 회전 합성이 가능하다. 사원수 곱셈이 약간 더 효율적일 수 있다.
수치 안정성 (반올림 오차)	연산 과정에서 반올림 오차가 누적되어 단위 사원수가 아니게 되더라도, 간단한 정규화 과정을 통해 유효한 회전 표현으로 복구하기 쉽다.	반올림 오차가 누적되면 행렬이 더 이상 직교 행렬의 성질(회전 변환의 성질)을 만족하지 않게 될 수 있으며, 이를 올바른 회전 행렬로 복구하는 과정이 더 복잡하다.
짐벌 락	짐벌 락 현상이 발생하지 않는다.	오일러 각을 사용할 경우 특정 각도에서 짐벌 락이 발생할 수 있으며, 회전 행렬 자체는 짐벌 락과 직접 관련 없지만 오일러 각과의 변환 과정에서 문제가 발생할 수 있다.

요약하자면, 사원수는 표현의 간결성, 축-각도 변환의 용이성, 부드러운 보간 능력, 수치적 안정성, 짐벌 락 회피 등의 장점을 가지며 특히 컴퓨터 그래픽스나 로보틱스 분야에서 널리 사용된다. 반면 회전 행렬은 선형 대수의 표준적인 도구로서 벡터에 직접 곱하여 변환을 적용하기 직관적이라는 장점이 있지만, 표현의 복잡성이나 수치적 문제 등에서 사원수에 비해 불리한 측면이 있다.

5. 2. 오일러 각과의 비교

3차원 회전을 표현하는 방법 중 하나인 오일러 각은 세 개의 각도를 사용한다. 이는 직관적으로 이해하기 쉬울 수 있지만, 특정 상황에서 문제가 발생한다. 오일러 각은 특정 각도에서 짐벌 락이라는 문제가 발생하는데,^[1] 이는 회전의 자유도 하나를 잃게 되는 현상이다. 예를 들어, 비행역학에서 항공기의 피치(pitch) 각도가 ±90°가 되면, 요(yaw)와 롤(roll)이 같은 움직임을 나타내게 된다. 이는 짐벌을 사용하는 관성 항법 시스템 등에서 치명적인 문제를 일으킬 수 있다.^[2]^[3]

사원수는 이러한 오일러 각의 단점을 보완하는 여러 장점을 가진다.

짐벌 락 회피: 사원수는 4개의 실수( $w, x, y, z$ , 단 $w^2 + x^2 + y^2 + z^2 = 1$ )를 사용하여 3차원 회전을 표현한다. 이 방식은 특정 각도에서 좌표계가 퇴화하는 문제가 없어 짐벌 락 현상을 근본적으로 피할 수 있다.^[2]^[3] 점 $(w, x, y, z)$ 는 벡터 $(x, y, z)$ 방향의 축을 중심으로 각도 $\alpha = 2 \cos^{-1} w = 2 \sin^{-1} \sqrt{x^2+y^2+z^2}$ 만큼 회전하는 것을 나타낸다.^[4]
표현의 간결성: 회전을 표현하는 데 사원수는 4개의 숫자를 사용하지만, 직교 행렬은 9개의 숫자를 사용한다. 따라서 사원수가 더 간결한 표현 방식이다.^[2]
변환의 용이성: 주어진 회전 축과 각도로 해당하는 사원수를 쉽게 계산할 수 있으며, 반대로 사원수로부터 회전 축과 각도를 알아내는 것도 비교적 간단하다. 이는 행렬이나 오일러 각 방식보다 편리한 점이다.^[2]
부드러운 보간: 비디오 게임 등에서 물체의 자세를 부드럽게 변화시켜야 할 때, 사원수는 구면 선형 보간(Spherical Linear Interpolation, Slerp)과 같은 기법을 사용하여 자연스러운 중간 회전을 쉽게 만들어낼 수 있다. 다른 표현 방식으로는 이러한 보간이 더 복잡하다.^[2]
수치적 안정성: 컴퓨터에서 여러 회전을 연속적으로 계산할 때 반올림 오차가 누적될 수 있다. 사원수는 약간의 오차가 발생하더라도 정규화 과정을 통해 유효한 회전으로 쉽게 복원할 수 있다. 반면, 행렬은 오차가 누적되면 직교성을 잃어버리기 쉬우며, 이를 다시 올바른 회전 행렬로 복원하는 것은 더 어렵다.^[2]

5. 3. 성능 비교

3차원 회전을 수행하는 데 사원수를 사용하는 방식과 다른 방법들(축/각도 또는 회전 행렬)을 사용하는 방식의 성능을 비교하면 다음과 같다.

저장 요구 사항
방법	저장 공간 (숫자 개수)
회전 행렬	9 또는 6
사원수	4 또는 3
축-각 표현	4 또는 3

회전은 단위 사원수로 표현되므로 사원수 구성 요소 중 3개만 독립적이다. 계산을 위해서는 일반적으로 네 개의 모든 요소가 필요하므로, 3개 요소만 저장했을 경우 네 번째 구성 요소를 복구하는 데 추가 비용이 발생한다. 마찬가지로 축-각 표현은 단위 방향 벡터에 각도(또는 각도의 함수)를 곱한 3성분 벡터로 저장할 수 있지만, 이를 계산에 사용하려면 추가적인 계산 비용이 발생한다. 회전 행렬의 경우, 3개의 열(또는 행) 벡터가 서로 직교하는 단위 벡터여야 하므로, 처음 두 벡터가 주어지면 세 번째 벡터는 외적을 사용하여 계산할 수 있다 (단, 부정 회전(improper rotation)을 허용하지 않는 경우).

회전 연산 합성 시 성능 비교 (두 회전 합성)
방법	곱셈 수	덧셈/뺄셈 수	총 연산 수
회전 행렬 (3x3 행렬 곱셈)	27	18	45
사원수 (사원수 곱셈)	16	12	28

단일 벡터 회전 연산 성능 비교^[21]^[22]
방법		곱셈 수	덧셈/뺄셈 수	sin/cos 호출 수	총 연산 수
회전 행렬 (벡터-행렬 곱)		9	6	0	15
사원수	중간 행렬 변환 없이	15	15	0	30
사원수	중간 행렬 변환 사용	21	18	0	39
축-각 표현	중간 행렬 변환 없이 (로드리게스 회전 공식 직접 사용)	18	13	2	31 + 2 함수 호출
축-각 표현	중간 행렬 변환 사용	21	16	2	37 + 2 함수 호출

벡터 $\vec{v}$ 를 회전시키는 기본적인 방법과 연산 비용은 다음과 같다.

# 회전 행렬: 3x3 회전 행렬 $R$ 과 3x1 벡터 $\vec{v}$ 의 행렬 곱셈 $R\vec{v}$ 를 계산한다. 곱셈 9회, 덧셈 6회가 필요하며, 단일 벡터를 회전시키는 가장 효율적인 방법이다.

# 사원수: 단위 사원수 $q = (w, \vec{r})$ 를 사용하여 $\vec{v}' = \vec{v} + 2\vec{r} \times (\vec{r} \times \vec{v} + w \vec{v})$ 공식을 적용한다. 곱셈 15회, 덧셈 15회가 필요하다 (또는 상수 2를 곱셈으로 간주하면 곱셈 18회, 덧셈 12회). 이는 사원수 곱셈 $\vec{v}' = q \vec{v} q^{-1}$ (벡터 $\vec{v}$ 를 순수 벡터 사원수로 간주)과 동일한 결과를 내지만 연산 효율이 더 좋다.

# 축-각 표현: 축-각 정보를 회전 행렬로 변환한 후 벡터와 곱한다. 축-각을 회전 행렬 $R$ 로 변환하는 데 곱셈 12회, 덧셈/뺄셈 10회, sin/cos 함수 호출 2회가 필요하다. 이후 벡터 회전에 곱셈 9회, 덧셈 6회가 추가되어 총 곱셈 21회, 덧셈/뺄셈 16회, 함수 호출 2회가 된다. 또는 로드리게스 회전 공식을 직접 사용할 수도 있다.

여러 개의 벡터( $n$ 개)를 동일한 회전으로 변환해야 하는 경우, 회전 표현(행렬, 사원수, 축-각)을 한 번 계산한 후 각 벡터에 적용하게 된다.

''n''개 벡터 회전 연산 성능 비교
방법		곱셈 횟수	덧셈/뺄셈 횟수	sin/cos 횟수	총 연산
회전 행렬		9n	6n	0	15n
사원수	중간 행렬 변환 없이	15n	15n	0	30n
사원수	중간 행렬 변환 사용	9n + 12	6n + 12	0	15n + 24
축-각 표현	중간 행렬 변환 없이 (로드리게스 공식)	18n	13n + 1	2	약 31n + 2 함수 호출
축-각 표현	중간 행렬 변환 사용	9n + 12	6n + 10	2	15n + 22 + 2 함수 호출

결론적으로, 단일 벡터를 회전시키는 데는 회전 행렬이 가장 빠르다. 여러 회전을 합성하는 경우에는 사원수가 더 효율적이다. 여러 벡터를 동일한 회전으로 변환할 때는 사원수를 회전 행렬로 미리 변환해두고 사용하는 것이 사원수 공식을 직접 반복 적용하는 것보다 효율적일 수 있다. 축-각 표현은 직접 사용하거나 행렬로 변환 시 삼각함수 계산 비용이 추가된다. 저장 공간 측면에서는 사원수나 축-각 표현이 회전 행렬보다 간결하다.

6. 사원수의 활용 사례

사원수는 3차원 공간에서의 회전을 효율적으로 표현하고 계산할 수 있어 컴퓨터 그래픽스, 로봇 공학, 항공우주공학 등 다양한 첨단 기술 분야에서 널리 활용되고 있다. 특히 복잡한 움직임이나 자세 제어가 필요한 시스템에서 중요한 역할을 한다.^[16]

사원수를 실제 응용 프로그램에 구현할 때는 주로 두 가지 곱셈 관례, 즉 해밀턴 관례와 슈스터 관례가 사용된다. 어떤 관례를 따르는지에 따라 사원수 곱셈의 순서나 부호가 달라질 수 있다.^[16] 아래 표는 각 관례를 따르는 대표적인 소프트웨어 및 라이브러리 목록이다.^[16]

사원수 곱셈 관례별 소프트웨어 및 라이브러리^[16]
해밀턴 곱셈 관례	슈스터 곱셈 관례

두 관례 중 어느 것을 사용하든 최종 결과물의 기능이나 정확성에는 차이가 없다. 하지만 일부 전문가들은 슈스터 관례가 역사적으로 더 오래된 해밀턴 관례에서 벗어나며, 수학이나 이론 물리학 분야의 표준과 다를 수 있다는 점에서 해밀턴 관례를 사용하는 것이 더 바람직하다고 주장하기도 한다.^[16]

7. 4차원 공간에서의 회전

단위 사원수 쌍 $\mathbf{z}_{\rm{L}} = a_{\rm{L}} + b_{\rm{L}}i + c_{\rm{L}}j + d_{\rm{L}}k$ 와 $\mathbf{z}_{\rm{R}} = a_{\rm{R}} + b_{\rm{R}}i + c_{\rm{R}}j + d_{\rm{R}}k$ 는 4차원 공간의 모든 회전을 나타낼 수 있다. 4차원 벡터 $\vec{v}$ 가 주어졌을 때, 이를 사원수 $\vec{v} = w + xi + yj + zk$ 로 표현하면 다음과 같이 회전시킬 수 있다.

: $f\left(\vec{v}\right) = \mathbf{z}_{\rm{L}} \vec{v} \mathbf{z}_{\rm{R}} = M_{\rm{L}}M_{\rm{R}} \vec{v} =\begin{pmatrix}a_{\rm{L}}&-b_{\rm{L}}&-c_{\rm{L}}&-d_{\rm{L}}\\b_{\rm{L}}& a_{\rm{L}}&-d_{\rm{L}}& c_{\rm{L}}\\c_{\rm{L}}& d_{\rm{L}}& a_{\rm{L}}&-b_{\rm{L}}\\d_{\rm{L}}&-c_{\rm{L}}& b_{\rm{L}}& a_{\rm{L}}\end{pmatrix}\begin{pmatrix}a_{\rm{R}}&-b_{\rm{R}}&-c_{\rm{R}}&-d_{\rm{R}}\\b_{\rm{R}}& a_{\rm{R}}& d_{\rm{R}}&-c_{\rm{R}}\\c_{\rm{R}}&-d_{\rm{R}}& a_{\rm{R}}& b_{\rm{R}}\\d_{\rm{R}}& c_{\rm{R}}&-b_{\rm{R}}& a_{\rm{R}}\end{pmatrix}\begin{pmatrix}w\\x\\y\\z\end{pmatrix},$

여기서 행렬 $M_{\rm{L}}$ 과 $M_{\rm{R}}$ 은 각각 왼쪽 및 오른쪽 사원수 곱셈을 나타내는 행렬이다. 이 두 행렬은 함께 $\mathbb{R}^4$ 에서의 회전에 대한 등경사 분해를 형성한다. 사원수 곱셈은 결합 법칙을 따르므로 다음과 같은 관계가 성립한다.

: $(\mathbf{z}_{\rm{L}} \vec{v}) \mathbf{z}_{\rm{R}} = M_{\rm{R}}M_{\rm{L}}\vec{v} = M_{\rm{L}}M_{\rm{R}}\vec{v} = \mathbf{z}_{\rm{L}} (\vec{v} \mathbf{z}_{\rm{R}})$ .

따라서 두 행렬 $M_{\rm{L}}$ 과 $M_{\rm{R}}$ 은 서로 가환해야 한다. 이는 4차원 회전 군 내에 두 개의 교환 가능한 부분군이 존재함을 의미한다. 임의의 4차원 회전은 6개의 자유도를 가지며, 각 행렬( $M_{\rm{L}}, M_{\rm{R}}$ )은 이 6개의 자유도 중 3개씩을 결정한다.

4차원 회전의 생성원은 아래와 같이 사원수 쌍으로 표현될 수 있으므로, 모든 4차원 회전 역시 사원수 쌍으로 표현될 수 있다.

: $\begin{align}\mathbf{z}_{\rm{L}} \vec{v} \mathbf{z}_{\rm{R}} &=\begin{pmatrix}1 &-dt_{ab}&-dt_{ac}&-dt_{ad}\\dt_{ab}&1 &-dt_{bc}&-dt_{bd}\\dt_{ac}& dt_{bc}&1 &-dt_{cd}\\dt_{ad}& dt_{bd}& dt_{cd}&1\end{pmatrix}\begin{pmatrix} w\\ x\\ y\\ z \end{pmatrix} \\[3pt]\mathbf{z}_{\rm{L}} &=1+{dt_{ab}+dt_{cd}\over 2}i+{dt_{ac}-dt_{bd}\over 2}j+{dt_{ad}+dt_{bc}\over 2}k \\[3pt]\mathbf{z}_{\rm{R}} &=1+{dt_{ab}-dt_{cd}\over 2}i+{dt_{ac}+dt_{bd}\over 2}j+{dt_{ad}-dt_{bc}\over 2}k\end{align}$

8. 같이 보기

사원수 (Ken Shoemake)
로제타 코드의 75개 이상의 컴퓨터 언어에서의 간단한 사원수 유형 및 연산
사원수 데모 (John C. Hart)
사원수, 보간법 및 애니메이션 (Eik B. Dam, Martin Koch, Martin Lillholm, 1998)
3차원 공간에서의 사원수와 회전: 대수와 기하학적 해석 (Vicci Leandra, 2001)
사원수 곱셈의 복잡성, TR75-245 (Thomas Howell, Jean-Claude Lafon, 1975, 코넬 대학교)
단위 사원수와 회전에 대한 몇 가지 참고 사항 (Berthold K.P. Horn, 2001)
회전의 단위 사원수 표현 - 부록 A, 사원수를 이용한 미분 - 부록 B (Byung-Uk Lee, Ph. D. 논문, 1991, 스탠포드 대학교)
연결 리 군의 몇 가지 예 (Rod Vance)
사원수 회전의 시각적 표현

참조

_[1] 논문 Animating Rotation with Quaternion Curves https://www.cs.cmu.e[...]
_[2] 서적 Introduction to Theoretical Kinematics https://books.google[...] MIT Press
_[3] 서적 Computational Rigid Vehicle Dynamics Krieger Publishing Co.
_[4] 서적 Quaternions and rotation Sequences: a Primer with Applications to Orbits, Aerospace, and Virtual Reality Princeton University Press
_[5] 논문 The Bingham Distribution of Quaternions and Its Spherical Radon Transform in Texture Analysis 2004-11
_[6] 서적 Euclidean and non-Euclidean Geometry Cambridge University Press 1987
_[7] 서적 Hypercomplex numbers Springer-Verlag 1989
_[8] 서적 Visualizing Quaternions Morgan Kaufmann Publishers 2006
_[9] 서적 On Quaternions and Octonions A.K. Peters 2003
_[10] 웹사이트 comp.graphics.algorithms FAQ http://www.faqs.org/[...] 2017-07-02
_[11] 간행물 Des lois géométriques qui régissent les déplacements d'un système solide dans l'espace, et la variation des coordonnées provenant de ses déplacements con- sidérés indépendamment des causes qui peuvent les produire 1840
_[12] 간행물 On quaternions or a new system of imaginaries in algebra http://www.maths.tcd[...] Trinity College, Dublin 1844-1850
_[13] 학위논문 Stereo Matching of Skull Landmarks Stanford University 1991
_[14] 논문 Hamilton, Rodrigues, and the Quaternion Scandal
_[15] 서적 Rotations, Quaternions, and Double Groups Dover Publications
_[16] 논문 Why and How to Avoid the Flipped Quaternion Multiplication 2018
_[17] 논문 A Survey of attitude representations 1993
_[18] 웹사이트 MATLAB Aerospace Toolbox quatrotate https://www.mathwork[...]
_[19] 서적 Advanced Animation and Rendering Techniques: Theory and Practice ACM Press
_[20] 논문 New method for extracting the quaternion from a rotation matrix 2000-11
_[21] 문서 Rotation Representations and performance issues
_[22] 웹사이트 Bitbucket https://bitbucket.or[...]
_[23] 논문 Animating Rotation with Quaternion Curves https://www.cs.cmu.e[...]
_[24] 서적 Introduction to Theoretical Kinematics https://books.google[...] MIT Press
_[25] 서적 Computational Rigid Vehicle Dynamics Krieger Publishing Co.
_[26] 서적 Quaternions and rotation Sequences: a Primer with Applications to Orbits, Aerospace, and Virtual Reality Princeton University Press
_[27] 논문 The Bingham Distribution of Quaternions and Its Spherical Radon Transform in Texture Analysis 2004-11

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com