맨위로가기

시계열

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

시계열은 시간의 흐름에 따라 기록된 일련의 데이터 포인트를 분석하는 통계적 기법이다. 시계열 분석은 주파수 영역과 시간 영역 방법으로 나뉘며, 모수적 및 비모수적 접근 방식, 선형 및 비선형 방법, 단변량 및 다변량 분석 등 다양한 분석 방법이 존재한다. 시계열 분석은 스펙트럼 분석, 웨이블릿 분석, 자기 상관 및 상호 상관 분석을 포함하며, 자기상관 함수, 푸리에 변환, 디지털 필터, 인공 신경망 등 다양한 도구를 활용한다. 시계열은 패널 데이터의 한 유형이며, 예측, 분류, 분할, 군집화 등 다양한 분석 목적에 사용된다. 시계열 모델에는 AR, MA, ARMA, ARIMA, VAR, ARCH, HMM 등이 있으며, 정상성 및 에르고딕성을 조건으로 분석이 이루어진다. 시계열은 주가, 환율, 기상 데이터 등 다양한 산업 분야에서 미래 예측을 위해 활용된다.

2. 시계열 분석 방법

시계열 분석 방법은 크게 주파수 영역 방법과 시간 영역 방법으로 나눌 수 있다. 주파수 영역 방법에는 스펙트럼 분석 및 웨이블릿 분석이 포함되고, 시간 영역 방법에는 자기 상관 및 상호 상관 분석이 포함된다. 시간 영역에서는 스케일링된 상관관계를 사용하여 필터와 유사한 방식으로 상관관계 및 분석을 수행할 수 있으며, 이는 주파수 영역에서 작동할 필요성을 줄여준다.

시계열 분석 기법은 모수 추정과 비모수 통계 방법으로 나눌 수 있다. 모수적 접근 방식은 기본적인 정상 확률 과정을 설명하는 모델의 매개변수를 추정하는 반면, 비모수적 접근 방식은 과정의 공분산 또는 스펙트럼을 명시적으로 추정한다.

시계열 분석 방법은 선형 회귀와 비선형 회귀, 단변량 분석과 다변량 분석으로도 나눌 수 있다.

2. 1. 주파수 영역 방법

주파수 영역 방법은 데이터를 주파수 성분으로 분해하여 분석하는 방법으로, 스펙트럼 분석 및 웨이블릿 분석을 포함한다. 이 방법은 푸리에 변환을 사용하여 신호를 주파수 영역에서 분석하고 필터링하며, 스펙트럼 밀도 추정을 기반으로 한다.

제2차 세계 대전 동안 노버트 위너, 루돌프 E. 칼만, 데니스 가보 등은 신호에서 노이즈를 제거하고 특정 시점의 신호 값을 예측하기 위해 주파수 영역 방법을 발전시켰다.[10][11]

2. 1. 1. 스펙트럼 분석

스펙트럼 분석은 시계열 데이터에 포함된 주기적인 변동을 파악하는 데 유용한 방법이다. 이 접근 방식은 푸리에 변환을 사용하여 주파수 영역에서 신호를 조화 분석 및 필터링하고 스펙트럼 밀도 추정을 기반으로 할 수 있다. 이는 제2차 세계 대전 동안 수학자 노버트 위너, 전기 기술자 루돌프 E. 칼만, 데니스 가보 등에 의해 신호에서 노이즈를 필터링하고 특정 시점에서 신호 값을 예측하는 데 크게 가속화되었다.

스펙트럼 분석을 통해 계절성과 관련이 없는 주기적 동작을 검토할 수 있다. 예를 들어, 흑점 활동은 11년 주기로 변동한다.[10][11] 다른 일반적인 예로는 천체 현상, 기상 패턴, 신경 활동, 상품 가격 및 경제 활동 등이 있다.

시계열 데이터를 분석하는 도구는 다음과 같다.

2. 1. 2. 웨이블릿 분석

웨이블릿 분석은 시간에 따라 변하는 주파수 특성을 분석하는 데 효과적인 방법이다. 시계열 데이터를 분석하는 도구 중 시간-주파수 해석 기법은 다음과 같다.

2. 2. 시간 영역 방법

시간 영역 방법은 시간의 흐름에 따른 데이터 변화를 직접 분석하는 방법으로, 자기 상관 분석, 상호 상관 분석 등이 있다. 시간 영역에서는 스케일링된 상관관계를 사용하여 필터와 유사한 방식으로 상관관계 및 분석을 수행할 수 있으며, 이는 주파수 영역에서 작동할 필요성을 줄여준다.

시계열 분석 기법은 모수 추정과 비모수 통계 방법으로 나눌 수 있다. 모수적 접근 방식은 기본 정상 확률 과정이 소수의 매개변수를 사용하여 설명할 수 있는 특정 구조를 가지고 있다고 가정한다. 반면, 비모수적 접근 방식은 과정이 특정 구조를 가지고 있다고 가정하지 않고 과정의 공분산 또는 스펙트럼을 명시적으로 추정한다.

시계열 분석 방법은 선형 회귀와 비선형 회귀, 단변량 분석과 다변량 분석으로도 나눌 수 있다.

2. 2. 1. 자기 상관 분석

자기 상관 분석은 과거 데이터가 현재 데이터에 미치는 영향을 파악하는 데 사용된다. 시계열 데이터를 분석하는 도구에는 자기상관 함수와 스펙트럼 밀도 함수가 있다.

2. 2. 2. 상호 상관 분석

자기상관과 스펙트럼 밀도 함수는 두 시계열 데이터 간의 연관성을 분석하는 데 사용된다.[1]

2. 3. 모수적 방법과 비모수적 방법

시계열 분석 기법은 모수 추정과 비모수 통계 방법으로 나눌 수 있다. 모수적 접근 방식은 기본 정상 확률 과정이 자기 회귀 또는 이동 평균 모델과 같이 소수의 매개변수를 사용하여 설명할 수 있는 특정 구조를 가지고 있다고 가정한다. 이러한 접근 방식에서는 확률 과정을 설명하는 모델의 매개변수를 추정하는 것이 과제이다. 반대로, 비모수적 접근 방식은 과정이 특정 구조를 가지고 있다고 가정하지 않고 과정의 공분산 또는 스펙트럼을 명시적으로 추정한다.

2. 4. 선형 분석과 비선형 분석

시계열 데이터는 그 특성에 따라 선형 분석 또는 비선형 분석을 적용하여 분석할 수 있다. 자기 회귀 모델(AR), 이동 평균 모델(MA), 자기 회귀 이동 평균 모델(ARMA), 자기 회귀 누적 이동 평균 모델(ARIMA) 등은 과거 데이터와 노이즈에 선형적으로 의존하는 선형 모델이다.[50][51] 반면, 과거 데이터에 대한 비선형적인 의존은 카오스 이론을 기반으로 한 분석이 필요하며, 이는 비선형 분석에 속한다.

상태 공간 모델은 상태(관측 불가능)를 x_t, 관측값(관측 가능)을 y_t, 시스템 노이즈(상태 천이의 노이즈)를 v_t, 관측 노이즈를 w_t로 하여 시계열 y_t를 표현한다.

:

\begin{align}

x_t &= f_t(x_{t-1}, v_t) \\

y_t &= h_t(x_t, w_t)

\end{align}



이 모델은 입자 필터(몬테카를로 방법)를 사용하여 상태 x_t의 확률 분포를 구할 수 있다.

만약 상태 및 관측값이 실수 열 벡터이고, 함수 f_t와 h_t가 선형이며, 시스템 노이즈 v_t와 관측 노이즈 w_t가 다변량 정규 분포를 따르는 경우에는 다음과 같이 표현할 수 있다.

:

\begin{align}

x_t &= F_t x_{t-1} + G_t v_t \\

y_t &= H_t x_t + w_t

\end{align}



이 모델은 칼만 필터를 통해 상태 x_t의 확률 분포(다변량 정규 분포)의 엄밀해를 구할 수 있으며, ARMA나 ARIMA도 이 선형 모델로 다룰 수 있다.[50][51]

3. 패널 데이터

시계열은 패널 데이터의 한 유형이다. 패널 데이터는 여러 개체에 대해 시간에 따라 반복 측정된 데이터를 의미하는 반면, 시계열 데이터 집합은 1차원 패널(횡단면 데이터 집합과 같음)이다. 데이터 집합은 패널 데이터와 시계열 데이터의 특성을 모두 나타낼 수 있다. 이를 구별하는 한 가지 방법은 하나의 데이터 레코드를 다른 레코드와 구별하는 요소가 무엇인지 묻는 것이다. 답이 시간 데이터 필드인 경우, 이는 시계열 데이터 집합 후보이다. 고유한 레코드를 결정하는 데 시간 데이터 필드와 시간과 관련 없는 추가 식별자(예: 학생 ID, 주식 기호, 국가 코드)가 필요한 경우, 이는 패널 데이터 후보이다.

4. 분석

시계열 분석은 시간에 따라 측정된 데이터를 해석하고, 그 데이터가 왜 그렇게 되었는지, 그리고 미래를 예측하는 데 사용되는 기법이다. 예를 들어, 과거 주식 가격의 변화를 보고 미래 가격을 예측하는 데 사용될 수 있다.[8]

시계열 분석은 다양한 목적을 가질 수 있으며, 여러 유형의 데이터 분석 방법이 사용된다. 주요 목적은 다음과 같다:


  • 예측: 과거 데이터를 기반으로 미래를 예측한다. 예를 들어, 주식 가격 예측에 활용될 수 있다.
  • 신호 감지: 데이터에서 특정 신호를 찾아낸다.
  • 군집 분석: 비슷한 패턴을 가진 시계열 데이터를 그룹으로 묶는다.
  • 이상 감지: 일반적인 패턴에서 벗어나는 이상치를 찾아낸다.


이러한 분석에는 푸리에 변환, 자기상관, 주성분 분석, 신경망 등 다양한 도구가 사용된다.

4. 1. 탐색적 분석

미국 결핵 사망자 시계열 (1954-2021)


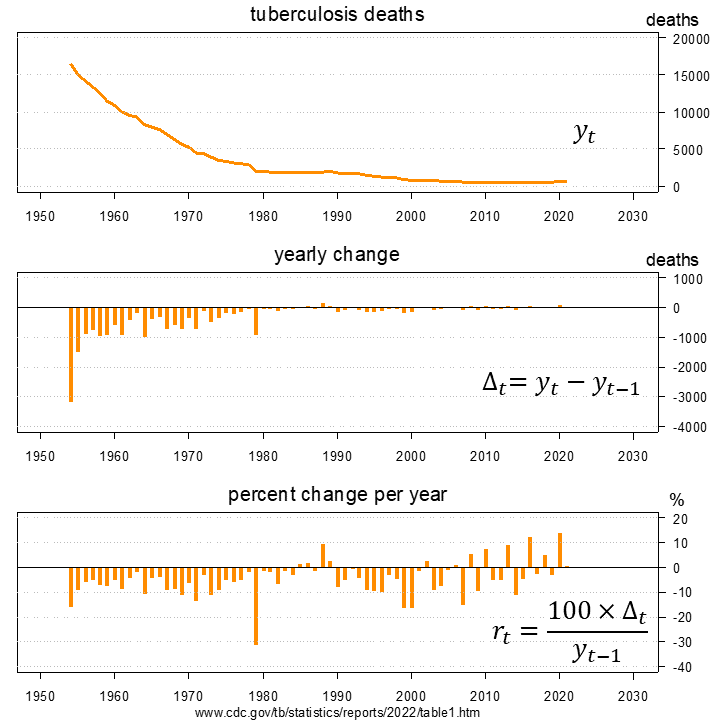
정규 시계열은 선 그래프를 사용하여 수동으로 검사할 수 있다. 위 그래프는 미국에서 결핵 사망자 수를 나타내며,[8] 연간 변화 및 전년 대비 백분율 변화를 함께 보여준다. 총 사망자 수는 1980년대 중반까지 매년 감소했으며, 그 이후에는 때때로 증가했는데, 종종 비율적으로는 상당히 컸지만, 절대적인 수치는 그렇지 않았다.

기업 데이터 분석가에 대한 연구에 따르면 탐색적 시계열 분석에는 두 가지 과제가 있다. 흥미로운 패턴의 형태를 발견하는 것과 이러한 패턴에 대한 설명을 찾는 것이다.[9] 시계열 데이터를 히트 맵 행렬로 표현하는 시각적 도구는 이러한 문제를 극복하는 데 도움이 될 수 있다.

4. 2. 추정, 필터링, 평활화

푸리에 변환을 사용하여 주파수 영역에서 신호를 조화 분석 및 필터링하고 스펙트럼 밀도 추정을 기반으로 데이터를 분석할 수 있다. 제2차 세계 대전 동안 노버트 위너, 루돌프 E. 칼만, 데니스 가보 등은 신호에서 노이즈를 필터링하고 특정 시점에서 신호 값을 예측하는 기술을 개발하였다.[10][11]

칼만 필터와 같이 시간 도메인에서 동일한 효과를 얻을 수 있다. 자세한 내용은 필터링 및 평활화 기법을 참고하라.

시계열 데이터를 분석하는 도구는 다음과 같다.

  • 자기상관 함수와 스펙트럼 밀도 함수
  • 주파수 영역의 계열 분석으로서의 푸리에 변환
  • 노이즈를 제거하는 디지털 필터의 사용
  • 주성분 분석 (또는 경험 직교 함수 분석)
  • 인공 신경망
  • 시간-주파수 해석 기법:
  • 연속 웨이블릿 변환
  • 단시간 푸리에 변환
  • Chirplet 변환
  • 비정수차 푸리에 변환
  • 카오스 해석
  • 상관 차원
  • 리커런스 플롯
  • 재귀 정량화 분석
  • 랴푸노프 지수
  • 상태 공간 모델
  • 칼만 필터, 확장 칼만 필터, 앙상블 칼만 필터
  • 입자 필터


자기 상관 분석을 통해 시계열 종속성을 검토하고, 스펙트럼 분석을 통해 계절성과 관련이 없는 주기적 동작을 검토할 수 있다. 예를 들어, 흑점 활동은 11년 주기로 변동한다.[10][11] 추세 추정 및 시계열 분해를 참조하여 추세, 계절성, 느리고 빠른 변동, 주기적 불규칙성을 나타내는 구성 요소로 분리할 수 있다.

상태 공간 모델은 상태(관측 불가능)를 x_t, 관측값(관측 가능)을 y_t, 시스템 노이즈(상태 천이의 노이즈)를 v_t, 관측 노이즈를 w_t로 하여, 다음과 같이 시계열 y_t를 표현하는 모델이다.[50][51]

:

\begin{align}

x_t &= f_t(x_{t-1}, v_t) \\

y_t &= h_t(x_t, w_t)

\end{align}



이 모델은 입자 필터(몬테카를로 방법)를 사용하여 상태 x_t의 확률 분포를 구할 수 있다.

상태 및 관측값이 실수 열 벡터이고, 함수 f_t와 h_t가 선형(행렬 곱셈)이며, 시스템 노이즈 v_t와 관측 노이즈 w_t가 다변량 정규 분포를 따르는 경우에는 다음과 같다.

:

\begin{align}

x_t &= F_t x_{t-1} + G_t v_t \\

y_t &= H_t x_t + w_t

\end{align}



이 모델은 칼만 필터로 엄밀해를 구할 수 있다. ARMA나 ARIMA도 이 선형 모델로 다룰 수 있다.

4. 3. 곡선 적합

곡선 맞춤[12][13]은 일련의 데이터 점에 가장 "적합한" 곡선 또는 수학적 함수를 구성하는 과정이며,[14] 제약 조건이 적용될 수도 있다.[15][16] 곡선 맞춤은 데이터에 정확하게 맞는 보간법[17][18], 또는 데이터에 근사적으로 맞는 "부드러운" 함수를 구성하는 평활화[19][20]를 포함할 수 있다. 관련된 주제는 회귀 분석[21][22]으로, 무작위 오차로 관찰된 데이터에 맞춰진 곡선에 얼마나 많은 불확실성이 있는지와 같은 통계적 추론 문제에 더 중점을 둔다. 맞춰진 곡선은 데이터 시각화,[23][24] 데이터가 없는 함수의 값을 추론하고,[25] 두 개 이상의 변수 간의 관계를 요약하는 데 도움이 될 수 있다.[26] 외삽법은 관찰된 데이터의 범위를 넘어 맞춰진 곡선을 사용하는 것을 말하며,[27] 이는 관찰된 데이터만큼 곡선을 구성하는 데 사용된 방법을 반영할 수 있으므로 불확실성[28]의 정도를 받는다.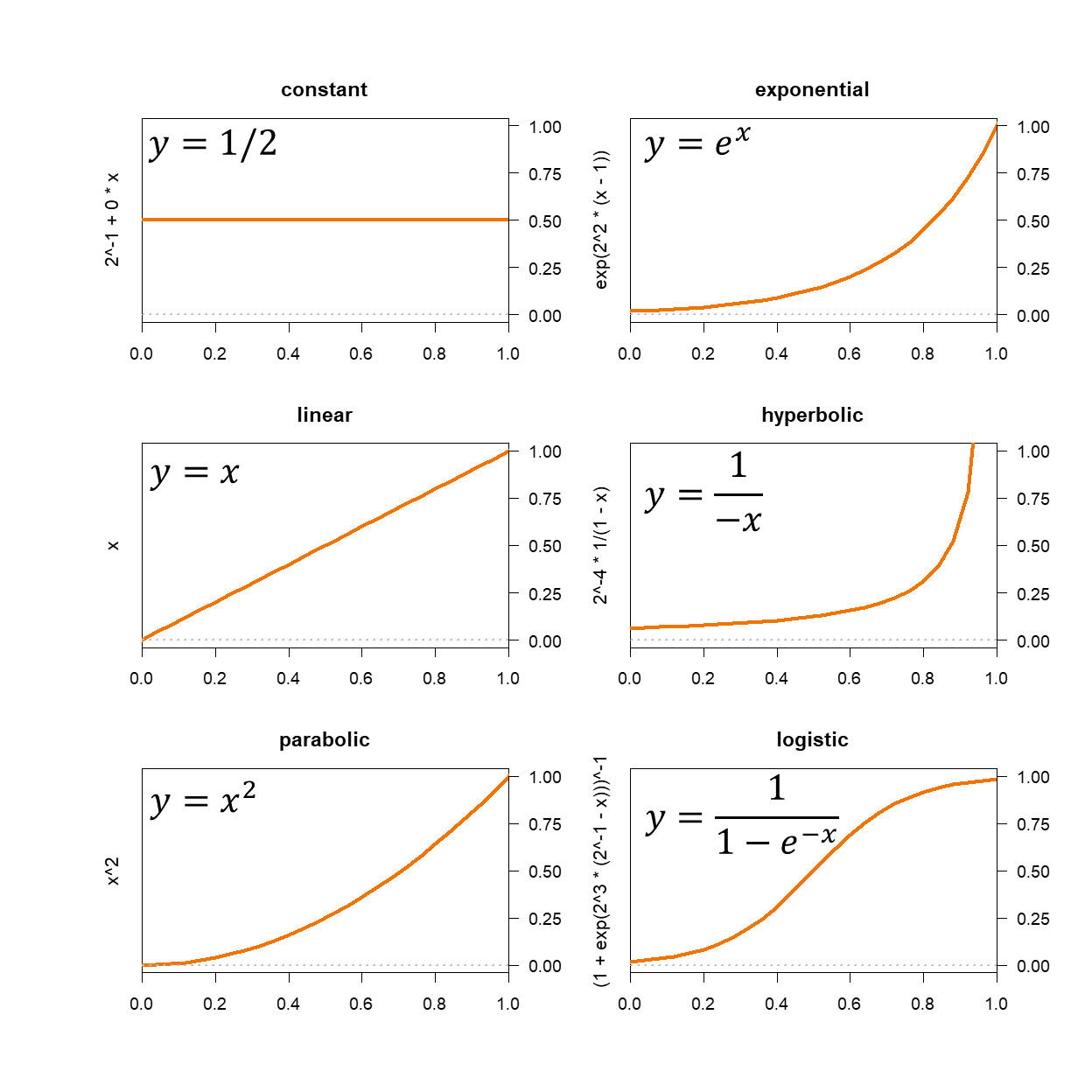

성장 방정식


경제 시계열의 구성에는 이전 및 이후 날짜의 값("기준") 사이의 보간법을 사용하여 일부 날짜에 대한 일부 구성 요소의 추정이 포함된다. 보간법은 두 개의 알려진 양(과거 데이터) 사이의 알려지지 않은 양을 추정하거나, 사용 가능한 정보에서 누락된 정보에 대한 결론을 도출하는 것이다("행간을 읽기").[29] 보간법은 누락된 데이터를 둘러싼 데이터가 있고, 해당 추세, 계절성 및 장기적인 주기가 알려진 경우에 유용하다. 이는 관련 시리즈를 사용하여 수행되는 경우가 많으며, 모든 관련 날짜에 대해 알려져 있다.[30] 또는 구간별 다항식 함수가 부드럽게 함께 맞도록 시간 간격으로 맞춰지는 다항식 보간법 또는 스플라인 보간법이 사용된다. 보간법과 밀접하게 관련된 또 다른 문제는 복잡한 함수를 단순한 함수로 근사하는 것이다(회귀라고도 함). 회귀와 보간법의 주요 차이점은 다항 회귀는 전체 데이터 세트를 모델링하는 단일 다항식을 제공하는 반면, 스플라인 보간법은 데이터 세트를 모델링하기 위해 여러 다항식으로 구성된 구간별 연속 함수를 생성한다는 것이다.

외삽법은 원래 관찰 범위를 넘어 다른 변수와의 관계를 기반으로 변수의 값을 추정하는 과정이다. 알려진 관찰 간의 추정치를 생성하는 보간법과 유사하지만, 외삽법은 불확실성이 더 크고 의미 없는 결과를 생성할 위험이 더 높다.

4. 4. 함수 근사

함수 근사는 알려진 함수 또는 알려지지 않은 함수를 특정 형태의 함수로 근사하는 방법이다.

함수 근사에는 크게 두 가지 종류가 있다.

  • 첫째, 대상 함수가 알려진 경우, 근사 이론을 통해 다항식이나 유리 함수와 같은 특정 종류의 함수를 사용하여 특수 함수와 같이 특정 알려진 함수를 근사하는 방법을 연구한다. 이러한 함수들은 계산이 저렴하고, 연속성을 가지며, 적분 및 극한 값 등을 구하기 쉬운 특징을 가지고 있다.

  • 둘째, 대상 함수 ''g''가 알려지지 않은 경우, (''x'', ''g''(''x'')) 형태의 점 집합(시계열)만이 주어질 수 있다. 이때, ''g''의 정의역과 공역의 구조에 따라 ''g''를 근사하는 다양한 기법을 적용할 수 있다.
  • ''g''가 실수에 대한 연산인 경우: 보간법, 외삽법, 회귀 분석, 곡선 맞춤 등을 사용할 수 있다.
  • ''g''의 공역이 유한 집합인 경우: 분류 문제를 다룬다.


이와 관련된 문제로 ''온라인'' 시계열 근사[31]가 있는데, 이는 한 번의 데이터 처리로 요약하고 최악의 경우 오차 범위를 가지는 다양한 시계열 쿼리를 지원할 수 있는 근사 표현을 구성하는 것이다.

회귀, 분류, 적합도 근사와 같은 문제들은 통계적 학습 이론에서 지도 학습 문제로 통합적으로 다루어진다.

일반적으로 크기가 증가할 것으로 예상되는 경우, 위 그림에 있는 곡선 중 하나(또는 여러 곡선)에 맞춰 매개변수를 추정할 수 있다.

경제 시계열을 구성할 때는 이전 및 이후 날짜 값("기준") 사이의 보간법을 사용하여 특정 날짜에 대한 구성 요소 추정치를 포함한다. 보간법은 과거 데이터와 같이 두 개의 알려진 값 사이에 있는 알려지지 않은 값을 추정하거나, 사용 가능한 정보에서 누락된 정보에 대한 결론을 도출하는 것이다.[29] 보간법은 누락된 데이터를 둘러싼 데이터가 있고, 해당 추세, 계절성 및 장기적인 주기가 알려진 경우에 유용하다. 관련 시리즈를 사용하거나,[30] 구간별 다항식 함수가 부드럽게 연결되도록 시간 간격으로 맞춰지는 다항식 보간법 또는 스플라인 보간법을 사용한다.

외삽법은 원래 관찰 범위를 넘어 다른 변수와의 관계를 기반으로 변수의 값을 추정하는 것이다. 이는 알려진 관찰 값 사이에서 추정치를 생성하는 보간법과 유사하지만, 외삽법은 불확실성이 더 크고 의미 없는 결과를 낼 위험이 더 높다.

4. 5. 예측 및 예측

통계학에서 예측은 통계적 추론의 한 부분이다. 예측적 추론은 통계적 추론에 대한 특별한 접근 방식이지만, 예측은 다양한 통계적 추론 방법 내에서 수행될 수 있다. 통계학은 모집단의 표본에 대한 지식을 전체 모집단 및 관련 모집단으로 이전하는 수단을 제공하며, 반드시 시간 경과에 따른 예측과 동일하지는 않다. 정보를 시간 경과에 따라, 특정 시점으로 이전하는 과정을 예측이라고 한다.[7]

미래 시계열 예측 방법은 다음과 같다.

  • 미래의 비특정 기간에 걸쳐 발생할 수 있는 여러 버전의 시계열을 생성하는 완전한 형태의 통계 모델 (확률적 시뮬레이션).
  • 가장 최근 결과에 대한 지식을 바탕으로 가까운 미래의 시계열의 가능성 있는 결과를 설명하는 간단하거나 완전한 형태의 통계 모델 (예측).
  • 줄리아, 파이썬, R, SAS, SPSS 등과 같은 자동화된 통계 소프트웨어 패키지 및 프로그래밍 언어를 사용하여 시계열 예측 수행.
  • 아파치 스파크와 Spark-TS 라이브러리(제3자 패키지)를 사용하여 대규모 데이터에 대한 예측 수행.


'''시계열 예측'''은 알려진 과거 사건을 기반으로 미래 모델을 구축하고, 측정 전에 미래 데이터 포인트를 예측하는 것이다. 예를 들어 주식의 과거 가격 추이로부터 미래 가격을 예측하는 것이 있다.

4. 6. 분류

통계적 분류

시계열 패턴을 특정 범주에 할당하는 것으로, 예를 들어 수화의 일련의 손 움직임을 기반으로 단어를 식별하는 것과 같다.

4. 7. 분할

시계열을 일련의 세그먼트로 분할하는 것을 말한다. 시계열은 각자 고유한 특성을 가진 개별 세그먼트의 시퀀스로 표현될 수 있는 경우가 많다. 예를 들어, 회의 통화의 오디오 신호는 각 사람이 말하는 시간에 해당하는 조각으로 분할될 수 있다. 시계열 분할의 목표는 시계열에서 세그먼트 경계 지점을 식별하고 각 세그먼트와 관련된 동적 특성을 특징짓는 것이다. 이 문제에 접근하기 위해 변화점 감지를 사용하거나, 시계열을 마르코프 점프 선형 시스템과 같은 보다 정교한 시스템으로 모델링할 수 있다.

4. 8. 군집화

시계열 데이터는 군집화(클러스터링)될 수 있지만, 부분 시퀀스 군집화를 고려할 때는 특별한 주의가 필요하다.[33][34]

시계열 군집화는 다음과 같이 나눌 수 있다.

  • 전체 시계열 군집화 (여러 시계열에서 군집을 찾는 경우)
  • 부분 시퀀스 시계열 군집화 (단일 시계열을 슬라이딩 윈도우를 사용하여 여러 조각으로 분할)
  • 시간점 군집화


부분 시계열 군집화는 슬라이딩 윈도우를 사용한 청킹(chunking)을 이용한 특징 추출 때문에 불안정하고 무작위적인 군집을 생성한다.[35] 군집 중심(군집 내 시계열의 평균, 역시 시계열)이 임의로 이동된 사인(sine) 패턴을 따른다는 것이 발견되었다(데이터 세트에 관계없이, 심지어 무작위 보행의 경우에도). 이는 군집 중심이 항상 대표적이지 않은 사인파이기 때문에, 발견된 군집 중심이 데이터 세트를 설명하지 못한다는 것을 의미한다.

5. 모델

시계열 데이터 모델은 다양한 형태를 가지며, 확률 과정을 나타낸다. 주요 모델은 다음과 같다.


  • 선형 모델: 자기 회귀 모델(AR), 이동 평균 모델(MA), 자기 회귀 이동 평균 모델(ARMA), 자기 회귀 누적 이동 평균 모델(ARIMA), 자기 회귀 분수 적분 이동 평균 모델(ARFIMA), 벡터 자기 회귀 모델(VAR) 등
  • 비선형 모델: 비선형 자기 회귀 외생 모델, 자기 회귀 조건부 이분산성(ARCH) 모델 (GARCH, TARCH, EGARCH, FIGARCH, CGARCH 등), 이중 확률 모델
  • 기타 모델: 은닉 마르코프 모델(HMM), 상태 공간 모델


이 외에도 웨이블릿 변환 기반 방법, 마르코프 스위칭 멀티프랙탈 (MSMF) 기술 등이 연구되고 있다.[39] 파이썬 패키지 sktime에는 이러한 모델 중 다수가 구현되어 있다.

5. 1. 자기 회귀 모델 (AR)

자기 회귀 모델(AR)은 현재 값이 이전 값에 선형적으로 의존하는 모델이다.[36]

5. 2. 이동 평균 모델 (MA)

이동 평균 모델(MA)은 현재 값이 이전 오차에 선형적으로 의존하는 모델이다.[36]

5. 3. 자기 회귀 이동 평균 모델 (ARMA)

자기 회귀 모델(AR)과 이동 평균 모델(MA)을 결합한 것이 ARMA 모델이다.[36] 이 모델은 이전 데이터 포인트에 선형적으로 의존한다.

5. 4. 자기 회귀 누적 이동 평균 모델 (ARIMA)

ARIMA 모델은 자기 회귀 모델(AR), 이동 평균(MA) 모델을 결합한 ARMA 모델에 적분(I)을 더한 것이다.[36] 이들은 과거의 데이터 열 및 노이즈에 선형적으로 의존한다.

5. 5. 자기 회귀 분수 적분 이동 평균 모델 (ARFIMA)

ARIMA 모델은 자기 회귀 모델(AR), 적분(I) 모델, 이동 평균 모델(MA)을 결합한 것이다. 자기 회귀 분수 적분 이동 평균(ARFIMA) 모델은 이 세 가지를 일반화한다.[36]

5. 6. 벡터 자기 회귀 모델 (VAR)

자기 회귀 모델(AR)과 이동 평균 모델(MA)을 결합한 자기 회귀 이동 평균 모델(ARMA)은 다변량 시계열 데이터를 분석하기 위해 벡터 자기 회귀(VAR) 모델로 확장될 수 있다.[36]

5. 7. 비선형 모델

카오스 시계열을 생성할 가능성 때문에, 계열 수준이 이전 데이터 포인트에 비선형적으로 의존하는 것은 흥미롭다.[37][38] 실증적 연구에 따르면, 비선형 자기 회귀 외생 모델과 같이 비선형 모델에서 파생된 예측을 사용하는 것이 선형 모델에서 파생된 예측보다 유리하다.

시간에 따른 분산의 변화(이분산성)를 나타내는 모델은 다른 유형의 비선형 시계열 모델이다. 이러한 모델은 자기 회귀 조건부 이분산성 (ARCH)을 나타내며, GARCH, TARCH, EGARCH, FIGARCH, CGARCH 등 다양한 표현을 포함한다. 여기서 변동성의 변화는 관찰된 계열의 최근 과거 값과 관련되거나 예측된다. 이는 변동성이 이중 확률 모델에서와 같이 별도의 시간 변화 프로세스에 의해 구동되는 것으로 모델링될 수 있는, 국소적으로 변동하는 변동성의 다른 가능한 표현과는 대조적이다.

5. 8. 은닉 마르코프 모델 (HMM)

은닉 마르코프 모델 (HMM)은 관찰되지 않은(은닉된) 상태를 가진 마르코프 과정을 가정하는 통계적 마르코프 모델이다. HMM은 가장 단순한 동적 베이지안 네트워크로 간주될 수 있다. HMM 모델은 말해진 단어의 시계열을 텍스트로 변환하는 데 널리 사용되며, 음성 인식에 널리 사용된다.[39]

6. 조건

시계열 이론은 대부분 다음 두 가지 조건을 기반으로 한다.


  • 정상성 과정
  • 에르고딕 과정


에르고딕 과정은 정상성 과정을 함축하지만, 그 역은 반드시 성립하지 않는다. 정상성은 평균과 분산이 시간에 따라 변하지 않는 과정을 말하며, 엄밀 정상성과 광의 정상성(혹은 2차 정상성)으로 분류된다. 정상성과 에르고딕성 두 조건 모두에서 모형과 응용 프로그램을 개발할 수 있지만, 광의 정상성의 경우 모형은 부분적으로만 지정될 수 있다.[40]

또한, 시계열 분석은 시계열이 계절 정상성을 가지거나 비정상적인 경우에도 적용될 수 있다. 주파수 성분의 진폭이 시간에 따라 변하는 상황은 시간-주파수 분석으로 처리할 수 있는데, 이는 시계열 또는 신호의 시간-주파수 표현을 활용한다.[40]

6. 1. 정상성 과정

정상성 과정은 평균과 분산이 시간에 따라 변하지 않는 과정을 말한다. 정상성 과정은 엄밀 정상성과 광의 정상성 또는 2차 정상성으로 분류된다.[40] 두 경우 모두에서 모형과 응용 프로그램을 개발할 수 있지만, 광의 정상성의 경우 모형은 부분적으로만 지정된 것으로 간주될 수 있다.[40]

6. 2. 에르고딕 과정

에르고딕성은 정상성 과정을 함축하지만, 그 역이 반드시 성립하는 것은 아니다.[40]

7. 도구

시계열 데이터를 조사하기 위한 도구는 다음과 같다.


  • 자기상관 함수 및 스펙트럼 밀도 함수 (또한 상관 함수 및 교차 스펙트럼 밀도 함수) 고려[41]
  • 느린 구성 요소의 기여를 제거하기 위한 확장 교차 및 자기 상관 함수[41]
  • 시계열을 주파수 영역에서 조사하기 위해 푸리에 변환 수행
  • 군집 분석 수행[42]
  • 시계열에 (일반화된) 조화 신호가 포함되어 있는지 여부에 따라 시계열의 이산, 연속 또는 혼합 스펙트럼
  • 원치 않는 잡음을 제거하기 위해 필터 사용
  • 주성분 분석 (또는 경험적 직교 함수 분석)
  • 특이 스펙트럼 분석
  • "구조적" 모델:
  • * 일반 상태 공간 모델
  • * 관찰되지 않은 구성 요소 모델
  • 기계 학습
  • * 인공 신경망
  • * 지지 벡터 머신
  • * 퍼지 논리
  • * 가우시안 프로세스
  • * 유전자 프로그래밍
  • * 유전자 발현 프로그래밍
  • * 은닉 마르코프 모델
  • * 다중 표현 프로그래밍
  • 대기열 이론 분석
  • 관리도
  • * Shewhart 개별 관리도
  • * CUSUM 차트
  • * EWMA 차트
  • 추세 제거 변동 분석
  • 비선형 혼합 효과 모델링
  • 동적 시간 워핑[43]
  • 동적 베이즈 네트워크
  • 시간-주파수 분석 기법:
  • * 고속 푸리에 변환
  • * 연속 웨이블릿 변환
  • * 단시간 푸리에 변환
  • * Chirplet 변환
  • * 분수 푸리에 변환
  • 카오스 분석
  • * 상관 차원
  • * 재귀 플롯
  • * 재귀 정량화 분석
  • * 랴푸노프 지수
  • * 엔트로피 인코딩

8. 측정

시계열 분류 또는 회귀 분석에 사용할 수 있는 특징은 다음과 같다.[44]


  • '''단변량 선형 척도'''
  • 적률
  • 스펙트럼 대역 전력
  • 스펙트럼 에지 주파수
  • 누적된 에너지
  • 자기상관 함수의 특성
  • 요르트 파라미터
  • FFT 파라미터
  • 자기 회귀 모형 파라미터
  • 만-켄달 검정
  • '''단변량 비선형 척도'''
  • 상관 관계 합을 기반으로 하는 척도
  • 상관 차원
  • 상관 적분
  • 상관 밀도
  • 상관 엔트로피
  • 근사 엔트로피[45]
  • 표본 엔트로피
  • Ентропія Фур'є|Fourier entropyuk
  • 웨이블릿 엔트로피
  • 분산 엔트로피
  • 변동 분산 엔트로피
  • 레니 엔트로피
  • 고차 방법
  • 한계 예측 가능성
  • 동적 유사성 지수
  • 상태 공간 비유사성 척도
  • 랴푸노프 지수
  • 순열 방법
  • 국소 흐름
  • '''기타 단변량 척도'''
  • 알고리즘 복잡도
  • 콜모고로프 복잡도 추정치
  • 은닉 마르코프 모형 상태
  • 거친 경로 시그니처[46]
  • 대리 시계열 및 대리 보정
  • 반복 손실 (비정상성의 정도)
  • '''이변량 선형 척도'''
  • 최대 선형 상호 상관
  • 선형 코히어런스
  • '''이변량 비선형 척도'''
  • 비선형 상호 의존성
  • 동적 견인 (물리학)
  • 위상 동기화 척도
  • 위상 잠금 척도
  • '''유사성 척도'''[47]
  • 상호 상관
  • 동적 시간 워핑[43]
  • 은닉 마르코프 모형
  • 편집 거리
  • 총 상관 관계
  • 뉴이-웨스트 추정량
  • 프레이스-윈스턴 변환
  • 거리 공간에서 벡터로 표현되는 데이터
  • 민코프스키 거리
  • 마할라노비스 거리
  • 포락선이 있는 시계열로 해석되는 데이터
  • 전역 표준 편차
  • 국소 표준 편차
  • 윈도우 표준 편차
  • 확률적 계열로 해석되는 데이터
  • 피어슨 곱 모멘트 상관 계수
  • 스피어만 순위 상관 계수
  • 확률 분포 함수로 해석되는 데이터
  • 콜모고로프-스미르노프 검정
  • 크라메르-본 미세스 기준

9. 시각화

시계열은 겹쳐진 차트와 분리된 차트의 두 가지 범주로 시각화할 수 있다. 겹쳐진 차트는 모든 시계열을 동일한 레이아웃에 표시하는 반면, 분리된 차트는 서로 다른 레이아웃에 표시하지만 비교를 위해 정렬된다.[48]


  • 엮은 그래프
  • 꺾은선 그래프
  • 기울기 그래프
  • GapChart|갭 차트프랑스어
  • 호라이즌 그래프
  • 축소된 선 그래프(스몰 멀티플)
  • 실루엣 그래프
  • 원형 실루엣 그래프

10. 산업계에서의 용도

시간에 따라 측정되는 모든 데이터는 시계열로 볼 수 있다. 종합 주가지수, 매일매일의 유가 변동, 환율 등 모든 데이터가 이에 해당한다. 따라서 시계열 해석은 미래를 예측하는 데 중요한 도구가 될 수 있다.[1] 예를 들어, 주식의 과거 가격 추이로 미래 가격을 예측할 수 있다.[2]

경영 애널리스트들은 이러한 도구를 활용하여 경영에 활용한다. 예를 들어, 에너지 트레이더는 평년 날씨와 단기 일기 예보를 바탕으로 전력 소비량을 예측한다.[3]

참조

[1] 서적 Proceedings of the 8th ACM SIGMOD workshop on Research issues in data mining and knowledge discovery ACM Press
[2] 논문 Clustering of time series data—a survey 2005-11
[3] 논문 Time-series clustering – A decade review 2015-10
[4] 논문 AngClust: Angle Feature-Based Clustering for Short Time Series Gene Expression Profiles 2023-04
[5] 서적 Proceedings of the eighth ACM SIGKDD international conference on Knowledge discovery and data mining 2002
[6] 서적 Foundations of Data Organization and Algorithms https://figshare.com[...] 1993
[7] 논문 Ordinal Time Series Forecasting of the Air Quality Index 2021-09-04
[8] 웹사이트 Table 1 | Reported TB in the US 2022| Data & Statistics | TB | CDC http://www.cdc.gov/t[...] 2024-08-27
[9] 서적 2016 IEEE Symposium on Visual Languages and Human-Centric Computing (VL/HCC) 2016
[10] 서적 Fourier Analysis of Time Series: An Introduction Wiley 1976
[11] 서적 Applied Statistical Time Series Analysis Prentice-Hall 1988
[12] 서적 Practical Handbook of Curve Fitting CRC Press 1994
[13] 서적 Curve Fitting for Programmable Calculators SYNTEC 1984
[14] 서적 Advanced Techniques of Population Analysis Springer Science & Business Media 1992
[15] 서적 The Signal and the Noise]: Why So Many Predictions Fail-but Some Don't. https://archive.org/[...]
[16] 서적 Data Preparation for Data Mining Morgan Kaufmann 1999
[17] 문서 Numerical Methods in Engineering with MATLAB®.
[18] 서적 Numerical Methods in Engineering with Python 3 Cambridge University Press 2013
[19] 서적 Numerical Methods of Curve Fitting Cambridge University Press 2012
[20] 문서 Mollifier
[21] 서적 Fitting Models to Biological Data Using Linear and Nonlinear Regression: A Practical Guide to Curve Fitting Oxford University Press 2004
[22] 문서 Regression Analysis
[23] 서적 Visual Informatics: Bridging Research and Practice 2009
[24] 서적 Numerical Methods for Nonlinear Engineering Models Springer Science & Business Media 2009
[25] 서적 Spectroscopy 1976
[26] 서적 Encyclopedia of Research Design https://books.google[...] SAGE 2010
[27] 서적 Community Analysis and Planning Techniques Rowman & Littlefield Publishers 1990
[28] 간행물 An Introduction to Risk and Uncertainty in the Evaluation of Environmental Investments U.S. Army Corps of Engineers 1996-03
[29] 서적 Numerical Methods for Scientists and Engineers Courier Corporation 2012
[30] 논문 The Interpolation of Time Series by Related Series 1962-12
[31] 서적 2010 IEEE 26th International Conference on Data Engineering (ICDE 2010) 2010
[32] 웹사이트 Time Series Analysis with Spark https://databricks.c[...] Databricks 2020-03-18
[33] 논문 A Review of Subsequence Time Series Clustering 2014
[34] 논문 AngClust: Angle Feature-Based Clustering for Short Time Series Gene Expression Profiles 2023-04
[35] 논문 Clustering of time-series subsequences is meaningless: implications for previous and future research 2005-08
[36] 서적 The Nature of Mathematical Modeling https://archive.org/[...] Cambridge University Press
[37] 서적 Nonlinear Time Series Analysis Cambridge University Press 2004
[38] 서적 Analysis of Observed Chaotic Data Springer 1997-11-25
[39] 간행물 Using wavelet tools to analyse seasonal variations from InSAR time-series data: a case study of the Huangtupo landslide http://link.springer[...] 2016-06
[40] 문서 "Time-Frequency Signal Analysis and Processing: A Comprehensive Reference" Elsevier Science 2003
[41] 간행물 Scaled correlation analysis: a better way to compute a cross-correlogram 2012-03
[42] 간행물 AngClust: Angle Feature-Based Clustering for Short Time Series Gene Expression Profiles 2023-04
[43] 간행물 Dynamic programming algorithm optimization for spoken word recognition 1978-02
[44] 간행물 Seizure prediction: the long and winding road
[45] 웹사이트 Measuring the 'Complexity' of a time series http://www.nbb.corne[...]
[46] arXiv A Primer on the Signature Method in Machine Learning 2016
[47] 서적 Proceedings of the 25th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (IEEE Cat. No.03CH37439) 2003
[48] 웹사이트 The TimeViz Browser:A Visual Survey of Visualization Techniques for Time-Oriented Data http://survey.timevi[...] 2014-06-01
[49] 문서 広辞苑第五版【時系列】
[50] 서적 時系列解析入門 岩波書店
[51] 서적 予測にいかす統計モデリングの基礎―ベイズ統計入門から応用まで 講談社


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com