주접속

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
3. 성질
- 3.1. 곡률
- 3.2. 게이지 변환
4. 주접속의 모듈러스 공간
5. 예
- 5.1. 자명한 주다발
- 5.2. 한원소 공간 위의 주접속
6. 응용
참조

1. 개요

주접속은 매끄러운 다양체 위의 리 군에 대한 주다발에서 정의되는 개념으로, 다양한 방식으로 정의될 수 있으며, 리 대수 값 미분 형식, 에레스만 접속, 벡터 다발, 국소 자명화를 통해 정의될 수 있다. 주접속은 등변성 및 재생성 조건을 만족하는 리 대수 값의 1차 미분 형식으로, 곡률과 게이지 변환과 같은 중요한 성질을 갖는다. 주접속의 모듈러스 공간은 아핀 공간이며, 게이지 변환군은 이 공간에 작용한다. 주접속은 자명한 주다발과 한원소 공간 위의 주다발 등에서 구체적인 예시를 찾아볼 수 있으며, 이론물리학 등 다양한 분야에 응용된다.

더 읽어볼만한 페이지

올다발 - 주다발
주다발은 위상 공간을 밑공간으로, 위상군을 올로 가지며, 연속적인 군 작용을 통해 정의되는 올다발로, 위상수학, 미분기하학, 게이지 이론 등에서 활용된다.
올다발 - 단면 (올다발)
단면은 올다발의 정의를 만족하는 함수로, 함수의 그래프를 일반화한 개념이며, 매끄러운 올다발에서는 매끄러운 단면을 정의할 수 있고, 전역 단면의 존재 여부는 호모토피 이론에서 중요한 연구 대상이다.
미분기하학 - 가우스 곡률
가우스 곡률은 3차원 유클리드 공간에 놓인 곡면의 두 주곡률의 곱으로, 곡면의 형태를 나타내는 지표이며 곡면 자체의 길이 측정만으로 결정되는 내재적인 값이다.
미분기하학 - 가우스의 빼어난 정리
가우스의 빼어난 정리는 곡면의 가우스 곡률이 외부 공간이 아닌 곡면 자체의 리만 계량만으로 결정된다는 정리로, 곡면의 변형 시 가우스 곡률이 보존됨을 의미하며, 지도 제작의 불가능성 증명과 고차원 리만 다양체 일반화에 응용되어 미분기하학과 일반 상대성 이론의 기초가 된다.

2. 정의

리 군 $G$ 와 그 리 대수 $\mathfrak{lie}(G)$ 가 주어지고, 매끄러운 다양체 $M$ 위의 매끄러운 주다발 $\pi\colon P\twoheadrightarrow M$ 가 주어졌을 때, 주접속은 다음과 같은 여러 동치인 방법으로 정의될 수 있다.

미분 형식: 주접속은 특정 조건을 만족시키는, $\mathfrak{lie}(G)$ 값의 1차 미분 형식 $\omega\in\Omega^1(P;\mathfrak{lie}(G))$ 으로 정의될 수 있다.
에레스만 접속: 주접속은 특정 호환 조건을 만족시키는 에레스만 접속 $H\subseteq\mathrm TP$ 으로 정의될 수 있다.
벡터 다발: 주접속은 $\mathrm TM$ 위의 특정한 올다발의 특정한 매끄러운 단면으로 정의될 수 있다.
국소 자명화: 주접속은 주다발의 국소 자명화에 대하여 각 조각 위의 $\mathfrak{lie}(G)$ 값의 1차 미분 형식들의 족으로 정의될 수 있다.

2. 1. 미분 형식을 통한 정의

P

의 '''주접속'''

\omega\in\Omega^1(P;\mathfrak{lie}(G))

는

P

위의

\mathfrak{lie}(G)

값을 가진 1차 미분 형식으로, 다음 두 가지 성질을 만족시킨다.^[3]

:

\operatorname{Ad}(g)(\cdot g)^*\omega=\omega\qquad\forall g\in G

:

\omega(X_\xi)=\xi\qquad\forall \xi\in\mathfrak{lie}(G)

여기서

$(\cdot g)\colon P\to P$ 는 군의 오른쪽 작용을 나타내는 매끄러운 함수 $h\mapsto h\cdot g$ 이다.
$(\cdot g)^*\omega\in\Omega^1(P;\mathfrak{lie}(G))$ 는 1차 미분 형식 $\omega$ 의, $(\cdot g)$ 에 대한 당김이다.
$\operatorname{Ad}(g)\colon\mathfrak{lie}(G)\to\mathfrak{lie}(G)$ 는 $g\in G$ 의 딸림표현이다.
$X_\xi\in\Gamma(\mathrm TP)$ 는 $G$ 의, $P$ 위의 오른쪽 작용을 생성하는 벡터장이다.

주 주다발 연결 형식 $\omega$ 는 주다발 $P$ 의 접다발 $TP$ 에 대한 투영 연산자로 생각할 수 있다. 연결 형식의 커널은 관련 Ehresmann 연결에 대한 수평 부분 공간으로 제공된다.

연결은 주다발 $P$ 의 모든 접선 공간에 대한 수평 부분 공간 $H_p\subset T_pP$ 을 선택하여 동등하게 지정된다.

주 주다발 연결은 $P$ 에서 $G$ 의 오른쪽 작용과 호환되어야 한다. 이것은 오른쪽 곱셈 $R_g$ 이 수평 부분 공간을 서로 가져가는 것으로 시각화할 수 있다. 연결 형식 $\omega$ 로 해석된 수평 부분 공간 $H\subset TP$ 의 이러한 등변성은 특징적인 등변성 속성을 초래한다.

주 ''G''-다발

\pi : P \to M

(

M

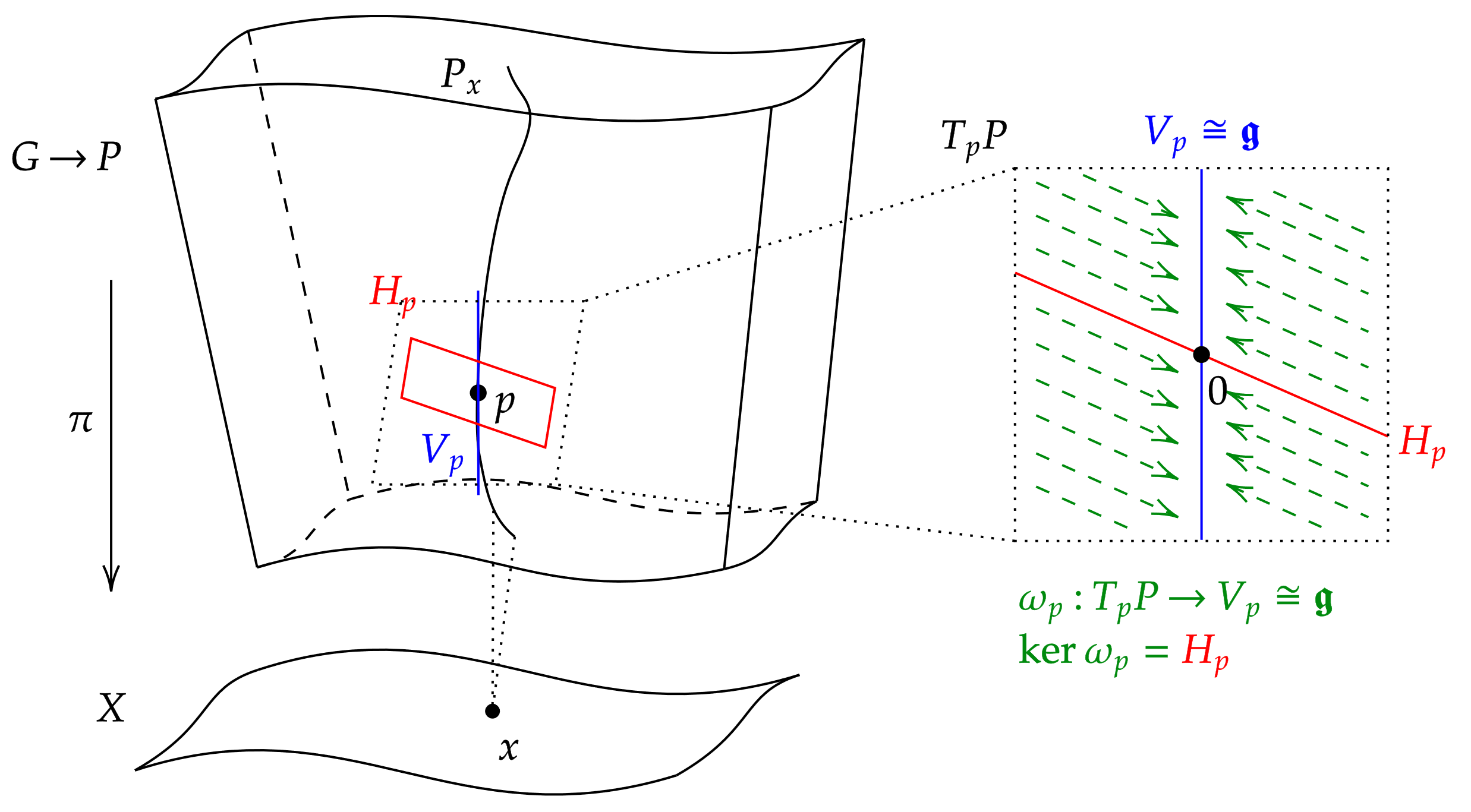
은 미분 다양체)에 대한 '''주 ''G''-접속'''은

G

의

\mathfrak{g}

리 대수 값을 갖는

P

위의 미분 1-형식

\omega

이며, 다음 두 가지 조건을 만족시킨다.

#

\omega

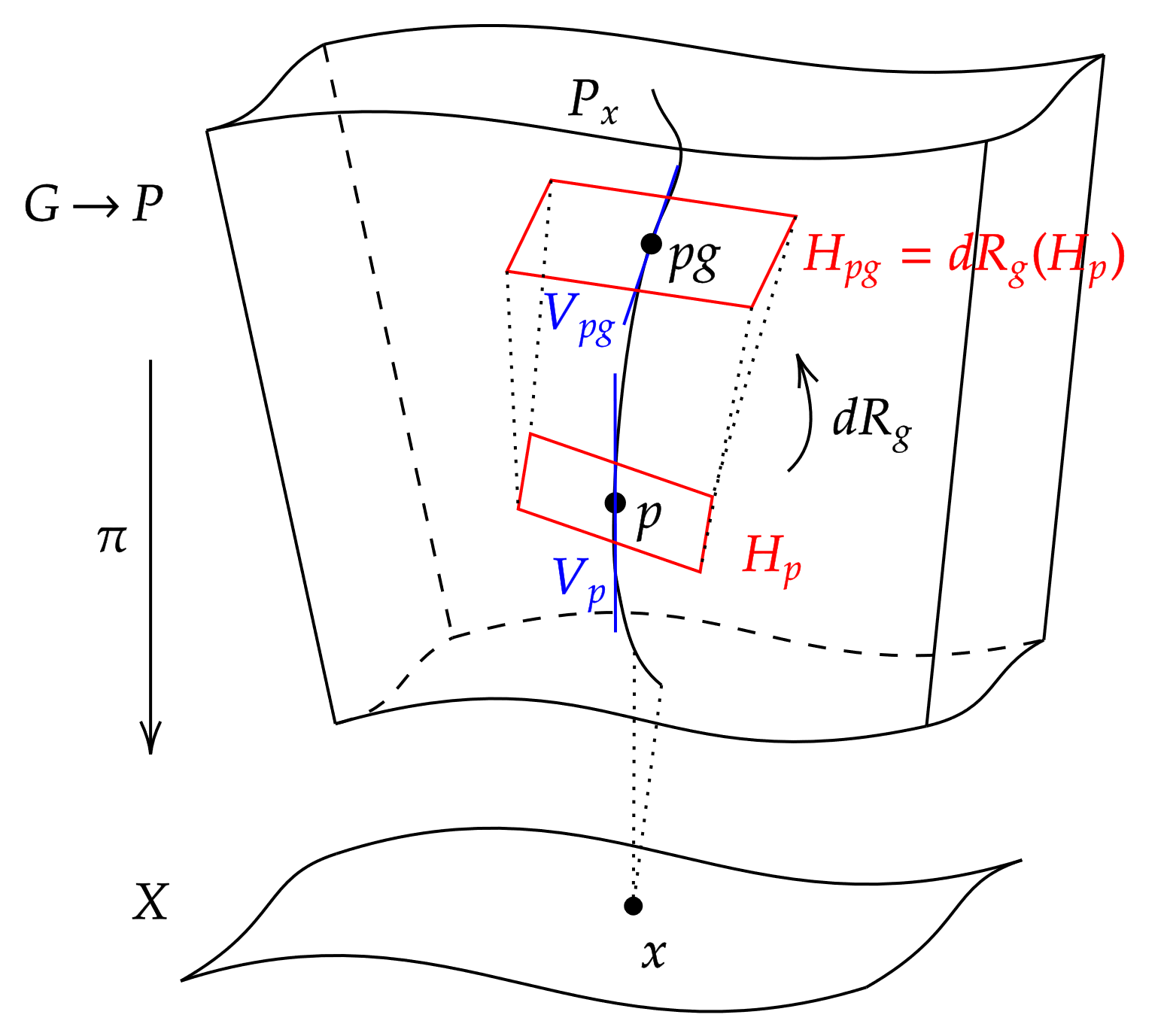
는 ''G''-등변성'''을 갖는다. 즉,

\hbox{Ad}_g(R_g^*\omega)=\omega

이다. 여기서

R_g

는

g

에 의한 오른쪽 곱셈이고,

\operatorname{Ad}_g

는

\mathfrak{g}

에 대한 딸림표현이다.

#

\omega

는 '''기본 벡터 필드'''의 '''리 대수 생성자'''를 '''재생'''한다. 즉,

\xi\in \mathfrak{g}

에 대해

X_\xi

가 ''P''에 대한 ''G'' 작용을 미분하여 ''ξ''와 연관된 벡터 필드이면,

\omega(X_\xi)=\xi

이다.

이때,

\omega

자체는 주접속의 '''연결 형식''' 또는 '''연결 1-형식'''이라고 불리기도 한다.

2. 2. 에레스만 접속을 통한 정의

주 ''G''-다발 미분 다양체

M

에서, $\pi : P \to M$가 있을 때,

P

에 대한 '''주'''

G

'''-연결'''은

G

의

\mathfrak g

리 대수 값의

P

에 대한 미분 1-형식으로,

G

'''-등변성'''이고

P

에 대한 '''기본 벡터 필드'''의 '''리 대수 생성자'''를 '''재생'''한다.

즉, 다음과 같은

\Omega^1(P,\mathfrak g)\cong C^\infty(P, T^*P\otimes\mathfrak g)

의 원소 ''ω''이다.

#

\hbox{Ad}_g(R_g^*\omega)=\omega

. 여기서

R_g

는

g

에 의한 오른쪽 곱셈을 나타내고,

\operatorname{Ad}_g

는

\mathfrak g

에 대한 수반 표현이다(명시적으로,

\operatorname{Ad}_gX = \frac{d}{dt}g\exp(tX)g^{-1}\bigl|_{t=0}

).

# 만약

\xi\in \mathfrak g

이고

X_\xi

가 ''P''에 대한 ''G'' 작용을 미분하여 ''ξ''와 연관된 벡터 필드이면,

\omega(X_\xi)=\xi

이다. (''P''에서 동일하게)

때로는 ''주

G

-연결''이라는 용어는 쌍

(P,\omega)

를 지칭하며,

\omega

자체는 주 연결의 '''연결 형식''' 또는 '''연결 1-형식'''이라고 불린다.

P

의 에레스만 접속

H\subseteq\mathrm TP

가 다음 조건을 만족시킨다면,

H

를 '''주접속'''이라고 한다.

:

H_{p\cdot g}=(\mathrm T(\cdot g))(H_p)\qquad\forall p\in P,\;g\in G

여기서

$(\cdot g)\colon\colon P\to P$ 는 $g$ 의 $P$ 위의 오른쪽 작용이다.
$\mathrm T(\cdot g)\colon\mathrm TP\to\mathrm TP$ 는 위 매끄러운 함수의 미분이다.

미분 형식을 통한 정의에 따른 주접속

\omega\in\Omega^1(P;\mathfrak{lie}(G))=\Gamma(\mathrm T^*P\otimes\mathfrak{lie}(G))

가 주어졌을 때, 이에 대응하는 에레스만 접속은 다음과 같다. 우선, 임의의

m\in M

에 대하여,

G

의 오른쪽 작용을 생성하는 벡터장의 족을

:

X\colon \mathfrak{lie}(G)\to\Gamma(\mathrm TP)

:

X\colon x\mapsto X_x

로 표기한다. 그러면, 위 작용이 정추이적 작용이므로,

X

의 상은

P

의 수직 벡터 다발

\mathrm VP=\ker(\mathrm T\pi)\subseteq\mathrm TP

과 같으며, 이는 벡터 다발의 표준적인 동형 사상

:

P\times\mathfrak{lie}(G)\to\mathrm VP

를 정의한다. (좌변은 올이

\mathfrak{lie}(G)

인 자명한 벡터 다발이다.) 따라서,

\omega

를

\mathrm T^*P\otimes\mathrm VP

의 단면으로 여길 수 있으며,

\omega

는 벡터 다발 사상

:

\omega\colon\mathrm TP\to\mathrm VP\subseteq\mathrm TP

를 정의한다. 이는 멱등 함수이며 (

\omega\circ\omega=\omega

), 따라서 그 핵으로 완전히 명시된다. 그 핵

\ker\omega\subseteq\mathrm TP

은 에레스만 접속이다.

주 주속

G

-접속

\omega

는 다음과 같은 방식으로

P

에 대한 에레스만 접속을 결정한다. 먼저

P

에 대한

G

작용을 생성하는 기본 벡터장은 올다발

V

에서

P\times\mathfrak g

로의 번들 동형 사상을 제공하며(

P

의 항등원을 덮는다), 여기서

V=\ker(d\pi)

는 접선 사상

{\mathrm d}\pi\colon TP\to TM

의 커널이며, 이는

P

의 수직 다발이라고 불린다. 결과적으로

\omega

는

V

에 대한 항등원인 번들 사상

v:TP\rightarrow V

를 고유하게 결정한다. 이러한 투영

v

는 커널에 의해 고유하게 결정되며, 커널은

TP

의 매끄러운 부분다발

H

( 수평 다발이라고 함)이며

TP=V\oplus H

가 된다. 이것이 에레스만 접속이다.

반대로,

P

에 대한 에레스만 접속

H\subset TP

(또는

v:TP\rightarrow V

)는

H_{pg}=\mathrm d(R_g)_p(H_{p})

라는 의미에서

G

-등변량일 때만 주

G

-접속

\omega

를 정의한다.

2. 3. 벡터 다발을 통한 정의

딸림표현의 연관 벡터 다발^[4]

:

\operatorname{ad}(P) = P \times_G \mathfrak{lie}(G)

을 생각하자. 또한,

G

는 접다발

TP

위에 오른쪽 군 작용을 가지며, 이에 따라 몫공간

TP/G

를 정의할 수 있다.

벡터장의 밂 $\pi_* \colon TP/G \twoheadrightarrow TM$ 는 매끄러운 올다발을 이룬다.
$TP/G \twoheadrightarrow M$ 은 매끄러운 벡터 다발을 이룬다.

올다발

TP/G\twoheadrightarrow TM

을 '''주접속 다발'''(bundle of principal connections^영어)이라고 한다.^[3]

이는 다음과 같은 표준적인

M

위의 매끄러운 벡터 다발들의 짧은 완전열을 이룬다.^[4]

:

0 \to \operatorname{ad}(P) \,\xrightarrow\iota\, \frac{TP}G \,\xrightarrow{\pi_*}\, TM \to 0

이 경우,

P

의 '''주접속'''은 위 짧은 완전열의 분할이다. 즉, 아벨 범주의 분할 보조정리에 따라, 다음과 같은 두 데이터가 서로 동치이며, 이는 주접속의 데이터와 같다.

$\iota\colon\operatorname{ad}(P) \to TP/G$ 의 왼쪽 역사상인 $M$ -매끄러운 벡터 다발 사상 $A \colon TP/G \to \operatorname{ad}(P)$
$\pi_* \colon TP/G \twoheadrightarrow TM$ 의 오른쪽 역사상인 $M$ -매끄러운 벡터 다발 사상 $A \colon TM \to TP/G$ ^[3]

짧은 완전열의 성질에 따라, 두 주접속의 차는 매끄러운 벡터 다발 사상

TM \to \operatorname{ad}(P)

를 정의하며, 이는 벡터 값 미분 형식

:

\Omega^1(M;\operatorname{ad}(P))

의 원소와 같다. 즉, 주접속의 모듈라이 공간은 이 실수 벡터 공간에 대한 아핀 공간이다.

2. 4. 국소 자명화를 통한 정의

주접속은 주다발의 국소 자명화에 따라, 각 좌표 조각 위에서 정의되는 리 대수 값 1차 미분 형식들의 모음으로 표현될 수 있으며, 이들은 게이지 변환에 의해 서로 연관된다.

\pi

를 자명화할 수 있게 충분히 섬세한

M

의 열린 덮개

(U_i)_{i\in I}

를 골랐다고 하자. 그렇다면,

P

의 주접속은 다음과 같은 데이터로 주어진다.

각 $i \in I$ 에 대하여, 리 대수 값 1차 미분 형식 $A_i \in \Omega^1(U_i; \mathfrak{lie}(G))$

이는 다음 조건을 만족시켜야 한다.

임의의 $i, j\in I$ 에 대하여, 만약 $U_i \cap U_j \ne 0$ 이라면, 어떤 매끄러운 함수 $g_{ij} \colon U_i \cap U_j \to G$ 에 대하여, 다음이 성립해야 한다.

:

A_j = \operatorname{Ad}(g_{ij})^{-1} A_i + g_{ij}^{-1} \mathrm dg_{ij}

여기서

$\mathfrak{lie}(G)$ 는 리 군에 대응되는 실수 리 대수이다.
$\operatorname{Ad} \colon G \to \operatorname{GL}(\mathfrak{lie}(G))$ 는 리 군의, 스스로의 리 대수 위의 딸림표현이다.

같은 열린 덮개

(U_i)_{i\in I}

위에 정의된 두 주접속

(A_i)_{i\in I}

,

(A'_i)_{i\in I}

에 대하여, 만약 어떤 매끄러운 함수들의 족

:

(g_i \colon U_i \to G)_{i\in I}

에 대하여

:

A'_i = \operatorname{Ad}(g_i)^{-1} A_i + g_i^{-1} \mathrm dg_i

라면,

A

와

A'

을 같은 주접속으로 간주한다.

이러한 정의는 이론물리학에서 자주 쓰이며, 물리학에서 위와 같은 동치 관계를 '''게이지 변환'''이라고 한다.

이 정의는 다른 정의들과 동치이다. 구체적으로, 주접속을

P

위에 정의된 1차 미분 형식

A \in \Omega^1(P;\mathfrak{lie}(G))

으로 정의하였다고 하자. 이 경우, 열린 덮개

(U_i)_{i\in I}

에 대한 국소 자명화는 각

i \in I

에 대한 매끄러운 단면

s_i \in \Gamma(U,P)

으로 주어진다. 이 경우,

:

A_i = s_i^*A \in \Omega^1(U_i;\mathfrak{lie}(G))

로 놓으면 국소 자명화를 통한 정의를 얻는다. 이 과정에서, 만약 사용한 자명화를

:

s'_i = s_ig_i

와 같이 바꾸면

:

A'_i = (s'_i)^*A = \operatorname{Ad}(g_i)^{-1} A_i + g_i^{-1} \mathrm dg_i

가 되어, 같은 주접속을 얻는다.

주 주다발 ''

P

''의 자명화 단면은 ''

M

''의 열린 부분 집합 ''

U

'' 위의 ''

P

''의 단면 ''s''로 주어진다. 그러면 주 접속의 당김 ''s''^*''ω''는

\mathfrak g

값을 갖는 ''

U

'' 위의 1-형식이다.

단면 ''s''가 부드러운 사상 ''g'':''M''→''G''에 의해 정의된 새로운 단면 (''sg'')(''x'') = ''s''(''x'')''g''(''x'')로 대체되면

(sg)^* \omega = \operatorname{Ad}(g)^{-1}s^* \omega + g^{-1} dg

가 된다. 주 접속은 이러한

\mathfrak g

값을 갖는 1-형식들의 집합에 의해 유일하게 결정되며, 이러한 1-형식들은 특히 오래된 문헌이나 물리학 관련 문헌에서 '''접속 형식''' 또는 '''접속 1-형식'''이라고도 불린다.^[1]

이 명제는 자명하지 않은 다발

E \to X

에 대해 열린 덮개

\mathcal{U} = \{U_a\}_{a \in I}

를 고려하고, 자명화

\{\phi_a\}_{a \in I}

와 변환 함수

\{g_{ab}\}_{a,b\in I}

를 사용하여 더욱 정교하게 다듬을 수 있다. 그러면

E

위의 접속과 다음 1-형식의 모음 사이에 일대일 대응이 존재한다.

$\{A_a \in \Omega_1(U_a,\mathfrak{g}) \}_{a \in I}$

이 형식은 교차점

U_{ab}

에서 다음 조건을 만족한다.

$A_b = Ad(g_{ab}^{-1})\circ A_a + g_{ab}^*\omega_0$

여기서

\omega_0

는

G

위의 마우러-카르탕 형식이며, 행렬 형태로

\omega_0 = g^{-1}dg

이다.^[2]

3. 성질

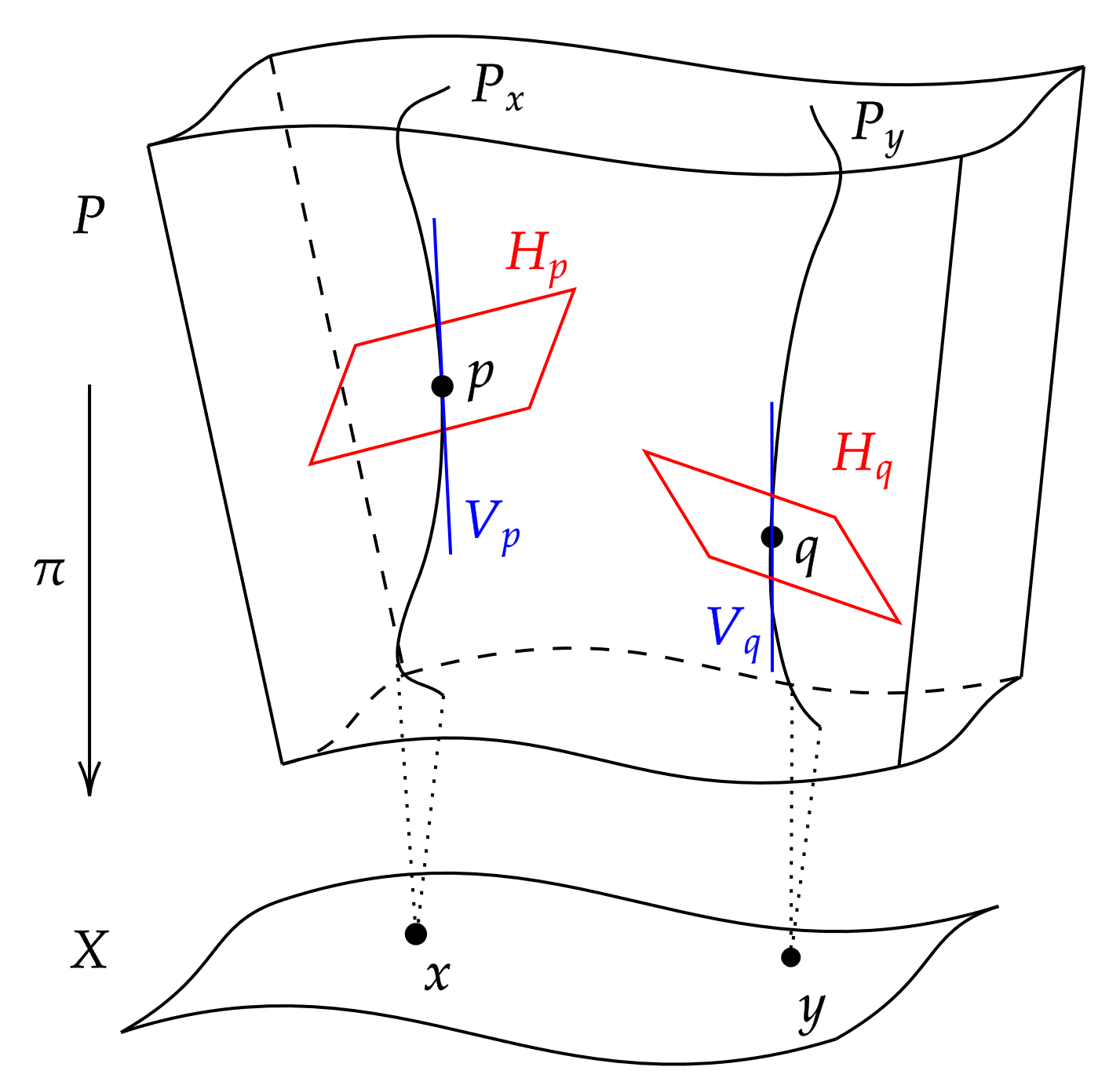
만약 ''ω''와 ''ω''′가 주 다발 ''P'' 위의 주 접속이라면, 그 차이 ''ω''′ − ''ω''^영어는 $\mathfrak g$ 값을 갖는 ''P'' 위의 1-형식이다. 이는 ''G''-등변(equivariant)일 뿐만 아니라, ''P''의 수직 다발 ''V''의 임의의 단면에 대해 0이 되는 의미에서 수평(horizontal)하다. 따라서 이는 기저(base)이며, 수반 다발

: $\mathfrak g_P:=P\times^G\mathfrak g.$

값을 갖는 ''M'' 위의 1-형식에 의해 결정된다.

반대로, 이러한 1-형식은 (당겨오기를 통해) ''P'' 위의 ''G''-등변 수평 1-형식을 정의하며, 주 ''G''-접속의 공간은 이 1-형식의 공간에 대한 아핀 공간이다.

3. 1. 곡률

주접속

\omega\in\Omega^1(P;\mathfrak{lie}(G))

의 '''곡률'''(curvature^영어)

\Omega \in \Omega^2(P;\mathfrak{lie}(G))

는 다음과 같다.

:

\Omega=d\omega+\frac12[\omega\wedge\omega]

여기서

[\cdot\wedge\cdot]

는 리 괄호와 외적을 결합한 연산으로,

[\alpha\otimes x\wedge\beta\otimes y]=(\alpha\wedge\beta)\otimes[x,y]

와 같이 정의한다.

곡률은 벡터 값 미분 형식

:

F \in \Omega^2(M;\operatorname{ad}(P))

를 정의하며,^[4] 이 데이터는 곡률의 개념과 동치이다.

곡률이 0인 주접속을 '''평탄 주접속'''이라고 한다.

주 주접속 *ω*의 곡률 형식은 다음과 같이 정의된

\mathfrak g

값을 갖는 2-형식 Ω이다.

:

\Omega=d\omega +\tfrac12 [\omega\wedge\omega].

이는 *G*에 대한 등변이며 수평이므로,

\mathfrak g_P

값을 갖는 *M* 위의 2-형식에 해당한다. 곡률을 이 양과 동일시하는 것을 때로는 "(카르탕의) 제2 구조 방정식"이라고 한다.^[2] 역사적으로 구조 방정식의 출현은 카르탕 접속의 개발에서 발견된다. 리 군의 맥락으로 옮겨지면, 구조 방정식은 마우러-카르탕 방정식으로 알려져 있다. 즉, 동일한 방정식이지만 다른 설정과 표기법을 사용한다.

연결

\omega

의 곡률 형식

\Omega = 0

일 때, 해당 연결을 '''평탄'''하다고 말한다. 평탄 연결을 갖는 주다발을 유용하게 특징지을 수 있는데, 즉 주

G

-다발

\pi: E \to X

가 평탄 연결을 가질 필요충분조건은, 모든 천이 함수가

$g_{ab}: U_a\cap U_b \to G$

상수인 열린 덮개

\{U_a\}_{a\in I}

와 사소화

\left\{ \phi_a \right\}_{a \in I}

가 존재하는 것이다. 이는 매끄러운 다양체 위에 평탄한 주

G

-다발을 구성하는 방법을 제공하기 때문에 유용하다. 즉, 열린 덮개를 취하고 상수 천이 함수를 사용하여 사소화를 정의하는 것이다.

3. 2. 게이지 변환

게이지 변환군은 다음과 같은 연관 다발

\operatorname{Ad}(P)

를 생각하여 정의할 수 있다.^[4]

:

\operatorname{Ad}(P)=P\times_G G

이는

G

의, 스스로 위의 켤레 작용

:

g\mapsto (h\mapsto ghg^{-1})

에 대한,

P

의 연관 다발이다.

\operatorname{Ad}(P)

의 매끄러운 단면들의 공간은 다음과 같은 매끄러운 함수의 공간으로 여겨질 수 있다.^[4]

:

\Gamma^\infty(M,\operatorname{Ad}(P)) \cong \{\phi\in\mathcal C^\infty(P,G)\colon \phi(p\cdot g)=g^{-1}\phi(p)g\} \cong\operatorname{Aut}(P)

\mathcal G=\Gamma^\infty(M,\operatorname{Ad}(P))

는 점별 곱셈을 통해 위상군을 이루며, 그 원소를 '''게이지 변환'''이라고 한다.

4. 주접속의 모듈러스 공간

$G$ -주다발 $P\twoheadrightarrow M$ 위의 주접속의 모듈라이 공간 $\mathcal A$ 는 다음 벡터 공간에 대한 아핀 공간이다.^[4]

: $\operatorname T_A\mathcal A \cong \Omega^1(M;\operatorname{ad}(P))$

여기서 $\operatorname{ad}(P) = P\times_G\mathfrak{lie}(G)$ 는 딸림표현에 대한 연관 벡터 다발이다.^[4]

게이지 변환군 $\mathcal G\cong\operatorname{Aut}(P)$ 는 $\mathcal A$ 위에 다음과 같이 자연스럽게 작용한다.

: $\phi\cdot A=\phi^*A \qquad(A\in\Omega^1(M;\operatorname{ad}(P)),\;\phi\in\operatorname{Aut}(P)\cong\mathcal G)$

만약 ''ω''와 ''ω''′가 주 다발 ''P'' 위의 주 접속이라면, 차이 ''ω''′ − ''ω''는 $\mathfrak g$ 값을 갖는 ''P'' 위의 1-형식이다. 이는 ''G''-등변이고, ''P''의 수직 다발 ''V''의 임의의 단면에 대해 0이 되는 의미에서 '''수평'''하다. 따라서 이는 '''기저'''이며, 수반 다발

: $\mathfrak g_P:=P\times^G\mathfrak g.$

값을 갖는 ''M'' 위의 1-형식에 의해 결정된다.

반대로, 이러한 1-형식은 (당겨오기를 통해) ''P'' 위의 ''G''-등변 수평 1-형식을 정의하며, 주 ''G''-접속의 공간은 이 1-형식의 공간에 대한 아핀 공간이다.

주 주다발 $G$ 다발 $\pi: E \to M$ 에 대해, $E$ 의 접속 집합은 벡터 공간 $\Omega^1(M,E_\mathfrak{g})$ 에 대한 아핀 공간^[1]이며, 여기서 $E_\mathfrak{g}$ 는 수반 벡터 다발이다. 즉, 임의의 두 접속 $\omega_0, \omega_1$ 에 대해 다음을 만족하는 형식 $A \in \Omega^1(M, E_\mathfrak{g})$ 이 존재한다.

> $\omega_0 = \omega_1 + A$

접속의 집합은 $\mathcal{A}(E)$ 로 표기하며, 문맥이 명확할 경우 단순히 $\mathcal{A}$ 로 표기한다.

5. 예

자명한 주다발 $P = M \times G$ 의 경우, 표준적인 자명한 주접속 $A = 0$ 이 존재한다. 이때 주접속의 모듈러스 공간은 리 대수 값 미분 형식의 실수 벡터 공간 $\Omega^1(M;\mathfrak{lie}(G))$ 를 이루며, 주접속은 단순히 리 대수 값 미분 형식으로 간주할 수 있다.^[1]

자명한 주 $G$ -다발 $\pi:E \to X$ ( $E = G\times X$ )에서 표준적인 접속^[1]은 마우러-카르탕 접속 $\omega_{MC} \in \Omega^1(E,\mathfrak{g})$ 이며, 점 $(g,x) \in G\times X$ 에서 다음과 같이 정의된다.

: $(\omega_{MC})_{(g,x)} = (L_{g^{-1}}\circ \pi_1)_*$ ( $x \in X, g \in G$ )

이는 다음 합성 함수로 표현된다.

: $T_{(g,x)}E \xrightarrow{\pi_{1*}} T_gG \xrightarrow{(L_{g^{-1}})_*} T_eG = \mathfrak{g}$

여기서 $\omega_0 = (L_{g^{-1}})_*: T_gG \to T_eG = \mathfrak{g}$ 는 리 군 $G$ 상의 마우러-카르탕 형식이며, $\omega_{MC} = \pi_1^*\omega_0$ 이다.

사소한 주 $G$ -다발 $\pi:E \to X$ 에서 항등 단면 $i: X \to G\times X$ ( $i(x) = (e,x)$ )는 $E$ 의 접속과 $X$ 위의 $\mathfrak{g}$ -값 1-형식 사이에 일대일 대응을 정의한다.

: $i^*:\Omega^1(E,\mathfrak{g}) \to \Omega^1(X,\mathfrak{g})$

$X$ 위의 $\mathfrak{g}$ -값 1-형식 $A$ 에 대해, 다음 조건을 만족하는 유일한 1-형식 $\tilde{A}$ 가 존재한다.

# $\tilde{A}(X) = 0$ ( $X \in T_xE$ 는 수직 벡터)

# 모든 $g \in G$ 에 대해 $R_g^*\tilde{A} = \text{Ad}(g^{-1}) \circ \tilde{A}$

이 1-형식과 마우러-카르탕 접속의 합 $\omega_{MC} + \tilde{A}$ 을 통해 $E$ 의 접속을 구성할 수 있다.

한원소 공간 $M = \{\bullet\}$ 인 경우,

주다발 $P\twoheadrightarrow\{\bullet\}$ 은 $G$ -torsor^영어(토서, 군에서 원점을 망각한 구조)이다.
$\operatorname{ad}(P) = \mathfrak{lie}(G)$ 이다.
$\operatorname{TP}/G = \operatorname{Vect}(P)^G$ 는 $P$ 위에서 $G$ -오른쪽 군 작용에 대해 불변인 벡터장들의 실수 벡터 공간이며, $\mathfrak{lie}(G)$ 와 표준적으로 대응한다. (리 대수의 원소는 군 작용에 대한 불변 벡터장을 정의하며, 이는 전단사 함수를 이룬다.)

따라서 이 경우 주접속은 유일하게 존재하며, 주접속 자체는 게이지 불변이다.

P

위의 1차 미분 형식으로서, 이는 마우러-카르탕 형식이다.

5. 1. 자명한 주다발

만약

P = M \times G

가 자명한 주다발일 경우,

\operatorname{ad}(P) = M\times\mathfrak{lie}(G)

는 자명한 벡터 다발이며, 표준적인 자명한 주접속

A = 0

이 존재한다. 따라서, 이 경우 주접속의 모듈러스 공간은 리 대수 값 미분 형식의 실수 벡터 공간

\Omega^1(M;\mathfrak{lie}(G))

를 이루며, 주접속을 단순히 리 대수 값 미분 형식으로 간주할 수 있다.^[1]

자명한 주

G

-다발

\pi:E \to X

(

E = G\times X

)에 대해, 표준적인 접속^[1]은 마우러-카르탕 접속(Maurer-Cartan connection)

\omega_{MC} \in \Omega^1(E,\mathfrak{g})

이며, 다음과 같이 정의된다. 점

(g,x) \in G\times X

에 대해,

$(\omega_{MC})_{(g,x)} = (L_{g^{-1}}\circ \pi_1)_*$ for $x \in X, g \in G$

이는 다음의 합성이다.

$T_{(g,x)}E \xrightarrow{\pi_{1*}} T_gG \xrightarrow{(L_{g^{-1}})_*} T_eG = \mathfrak{g}$

여기서,

$\omega_0 = (L_{g^{-1}})_*: T_gG \to T_eG = \mathfrak{g}$

는 리 군

G

상의 마우러-카르탕 형식이며

\omega_{MC} = \pi_1^*\omega_0

이다.

주어진 사소한 주

G

-다발

\pi:E \to X

에 대해, 항등 단면

i: X \to G\times X

(

i(x) = (e,x)

)는 연결

E

와

X

위의

\mathfrak{g}

-값 1-형식 사이의 일대일 대응을 정의한다.

$i^*:\Omega^1(E,\mathfrak{g}) \to \Omega^1(X,\mathfrak{g})$

^[1]

X

위의

\mathfrak{g}

-값 1-형식

A

에 대해, 다음을 만족하는 고유한 1-형식

\tilde{A}

가 존재한다.

#

\tilde{A}(X) = 0

(

X \in T_xE

는 수직 벡터)

# 모든

g \in G

에 대해

R_g^*\tilde{A} = \text{Ad}(g^{-1}) \circ \tilde{A}

이 1-형식을 통해 다음 합을 취하여

E

의 연결을 구성할 수 있다.

$\omega_{MC} + \tilde{A}$

이는

E

에 대한 실제 연결을 제공한다.

5. 2. 한원소 공간 위의 주접속

만약

M = \{\bullet\}

이 한원소 공간이라고 하자. 이 경우,

주다발 $P\twoheadrightarrow\{\bullet\}$ 은 $G$ -토서(torsor^영어, 군에서 원점을 망각한 구조)이다.
표준적으로 $\operatorname{ad}(P) = \mathfrak{lie}(G)$ 이다.
$\operatorname{TP}/G = \operatorname{Vect}(P)^G$ 는 $P$ 위의, $G$ -오른쪽 군 작용에 대하여 불변인 벡터장들의 실수 벡터 공간이며, 이 역시 $\mathfrak{lie}(G)$ 와 표준적으로 대응한다. (리 대수의 원소는 이에 대한 군 작용으로서 불변 벡터장을 정의하며, 이는 전단사 함수를 이룬다.)

따라서, 이 경우 주접속이 유일하게 존재하며, 주접속 자체가 게이지 불변이다.

P

위의 1차 미분 형식으로서, 이는 마우러-카르탕 형식이다.

6. 응용

주접속은 다양한 분야에서 활용된다. 특히, 주접속의 개념은 게이지 이론을 기술하는 데 필수적이며, 현대 이론 물리학, 특히 양자장론에서 게이지 대칭과 함께 근본적인 상호작용을 기술하는 데 핵심적인 역할을 한다.

임의의 선형 표현 ''W''에 대해 ''M'' 위에 $P\times^G W$ 라는 연관 벡터 다발이 존재하며, 주접속은 이러한 벡터 다발에 대한 공변 미분을 유도한다. 이 공변 미분은 ''M'' 위의 $P\times^G W$ 단면 공간이 ''P'' 위의 ''G''-등변 ''W'' 값 함수 공간과 동형이라는 사실을 사용하여 정의할 수 있다. 더 일반적으로, $P\times^G W$ 값을 갖는 ''k''-형식의 공간은 ''P'' 위의 ''G''-등변이고 수평적인 ''W'' 값 ''k''-형식의 공간과 동일시된다. ''α''가 그러한 ''k''-형식인 경우, 그 외미분 d''α''는 ''G''-등변이지만 더 이상 수평적이지 않다. 그러나 d''α''+''ω''Λ''α''의 조합은 수평적이다. 이것은 ''M'' 위의 $P\times^G W$ 값 ''k''-형식에서 ''M'' 위의 $P\times^G W$ 값 (''k''+1)-형식으로의 외공변 미분 d^''ω''을 정의한다. 특히, ''k''=0일 때, $P\times^G W$ 에 대한 공변 미분을 얻는다.

만약 주다발 ''P''가 틀다발이거나 (더 일반적으로) 땜납 형식을 가지면, 접속은 아핀 접속의 예시가 되며, 곡률은 유일한 불변량이 아니다. 왜냐하면 주어지는 땜납 형식 ''θ''의 추가적인 구조, 즉 ''P'' 위의 등변 '''R'''^''n''-값을 가지는 1-형식을 고려해야 하기 때문이다. 특히, ''P'' 위의 꼬임 형식은 다음과 같이 정의되는 '''R'''^''n''-값을 가지는 2-형식 Θ이다.

: $\Theta=\mathrm d\theta+\omega\wedge\theta.$

Θ는 ''G''-등변이고 수평이므로, ''M'' 위의 접선 값을 가지는 2-형식으로 내려가며, 이를 ''꼬임''이라고 부른다. 이 방정식은 때때로 ''(카르탕의) 첫 번째 구조 방정식''이라고 불린다.

참조

_[1] 웹사이트 Fibre Bundles and Chern-Weil Theory http://www.johno.dk/[...] 2003-08
_[2] 논문 Gravitation, gauge theories and differential geometry https://www.research[...] 1980
_[3] 저널 Theory of connections 1957
_[4] 저널 The Yang-Mills Equations over Riemann Surfaces 1983-03-17

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com