맨위로가기

역함수 정리

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

역함수 정리는 미적분학의 중요한 정리로, 함수가 특정 조건을 만족할 경우 국소적으로 역함수를 갖는다는 것을 보여준다. 구체적으로, 양의 정수 k와 열린 근방, 그리고 C^k 함수가 주어졌을 때, 함수의 야코비 행렬식이 0이 아니면, 함수는 국소적으로 C^k 미분동형사상이다. 즉, 함수의 역함수가 존재하고, 그 역함수 역시 C^k 함수이다.

이 정리는 일변수 및 다변수 함수에 모두 적용되며, 일변수 함수의 경우, 함수가 특정 점에서 0이 아닌 도함수를 갖는 연속 미분 가능 함수이면, 그 점의 근방에서 단사 함수이고, 역함수는 그 점 근처에서 연속 미분 가능하며, 역함수의 도함수는 원래 함수의 도함수의 역수와 같다. 다변수 함수의 경우, 연속 미분 가능 함수의 도함수가 가역적이면, 그 함수의 근방에서 전단사 함수가 되며, 역함수 역시 연속 미분 가능하고, 역함수의 도함수는 원래 도함수의 역행렬과 같다.

역함수 정리는 음함수 정리, 미분 기하학에서의 정칙값의 역상이 다양체임을 보이는 데 사용되며, 바나흐 공간 및 바나흐 다양체로 일반화될 수 있다. 또한, 상수 랭크 정리, 복소해석학의 홀로모픽 사상, 그리고 다항 함수에도 적용될 수 있다. 그러나 함수의 도함수가 연속적이라는 가정을 없애면, 함수는 가역적이지 않을 수도 있다.

더 읽어볼만한 페이지

  • 역함수 - 분위수함수
    분위수 함수는 주어진 누적 분포 함수 값 p를 초과하는 값 중 최소값을 반환하며, 통계적 응용, 몬테카를로 방법, 전산 금융 등 다양한 분야에서 활용된다.
  • 역함수 - 분지점
    분지점은 복소해석학과 대수 기하학에서 함수의 국소적 성질이 변하는 지점을 의미하며, 리만 곡면 사이의 정칙 함수에서 함수가 국소적으로 피복 공간이 되지 못하는 점으로 정의되고, 다가 함수의 역함수를 정의하기 위해 분지 절단 과정을 거치며, 함수의 다중값성을 이해하고 분석적 성질을 파악하는 데 중요한 도구로 활용된다.
  • 미적분학 정리 - 연쇄 법칙
    연쇄 법칙은 둘 이상의 미분 가능한 함수 합성의 미분법을 제공하며, z의 y에 대한 순간적인 변화율과 y의 x에 대한 순간적인 변화율을 곱하여 z의 x에 대한 순간적인 변화율을 계산하는 직관적인 아이디어를 바탕으로 실변수 함수, 다변수 함수 등 다양한 경우에 적용된다.
  • 미적분학 정리 - 미적분학의 기본 정리
    미적분학의 기본 정리는 미분과 적분 사이의 관계를 설명하는 미적분학의 핵심 정리로서, 제1 기본 정리와 제2 기본 정리로 구성되며, 17세기에 발전되어 르베그 적분 등으로 일반화된다.
역함수 정리
개요
분야수학, 미적분학
하위 분야실해석학, 복소해석학
설명
내용어떤 함수가 주어진 점에서 국소적으로 전단사이고, 그 점에서 도함수가 0이 아니면, 그 점 근방에서 역함수가 존재하고 미분 가능하다는 정리이다.
관련 개념전단사 함수, 미분 가능 함수, 도함수
형식적 표현
단변수 함수실수 값 함수 f가 점 a에서 미분 가능하고 f'(a) ≠ 0이면, a를 포함하는 열린 구간 I에서 f는 전단사이고, 역함수 f⁻¹: f(I) → I는 f(a)에서 미분 가능하다.
다변수 함수F: U → V가 유클리드 공간 사이의 C¹ 함수이고, 점 p에서 F의 야코비 행렬이 가역 행렬이면, p를 포함하는 열린 집합 S에서 F는 전단사이고, 역함수 F⁻¹: F(S) → S는 F(p)에서 미분 가능하다.
응용
활용역함수의 도함수를 구하는 데 사용된다.
음함수 정리를 증명하는 데 사용된다.
미분기하학에서 좌표 변환을 다루는 데 사용된다.
관련 정리
연관된 정리음함수 정리

2. 정의

양의 정수 k 및 열린 근방 \mathbf a\in U\subseteq\mathbb R^n 및 \mathcal C^k 함수 \mathbf f\colon U\to\mathbb R^n가 다음을 만족시킨다고 하자.

:\det\mathrm D\mathbf f(\mathbf a)\ne 0

여기서 좌변은 \mathbf f의 \mathbf a에서의 야코비 행렬식이다. 그렇다면, \mathbf f는 \mathbf a에서 국소 \mathcal C^k 미분동형사상이다. 즉, 다음을 만족시키는 열린 근방 \mathbf a\in V\subseteq U가 존재한다.


  • \mathbf f(V)는 열린집합이다.
  • \mathbf f|_V는 단사 함수이다.
  • \mathbf g\colon\mathbf f(V)\to\mathbb R^n, \mathbf f(\mathbf x)\mapsto\mathbf x는 \mathcal C^k 함수이다.

이를 '''역함수 정리'''라고 한다.[30]

단일 변수의 함수에 대해, 정리는 f가 점 a에서 0이 아닌 도함수를 가진 연속 미분 가능 함수이면, f는 a의 근방에서 단사 함수(또는 상으로의 전사 함수)이고, 역함수는 b=f(a) 근처에서 연속 미분 가능하며, b에서의 역함수의 도함수는 a에서의 f의 도함수의 역수와 같다고 말한다.

:\bigl(f^{-1}\bigr)'(b) = \frac{1}{f'(a)} = \frac{1}{f'(f^{-1}(b))}.

함수 f가 f'(a) = 0인 경우에도 점 a 근처에서 단사 함수일 수 있다. 예시는 f(x) = (x - a)^3이다. 사실, 그러한 함수에 대해 역함수는 b = f(a)에서 미분 가능할 수 없는데, 만약 f^{-1}이 b에서 미분 가능하다면, 연쇄 법칙에 의해 1 = (f^{-1} \circ f)'(a) = (f^{-1})'(b)f'(a)가 되어 f'(a) \ne 0이 되기 때문이다.

둘 이상의 변수의 함수에 대해, 정리는 f가 \mathbb{R}^n의 열린 부분 집합 A에서 \R^n으로의 연속 미분 가능 함수이고, 점 a에서 도함수 f'(a)가 가역적(즉, a에서의 f의 야코비 행렬의 행렬식이 0이 아님)이면, A 내의 a의 근방 U와 b = f(a)의 근방 V가 존재하여 f(U) \subset V이고 f : U \to V가 전단사 함수라고 말한다.[1] f=(f_1,\ldots,f_n)이라고 쓰면, 이는 n개의 방정식 y_i = f_i(x_1, \dots, x_n) 시스템이 x \in U, y \in V일 때 x_1, \dots, x_n에 대한 유일한 해를 갖는다는 의미이다. 정리가 f'가 가역적일 때 f가 상으로의 전단사 함수라고 말하는 것이 아니라 f'가 가역적일 때 국소적으로 전단사 함수라고 말한다는 점에 유의해야 한다.

또한, 정리는 역함수 f^{-1} : V \to U가 연속 미분 가능하고, b=f(a)에서의 도함수는 f'(a)의 역사상, 즉,

:(f^{-1})'(b) = f'(a)^{-1}.

다시 말해, Jf^{-1}(b), Jf(a)가 (f^{-1})'(b), f'(a)를 나타내는 야코비 행렬이라면, 이는 다음을 의미한다.

:Jf^{-1}(b) = Jf(a)^{-1}.

정리의 어려운 부분은 f^{-1}의 존재성과 미분 가능성이다. 이것을 가정하면, 역도함수 공식은 f^{-1}\circ f = I에 적용된 연쇄 법칙으로부터 나온다. 역을 취하는 것은 무한히 미분 가능하기 때문에, 역함수의 도함수에 대한 공식은 f가 k번 연속 미분 가능하고, 점 a에서 가역적 도함수를 가지면, 역함수 또한 k번 연속 미분 가능하다는 것을 보여준다. 여기서 k는 양의 정수 또는 \infty이다.

역함수 정리에는 두 가지 변형이 있다.[1] 연속 미분 가능한 사상 f : U \to \mathbb{R}^m이 주어지면, 첫 번째는 다음과 같다.

  • 도함수 f'(a)가 전사 함수(즉, 이를 나타내는 야코비 행렬의 랭크가 m)이면, b = f(a)의 근방 V에서 f \circ g = I인 연속 미분 가능 함수 g가 존재한다.

두 번째는 다음과 같다.

  • 도함수 f'(a)가 단사 함수이면, b = f(a)의 근방 V에서 g \circ f = I인 연속 미분 가능 함수 g가 존재한다.


첫 번째 경우(f'(a)가 전사 함수일 때), 점 b = f(a)는 정칙값이라고 한다. m = \dim \ker(f'(a)) + \dim \operatorname{im}(f'(a))이므로, 첫 번째 경우는 b = f(a)가 임계점 a의 상에 있지 않다는 것과 같다(임계점은 f'(a)의 커널이 0이 아닌 점이다). 첫 번째 경우의 진술은 침몰 정리의 특수한 경우이다.

이러한 변형은 역함수 정리의 재진술이다. 실제로, f'(a)가 전사 함수인 첫 번째 경우에, f'(a) \circ T = I인 (단사) 선형 사상 T를 찾을 수 있다. h(x) = a + Tx를 정의하면 다음을 얻는다.

:(f \circ h)'(0) = f'(a) \circ T = I.

따라서, 역함수 정리에 의해, f \circ h는 0 근처에서 역함수를 가진다. 즉, f \circ h \circ (f \circ h)^{-1} = I는 b 근처에 있다. 두 번째 경우(f'(a)가 단사 함수)는 유사한 방식으로 볼 수 있다.

일변수 함수에 대한 역함수 정리는 다음과 같다.

: ''C''1급 함수 ''f''의 점 ''a''에서의 미분 계수가 0이 아닐 때, ''f''는 ''a''의 근방에서 가역이 되며, 이 역함수 ''f''−1도 또한 ''C''1 급이 된다. 이 때 ''f''−1는 다음 식을 만족한다.

:\((1)\qquad \left( f^{-1} \right)' \Bigl( f(a) \Bigr) = \frac{1}{ f'(a) }\)

다변수 함수에 대한 역함수 정리는 다음과 같다.

: ''U'' ⊂ '''R'''''n''를 열린 집합, ''F'' : ''U'' → '''R'''''n''를 ''C''1급 함수라고 할 때, ''F''의 점 ''p'' ∈ ''U''에서의 야코비 행렬 ''JF''(''p'')가 정칙일 때, ''F''는 ''p''의 근방에서 가역이 되며, 이 역함수 ''F''−1도 또한 ''C''1급이 된다.

: 이 때 ''F''−1는 다음 식을 만족한다. 여기서 [A]^{-1}는 ''A''의 역행렬, J_F(p)는 ''F''의 점 ''p''에서의 야코비 행렬이다.

:\((2)\qquad J_{F^{-1}} \Bigl( F(p) \Bigr) = \Bigl[ J_{F}(p) \Bigr]^{-1}

식(2)는 다음 연쇄 법칙의 식으로부터 유도할 수도 있다. 여기서 ''G'', ''H''는 각각 ''H''(''p''), ''p''에서 전미분을 갖는 함수이다.

:\((3)\qquad J_{G \circ H} (p) = J_G \Bigl( H(p) \Bigr) \cdot J_H(p)

식(3)의 ''G'', ''H''를 각각 ''F''−1, ''F''로 놓으면, G \circ H가 항등 사상이 되므로 그 야코비 행렬(좌변) J_{G \circ H}(p)는 단위 행렬이 된다. 이것을 J_{F^{-1}} \Bigl( F(p) \Bigr)에 대해 풀면 식(2)가 유도된다. 여기서, 역함수 정리가 ''p''에서의 ''F''−1의 전미분의 존재를 보이는 반면, 연쇄 법칙은 ''H''(= ''F'')의 전미분의 존재를 가정하고 있다. 역함수 ''F''−1가 존재한다는 것은, ''x'', ''y''를 각각 ''p'', ''F''(''p'')의 충분히 작은 근방이라고 할 때 ''n''개의 연립 방정식

:\((4)\qquad \begin{cases}

y_1 &= F_1( x_1, \cdots, x_n ) \\

&\,\vdots \\

y_n &= F_n( x_1, \cdots, x_n )

\end{cases}

의 해 ''x''1, …, ''x''n''이 ''y''1, …, ''y''n''에 의해 기술될 수 있는 것과 같다.

2. 1. 일변수 함수의 경우

열린구간 \(a \in I \subseteq \mathbb{R}\) 및 \(\mathcal{C}^k\) 함수 \(f \colon I \to \mathbb{R}\)가 \(f'(a) \ne 0\)를 만족하면, \(f\)는 \(a\)에서 국소 \(\mathcal{C}^k\) 미분동형사상이다. 즉, 다음을 만족시키는 열린구간 \(a \in J \subseteq I\)가 존재한다.

  • \(f(J)\)는 열린구간이다.
  • \(f|_J\)는 단사 함수이다.
  • \(g \colon f(J) \to \mathbb{R}\), \(f(x) \mapsto x\)는 \(\mathcal{C}^k\) 함수이다.


\(D \subseteq \mathbb{R}\)가 열린 집합이고, \(x_0 \in D\), \(f: D \to \mathbb{R}\)가 \(D\)에서 정의된 연속 미분 가능한 함수이며, \(f'(x_0) \ne 0\)이라고 가정하자. 그러면 \(f\)가 \(I\)를 열린 구간 \(J = f(I)\) 위로 전단사로 사상하고, 역함수 \(f^{-1} : J \to I\)가 연속 미분 가능하며, 모든 \(y \in J\)에 대해, \(x \in I\)가 \(f(x) = y\)를 만족하면, \((f^{-1})'(y) = \dfrac{1}{f'(x)}\)를 만족하는 열린 구간 \(I\)가 존재한다.

일반성을 잃지 않고 \(f'(x_0) > 0\)라고 가정할 수 있다. \(D\)가 열린 집합이고 \(f'\)가 \(x_0\)에서 연속이므로, \((x_0 - r, x_0 + r) \subseteq D\)이고 다음을 만족하는 \(r > 0\)가 존재한다.

\(|f'(x) - f'(x_0)| < \dfrac{f'(x_0)}{2} \qquad \text{for all } |x - x_0| < r.\)

특히,

\(f'(x) > \dfrac{f'(x_0)}{2} >0 \qquad \text{for all } |x - x_0| < r.\)

이것은 \(f\)가 모든 \(|x - x_0| < r\)에 대해 단조 증가함을 보여준다. \(\delta > 0\)를 \(\delta < r\)을 만족하도록 하면, \([x - \delta, x + \delta] \subseteq (x_0 - r, x_0 + r)\)이다. 중간값 정리에 의해, \(f\)가 구간 \([x - \delta, x + \delta]\)를 \([f(x - \delta), f(x + \delta)]\) 위로 전단사로 사상함을 알 수 있다. \(I = (x-\delta, x+\delta)\) 및 \(J = (f(x - \delta),f(x + \delta))\)라고 하면, \(f: I \to J\)는 전단사이고 역함수 \(f^{-1}: J \to I\)가 존재한다. \(f^{-1}: J \to I\)가 미분 가능하다는 사실은 \(f\)의 미분 가능성에서 따른다.

일변수 함수에 대한 역함수 정리는 다음과 같다.

''C''1급 함수 ''f''의 점 ''a''에서의 미분 계수가 0이 아닐 때, ''f''는 ''a''의 근방에서 가역이 되며, 이 역함수 ''f''−1도 또한 ''C''1 급이 된다. 이 때 ''f''−1는 다음 식을 만족한다.

:\((1)\qquad \left( f^{-1} \right)' \Bigl( f(a) \Bigr) = \frac{1}{ f'(a) }\)

2. 2. 다변수 함수의 경우

'''R'''''n''의 열린 집합 ''U''에 대하여, ''C''1급 함수 ''F'' : ''U'' → '''R'''''n''가 있을 때, 점 ''p'' ∈ ''U''에서 ''F''의 야코비 행렬 ''JF''(''p'')가 정칙행렬이면, ''F''는 ''p''의 근방에서 가역이 되며, 그 역함수 ''F''-1 역시 ''C''1급이 된다.

이 때, ''F''-1는 다음 식을 만족한다. 여기서 [''A'']-1는 ''A''의 역행렬, J_F(p)는 ''F''의 점 ''p''에서의 야코비 행렬이다.

:(2)\qquad J_{F^{-1}} \Bigl( F(p) \Bigr) = \Bigl[ J_{F}(p) \Bigr]^{-1}

식 (2)는 연쇄 법칙을 통해 유도할 수 있다. ''G'', ''H''가 각각 ''H''(''p''), ''p''에서 전미분을 갖는 함수라면, 다음 식이 성립한다.

:(3)\qquad J_{G \circ H} (p) = J_G \Bigl( H(p) \Bigr) \cdot J_H(p)

식 (3)에서 ''G'', ''H''를 각각 ''F''-1, ''F''로 놓으면, G \circ H는 항등 사상이 되므로 그 야코비 행렬(좌변) J_{G \circ H}(p)는 단위 행렬이 된다. 이를 J_{F^{-1}} \Bigl( F(p) \Bigr)에 대해 풀면 식 (2)가 유도된다.

역함수 ''F''-1가 존재한다는 것은, ''x'', ''y''를 각각 ''p'', ''F''(''p'')의 충분히 작은 근방이라고 할 때, ''n''개의 연립 방정식

:(4)\qquad \begin{cases}

y_1 &= F_1( x_1, \cdots, x_n ) \\

&\,\vdots \\

y_n &= F_n( x_1, \cdots, x_n )

\end{cases}

의 해 ''x''1, …, ''x''n''이 ''y''1, …, ''y''n''에 의해 기술될 수 있는 것과 같다.

3. 증명

축약 사상(바나흐 고정점 정리)을 이용한 증명은 앙리 카르탕, 장 디외도네, 세르주 랭, 로제 고드망 및 라르스 횸란데르의 책에서 찾을 수 있다.[1][7] T. Tao에 따르면,[8] 축약 사상 정리의 결과를 사용하여 증명할 수 있다.

임의의 \mathbf y\in\mathbb R^n에 대하여, 함수 \mathbf F_{\mathbf y}\colon U\to\mathbb R^n를 다음과 같이 정의한다.

:\mathbf F_{\mathbf y}(\mathbf x)=\mathbf x+(\mathrm D\mathbf f(\mathbf a))^{-1}(\mathbf y-\mathbf f(\mathbf x))

\qquad\forall\mathbf x\in U

그러면 다음이 성립한다.

:\mathrm D\mathbf F_{\mathbf y}(\mathbf x)=(\mathrm D\mathbf f(\mathbf a))^{-1}(\mathrm D\mathbf f(\mathbf a)-\mathrm D\mathbf f(\mathbf x))

\qquad\forall\mathbf x\in U,\;\mathbf y\in\mathbb R^n

\mathrm D\mathbf f가 연속 함수이므로, 다음을 만족시키는 열린 근방 \mathbf a\in V\subseteq U가 존재한다.

:\Vert\mathrm D\mathbf f(\mathbf a)-\mathrm D\mathbf f(\mathbf x)\Vert<\frac 1{2\Vert\mathrm D\mathbf f(\mathbf a))^{-1}\Vert}

즉, 다음이 성립한다.

:\Vert\mathrm D\mathbf F_{\mathbf y}(\mathbf x)\Vert<\frac 12

\qquad\forall\mathbf x\in V,\;\mathbf y\in\mathbb R^n

이는 다음을 의미한다.

:\Vert\mathbf F_{\mathbf y}(\mathbf x)-\mathbf F_{\mathbf y}(\mathbf x')\Vert\le\frac 12\Vert\mathbf x-\mathbf x'\Vert

\qquad\forall\mathbf x,\mathbf x'\in V,\;\mathbf y\in\mathbb R^n

\mathbf f|_V가 단사 함수임을 보이기 위해, \mathbf x,\mathbf x'\in V가 \mathbf f(\mathbf x)=\mathbf f(\mathbf x')를 만족한다고 가정하면, \mathbf x,\mathbf x'는 모두 \mathbf F_{\mathbf f(\mathbf x)}의 고정점이다. 즉, \mathbf F_{\mathbf f(\mathbf x)}(\mathbf x)=\mathbf x이며 \mathbf F_{\mathbf f(\mathbf x)}(\mathbf x')=\mathbf x'이다. 이를 위에 대입하면, \mathbf x=\mathbf x'를 얻는다. 따라서 \mathbf f|_V는 단사 함수이다.

\mathbf f(V)가 열린집합임을 보이기 위해, 임의의 \mathbf x'\in V에 대하여, \operatorname B(\mathbf f(\mathbf x'),\epsilon)\subseteq\mathbf f(V)인 \epsilon>0을 찾는다. 이를 위해 임의의 \mathbf y\in\operatorname B(\mathbf f(\mathbf x'),\epsilon)에 대하여, \mathbf F_{\mathbf y}가 V에서 고정점을 가지는 것을 보인다. \delta>0가 \bar\operatorname B(\mathbf x',\delta)\subseteq V를 만족시킨다고 하면, 임의의 \mathbf y\in\operatorname B(\mathbf f(\mathbf x'),\epsilon)에 대하여 \mathbf F_\mathbf y(\operatorname B(\mathbf x',\delta))\subseteq \operatorname B(\mathbf x',\delta)가 성립함을 보인다. \epsilon=\delta/2\Vert(\mathrm D\mathbf f(\mathbf a))^{-1}\Vert를 취하면, 임의의 \mathbf y\in\bar\operatorname B(\mathbf f(\mathbf x'),\epsilon) 및 \mathbf x\in\operatorname B(\mathbf x',\delta)에 대하여, 다음이 성립한다.

:\begin{align}\Vert\mathbf F_{\mathbf y}(\mathbf x)-\mathbf x'\Vert

&\le\Vert\mathbf F_{\mathbf y}(\mathbf x)-\mathbf F_{\mathbf y}(\mathbf x')\Vert+

\Vert\mathbf F_{\mathbf y}(\mathbf x')-\mathbf x'\Vert\\

&\le\frac 12\Vert\mathbf x-\mathbf x'\Vert+

\Vert(\mathrm D\mathbf f(\mathbf a))^{-1}(\mathbf y-\mathbf f(\mathbf x'))\Vert\\

&<\delta

\end{align}

즉, \mathbf F_{\mathbf y}(\mathbf x)\in\bar\operatorname B(\mathbf x',\delta)이다. 즉, \mathbf F_{\mathbf y}는 \bar\operatorname B(\mathbf x',\delta) 위의 축약 사상이며, 바나흐 고정점 정리에 따라, \mathbf F_{\mathbf y}는 고정점 \mathbf x\in\bar\operatorname B(\mathbf x',\delta)를 갖는다. 따라서, \mathbf y=\mathbf f(\mathbf x)\in\mathbf f(\bar\operatorname B(\mathbf x',\delta))\subseteq\mathbf f(V)이며, \mathbf f(V)는 열린집합이다.

임의의 \mathbf x\in V에 대하여, \mathrm D\mathbf f(\mathbf x)가 가역 행렬임을 보이기 위해, \mathbf h\in\mathbb R^n가 \mathrm D\mathbf f(\mathbf x)\mathbf h=\mathbf 0을 만족시킨다고 가정하면, 다음이 성립한다.

:\begin{align}0

&=\Vert\mathrm D\mathbf f(\mathbf x)\mathbf h\Vert\\

&\ge\Vert\mathrm D\mathbf f(\mathbf a)\mathbf h\Vert-

\Vert(\mathrm D\mathbf f(\mathbf a)-\mathrm D\mathbf f(\mathbf x))\mathbf h\Vert\\

&\ge\frac{\Vert\mathbf h\Vert}{\Vert(\mathrm D\mathbf f(\mathbf a))^{-1}\Vert}-

\Vert\mathrm D\mathbf f(\mathbf a)-\mathrm D\mathbf f(\mathbf x)\Vert\Vert\mathbf h\Vert\\

&\ge\frac{\Vert\mathbf h\Vert}{2\Vert(\mathrm D\mathbf f(\mathbf a))^{-1}\Vert}\\

\end{align}

즉, \mathbf h=\mathbf 0이다. 따라서 \mathrm D\mathbf f(\mathbf x)는 가역 행렬이다.

\mathbf g\colon\mathbf f(V)\to\mathbb R^n, \mathbf f(\mathbf x)\to\mathbf x가 \mathcal C^k 함수임을 보이기 위해, 임의의 \mathbf y,\mathbf y+\mathbf k\in\mathbf f(V)에 대하여, \mathbf y=\mathbf f(\mathbf x) 또한 \mathbf y+\mathbf k=\mathbf f(\mathbf x+\mathbf h)인 \mathbf x,\mathbf x+\mathbf h\in V를 취한다. 그러면 다음이 성립한다.

:\begin{align}\frac 12\Vert\mathbf h\Vert

&\ge\Vert\mathbf F_{\mathbf y}(\mathbf x+\mathbf h)-\mathbf F_{\mathbf y}(\mathbf x)\Vert\\

&=\Vert\mathbf h-(\mathrm D\mathbf f(\mathbf a))^{-1}\mathbf k\Vert\\

&\ge\Vert\mathbf h\Vert-\Vert(\mathrm D\mathbf f(\mathbf a))^{-1}\Vert\Vert\mathbf k\Vert

\end{align}

즉, \Vert\mathbf k\Vert\ge\Vert\mathbf h\Vert/(2\Vert(\mathrm D\mathbf f(\mathbf a))^{-1}\Vert)이다. 따라서 다음이 성립한다.

:\begin{align}\limsup_{\mathbf k\to\mathbf 0}

\frac{\Vert\mathbf g(\mathbf y+\mathbf k)-\mathbf g(\mathbf y)-

(\mathrm D\mathbf f(\mathbf x))^{-1}\mathbf k\Vert}{\Vert\mathbf k\Vert}

&=\limsup_{\mathbf k\to\mathbf 0}

\frac{\Vert\mathbf h-(\mathrm D\mathbf f(\mathbf x))^{-1}(\mathbf f(\mathbf x+\mathbf h)-\mathbf f(\mathbf x))\Vert}{\Vert\mathbf k\Vert}\\

&\le\limsup_{\mathbf h\to\mathbf 0}

\frac{\Vert(\mathrm D\mathbf f(\mathbf x))^{-1}\Vert}{\Vert(\mathrm D\mathbf f(\mathbf a))^{-1}\Vert}

\frac{\Vert\mathbf f(\mathbf x+\mathbf h)-\mathbf f(\mathbf x)-(\mathrm D\mathbf f(\mathbf x))^{-1}\mathbf h\Vert}{\Vert\mathbf h\Vert}\\

&=0

\end{align}

즉, \mathrm D\mathbf g(\mathbf x)=(\mathrm D\mathbf f(\mathbf g(\mathbf y))^{-1}이며, \mathbf g는 \mathcal C^k 함수이다.

3. 1. 축약 사상 원리 (바나흐 고정점 정리) 이용

임의의 \mathbf y\in\mathbb R^n에 대하여, 함수 \mathbf F_{\mathbf y}\colon U\to\mathbb R^n를 다음과 같이 정의한다.

:\mathbf F_{\mathbf y}(\mathbf x)=\mathbf x+(\mathrm D\mathbf f(\mathbf a))^{-1}(\mathbf y-\mathbf f(\mathbf x))

\qquad\forall\mathbf x\in U

그러면 다음이 성립한다.

:\mathrm D\mathbf F_{\mathbf y}(\mathbf x)=(\mathrm D\mathbf f(\mathbf a))^{-1}(\mathrm D\mathbf f(\mathbf a)-\mathrm D\mathbf f(\mathbf x))

\qquad\forall\mathbf x\in U,\;\mathbf y\in\mathbb R^n

\mathrm D\mathbf f가 연속 함수이므로, 다음을 만족시키는 열린 근방 \mathbf a\in V\subseteq U가 존재한다.

:\Vert\mathrm D\mathbf f(\mathbf a)-\mathrm D\mathbf f(\mathbf x)\Vert<\frac 1{2\Vert\mathrm D\mathbf f(\mathbf a))^{-1}\Vert}

즉, 다음이 성립한다.

:\Vert\mathrm D\mathbf F_{\mathbf y}(\mathbf x)\Vert<\frac 12

\qquad\forall\mathbf x\in V,\;\mathbf y\in\mathbb R^n

이는 다음을 의미한다.

:\Vert\mathbf F_{\mathbf y}(\mathbf x)-\mathbf F_{\mathbf y}(\mathbf x')\Vert\le\frac 12\Vert\mathbf x-\mathbf x'\Vert

\qquad\forall\mathbf x,\mathbf x'\in V,\;\mathbf y\in\mathbb R^n

\mathbf f|_V가 단사 함수임을 보이기 위해, \mathbf x,\mathbf x'\in V가 \mathbf f(\mathbf x)=\mathbf f(\mathbf x')를 만족한다고 가정하면, \mathbf x,\mathbf x'는 모두 \mathbf F_{\mathbf f(\mathbf x)}의 고정점이다. 즉, \mathbf F_{\mathbf f(\mathbf x)}(\mathbf x)=\mathbf x이며 \mathbf F_{\mathbf f(\mathbf x)}(\mathbf x')=\mathbf x'이다. 이를 위에 대입하면, \mathbf x=\mathbf x'를 얻는다. 따라서 \mathbf f|_V는 단사 함수이다.

\mathbf f(V)가 열린집합임을 보이기 위해, 임의의 \mathbf x'\in V에 대하여, \operatorname B(\mathbf f(\mathbf x'),\epsilon)\subseteq\mathbf f(V)인 \epsilon>0을 찾는다. 이를 위해 임의의 \mathbf y\in\operatorname B(\mathbf f(\mathbf x'),\epsilon)에 대하여, \mathbf F_{\mathbf y}가 V에서 고정점을 가지는 것을 보인다. \delta>0가 \bar\operatorname B(\mathbf x',\delta)\subseteq V를 만족시킨다고 하면, 임의의 \mathbf y\in\operatorname B(\mathbf f(\mathbf x'),\epsilon)에 대하여 \mathbf F_\mathbf y(\operatorname B(\mathbf x',\delta))\subseteq \operatorname B(\mathbf x',\delta)가 성립함을 보인다. \epsilon=\delta/2\Vert(\mathrm D\mathbf f(\mathbf a))^{-1}\Vert를 취하면, 임의의 \mathbf y\in\bar\operatorname B(\mathbf f(\mathbf x'),\epsilon) 및 \mathbf x\in\operatorname B(\mathbf x',\delta)에 대하여, 다음이 성립한다.

:\begin{align}\Vert\mathbf F_{\mathbf y}(\mathbf x)-\mathbf x'\Vert

&\le\Vert\mathbf F_{\mathbf y}(\mathbf x)-\mathbf F_{\mathbf y}(\mathbf x')\Vert+

\Vert\mathbf F_{\mathbf y}(\mathbf x')-\mathbf x'\Vert\\

&\le\frac 12\Vert\mathbf x-\mathbf x'\Vert+

\Vert(\mathrm D\mathbf f(\mathbf a))^{-1}(\mathbf y-\mathbf f(\mathbf x'))\Vert\\

&<\delta

\end{align}

즉, \mathbf F_{\mathbf y}(\mathbf x)\in\bar\operatorname B(\mathbf x',\delta)이다. 즉, \mathbf F_{\mathbf y}는 \bar\operatorname B(\mathbf x',\delta) 위의 축약 사상이며, 바나흐 고정점 정리에 따라, \mathbf F_{\mathbf y}는 고정점 \mathbf x\in\bar\operatorname B(\mathbf x',\delta)를 갖는다. 따라서, \mathbf y=\mathbf f(\mathbf x)\in\mathbf f(\bar\operatorname B(\mathbf x',\delta))\subseteq\mathbf f(V)이며, \mathbf f(V)는 열린집합이다.

임의의 \mathbf x\in V에 대하여, \mathrm D\mathbf f(\mathbf x)가 가역 행렬임을 보이기 위해, \mathbf h\in\mathbb R^n가 \mathrm D\mathbf f(\mathbf x)\mathbf h=\mathbf 0을 만족시킨다고 가정하면, 다음이 성립한다.

:\begin{align}0

&=\Vert\mathrm D\mathbf f(\mathbf x)\mathbf h\Vert\\

&\ge\Vert\mathrm D\mathbf f(\mathbf a)\mathbf h\Vert-

\Vert(\mathrm D\mathbf f(\mathbf a)-\mathrm D\mathbf f(\mathbf x))\mathbf h\Vert\\

&\ge\frac{\Vert\mathbf h\Vert}{\Vert(\mathrm D\mathbf f(\mathbf a))^{-1}\Vert}-

\Vert\mathrm D\mathbf f(\mathbf a)-\mathrm D\mathbf f(\mathbf x)\Vert\Vert\mathbf h\Vert\\

&\ge\frac{\Vert\mathbf h\Vert}{2\Vert(\mathrm D\mathbf f(\mathbf a))^{-1}\Vert}\\

\end{align}

즉, \mathbf h=\mathbf 0이다. 따라서 \mathrm D\mathbf f(\mathbf x)는 가역 행렬이다.

\mathbf g\colon\mathbf f(V)\to\mathbb R^n, \mathbf f(\mathbf x)\to\mathbf x가 \mathcal C^k 함수임을 보이기 위해, 임의의 \mathbf y,\mathbf y+\mathbf k\in\mathbf f(V)에 대하여, \mathbf y=\mathbf f(\mathbf x) 또한 \mathbf y+\mathbf k=\mathbf f(\mathbf x+\mathbf h)인 \mathbf x,\mathbf x+\mathbf h\in V를 취한다. 그러면 다음이 성립한다.

:\begin{align}\frac 12\Vert\mathbf h\Vert

&\ge\Vert\mathbf F_{\mathbf y}(\mathbf x+\mathbf h)-\mathbf F_{\mathbf y}(\mathbf x)\Vert\\

&=\Vert\mathbf h-(\mathrm D\mathbf f(\mathbf a))^{-1}\mathbf k\Vert\\

&\ge\Vert\mathbf h\Vert-\Vert(\mathrm D\mathbf f(\mathbf a))^{-1}\Vert\Vert\mathbf k\Vert

\end{align}

즉, \Vert\mathbf k\Vert\ge\Vert\mathbf h\Vert/(2\Vert(\mathrm D\mathbf f(\mathbf a))^{-1}\Vert)이다. 따라서 다음이 성립한다.

:\begin{align}\limsup_{\mathbf k\to\mathbf 0}

\frac{\Vert\mathbf g(\mathbf y+\mathbf k)-\mathbf g(\mathbf y)-

(\mathrm D\mathbf f(\mathbf x))^{-1}\mathbf k\Vert}{\Vert\mathbf k\Vert}

&=\limsup_{\mathbf k\to\mathbf 0}

\frac{\Vert\mathbf h-(\mathrm D\mathbf f(\mathbf x))^{-1}(\mathbf f(\mathbf x+\mathbf h)-\mathbf f(\mathbf x))\Vert}{\Vert\mathbf k\Vert}\\

&\le\limsup_{\mathbf h\to\mathbf 0}

\frac{\Vert(\mathrm D\mathbf f(\mathbf x))^{-1}\Vert}{\Vert(\mathrm D\mathbf f(\mathbf a))^{-1}\Vert}

\frac{\Vert\mathbf f(\mathbf x+\mathbf h)-\mathbf f(\mathbf x)-(\mathrm D\mathbf f(\mathbf x))^{-1}\mathbf h\Vert}{\Vert\mathbf h\Vert}\\

&=0

\end{align}

즉, \mathrm D\mathbf g(\mathbf x)=(\mathrm D\mathbf f(\mathbf g(\mathbf y))^{-1}이며, \mathbf g는 \mathcal C^k 함수이다.

바나흐 고정점 정리(축약 사상 원리)를 이용한 증명은 앙리 카르탕, 장 디외도네, 세르주 랭, 로제 고드망 및 라르스 횸란데르의 책에서 찾을 수 있다.[1][7] T. Tao에 따르면,[8] 축약 사상 정리의 결과를 사용하여 증명할 수 있다.

3. 2. 평균값 정리 이용

역함수 정리는 중요한 결과이므로 여러 증명이 제시되어 왔다. 교과서에서 가장 흔히 볼 수 있는 증명은 축약 사상의 원리 (바나흐 고정점 정리라고도 불림)에 의존한다.[25] 이 정리는 상미분 방정식의 해의 증명에서도 중요한 단계로 사용될 수 있다. 이 정리는 무한 차원(바나흐 공간)의 경우에도 적용되므로, 역함수 정리의 무한 차원 버전 증명에 사용되는 도구이다.

다른 증명(유한 차원에서만 유효)으로, 콤팩트 집합 위의 함수에 대한 최댓값 정리를 중요한 도구로 사용하는 것이 있다.[25] 또 다른 증명으로, 뉴턴법을 사용하는 것이 있는데, 이점은 정리의 한 버전을 얻을 수 있다는 것이다. 즉, 함수의 미분 크기의 상한이 주어지면, 함수가 가역적인 근방의 크기에 대한 평가를 얻을 수 있다.[26]

3. 3. 최대 최소 정리 이용

역함수 정리는 중요한 결과이므로 여러 증명이 제시되어 왔다. 최댓값 정리를 중요한 도구로 사용하는 증명도 존재한다.[25] 이 증명 방법은 콤팩트 집합 위의 함수에 대한 최대 최소 정리를 이용한다. 뉴턴법을 사용하는 증명 방법도 있는데, 이 방법은 정리의 effective한 버전을 얻을 수 있다는 장점이 있다.[26] 즉, 함수의 미분 크기의 상한이 주어지면, 함수가 가역적인 근방의 크기에 대한 평가를 얻을 수 있다.

3. 4. 실수 닫힌 체 이용

역함수 정리는 실수 닫힌 체 ''k'' (또는 O-최소 구조)에서도 성립한다.[24] 정확히 말하면, 이 정리는 연속적으로 미분 가능한 k^n의 열린 부분 집합 사이의 반대수적(또는 정의 가능한) 사상에 대해 성립한다.

일반적인 역함수 정리 증명은 코시 완비성에 의존하는 바나흐 고정점 정리를 사용한다. 하지만, 완비성을 필요로 하지 않는 최대 최소 정리를 사용하여 증명할 수도 있다. 우선, B(0, r/4) \subset f(B(0, r))임을 보인다. B(0, r/4)의 점 y가 주어지면, \overline{B}(0, r)의 근방에서 정의된 함수 P(x) = |f(x) - y|^2을 고려한다. P'(x) = 0이면, 0 = P'(x) = 2[f_1(x) - y_1 \cdots f_n(x) - y_n]f'(x)이고 f'(x)가 가역적이므로 f(x) = y이다. 최대 최소 정리에 의해 P는 닫힌 공 \overline{B}(0, r)의 어떤 점 x_0에서 최소값을 갖는데, 2^{-1}|x| \le |f(x)|을 사용하여 B(0, r)에 속함을 보일 수 있다. P'(x_0) = 0이므로 f(x_0) = y가 되어, 포함 관계가 증명된다.

또 다른 방법으로는, 타르스키의 원리에 의해 실수에 대한 정리를 유추할 수도 있다.

4. 따름정리

역함수 정리는 다음과 같은 연립 방정식을 푸는 데 사용될 수 있다.

:\begin{align}

&f_1(x) = y_1 \\

&\quad \vdots\\

&f_n(x) = y_n,\end{align}

즉, 야코비 행렬이 가역행렬일 경우 x = (x_1, \dots, x_n)에 대한 함수로 y_1, \dots, y_n을 표현하는 것이다. 음함수 정리는 보다 일반적인 연립 방정식을 푸는 것을 허용한다.[9]

:\begin{align}

&f_1(x, y) = 0 \\

&\quad \vdots\\

&f_n(x, y) = 0\end{align}

x에 대한 y에 대해. 더욱 일반적이지만, 이 정리는 실제로 역함수 정리의 결과이다.

미분 기하학에서, 역함수 정리는 매끄러운 사상 아래에서 정칙값의 역상이 다양체임을 보이기 위해 사용된다.[10]

더 일반적으로, 이 정리는 매끄러운 사상 f : P \to E가 부분 다양체 M \subset E에 횡단적이면, 역상 f^{-1}(M) \hookrightarrow P가 부분 다양체임을 보여준다.[11]

== 열린 함수 관련 ==

열린집합 U\subseteq\mathbb R^n 및 \mathcal C^1 함수 \mathbf f\colon U\to\mathbb R^n가 다음을 만족시킨다고 하자.

:\det\mathrm D\mathbf f(\mathbf x)\ne 0\qquad\forall\mathbf x\in U

그렇다면, \mathbf f는 열린 함수이다. 즉, 모든 열린집합 \widetilde U\subseteq U의 상 \mathbf f(\widetilde U)은 역시 열린집합이다.

== (대역) 미분동형사상 관련 ==

열린집합 U\subseteq\mathbb R^n 및 단사 \mathcal C^k 함수 \mathbf f\colon U\to\mathbb R^n가 다음을 만족한다고 가정하자.

:\det\mathrm D\mathbf f(\mathbf x)\ne 0\qquad\forall\mathbf x\in U

그러면, \mathbf f는 \mathcal C^k 미분동형사상이다. 즉, 다음이 성립한다.


  • \mathbf f(U)는 열린집합이다.
  • \mathbf f^{-1}\colon f(U)\to\mathbb R^n은 역시 \mathcal C^k 함수이다.


역함수 정리는 국소적인 결과이며, 각 점에 적용된다. 이 정리는 함수 f가 국소적으로 전단사(또는 어떤 종류의 국소적 미분동형사상)임을 보여준다.

만약 A가 점이라면, 위는 일반적인 역함수 정리이다. 역함수 정리는 미분 다양체 간의 미분 가능한 사상과 관련하여 다시 표현할 수 있다. 미분 가능한 사상 F: M \to N (클래스 C^1)에 대해, F의 미분

:dF_p: T_p M \to T_{F(p)} N

가 M의 점 p에서 선형 동형 사상이면,

:F|_U: U \to F(U)

가 미분 동형 사상이 되도록 하는 p의 열린 근방 U가 존재한다.

만약 F의 도함수가 M의 모든 점 p에서 동형 사상이면, 사상 F는 국소 미분 동형 사상이다.

4. 1. 열린 함수 관련

열린집합 U\subseteq\mathbb R^n 및 \mathcal C^1 함수 \mathbf f\colon U\to\mathbb R^n가 다음을 만족시킨다고 하자.

:\det\mathrm D\mathbf f(\mathbf x)\ne 0\qquad\forall\mathbf x\in U

그렇다면, \mathbf f는 열린 함수이다. 즉, 모든 열린집합 \widetilde U\subseteq U의 상 \mathbf f(\widetilde U)은 역시 열린집합이다.

4. 2. (대역) 미분동형사상 관련

열린집합 U\subseteq\mathbb R^n 및 단사 \mathcal C^k 함수 \mathbf f\colon U\to\mathbb R^n가 다음을 만족한다고 가정하자.

:\det\mathrm D\mathbf f(\mathbf x)\ne 0\qquad\forall\mathbf x\in U

그러면, \mathbf f는 \mathcal C^k 미분동형사상이다. 즉, 다음이 성립한다.

  • \mathbf f(U)는 열린집합이다.
  • \mathbf f^{-1}\colon f(U)\to\mathbb R^n은 역시 \mathcal C^k 함수이다.


역함수 정리는 국소적인 결과이며, 각 점에 적용된다. 이 정리는 함수 f가 국소적으로 전단사(또는 어떤 종류의 국소적 미분동형사상)임을 보여준다.

만약 A가 점이라면, 위는 일반적인 역함수 정리이다. 역함수 정리는 미분 다양체 간의 미분 가능한 사상과 관련하여 다시 표현할 수 있다. 미분 가능한 사상 F: M \to N (클래스 C^1)에 대해, F의 미분

:dF_p: T_p M \to T_{F(p)} N

가 M의 점 p에서 선형 동형 사상이면,

:F|_U: U \to F(U)

가 미분 동형 사상이 되도록 하는 p의 열린 근방 U가 존재한다.

만약 F의 도함수가 M의 모든 점 p에서 동형 사상이면, 사상 F는 국소 미분 동형 사상이다.

5. 예시

다음과 같이 정의된 벡터값 함수 F:'''R'''2 → '''R'''2를 고려해 보자.

: F(x,y) = ex cos y], [ex sin y

점 (x, y)에서의 야코비 행렬은 다음과 같다.

: JF(x,y) = ex cos y, -ex sin y], [ex sin y, ex cos y

행렬식은 다음과 같다.

: det JF(x,y) = e2xcos2y + e2xsin2y = e2x

행렬식 e2x는 모든 곳에서 0이 아니다. 따라서 역함수 정리에 의해, '''R'''2의 모든 점 p에 대해, F가 가역인 p의 근방이 존재한다. 이는 F가 전체 정의 구역에서 가역임을 의미하지는 않는다. 이 경우 F는 주기적이기 때문에 단사 함수조차 아니다: F(x,y) = F(x, y+2π).

5. 1. 미분동형사상이 아닌 국소 미분동형사상

함수 \mathbf f\colon\mathbb R^2\to\mathbb R^2를 다음과 같이 정의하자.

:\mathbf f(x,y)=(e^x\cos y,e^x\sin y)\qquad\forall x,y\in\mathbb R

이 함수는 \mathcal C^\infty 함수이며, 야코비 행렬의 행렬식은 다음과 같다.

:\det\mathrm D\mathbf f(x,y)=e^{2x}\ne 0

음함수 정리에 따라, \mathbf f는 모든 점에서 국소 \mathcal C^\infty 미분동형사상이다. 그러나 \mathbf f는 삼각 함수의 주기성에 따라 단사 함수가 아니므로, 미분동형사상이 아니다.

벡터값 함수 F(x,y)= \begin{bmatrix} {e^x \cos y}\\ {e^x \sin y}\\ \end{bmatrix}는 주기적이기 때문에 단사 함수가 아니다. 즉, F(x,y)=F(x,y+2\pi)\!이다.

5. 2. 야코비 행렬식이 0인 점을 갖는 C0 미분동형사상

함수 f : ℝ2 → ℝ2를 다음과 같이 정의하자.
f(x, y) = (x3, y) (∀ x, y ∈ ℝ)

그러면 f는 연속 함수이며, 다음과 같은 연속 역함수 f-1를 갖는다.
f-1(u, v) = (u1/3, v) (∀ u, v ∈ ℝ)

즉, f는 C0 미분동형사상이다. 그러나 det Df(0, 0) = 0이다. 즉, C0 미분동형사상은 야코비 행렬식이 0인 점을 가질 수 있다. k > 0일 경우, Ck 미분동형사상은 야코비 행렬식이 0인 점을 가지지 않는다.

6. 응용

6. 1. 음함수 정리

역함수 정리는 연립 방정식 f_1(x) = y_1, \dots, f_n(x) = y_n을 푸는 데 사용될 수 있다. 즉, 야코비 행렬이 가역행렬일 경우 x = (x_1, \dots, x_n)에 대한 함수로 y_1, \dots, y_n을 표현하는 것이다.[9] 음함수 정리는 보다 일반적인 연립 방정식 f_1(x, y) = 0, \dots, f_n(x, y) = 0을 푸는 것을 허용한다.[9]

음함수 정리는 역함수 정리의 결과이다.[9] 지도 f : \mathbb{R}^n \times \mathbb{R}^m \to \mathbb{R}^m가 주어졌을 때, f(a, b) = 0이고, f가 (a, b)의 근방에서 연속적으로 미분 가능하며, b에서의 y \mapsto f(a, y)의 도함수가 가역행렬이면, 어떤 근방 U, V에서 미분 가능한 지도 g : U \to V가 존재하여 f(x, g(x)) = 0이다. 게다가 f(x, y) = 0, x \in U, y \in V이면 y = g(x)이다. 즉, g(x)는 유일한 해이다.[9]

이를 확인하기 위해, 지도 F(x, y) = (x, f(x, y))를 고려한다. 역함수 정리에 따르면, F : U \times V \to W는 어떤 근방 U, V, W에 대한 역 G를 갖는다. 그러면 (x, y) = F(G_1(x, y), G_2(x, y)) = (G_1(x, y), f(G_1(x, y), G_2(x, y)))를 얻는다. 따라서 x = G_1(x, y)와 y = f(x, G_2(x, y))이다. g(x) = G_2(x, 0)는 필요한 속성을 갖는다.[9]

6. 2. 다양체 구조

미분 기하학에서, 역함수 정리는 매끄러운 사상 아래에서 정칙값의 역상이 다양체임을 보이는 데 사용된다.[10]

f : U \to \mathbb{R}^r을 \mathbb{R}^n의 열린 부분 집합에서 매끄러운 사상이라고 가정하자. f^{-1}(b)에서 점 a를 고정하고, \mathbb{R}^n의 좌표를 순열하여 행렬 \left [ \frac{\partial f_i}{\partial x_j}(a) \right]_{1 \le i, j \le r}가 랭크 r을 갖는다고 가정한다. 그러면 사상 F : U \to \mathbb{R}^r \times \mathbb{R}^{n-r} = \mathbb{R}^n, \, x \mapsto (f(x), x_{r+1}, \dots, x_n)는 F'(a)가 랭크 n을 갖도록 한다. 역함수 정리에 의해, (b, a_{r+1}, \dots, a_n)의 근방 V \times W에서 정의된 F의 매끄러운 역 G를 찾을수 있다.

(f \circ G)(x_1, \dots, x_n) = (x_1, \dots, x_r)이 성립한다. 즉, G에 의한 좌표 변환 후, f는 좌표 투영이다. (침강 정리 참조) G : V \times W \to U' = G(V \times W)가 전단사이기 때문에, 사상 g = G(b, \cdot) : W \to f^{-1}(b) \cap U', \, (x_{r+1}, \dots, x_n) \mapsto G(b, x_{r+1}, \dots, x_n)는 매끄러운 역을 갖는 전단사이다. 즉, g는 a 주변에서 f^{-1}(b)의 국소 매개화를 제공한다. 따라서, f^{-1}(b)는 다양체이다.

더 일반적으로, 이 정리는 매끄러운 사상 f : P \to E가 부분 다양체 M \subset E에 횡단적이면, 역상 f^{-1}(M) \hookrightarrow P가 부분 다양체임을 보여준다.[11]

역함수 정리는 미분가능 다양체 사이의 미분가능 사상으로 일반화할 수 있다. 미분가능 사상 ''F'': ''M'' → ''N'' 에 대해, ''F'' 의 미분 사상 dF_p \colon T_p M \to T_{F(p)} N이 ''M'' 의 점 ''p'' 에서 선형 동형이면, ''p'' 의 열린 근방 ''U'' 가 존재하여, F|_U \colon U \to F(U)는 미분 동형 사상이 된다. ''M'' 과 ''N'' 은 ''p'' 에서 같은 차원을 가져야 한다. ''F'' 의 미분이 ''M'' 의 모든 점 ''p'' 에서 동형이면, 사상 ''F'' 는 국소 미분 동형 사상이다.

7. 일반화

7. 1. 바나흐 공간

바나흐 공간 ''X''와 ''Y'' 사이의 미분 가능한 사상으로 역함수 정리를 일반화할 수 있다.[20] ''U''를 ''X''에서 원점의 열린 근방이라고 하고, F: U \to Y\!를 연속적으로 미분 가능한 함수라고 하자. 그리고 0에서의 ''F''의 프레셰 미분 dF_0: X \to Y\!가 ''X''에서 ''Y''로의 유계 선형 동형사상이라고 가정하자. 그러면 ''Y''에서 F(0)\!의 열린 근방 ''V''와 모든 ''y'' in ''V''에 대해 F(G(y)) = y를 만족하는 연속적으로 미분 가능한 사상 G: V \to X\!가 존재한다. 게다가 G(y)\!는 방정식 F(x) = y\!의 유일하고 충분히 작은 해 ''x''이다.

바나흐 다양체에 대한 역함수 정리도 있다.[21]

7. 2. 바나흐 다양체

역함수 정리는 바나흐 공간 ''X''와 ''Y'' 사이의 미분 가능한 사상으로 일반화될 수 있다.[20] ''U''를 ''X''에서 원점의 열린 근방이라고 하고, F: U \to Y\!를 연속적으로 미분 가능한 함수라고 하자. 그리고 0에서의 ''F''의 프레셰 미분 dF_0: X \to Y\!가 ''X''에서 ''Y''로의 유계 선형 동형사상이라고 가정하자. 그러면 ''Y''에서 F(0)\!의 열린 근방 ''V''와 모든 ''y'' in ''V''에 대해 F(G(y)) = y를 만족하는 연속적으로 미분 가능한 사상 G: V \to X\!가 존재한다. 게다가 G(y)\!는 방정식 F(x) = y\!의 유일하고 충분히 작은 해 ''x''이다.

바나흐 다양체에 대한 역함수 정리도 있다.[21][27]

7. 3. 상수 랭크 정리

역함수 정리(및 음함수 정리)는 어떤 점 주위에서 일정한 계수를 가지는 매끄러운 사상이 그 점 근처에서 특정 형태의 정규형을 가짐을 말하는 상수 랭크 정리의 특수한 경우로 볼 수 있다.[22][28]

매끄러운 사상 F:M\to N이 점 p\in M 근처에서 계수가 일정하다면, p의 열린 근방 U와 F(p)의 열린 근방 V가 존재하여 미분동형사상 u:T_pM\to U 및 v:T_{F(p)}N\to V로 F(U)\subseteq V이고, 미분 dF_p:T_pM\to T_{F(p)}N가 v^{-1}\circ F\circ u와 같아지는 것을 택할 수 있다. 즉, F는 p 근처에서 그 미분 "처럼 보인다"는 것이다. p 근처에서 상수 계수를 갖는 점 p\in M의 집합은 M의 열린 조밀 부분 집합이다. 이는 계수 함수의 반연속성의 결과이다. 따라서 상수 랭크 정리는 정의역의 일반적인 점에 적용된다.

F의 미분이 점 p에서 단사(또는 전사)라면 p의 근방에서도 단사(또는 전사)이므로 F의 계수는 해당 근방에서 상수이고, 상수 랭크 정리가 적용된다.

7. 4. 정칙 함수

복소해석학에서 홀로모픽 사상에 대한 역함수 정리는 다음과 같다.[17][18]

:U, V \subset \mathbb{C}^n을 0 \in U이고 f : U \to V는 변수 z_i, \overline{z}_i에서 야코비 행렬이 0에서 가역인(행렬식이 0이 아닌) 홀로모픽 사상이라고 하자. 그러면 f는 0의 어떤 근방 W에서 단사이고 역 f^{-1} : f(W) \to W는 홀로모픽이다.

이 정리는 일반적인 역함수 정리에서 유도된다. J_{\mathbb{R}}(f)를 변수 x_i, y_i에서 f의 야코비 행렬, J(f)를 z_j, \overline{z}_j에서 그 야코비 행렬로 나타내면 \det J_{\mathbb{R}}(f) = |\det J(f)|^2를 얻고, 이는 가정에 의해 0이 아니다. 따라서 일반적인 역함수 정리에 의해 f는 0 근방에서 단사이고 연속적으로 미분 가능한 역함수를 갖는다.

연쇄 법칙에 의해, w = f(z)일 때,

:\frac{\partial}{\partial \overline{z}_j} (f_j^{-1} \circ f)(z) = \sum_k \frac{\partial f_j^{-1}}{\partial w_k}(w) \frac{\partial f_k}{\partial \overline{z}_j}(z) + \sum_k \frac{\partial f_j^{-1}}{\partial \overline{w}_k}(w) \frac{\partial \overline{f}_k}{\partial \overline{z}_j}(z)

좌변과 우변의 첫 번째 항은 f_j^{-1} \circ f와 f_k가 홀로모픽이기 때문에 0이다. 따라서, 각 k에 대해 \frac{\partial f_j^{-1}}{\partial \overline{w}_k}(w) = 0이다.

단사 매끄러운 함수가 매끄럽지 않은 역함수를 가질 수 있지만(예: 실수 변수에서 f(x) = x^3), 홀로모픽 함수에서는 발생하지 않는다. f : U \to V가 \mathbb{C}^n의 열린 부분 집합 사이의 단사 홀로모픽 사상인 경우, f^{-1} : f(U) \to U는 홀로모픽이다.[19]

'''C'''''n'' 의 열린 집합 ''U''에서 '''C'''''n''으로 가는 정칙 함수 ''F''의 야코비 행렬이 점 ''p''에서 가역적이면, ''F''는 ''p'' 근방에서 가역 함수이고, 이 역함수는 다시 정칙 함수이다.[29]

7. 5. 다항 함수

만약 야코비안 추측이 참이라면, 이는 다항식에 대한 역함수 정리의 변형이 될 것이다. 야코비안 추측은 벡터 값을 갖는 다항식 함수가 가역 다항식(즉, 0이 아닌 상수)인 야코비 행렬식을 갖는다면, 그 역함수 또한 다항식 함수라는 것을 명시한다. 이는 두 변수의 경우에서도 참인지 거짓인지 알려져 있지 않으며, 다항식 이론의 주요 미해결 문제이다.

8. 한계

함수의 도함수가 연속적이라는 가정을 없앤다면, 함수는 더 이상 가역적일 필요가 없다. 예를 들어 f(x) = x + 2x^2\sin(\tfrac1x)이고 f(0)= 0은 불연속 도함수를 가지며,

f'\!(x) = 1 -2\cos(\tfrac1x) + 4x\sin(\tfrac1x)이고 f'\!(0) = 1인데, 이는 x=0에 임의로 가까워지면서 사라진다. 이러한 임계점들은 f의 국소 극대/극소점들이므로, f는 x=0을 포함하는 어떤 구간에서도 일대일 함수가 아니며 (따라서 가역적이지도 않다). 직관적으로, 기울기 f'\!(0)=1은 근처 점들로 전파되지 않으며, 여기서의 기울기는 약하지만 빠른 진동에 의해 지배된다.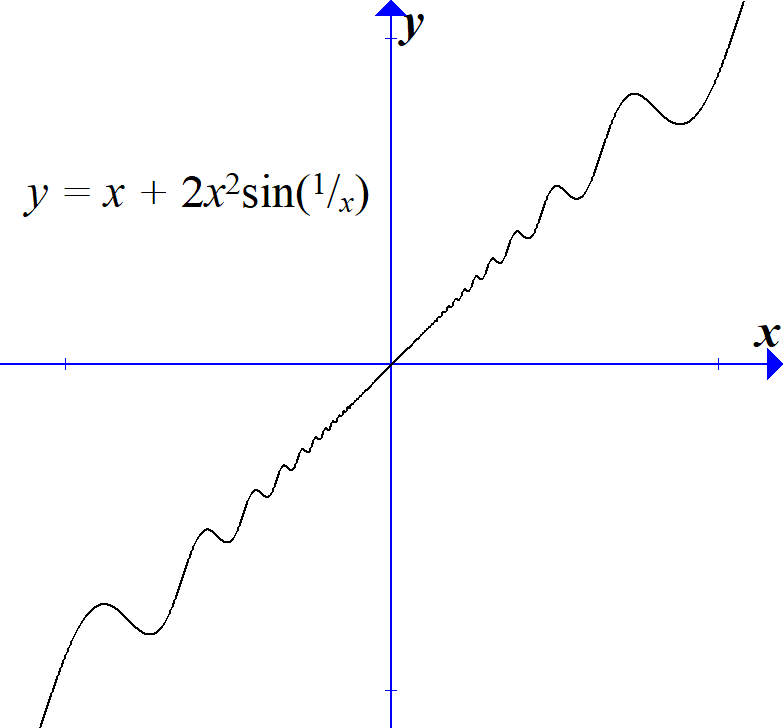


9. 역사

10. 같이 보기

11. 참고 문헌

12. 외부 링크

참조

[1] 서적 The Analysis of Linear Partial Differential Operators I: Distribution Theory and Fourier Analysis Springer
[2] 서적 Partial Differential Equations: Methods and Applications Prentice Hall
[3] 웹사이트 The inverse function theorem for everywhere differentiable maps https://terrytao.wor[...] 2011-09-12
[4] 웹사이트 Inverse Function Theorem https://r-grande.git[...]
[5] 간행물
[6] 서적 Vector Analysis, Linear Algebra, and Differential Forms: A Unified Approach
[7] 서적 Calcul Differentiel Éditions Hermann
[8] 서적 Analysis. II Hindustan Book Agency
[9] 간행물
[10] 간행물
[11] 웹사이트 Transversality https://sites.math.n[...]
[12] 서적 Calculus on Manifolds
[13] 간행물
[14] 웹사이트 Lectures on differential topology https://www.utsc.uto[...]
[15] 웹사이트 On a proof of the existence of tubular neighborhoods. https://mathoverflow[...] 2017-04-13
[16] 서적 Differential Topology Prentice-Hall Inc.
[17] 간행물
[18] 서적 From Holomorphic Functions to Complex Manifolds https://books.google[...] Springer
[19] 간행물
[20] 서적 Optimization by Vector Space Methods https://books.google[...] John Wiley & Sons
[21] 서적 Differential Manifolds Springer
[22] 서적 An Introduction to Differentiable Manifolds and Riemannian Geometry https://archive.org/[...] Academic Press
[23] 서적 Implicit Functions and Solution Mappings: A View from Variational Analysis Springer-Verlag 2014
[24] 서적 Tame Topology and O-minimal Structures. London Mathematical Society lecture note series, no. 248 Cambridge University Press
[25] 서적 Calculus on Manifolds
[26] 서적 Vector Analysis, Linear Algebra, and Differential Forms: a unified approach Matrix Editions
[27] 간행물
[28] 서적 An Introduction to Differentiable Manifolds and Riemannian Geometry Academic Press
[29] 서적 From Holomorphic Functions to Complex Manifolds https://books.google[...] Springer-Verlag
[30] 서적 해석학 입문 경문사 2007


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com