오일러-마스케로니 상수

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사
3. 정의
4. 성질
5. 알려진 자릿수
6. 일반화
참조

1. 개요

오일러-마스케로니 상수는 1734년 레온하르트 오일러가 처음 정의한 수학 상수이다. 이 상수는 조화 급수와 자연 로그의 차이의 극한으로 정의되며, 약 0.57721의 값을 갖는다. 오일러-마스케로니 상수는 감마 함수, 리만 제타 함수 등 다양한 수학적 개념과 관련이 있으며, 유리수인지 무리수인지 여부는 아직 밝혀지지 않았다. 이 상수는 슈틸티예스 상수, 오일러의 일반화된 상수 등으로 일반화될 수 있으며, 오일러-레머 상수와 마세르-그라맹 상수와 같은 관련 상수들도 존재한다. 현재까지 소수점 아래 수억 자리까지 계산되었다.

더 읽어볼만한 페이지

실수 - 데데킨트 절단
데데킨트 절단은 유리수 집합을 특정 조건에 따라 두 부분집합으로 나누어 무리수를 정의하고 실수의 완비성을 구성하는 방법으로, 순서 집합 완비화나 초현실수 구성 등 다양한 수학적 개념으로 확장된다.
실수 - 실수의 구성
실수의 구성은 체, 순서, 완비성 공리를 만족하는 수 체계인 실수를 엄밀하게 정의하기 위한 수학적 방법들을 설명하며, 데데킨트 절단, 코시 수열, 초실수 등의 도구를 활용하여 실수의 고유한 성질을 강조한다.
레온하르트 오일러 - 오일러-라그랑주 방정식
오일러-라그랑주 방정식은 변분법으로 범함수의 정류점을 찾는 편미분 방정식으로, 라그랑주 역학 등 다양한 분야에 활용되며 뉴턴 역학을 일반화한 것으로 여겨진다.
레온하르트 오일러 - 오일러 방법
오일러 방법은 레온하르트 오일러가 제시한 미분 방정식의 해를 구하는 수치 해석 방법으로, 초기값을 이용하여 시간 간격을 나누어 해를 계산하며, 테일러 급수를 활용하여 공식을 유도하고, 간단한 알고리즘 덕분에 과거에 널리 사용되었고 현재에도 수치 해석의 기본 원리를 설명하는 데 중요한 역할을 한다.
수론의 미해결 문제 - 리만 가설
리만 가설은 리만 제타 함수의 자명하지 않은 모든 영점의 실수부가 1/2이라는 추측으로, 힐베르트 문제와 클레이 수학 연구소의 밀레니엄 문제 중 하나이며 정수론과 복소해석학을 연결하는 다양한 수학적 명제들과 동치이다.
수론의 미해결 문제 - 쌍둥이 소수
쌍둥이 소수는 2만큼 차이나는 두 소수의 쌍으로, 무한성 여부는 미해결 문제이며 역수 합은 브룬 상수로 수렴하고 큰 쌍둥이 소수들이 발견되고 있다.

오일러-마스케로니 상수
일반 정보
이름	오일러-마스케로니 상수
다른 이름	오일러 상수, 오일러 감마 상수
기호	γ
발견 연도	1734년
발견자	레온하르트 오일러
관련 분야	수론 해석학
값	0.5772156649...
영어 이름	Euler-Mascheroni constant, Euler's constant, Euler's gamma
정의
정의식	γ := lim (n → ∞) (∑(k=1 to n) 1/k - ln(n)) = ∫(1 to ∞) (1/⌊x⌋ - 1/x) dx
성질
종류	무리수인지 여부가 밝혀지지 않음
같이 보기
관련 항목	오일러 수

2. 역사

레온하르트 오일러가 1734년에 〈조화급수에 대한 고찰〉(De Progressionibus harmonicis observationes^la)이라는 논문에서 오늘날 오일러-마스케로니 상수로 불리는 수를 최초로 정의하였다. 오일러는 이 상수를 ''C'' 또는 ''O''로 표시했다. 이탈리아의 수학자 로렌초 마스케로니(Lorenzo Mascheroni^it)도 1790년 이 수를 언급하였고, ''A'' 또는 ''a''라는 기호를 사용하였다.

오일러-마스케로니 상수는 보통 소문자 감마 ''γ''로 표기된다. 이 기호는 오일러나 마스케로니의 저서에는 등장하지 않으나, 이후 이 수가 대문자 감마로 표기되는 감마 함수와 깊은 관계를 가진다는 사실이 발견되면서 소문자 감마가 사용되게 되었다. 소문자 감마 기호가 사용된 최초의 논문은 1835년에 작성되었고, 1837년 출판되었다.^[106]

오일러는 처음 이 상수의 값을 소수점 6자리까지 계산했다. 1781년에는 소수점 16자리까지 계산했다. 이탈리아 수학자 로렌초 마스케로니는 이 상수를 소수점 32자리까지 계산하려 했지만, 20~22번째와 31~32번째 소수점에서 오류를 범했다. 그는 20번째 자리부터 ...'''181'''12090082'''39'''로 계산했지만, 실제 값은 ...'''065'''12090082'''40'''이다. 1809년에는 요한 게오르크 폰 졸트너가 소수점 아래 22자리까지 계산을 수행했으며, 기호 ''H''를 사용했다.

독일 수학자 카를 안톤 브레치나이더는 1835년에 기호 ''γ''를 사용했고,^[106] 오거스터스 드 모건은 1836년부터 1842년까지 부분적으로 출판된 교과서에서 이를 사용했다.

인도의 수학자 스리니바사 라마누잔도 오일러-마스케로니 상수에 관한 연구를 진행하여 1917년에 논문을 발표했다.^[1] 다비트 힐베르트는 ''γ''의 무리성을 "접근할 수 없는" 미해결 문제로 언급했고, 영국 수학자 고드프리 하디는 이를 증명하는 사람에게 옥스퍼드의 사빌 의장직을 넘겨주겠다고 제안했다고 한다.^[48]

3. 정의

Euler–Mascheroni constant^영어 $\gamma$(감마)는 다음과 같은 극한으로 정의된다.

:$\gamma = \lim_{n\to\infty } \left(\sum_{k=1}^n\frac1k - \ln n\right)=\int_1^\infty\left(\frac1{\lfloor x\rfloor}-\frac1x\right)\,dx$

그 값은 다음과 같다.

:0.57721 56649 01532 86060 65120 90082 40243 10421 59335 93992 …

레온하르트 오일러는 유한항의 조화 급수의 근사식에 대한 관심에서 조화 급수의 증가가 극한에서 로그 함수와 같다는 것을 증명했다. 즉, 조화 급수와 로그 함수의 차이는 어떤 상수로 수렴하며, 그것이 나중에 오일러-마스케로니 상수로 불리게 되었다. 오일러는 이 값을 소수점 6자리까지 구했다. 그 후 로렌초 마스케로니가 32번째 자리까지 구했고 (단, 정확했던 것은 20번째 자리까지), $\gamma$ 기호로 나타냈다.^[102]

4. 성질

오일러-마스케로니 상수가 유리수인지 여부는 아직 알려져 있지 않다. 연분수 분석에 따르면, 만약 이 상수가 유리수라면 그 분모는 적어도 10²⁴²⁰⁸⁰ 이상이다.

4. 1. 감마 함수와의 관계

감마 함수와는 다음과 같은 관계가 있다.

:

\gamma = -\lim_{z\to 0} \left\{\Gamma(z) - \frac1{z} \right\}= -\lim_{z\to 0} \left\{\Psi(z)   + \frac1{z} \right\}.

디감마 함수

\Psi(z)

는 감마 함수의 로그 도함수이며,

z=1

에서

\Psi(1) = -\gamma

이다.^[102]

4. 2. 리만 제타 함수와의 관계

리만 제타 함수와는 다음과 같은 관계가 있다.

:

\begin{align}\gamma &= \sum_{m=2}^{\infty} (-1)^m\frac{\zeta(m)}{m} \\&= \ln \left ( \frac{4}{\pi} \right ) + \sum_{m=2}^{\infty} (-1)^m\frac{\zeta(m)}{2^{m-1}m} \\&= \lim_{s \to 1^+} \sum_{n=1}^\infty \left ( \frac{1}{n^s}-\frac{1}{s^n} \right )  = \lim_{s \to 1} \left ( \zeta(s) - \frac{1}{s-1} \right ) \end{align}

다음은 오일러-마스케로니 상수와 관련된 추가적인 관계들이다.

감마 함수와 바르네스 G-함수에 대한 바이어슈트라스 곱 공식.^[3]^[4]
$\Gamma(1/x)$ 의 점근 전개.
유리수 값에서의 디감마 함수의 값 평가.^[5]
리만 제타 함수의 로랑 급수 전개에서 슈틸체스 상수의 첫 번째 값.^[6]
리만 제타 함수의 미분 및 디리클레 베타 함수의 미분 값.^[26]^[49]
라플라스 변환 및 멜린 변환과의 관련성.^[7]^[8]
조화 급수를 유한 값으로 정규화/재정규화하는 데 사용.
지수 적분 및 로그 적분 함수를 포함하는 식.^[9]^[10]
코사인 적분의 정의.^[9]
베셀 함수와의 관련성.^[11]^[12]^[13]^[14]
수정된 스트루베 함수의 점근 전개.^[15]
다른 특수 함수와의 관련성.^[16]^[17]
오일러 피 함수에 대한 부등식.^[18]
약수 함수의 성장률.^[19]
리만 가설의 공식.^[29]^[20]
메르텐스 정리의 세 번째 정리.^[51]
마이셀-메르텐스 상수의 계산.^[21]
특정 소수 간격에 대한 하한.^[22]
1부터 주어진 ''n''까지의 모든 수의 평균 약수 개수에 대한 근사.^[28]
메르센 소수의 빈도에 관한 렌스트라-포머란스-와그스태프 추측.^[23]
유클리드 호제법의 효율성에 대한 추정.^[24]
뫼비우스 함수와 폰 망골트 함수를 포함하는 합.

4. 3. 적분 표현

다음 적분 식으로도 오일러-마스케로니 상수를 얻을 수 있다.^[3]^[4]^[5]^[6]^[26]^[49]^[7]^[8]^[9]^[10]^[11]^[12]^[13]^[14]

:

\begin{align}\gamma &= - \int_0^\infty { e^{-x} \ln x }\,dx \\&= -\int_0^1 \ln\ln\left (\frac{1}{x}\right) dx \\&=  \int_0^\infty \left (\frac1{e^x-1}-\frac1{xe^x} \right)dx = \int_0^1\left(\frac 1{\ln x} + \frac 1{1-x}\right)dx\\&=  \int_0^\infty \left (\frac1{1+x^k}-e^{-x} \right)\frac{dx}{x},\quad k>0.\end{align}

:

\int_0^\infty {e^{-x^2} \ln x}\,dx = -\frac{(\gamma+2\ln 2)\sqrt{\pi}}{4}

:

\int_0^\infty {e^{-x} \ln^2 x}\,dx = \gamma^2 + \frac{\pi^2}{6} .

오일러-마스케로니 상수의 값은 다음 정적분으로도 구할 수 있다.

:

\begin{align}\gamma&=-\Gamma'(1)\\&=-\int_{0}^{\infty}e^{-t}\log{t}dt\\&=-\int_{0}^{1}\log\log\frac{1}{u}du\qquad(u=e^{-t})\\&=-\int_{-\infty}^{\infty}ue^{u-e^u}du\qquad(u=\log{t})\\\end{align}

또는

:

\begin{align}\log{t}&=\int_{1}^{t}\frac{1}{s}ds\\&=\int_{1}^{t}\int_{0}^{\infty}e^{-su}duds\\&=\int_{0}^{\infty}\int_{1}^{t}e^{-su}dsdu\\&=\int_{0}^{\infty}\frac{e^{-u}-e^{-tu}}{u}du\\\end{align}

를 사용하면

:

\begin{align}\gamma&=-\int_{0}^{\infty} e^{-t} \log{t}dt\\&=-\int_{0}^{\infty}\int_{0}^{\infty}\frac{e^{-u}-e^{-tu}}{u}du\;e^{-t}dt\\&=\int_{0}^{\infty}\int_{0}^{\infty}\frac{e^{-tu}-e^{-u}}{u}du\;e^{-t}dt\\&=\int_{0}^{\infty}\left(\int_{0}^{\infty}\frac{e^{-t(u+1)}}{u}dt-\int_{0}^{\infty}\frac{e^{-u}e^{-t}}{u}dt\right)du\\&=\int_{0}^{\infty}\left(\frac{1}{u(u+1)}-\frac{e^{-u}}{u}\right)du\\\end{align}

가 되고,

\delta\to+0

일 때

:

\begin{align}\left|\int_{\delta}^{e^\delta-1}\frac{1}{u(u+1)}du\right|&\le\left|\int_{\delta}^{e^\delta-1}\frac{1}{\delta}du\right|\\&=O(\delta)\\\end{align}

이므로

:

\begin{align}\gamma&=\lim_{\delta\to+0}\int_{\delta}^{\infty}\left(\frac{1}{u(u+1)}-\frac{e^{-u}}{u}\right)du\\&=\lim_{\delta\to+0}\int_{\delta}^{\infty}\frac{1}{u(u+1)}du-\int_{\delta}^{\infty}\frac{e^{-s}}{s}ds\\&=\lim_{\delta\to+0}\int_{e^\delta-1}^{\infty}\frac{1}{u(u+1)}du-\int_{\delta}^{\infty}\frac{e^{-s}}{s}ds\\&=\lim_{\delta\to+0}\int_{\delta}^{\infty}\frac{e^t}{(e^t-1)e^t}dt-\int_{\delta}^{\infty}\frac{e^{-s}}{s}ds\qquad(u=e^t-1)\\&=\lim_{\delta\to+0}\int_{\delta}^{\infty}\frac{e^{-t}}{1-e^{-t}}dt-\int_{\delta}^{\infty}\frac{e^{-s}}{s}ds\\&=\int_{0}^{\infty}\left(\frac{e^{-t}}{1-e^{-t}}-\frac{e^{-t}}{t}\right)dt\end{align}

가 된다.

4. 4. 급수 표현

오일러 상수는 다음과 같은 급수 표현을 갖는다. 여기서

\zeta(s)

는 리만 제타 함수이다.

:

\gamma = \sum_{n=2}^{\infty}\frac{(-1)^n\zeta(n)}{n}

:

\gamma = 1 - \sum_{n=2}^{\infty}\frac{\zeta(n)-1}{n}

:

\gamma = \sum_{n=2}^{\infty}\frac{(n-1)(\zeta(n)-1)}{n}

:

\gamma = \ln 2 - \sum_{n=1}^{\infty}\frac{\zeta(2n+1)}{2^{2n}(2n+1)}

:

\gamma = \displaystyle\sum_{n=2}^{\infty}\frac{(-1)^n\zeta(n)}{m^{n-1}n}-m\ln\Gamma\left(\frac{m+1}{m}\right)

(여기서

m\in\mathbb{R}\setminus\left\{0,-1,-\dfrac{1}{k+1}\ (k\in\mathbb{Z}\setminus\{-1\})\right\}

)

:

\gamma = \lim_{m\rightarrow0}\left(\displaystyle\sum_{n=2}^{\infty}\frac{(-1)^n\zeta(n)}{m^{n-1}n}-m\ln\Gamma\left(\frac{m+1}{m}\right)\right)

^[103]

:

\gamma = \lim_{m\rightarrow -1}\left(\displaystyle\sum_{n=2}^{\infty}\frac{(-1)^n\zeta(n)}{m^{n-1}n}-m\ln\Gamma\left(\frac{m+1}{m}\right)\right)

^[104]

:

\gamma = \lim_{m\rightarrow(-1)/(k+1)}\left(\displaystyle\sum_{n=2}^{\infty}\frac{(-1)^n\zeta(n)}{m^{n-1}n}-m\ln\Gamma\left(\frac{m+1}{m}\right)\right)

(여기서

k\in\mathbb{Z}\setminus\{-1\}

)^[105]

:

\gamma = \frac{3}{2} - \ln 2 - \sum_{n=2}^{\infty}\frac{(-1)^n (n - 1)(\zeta(n)-1)}{n}

:

\gamma = 1 - \ln 2 + \sum_{n=2}^{\infty}\frac{(-1)^n(\zeta(n)-1)}{n}

5. 알려진 자릿수

레온하르트 오일러는 이 상수의 값을 소수점 아래 여섯 자리까지 처음으로 계산했다. 1781년, 오일러는 소수점 아래 16자리까지 계산했다. 이탈리아의 수학자 로렌초 마스케로니는 소수점 아래 32자리까지 계산을 시도했지만, 20~22번째 자리와 31~32번째 자리에서 오류를 범했다. 마스케로니는 20번째 자리부터 ...'''181'''12090082'''39'''로 계산했으나, 올바른 값은 ...'''065'''12090082'''40'''이었다.^[107]

오일러-마스케로니 상수의 알려진 십진 자릿수
일자	십진 자릿수	발견자
1734년	5	레온하르트 오일러
1735년	15	레온하르트 오일러
1781년	16	레온하르트 오일러
1790년	32	로렌초 마스케로니
1809년	22	요한 게오르크 폰 졸트너
1811년	22	카를 프리드리히 가우스
1812년	40	프리드리히 베른하르트 고트프리드 니콜라이
1857년	34	크리스티안 프레드릭 린드만
1861년	41	루드윅 오팅거
1867년	49	윌리엄 샹크스
1871년	99	제임스 위트브레드 리 글레이셔
1871년	101	윌리엄 샹크스
1877년	262	존 쿠치 애덤스
1952년	328	존 렌치
1961년	1050	헬무트 피셔와 칼 롱인 젤러
1962년	1271	도널드 커누스
1962년	3566	듀라 W. 스위니
1973년	4879	윌리엄 A. 베이어와 마이클 워터먼
1977년	20700	리차드 P. 브렌트
1980년	30100	리차드 P. 브렌트와 에드윈 맥밀런
1993년	172000	조나단 보웨인
1999년	108000000	페르릭 데미첼과 하비에르 구르동
2009년 3월 13일	29844489545	알랙산더 J. 리와 래이먼드 찬
2013년 12월 22일	119,377,958,182	알랙산더 J. 리
2016년 3월 15일	160,000,000,000	페터 트뤼프
2016년 5월 18일	250,000,000,000	론 왓킨스
2017년 8월 23일	477,511,832,674	론 왓킨스
2020년 5월 26일	600,000,000,100	김승민과 이언 커트리스^[107]

6. 일반화

는 디감마 함수 와 관련이 있으며, 따라서 두 함수 모두 1에서 평가될 때 감마 함수 의 도함수와도 관련이 있다. 따라서 다음이 성립한다.

: $-\gamma = \Gamma'(1) = \Psi(1).$

이는 다음 극한과 같다.

: $\begin{align}-\gamma &= \lim_{z\to 0}\left(\Gamma(z) - \frac1{z}\right) \\&= \lim_{z\to 0}\left(\Psi(z) + \frac1{z}\right).\end{align}$

추가적인 극한 결과는 다음과 같다.^[6]

: $\begin{align} \lim_{z\to 0}\frac1{z}\left(\frac1{\Gamma(1+z)} - \frac1{\Gamma(1-z)}\right) &= 2\gamma \\\lim_{z\to 0}\frac1{z}\left(\frac1{\Psi(1-z)} - \frac1{\Psi(1+z)}\right) &= \frac{\pi^2}{3\gamma^2}. \end{align}$

베타 함수와 관련된 극한 (감마 함수로 표현됨)은 다음과 같다.

: $\begin{align} \gamma &= \lim_{n\to\infty}\left(\frac{ \Gamma\left(\frac1{n}\right) \Gamma(n+1)\, n^{1+\frac1{n}}}{\Gamma\left(2+n+\frac1{n}\right)} - \frac{n^2}{n+1}\right) \\&= \lim\limits_{m\to\infty}\sum_{k=1}^m{m \choose k}\frac{(-1)^k}{k}\log\big(\Gamma(k+1)\big). \end{align}$

6. 1. 슈틸티예스 상수

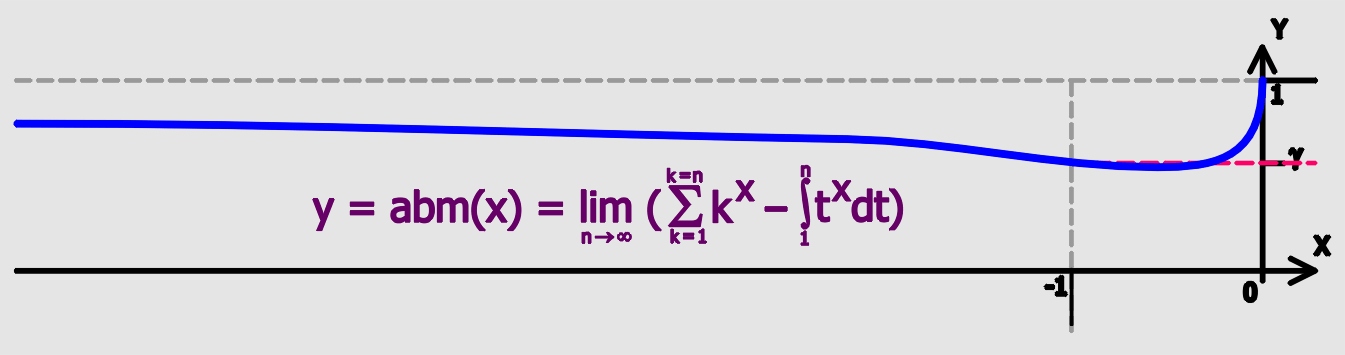
오일러-마스케로니 상수(일반적으로 그냥 오일러 상수)는 슈틸티예스 상수로 일반화될 수 있다.^[6] 슈틸티예스 상수는 리만 제타 함수의 로랑 급수 전개에 나타난다.^[6]

''오일러의 일반화된 상수''는 다음과 같이 주어진다.

\gamma_\alpha = \lim_{n\to\infty}\left(\sum_{k=1}^n \frac1{k^\alpha} - \int_1^n \frac1{x^\alpha}\,dx\right)

0 < α < 1 에 대해, γ는 특수한 경우 α = 1이다. α > 1 에 대해 확장하면 다음과 같다.

\gamma_{\alpha} = \zeta(\alpha) - \frac1{\alpha-1}

극한은 다음과 같다.

\gamma = \lim_{a\to 1}\left(\zeta(a) - \frac1{a-1}\right)

이것은 다음과 같이 더 일반화될 수 있다.

c_f = \lim_{n\to\infty}\left(\sum_{k=1}^n f(k) - \int_1^n f(x)\,dx\right)

임의의 감소 함수 f에 대해. 다음을 설정하면

f_n(x) = \frac{(\log x)^n}{x}

리만 제타 함수의 로랑 급수 전개에 나타나는 슈틸티예스 상수 γ_n이 발생한다.

:

\zeta(1+s)=\frac{1}{s}+\sum_{n=0}^\infty \frac{(-1)^n}{n!} \gamma_n s^n.

γ₀ = γ = 0.577...

n	γ_n의 근사값	OEIS
0	+0.5772156649015
1	-0.0728158454836
2	-0.0096903631928
3	+0.0020538344203
4	+0.0023253700654
100	-4.2534015717080 × 10¹⁷
1000	-1.5709538442047 × 10⁴⁸⁶

6. 2. 오일러-레머 상수

Euler–Lehmer constant^영어인 오일러-레머 상수는 공통 합동식의 역수의 합으로 주어진다.^[48]

:

\gamma(a,q) = \lim_{x\to \infty}\left (\sum_{0

기본적인 성질은 다음과 같다.

:

\begin{align}&\gamma(0,q) = \frac{\gamma -\log q}{q}, \\&\sum_{a=0}^{q-1} \gamma(a,q)=\gamma, \\&q\gamma(a,q) = \gamma-\sum_{j=1}^{q-1}e^{-\frac{2\pi aij}{q}}\log\left(1-e^{\frac{2\pi ij}{q}}\right),\end{align}

만약 최대공약수 이면,

:

q\gamma(a,q) = \frac{q}{d}\gamma\left(\frac{a}{d},\frac{q}{d}\right)-\log d.

6. 3. 마세르-그라맹 상수

오일러 상수의 2차원 일반화는 마세르-그라맹 상수이다.^[61] 이는 복소 평면에서 최소 ''k''개의 가우스 정수를 포함하는 원반의 최소 반지름

r_k

를 이용하여 다음과 같은 극한 차이로 정의된다.

:

\delta = \lim_{n\to\infty} \left( -\log n + \sum_{k=2}^n \frac{1}{\pi r_k^2} \right)

현재까지 알려진 바로는,

1.819776 < \delta < 1.819833

이다.^[62]

참조

_[1] 논문 Ramanujan and Euler's Constant https://maths-people[...] 1994
_[2] 웹사이트 The Euler constant: γ http://numbers.compu[...] 2024-11-01
_[3] 논문 Leonhard Euler's Integral: A Historical Profile of the Gamma Function http://mathdl.maa.or[...] 2016-12-03
_[4] 웹사이트 DLMF: §5.17 Barnes' 𝐺-Function (Double Gamma Function) ‣ Properties ‣ Chapter 5 Gamma Function https://dlmf.nist.go[...] 2024-11-01
_[5] 웹사이트 Digamma Function https://mathworld.wo[...] 2024-10-30
_[6] 웹사이트 Stieltjes Constants https://mathworld.wo[...] 2024-11-01
_[7] 서적 Laplace transforms Allen & Unwin 1973
_[8] 웹사이트 DLMF: §2.5 Mellin Transform Methods ‣ Areas ‣ Chapter 2 Asymptotic Approximations https://dlmf.nist.go[...] 2024-11-01
_[9] 웹사이트 DLMF: §6.6 Power Series ‣ Properties ‣ Chapter 6 Exponential, Logarithmic, Sine, and Cosine Integrals https://dlmf.nist.go[...] 2024-11-01
_[10] 웹사이트 Logarithmic Integral https://mathworld.wo[...] 2024-11-01
_[11] 웹사이트 DLMF: §10.32 Integral Representations ‣ Modified Bessel Functions ‣ Chapter 10 Bessel Functions https://dlmf.nist.go[...] 2024-11-01
_[12] 웹사이트 DLMF: §10.22 Integrals ‣ Bessel and Hankel Functions ‣ Chapter 10 Bessel Functions https://dlmf.nist.go[...] 2024-11-01
_[13] 웹사이트 DLMF: §10.8 Power Series ‣ Bessel Functions and Hankel Functions ‣ Chapter 10 Bessel Functions https://dlmf.nist.go[...] 2024-11-01
_[14] 웹사이트 DLMF: §10.24 Functions of Imaginary Order ‣ Bessel and Hankel Functions ‣ Chapter 10 Bessel Functions https://dlmf.nist.go[...] 2024-11-01
_[15] 웹사이트 DLMF: §11.6 Asymptotic Expansions ‣ Struve and Modified Struve Functions ‣ Chapter 11 Struve and Related Functions https://dlmf.nist.go[...] 2024-11-01
_[16] 웹사이트 DLMF: §13.2 Definitions and Basic Properties ‣ Kummer Functions ‣ Chapter 11 Confluent Hypergeometric Functions https://dlmf.nist.go[...] 2024-11-01
_[17] 웹사이트 DLMF: §9.12 Scorer Functions ‣ Related Functions ‣ Chapter 9 Airy and Related Functions https://dlmf.nist.go[...] 2024-11-01
_[18] 논문 Approximate formulas for some functions of prime numbers https://projecteucli[...] 1962
_[19] 서적 An introduction to the theory of numbers Oxford University Press 2008
_[20] 논문 Grandes valeurs de la fonction somme des diviseurs et hypothèse de Riemann http://zakuski.utsa.[...] 1984
_[21] 웹사이트 Mertens Constant https://mathworld.wo[...] 2024-11-01
_[22] 논문 Very Large Gaps between Consecutive Primes https://www.scienced[...] 1997-04-01
_[23] 웹사이트 Heuristics: Deriving the Wagstaff Mersenne Conjecture https://t5k.org/mers[...] 2024-11-01
_[24] 웹사이트 Porter's Constant https://mathworld.wo[...] 2024-11-01
_[25] 웹사이트 Eulers Constant https://num.math.uni[...] 2024-10-19
_[26] 서적 Mathematical Constants https://books.google[...] Cambridge University Press 2003-08-18
_[27] 웹사이트 Some of the most famous open problems in number theory https://webusers.imj[...] 2023
_[28] 서적 The Book of Numbers https://books.google[...] Springer Science & Business Media 1998-03-16
_[29] 웹사이트 On Euler's Constant https://webusers.imj[...] 2023
_[30] 논문 Generalized Euler constants Cambridge University Press 2008
_[31] 웹사이트 Euler-Mascheroni Constant Digits https://mathworld.wo[...] 2024-10-19
_[32] 논문 Computation of the Regular Continued Fraction for Euler's Constant https://www.jstor.or[...] 1977
_[33] 웹사이트 Euler-Mascheroni Constant Continued Fraction https://mathworld.wo[...] 2024-09-23
_[34] 간행물 On a continued fraction expansion for Euler's constant 2013-12-29
_[35] 웹사이트 Euler-Mascheroni Constant Approximations https://mathworld.wo[...] 2024-10-19
_[36] arXiv 6+infinity new expressions for the Euler-Mascheroni constant
_[37] journal Another relation between π, e, γ and ζ(n) https://doi.org/10.1[...]
_[38] journal Double Integrals for Euler's Constant and $\textstyle \frac{4}{\pi}$ and an Analog of Hadjicostas's Formula https://doi.org/10.2[...] 2024-04-27
_[39] journal Ramanujan's formula for the harmonic number https://www.scienced[...] 2024-04-27
_[40] journal An approximate expression for the value of 1 + 1/2 + 1/3 + ... + 1/r https://books.google[...]
_[41] arXiv Ramanujan's Harmonic Number Expansion into Negative Powers of a Triangular Number
_[42] journal On the Stirling expansion into negative powers of a triangular number https://www.research[...]
_[43] journal Sur la série harmonique http://eudml.org/doc[...] Carilian-Goeury et Vor Dalmont
_[44] book An Introduction to the Theory of Infinite Series https://www.dbraulib[...] American Mathematical Society
_[45] book A Course of Modern Analysis
_[46] journal Proof without Words: Sum of Reciprocals of Triangular Numbers
_[47] book Riemann's Zeta Function Academic Press
_[48] 웹사이트 Euler-Mascheroni Constant https://mathworld.wo[...] 2024-10-19
_[49] journal Rediscovery of Malmsten's integrals, their evaluation by contour integration methods and some related results https://link.springe[...] 2014-10-01
_[50] 간행물 Vacca-type series for values of the generalized-Euler-constant function and its derivative 2008-08-04
_[51] 웹사이트 Mertens Theorem https://mathworld.wo[...] 2024-10-08
_[52] journal Ueber die richtige Werthbestimmung der Constante des Integrallogarithmus. https://www.degruyte[...] 1862-01-01
_[53] journal I. On the calculation of the numerical value of Euler's constant, which Professor Price, of Oxford, calls E https://royalsociety[...] 1867-12-31
_[54] 웹사이트 Bernoullische Zahlen und Eulersche Konstante https://zbmath.org/?[...] 2024-10-27
_[55] journal On the computation of Euler's constant 1963
_[56] journal Error Analysis of a Computation of Euler's Constant https://www.jstor.or[...] 1974
_[57] journal Some new algorithms for high-precision computation of Euler's constant https://www.ams.org/[...] 1980
_[58] 웹사이트 The Euler constant: γ https://scipp.ucsc.e[...] 2024-10-27
_[59] 웹사이트 The Euler constant: γ https://scipp.ucsc.e[...] 2024-10-27
_[60] 웹사이트 The Euler constant: γ https://scipp.ucsc.e[...] 2024-10-27
_[61] 웹사이트 Masser-Gramain Constant https://mathworld.wo[...] 2024-10-19
_[62] 웹사이트 Numerical approximation of the Masser-Gramain constant to four decimal digits https://www.lri.fr/~[...] 2024-10-03
_[63] OEIS
_[64] book The differential and integral calculus Baldwin and Craddoc 1836–1842
_[65] book The Dilemma of Einstein, Podolsky and Rosen – 60 Years Later Israel Physical Society 1996
_[66] book Algorithmic Number Theory Springer 1998
_[67] thesis Entwurf und Entwicklung einer objektorientierten Bibliothek für algorithmische Zahlentheorie https://www-old.cdc.[...] Universität des Saarlandes 1997
_[68] journal Criteria for irrationality of Euler's constant 2003
_[69] journal Applications of a theorem by A. B. Shidlovski https://carmamaths.o[...] 1968-06-04
_[70] journal Euler–Lehmer constants and a conjecture of Erdos 2010
_[71] arXiv On linear forms containing the Euler constant 2009-02-28
_[72] 간행물 On the arithmetic nature of the values of the gamma function, Euler's constant, and Gompertz's constant https://projecteucli[...] 2012
_[73] 간행물 Transcendence of Generalized Euler Constants https://www.jstor.or[...] 2013
_[74] 서적 Die Eulersche Konstante {{math|γ}} und verwandte Zahlen University of Göttingen 2005
_[75] 간행물 An antisymmetric formula for Euler's constant http://home.earthlin[...] 2006-05-29
_[76] 간행물 Double integrals for Euler's constant and $\log \frac{4}{\pi}$ and an analog of Hadjicostas's formula 2005
_[77] 서적 New Vacca-type rational series for Euler's constant and its 'alternating' analog $\log \frac{4}{\pi}$ 2005-08-01
_[78] 간행물 Euler's constant, {{math|''q''}}-logarithms, and formulas of Ramanujan and Gosper 2006
_[79] 간행물 A Quicker Convergence to Euler's Constant 1993-05
_[80] 간행물 Expansions of generalized Euler's constants into the series of polynomials in {{math|π⁻²}} and into the formal enveloping series with rational coefficients only 2016
_[81] 간행물 A new analytical expression for the number π and some historical considerations 1910
_[82] 간행물 Nuova serie per la costante di Eulero, {{math|''C''}} = 0,577...". Rendiconti, Accademia Nazionale dei Lincei, Roma, Classe di Scienze Fisiche 1926
_[83] 간행물 On Dr. Vacca's series for {{math|''γ''}} 1910
_[84] 간행물 Note on Dr. Vacca's series for {{math|''γ''}} 1912
_[85] 간행물 On certain series of Mr. Hardy 1927
_[86] 간행물 Three notes on Ser's and Hasse's representations for the zeta-functions http://math.colgate.[...] 2018
_[87] 서적 Summability Calculus. A Comprehensive Theory of Fractional Finite Sums Springer 2018
_[88] OEIS Absolute value of the numerators of a series converging to Euler's constant
_[89] OEIS Denominators of a series converging to Euler's constant
_[90] 서적 Excursions in Multiplicative Number Theory https://books.google[...] Birkhäuser/Springer 2022
_[91] OEIS Decimal expansion of exp(gamma)
_[92] 간행물 Integral Representations for the Euler–Mascheroni Constant {{math|''γ''}} 2010-09-01
_[93] arXiv An infinite product for {{math|''e{{sup|γ}}''}} via hypergeometric formulas for Euler's constant, {{math|''γ''}} 2003
_[94] 간행물 Euler's Constant to 1271 Places https://www.jstor.or[...] American Mathematical Society 1962-07
_[95] 웹사이트 Large Computations http://www.numberwor[...] 2011-03-07
_[96] 웹사이트 Records Set by y-cruncher http://www.numberwor[...] 2018-04-30
_[97] 웹사이트 Euler-Mascheroni Constant https://ehfd.github.[...] 2020-02-15
_[98] 간행물 Allen Orr and the genetics of adaptation 2021-10
_[99] 간행물 A fragment on Euler's constant in Ramanujan's lost notebook https://scholarworks[...] 2008-01
_[100] OEIS Decimal expansion of Euler's constant (or the Euler-Mascheroni constant), gamma
_[101] 문서 Weisstein
_[102] 웹사이트 Jeff Miller, Earliest Uses of Various Mathematical Symbols http://members.aol.c[...]
_[103] 문서 Limit[Sum[(-1)^n Zeta[n]/(m^(n - 1)n), {n, 2, Infinity}] - m Log[Gamma[(m + 1)/m]]
_[104] 문서 Limit[Sum[(-1)^n Zeta[n]/(m^(n - 1)n), {n, 2, Infinity}] - m Log[Gamma[(m + 1)/m]]
_[105] 문서 Limit[Sum[(-1)^n Zeta[n]/(m^(n - 1)n), {n, 2, Infinity}] - m Log[Gamma[(m + 1)/m]], m -> -1/(k+1)]=EulerGamma
_[106] 저널 Theoriae logarithmi integralis lineamenta nova 1837
_[107] 웹사이트 Euler–Mascheroni constant world record by Seungmin Kim https://ehfd.github.[...]
_[108] 웹사이트 y-cruncher by Alexander Yee https://web.archive.[...]

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com