발산 정리

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
- 2.1. 수식 표현
3. 역사
- 3.1. 발견 과정 (일본어 위키 텍스트 기반)
4. 유체 흐름을 이용한 설명 (영어 위키 텍스트 기반)
- 4.1. 보존 법칙과의 관계
5. 수학적 표현 (영어 위키 텍스트 기반)
- 5.1. 공식
6. 증명 (영어 위키 텍스트 기반)
7. 활용
- 7.1. 전자기학 응용 (일본어 위키 텍스트 기반)
  - 7.1.1. 맥스웰 방정식
8. 일반화
- 8.1. 일반화된 스토크스 정리와의 관계 (일본어 위키 텍스트 기반)
9. 예제
참조

1. 개요

발산 정리는 유계 영역의 폐포에서 정의된 벡터장의 발산에 대한 부피 적분을, 해당 영역의 경계면을 통과하는 벡터장의 면적분으로 나타내는 정리이다. 이 정리는 유체 흐름, 전자기학, 중력 등 다양한 물리 현상을 설명하는 데 활용되며, 가우스 법칙과 같은 중요한 법칙들을 유도하는 데 사용된다. 발산 정리는 일반화된 스토크스 정리의 특수한 경우이며, 미적분학의 기본 정리와 그린 정리와도 관련이 있다.

더 읽어볼만한 페이지

미적분학 정리 - 연쇄 법칙
연쇄 법칙은 둘 이상의 미분 가능한 함수 합성의 미분법을 제공하며, z의 y에 대한 순간적인 변화율과 y의 x에 대한 순간적인 변화율을 곱하여 z의 x에 대한 순간적인 변화율을 계산하는 직관적인 아이디어를 바탕으로 실변수 함수, 다변수 함수 등 다양한 경우에 적용된다.
미적분학 정리 - 미적분학의 기본 정리
미적분학의 기본 정리는 미분과 적분 사이의 관계를 설명하는 미적분학의 핵심 정리로서, 제1 기본 정리와 제2 기본 정리로 구성되며, 17세기에 발전되어 르베그 적분 등으로 일반화된다.
벡터 미적분학 - 벡터장
벡터장은 유클리드 공간이나 미분다양체의 각 점에 벡터를 대응시키는 사상으로, 유클리드 공간에서는 벡터값 함수로 표현되고 미분다양체에서는 접다발의 단면이나 도함수로 정의되며, 물리학, 기상, 유체역학, 전자기학, 컴퓨터 그래픽스 등 다양한 분야에서 응용된다.
벡터 미적분학 - 기울기 (벡터)
기울기(벡터)는 스칼라장의 특정 지점에서 값이 가장 빠르게 증가하는 방향과 변화율을 나타내는 벡터로, 함수의 등위면에 수직이며 크기는 해당 방향의 변화율을 나타내고, 스칼라 함수의 각 성분에 대한 편미분으로 구성되며 나블라 연산자로 표현된다.
수리물리학 - 라플라스 변환
라플라스 변환은 함수 f(t)를 복소수 s를 사용하여 적분을 통해 다른 함수 F(s)로 변환하는 적분 변환이며, 선형성을 가지고 미분방정식 풀이 등 공학 분야에서 널리 사용된다.
수리물리학 - 불확정성 원리
불확정성 원리는 1927년 베르너 하이젠베르크가 발표한 양자역학의 기본 원리로, 입자의 위치와 운동량 등 짝을 이루는 물리량들을 동시에 정확하게 측정하는 것이 불가능하며, 두 물리량의 불확정성은 플랑크 상수에 의해 제한된다.

발산 정리
개요
이름	발산 정리
다른 이름	가우스 정리 오스트로그라드스키 정리
분야	미적분학
설명
내용	발산정리는 벡터장의 발산과 표면적분을 연관시키는 정리이다.
공식	∫∫S F ⋅ n dS = ∫∫∫V (∇ ⋅ F) dV
의미	닫힌 곡면 S를 통과하는 벡터장 F의 유출량은 부피 V에 대한 F의 발산의 적분과 같다.
역사
발명가	카를 프리드리히 가우스, 미하일 오스트로그라드스키
발명 시기	19세기 초
응용
분야	유체역학 전자기학 열역학

2. 정의

3차원 유클리드 공간에서, 유계 영역의 폐포 $D$ 와 그 경계면 $\partial D$ 에 대해, $\mathcal C^1$ 함수인 벡터장 $\mathbf F$ 에 대해 발산 정리가 성립한다. 이 정리는 스토크스의 정리로부터 유도할 수 있다.^[4]^[5]

발산 정리는 벡터장이 영역 $V$ 의 표면에서 유출되는 양이 영역 전체에서의 벡터장의 발산 값의 적분과 같음을 나타낸다. div라는 연산이 '발산'(혹은 '용출량')이라고 불리는 이유이기도 하다.

2. 1. 수식 표현

유계 영역의 폐포

D\subseteq\mathbb R^n

의 외향 경계면

\partial D

가 유한 개의 조각마다 매끄러운 단순 닫힌곡면들로 이루어졌다고 하자. 또한,

\mathbf F\colon D\to\mathbb R^n

가

\mathcal C^1

함수라고 하면, '''발산 정리'''에 따라 다음이 성립한다.^[4]^[5]

:

\oint_{\partial D}\mathbf F\cdot d\mathbf S=\int_D\nabla\cdot\mathbf FdV

여기서

:

\operatorname{div}\mathbf F=\nabla\cdot\mathbf F=\frac{\partial F_1}{\partial x_1}+\cdots+\frac{\partial F_n}{\partial x_n}

은 발산이다.

\mathbb{R}^n

의 부분 집합

V

가 콤팩트 공간이고 조각적 매끄러운 경계

S

를 갖는다고 가정하자(

\partial V = S

).

n=3

인 경우,

V

는 3차원 공간의 부피를 나타낸다. 만약

\mathbf{F}

가

V

의 근방에서 정의된 연속적으로 미분 가능한 벡터장이라면, 다음이 성립한다.

:

\iiint_V\left(\mathbf{\nabla}\cdot\mathbf{F}\right)\,\mathrm{d}V=

\scriptstyle S

(\mathbf{F}\cdot\mathbf{\hat{n}})\,\mathrm{d}S .

좌변은 부피

V

에 대한 부피 적분이고, 우변은 부피

V

의 경계에 대한 곡면 적분이다. 닫힌 가측 집합

\partial V

는 바깥쪽을 향하는 법선에 의해 방향이 지정되며,

\mathbf{\hat{n}}

은 경계

\partial V

의 거의 모든 지점에서 바깥쪽을 향하는 단위 법선이다.

'''R'''³에서 정의된 매끄러운 벡터장

\boldsymbol{F}=(F_1,F_2,F_3)

에 대해 ''F''의 '''발산''' div ''F''는 다음과 같이 정의된다.

:

\operatorname{div}\boldsymbol{F}:=\frac{\partial F_1}{\partial x}+\frac{\partial F_2}{\partial y}+\frac{\partial F_3}{\partial z}

발산은 ∇(델)를 사용하면 다음과 같이 표현된다.

:

\operatorname{div}\boldsymbol{F}=\boldsymbol{\nabla}\cdot\boldsymbol{F}

''V''를 '''R'''³에서 매끄러운 경계 ∂''V''를 갖는 유계 영역으로 하고, ''F''를 ''V''의 폐포에서 정의된 매끄러운 벡터장이라고 하면, 다음이 성립한다.

:

\iiint_V \operatorname{div} \boldsymbol{F}\,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z=\iint_{\partial V} \boldsymbol{F}\!\cdot\!\boldsymbol{n}\,\mathrm{d}S

여기서

\boldsymbol{n}

은

V

의 외향 단위 법선 벡터이다.

3. 역사

발산 정리는 여러 수학자에 의해 독립적으로 발견되었다. 미하일 오스트로그라츠키(Михаил Васильевич Остроградский^ru)가 발산 정리의 증명을 가장 먼저 발표했다. 오스트로그라츠키는 부피적분을 표면적분으로 바꾸는 도구로서 발산 정리를 이용했다.^[24] 카를 프리드리히 가우스 또한 중력 이론에 대해 연구할 당시 이 정리를 증명했으나, 그의 결과는 수년간 출판되지 않았다.^[24]

3. 1. 발견 과정 (일본어 위키 텍스트 기반)

1762년에 조제프루이 라그랑주가 발산 정리를 처음 발견했다.^[14]^[22] 라그랑주는 유체 역학 연구에서 표면 적분을 사용했으며, 1760년에 표면 적분의 개념을 도입했고, 1811년 그의 저서 ''해석역학''의 두 번째 판에서 더 일반적인 용어로 다시 소개했다.^[13] 이후 카를 프리드리히 가우스(1813년), 조지 그린(1825년), 미하일 오스트로그라츠키(1831년)가 각각 독립적으로 재발견했다.^[22]

가우스는 1813년 타원체에 대한 중력의 인력을 연구하면서 표면 적분을 사용했고, 이때 발산 정리의 특수한 경우를 증명했으며, 1833년과 1839년에 추가적인 특수한 경우를 증명했다.^[15]^[13]^[16] 그린은 1828년 ''전기 및 자기 이론에 대한 수학적 분석의 적용에 관한 에세이''에서 특수한 경우를 증명했다.^[18]^[16]

그러나 발산 정리의 일반적인 경우를 처음으로 증명한 사람은 미하일 오스트로그라츠키였다. 그는 1826년 열 흐름에 대한 연구의 일환으로 발산 정리를 증명했다.^[17] 오스트로그라츠키는 1828년에 파리에서 구두 발표했지만, 그 내용은 공표되지 않았고, 1831년 상트페테르부르크에서의 학회 보고만 남아 있다.^[23] 그는 부피적분을 표면적분으로 바꾸는 도구로서 발산정리를 이용했다. 가우스 또한 중력이론에 대해 연구할 당시 이미 이 정리를 증명했지만, 그의 결과는 수년간 출판되지 않았다.^[24]

이 외에도 시메옹 드니 푸아송이 1824년 탄성에 관한 논문에서, 프레데릭 사루스가 1828년 부유하는 물체에 대한 연구에서 특수한 경우를 증명했다.^[19]^[16]

4. 유체 흐름을 이용한 설명 (영어 위키 텍스트 기반)

벡터장은 종종 유체 (기체 또는 액체)의 속도장의 예시를 사용하여 설명된다. 움직이는 액체는 각 지점에서 벡터로 표현될 수 있는 속도(속도와 방향)를 가지므로, 임의의 순간에 액체의 속도는 벡터장을 형성한다. 액체 덩어리 내부에 있는 가상의 닫힌 표면 ''S''를 고려하면, 이 표면은 액체의 부피를 둘러싸고 있다. 임의의 시간에 부피에서 유출되는 액체의 플럭스는 이 표면을 가로지르는 유체의 부피 유속, 즉 표면에서의 속도의 표면 적분과 같다.

액체는 압축할 수 없으므로 닫힌 부피 내의 액체량은 일정하다. 소스 또는 싱크가 없는 경우 ''S''에서 유출되는 액체의 플럭스는 0이다. 액체가 움직이면 표면 ''S''의 일부 지점에서 부피로 흘러 들어가고 다른 지점에서 부피 밖으로 흘러 나갈 수 있지만, 임의의 순간에 유입 및 유출되는 양은 같으므로 부피에서 유출되는 액체의 ''순'' 플럭스는 0이다.

그러나 파이프와 같이 액체가 유입되는 액체의 ''소스''가 닫힌 표면 안에 있는 경우, 추가 액체는 주변 액체에 압력을 가하여 모든 방향으로 외부로 흐르게 한다. 이로 인해 표면 ''S''를 통해 순 유출이 발생한다. ''S''를 통해 외부로 흐르는 플럭스는 파이프에서 ''S''로 유입되는 유체의 부피 유속과 같다. 마찬가지로 ''S'' 내부에 액체를 배출하는 파이프와 같은 ''싱크'' 또는 배수구가 있는 경우, 액체의 외부 압력은 배수구 위치를 향해 안쪽으로 향하는 액체 전체의 속도를 유발한다. 표면 ''S''를 통해 안쪽으로 유입되는 액체의 부피 유속은 싱크에 의해 제거되는 액체의 유속과 같다.

''S'' 내부에 여러 개의 액체 소스와 싱크가 있는 경우, 표면을 통과하는 플럭스는 소스에 의해 추가된 액체의 부피 유속을 합산하고 싱크에 의해 배수된 액체의 유속을 뺀 값으로 계산할 수 있다. 소스 또는 싱크를 통한 액체의 부피 유속(싱크를 통한 유량에는 음의 부호가 부여됨)은 파이프 입구에서의 속도장의 ''발산''과 같으므로, ''S''로 둘러싸인 부피 전체의 액체의 발산을 합산(적분)하면 ''S''를 통과하는 플럭스의 부피 유속과 같다. 이것이 발산 정리이다.^[2]

4. 1. 보존 법칙과의 관계

발산 정리는 모든 보존 법칙에 사용될 수 있으며, 이는 모든 싱크와 소스의 총 부피, 즉 발산의 부피 적분이 부피의 경계를 가로지르는 순 유량과 같다고 명시한다.^[3]

5. 수학적 표현 (영어 위키 텍스트 기반)

3차원 공간에서 발산 정리는 부피 적분과 면적분 사이의 관계를 나타낸다. Divergence theorem^영어에 따르면, 어떤 영역을 둘러싼 닫힌 곡면을 통과하는 벡터장의 흐름은, 그 영역 내에서 벡터장의 발산의 총합과 같다.^[4]^[5]

직관적으로 설명하면, 발산 정리 공식의 좌변은 주어진 부피( $V$ ) 내의 모든 소스(source)의 총합을 나타내고, 우변은 그 부피의 경계( $\partial V$ )를 가로지르는 총 흐름을 나타낸다.

5. 1. 공식

유계 영역의 폐포

D\subseteq\mathbb R^n

의 외향 경계면

\partial D

가 유한 개의 조각마다 매끄러운 단순 닫힌곡면들로 이루어졌다고 하자. (경계면이 하나의 닫힌곡면일 필요충분조건은

D

가 축약 가능 공간임이다.) 또한,

\mathbf F\colon D\to\mathbb R^n

가

\mathcal C^1

함수라고 하자. 그렇다면, '''발산 정리'''에 따르면, 다음이 성립한다.

:

\oint_{\partial D}\mathbf F\cdot d\mathbf S=\int_D\nabla\cdot\mathbf FdV

여기서

:

\operatorname{div}\mathbf F=\nabla\cdot\mathbf F=\frac{\partial F_1}{\partial x_1}+\cdots+\frac{\partial F_n}{\partial x_n}

은 발산이다.

V

가

\mathbb{R}^n

의 부분 집합이라고 가정하자. (

n=3

인 경우,

V

는 3차원 공간의 부피를 나타낸다). 이 부분 집합은 콤팩트 공간이고 조각적 매끄러운 경계

S

를 갖는다(

\partial V = S

로 표시). 만약

\mathbf{F}

가

V

의 근방에서 정의된 연속적으로 미분 가능한 벡터장이라면:^[4]^[5]

:

\iiint_V\left(\mathbf{\nabla}\cdot\mathbf{F}\right)\,\mathrm{d}V=\oint_{\partial V}(\mathbf{F}\cdot\mathbf{\hat{n}})\,\mathrm{d}S

좌변은 부피

V

에 대한 부피 적분이고, 우변은 부피

V

의 경계에 대한 곡면 적분이다. 닫힌 가측 집합

\partial V

는 바깥쪽을 향하는 법선에 의해 방향이 지정되며,

\mathbf{\hat{n}}

은 경계

\partial V

의 거의 모든 지점에서 바깥쪽을 향하는 단위 법선이다. (

\mathrm{d} \mathbf{S}

는

\mathbf{n} \mathrm{d} S

의 축약형으로 사용될 수 있다.) 위의 직관적인 설명에 따르면, 방정식의 좌변은 부피

V

내의 소스(source)의 총합을 나타내고, 우변은 경계

S

를 가로지르는 총 흐름을 나타낸다.

'''R'''³에서 정의된 매끄러운 벡터장

\boldsymbol{F}=(F_1,F_2,F_3)

에 대해 ''F''의 '''발산''' div ''F''를

:

\operatorname{div}\boldsymbol{F}:=\frac{\partial F_1}{\partial x}+\frac{\partial F_2}{\partial y}+\frac{\partial F_3}{\partial z}

로 정의한다. 발산은 델(nabla)을 사용하면,

:

\operatorname{div}\boldsymbol{F}=\boldsymbol{\nabla}\cdot\boldsymbol{F}

로 표현되며, 벡터의 내적이 된다.

''V''를 '''R'''³에서 매끄러운 (여기서는 ''C''¹급이면 충분하다) 경계 ∂''V''를 갖는 유계 영역 (= 연결된 열린 집합)으로 하고, ''F''를 ''V''의 폐포에서 정의된 매끄러운 벡터장이라고 하면,

:

\iiint_V \operatorname{div} \boldsymbol{F}\,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z=\iint_{\partial V} \boldsymbol{F}\!\cdot\!\boldsymbol{n}\,\mathrm{d}S

가 성립한다. 여기서, ''n''은 ''V''의 외향 단위 법선 벡터로 한다. 또한, 정리가 성립하기 위해서는 ∂''V''가 구분적으로 ''C''¹ 급이면 충분하다.

이 정리는 div라는 연산이 발산 (혹은 ''용출량'')이라고 불리는 이유이기도 하다. 우변은 벡터장이 영역 ''V''의 표면에서 유출되는 양이며, 이것이 좌변이 나타내는 영역 전체에서의 벡터장의 발산 값의 적분과 같음을 나타낸다.

이 정리는 일반적인 스토크스의 정리로부터 유도할 수 있다.

6. 증명 (영어 위키 텍스트 기반)

유클리드 공간의 열린 유계 부분 집합에 대한 증명과 경계를 가진 콤팩트 리만 다양체에 대한 증명은 다음과 같다.^[8]^[9]

'''유클리드 공간의 열린 유계 부분 집합에 대한 증명'''^[8]

먼저, $u \in C_c^1(\mathbb{R}^n)$ 인 경우로 축소한다. $\overline{\Omega}$ 에서 $\phi = 1$ 이 되도록 $\phi \in C_c^{\infty}(O)$ 를 선택한다. $\phi u \in C_c^{1}(O) \subset C_c^1(\mathbb{R}^n)$ 이고 $\overline{\Omega}$ 에서 $\phi u = u$ 이므로, $\phi u$ 에 대한 정리를 증명하는 것으로 충분하다. 따라서 $u \in C_c^1(\mathbb{R}^n)$ 라고 가정할 수 있다.

임의의 $x_0 \in \partial \Omega$ 를 취한다. $\overline{\Omega}$ 이 $C^1$ 경계를 갖는다는 가정은 $\mathbb{R}^n$ 의 $x_0$ 의 열린 근방 $U$ 가 존재하여 $\partial \Omega \cap U$ 가 $C^1$ 함수의 그래프이고 $\Omega \cap U$ 가 이 그래프의 한쪽에 놓인다는 것을 의미한다. 더 정확하게는, $\Omega$ 의 평행 이동과 회전 후에, $r > 0$ 및 $h > 0$ 과 $C^1$ 함수 $g : \mathbb{R}^{n - 1} \to \mathbb{R}$ 이 존재하여 표기법으로

$x' = (x_1, \dots, x_{n - 1}),$

다음이 성립한다.

$U = \{x \in \mathbb{R}^n : |x'| < r \text{ and } |x_n - g(x')| < h\}$

그리고 $x \in U$ 에 대해,

$\begin{align}x_n = g(x') & \implies x \in \partial \Omega, \\$

h < x_n - g(x') < 0 & \implies x \in \Omega, \\

0 < x_n - g(x') < h & \implies x \notin \Omega. \\\end{align}

\partial \Omega

가 콤팩트하므로, 위 형태의 유한 개의 근방

U_1, \dots, U_N

으로

\partial \Omega

을 덮을 수 있다.

\{\Omega, U_1, \dots, U_N\}

이

\overline{\Omega} = \Omega \cup \partial \Omega

의 열린 덮개임을 주목한다. 이 덮개에 종속적인

C^{\infty}

분할의 합을 사용함으로써,

u

가

\Omega

내에서 콤팩트한 지지도를 갖거나

u

가 어떤

U_j

내에서 콤팩트한 지지도를 갖는 경우에 정리를 증명하는 것으로 충분하다.

만약

u

가

\Omega

내에서 콤팩트한 지지도를 갖는다면, 모든

i \in \{1, \dots, n\}

에 대해,

\int_{\Omega} u_{x_i}\,dV = \int_{\mathbb{R}^n}u_{x_i}\,dV = \int_{\mathbb{R}^{n - 1}} \int_{-\infty}^{\infty}u_{x_i}(x)\,dx_i\,dx' = 0

(미적분학의 기본 정리)이고

\int_{\partial \Omega}u\nu_i\,dS = 0

(

u

가

\partial \Omega

의 근방에서 사라지므로)이다. 따라서 이 경우 정리는 성립한다.

이제

u

가 어떤

U_j

내에서 콤팩트한 지지도를 갖는다고 가정한다. 표기법을

U = U_j

로 변경하고, 위에서

U

를 설명하는 데 사용된 표기법을 사용한다. 이는

\Omega

을 회전하고 평행 이동했음을 의미하지만, 정리는 좌표의 회전과 평행 이동에 불변하므로 유효하다.

u(x) = 0

(

|x'| \geq r

또는

|x_n - g(x')| \geq h

인 경우)이므로, 각

i \in \{1, \dots, n\}

에 대해

\begin{align}\int_{\Omega}u_{x_i}\,dV &= \int_

7. 활용

발산 정리는 많은 물리 법칙들을 미분 형태와 적분 형태로 표현할 수 있게 해준다. 정전기학에서의 가우스 법칙, 자기학에 대한 가우스 법칙, 중력에 대한 가우스 법칙 등이 그 예시이다.^[12]연속 방정식은 유체역학, 전자기학, 양자역학, 상대성 이론 등 여러 분야에서 질량, 운동량, 에너지, 확률 등 다양한 양의 보존을 설명한다. 일반적으로 보존되는 양의 흐름의 발산은 해당 양의 '소스' 또는 '싱크' 분포와 같다고 표현된다. 발산 정리는 이러한 방정식을 미분 형태(발산)와 적분 형태(플럭스)로 나타낼 수 있게 한다.^[12]제곱 반비례 법칙은 가우스 법칙 형태(미분 및 적분 형태)로도 표현 가능하다. 쿨롱의 법칙에서 유도되는 정전기학에서의 가우스 법칙과 만유인력의 법칙에서 유도되는 중력에 대한 가우스 법칙이 그 예시이다. 제곱 반비례 공식에서 가우스 법칙 형태의 방정식을 유도하거나, 그 반대의 과정은 두 경우 모두 동일하다.

7. 1. 전자기학 응용 (일본어 위키 텍스트 기반)

발산 정리는 전자기학에서 전하에서 솟아나는 전장에 대한 가우스 법칙을 수학적으로 표현하는 데 사용된다.

7. 1. 1. 맥스웰 방정식

전자기학에서 발산 정리를 응용하여, 전하에서 솟아나는 전장에 대한 가우스 법칙을 수학적으로 기술할 수 있다(⇒ 맥스웰 방정식).^[1]:

\oint_S \boldsymbol{E} \cdot \mathrm{d} \boldsymbol{S} = \frac{Q}{\varepsilon _0} = \frac{1}{\varepsilon _0} \int_V \rho\, \mathrm{d} V

적분 형태 표현^[1]

:

\operatorname{div} \boldsymbol{E} = \frac{\rho}{\varepsilon _0}

미분 형태 표현 (정전장의 가우스 발산 정리)^[1]

8. 일반화

아인슈타인 표기법으로 정리를 작성하면 다음과 같다.

: $\iiint_V \dfrac{\partial \mathbf{F}_i}{\partial x_i} \, \mathrm{d}V= \oint_S \mathbf{F}_i n_i\, \mathrm{d}S$

벡터장 ${\mathbf{F}}$를 랭크-n 텐서장 ${\mathbf{T}}$로 바꾸면 다음과 같이 일반화할 수 있다.^[20]

: $\iiint_V \dfrac{\partial T_{i_1i_2\cdots i_q\cdots i_n}}{\partial x_{i_q}} \, \mathrm{d}V= \oint_S T_{i_1i_2\cdots i_q\cdots i_n}n_{i_q}\, \mathrm{d}S .$

여기서 각 항에서 적어도 하나의 지수에 대해 텐서 축약이 발생한다. 이 형태의 정리는 여전히 3차원이며, 각 지수는 1, 2, 3의 값을 갖는다. 일반 상대성 이론의 4차원 시공간과 같이 더 높거나 낮은 차원으로 일반화할 수 있다.^[21]

8. 1. 일반화된 스토크스 정리와의 관계 (일본어 위키 텍스트 기반)

일반화된 스토크스 정리를 사용하면 벡터장 '''F'''의 발산에 대한 n차원 부피 적분을 영역 U에 대해 (n-1)차원 면적분으로 나타낼 수 있다.

:

\underbrace{ \int \cdots \int_U }_n \nabla \cdot \mathbf{F} \, \mathrm{d}V = \underbrace{ \oint_{} \cdots \oint_{\partial U} }_{n-1} \mathbf{F} \cdot \mathbf{n} \, \mathrm{d}S

이 방정식은 발산 정리라고도 한다.

n = 2일 때, 이는 그린 정리와 같다.

n = 1일 때, 이는 미적분학의 기본 정리 2부로 축소된다.

발산 정리는 일반화된 스토크스 정리에서 2차 미분 형식 ω를 고려한 경우에 해당한다.

:

\int_{\partial V} \omega = \int_V \mathrm{d}\omega

여기서 ω는

:

\omega:= F_1\mathrm{d}y \wedge \mathrm{d}z + F_2 \mathrm{d}z \wedge \mathrm{d}x +F_3 \mathrm{d}x \wedge \mathrm{d}y

이며, 그 외미분은 다음 식으로 주어진다.

:

\mathrm{d} \omega :=\biggl ( \frac{\partial F_1}{\partial x} + \frac{\partial F_2}{\partial y} + \frac{\partial F_3}{\partial z}\biggr ) \mathrm{d}x \wedge \mathrm{d}y \wedge \mathrm{d}z

9. 예제

발산 정리는 부피를 완전히 둘러싸는 닫힌 곡면과 같은 왼쪽의 곡면을 통해 흐르는 플럭스를 계산하는 데 사용할 수 있다. 오른쪽과 같이 경계가 있는 곡면을 통해 흐르는 플럭스를 직접 계산할 수는 ''없다''. (곡면은 파란색, 경계는 빨간색)

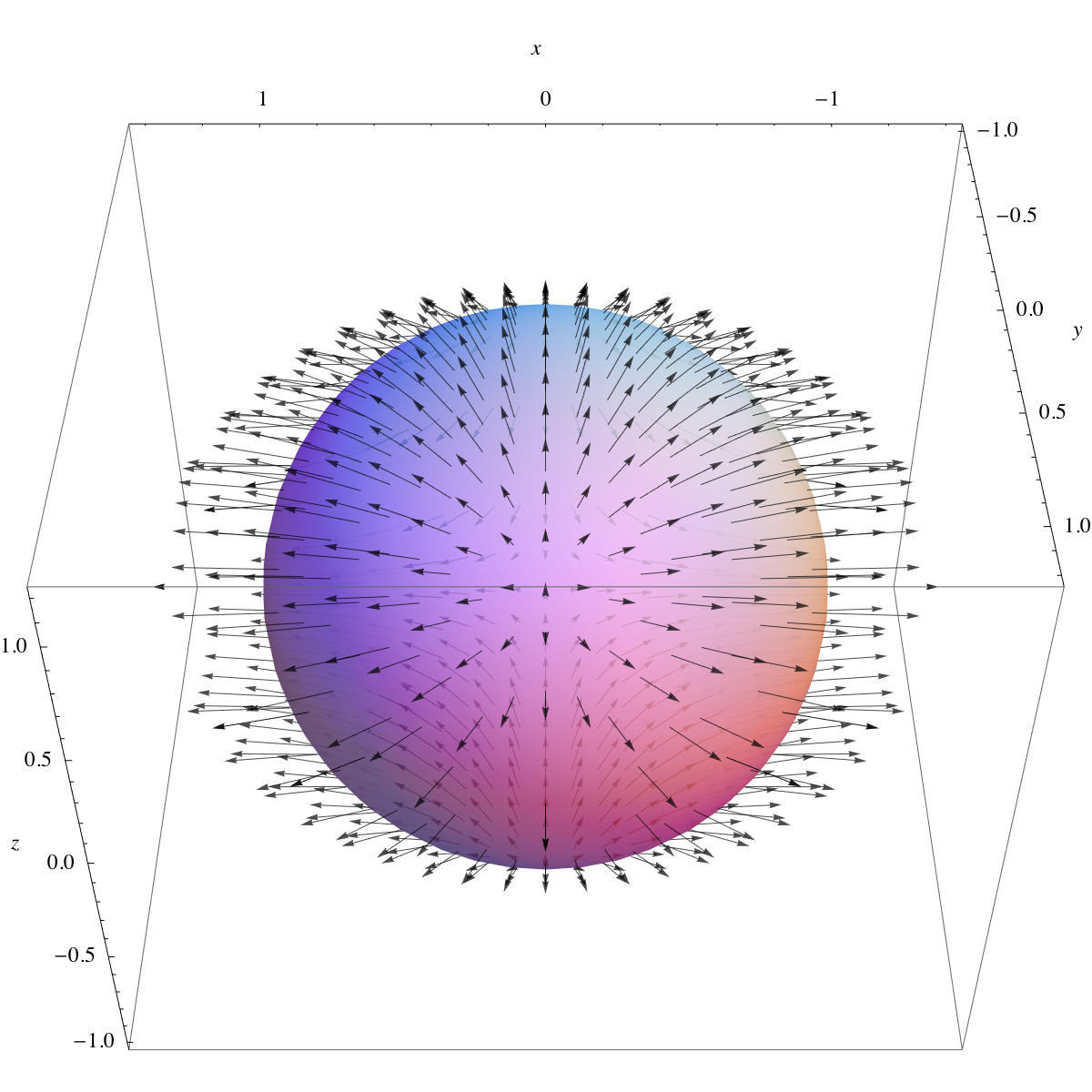
다음과 같은 값을 계산한다고 가정해 보자.

:

\mathbf{F}\cdot\mathbf{n} \, \mathrm{d}S,

여기서 는 다음과 같이 정의된 단위 구이다.

:

S = \left \{ (x,y, z) \in \mathbb{R}^3 \ : \ x^2+y^2+z^2 = 1 \right \},

그리고 는 벡터장이다.

:

\mathbf{F} = 2x\mathbf{i}+y^2\mathbf{j}+z^2\mathbf{k}.

이 적분을 직접 계산하는 것은 매우 어렵지만, 발산 정리를 사용하면 결과를 쉽게 유도할 수 있다. 발산 정리에 따르면 이 적분은 다음과 같다.

:

(\nabla \cdot \mathbf{F})\,\mathrm{d}V = 2 (1 + y + z)\, \mathrm{d}V = 2 \mathrm{d}V + 2 y\, \mathrm{d}V + 2 z\, \mathrm{d}V,

여기서 는 단위 공이다.

:

W = \left \{ (x,y, z) \in \mathbb{R}^3 \ : \ x^2+y^2+z^2\leq 1 \right \}.

함수 는 의 한 반구에서는 양수이고 다른 반구에서는 음수이므로, 그 총 적분은 0이다. 에 대해서도 마찬가지이다.

:

y\, \mathrm{d}V =  z\, \mathrm{d}V = 0.

따라서,

:

단위 공 의 부피가 이기 때문이다.

참조

_[1] 논문 The history of Stokes's theorem
_[2] 서적 Encyclopaedia of Physics VHC
_[3] 서적 Mathematics of Classical and Quantum Physics https://archive.org/[...] Dover Publications
_[4] 서적 Advanced Engineering Mathematics, 3rd Ed. McGraw-Hill
_[5] 서적 Advanced Engineering Mathematics https://archive.org/[...] John Wiley and Sons 2011
_[6] 웹사이트 Notes on Vector Calculus https://web.williams[...] Prof. Steven Miller's webpage, Williams College 2007-05
_[7] 서적 Electricity and Magnetism https://books.google[...] Cambridge Univ. Press 2013
_[8] 서적 Universitext Springer London
_[9] 서적 Applied Mathematical Sciences Springer New York
_[10] 서적 Vector Analysis McGraw Hill
_[11] 웹사이트 MathWorld http://mathworld.wol[...]
_[12] 서적 McGraw Hill Encyclopaedia of Physics https://archive.org/[...] McGraw Hill
_[13] 서적 A History of Mathematics: An Introduction Addison-Wesley
_[14] 간행물 Nouvelles recherches sur la nature et la propagation du son J.A. Serret, ed., ''Oeuvres de Lagrange'' 1762
_[15] 간행물 Theoria attractionis corporum sphaeroidicorum ellipticorum homogeneorum methodo nova tractata, https://books.google[...] Commentationes societatis regiae scientiarium Gottingensis recentiores 1813
_[16] 논문 A History of Stokes' Theorem 1979-05
_[17] 간행물 Démonstration d'un théorème du calcul intégral Историко-математические исследования 1826
_[18] 서적 An Essay on the Application of Mathematical Analysis to the Theories of Electricity and Magnetism T. Wheelhouse 1838
_[19] 간행물 Mémoire sur la théorie du magnétisme Mémoires de l'Académie des sciences de l'Institut de France 1826
_[20] 서적 Mathematical methods for physics and engineering https://archive.org/[...] Cambridge University Press
_[21] 서적 Gravitation W.H. Freeman & Co
_[22] 간행물 Allgemeine Lehrsätze in Beziehung auf die im verkehrten Verhältnisse des Quadrats der Entfernung wirkenden Anziehungs- und Abstossungs-kräfte https://books.google[...] Res. Beob. magn. Vereins 1840
_[23] 간행물 Note sur la théorie de la chaleur Mém. Acad Sci. St.-Pétersb 1831
_[24] 서적

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com