푸리에 급수

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사
3. 정의
4. 성질
5. 응용
- 5.1. 다양한 분야에서의 활용
- 5.2. 확장된 푸리에 급수
6. 추가 정보
참조

1. 개요

푸리에 급수는 주기 함수를 삼각 함수 또는 복소 지수 함수의 급수로 나타낸 것이다. 조제프 푸리에가 열 방정식을 풀기 위해 도입했으며, 임의의 (구간별로 매끄러운) 함수를 삼각 급수로 표현할 수 있다는 것을 발견했다. 푸리에 급수는 전기 공학, 신호 처리, 이미지 처리 등 다양한 분야에 응용되며, 함수의 직교성, 파르세발의 등식과 같은 성질을 갖는다. 푸리에 급수는 콤팩트 군, 리만 다양체 등 다양한 수학적 공간으로 확장될 수 있으며, 2차원 및 3차원 푸리에 급수는 이미지 압축 및 결정 구조 분석에 활용된다.

더 읽어볼만한 페이지

조제프 푸리에 - 푸리에 변환
푸리에 변환은 복소 함수를 주파수 성분으로 분해하는 적분 변환으로, 푸리에 급수의 확장 개념이며, 시간-주파수 영역 변환, 선형성, 컨볼루션 정리, 불확정성 원리 등의 성질을 가지며 다양한 분야에 활용된다.
조제프 푸리에 - 푸리에 역변환 정리
푸리에 역변환 정리는 푸리에 변환된 함수를 시간 영역으로 되돌리는 변환으로, 신호 및 이미지 처리 분야에서 활용되며, 오일러 공식을 사용하여 복소 지수 함수로 표현된다.
푸리에 급수 - 톱니파
톱니파는 선형적으로 증가하다 급격히 떨어지는 파형으로, 신디사이저 음색 생성, 전원 공급 장치 전압 조정, 각도 계산, 래스터 그래픽 생성 등에 활용된다.
푸리에 급수 - 방형파
방형파는 높은 레벨과 낮은 레벨 사이를 즉시 전환하는 주기적인 파형으로, 디지털 회로의 클럭 신호로 사용되지만 고조파를 다량 포함하며, 실제 회로에서는 이상적인 구현이 어렵다.
급수 - 테일러 급수
테일러 급수는 매끄러운 함수를 무한 멱급수로 나타내는 방법으로, 함수의 미분 계수를 사용하여 함수를 근사하며, a=0일 때의 테일러 급수를 매클로린 급수라고 한다.
급수 - 멱급수
멱급수는 실수 또는 복소수 체에서 정의되며, 수렴 영역과 반지름을 가지며 미분, 적분, 사칙연산이 가능하고 해석 함수와 관련되어 상미분 방정식의 해를 구하는 데 활용된다.

푸리에 급수
기본 정보
푸리에 급수의 부분합의 애니메이션
분야	수학, 물리학, 공학
하위 분야	조화 해석
명명자	조제프 푸리에
발견 시기	1807년
정의
정의	주기 함수를 삼각 함수의 합으로 표현
수학적 표현
일반적인 형태	f(x) = a₀/2 + Σ[n=1 to ∞] (aₙcos(nx) + bₙsin(nx))
계수 a₀	(1/π) ∫[-π to π] f(x) dx
계수 aₙ	(1/π) ∫[-π to π] f(x) cos(nx) dx
계수 bₙ	(1/π) ∫[-π to π] f(x) sin(nx) dx
응용 분야
응용 분야	신호 처리 음성 인식 이미지 처리 데이터 압축 진동 해석 양자 역학
관련 항목
관련 항목	푸리에 변환 조화 해석 스펙트럼 분석 직교 함수 힐베르트 공간

2. 역사

조제프 푸리에는 프랑스의 과학자이자 수학자로, 열 방정식을 풀기 위해 푸리에 급수를 도입하였고, 프랑스 혁명에도 참가했다.^[29] 푸리에 급수는 장바티스트 조제프 푸리에(1768–1830)의 이름을 따서 명명되었으며, 그는 삼각 급수 연구에 중요한 기여를 했다. 레온하르트 오일러, 장 르 롱 달랑베르, 다니엘 베르누이도 이 분야를 연구했다. 푸리에는 1807년 ''Mémoire sur la propagation de la chaleur dans les corps solides''(고체 내 열의 전파에 관한 논문)에서 푸리에 해석과 푸리에 급수를 처음 발표했고, 1822년에는 ''Théorie analytique de la chaleur''(열의 해석적 이론)을 발표했다.

원래 푸리에 급수는 열 방정식을 풀기 위한 것이었지만, 이후에는 상수 계수를 갖는 선형 미분 방정식 등 다양한 수학 및 물리적 문제에 적용될 수 있다는 것이 밝혀졌다. 이 경우 고유해는 정현파이다. 푸리에 급수는 전기 공학, 진동 분석, 음향학, 광학, 신호 처리, 이미지 처리, 양자 역학, 계량 경제학^[9], 쉘 이론^[10] 등에서 다양하게 응용되고 있다.

2. 1. 푸리에 급수의 기원

프랑스의 과학자이자 수학자인 조제프 푸리에가 열 방정식을 풀기 위해 푸리에 급수를 도입하였다.^[29]

푸리에 급수는 장바티스트 조제프 푸리에(1768–1830)의 이름을 따서 명명되었으며, 그는 삼각 급수 연구에 중요한 기여를 했다. 레온하르트 오일러, 장 르 롱 달랑베르, 다니엘 베르누이도 삼각 급수를 연구했지만,^[29] 푸리에는 임의의 함수를 삼각 급수로 표현할 수 있다고 주장했다.

푸리에는 1807년 "고체 내 열의 전파에 관한 논문"에서 푸리에 해석, 특히 푸리에 급수를 처음 발표했고,^[4] 1822년에는 "열의 해석적 이론"을 발표했다.^[29]

열 방정식은 편미분 방정식이다. 푸리에 이전에는 열원의 동작이 단순한 사인 또는 코사인파인 경우에만 열 방정식의 일반적인 해가 알려져 있었다. 푸리에는 복잡한 열원을 단순한 사인파와 코사인파의 중첩으로 모델링하고, 해당 고유해의 중첩으로 해를 쓰는 아이디어를 제시했는데, 이 중첩 또는 선형 결합을 푸리에 급수라고 한다.

현대적인 관점에서 볼 때, 푸리에의 결과는 19세기 초에 함수와 적분에 대한 정확한 개념이 부족했기 때문에 다소 비형식적이었다. 나중에 페터 구스타프 르줴네 디리클레^[5]와 베른하르트 리만^[6]^[7]^[8]은 푸리에의 결과를 더 정확하고 형식적으로 표현했다.

푸리에는 모든 함수가 삼각 급수로 표현될 수 있다고 주장했는데, 이는 당시 수학계에 받아들여지지 않았다. 그러나 푸리에 급수론은 19세기 수학에서 해석학 엄밀화에 큰 영향을 미쳤고, 푸리에 변환 등의 기법을 낳아 이미지 처리, 데이터 압축 등 현대 과학의 기초 기술로 발전해 갔다.

2. 2. 푸리에 급수 이론의 발전

푸리에가 열 방정식을 풀기 위해 도입한 푸리에 급수는, 당시 수학계에 큰 반향을 일으켰다. 푸리에는 모든 함수가 삼각 급수로 표현될 수 있다고 주장했는데, 이는 당시 함수와 적분에 대한 개념이 명확하지 않았기 때문에 다소 비형식적인 결과였다.^[4]

푸리에의 주장은 당시 수학계에서 받아들여지지 않았으나, 이후 페터 구스타프 르줴네 디리클레^[5]와 베른하르트 리만^[6]^[7]^[8] 등에 의해 더 정확하고 형식적으로 표현되었다.

푸리에 급수 이론은 실수, 함수, 수렴, 적분 등의 개념을 재검토하게 만들었으며, 19세기 수학의 엄밀화에 큰 영향을 미쳤다. 또한, 푸리에 변환과 같은 기법을 낳아 이미지 처리, 데이터 압축, CT, MRI 등 현대 과학 기술의 기초를 제공했다.

2. 3. 한국에서의 푸리에 급수 활용

푸리에 급수는 한국의 디지털 신호 처리, 통신, 영상 처리 기술 발전에 중요한 기반이 되었다. 특히, 이동통신, 디지털 방송, 의료 영상 등 다양한 분야에서 푸리에 급수를 활용한 기술이 개발 및 상용화되었다.

3. 정의

푸리에 급수는 주기함수를 기본적인 조화함수인 삼각함수 또는 복소 지수 함수의 급수로 나타낸 것이다. Fourier coefficient|푸리에 계수^영어를 결정하는 과정을 '해석', 관련된 삼각 함수 급수(또는 그 다양한 근사)를 구성하는 과정을 '합성'이라고 한다.

$f$ 에 수렴하는 푸리에 급수를 얻을 수 있을 때 $f$ 는 '푸리에 전개 가능하다'고 하는데, $f$ 에 대한 형식적인 푸리에 급수가 수렴하는지, 수렴한다고 해도 실제로 $f$ 에 수렴하는지 등의 복잡한 논의가 필요하며, 이는 푸리에 급수의 수렴성 문제라고 불린다.

3. 1. 푸리에 급수의 기본 정의

주기함수를 기본적인 조화함수인 삼각함수 또는 복소 지수 함수의 급수로 나타낸 것이다. 주기함수

f\colon\mathbb R\to\mathbb C

가

T

의 주기를 가진다고 할 때, 다음이 성립한다.

:

f(x)=f(x+T)

또한,

f

가 모든 유한 구간(finite interval^영어)에서 제곱적분 가능하다고 가정한다. 즉, 임의의

a,b\in\mathbb R

에 대하여,

:

\int_a^b|f|^2\,dx

가 유한한 값으로 존재한다. 이때,

f

의 '''푸리에 계수'''(Fourier coefficient^영어)

g_n

은 다음과 같이 정의된다.

:

g_n=\frac1{T}\int_{t_{0}}^{t_{0} + T}\exp\left(-\frac{2n\pi{i}x}{T}\right)f(x)\,dx,\quad t_{0} \in \mathbb{R}.

그러면 임의의

x\in\mathbb R

에 대하여 다음 식이 성립하지 않는

x

의 집합은 르베그 측도 0을 가진다.

:

f(x)=\sum_{n=-\infty}^{\infty}g_n\exp\left(\frac{2n\pi{i}x}{T}\right)

.

만약

f

가 연속미분가능 (

C^1

) 함수라면 (즉,

f

의 도함수가 존재하고 연속적인 경우)

f

의 푸리에 급수는 모든

x

에서

f(x)

로 수렴한다.

복소수 값을 갖는 함수

s(x)

가 길이

P

의 구간에서 정의될 때, 이 함수의 푸리에 급수는 다음과 같은 형태의 삼각 함수 급수로 나타낼 수 있다.

:

s(x) = \sum_{n=-\infty}^\infty c_{_n} e^{i 2\pi \tfrac{n}{P} x },

여기서 ''푸리에 계수''

c_{_n}

는 다음과 같은 적분으로 정의되는 복소수이다.

:

c_{_n} = \frac{1}{P}\int_0^P s(x)\ e^{-i 2\pi \tfrac{n}{P} x }\,dx.

이러한 전개의 존재는 디리클레 충분 조건에 의해 보장된다.

#

s(x)

는

[0,P]

구간에서 절대 적분 가능해야 한다.

#

s(x)

는 구간별 연속이어야 하며, 유한 개의 유한 불연속점을 허용한다.

#

s(x)

는

[0,P]

구간에서 극값의 개수가 유한해야 한다.

주어진 함수의 푸리에 계수를 결정하는 과정을 '''''해석''''', 관련된 삼각 함수 급수(또는 그 다양한 근사)를 구성하는 과정을 '''''합성''''''이라고 한다.

푸리에 급수는 여러 동등한 형태로 작성될 수 있으며, 여기서는

s(x)

의

N

번째 부분합

s_{_N}(x)

로 표시된다.^[12]

그림 1. 위 그래프는 빨간색 구간 0에서 P까지만 정의된 비주기 함수 $s(x)$ 를 파란색으로 나타낸 것이다. 이 함수는 이 구간에서 분석되어 아래 그래프의 푸리에 급수를 생성할 수 있다. 푸리에 급수는 원래 함수 $s(x)$ 가 주기가 아니더라도 항상 주기 함수이다.

고조파는 정수

n

으로 인덱싱되며, 이는 해당 정현파가 구간

P

에서 만드는 사이클의 수이다. 따라서 정현파는 다음과 같다.

$x$ 와 동일한 단위로 $\tfrac{P}{n}$ 와 같은 파장.
$x$ 의 역 단위로 $\tfrac{n}{P}$ 와 같은 주파수.

이 급수는 하나 이상의 조화 주파수의 합인 함수를 나타낼 수 있다.

N\to\infty

의 극한에서, 삼각 함수 급수는 무한대의 항으로 인해 중간 주파수 및/또는 비정현파 함수도 나타낼 수 있다. 계수는 음악 신디사이저나 파형의 시간 샘플과 같이 주어지거나 가정될 수 있다. 후자의 경우, 푸리에 급수의 지수 형태는 변수

x

가 시간을 대신하여 주파수를 나타내는 이산 시간 푸리에 변환을 합성한다. 일반적으로 계수는 길이가

P

인 간격을 정의역으로 하는 주어진 함수

s(x)

의 ''분석''에 의해 결정된다.

\tfrac{2}{P}

스케일 인수는 삼각 함수의 직교성을 활용하여 도출된다.^[13] 오일러 공식에 의해 다음이 성립한다.

:

\cos x = \frac{e^{ix} + e^{-ix}}{2}, \quad \sin x = \frac{e^{ix} - e^{-ix}}{2i},

이에따라 지수형태 계수는 다음과 같이 표현 가능하다.

:

c_{_n} = \begin{cases}\tfrac{1}{2}(a_{_n} -i b_{_n}) & \text{if } n > 0,\\a_{_n} & \text{if } n = 0,\\\tfrac{1}{2}(a_{_{-n}} + i b_{_{-n}}) & \text{if } n < 0,\\\end{cases}

여기서

c_{0}

는 간격

P

에서

s

의 평균값이다. 반대로, 역관계는 다음과 같다.

:

\begin{aligned} a_{_0} &= c_{_0} &\\a_{_n} &= c_{_n}+c_{_{-n}} \qquad &\textrm{for}~ n > 0 \\b_{_n} &= i(c_{_n}-c_{_{-n}}) \qquad &\textrm{for}~ n > 0 \end{aligned}

위 그림과 같이 사인과 코사인은 직교 집합을 이룬다. 사인, 코사인, 이들의 곱의 적분은 $m$ , $n$ 또는 함수가 다를 때는 0이고 (녹색과 빨간색 영역이 같아서 상쇄됨), $m$ 과 $n$ 이 같고 사용된 함수가 동일할 때만 π이다. 적분이 1과 같으면 (즉, 각 함수를 $1/\sqrt{\pi}$ 로 스케일링해야 함), 이들은 정규 직교 집합을 형성한다.

f

에 수렴하는 푸리에 급수를 얻을 수 있을 때

f

는 '''푸리에 전개 가능하다'''고 하는데,

f

에 대한 형식적인 푸리에 급수가 수렴하는지, 수렴한다고 해도 실제로

f

에 수렴하는지 등의 복잡한 논의가 필요하며, 이는 푸리에 급수의 수렴성 문제라고 불린다. 이하에서는 이를 고려하지 않고 형식적으로 서술한다.

f

는 실수

x

를 변수로 하는 실숫값 함수이며, 주기는

2\pi

인 주기 함수라고 가정한다.

:

\begin{align}a_n &= \frac{1}{\pi} \int_{-\pi}^{\pi} f\left(t \right) \cos nt\,dt, \left(n = 0,1,2,3,\dots \right) \\b_n &= \frac{1}{\pi} \int_{-\pi}^{\pi} f\left(t \right) \sin nt\,dt, \left(n = 1,2,3,\dots \right)\end{align}

라고 놓고,

a_n

을

f

의 '''푸리에 코사인 계수'''(''Fourier cosine coefficient''),

b_n

을

f

의 '''푸리에 사인 계수'''(''Fourier sine coefficient'')라고 한다.

이들을 사용하여 나타낸 삼각 급수

:

{a_0 \over 2} + \sum_{n=1}^{\infty} \left(a_n \cos nx + b_n \sin nx \right)

를 '''푸리에 급수'''(''Fourier series'') 또는 '''푸리에 급수 전개'''(''Fourier series expansion'')라고 한다. 코사인 항만 있는

:

{a_0 \over 2} + \sum_{n=1}^{\infty} a_n \cos nx

를 '''푸리에 코사인 급수'''라고 하며, 사인 항만 있는

:

\sum_{n=1}^{\infty} b_n \sin nx

를 '''푸리에 사인 급수'''라고 한다.

푸리에 계수를 결정하는 적분 구간

-\pi < x < \pi

로 제한하여

f

를 볼 때,

f

가 푸리에 급수로 나타낼 수 있는 우함수이면, 그 푸리에 급수는 코사인 급수가 되며,

f(x)

가 푸리에 급수로 나타낼 수 있는 기함수이면, 그 푸리에 급수는 사인 급수가 된다.

오일러 공식을 사용하면, 복소수형 푸리에 급수를 얻을 수 있다.

f

도 복소수 값을 가질 수 있다.

:

c_n = \frac{1}{2\pi} \int_{-\pi}^{\pi} f(t) \exp(-int) dt, \left(n = 0,\pm 1,\pm 2,\dots \right)

를,

f

의 '''푸리에 계수'''(''Fourier coefficient'')라고 하며, 이를 사용하여 쓰여진 다항식

:

\sum_{n=-m}^m c_n e^{inx}

를,

m

차 '''푸리에 다항식'''(''Fourier polynomial'')이라고 한다. 이

m

을

+\infty

로 한 극한

:

\sum_{n=-\infty}^{\infty} c_n e^{inx}= \lim_{m\to +\infty} \sum_{n=-m}^m c_n e^{inx}

을 '''푸리에 급수'''라고 한다. 좌변은

:

\sum_{n=-\infty}^{\infty} c_n e^{inx}= \lim_{k,m\to +\infty} \sum_{n=-k}^m c_n e^{inx}

의 의미는 '''아닌''' 것에 주의해야 한다.

3. 2. 다양한 형태의 푸리에 급수

푸리에 급수는 주기함수를 삼각함수나 복소 지수 함수의 급수로 나타낸 것이다. 푸리에 급수는 다양한 형태로 표현될 수 있다.^[12]

'''사인-코사인 형태'''

:

s_{_N}(x) = a_{_0} + \sum_{n=1}^N \left(a_{_n} \cos \left(2 \pi \tfrac{n}{P} x \right) +b_{_n} \sin \left(2 \pi \tfrac{n}{P} x  \right) \right)

'''지수 형태'''

:

s_{_N}(x) = \sum_{n=-N}^N c_{_n} \ e^{i 2\pi \tfrac{n}{P}x}

'''주기 변환'''

주기가

2\pi

인 주기 함수

f

에 대한 푸리에 급수는 변수 변환

x = (\pi/L)y

를 통해 주기

2L

인 주기 함수

g(y) = f((\pi/L)y)

의

-L \le y \le L

구간에서의 정의로 변환할 수 있다.

:

\begin{align}a_n &= {1 \over L} \int_{-L}^L g\left(s\right) \cos\left(\frac{n \pi s}{L} \right) ds, \left(n = 0,1,2,3,\dots \right) \\b_n &= \frac{1}{L} \int_{-L}^L g\left(s\right) \sin\left(\frac{n \pi s}{L} \right) ds, \left(n = 1,2,3,\dots \right) \\g(y) &= \frac{a_0}{2} + \sum_{n=1}^{\infty} \left(a_n \cos\left(\frac{n\pi y}{L}\right) + b_n \sin\left(\frac{n \pi y}{L}\right)\right) \\c_n &= \frac{1}{2L} \int_{-L}^L g\left(s \right) \exp\left(-\frac{in\pi s}{L}\right) ds, \left(n = 0,\pm 1,\pm 2,\dots \right) \\g(y) &= \sum_{n=-\infty}^{\infty} c_n \exp\left(\frac{in\pi y}{L}\right) = \lim_{m\to +\infty} \sum_{n=-m}^m c_n \exp\left(\frac{in\pi y}{L}\right)\end{align}

3. 3. 푸리에 급수의 수렴성

푸리에 급수는 주기함수를 기본적인 삼각함수나 복소 지수 함수의 급수로 나타내는 방법이다. 푸리에 급수가 수렴하기 위한 충분 조건에는 디리클레 조건이 있다.
디리클레 조건^[20]^[21]^[22]^[23]

함수는 유한한 구간에서 유한 개의 불연속점을 가져야 한다.
함수는 유한한 구간에서 유한 개의 극값을 가져야 한다.

이러한 조건을 만족하면 푸리에 급수는 거의 모든 점에서 원래 함수로 점별 수렴한다. 여기서 '거의 모든 점'이라는 것은 르베그 측도가 0인 집합을 제외한 모든 점을 의미한다.

만약 함수가 연속이고 그 도함수가 제곱 적분 가능하다면, 푸리에 급수는 절대적이고 균등하게 원래 함수로 수렴한다.^[19] 즉, 모든 점에서 원래 함수 값으로 수렴하며, 그 수렴 속도가 일정하다.

공학 분야에서는 푸리에 급수가 도약 불연속점을 제외하고는 수렴한다고 가정하는 경우가 많다. 이는 공학에서 다루는 함수들이 일반적으로 더 "잘 동작"하기 때문이다.

하지만, 연속 함수임에도 불구하고 푸리에 급수가 특정 점에서 수렴하지 않는 경우가 존재할 수 있다. 안드레이 콜모고로프는 푸리에 급수가 거의 모든 곳에서 발산하는 함수의 예를 제시하기도 했다.^[24]

기브스 현상은 푸리에 급수가 불연속점 근처에서 원래 함수와 큰 오차를 보이는 현상이다.
정리

''' $L^2$ 수렴''': 함수 $s$ 가 $L^2 (P)$ 에 속하면, $s$ 의 푸리에 급수 $s_{_N}$ 는 $N \to \infty$ 일 때 $L^2 (P)$ 에서 $s$ 로 수렴한다. 즉,

:

\lim_{N\to \infty}\|s_{_N} - s\|_2=0.

'''균등 수렴''': 함수 $s$ 가 연속적으로 미분가능하면 ( $s \in C^1(\mathbb{R})$ ), $s_{_N}$ 는 균등 수렴으로 $s$ 로 수렴한다.

4. 성질

여러 함수들의 푸리에 계수를 논의하기 위해 $c_{_n}$ 표기는 부적절하다. 따라서 관례적으로 함수( $s,$ 이 경우)의 수정된 형태, 예를 들어 $\widehat{s}(n)$ 또는 $S[n],$ 으로 대체하며, 종종 첨자 표기 대신 함수 표기를 사용한다.

: $\begin{align}s(x) &= \sum_{n=-\infty}^\infty \widehat{s}(n)\cdot e^{i 2\pi \tfrac{n}{P} x} && \scriptstyle \text{일반적인 수학 표기법} \\&= \sum_{n=-\infty}^\infty S[n]\cdot e^{i 2\pi \tfrac{n}{P} x} && \scriptstyle \text{일반적인 공학 표기법}\end{align}$

공학에서는, 특히 변수 $x$ 가 시간을 나타낼 때, 계수 시퀀스를 주파수 영역 표현이라고 한다. 이 함수의 영역이 이산 주파수 집합임을 강조하기 위해 종종 대괄호를 사용한다.

또 다른 일반적으로 사용되는 주파수 영역 표현은 푸리에 급수 계수를 사용하여 변조 디랙 콤을 변조한다.

: $S(f) \ \triangleq \ \sum_{n=-\infty}^\infty S[n]\cdot \delta \left(f-\frac{n}{P}\right),$

여기서 $f$ 는 연속적인 주파수 영역을 나타낸다. 변수 $x$ 의 단위가 초일 때, $f$ 의 단위는 헤르츠이다. 콤의 "이빨"은 $\tfrac{1}{P}$ 의 배수(즉, 고조파)로 간격을 두며, 이를 기본 주파수라고 한다. $s(x)$ 는 푸리에 역변환을 통해 이 표현에서 복구할 수 있다.

: $\begin{align}\mathcal{F}^{-1}\{S(f)\} &= \int_{-\infty}^\infty \left( \sum_{n=-\infty}^\infty S[n]\cdot \delta \left(f-\frac{n}{P}\right)\right) e^{i 2 \pi f x}\,df, \\[6pt]&= \sum_{n=-\infty}^\infty S[n]\cdot \int_{-\infty}^\infty \delta\left(f-\frac{n}{P}\right) e^{i 2 \pi f x}\,df, \\[6pt]&= \sum_{n=-\infty}^\infty S[n]\cdot e^{i 2\pi \tfrac{n}{P} x} \ \ \triangleq \ s(x).\end{align}$

따라서 구성된 함수 $S(f)$ 는 '''푸리에 변환'''이라고도 하지만, 주기 함수의 푸리에 적분은 고조파 주파수에서 수렴하지 않는다.

만약 $S$ 가 적분가능하다면, $\lim_{|n| \to \infty} S[n]=0$ , $\lim_{n \to +\infty} a_n=0$ 이고 $\lim_{n \to +\infty} b_n=0$ 이다. 이 결과는 리만-르베그 보조정리로 알려져 있다.

삼각함수 또는 복소 지수 함수는 서로 직교하는 성질을 가지며, 이는 푸리에 계수를 계산하는 데 중요한 역할을 한다. 내적 공간에서 정의되는 직교성은 푸리에 급수를 힐베르트 공간 이론으로 확장하는 기반이 된다.^[15]

함수 $f$ 가 제곱 적분 가능하면, 다음 등식이 성립한다.

: ${1 \over \pi}\int_{-\pi}^{\pi} |f(t)|^2 dt = {{a_0}^2 \over 2} + \sum_{n=1}^\infty ( {a_n}^2 + {b_n}^2 ) = 2 \sum_{n=-\infty}^{\infty} |c_n|^2.$

이 식을 파르세발의 등식이라고 한다. 파르세발의 등식은 함수의 에너지(또는 제곱 적분)와 푸리에 계수의 제곱 합 사이의 관계를 나타내는 중요한 등식이며, 신호 처리에서 에너지 보존 법칙을 설명하는 데 사용된다.

다음 표는 시간 영역에서의 몇 가지 수학적 연산과 푸리에 급수 계수에서 해당하는 효과를 보여준다.

속성	시간 영역	주파수 영역 (지수 형태)	비고	참고 문헌
선형성	$a\cdot s(x) + b\cdot r(x)$	$a\cdot S[n] + b\cdot R[n]$	$a,b \in \mathbb{C}$
시간 반전 / 주파수 반전	$s(-x)$	$S[-n]$	^[16]
시간 켤레	$s^*(x)$	$S^*[-n]$	^[16]
시간 반전 & 켤레	$s^*(-x)$	$S^*[n]$
시간 영역의 실수부	$\operatorname{Re}{(s(x))}$	$\frac{1}{2}(S[n] + S^*[-n])$
시간 영역의 허수부	$\operatorname{Im}{(s(x))}$	$\frac{1}{2i}(S[n] - S^*[-n])$
주파수 영역의 실수부	$\frac{1}{2}(s(x)+s^*(-x))$	$\operatorname{Re}{(S[n])}$
주파수 영역의 허수부	$\frac{1}{2i}(s(x)-s^*(-x))$	$\operatorname{Im}{(S[n])}$
시간 이동 / 주파수 변조	$s(x-x_0)$	$S[n] \cdot e^{-i 2\pi\tfrac{x_0}{P}n}$	$x_0 \in \mathbb{R}$	^[16]
주파수 이동 / 시간 변조	$s(x) \cdot e^{i 2\pi \frac{n_0}{P}x}$	$S[n-n_0] \!$	$n_0 \in \mathbb{Z}$	^[16]

실수 값을 갖는 함수의 변환은 켤레 대칭 함수이다. 반대로, 켤레 대칭 변환은 실수 시간 영역을 의미한다.

허수 값을 갖는 함수의 변환은 켤레 반대칭 함수이며 그 반대도 마찬가지이다.

켤레 대칭 함수의 변환은 실수 값을 갖는 함수이며 그 반대도 마찬가지이다.

켤레 반대칭 함수의 변환은 허수 값을 갖는 함수이며 그 반대도 마찬가지이다.^[14]

4. 1. 직교성

Trigonometric function^영어(삼각함수) 또는 복소 지수 함수는 서로 직교하는 성질을 가지며, 이는 푸리에 계수를 계산하는 데 중요한 역할을 한다. 내적 공간에서 정의되는 직교성은 푸리에 급수를 힐베르트 공간 이론으로 확장하는 기반이 된다.^[15]

제곱 적분 가능 함수의 공간 ''L''²(−π, π)에서 내적은 다음과 같이 정의된다.

:

\left\langle f(x),g(x) \right\rangle := {1 \over \pi} \int_{-\pi}^{\pi} f(x) g(x)^* dx

여기서 ''g''(''x'')^*는 ''g''(''x'')의 복소 켤레이며, 실수값일 때는 ''g''(''x'')와 같다.

이 내적을 이용하여 자연수 ''m'', ''n'' ≥ 1에 대해 다음과 같은 직교 관계를 얻을 수 있다.

:

\begin{align}\langle \cos mx, \cos nx \rangle &= \delta_{mn}\\\langle \sin mx, \sin nx \rangle &= \delta_{mn}\\\langle \cos mx, \sin nx \rangle &= 0\\\langle 1, 1 \rangle &= 2\\\langle 1, \cos mx \rangle &= 0\\\langle 1, \sin mx \rangle &= 0\end{align}

여기서 δ_''mn''는 크로네커 델타이며, 내적 안에 사용된 1은 ''x''에 의존하지 않고 1을 값으로 갖는 상수 함수를 의미한다.

이러한 관계로부터 다음 함수 집합은 정규 직교 함수 열이 되며, ''L''²(−π, π)의 정규 직교 기저가 된다.

:

\left\{\frac{1}{\sqrt{2}}, \cos x, \sin x, \cos 2x, \sin 2x, \cos 3x, \sin 3x,\ldots \right\}

푸리에 급수의 cos ''nx'', sin ''nx'' 계수는 다음과 같이 계산된다.

:

\begin{align} a_n &= \langle f(x), \cos nx \rangle \\b_n &= \langle f(x), \sin nx \rangle \end{align}

또한, 임의의 자연수 ''m''에 대해 다음이 성립하면 ''f''(''x'') = 0이 되므로, 이 직교 함수 열은 완비 함수 열이 되며, 이 내적에 의해 ''L''²(−π, π)는 힐베르트 공간이 된다.

:

\begin{align} \langle f(x), \cos mx \rangle &= 0 \\\langle f(x), \sin mx \rangle &= 0 \end{align}

복소수형 푸리에 급수의 경우, 정수 ''m'', ''n''에 대해 다음과 같은 직교 관계가 성립한다.

:

\langle e^{imx}, e^{inx} \rangle = 2\pi\delta_{mn}

그리고 {''e''^''imx''}는 완비 함수 열이 된다.

힐베르트 공간 ''X''와 그 정규 직교계 {''e''_''k''}에서 ''x'' ∈ ''X''의 내적

\langle x, e_k\rangle

를 '''푸리에 계수'''라고 한다. 이때, '''베셀 부등식'''이 성립한다.

:

\|x \|_{2}^{2} \ge \sum_k \left|\langle x,e_k \rangle \right|^2

{''e''_''k''}가 ''X''의 기저가 되면, 다음 급수를 '''푸리에 급수'''라고 한다.

:

\sum_k \langle x,e_k \rangle e_k =\left\langle x,e_1 \right\rangle e_1 +  \left\langle x,e_2 \right\rangle e_2 + \cdots

이 급수가 원래의 ''x''와 같을 때 푸리에 전개할 수 있다고 하며, 이때 '''플랑셰렐 등식'''이 성립한다.

:

\|x \|_2^2 = \sum_k \left|\langle x,e_k \rangle \right|^2

힐베르트 공간 ''X''에 대해 다음 세 조건은 서로 동치이다.

임의의 ''x'' ∈ ''X''가 푸리에 전개 가능하다.
임의의 ''x'' ∈ ''X''에 대해 플랑셰렐 등식이 성립한다.
{''e''_''k''}가 ''X''의 정규 직교 기저이다.

실제로, 사인과 코사인은 직교 집합을 형성한다.^[15]

:

\int_{-\pi}^{\pi} \cos(mx)\, \cos(nx)\, dx = \frac{1}{2}\int_{-\pi}^{\pi} \cos((n-m)x)+\cos((n+m)x)\, dx = \pi \delta_{mn}, \quad m, n \ge 1,

:

\int_{-\pi}^{\pi} \sin(mx)\, \sin(nx)\, dx = \frac{1}{2}\int_{-\pi}^{\pi} \cos((n-m)x)-\cos((n+m)x)\, dx = \pi \delta_{mn}, \quad m, n \ge 1

(여기서 ''δ''_''mn''는 크로네커 델타)이고,

:

\int_{-\pi}^{\pi} \cos(mx)\, \sin(nx)\, dx = \frac{1}{2}\int_{-\pi}^{\pi} \sin((n+m)x)+\sin((n-m)x)\, dx = 0;

따라서 집합

:

\left\{\frac{1}{\sqrt{2}},\frac{\cos x}{\sqrt{2}},\frac{\sin x}{\sqrt{2}},\dots,\frac{\cos (nx)}{\sqrt{2}},\frac{\sin (nx)}{\sqrt{2}},\dots \right\},

또한

L^2([-\pi,\pi])

에 대한 정규 직교 기저를 형성한다.

4. 2. 파르세발의 등식

함수 가 제곱 적분 가능하면, 다음 등식이 성립한다.

:

{1 \over \pi}\int_{-\pi}^{\pi} |f(t)|^2 dt = {{a_0}^2 \over 2} + \sum_{n=1}^\infty ( {a_n}^2 + {b_n}^2 ) = 2 \sum_{n=-\infty}^{\infty} |c_n|^2.

이 식을 파르세발의 등식이라고 한다. 파르세발의 등식은 함수의 에너지(또는 제곱 적분)와 푸리에 계수의 제곱 합 사이의 관계를 나타내는 중요한 등식이며, 신호 처리에서 에너지 보존 법칙을 설명하는 데 사용된다.

4. 3. 변환 규칙

wikitext

다음 표는 시간 영역에서의 몇 가지 수학적 연산과 푸리에 급수 계수에서 해당하는 효과를 보여준다. 표기법:

복소 켤레는 별표로 표시된다.
$s(x),r(x)$ 는 $P$ 주기 함수 '''또는''' $x \in [0,P]$ 에 대해서만 정의된 함수를 나타낸다.
$S[n], R[n]$ 은 $s$ 와 $r$ 의 푸리에 급수 계수(지수 형태)를 나타낸다.

속성	시간 영역	주파수 영역 (지수 형태)	비고	참고 문헌
선형성	$a\cdot s(x) + b\cdot r(x)$	$a\cdot S[n] + b\cdot R[n]$	$a,b \in \mathbb{C}$
시간 반전 / 주파수 반전	$s(-x)$	$S[-n]$		^[16]
시간 켤레	$s^*(x)$	$S^*[-n]$		^[16]
시간 반전 & 켤레	$s^*(-x)$	$S^*[n]$
시간 영역의 실수부	$\operatorname{Re}{(s(x))}$	$\frac{1}{2}(S[n] + S^*[-n])$
시간 영역의 허수부	$\operatorname{Im}{(s(x))}$	$\frac{1}{2i}(S[n] - S^*[-n])$
주파수 영역의 실수부	$\frac{1}{2}(s(x)+s^*(-x))$	$\operatorname{Re}{(S[n])}$
주파수 영역의 허수부	$\frac{1}{2i}(s(x)-s^*(-x))$	$\operatorname{Im}{(S[n])}$
시간 이동 / 주파수 변조	$s(x-x_0)$	$S[n] \cdot e^{-i 2\pi\tfrac{x_0}{P}n}$	$x_0 \in \mathbb{R}$	^[16]
주파수 이동 / 시간 변조	$s(x) \cdot e^{i 2\pi \frac{n_0}{P}x}$	$S[n-n_0] \!$	$n_0 \in \mathbb{Z}$	^[16]

4. 4. 대칭성

실수 값을 갖는 함수

(s_{_{\text{RE}}}+s_{_{\text{RO}}})

의 변환은 켤레 대칭 함수

S_{RE}+i\ S_{IO}

이다. 반대로, 켤레 대칭 변환은 실수 시간 영역을 의미한다.

허수 값을 갖는 함수

(i\ s_{_{\text{IE}}}+i\ s_{_{\text{IO}}})

의 변환은 켤레 반대칭 함수

S_{RO}+i\ S_{IE}

이며 그 반대도 마찬가지이다.

켤레 대칭 함수

(s_{_{\text{RE}}}+i\ s_{_{\text{IO}}})

의 변환은 실수 값을 갖는 함수

S_{RE}+S_{RO}

이며 그 반대도 마찬가지이다.

켤레 반대칭 함수

(s_{_{\text{RO}}}+i\ s_{_{\text{IE}}})

의 변환은 허수 값을 갖는 함수

i\ S_{IE}+i\ S_{IO}

이며 그 반대도 마찬가지이다.^[14]

5. 응용

만약 S^영어가 적분가능하다면, $\lim_$

5. 1. 다양한 분야에서의 활용

푸리에 급수는 다양한 분야에 응용된다.

신호 처리: 음성, 음악, 통신 신호 등을 분석하고 처리하는 데 사용된다.^[9]
이미지 처리: 이미지 압축, 노이즈 제거, 특징 추출 등에 사용된다.^[9]
음향학: 소리의 분석, 합성, 음향 효과 생성 등에 사용된다.^[9]
양자 역학: 파동 함수를 분석하고, 에너지 준위를 계산하는 데 사용된다.^[9]

5. 2. 확장된 푸리에 급수

푸리에 급수는 다양한 수학적 공간으로 확장될 수 있다.

'''콤팩트 군에서의 푸리에 급수'''

합성곱을 점별 곱으로 변환하는 푸리에 변환의 성질을 이용하여, 모든 콤팩트 군에서 푸리에 급수를 만들 수 있다. 이는 푸리에 변환을 ''L''²(''G'') 형태의 공간으로 일반화하며, 푸리에 급수는 경우와 유사하게 존재하고 수렴한다. 페터-바일 정리는 콤팩트 군의 표현에 대한 결과를 제공하여, 콤팩트 군으로의 확장을 가능하게 한다.^[18]

'''리만 다양체에서의 푸리에 급수'''

콤팩트 리만 다양체에서는 라플라스-벨트라미 연산자를 이용한다. 이 연산자는 리만 다양체에 대한 라플라스 연산자에 해당하며, 이를 통해 열 방정식을 고려할 수 있다. 라플라스-벨트라미 연산자의 고유해를 기저로 사용하여 푸리에 급수를

L^2(X)

유형의 공간으로 일반화하며,

[-\pi,\pi]

경우와 유사하게 수렴한다. 예를 들어, 구에서는 구면 조화 함수가 푸리에 기저를 구성한다.

화학의 원자 궤도는 부분적으로 구면 조화 함수로 설명되며, 이를 사용하여 구에서 푸리에 급수를 생성할 수 있다.

'''국소 콤팩트 가환 (LCA) 군에서의 푸리에 급수'''

폰트랴긴 쌍대성을 이용하여 비콤팩트, 비가환군이 아닌 LCA 군으로 푸리에 변환을 일반화할 수 있다.

G

가 콤팩트이면 수렴하는 푸리에 급수를 얻고, 비콤팩트이면 푸리에 적분을 얻는다. 이는

\mathbb{R}

에서의 일반적인 푸리에 변환을 포함한다.

'''다변수 푸리에 급수'''

JPEG 이미지 압축 표준과 같이, 이미지 압축에서 2차원 이산 코사인 변환을 사용한다.

2차원 푸리에 급수는 다음과 같이 정의된다.

\begin{align}f(x,y) & = \sum_{j,k \in \Z} c_{j,k}e^{ijx}e^{iky},\\[5pt]c_{j,k} & = \frac{1}{4 \pi^2} \int_{-\pi}^\pi \int_{-\pi}^\pi f(x,y) e^{-ijx}e^{-iky}\, dx \, dy.\end{align}

'''브라베 격자에서의 푸리에 급수'''

3차원 브라베 격자는 결정 구조 분석 및 고체 물리학 연구에 사용된다. 결정 내부의 주기적인 퍼텐셜과 같은 함수는 푸리에 급수로 표현될 수 있다. 3차원 브라베 격자는 벡터 집합

\mathbf{R} = n_1\mathbf{a}_1 + n_2\mathbf{a}_2 + n_3\mathbf{a}_3

(

n_i

는 정수,

\mathbf{a}_i

는 선형 독립 벡터)로 정의된다. 주기성 조건

f(\mathbf{r}) = f(\mathbf{R}+\mathbf{r})

을 만족하는 함수

f(\mathbf{r})

의 푸리에 급수는 다음과 같이 표현된다.

f(\mathbf{r})=\sum_{\mathbf{G}} h(\mathbf{G}) \cdot e^{i \mathbf{G} \cdot \mathbf{r}},

h(\mathbf{G}) = \frac{1}{\mathbf{a}_1\cdot(\mathbf{a}_2 \times \mathbf{a}_3)}\int_{C} d\mathbf{r} f(\mathbf{r})\cdot e^{-i \mathbf{G} \cdot \mathbf{r}}

여기서

\mathbf{G}

는 역 격자 벡터,

C

는 원시 단위 세포,

\mathbf{a}_1\cdot(\mathbf{a}_2 \times \mathbf{a}_3)

는 원시 단위 세포의 부피이다.

6. 추가 정보

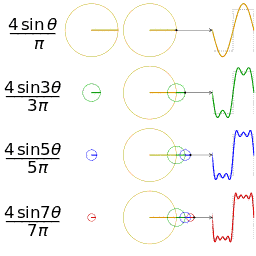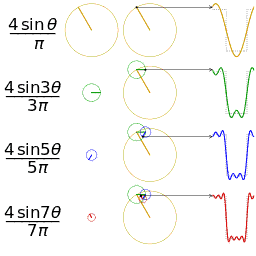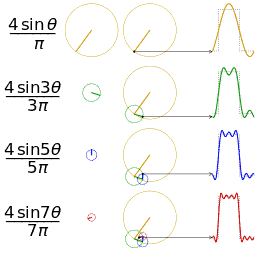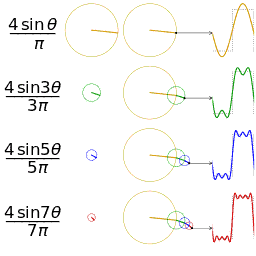
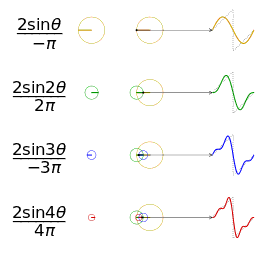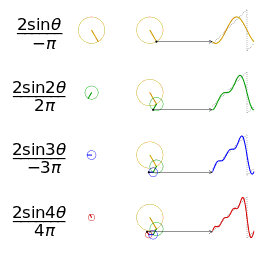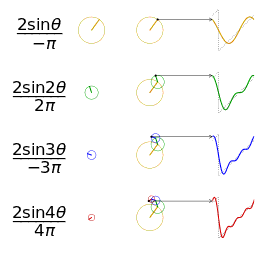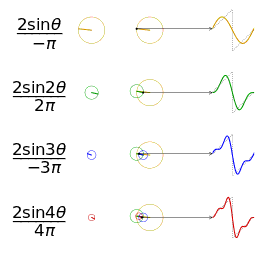
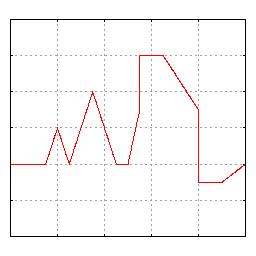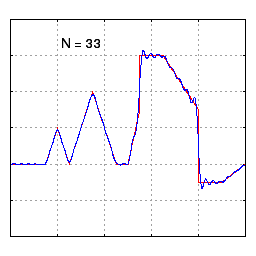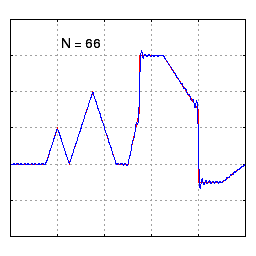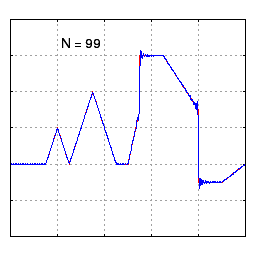
공학 분야에서는 푸리에 급수가 도약 불연속점을 제외하고 일반적으로 수렴한다고 가정한다. 이는 공학에서 다루는 함수들이 다른 분야의 함수들보다 더 안정적인 경향을 보이기 때문이다. 특히, 함수 $s$ 가 연속이고 그 도함수가 제곱 적분 가능하다면, 푸리에 급수는 $s(x)$ 로 절대적이고 균일하게 수렴한다.^[19] 함수가 특정 구간에서 제곱 적분 가능하다면, 푸리에 급수는 거의 모든 곳에서 해당 함수로 수렴한다.

항의 수가 증가함에 따라 사각파에 대한 근사가 어떻게 개선되는지를 보여주는 푸리에 급수의 부분합 (애니메이션)

항의 수가 증가함에 따라 톱니파에 대한 근사가 어떻게 개선되는지를 보여주는 푸리에 급수의 부분합 (애니메이션)

다소 임의적인 함수로의 수렴 예시. 수직 구간에서 "링잉"(깁스 현상)이 나타나는 것을 주목

하지만 푸리에 급수의 수렴성이 항상 보장되는 것은 아니다. 연속적인 주기 함수의 푸리에 급수가 특정 지점에서 수렴하지 않을 수도 있다는 사실은 많은 사람들을 놀라게 한다. 안드레이 콜모고로프는 1922년에 푸리에 급수가 거의 모든 곳에서 발산하는 함수의 예를 제시하기도 했다.^[24]

푸리에 급수가 0에서 발산하는 연속 함수의 예시도 존재한다.^[25] [0,π]에서 정의된 짝함수이자 2π-주기 함수 ''f''는 다음과 같이 표현될 수 있다.

:

f(x) = \sum_{n=1}^{\infty} \frac{1}{n^2} \sin\left[ \left( 2^{n^3} +1 \right) \frac{x}{2}\right].

이 함수의 푸리에 급수는 코사인 항만으로 구성되며, 계수는 특정 값에 도달할 때까지 증가하다가 감소하는 패턴을 보인다. 이로 인해 x=0에서 푸리에 급수는 수렴하지 않고 점점 더 높은 봉우리에 도달하게 된다.

참조

_[1] Dictionary Fourier
_[2] 서적 Trigonometric Series Cambridge University Press 2002
_[3] 서적 Routledge History of Philosophy Routledge
_[4] 서적 A History of Mathematics https://archive.org/[...] Macmillan
_[5] 간행물 Sur la convergence des séries trigonométriques qui servent à représenter une fonction arbitraire entre des limites données https://archive.org/[...]
_[6] 웹사이트 Ueber die Darstellbarkeit einer Function durch eine trigonometrische Reihe http://www.maths.tcd[...] 2008-05-19
_[7] citation Landmark Writings in Western Mathematics 1640–1940 https://books.google[...] Elsevier 1867
_[8] 서적 Theory of Complex Functions: Readings in Mathematics https://books.google[...] Springer 1991
_[9] 서적 Analysis of Economic Time Series. Economic Theory, Econometrics, and Mathematical Economics https://archive.org/[...] Elsevier
_[10] 서적 Stresses in Shells
_[11] 서적 Oeuvres de Fourier http://gallica.bnf.f[...] Gauthier-Villars et Fils 1888
_[12] Citation Fourier Series And Integrals https://math.mit.edu[...] Wellesley-Cambridge Press
_[13] 웹사이트 Trigonometrical series https://eudml.org/do[...] 2024-12-14
_[14] 웹사이트 Fourier Series (Part II) https://www.seas.upe[...] 2004
_[15] 서적 Mathematische Formelsammlung: für Ingenieure und Naturwissenschaftler Vieweg+Teubner Verlag
_[16] 서적 Continuous-Time Signals Springer
_[17] 웹사이트 Characterizations of a linear subspace associated with Fourier series https://mathoverflow[...] MathOverflow 2010-11-19
_[18] Youtube Vanishing of Half the Fourier Coefficients in Staggered Arrays https://www.youtube.[...]
_[19] 서적 Fourier Series https://books.google[...] Courier-Dover
_[20] 서적 Circuits, signals, and systems https://books.google[...] MIT Press
_[21] 서적 Advances in Electronics and Electron Physics https://books.google[...] Academic Press
_[22] 서적 Solid-state spectroscopy https://books.google[...] Springer
_[23] 서적 Brain and perception https://books.google[...] Lawrence Erlbaum Associates
_[24] 서적 An introduction to Harmonic Analysis Dover Publications, Inc. 1976
_[25] 서적 Les maths en tête. Analyse (2ème édition) Ellipses 2009
_[26] 웹사이트 Fourier Series and Boundary Value Problems http://www.math.iit.[...] Department of Applied Mathematics, Illinois Institute of Technology 2015
_[27] 서적 Analysis of Economic Time Series. Economic Theory, Econometrics, and Mathematical Economics Elsevier
_[28] 서적 Mathematische Formelsammlung: für Ingenieure und Naturwissenschaftler Vieweg+Teubner Verlag
_[29] 저널

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com