삼각측량법

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

삼각측량법은 두 지점 사이의 거리와 각도를 이용하여 대상 지점의 위치를 계산하는 방법이다. 고대 이집트에서부터 사용되었으며, 탈레스는 피라미드의 높이를 측정하는 데 활용했다. 근대에 들어 겜마 프리시우스가 지도 제작에 삼각 측량을 제안했고, 빌레브로르트 스넬은 현대적인 삼각망 측량을 시작했다. 이후 가우스는 삼각 측량에 헬리오트로프와 최소 제곱법을 도입하여 정확성을 높였다. 한국에서는 조선 시대부터 활용되었으며, 개항 이후 근대적 측량 기술 도입과 함께 토지 조사, 국토 개발 등에 기여했다. 현대에는 위성 측위 시스템에 의해 대체되었지만, 삼각점은 역사적 유산으로 남아 있다. 삼각측량법은 측량, 컴퓨터 비전, 항해, 천체측량 등 다양한 분야에서 활용된다.

더 읽어볼만한 페이지

위치 결정 - 위치 기반 서비스
위치 기반 서비스(LBS)는 이동통신, 무선 인터넷, GPS 기술을 이용하여 사용자의 위치 정보를 기반으로 내비게이션, 소셜 네트워크 서비스, 게임, 광고 등 다양한 부가 가치를 제공하는 서비스이다.
위치 결정 - 삼변측량
삼변측량은 기하학에서 원, 구, 삼각형의 기하를 이용하여 거리 측정을 통해 점의 위치를 결정하는 과정으로 정의되며, 측량에서는 진거리 및 의사거리 다변측량 기술을 통해 대상의 위치를 결정하는 데 사용되고, 실내 위치 추적 시스템, 항공 교통 관제, 로봇 공학 등 다양한 분야에 활용된다.
각 - 위도
위도는 지구 표면의 남북 위치를 각도로 나타내며, 지구를 회전 타원체로 가정했을 때 법선과 적도면이 이루는 각으로 측정하여 적도를 0°로 북극과 남극까지 나타내고, 기후와 지리적 특징 등에 영향을 미치는 다양한 종류가 존재한다.
각 - 등각 사상
등각 사상은 각도를 보존하는 사상으로, 2차원에서는 도함수가 0이 아닌 정칙 함수인 복소 함수가 해당되며, 3차원 이상에서는 상사 변환, 등거리 변환, 특수 등각 변환 등으로 분류되어 지도 제작, 항공우주 공학 등 다양한 분야에 응용된다.
유클리드 기하학 - 결정계
결정계는 결정 구조의 대칭성에 따라 7가지(삼사, 단사, 사방, 정방, 삼방, 육방, 입방)로 분류되며, 각 결정계는 고유한 대칭 요소와 점군의 대칭성을 갖는다.
유클리드 기하학 - 퐁슬레-슈타이너 정리
퐁슬레-슈타이너 정리는 자와 주어진 원(중심 포함)만 사용하여 자와 컴퍼스로 작도 가능한 모든 것을 작도할 수 있다는 기하학적 정리이다.

삼각측량법
개요
정의	일련의 연결된 삼각형들을 사용하여 평면상의 위치를 결정하는 측량 방법
활용	정확한 위치 결정 거리 및 면적 계산 지도 제작 지각 변동 연구
설명	기지점과 목표점 사이의 각도를 측정하여 위치를 결정함 최소 하나의 거리가 알려져 있어야 함 주로 토지, 해양, 항공 측량에 사용됨
역사
기원	고대 이집트 시대
발전	프톨레마이오스 (기원후 2세기): 천문학적 거리를 계산 스넬리우스 (1615년): 현대적인 삼각측량법 고안 켈빈 경 (19세기): 해저 케이블 지도 제작
원리
기본 원리	삼각형의 각과 한 변의 길이를 알면 나머지 변의 길이를 계산할 수 있음
사용되는 법칙	사인 법칙 코사인 법칙
방법
절차
필요한 장비	시준의 경위의 토털 스테이션 GPS 수신기
정확도 향상 방법
방법	여러 번 측정하여 평균값 사용 오차 발생 요인 제거 (기상 조건, 시준 오차 등) 정밀한 측량 장비 사용 기지점의 정확도 확보
응용 분야
토지 측량	지형도 제작 토지 경계 설정 건물 건설
해양 측량	해도 제작 해안선 조사 항로 설정
항공 측량	항공 사진 측량 지형 모델 제작 지도 갱신
기타	지각 변동 연구 터널 공사 댐 건설 교량 건설
장단점
장점	비교적 간단한 방법 넓은 지역에 적용 가능 높은 정확도
단점	기상 조건에 영향 받음 시준이 어려울 수 있음 오차 누적 가능성
관련 용어
관련 용어	기선 시준 방위각 고도각 삼각점 수준점
참고 문헌
참고 문헌	이재기, 최석근, 박경식, 정성혁 (2013). 측량학 (pp. 11-13). 박영사.

2. 역사

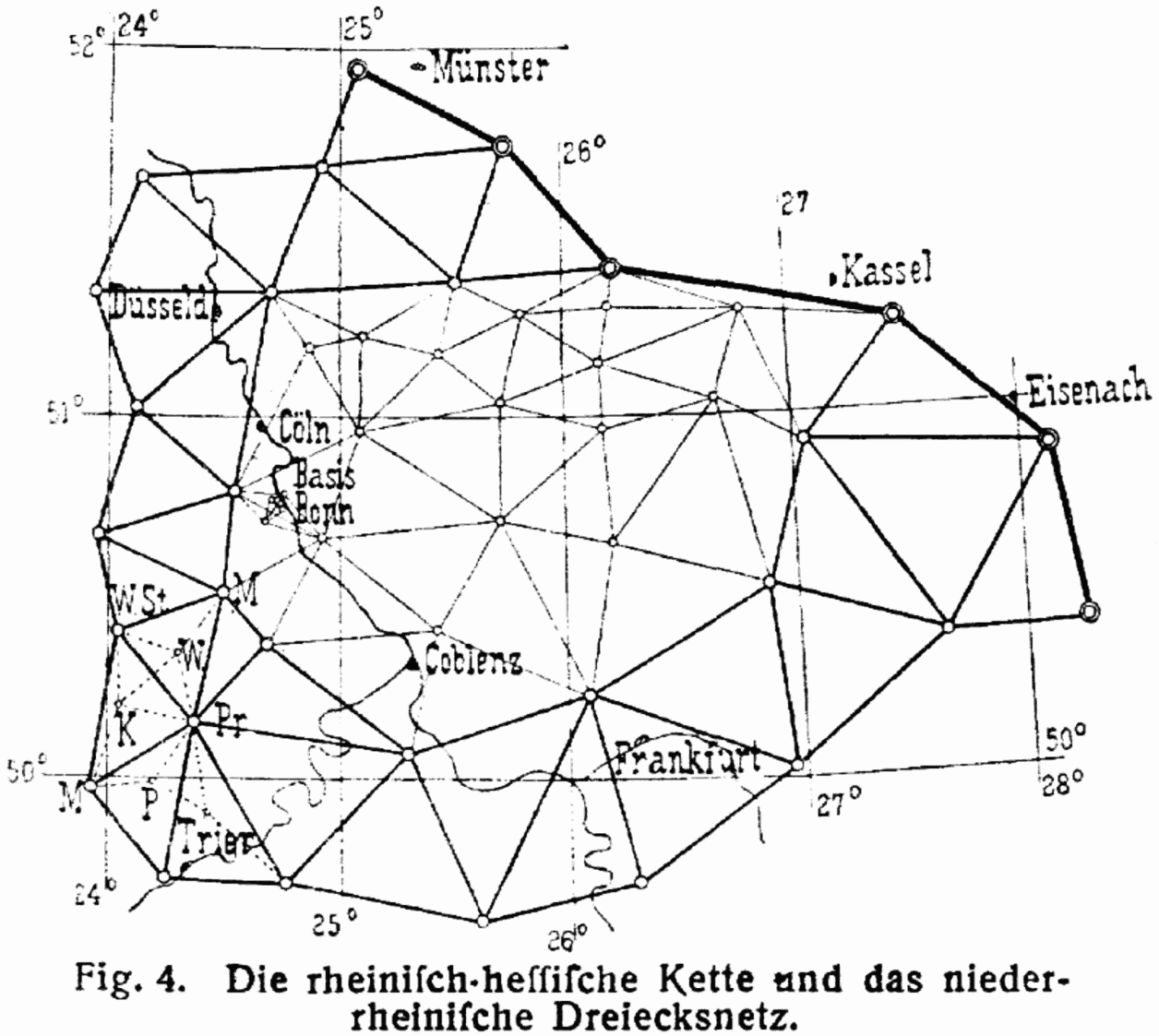
1533년 네덜란드의 지도 제작자 게르마 프리시우스는 지도를 만들기 위해 멀리 떨어진 장소를 정확하게 측정하는 방법으로 삼각 측량을 사용할 것을 제안했다. 이는 매우 큰 영향을 미쳐 독일, 오스트리아, 네덜란드 등으로 퍼져나갔다. 1579년 천문학자 티코 브라헤는 스칸디나비아에서 이 방법을 적용하여 벤 섬의 상세한 삼각 측량을 완성하고, 1584년에 섬의 토지 계획을 만들었다.

1615년 네덜란드 수학자 빌레브로르트 스넬(스넬리우스)은 알크마르에서 베르겐 옵 조움까지 약 110 km를 33개의 삼각형을 포함하는 사각형 연쇄를 이용하여 측정했다. 이 두 도시는 거의 같은 자오선상에 위치해 있었고, 위도로 1도 떨어져 있었으며, 이 측정을 통해 지구의 원둘레를 구할 수 있었다. 이 업적은 1617년 저서 ''Eratosthenes Batavus''(네덜란드의 에라토스테네스)에 나타나 있다. 스넬은 평면 공식을 지구의 둥근 모양에 맞춰 수정하는 방법과 삼각형 내부 점의 위치를 그 지점에서 삼각형 변이 이루는 각도로부터 계산하는 후방 교회법을 제시했다.

스넬의 자오선 측정은 정확하지 않았지만, 그가 고안한 측량 방법은 우수하여 각국에서 삼각 측량이 이루어졌다. 1669년부터 1670년까지 장 피카르는 파리 자오선상에서 위도 1도의 길이를 측량했다. 18세기 동안 카시니 가문에 의해 이 작업은 더욱 발전되었다. 1683년부터 1718년까지 조반니 카시니와 그의 아들 자크 카시니는 파리 자오선을 됭케르크에서 페르피냥까지 측량했다. 1733년부터 1740년까지 자크와 그의 아들은 전국토의 첫 삼각 측량을 실시하여 1745년에 정확한 원리에 기초한 최초의 프랑스 지도를 출판했다.

18세기 말, 다른 나라들도 전국토 지도를 만들기 위한 상세한 삼각망 측량을 시작했다. 1783년 영국은 그레이트 브리튼 섬의 기본 삼각 측량을 시작했지만, 1853년에 완료되었다. 1801년 시작된 인도 대 삼각 측량에서는 에베레스트 산과 히말라야 산맥의 산들을 삼각 측량하여 지도를 만들었다.

이 시기, 카를 프리드리히 가우스는 삼각 측량에 훌륭한 개량을 더했다.^[20] 1821년부터 1825년까지 가우스는 하노버 왕국의 삼각 측량을 위탁받았다. 1820년 가우스는 햇빛 반사로 위치를 나타내는 헬리오트로프(회조기)를 삼각 측량에 사용했다.^[21] 가우스는 최소 제곱법을 고안했다.^[22]

조선 시대에는 전통적인 측량 기술과 함께 삼각측량 원리가 활용되었다. 개항 이후 대한제국 시기에는 근대적인 측량 기술이 도입되어 토지 조사 사업에 삼각측량이 활용되었다. 일제강점기에는 조선총독부 주도로 전국적인 삼각측량이 실시되었는데, 이는 식민지 지배와 자원 수탈의 도구로 이용되었다는 비판을 받기도 한다.^[29] 광복 이후 대한민국 정부는 국토 재건과 개발을 위해 삼각측량을 적극 활용했으며, 1970년대부터 경제 개발 계획과 함께 전국적인 규모의 삼각측량이 이루어져 국가 기본도 제작에 중요한 기반이 되었다.

메이지 5년 공부성 측량사에 의한 영국인 맥스웰(혹은 맥베인)을 중심으로 한 도쿄 측량의 선행 사례가 있지만,^[28] 홋카이도 개척사의 개척 차관 구로다 기요타카의 초청으로 일본에 온 호러스 케플론은 홋카이도의 지리·기후를 조사하고 삼각 측량을 할 필요성을 지적했다.^[26] 이를 바탕으로 1873년부터 개척사 측량장에 임명된 제임스 R. 와슨 등 고용 외국인을 중심으로 유후츠 지방을 기점으로 측량이 진행되어 1875년 12월에 "홋카이도 실측도"가 간행되었다.^[27] 이는 일본에서 본격적인 삼각 측량에 의한 지도 제작의 선구적인 사례가 된다.^[29]

2. 1. 고대와 중세

삼각형을 사용하여 거리를 측정하는 방법은 고대까지 거슬러 올라간다. 기원전 6세기 고대 그리스의 철학자 탈레스는 피라미드 그림자의 길이를 측정하고, 동시에 자신의 그림자 길이를 측정하여 자신의 키와의 비율로부터 닮음인 삼각형을 사용하여 피라미드의 높이를 측정했다.^[8] 또한 절벽 위에서 바다에 보이는 배까지의 거리를, 수평 방향에 있는 알려진 폭포까지의 가시 수평 거리를 측정하고, 이를 절벽 전체 높이까지 확대하여 측정했다.^[9] 이러한 방법은 고대 이집트인에게도 알려져 있었다. 이보다 1000년 정도 오래된 린드 수학 파피루스에 나오는 문제 57번에서는 기울기를 거리와 높이의 비율로 정의하고 있으며, 이는 오늘날 기울기의 역수에 해당한다. 기울기와 각도는, 후대의 아랍의 알리다드의 전신인, 그리스인이 디옵트라라고 부르는 측정 막대기로 측정했다. 이 기구를 사용하여 떨어진 곳에서 거리를 측정하는 방법에 대한 이 시대의 상세한 설명은, 알렉산드리아의 헤론의 "디옵트라"에 있으며, 이는 아랍에서는 번역되어 남아 있었지만, 유럽에서는 사라졌다.

중국에서는 배수가 정확한 지도 제작의 6원칙의 5번째로 "직각과 예각을 측정"을 들었고, 이는 정확하게 거리를 측정하기 위해 필요한 것이었다.^[10] 또한 유휘는, 도달할 수 없는 장소까지의 높이를 구하는 방법으로, 앞서 언급한 계산 방법을 제시했다.^[11]^[12]

로마 시대의 토지 측량 전문가인 ''agromensores''에게는 삼각 측량이 사용되지 않았던 것이 분명하다. 그러나 아스트롤라베에 관한 아랍 문헌을 통해 중세 스페인에 도입되었다.^[13] 아부 라이한 비루니도 또한 삼각 측량을 이용하여 지구의 크기를 측정하거나, 다양한 장소 사이의 거리를 측정했다.^[14] 간소화된 로마 기술은, 전문 측량 기술자가 사용하는 더 세련된 기술과 공존했을 것으로 보인다. 그러나 이러한 기술이 라틴어로 번역되는 일은 드물었고, 11세기의 측량에 관한 매뉴얼 ''Geomatria incerti auctoris''가 몇 안 되는 예외였다. 이러한 기술은 유럽의 다른 지역은 매우 느리게 침투해 간 것으로 보인다.^[13] 스페인에서 이러한 기술의 인식이 확산되어 사용된 것은, 1300년경부터 각도를 측정하기 위해 전용으로 사용되었던 중세의 야곱의 지팡이라는 도구와, 현존하는 가장 오래된 것으로는 1296년의 것이 있는, 정밀하게 해안을 측량한 나침의 해도에 의해 증명될 것이다.

2. 2. 근대

네덜란드의 지도 제작자 겜마 프리시우스(Gemma Frisius)는 1533년에 지도를 만들기 위해 멀리 떨어진 장소를 정확하게 측정하는 방법으로 삼각 측량을 사용할 것을 제안했다. 이는 매우 큰 영향을 미쳐 기술은 독일, 오스트리아, 네덜란드 등으로 퍼져나갔다.^[15] 천문학자 티코 브라헤(Tycho Brahe)는 스칸디나비아에서 이 방법을 적용하여, 벤 섬의 상세한 삼각 측량을 1579년에 완성하고, 1584년에 섬의 토지 계획을 만들었다.^[16]

현대적인 체계적 삼각망의 사용은 1615년 네덜란드 수학자 빌레브로르트 스넬(스넬리우스)이 알크마르에서 베르겐 옵 조움까지 약 110 km를 33개의 삼각형을 포함하는 사각형 연쇄를 이용하여 측정한 것에서 시작되었다. 이 두 도시는 거의 같은 자오선상에 위치해 있었고, 위도로 1도 떨어져 있었으며, 이 측정을 통해 지구의 원둘레를 구할 수 있었다. 이 업적은 1617년의 저서 ''Eratosthenes Batavus''(네덜란드의 에라토스테네스)에 나타나 있다. 스넬은 평면에서의 공식을 어떻게 지구의 둥근 모양에 맞춰 수정할 것인가에 대한 방법을 계산했다. 그는 또한 삼각형 내부에 있는 점의 위치를, 그 지점에서 삼각형 변이 이루는 각도로부터 계산하는 후방 교회법을 제시했다.^[18]

스넬이 측정한 자오선은 정확하지 않았지만, 그가 고안한 측량 방법이 우수한 방법임이 알려지면서 각국에서 삼각 측량이 이루어졌다.^[19] 스넬의 방법은 1669년부터 1670년까지 파리 자오선상에서 위도 1도의 길이를 측량한 장 피카르에게 이어졌다. 18세기 동안 유명한 카시니 가문의 사람들에 의해 이 작업은 더욱 발전되었다. 1683년부터 1718년까지 조반니 카시니와 그의 아들 자크 카시니는 파리 자오선을 됭케르크에서 페르피냥까지 측량했다. 1733년부터 1740년까지 자크와 그의 아들은 전국토의 첫 삼각 측량을 실시하여 1745년에 정확한 원리에 기초한 최초의 프랑스 지도를 출판했다.

이 시점까지 삼각 측량 기술은 지역적인 지도 제작에 대해서는 충분히 확립되었다. 그러나 다른 나라가 전국토에 걸친 지도를 만들기 위한 상세한 삼각망 측량을 시작한 것은 18세기 말에 이르러서였다. 영국은 1783년에 그레이트 브리튼 섬의 기본이 되는 삼각 측량을 시작했지만, 완료된 것은 1853년이 되었다. 1801년에 시작된 인도 대 삼각 측량에서는 에베레스트 산과 그 밖의 히말라야 산맥의 산들을 삼각 측량하여 지도를 만들었다.

이 시기, 유명한 수학자 카를 프리드리히 가우스에 의해 삼각 측량에 훌륭한 개량이 더해져 다른 방법을 능가하게 되었다.^[20] 1821년부터 1825년에 걸쳐 가우스는 하노버 왕국의 삼각 측량을 위탁받았다. 1820년, 가우스는 햇빛의 반사에 의해 위치를 나타내는 헬리오트로프(회조기)를 삼각 측량에 사용했다.^[21] 가우스는 최소 제곱법을 고안했다.^[22]

2. 3. 한국의 삼각측량 역사

조선 시대에는 전통적인 측량 기술과 함께 삼각측량의 원리가 활용되었다. 개항 이후, 대한제국 시기에는 근대적인 측량 기술이 도입되었으며, 토지 조사 사업에 삼각측량이 활용되었다. 일제강점기에는 조선총독부 주도로 전국적인 삼각측량이 실시되었는데, 이는 식민지 지배와 자원 수탈의 도구로 이용되었다는 비판을 받기도 한다.^[29] 광복 이후, 대한민국 정부는 국토 재건과 개발을 위해 삼각측량을 적극적으로 활용했다. 1970년대부터는 경제 개발 계획과 함께 전국적인 규모의 삼각측량이 이루어졌으며, 이는 국가 기본도 제작에 중요한 기반이 되었다.

메이지 5년 공부성 측량사에 의한 영국인 맥스웰(혹은 맥베인)을 중심으로 한 도쿄 측량의 선행 사례가 있지만,^[28] 홋카이도 개척사의 개척 차관 구로다 기요타카의 초청으로 일본에 온 호러스 케플론은 홋카이도의 지리·기후를 조사하고 삼각 측량을 할 필요성을 지적했다.^[26] 이를 바탕으로 1873년부터 개척사 측량장에 임명된 제임스 R. 와슨 등 고용 외국인을 중심으로 유후츠 지방을 기점으로 측량이 진행되어 1875년 12월에 "홋카이도 실측도"가 간행되었다.^[27] 이는 일본에서 본격적인 삼각 측량에 의한 지도 제작의 선구적인 사례가 된다.^[29]

2. 4. 현대

현대에는 1980년대 이후 확립된 위성 측위 시스템(GPS)으로 인해 측량을 위한 대규모 삼각망은 대체되었다. 하지만 초기의 측량 기준점들은 여전히 역사적 유산으로 남아있다. 예를 들어, 1936년부터 1962년까지 진행된 그레이트 브리튼 섬 재삼각 측량을 위해 만들어진 콘크리트 삼각점이나, 1816년부터 1855년까지 이루어진 슈트루베 측지 아크의 삼각 측량을 위해 만들어져 현재 유네스코 세계 유산에 등록된 삼각점 등이 그 예이다.

천문학에서는 지구에서 별까지의 거리를 재는 데 삼각측량법이 사용되지만^[23], 거리가 멀어질수록 연주 시차가 작아져 1만 광년 정도가 한계이다.^[24] 따라서 다른 측정 방법을 병행하여 사용한다.^[25]

우주 탐사기는 통신용 안테나를 지구로 향하게 하기 위해 두 개의 항성을 이용한 삼각 측량으로 위치를 계산하는데, 이때 지구에 가깝고 매우 밝은 별인 태양과 카노푸스가 사용된다.

3. 기본 원리

삼각측량은 두 기준점 사이의 거리(기선)와 각 기준점에서 대상 지점까지의 각도를 측정하여 대상 지점의 위치를 계산하는 방법이다. 어떤 점과 두 개의 기준점이 이루는 삼각형의 변과 각도가 측정되어 있다면, 그 점의 좌표 및 거리를 구할 수 있다.

3. 1. 평면 삼각측량

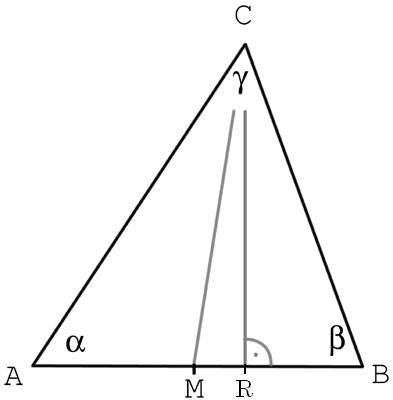
평면에서의 삼각측량은 사인 법칙과 코사인 법칙을 이용하여 거리를 계산한다. 어떤 점과 두 개의 기준점이 이루는 삼각형의 변과 각도가 측정되어 있다면, 그 점의 좌표 및 거리는 그 삼각형의 변의 길이를 계산하여 구할 수 있다.

α, β 와 AB의 길이는 주어진다.
C는 거리 RC 혹은 MC를 이용해 구할 수 있다.
'''RC:''' 사인법칙과 코사인법칙을 이용하여 C의 위치를 구할 수 있다.
$\gamma=180^\circ-\alpha-\beta$
$\frac{\sin\alpha}{BC}=\frac{\sin\beta}{AC}=\frac{\sin\gamma}{AB}$
AC와 BC를 다음과 같이 구할 수 있다.
$AC=\frac{AB\cdot\sin\beta}{\sin\gamma}$
$BC=\frac{AB\cdot\sin\alpha}{\sin\gamma}$
RC는 다음과 같이 구할 수 있다.
$RC=AC \cdot \sin\alpha$
혹은
$RC=BC \cdot \sin\beta$

'''MC'''는 피타고라스 정리를 이용하여 구할 수 있다.
$MR=AM-RB=\left(\frac{AB}{2}\right)-\left(BC \cdot \cos\beta\right)$
$MC=\sqrt{MR^2+RC^2}$

다음 수식은 평탄한 유클리드 평면에서 적용된다. 이는 거리가 지구의 곡면에 비해 유의미한 길이가 되면 부정확해지지만, 구면 삼각법을 사용하면 더 복잡한 계산 방법으로 구할 수 있다.

오른쪽 그림에 나타낸 바와 같이, 각도를 측정한 지점 간의 거리를

\ell

로 하면

:

\ell = \frac{d}{\tan \alpha} + \frac{d}{\tan \beta}

따라서

:

d =\frac {\ell} {(\frac{1}{\tan \alpha} + \frac{1}{\tan \beta})}

삼각 함수의 공식

\tan \alpha = \frac{\sin \alpha}{\cos \alpha}

및

\sin (\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta

를 적용하면, 이는

:

d = \frac{\sin\alpha \sin\beta}{\sin(\alpha + \beta)}\ell

와 같다. 이로부터, 관측점에서 미지의 점까지의 거리를 구하는 것은 용이하며, 모든 좌표도 얻을 수 있게 된다.

3. 2. 구면 삼각측량

어떤 점과 두 개의 기준점이 이루는 삼각형의 변과 각도가 측정되어 있다면, 그 점의 좌표 및 거리는 그 삼각형의 변의 길이를 계산하여 구할 수 있다.

다음 수식은 평탄한 유클리드 평면에서 적용된다. 이는 거리가 지구의 곡면에 비해 유의미한 길이가 되면 부정확해지지만, 구면 삼각법을 사용하면 더 복잡한 계산 방법으로 구할 수 있다.

4. 삼각망

삼각측량에 필요한 삼각점들을 연결하여 만든 여러 개의 삼각형 네트워크를 '''삼각망'''이라고 한다. 삼각망은 정삼각형에 가까울수록 좋으며, 내각은 25° ~ 130° 사이가 바람직하다.^[13] 삼각망에는 단열 삼각망, 사변형 삼각망, 유심 삼각망 등이 있다.

기선: 삼각측량의 출발선으로, 거리를 알고 있는 선분이다.
검기선: 측량 결과를 검정하는 데 사용되는, 거리를 알고 있는 선분이다.

삼각망에서 각의 이름은 다음과 같이 정의한다.

α: 다음 진행 방향으로 길이를 알고자 하는 선분을 마주보는 각
β: 기지선을 마주보는 각
γ: 나머지 각

4. 1. 단열 삼각망

삼각형을 일렬로 연결하여 폭이 좁고 길이가 긴 형태로 만든 것을 '''단열 삼각망'''이라고 한다. 하천, 도로, 철도, 노선, 터널같은 폭이 좁고 길이가 긴 지형에 적합하게 쓰인다. 정밀도는 떨어지나 신속한 측량이 가능하다.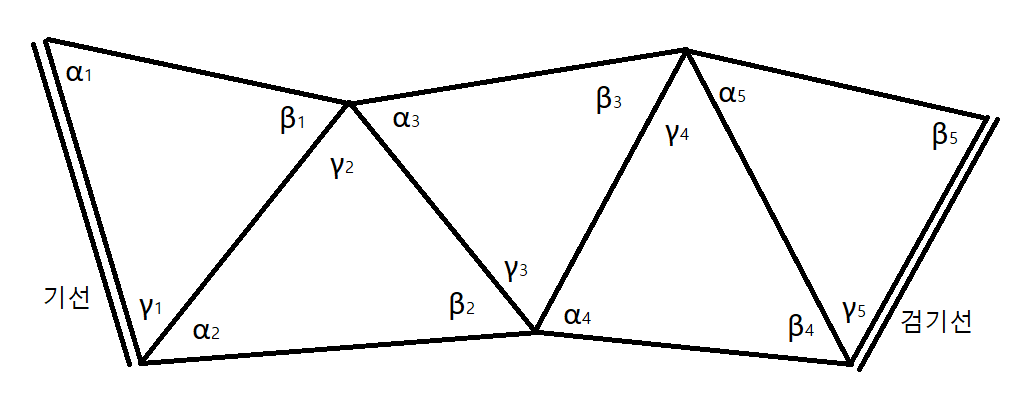

기선: 거리를 알고 있는 선으로 삼각측량의 출발선이 된다.
검기선: 거리를 알고 있는 선으로 측량 결과의 검정에 쓰인다.

; 각 이름

α: 다음 진행방향의 길이를 알고자 하는 선분을 마주보는 각
β: 기지선을 마주보는 각
γ: 나머지 각

4. 2. 사변형 삼각망

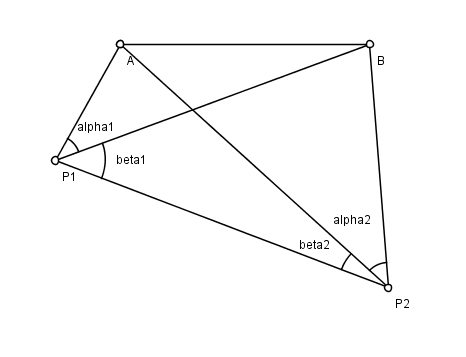
'''사변형 삼각망''' 또는 '''사변형망'''은 삼각형을 연결하여 사변형으로 만든 다음, 사변형을 연속적으로 이어가는 형태이다. 측량 면적이 작고 조건식 수가 많아 조정이 복잡하고 시간이 많이 걸리나, 정밀도가 높다.^[1] 폭이 좁고 길이가 긴 지형이면서 높은 정밀도를 요하는 경우에 사용된다.

4. 3. 유심 삼각망

삼각형의 측점 하나를 중심으로 삼각형이 둘러싸는 형태로 측량하는 것을 '''유심 삼각망'''이라고 한다. 유심 삼각망은 방대한 지역의 측량에 적절하며, 단열 삼각망과 사변형망의 중간 정도 정밀도를 가진다.^[1]

5. 조건

측량 결과가 허용 오차 이내에 있는 경우 조건식을 이용하여 관측각을 조정한다. 조건식에는 각조건, 변조건, 점조건이 있다.

각조건: 삼각형의 내각의 합이 180°임을 이용한다.
변조건: 삼각망의 임의 선분에 대해서, 어떤 경로를 거치든 계산 결과가 동일해야 함을 이용한다. 예를 들어 단열삼각망에서 기선으로부터 계산하든, 검기선으로부터 계산하든 같은 선분에 대해서는 계산 결과가 같아야 한다.
점조건: 임의 한 점을 둘러싼 각의 총합은 360°임을 이용한다.

6. 조정

삼각망의 종류에 따라 조정 방법이 약간씩 달라진다. 조정 과정에서 오차를 배분할 때, 단위 또는 절단오차 때문에 정확하게 오차를 배분하기 어려운 경우가 있다. 이때는 90°에 가장 가까운 각에 잔여 오차를 배분한다. 예를 들어 10″를 세 각에 배분해야 한다면, 우선 3″씩 배분하고 남은 1″를 90°에 가장 가까운 한 각에 배분한다.^[1]

6. 1. 사변형 망 조정

사변형 망 조정에는 엄밀법과 근사법이 있다. 토목공학에서는 근사법이 더 간편하고 자주 사용된다.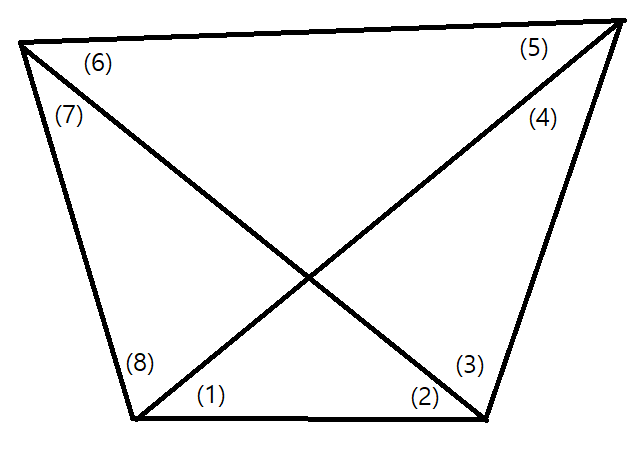

각 조건은 다음 세 가지이다.

# (1) + (2) = (5) + (6)

# (3) + (4) = (7) + (8)

# (1) + (2) + (3) + (4) + (5) + (6) + (7) + (8) = 360°

식의 좌우변이 같아야 오차가 없는 것이나, 오차가 생긴다고 하고, 각 식의 오차들을 ε₁, ε₂, ε₃라고 하자. 같은 기계로, 같은 정도로 관측하는 경우 경중률이 없으므로 발생 오차를 관측 횟수로 나누어 균등분배한다. 즉,

\frac{\epsilon_1}{4}, \frac{\epsilon_2}{4}, \frac{\epsilon_3}{8}

씩 배분하여 조정각을 구한다.

(1)의 조정각 $= (1) \mp \frac{\epsilon_1}{4} \mp \frac{\epsilon_3}{8}$
(2)의 조정각 $= (2) \mp \frac{\epsilon_1}{4} \mp \frac{\epsilon_3}{8}$
(3)의 조정각 $= (3) \mp \frac{\epsilon_2}{4} \mp \frac{\epsilon_3}{8}$
(4)의 조정각 $= (4) \mp \frac{\epsilon_2}{4} \mp \frac{\epsilon_3}{8}$
(5)의 조정각 $= (5) \mp \frac{\epsilon_1}{4} \mp \frac{\epsilon_3}{8}$
(6)의 조정각 $= (6) \mp \frac{\epsilon_1}{4} \mp \frac{\epsilon_3}{8}$
(7)의 조정각 $= (7) \mp \frac{\epsilon_2}{4} \mp \frac{\epsilon_3}{8}$
(8)의 조정각 $= (8) \mp \frac{\epsilon_2}{4} \mp \frac{\epsilon_3}{8}$

변조건에 의한 조정은 우선 각조건에 의해 조정된 조정각에 log sin을 취한 후 10을 더하고, 다음으로 정의되는 '''표차'''(tabular difference, d)를 구한다. 표차는 소수점 아래 8자리에서 반올림하여 7자리까지 나타낸다.

:

d_i = 2.106 \times 10^{-6} \cot \text{(조 정 각 )}

다음으로 ε₄를 구한다.

:

\epsilon_4 = \Sigma (\log \sin \text{홀 수 각} + 10) - \Sigma (\log \sin \text{짝 수 각} + 10)

변조건 조정량은

\frac{\epsilon_4}{\Sigma d}

이며, 이 값을 ε₄가 음수이면 홀수각에 조정량만큼 더해주고, 짝수각에는 조정량만큼 빼주면 된다. 변조건 조정까지 끝났으면 각들을 다 더해서 내각의 합인 360°가 나오는지 확인한다. 점조건은 사변형 망에서 사용되지 않는다.

6. 2. 단열 삼각망 조정

각 조건은 삼각형 내각의 합이 180°임을 이용하여 조정한다. 삼각망을 구성하는 각각의 삼각형 내각의 합을 구한 뒤, 180°와의 차이만큼 삼각형을 이루는 세 각에 분배해준다.

방향각 조건에 의한 조정은 검기선의 방향각 기지값이, 기선으로부터 계산해서 나온 검기선 방향각과 동일해야 한다는 것을 근거로 실시한다. 방향각은 다음 원리로 계산된다. (n은 삼각형 수)

: 현재 측선 방향각 = 전 측선 방향각 + 180 ± 교각 (진행 방향에 대해 왼쪽 방향 교각은 더해주고, 오른쪽 방향 교각은 빼준다)

: 계산을 통한 검기선 방향각 = 기선 방향각 + 180n + Σγ_{진행 방향 왼쪽} - Σγ_{진행 방향 오른쪽}

: 오차 ε₂ = 계산을 통한 검기선 방향각 - 기지값 검기선 방향각

α, β, γ각에 대해 조정량은 다음과 같다.

: ν_α = ε₂ / 2n

: ν_β = ε₂ / 2n

: ν_γ = ε₂ / n

다음으로 변 조건에 의한 조정을 실시한다. 변 조건에 의한 조정은 γ를 제외하고 α, β에 대해서만 실시한다. 첫 번째 측선 길이를 L₁, n번째 측선 길이를 L_n이라 할 때

: ε₃ = log L₁ - log L_n + Σ log sin α - Σ log sin β

: ν₄ = ν_α = ν_β = ε₃ / Σ d

조정량 ν₄를 적용한 조정각을 구했으면 삼각형마다 사인 법칙을 적용하여 변 길이를 구한다.^[1]

6. 3. 유심 삼각망 조정

유심다각망은 각 조건, 방향각 조건, 측점 조건, 변 조건에 의한 조정을 한다. 각 조건은 각 삼각형의 내각의 합이 180도가 되어야 한다는 것이다. 단열삼각망에서와 같은 방법으로 조정한다.

방향각 조건에 의한 조정은 기선의 방향각을 기초로 계산한 각 변의 방향각이 이미 알고 있는 방향각과 같아야 한다는 것을 이용하여 실시한다. 오차가 발생하고, 정도가 같은 측정을 했다면 보정량 ν₂는 마지막 측선까지 중심각 수 n으로 과부족량 ε₂를 나누어 분배한다.

:

\nu_2 = \frac{\epsilon_2 }{n}

측점 조건에 의한 조정은 다각형 중앙의 점 주위의 각을 모두 합하면 360도가 되어야 한다는 것을 이용한다. 360도가 안 된다면 과부족량을 중심각 수 n으로 나누어 조정한다.

변 조건에 의한 조정은 처음 기선의 길이와 계산을 통해 최종적으로 얻는 같은 위치의 변 길이가 같아야 한다는 것을 이용한다. 조정할 때는 중심각은 계산에 사용되지 않는다. 즉 삼각형 부분에서 다각형의 중심을 구성하는 각을 제외한 나머지 두 각만 이용한다. 기선의 길이를 b₁, 계산을 통해 나온 변 길이를 b_n, 다각형의 가장자리를 구성하는 두 각을 α_i, β_i라고 하면 다음 과정으로 조정을 진행한다.

:

b_n = \frac{\sin \alpha_1 \sin \alpha_2 \cdots \sin \alpha_n}{\sin \beta_1 \sin \beta_2 \cdots \sin \beta_n} b_1

b₁, b_n은 서로 같아야 한다. 즉

:

\frac{b_n}{b_1} = 1 = \frac{\sin \alpha_1 \sin \alpha_2 \cdots \sin \alpha_n}{\sin \beta_1 \sin \beta_2 \cdots \sin \beta_n}

양변에 로그를 취하여 변조건에 의해 발생하는 오차 ε₄를 계산한다.

:

\sum \log \sin \alpha - \sum \log \sin \beta = \epsilon_4

표차 d를 계산하고, 조정량을 계산한다.

:

\nu_{\alpha, \beta} = \frac{\epsilon_4}{\sum d}

7. 응용

점 A와 C에서 관찰한 각도와 두 점 사이의 기준선 b를 이용하여 먼 거리에 있는 물체 B의 위치를 구함

삼각측량은 다양한 분야에서 활용된다.

측량: 삼변측량법과 함께 측량에서 사용되는 방법으로, 알려진 지점에서의 각도를 측정하여 거리를 계산한다.
컴퓨터 비전: 컴퓨터 스테레오 비전과 광학 3차원 측정 시스템은 삼각측량법 원리를 사용하여 물체의 공간적 치수와 기하학적 구조를 결정한다.^[2]
천문학: 지구에서 별까지의 거리 계측에 사용되지만,^[23] 거리가 멀어지면 연주 시차가 작아져 1만 광년 정도가 한계이므로,^[24] 다른 계측법을 병용한다.^[25]
우주 탐사기: 통신용 안테나를 지구에 계속 향하게 하기 위해 두 개의 항성을 사용한 삼각 측량으로 위치를 계산한다. 주로 태양과 카노푸스가 사용된다.
일본의 측량: 홋카이도 개척 과정에서 호러스 케플론의 지적과 제임스 R. 와슨 등 고용 외국인을 중심으로 삼각 측량이 진행되었다.^[26]^[27] 이는 일본에서 본격적인 삼각 측량에 의한 지도 제작의 선구적인 사례이다.^[29]

위에 언급된 활용 분야 외에도 항해, 계량학, 천문 측지학, 양안시, 모델 로켓, 병기의 조준 등 다목적으로 사용된다.

7. 1. 측량

삼각측량법은 삼변측량법과 함께 측량에서 사용되는 방법이다. 삼변측량법이 점까지의 거리를 직접 측정하는 것과 달리, 삼각측량법은 알려진 지점에서의 각도만 측정한다. 각도와 거리 측정을 모두 사용하는 것을 삼각측량법이라고 한다.

어떤 점과 두 개의 기준점이 이루는 삼각형의 변과 각도가 측정되어 있다면, 그 점의 좌표 및 거리는 그 삼각형의 변의 길이를 계산하여 구할 수 있다.

오른쪽 그림과 같이, 각도를 측정한 지점 간의 거리를

\ell

로 하면 다음과 같다.

:

\ell = \frac{d}{\tan \alpha} + \frac{d}{\tan \beta}

따라서

:

d =\frac {\ell} {(\frac{1}{\tan \alpha} + \frac{1}{\tan \beta})}

삼각 함수의 공식

\tan \alpha = \frac{\sin \alpha}{\cos \alpha}

및

\sin (\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta

를 적용하면, 이는

:

d = \frac{\sin\alpha \sin\beta}{\sin(\alpha + \beta)}\ell

와 같다. 이로부터 관측점에서 미지의 점까지의 거리를 구하는 것은 용이하며, 모든 좌표도 얻을 수 있게 된다.

오늘날 삼각 측량은 측량, 항해, 계량학, 천문 측지학, 모델 로켓, 병기의 조준 등 다목적으로 사용된다.

삼각형을 이용하여 거리를 측정하는 것은 고대까지 거슬러 올라간다. 기원전 6세기의 고대 그리스 철학자 탈레스는 피라미드 그림자의 길이를 측정하고, 동시에 자신의 그림자 길이를 측정하여 자신의 키와의 비율로부터 닮음인 삼각형을 사용하여 피라미드의 높이를 측정했다^[8]。

7. 2. 컴퓨터 비전

컴퓨터 스테레오 비전과 광학 3차원 측정 시스템은 삼각측량법 원리를 사용하여 물체의 공간적 치수와 기하학적 구조를 결정한다.^[2] 기본적으로 이 구성은 물체를 관찰하는 두 개의 센서로 이루어진다. 센서 중 하나는 일반적으로 디지털 카메라 장치이며, 다른 하나는 카메라 또는 광선 프로젝터일 수 있다. 각 센서의 중심 및 대상물 표면상의 점이 공간상에 삼각형을 구성한다. 이 삼각형에서 센서 간의 거리가 기선 b로 알려져 있어야 한다. 이 기선과 센서에 투영되는 빛의 각도를 결정함으로써, 투영광의 교점의 3차원 좌표를 삼각 함수로부터 계산할 수 있다.

7. 3. 기타 응용 분야

오늘날 삼각측량은 측량, 항해, 계량학, 천문 측지학, 양안시, 모델 로켓, 병기의 조준 등 다목적으로 사용된다.

천문학에서 지구에서 별까지의 거리 계측에 사용되고 있지만,^[23] 거리가 멀어지면 연주 시차가 작아지기 때문에 1만 광년 정도가 한계이므로,^[24] 다른 계측법을 병용한다.^[25]

우주 탐사기는 통신용 안테나를 지구에 계속 향하게 하기 위해 두 개의 항성을 사용한 삼각 측량으로 위치를 계산하고 있지만, 지구에 가깝고 매우 밝은 항성으로서 태양과 카노푸스가 사용되고 있다.

일본에서는 홋카이도 개척사의 개척 차관 구로다 기요타카의 초청으로 일본에 온 호러스 케플론은 홋카이도의 개척에 있어 홋카이도의 지리·기후를 조사하고 삼각 측량을 할 필요성을 지적했다.^[26] 이를 바탕으로 개척사 측량장에 임명된 제임스 R. 와슨 등 고용 외국인을 중심으로 1873년부터 유후츠 지방을 기점으로 측량이 진행되어 1875년 12월에 "홋카이도 실측도"가 간행되었다.^[27] 1872년 공부성의 측량사에 의한 영국인 맥스웰(혹은 맥베인)을 중심으로 한 도쿄에서의 측량의 선행 사례는 있지만,^[28] 이것은 일본에서 본격적인 삼각 측량에 의한 지도 제작의 선구적인 사례가 된다.^[29]

참조

_[1] 웹사이트 מה בתמונה? (תשובה: נקודת טריאנגולציה) http://www.jeepolog.[...] 2007-07-08
_[2] 서적 Close-Range Photogrammetry and 3D Imaging https://books.google[...] De Gruyter 2013-11-27
_[3] 간행물 The Lives and Opinions of Eminent Philosophers https://en.wikisourc[...] 2008-02-22
_[4] 문서 Proclus, In Euclidem
_[5] 서적 Science and Civilization in China: Volume 3, Mathematics and the Sciences of the Heavens and the Earth Caves Books Ltd. 1986
_[6] 문서 Liu Hui, Haidao Suanjing
_[7] 간행물 A Surveying Problem Travels from China to Paris https://books.google[...] Mathematisches Forschungsinstitut, Oberwolfach, Germany 1997
_[8] 간행물 The Lives and Opinions of Eminent Philosophers http://www.classicpe[...] 2008-02-22
_[9] 문서 Proclus, In Euclidem
_[10] 서적 Science and Civilization in China: Volume 3, Mathematics and the Sciences of the Heavens and the Earth Caves Books Ltd. 1986
_[11] 문서 劉徽, 『海島算経』
_[12] 간행물 A Surveying Problem Travels from China to Paris https://books.google[...] Mathematisches Forschungsinstitut, Oberwolfach, Germany 1997
_[13] 서적 A History of Engineering in Classical and Medieval Times Croom Helm & La Salle, Illinois: Open Court 1984
_[14] MacTutor Abu Arrayhan Muhammad ibn Ahmad al-Biruni
_[15] 문서 地図の話
_[16] 간행물 Tycho Brahe, Cartography and Landscape in 16th Century Scandinavia https://books.google[...] 2004
_[17] 웹사이트 Saxton's Hampshire: Surveying http://www.geog.port[...] 2003
_[18] 문서 地図の話
_[19] 문서 地図の話
_[20] 문서 地図の話
_[21] 문서 地図の話
_[22] 문서 地図の話
_[23] 웹사이트 質問6-1）星までの距離はどうやって測定するの？ https://www.nao.ac.j[...]
_[24] 웹사이트 『三角測量原理』による"星までの距離"の測定と限界について。 http://journal.orixr[...]
_[25] 웹사이트 宇宙の質問箱-恒星編 https://www.kahaku.g[...]
_[26] 웹사이트 史跡「開拓使札幌本庁本庁舎跡および旧北海道庁本庁舎」保存活用計画(素案) http://www.pref.hokk[...] 2020-12-04
_[27] 웹사이트 北海道実測図 http://archives.c.fu[...] 2020-12-04
_[28] 학술지 明治初期の勇払基線と苫小牧の発展:わが国最初の系統的な基線測量と三角測量をめぐって https://doi.org/10.1[...] 日本地図学会
_[29] 웹사이트 開拓使三角測量一本木基点 https://bunka.nii.ac[...] 2020-12-04
_[30] 웹사이트 江戸の数学第一部和算の歴史第4章実学としての和算コラム測量の方法 https://www.ndl.go.j[...] 2020-12-06
_[31] 웹사이트 伊能忠敬が仰いだ山々 https://www.gsi.go.j[...] 2020-12-06
_[32] 웹인용 מה בתמונה? (תשובה: נקודת טריאנגולציה) http://www.jeepolog.[...] 2007-07-08
_[33] 웹인용 보관된 사본 http://dl.dongascien[...] 2018-06-10

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com