테일러 정리

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

테일러 정리는 함수를 다항식으로 근사하는 방법으로, 함수의 미분값을 사용하여 함수를 특정 점에서의 테일러 다항식으로 나타낸다. 이 정리는 페아노, 라그랑주, 코시, 적분 형태의 나머지 항을 포함하며, 함수의 근사, 해석, 그리고 여러 분야에서의 응용에 핵심적인 역할을 한다. 테일러 정리는 함수의 해석성과 밀접한 관련이 있으며, 특히 복소해석학에서 강력한 결과를 제공한다.

테일러 정리

개요

이름	테일러 정리
영어 이름	Taylor's theorem
분야	미적분학
설명	어떤 함수의 도함숫값을 이용하여 특정 점에서 함수값을 근사하는 방법

테일러 급수

정의	함수 f(x)의 a에서의 테일러 급수는 다음과 같이 정의된다.
급수 표현	f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!}(x-a)^n
중심	a는 테일러 급수의 중심이다.
나머지 항	테일러 급수는 무한 급수이므로, 실제로 계산할 때는 유한한 항까지만 계산하고 나머지는 오차항으로 처리한다. 이 오차항을 나머지 항이라고 한다.

활용

함수의 근사값 계산	테일러 정리를 이용하면 복잡한 함수의 값을 특정 점에서 근사적으로 계산할 수 있다.
함수의 성질 분석	테일러 급수를 이용하면 함수의 극값, 변곡점 등의 성질을 분석할 수 있다.
미분 방정식의 해 구하기	테일러 급수를 이용하여 미분 방정식의 해를 근사적으로 구할 수 있다.

매클로린 급수	매클로린 급수는 테일러 급수의 특수한 경우로, 중심이 0인 테일러 급수이다.
로피탈의 정리	로피탈의 정리는 테일러 정리를 이용하여 증명할 수 있다.
점근 분석	테일러 정리는 점근 분석에서 함수의 근사식을 구하는 데 사용된다.
제트	테일러 정리는 제트의 개념과 관련이 있다.

2. 정의

함수

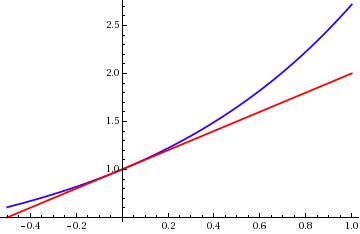
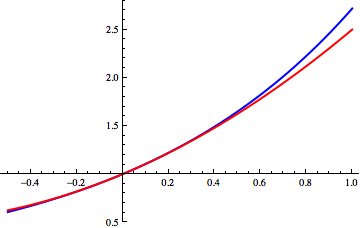
f(x)

가 점

x=a

에서 미분 가능하다면, 이 점 근처에서 함수를 선형 근사할 수 있다. 이는 다음 식을 만족하는 함수

h_1(x)

가 존재한다는 의미이다.

f(x) = f(a) + f'(a)(x - a) + h_1(x)(x - a), \quad \lim_{x \to a} h_1(x) = 0.

여기서

P_1(x) = f(a) + f'(a)(x - a)

는 점

a

근처에서

f(x)

의 선형 근사 다항식이며,

y=P_1(x)

의 그래프는

x = a

에서

y=f(x)

그래프의 접선이다. 근사 오차는

R_1(x) = f(x) - P_1(x) = h_1(x)(x - a)

로 주어지며,

x

가

a

에 가까워질수록

f'(a)(x-a)

항보다 훨씬 빠르게 0으로 수렴한다.

더 정확한 근사를 위해 2차 다항식을 사용할 수 있다.

P_2(x) = f(a) + f'(a)(x - a) + \frac{f

(a)}{2}(x - a)^2.
이 다항식은 $x=a$ 에서 $f(x)$ 와 함수값, 1계 도함수값, 2계 도함수값이 모두 같다. 테일러 정리는 충분히 작은 $a$ 의 이웃에서 2차 근사가 선형 근사보다 더 정확함을 보장한다. 구체적으로, 다음 식을 만족하는 함수 $h_2(x)$ 가 존재한다.
$f(x) = P_2(x) + h_2(x)(x - a)^2, \quad \lim_{x \to a} h_2(x) = 0.$
여기서 오차항 $R_2(x) = f(x) - P_2(x) = h_2(x)(x - a)^2$ 는 $x$ 가 $a$ 로 갈 때 $(x - a)^2$ 보다 빠르게 0으로 수렴한다.

이러한 아이디어를 일반화하여, 함수 $f(x)$ 를 주어진 점 $a$ 근처에서 더 높은 차수의 다항식으로 근사할 수 있다. $k$ 차 테일러 다항식은 $x=a$ 에서 함수 $f(x)$ 와 0차부터 $k$ 차까지의 도함수 값을 일치시키는 다항식이다.

테일러 정리의 가장 기본적인 형태는 다음과 같이 기술된다.
$k \ge 1$ 인 정수 $k$ 에 대해 함수 $f: \mathbb{R} \to \mathbb{R}$ 가 점 $a \in \mathbb{R}$ 에서 $k$ 번 미분가능하다고 하자. 그러면 다음을 만족하는 함수 $h_k: \mathbb{R} \to \mathbb{R}$ 가 존재한다.
$f(x) = \sum_{i=0}^k \frac{f^{(i)}(a)}{i!}(x-a)^i + h_k(x)(x-a)^k,$
그리고
$\lim_{x\to a} h_k(x) = 0.$

여기서 다항식
$P_k(x) = f(a) + f'(a)(x-a) + \frac{f$ (a)}{2!}(x-a)^2 + \cdots + \frac{f^{(k)}(a)}{k!}(x-a)^k
는 함수

f

의 점

a

에서의 $k$ 차 테일러 다항식이다. 테일러 다항식은

x \to a

일 때

f(x)

에 "점근적으로 가장 잘 맞는" 유일한

k

차 다항식이다. 즉, 만약 어떤

k

차 다항식

p(x)

와 함수

h_k(x)

에 대해

f(x) = p(x) + h_k(x)(x-a)^k

이고

\lim_{x\to a} h_k(x) = 0

가 성립한다면, 반드시

p(x) = P_k(x)

이다.

테일러 정리는 나머지 항(remainder term^영어)

R_k(x) = f(x) - P_k(x) = h_k(x)(x-a)^k

의 점근적 거동을 설명한다. 이는

f

를 테일러 다항식

P_k(x)

로 근사할 때 발생하는 근사 오차이다. 작은 o 표기법을 사용하면, 나머지 항의 성질은 다음과 같이 표현할 수 있다.

R_k(x) = o(|x-a|^{k}), \quad x\to a.

이는

x

가

a

로 접근할 때 나머지 항

R_k(x)

가

(x-a)^k

보다 더 빠르게 0으로 수렴함을 의미한다. 이 형태의 나머지 항을 특별히 페아노 나머지 항이라고 부른다.

함수

f

에 대한 추가적인 조건(예: 더 높은 차수의 미분 가능성 및 연속성) 하에서는 나머지 항

R_k(x)

를 더 구체적인 형태로 표현할 수 있다. 대표적으로 라그랑주 나머지 항, 코시 나머지 항, 적분 나머지 항 등이 있으며, 이들은 특정 구간에서 오차의 크기를 추정하는 데 유용하게 사용된다. 이러한 나머지 항의 구체적인 형태와 유도 과정은 하위 섹션에서 자세히 다룬다.

2.1. 페아노 나머지 항

함수 $f\colon(a-r,a+r)\to\mathbb R$ 가 점 $a$ 에서 $n$ 번 미분 가능하다면, 함수 $f(x)$ 는 다음과 같이 테일러 다항식과 나머지 항으로 표현될 수 있다.
: $f(x) = f(a) + f'(a)(x-a) + \frac{f$ (a)}{2!}(x-a)^2 + \cdots + \frac{f^{(n)}(a)}{n!}(x-a)^n + R_n(x)
여기서 $P_n(x) = f(a) + f'(a)(x-a) + \frac{f$ (a)}{2!}(x-a)^2 + \cdots + \frac{f^{(n)}(a)}{n!}(x-a)^n는 $n$ 차 테일러 다항식(-次-多項式, $n$ -th order Taylor polynomial^영어)이라고 하며, $R_n(x) = f(x) - P_n(x)$ 는 나머지 항(-項, remainder term^영어)이라고 한다.

페아노 나머지 항은 이 나머지 항 $R_n(x)$ 의 한 형태로, $x$ 가 $a$ 에 가까워질 때 나머지 항의 크기가 $(x-a)^n$ 보다 더 빠르게 0으로 수렴한다는 것을 나타낸다. 이는 작은 o 표기법을 사용하여 다음과 같이 표현한다.
: $R_n(x) = o(|x-a|^n) \quad (x \to a)$
위 식은 $\lim_{x\to a} \frac{R_n(x)}{(x-a)^n} = 0$ 임을 의미한다.

테일러 정리의 페아노 나머지 항 형태는 다음과 같이 기술될 수 있다.
$k \ge 1$ 인 정수 $k$ 에 대해 함수 $f: \mathbb{R} \to \mathbb{R}$ 가 점 $a \in \mathbb{R}$ 에서 $k$ 번 미분가능하다고 하자. 그러면 다음을 만족하는 함수 $h_k: \mathbb{R} \to \mathbb{R}$ 가 존재한다.
: $f(x) = \sum_{i=0}^k \frac{f^{(i)}(a)}{i!}(x-a)^i + h_k(x)(x-a)^k$
: $\lim_{x\to a} h_k(x) = 0$
여기서 $h_k(x)(x-a)^k$ 항을 페아노 나머지 항(-項, Peano remainder term^영어) 또는 페아노의 나머지 항이라고 부른다.

이 형태의 테일러 정리는 나머지 항 $R_k(x) = f(x) - P_k(x)$ 의 점근적 거동, 즉 $x$ 가 $a$ 로 갈 때 근사 오차가 어떻게 0에 가까워지는지를 설명한다.

또한, 주어진 함수 $f(x)$ 에 대해 $f(x) = p(x) + h_k(x)(x-a)^k$ 이고 $\lim_{x\to a} h_k(x) = 0$ 를 만족하는 $k$ 차 이하의 다항식 $p(x)$ 는 위에서 정의한 테일러 다항식 $P_k(x)$ 로 유일하다. 이는 테일러 다항식이 페아노 나머지 항의 관점에서 함수를 근사하는 "점근적으로 가장 잘 맞는" 유일한 다항식임을 의미한다.

2.2. 라그랑주 나머지 항

만약 함수 $f\colon[a',b']\to\mathbb R$ 가 $n$ 번 연속 미분 가능하고, 열린 구간 $(a',b')$ 에서 $(n+1)$ 계 도함수를 가진다면, 임의의 $a,x\in[a',b']$ 에 대하여 테일러 전개의 나머지 항 $R_n(x) = f(x) - \sum_{i=0}^{n} \frac{f^{(i)}(a)}{i!}(x-a)^i$ 는 다음과 같이 표현될 수 있다.
: $R_n(x) = \frac{f^{(n+1)}(\xi)}{(n+1)!}(x-a)^{n+1}$
여기서 $\xi$ 는 $a$ 와 $x$ 사이의 어떤 값이다. 즉, $\xi$ 는 $a$ 와 $x$ 를 양 끝점으로 하는 열린 구간 $(a, x)$ 또는 $(x, a)$ 안에 존재한다 ( $\xi\in\{a+\theta(x-a)\colon 0<\theta<1\}$ ).

이 형태의 나머지 항을 수학자 조제프루이 라그랑주의 이름을 따서 라그랑주 나머지항(-項, Lagrange remainder term^영어)이라고 부른다. 이는 평균값 정리를 일반화한 것으로 볼 수 있는데, 실제로 $n=0$ 인 경우 라그랑주 나머지항 공식은 평균값 정리와 동일한 형태가 된다. 테일러 정리의 이러한 형태는 나머지 항을 특정 점에서의 $(n+1)$ 계 도함수 값과 관련지어 표현할 수 있게 해주며, 주로 평균값 정리를 사용하여 증명된다.

2.3. 코시 나머지 항

구간 $I$ 에서 함수 $f$ 가 $(n+1)$ 번 연속 미분 가능하다고 가정하자. 이때 임의의 $a, x \in I$ 에 대해, 테일러 정리의 나머지 항 $R_n(x) = f(x) - P_n(x)$ 는 다음과 같은 형태로 표현될 수 있다.

: $R_n(x) = \frac{f^{(n+1)}(\xi)}{n!}(x-\xi)^n(x-a)$

여기서 $\xi$ 는 $a$ 와 $x$ 사이에 있는 어떤 값이다 ( $\xi\in\{a+\theta(x-a)\colon 0<\theta<1\}$ ). 이 형태의 나머지 항을 코시 나머지 항(Cauchy remainder term^영어)이라고 부른다.

코시 나머지 항은 코시의 평균값 정리를 이용하여 유도할 수 있다. 두 함수 $F(t)$ 와 $G(t)$ 를 다음과 같이 정의하자.

$F(t) = f(t) + f'(t)(x-t) + \frac{f''(t)}{2!}(x-t)^2 + \cdots + \frac{f^{(n)}(t)}{n!}(x-t)^n$
$G(t) = t-a$

여기서 $t$ 는 $a$ 와 $x$ 사이의 값이다. $F(t)$ 는 $t$ 에 대한 함수이며, 정의에 따라 $F(x) = f(x)$ 이고 $F(a)$ 는 $f(x)$ 의 $a$ 에서의 $n$ 차 테일러 다항식 $P_n(x)$ 와 같다. 따라서 $F(x) - F(a) = f(x) - P_n(x) = R_n(x)$ 이다.

$F(t)$ 와 $G(t)$ 의 도함수를 구하면 다음과 같다.

$F'(t) = \frac{f^{(n+1)}(t)}{n!}(x-t)^n$
$G'(t) = 1$

코시의 평균값 정리에 따르면, $a$ 와 $x$ 사이의 어떤 값 $\xi$ 에 대해 다음 식이 성립한다.

$\frac{F'(\xi)}{G'(\xi)} = \frac{F(x) - F(a)}{G(x) - G(a)}$

위에서 구한 $F'(t)$ , $G'(t)$ , $F(x)-F(a)=R_n(x)$ , $G(x)-G(a)=x-a$ 를 코시 평균값 정리 식에 대입하면,

$\frac{\frac{f^{(n+1)}(\xi)}{n!}(x-\xi)^n}{1} = \frac{R_n(x)}{x-a}$

이 식을 $R_n(x)$ 에 대해 정리하면 코시 나머지 항의 공식을 얻는다.

$R_n(x) = \frac{f^{(n+1)}(\xi)}{n!}(x-\xi)^n(x-a)$

이는 앞서 제시된 코시 나머지 항의 정의와 일치한다. 라그랑주 나머지 항은 동일한 유도 과정에서 $G(t) = (x-t)^{n+1}$ 을 선택하여 얻을 수 있다.

2.4. 적분 나머지 항

만약 $I$ 가 구간이며, $f\colon I\to\mathbb R$ 가 $(n+1)$ 번 연속 미분 가능 함수라면, 임의의 $a,x\in I$ 에 대하여, 다음이 성립한다.
: $f(x)=f(a)+f'(a)(x-a)+\frac{f$ (a)}{2!}(x-a)^2+\cdots+\frac{f^{(n)}(a)}{n!}(x-a)^n+R_n(x)
여기서 나머지항 $R_n(x)$ 는 다음과 같이 적분 형태로 표현될 수 있다.
: $R_n(x) = \frac 1{n!}\int_a^xf^{(n+1)}(t)(x-t)^n\mathrm dt$
이와 같은 나머지항을 적분 나머지항(積分-項, integral remainder form^영어)이라고 한다.

이 적분 형태의 나머지 항은 미적분학의 기본 정리와 부분 적분을 반복적으로 적용하여 유도할 수 있다.

먼저 미적분학의 기본 정리에 의해 다음이 성립한다.
: $f(x)=f(a)+ \int_a^x \, f'(t) \, dt.$
여기서 우변의 적분 항에 부분 적분을 적용하면 ( $u=f'(t), dv=dt$ 가 아니라, $u=f'(t), dv=-(x-t)'dt$ 즉 $v=-(x-t)$ 로 간주),
: $\begin{align}\int_a^x f'(t)\,dt &= \Big[-(x-t)f'(t)\Big]_a^x - \int_a^x -(x-t)f$ (t)\,dt \\&= (x-a)f'(a) + \int_a^x (x-t)f(t)\,dt\end{align}
이를 위 식에 대입하면 다음과 같다.
: $f(x) = f(a)+(x-a)f'(a)+\int_a^x \, (x-t)f$ (t) \, dt
이는 $n=1$ 일 때의 테일러 정리와 적분 나머지항 $R_1(x) = \int_a^x (x-t)f$ (t)\,dt을 보여준다.

같은 방식으로 적분 항 $\int_a^x (x-t)f$ (t)\,dt에 다시 한번 부분 적분을 적용하면 ( $u=f$ (t), dv=(x-t)dt = -\frac{1}{2}((x-t)^2)'dt 즉 $v = -\frac{1}{2}(x-t)^2$ 로 간주),
: $\begin{align}\int_a^x (x-t)f$ (t)\,dt &= \left[-\frac{1}{2}(x-t)^2 f(t)\right]_a^x - \int_a^x -\frac{1}{2}(x-t)^2 f(t) \, dt \\&= \frac{1}{2}(x-a)^2 f(a) + \int_a^x \frac{1}{2}(x-t)^2 f(t)\,dt\end{align}
이를 대입하면 다음과 같다.
: $f(x) = f(a) + (x-a)f'(a) + \frac{1}{2}(x-a)^2 f$ (a) + \int_a^x \frac{1}{2}(x-t)^2f(t)\,dt
이는 $n=2$ 일 때의 테일러 정리와 적분 나머지항 $R_2(x) = \int_a^x \frac{1}{2}(x-t)^2f$ (t)\,dt을 보여준다.

이 과정을 $n$ 번 반복하면 다음의 일반적인 공식을 얻을 수 있다.
: $f(x) = f(a) + \frac{f'(a)}{1!}(x-a) + \cdots + \frac{f^{(n)}(a)}{n!}(x-a)^n + \int_a^x \frac{f^{(n+1)} (t)}{n!} (x-t)^n\,dt$
여기서 마지막 항이 바로 적분 나머지항 $R_n(x)$ 이다.

이 유도 과정은 $f^{(n+1)}$ 이 리만 적분 가능하다는 조건 하에 성립한다. 만약 함수 $f$ 가 더 약한 조건인 $f^{(n)}$ 이 절대 연속이기만 하다면, $f^{(n+1)}$ 은 L''¹ 함수로 존재하며, 르베그 적분의 틀 안에서 미적분학의 기본 정리와 부분 적분을 사용하여 동일한 결과를 얻을 수 있다.

3. 다변수 함수의 경우

함수 $f: \mathbb{R}^n \to \mathbb{R}$ 가 점 $\boldsymbol{a} \in \mathbb{R}^n$ 에서 $k$ 번 연속 미분 가능할 경우, 다중 지표 표기법을 사용하여 테일러 정리를 다음과 같이 나타낼 수 있다. 이때 $h_\alpha : \mathbb{R}^n \to \mathbb{R}$ 는 $\lim_{\boldsymbol{x}\to \boldsymbol{a}}h_\alpha(\boldsymbol{x})=0$ 을 만족하는 함수이다.

$\begin{align}& f(\boldsymbol{x}) = \sum_{|\alpha|\leq k} \frac{D^\alpha f(\boldsymbol{a})}{\alpha!} (\boldsymbol{x}-\boldsymbol{a})^\alpha + \sum_{|\alpha|=k} h_\alpha(\boldsymbol{x})(\boldsymbol{x}-\boldsymbol{a})^\alpha \\\end{align}$

만약 함수 $f : \mathbb{R}^n \to \mathbb{R}$ 가 닫힌 공 $B = \{ \mathbf{y} \in \mathbb{R}^n : \left\|\mathbf{a}-\mathbf{y}\right\| \leq r\}$ (여기서 $r > 0$ )에서 $k + 1$ 번 연속 미분 가능하다면, 나머지 항을 $(k+1)$ 차 편도함수를 이용한 적분 형태로 정확하게 표현할 수 있다.

$\begin{align}& f( \boldsymbol{x} ) = \sum_{|\alpha|\leq k} \frac{D^\alpha f(\boldsymbol{a})}{\alpha!} (\boldsymbol{x}-\boldsymbol{a})^\alpha + \sum_{|\beta|=k+1} R_\beta(\boldsymbol{x})(\boldsymbol{x}-\boldsymbol{a})^\beta, \\& R_\beta( \boldsymbol{x} ) = \frac$

👆

좌우로 밀어서 보기

{\beta!} \int_0^1 (1-t)^{|\beta|-1}D^\beta f \big(\boldsymbol{a}+t( \boldsymbol{x}-\boldsymbol{a} )\big) \, dt.\end{align}

이 경우, 콤팩트 집합

B

에서

(k+1)

차 편도함수의 연속성으로 인해 나머지 항

R_\beta(\boldsymbol{x})

에 대해 다음의 균등한 추정(uniform estimate)을 얻을 수 있다.

\left|R_\beta(\boldsymbol{x})\right| \leq \frac{1}{\beta!} \max_

👆

좌우로 밀어서 보기

\max_{\boldsymbol{y}\in B} |D^\alpha f(\boldsymbol{y})|, \qquad \boldsymbol{x}\in B.

예를 들어, 충분히 매끄러운 함수

f:\mathbb R^2\to\mathbb R

의 점

\boldsymbol{a}

에서의 3차 테일러 다항식은

\boldsymbol{v} = \boldsymbol{x}-\boldsymbol{a}

로 두면 다음과 같다.

\begin{align}P_3(\boldsymbol{x}) = f ( \boldsymbol{a} ) + {} &\frac{\partial f}{\partial x_1}( \boldsymbol{a} ) v_1 + \frac{\partial f}{\partial x_2}( \boldsymbol{a} ) v_2 + \frac{\partial^2 f}{\partial x_1^2}( \boldsymbol{a} ) \frac {v_1^2}{2!} +  \frac{\partial^2 f}{\partial x_1 \partial x_2}( \boldsymbol{a} ) v_1 v_2 + \frac{\partial^2 f}{\partial x_2^2}( \boldsymbol{a} ) \frac{v_2^2}{2!}  \\& + \frac{\partial^3 f}{\partial x_1^3}( \boldsymbol{a} ) \frac{v_1^3}{3!} + \frac{\partial^3 f}{\partial x_1^2 \partial x_2}( \boldsymbol{a} ) \frac{v_1^2 v_2}{2!} + \frac{\partial^3 f}{\partial x_1 \partial x_2^2}( \boldsymbol{a} ) \frac{v_1 v_2^2}{2!} + \frac{\partial^3 f}{\partial x_2^3}( \boldsymbol{a} ) \frac{v_2^3}{3!}\end{align}

3.1. 페아노 나머지 항

만약 함수 $f\colon\operatorname B_{\mathbb R^d}(\mathbf a,r)\to\mathbb R$ 의 모든 $n$ 계 편도함수가 연속 함수라면, 점 $\mathbf a$ 근방에서 다음과 같은 테일러 전개가 성립한다.
: $f(\mathbf x)=\sum_{k=0}^n\frac 1{k!}\sum_{j_1=1}^d\cdots\sum_{j_k=1}^d\frac{\partial^kf(\mathbf a)}{\partial x_{j_1}\cdots\partial x_{j_k}}(x_{j_1}-a_{j_1})\cdots(x_{j_k}-a_{j_k})+o(\Vert\mathbf x-\mathbf a\Vert^n)\qquad(\mathbf x\to\mathbf a)$
여기서 나머지 항 $o(\Vert\mathbf x-\mathbf a\Vert^n)$ 는 란다우 표기법으로, $\mathbf x$ 가 $\mathbf a$ 로 접근할 때 $\Vert\mathbf x-\mathbf a\Vert^n$ 보다 더 빠르게 0으로 수렴하는 함수를 의미한다. 이를 페아노 나머지 항 형태라고 한다.

특히, 함수 $f\colon \mathbb{R}^n \to \mathbb{R}$ 가 점 $\boldsymbol{a} \in \mathbb{R}^n$ 에서 미분 가능하다는 것은 다음 조건과 동치이다.
: $f(\boldsymbol{x}) = f(\boldsymbol{a}) + L(\boldsymbol{x}-\boldsymbol{a}) + h(\boldsymbol{x})|\mathbf{x}-\mathbf{a}|,\qquad \lim_{\boldsymbol{x}\to\boldsymbol{a}}h(\boldsymbol{x})=0$
위 식을 만족하는 선형 범함수 $L\colon \mathbb{R}^n \to \mathbb{R}$ 과 함수 $h\colon \mathbb{R}^n \to \mathbb{R}$ 가 존재해야 한다. 이때, $L = df(\boldsymbol{a})$ 는 점 $\boldsymbol{a}$ 에서의 $f$ 의 유일한 미분이다. 또한, $f$ 의 $\boldsymbol{a}$ 에서의 편미분이 존재하며, 미분은 다음과 같이 편미분으로 표현된다.
: $df( \boldsymbol{a} )( \boldsymbol{v} ) = \frac{\partial f}{\partial x_1}(\boldsymbol{a})v_1 + \cdots + \frac{\partial f}{\partial x_n}(\boldsymbol{a})v_n$

다변수 테일러 정리를 더 간결하게 표현하기 위해 다음과 같은 다중 지수 표기법을 도입하기도 한다. $\alpha \in \mathbb{N}^n$ 와 $\boldsymbol{x} \in \mathbb{R}^n$ 에 대해,
: $|\alpha| = \alpha_1+\cdots+\alpha_n, \quad \alpha!=\alpha_1!\cdots\alpha_n!, \quad \boldsymbol{x}^\alpha=x_1^{\alpha_1}\cdots x_n^{\alpha_n}.$

만약 함수 $f\colon \mathbb{R}^n \to \mathbb{R}$ 의 모든 $k$ 계 편도함수가 점 $\boldsymbol{a} \in \mathbb{R}^n$ 에서 연속이라면, 클레로의 정리에 따라 $\boldsymbol{a}$ 에서 혼합 편미분의 순서를 바꿀 수 있다. 따라서 고계 편도함수에 대한 다음 표기가 정당화된다.
: $D^\alpha f = \frac{\partial^$

👆

좌우로 밀어서 보기

f}{\partial x_1^{\alpha_1}\cdots \partial x_n^{\alpha_n}}, \qquad |\alpha|\leq k
이는

f

의 모든 (

k-1

)계 편도함수가

\boldsymbol{a}

의 어떤 근방에서 존재하고

\boldsymbol{a}

에서 미분 가능할 때도 마찬가지로 성립한다. 이때

f

는 점 $\boldsymbol{a}$ 에서 $k$ 번 미분 가능하다고 한다.

3.2. 라그랑주 나머지 항

$D\subseteq\mathbb R^d$ 가 연결된 열린집합이고, 함수 $f\colon D\to\mathbb R$ 의 모든 $(n+1)$ 계 편도함수가 연속 함수라고 가정하자. 또한, 두 점 $\mathbf a, \mathbf x \in D$ 에 대해 이 두 점을 잇는 선분, 즉 $\{\mathbf a+t(\mathbf x-\mathbf a) \mid t\in[0,1]\}$ 전체가 $D$ 에 포함된다고 하자.

이 조건에서, 다변수 함수 $f(\mathbf x)$ 를 점 $\mathbf a$ 근방에서 테일러 다항식으로 근사할 때 발생하는 나머지 항 $R_n(\mathbf x)$ 는 라그랑주 형태로 표현될 수 있다. 테일러 정리에 따르면 $f(\mathbf x)$ 는 다음과 같이 나타낼 수 있다.

: $f(\mathbf x) = \sum_{k=0}^n \frac{1}{k!} \sum_{j_1=1}^d \cdots \sum_{j_k=1}^d \frac{\partial^k f(\mathbf a)}{\partial x_{j_1}\cdots\partial x_{j_k}} (x_{j_1}-a_{j_1})\cdots(x_{j_k}-a_{j_k}) + R_n(\mathbf x)$

여기서 라그랑주 나머지 항 $R_n(\mathbf x)$ 는 다음과 같다.

: $R_n(\mathbf x) = \frac{1}{(n+1)!} \sum_{j_1=1}^d \cdots \sum_{j_{n+1}=1}^d \frac{\partial^{n+1} f(\boldsymbol\xi)}{\partial x_{j_1}\cdots\partial x_{j_{n+1}}} (x_{j_1}-a_{j_1})\cdots(x_{j_{n+1}}-a_{j_{n+1}})$

이 식에서 $\boldsymbol\xi$ 는 점 $\mathbf a$ 와 $\mathbf x$ 를 잇는 선분 위에 존재하는 어떤 점이다. 즉, $\boldsymbol\xi = \mathbf a + \theta(\mathbf x - \mathbf a)$ 를 만족하는 $\theta$ 가 $0$ 과 $1$ 사이에 존재한다 ( $0 < \theta < 1$ ). 이 형태는 일변수 함수의 테일러 정리에서 나타나는 라그랑주 나머지 항과 유사하며, $(n+1)$ 계 편도함수를 이용하여 나머지 항을 구체적으로 나타낸다.

3.3. 적분 나머지 항

미적분학의 기본 정리에 따르면, 함수 $f$ 의 도함수 $f'$ 이 르베그 적분 가능하다면 다음과 같이 쓸 수 있다.
: $f(x)=f(a)+ \int_a^x \, f'(t) \, dt.$
여기서 $f^{(k)}$ 가 절대 연속이라고 가정하면, 그 도함수 $f^{(k+1)}$ 는 $L^1$ 함수로 존재하므로 미적분학의 기본 정리와 부분 적분을 사용할 수 있다.

부분 적분을 반복 적용하면 다음과 같은 결과를 얻는다.
: $\begin{align}f(x) &= f(a)+\int_a^x f'(t) \, dt \\&= f(a) + \left[ (x-t)f'(t) \right]_a^x + \int_a^x (x-t)f$ (t) \, dt \\&= f(a)+(x-a)f'(a)+\int_a^x \, (x-t)f(t) \, dt.\end{align}
이는 $k=1$ 일 때 테일러 정리의 적분 형태와 같다.

일반적인 명제는 수학적 귀납법을 사용하여 증명할 수 있다. $k$ 에 대해 다음 식이 성립한다고 가정하자.
: $f(x) = f(a) + \frac{f'(a)}{1!}(x - a) + \cdots + \frac{f^{(k)}(a)}{k!}(x - a)^k + \int_a^x \frac{f^{(k+1)} (t)}{k!} (x - t)^k \, dt.$
나머지 항을 부분 적분하면 다음과 같다.
: $\begin{align}\int_a^x \frac{f^{(k+1)} (t)}{k!} (x - t)^k \, dt = & - \left[ \frac{f^{(k+1)} (t)}{(k+1)k!} (x - t)^{k+1} \right]_a^x + \int_a^x \frac{f^{(k+2)} (t)}{(k+1)k!} (x - t)^{k+1} \, dt \\= & \ \frac{f^{(k+1)} (a)}{(k+1)!} (x - a)^{k+1} + \int_a^x \frac{f^{(k+2)} (t)}{(k+1)!} (x - t)^{k+1} \, dt.\end{align}$
위 결과를 원래 식에 대입하면, $k$ 에 대해 성립하는 식이 $k+1$ 에 대해서도 성립함을 알 수 있다. $k=1$ 일 때 성립하므로, 모든 양의 정수 $k$ 에 대해 성립한다.

다변수 함수의 경우에도 유사한 형태의 적분 나머지 항을 정의할 수 있다. 만약 $D\subseteq\mathbb R^d$ 가 연결 열린집합이며, $f\colon D\to\mathbb R$ 의 모든 $(n+1)$ 계 편도함수가 연속 함수이고, 임의의 $t\in[0,1]$ 에 대하여 $\mathbf a+t(\mathbf x-\mathbf a)\in D$ 라면, 다음이 성립한다.
: $f(\mathbf x)=\sum_{k=0}^n\frac 1{k!}\sum_{j_1=1}^d\cdots\sum_{j_k=1}^d\frac{\partial^kf(\mathbf a)}{\partial x_{j_1}\cdots\partial x_{j_k}}(x_{j_1}-a_{j_1})\cdots(x_{j_k}-a_{j_k})+R_n(\mathbf x)$
여기서 나머지 항 $R_n(\mathbf x)$ 은 다음과 같이 적분 형태로 주어진다.
: $R_n(\mathbf x) = \frac 1{n!}\int_0^1\sum_{j_1=1}^d\cdots\sum_{j_{n+1}=1}^d\frac{\partial^{n+1}f(\mathbf a+t(\mathbf x-\mathbf a))}{\partial x_{j_1}\cdots\partial x_{j_{n+1}}}(x_{j_1}-a_{j_1})\cdots(x_{j_{n+1}}-a_{j_{n+1}})(1-t)^n\mathrm dt$

다중 지수 표기법을 사용하면 다변수 테일러 정리를 더 간결하게 표현할 수 있다. 함수 $f : \mathbb{R}^n \to \mathbb{R}$ 가 닫힌 공 $B = \{ \mathbf{y} \in \mathbb{R}^n : \left\|\mathbf{a}-\mathbf{y}\right\| \leq r\}$ 에서 $k + 1$ 번 연속 미분 가능하다고 하자. 여기서 $r > 0$ 이다. 그러면 $f$ 의 $(k+1)$ 차 편도함수를 이용하여 나머지 항에 대한 정확한 공식을 유도할 수 있다. 즉,
: $\begin{align}& f( \boldsymbol{x} ) = \sum_{|\alpha|\leq k} \frac{D^\alpha f(\boldsymbol{a})}{\alpha!} (\boldsymbol{x}-\boldsymbol{a})^\alpha + \sum_{|\beta|=k+1} R_\beta(\boldsymbol{x})(\boldsymbol{x}-\boldsymbol{a})^\beta, \\& R_\beta( \boldsymbol{x} ) = \frac$

👆

좌우로 밀어서 보기

{\beta!} \int_0^1 (1-t)^{|\beta|-1}D^\beta f \big(\boldsymbol{a}+t( \boldsymbol{x}-\boldsymbol{a} )\big) \, dt.\end{align}
이 경우, 콤팩트 집합

B

에서

(k+1)

차 편도함수의 연속성으로 인해 다음의 균등한 추정(uniform estimate)을 즉시 얻을 수 있다.
:

\left|R_\beta(\boldsymbol{x})\right| \leq \frac{1}{\beta!} \max_

👆

좌우로 밀어서 보기

\max_{\boldsymbol{y}\in B} |D^\alpha f(\boldsymbol{y})|, \qquad \boldsymbol{x}\in B.

4. 증명

테일러 정리는 다양한 방식으로 증명될 수 있으며, 사용되는 미적분학의 도구나 목표로 하는 나머지 항의 형태에 따라 여러 가지 증명 방법이 존재한다. 주요 증명 방법들은 다음과 같다.

* [[로피탈의 정리]] 활용: 페아노 나머지 항 형태의 테일러 정리를 증명하는 데 주로 사용된다. 함수 $f(x)$ 와 그 테일러 다항식 $P_k(x)$ 의 차이 $f(x) - P_k(x)$ 가 $x=a$ 에서 $k-1$ 차 도함수까지 0이 된다는 성질을 이용하여, 극한값 $\lim_{x\to a} \frac{f(x) - P_k(x)}{(x-a)^k}$ 을 계산할 때 로피탈의 정리를 $k$ 번 반복 적용하여 극한값이 0임을 보인다.

* [[코시 평균값 정리]] 활용: 라그랑주 나머지 항이나 코시 나머지 항 형태를 유도하는 데 사용된다. 보조 함수 $F(t)$ 와 $G(t)$ 를 적절히 정의하고, 이 함수들에 코시 평균값 정리를 적용하여 나머지 항 $R_{k+1}(x) = f(x) - P_k(x)$ 를 특정 형태( $\frac{f^{(k+1)}(\xi)}{(k+1)!}(x-a)^{k+1}$ 등)로 표현한다. 함수 $G(t)$ 를 어떻게 선택하느냐에 따라 라그랑주 나머지 항 또는 코시 나머지 항을 얻을 수 있다.

* [[미적분학의 기본 정리]]와 [[부분 적분]] 활용: 적분 나머지 항 형태를 유도하는 데 사용된다. $f(x) = f(a) + \int_a^x f'(t) dt$ 라는 미적분학의 기본 정리에서 시작하여, 적분 항에 부분 적분을 반복적으로 적용하면 테일러 다항식의 각 항과 적분 형태의 나머지 항 $R_k(x) = \frac{1}{k!} \int_a^x (x-t)^k f^{(k+1)}(t) dt$ 를 얻을 수 있다.

* [[다변수 함수]]의 경우: 다변수 함수의 테일러 정리는 일변수 함수의 테일러 정리를 이용하여 증명하는 경우가 많다. 두 점 $\mathbf{a}$ 와 $\mathbf{x}$ 를 잇는 선분 위에서 함수를 일변수 함수 $g(t) = f(\mathbf{a} + t(\mathbf{x}-\mathbf{a}))$ 로 제한한 뒤, 이 함수 $g(t)$ 에 일변수 테일러 정리를 적용한다. 이때 $g(t)$ 의 도함수를 계산하기 위해 연쇄 법칙과 다중 지표 표기법이 사용된다.

각 증명 방법에 대한 자세한 내용은 해당 하위 섹션에서 확인할 수 있다. 또한, 테일러 다항식이 주어진 조건을 만족하는 유일한 다항식이라는 유일성 증명도 존재한다.

4.1. 페아노 나머지 항의 증명

함수 $f$ 가 점 $a \in \mathbb{R}$ 에서 $k$ 번 미분가능하다고 하자. 페아노 나머지 항 형태의 테일러 정리는 함수 $f(x)$ 가 $k$ 차 테일러 다항식 $P_k(x)$ 와 나머지 항 $h_k(x)(x-a)^k$ 의 합으로 표현될 수 있으며, 이 나머지 항이 $(x-a)^k$ 보다 빠르게 0으로 수렴함을 의미한다. 즉, 다음을 만족하는 함수 $h_k(x)$ 가 존재한다는 것이다.
$f(x) = P_k(x) + h_k(x)(x-a)^k = \sum_{i=0}^k \frac{f^{(i)}(a)}{i!}(x-a)^i + h_k(x)(x-a)^k$
그리고
$\lim_{x\to a} h_k(x) = 0.$

이것은 다음 극한 식이 성립하는 것과 동치이다.
$\lim_{x\to a}\frac{f(x)-P_k(x)}{(x-a)^k}=0$

이 극한값을 증명하기 위해 함수 $h_k(x)$ 를 다음과 같이 정의한다.
$h_k(x) = \begin{cases}\dfrac{f(x) - P_k(x)}{(x-a)^k} & x\not=a\\0&x=a\end{cases}$
여기서 $P_k(x) = f(a) + f'(a)(x-a) + \frac{f''(a)}{2!}(x-a)^2 + \cdots + \frac{f^{(k)}(a)}{k!}(x-a)^k$ 는 $f$ 의 $a$ 에서의 $k$ 차 테일러 다항식이다. 이제 $\lim_{x\to a} h_k(x) = 0$ 임을 보이면 증명이 완료된다.

증명은 로피탈의 정리를 반복적으로 적용하는 것을 기반으로 한다. 테일러 다항식의 정의에 의해, 각 $j=0, 1, \dots, k$ 에 대해 $f^{(j)}(a)=P_k^{(j)}(a)$ 이다. 따라서 $j=0, 1, \dots, k-1$ 에 대해 분자 $f(x) - P_k(x)$ 와 그 $j$ 차 도함수는 $x=a$ 에서 0이 된다. 분모 $(x-a)^k$ 와 그 $j$ 차 도함수 ( $j \le k-1$ ) 역시 $x=a$ 에서 0이 된다. 함수 $f$ 가 점 $a$ 에서 $k$ 번 미분 가능하다는 것은 $a$ 의 근방에서 $k-1$ 번 미분 가능하다는 것을 의미하므로, 분자와 그 $k-2$ 개의 도함수는 $a$ 의 근방에서 미분 가능하다. 분모 또한 이 조건을 만족하며 $x \ne a$ 일 때 0이 아니므로, 로피탈의 정리를 $k-1$ 번 적용할 수 있다.

$정의}) \\&= 0\end{align}$
따라서 $\lim_{x\to a} h_k(x) = 0$ 이며, 페아노 나머지 항의 성질이 증명되었다.

4.1.1. 테일러 다항식의 유일성의 증명

함수 $f(x)$ 가 점 $a$ 근방에서 다음과 같이 $n$ 차 다항식과 페아노 나머지 항의 합으로 표현될 수 있다고 가정하자.
: $f(x)=a_0+a_1(x-a)+a_2(x-a)^2+\cdots+a_n(x-a)^n+o(x-a)^n\qquad(x\to a)$
여기서 $a_0, a_1, \dots, a_n \in \mathbb{R}$ 는 상수이며, $o(x-a)^n$ 은 $x \to a$ 일 때 $(x-a)^n$ 보다 더 빠르게 0으로 수렴하는 항을 의미한다 ( $\lim_{x\to a} \frac{o(x-a)^n}{(x-a)^n} = 0$ ). 이러한 표현에서 다항식 $P_n(x) = a_0+a_1(x-a)+\cdots+a_n(x-a)^n$ 부분이 유일하게 테일러 다항식임을 보이자.

먼저, 위 식의 양변에 $x \to a$ 극한을 취하면, $(x-a)^k$ (단, $k \ge 1$ ) 항들과 $o(x-a)^n$ 항은 모두 0으로 수렴하므로 다음을 얻는다.
: $\lim_{x\to a} f(x) = a_0$
만약 함수 $f$ 가 점 $a$ 에서 연속이라면 $\lim_{x\to a} f(x) = f(a)$ 이므로, $a_0 = f(a)$ 이다. 이는 테일러 다항식의 0차항 계수 $\frac{f^{(0)}(a)}{0!}$ 와 같다.

다음으로, $a_0 = f(a)$ 를 원래 식에 대입하고 양변에서 $f(a)$ 를 뺀 뒤 $(x-a)$ 로 나누면 다음과 같다.
: $\frac{f(x)-f(a)}{x-a}=a_1+a_2(x-a)+\cdots+a_n(x-a)^{n-1}+\frac{o(x-a)^n}{x-a}\qquad(x\to a)$
$\frac{o(x-a)^n}{x-a} = o(x-a)^{n-1}$ 이므로 ( $\lim_{x\to a} \frac{o(x-a)^n/(x-a)}{(x-a)^{n-1}} = \lim_{x\to a} \frac{o(x-a)^n}{(x-a)^n} = 0$ ), 식은 다음과 같이 정리된다.
: $\frac{f(x)-f(a)}{x-a}=a_1+a_2(x-a)+\cdots+a_n(x-a)^{n-1}+o(x-a)^{n-1}\qquad(x\to a)$
이 식의 양변에 다시 $x \to a$ 극한을 취하면,
: $\lim_{x\to a} \frac{f(x)-f(a)}{x-a} = a_1$
미분의 정의에 의해 좌변은 $f'(a)$ 와 같으므로 (함수 $f$ 가 $a$ 에서 미분 가능하다면), $a_1 = f'(a)$ 이다. 이는 테일러 다항식의 1차항 계수 $\frac{f^{(1)}(a)}{1!}$ 와 같다.

같은 방법으로 $a_1 = f'(a)$ 를 대입하고 식을 변형하여 $(x-a)^2$ 로 나누면 다음과 같다.
: $\frac{f(x)-f(a)-f'(a)(x-a)}{(x-a)^2}=a_2+a_3(x-a)+\cdots+a_n(x-a)^{n-2}+o(x-a)^{n-2}\qquad(x\to a)$
여기에 $x \to a$ 극한을 취하면,
: $\lim_{x\to a} \frac{f(x)-f(a)-f'(a)(x-a)}{(x-a)^2} = a_2$
만약 $f$ 가 $a$ 에서 두 번 미분 가능하다면, 로피탈의 정리를 적용하거나 고계 도함수의 정의를 이용하여 좌변이 $\frac{f$ (a)}{2}와 같음을 보일 수 있다. 따라서 $a_2 = \frac{f$ (a)}{2!}이다. 이는 테일러 다항식의 2차항 계수와 같다.

이 과정을 계속 반복하면, 함수 $f$ 가 $a$ 에서 $n$ 번 미분 가능하다는 가정 하에, 모든 $k \in \{0, 1, \dots, n\}$ 에 대하여 계수 $a_k$ 가 다음과 같이 유일하게 결정됨을 알 수 있다.
: $a_k = \frac{f^{(k)}(a)}{k!}$
이는 정확히 $a$ 에서의 $n$ 차 테일러 다항식의 계수이다. 따라서 함수 $f(x)$ 를 점 $a$ 근방에서 $n$ 차 다항식과 페아노 나머지 항 $o(x-a)^n$ 의 합으로 표현할 때, 그 다항식 부분은 테일러 다항식으로 유일하게 결정된다.

4.2. 라그랑주 나머지 항의 증명

코시 평균값 정리를 이용하여 라그랑주 나머지 항을 증명할 수 있다. 편의상 $a 라고 가정한다.$

먼저, 어떤 실수 값을 가지는 함수 G가 닫힌 구간 $[a, x]$ 에서 연속이고, 열린 구간 $(a, x)$ 에서 미분 가능하며, 그 도함수 G''의 값이 열린 구간에서 0이 아니라고 가정하자.

다음으로 함수 F를 다음과 같이 정의한다.
: $F(t) = f(t) + f'(t)(x-t) + \frac{f$ (t)}{2!}(x-t)^2 + \cdots + \frac{f^{(k)}(t)}{k!}(x-t)^k
여기서 F는 닫힌 구간 $[a, x]$ 에서 연속이고, 열린 구간 $(a, x)$ 에서 미분 가능하다.

코시 평균값 정리에 따르면, 다음을 만족하는 점 $\xi \in (a, x)$ 가 존재한다.
: $(*) \quad \frac{F'(\xi)}{G'(\xi)} = \frac{F(x)-F(a)}{G(x)-G(a)}$

여기서 분자 $F(x)-F(a)$ 는 $f(x)$ 에 대한 테일러 다항식의 나머지 항 $R_{k+1}(x)$ 와 정확히 일치한다. ( $R_{k+1}(x) = f(x) - P_k(x)$ , $P_k(x)$ 는 k차 테일러 다항식)

이제 F의 도함수를 계산하면 다음과 같다.
: $\begin{align}F'(t) &= f'(t) + \big(f$ (t)(x-t) - f'(t)\big) + \left(\frac{f^{(3)}(t)}{2!}(x-t)^2 - \frac{f^{(2)}(t)}{1!}(x-t)\right) + \cdots \\&\quad \cdots + \left( \frac{f^{(k+1)}(t)}{k!}(x-t)^k - \frac{f^{(k)}(t)}{(k-1)!}(x-t)^{k-1}\right) \\&= \frac{f^{(k+1)}(t)}{k!}(x-t)^k\end{align}

이 $F'(t)$ 를 식 (*)에 대입하고 $R_{k+1}(x)$ 에 대해 정리하면 다음을 얻는다.
: $R_{k+1}(x) = (G(x)-G(a)) \frac{F'(\xi)}{G'(\xi)} = \frac{f^{(k+1)}(\xi)}{k!}(x-\xi)^k \frac{G(x)-G(a)}{G'(\xi)}$

이것은 나머지 항에 대한 일반적인 형태이다. 여기서 특정 함수 G를 선택하여 라그랑주 나머지 항을 유도할 수 있다.

G(t) = (x − t)^k+1 로 두면, G(x) = 0 이고 G(a) = (x − a)^k+1 이다. 또한 도함수는 G''(t) = −(k+1)(x − t)^k 이다. 이를 위 나머지 항 공식에 대입하면 다음과 같다.

$R_{k+1}(x) = \frac{f^{(k+1)}(\xi)}{k!}(x-\xi)^k \frac{0 - (x-a)^{k+1}}{-(k+1)(x-\xi)^k} = \frac{f^{(k+1)}(\xi)}{k!} \frac{(x-a)^{k+1}}{k+1} = \frac{f^{(k+1)}(\xi)}{(k+1)!}(x-a)^{k+1}$

이것이 바로 라그랑주 나머지 항이다. 참고로, G(t) = t − a 로 두면 코시 나머지 항을 얻을 수 있다.

4.3. 적분 나머지 항의 증명

미적분학의 기본 정리에 따라 다음이 성립한다.
: $f(x)=f(a)+\int_a^xf'(t)\mathrm dt$
여기에 부분 적분을 반복적으로 적용하면 다음과 같은 과정을 거쳐 테일러 다항식과 적분 형태의 나머지 항을 얻을 수 있다.

먼저, 위 식의 적분 항에 $u = f'(t)$ , $dv = dt$ 로 놓고 부분 적분을 시도하는 대신, 적분 변수 $t$ 에 대해 $d(x-t) = -dt$ 임을 이용하여 다음과 같이 변형하여 부분 적분을 적용한다.
: $\begin{align}f(x)&=f(a)-\int_a^xf'(t)\mathrm d(x-t)\\&=f(a)-\left[f'(t)(x-t)\right]_a^x + \int_a^x(x-t)f$ (t)\mathrm dt \quad (\because \text{부분 적분})\\&=f(a)+f'(a)(x-a)+\int_a^x(x-t)f(t)\mathrm dt\end{align}
여기서 얻어진 적분 항 $\int_a^x(x-t)f$ (t)\mathrm dt에 다시 한 번 $d(x-t)^2 = -2(x-t)dt$ 임을 이용하여 변형하고 부분 적분을 적용한다.
: $\begin{align}f(x)&=f(a)+f'(a)(x-a)-\frac 12\int_a^xf$ (t)\mathrm d(x-t)^2\\&=f(a)+f'(a)(x-a)-\frac 12\left[f(t)(x-t)^2\right]_a^x + \frac 12\int_a^x(x-t)^2f(t)\mathrm dt \quad (\because \text{부분 적분})\\&=f(a)+f'(a)(x-a)+\frac{f(a)}2(x-a)^2+\frac 12\int_a^x(x-t)^2f(t)\mathrm dt\end{align}
이 과정을 $n$ 번 반복하면 다음과 같은 일반적인 형태를 얻는다.
: $\begin{align}f(x)&=f(a)+f'(a)(x-a)+\frac{f''(a)}{2!}(x-a)^2+\cdots+\frac{f^{(n)}(a)}{n!}(x-a)^n+R_n(x)\end{align}$
이때 나머지 항 $R_n(x)$ 는 다음과 같은 적분 형태로 주어진다.
: $R_n(x) = \frac 1{n!}\int_a^x(x-t)^nf^{(n+1)}(t)\mathrm dt$
따라서 위와 같이 미적분학의 기본 정리와 부분 적분을 반복 적용하여 적분 나머지 항을 갖는 테일러 정리를 증명할 수 있다. 이 적분 형태의 나머지 항에 적분 평균값 정리 중 하나인 제1 적분 평균값 정리를 적용하면 라그랑주 나머지 항을 유도할 수 있다.

4.4. 코시 나머지 항의 증명

적분 나머지항에 제1 적분 평균값 정리를 적용하면 다음을 얻는다.
: $\begin{align}\frac 1{n!}\int_a^xf^{(n+1)}(t)(x-t)^n\mathrm dt&=\frac{f^{(n+1)}(\xi)}{n!}(x-\xi)^n\int_a^x\mathrm dt\\&=\frac{f^{(n+1)}(\xi)}{n!}(x-\xi)^n(x-a)\end{align}$
여기서 $\xi$ 는 $a$ 와 $x$ 사이의 어떤 값이다 ( $\xi\in\{a+\theta(x-a)\colon 0<\theta<1\}$ ). 따라서 코시 나머지항 형태의 테일러 정리가 성립한다.

4.5. 다변수 함수의 경우의 증명

다변수 함수의 테일러 정리는 일변수 함수의 테일러 정리를 확장하여 증명할 수 있다. 여러 형태의 나머지 항에 대한 증명이 가능하며, 여기서는 라그랑주 나머지 항과 적분 형태의 나머지 항을 유도하는 과정을 중심으로 설명한다.

증명의 기본 아이디어는 함수 $f: \mathbb{R}^n \to \mathbb{R}$ 를 점 $\mathbf{a}$ 와 $\mathbf{x}$ 를 잇는 선분 위로 제한하여 일변수 함수 $g(t)$ 를 정의하고, 이 함수에 일변수 테일러 정리를 적용하는 것이다.

먼저 $\mathbf{a}$ 와 $\mathbf{x}$ 사이의 선분을 $\mathbf{u}(t) = \mathbf{a} + t(\mathbf{x} - \mathbf{a})$ (단, $0 \le t \le 1$ )로 매개변수화하고, 일변수 함수 $g(t) = f(\mathbf{u}(t)) = f(\mathbf{a} + t(\mathbf{x} - \mathbf{a}))$ 를 정의한다. 만약 $f$ 가 $\mathbf{a}$ 를 포함하는 어떤 닫힌 공 $B$ 에서 $k+1$ 번 연속 미분 가능하다면, $g(t)$ 는 $[0, 1]$ 에서 $k+1$ 번 연속 미분 가능하다.

1. 라그랑주 나머지 항 형태의 증명

함수 $g(t)$ 에 라그랑주 나머지 항을 포함하는 일변수 테일러 정리를 적용하면, 어떤 $\theta \in (0, 1)$ 에 대해 다음이 성립한다.
: $g(1) = \sum_{j=0}^n \frac{g^{(j)}(0)}{j!} + \frac{g^{(n+1)}(\theta)}{(n+1)!}$
여기서 $g(1) = f(\mathbf{x})$ 이고 $g(0) = f(\mathbf{a})$ 이다. 연쇄 법칙과 다중 지표 표기법을 사용하여 $g(t)$ 의 $j$ 계 도함수를 계산하면 다음과 같다.
: $g^{(j)}(t) = \sum_{|\alpha|=j} \frac{j!}{\alpha!} (D^\alpha f)(\mathbf{a} + t(\mathbf{x} - \mathbf{a})) (\mathbf{x} - \mathbf{a})^\alpha$
여기서 $\alpha = (\alpha_1, \dots, \alpha_n)$ 는 다중 지표, $|\alpha| = \sum \alpha_i$ , $\alpha! = \prod \alpha_i!$ , $\mathbf{y}^\alpha = \prod y_i^{\alpha_i}$ , $D^\alpha f = \frac{\partial^$

👆

좌우로 밀어서 보기

f}{\partial x_1^{\alpha_1} \cdots \partial x_n^{\alpha_n}}이다.

t=0

일 때와

t=\theta

일 때의 도함수를 위 테일러 전개식에 대입하면,
:

g^{(j)}(0) = \sum_{|\alpha|=j} \frac{j!}{\alpha!} (D^\alpha f)(\mathbf{a}) (\mathbf{x} - \mathbf{a})^\alpha

g^{(n+1)}(\theta) = \sum_{|\beta|=n+1} \frac{(n+1)!}{\beta!} (D^\beta f)(\mathbf{a} + \theta(\mathbf{x} - \mathbf{a})) (\mathbf{x} - \mathbf{a})^\beta

이를 정리하면 라그랑주 나머지 항 형태의 다변수 테일러 정리를 얻는다.
:

f(\mathbf{x}) = \sum_{|\alpha| \le n} \frac{D^\alpha f(\mathbf{a})}{\alpha!} (\mathbf{x} - \mathbf{a})^\alpha + \sum_{|\beta|=n+1} \frac{D^\beta f(\mathbf{a} + \theta(\mathbf{x} - \mathbf{a}))}{\beta!} (\mathbf{x} - \mathbf{a})^\beta

2. 적분 나머지 항 형태의 증명

함수

g(t)

에 적분 나머지 항을 포함하는 일변수 테일러 정리를 적용하면 다음과 같다.
:

g(1) = g(0) + \sum_{j=1}^k \frac{1}{j!} g^{(j)}(0) + \int_0^1 \frac{(1-t)^k}{k!} g^{(k+1)}(t) dt

위에서 구한

g^{(j)}(t)

공식을

t=0

일 때와

g^{(k+1)}(t)

에 대해 대입하고 정리하면,
:

f(\mathbf{x}) = f(\mathbf{a}) + \sum_{j=1}^k \frac{1}{j!} \sum_{|\alpha|=j} \frac{j!}{\alpha!} (D^\alpha f)(\mathbf{a}) (\mathbf{x} - \mathbf{a})^\alpha + \int_0^1 \frac{(1-t)^k}{k!} \sum_{|\beta|=k+1} \frac{(k+1)!}{\beta!} (D^\beta f)(\mathbf{a} + t(\mathbf{x} - \mathbf{a})) (\mathbf{x} - \mathbf{a})^\beta dt

이를 다중 지표 표기법을 사용하여 정리하면 다음과 같은 적분 나머지 항 형태의 테일러 정리를 얻는다.
:

f(\mathbf{x}) = \sum_{|\alpha| \le k} \frac{(D^\alpha f)(\mathbf{a})}{\alpha!} (\mathbf{x} - \mathbf{a})^\alpha + \sum_{|\beta|=k+1} R_\beta(\mathbf{x}) (\mathbf{x} - \mathbf{a})^\beta

여기서 나머지 항

R_\beta(\mathbf{x})

는 다음과 같이 주어진다.
:

R_\beta(\mathbf{x}) = \frac

👆

좌우로 밀어서 보기

{\beta!} \int_0^1 (1-t)^{|\beta|-1} (D^\beta f)(\mathbf{a} + t(\mathbf{x} - \mathbf{a})) dt
단,

|\beta|=k+1

이다.

5. 역사적 배경

주어진 원본 소스(`source`)에는 '역사적 배경' 섹션에 해당하는 내용이 포함되어 있지 않습니다. 원본 소스는 테일러 정리의 수학적 정의, 테일러 다항식, 나머지 항의 다양한 형태(피아노, 라그랑주, 코시, 슐뢰밀히, 적분 형태) 및 관련 추정 등 수학적 세부 사항만을 다루고 있습니다. 따라서 제공된 정보만으로는 '역사적 배경' 섹션을 작성할 수 없습니다.

5.1. 초기 역사

주어진 원본 소스(`source`)에는 '초기 역사' 섹션에 해당하는 내용이 포함되어 있지 않습니다. 원본 소스는 테일러 정리의 나머지 항에 대한 다양한 형태(라그랑주, 코시, 슐뢰밀히, 적분 형태), 나머지 항의 추정, 그리고 지수 함수 근사 예시에 대한 수학적 세부 사항을 다루고 있습니다. 따라서 제공된 정보만으로는 '초기 역사' 섹션을 작성할 수 없습니다.

6. 주요 특징

함수가 특정 지점에서 충분히 미분 가능하다면, 그 지점 주변에서 함수의 값을 다항식으로 근사할 수 있다는 것이 테일러 정리의 핵심 아이디어이다. 일반적으로 사용하는 다항식의 차수가 높아질수록, 즉 함수의 더 높은 차수의 도함수 정보까지 활용할수록 근사의 정확도는 높아진다. 이렇게 만들어진 근사 다항식을 테일러 다항식이라고 부른다.

하지만 다항식 근사는 필연적으로 원래 함수와의 오차를 포함하며, 이를 [[나머지 항]](remainder term)이라고 한다. 테일러 정리는 이 나머지 항의 크기가 어떻게 되는지, 즉 근사가 얼마나 정확한지를 수학적으로 분석하는 방법을 제공한다. 기본적으로 테일러 정리는 근사 오차가 특정 항( $(x-a)^k$ 형태)보다 빠르게 0으로 수렴한다는 점근적인 성질을 알려준다. 즉, 근사하려는 지점에 충분히 가깝다면 오차는 매우 작아진다.

그러나 모든 함수가 테일러 다항식으로 잘 근사되는 것은 아니다. 함수가 무한히 미분 가능하더라도 해석적 함수가 아닌 경우에는 다항식의 차수를 높여도 근사 정확도가 개선되지 않거나, 특정 구간에서만 근사가 유효할 수 있다.

근사 오차의 구체적인 크기를 파악하고 제어하기 위해 나머지 항에 대한 다양한 형태(라그랑주 형태, 코시 형태 등)가 연구되었다. 이러한 형태들을 이용하면 특정 구간에서 오차의 상한을 추정할 수 있으며, 이는 테일러 근사의 신뢰도를 평가하고 실제 문제에 적용하는 데 매우 중요하다. 예를 들어, 특정 정확도 요구사항을 만족시키기 위해 필요한 테일러 다항식의 최소 차수를 결정하거나, 주어진 차수의 다항식이 특정 오차 범위 내에서 유효한 구간을 찾는 데 활용될 수 있다.

6.1. 기술적 측면

테일러 정리는 함수를 특정 점 주변에서 다항식으로 근사하는 방법을 제공하는 중요한 수학적 도구이다. 어떤 함수가 한 점에서 미분 가능하다면, 그 점에서의 함수값과 도함수 값을 이용하여 선형 근사(1차 다항식, 즉 접선)를 구할 수 있다. 이는 가장 기본적인 형태의 근사이다.

더 정확한 근사가 필요할 경우, 함수의 2계, 3계 등 더 높은 차수의 도함수 정보를 활용하여 2차, 3차 또는 그 이상의 고차 다항식으로 함수를 근사할 수 있다. 이렇게 구성된 다항식을 테일러 다항식이라고 부른다. 일반적으로 다항식의 차수가 높아질수록 특정 점 근처에서 원래 함수를 더 잘 근사하게 된다.

하지만 다항식 근사는 필연적으로 원래 함수와의 차이, 즉 오차를 수반한다. 이 오차를 나머지 항이라고 부르며, 테일러 정리는 이 나머지 항의 크기와 성질을 분석하는 수학적 틀을 제공한다. 즉, 테일러 정리는 함수를 얼마나 정확하게 다항식으로 근사할 수 있는지, 그리고 그 오차가 어떻게 변화하는지를 이해하는 데 핵심적인 역할을 한다. 테일러 다항식의 구체적인 구성 방법과 나머지 항의 다양한 형태 및 분석은 하위 섹션에서 더 자세히 다룬다.

6.1.1. 구성 요소

실수 값을 갖는 함수

f(x)

가 점

x=a

에서 미분 가능하다면, 이 점 근처에서 선형 근사를 가질 수 있다. 이는 다음을 만족하는 함수 h₁(x)가 존재한다는 것을 의미한다.

f(x) = f(a) + f'(a)(x - a) + h_1(x)(x - a), \quad \lim_{x \to a} h_1(x) = 0.

여기서

P_1(x) = f(a) + f'(a)(x - a)

는 점 a 근처의 x에 대한

f(x)

의 1차 테일러 다항식 또는 선형 근사이다. 그래프

y=P_1(x)

는 x = a에서 그래프

y=f(x)

에 대한 접선이다. 이때 근사 오차, 즉 나머지 항은 다음과 같다.

R_1(x) = f(x) - P_1(x) = h_1(x)(x - a).

x가 a에 가까워질수록, 이 오차

R_1(x)

는

f'(a)(x{-}a)

항보다 훨씬 빠르게 0에 가까워지므로,

f(x)\approx P_1(x)

는 유용한 근사가 된다.

더 나은 근사를 위해 선형 함수 대신 2차 다항식을 사용할 수 있다.

P_2(x) = f(a) + f'(a)(x - a) + \frac{f

(a)}{2}(x - a)^2.

이 2차 테일러 다항식은 $x=a$ 에서 $f(x)$ 의 값뿐만 아니라 1계 및 2계 미분값까지 일치시킨다. 테일러 정리는 2차 근사가 $x=a$ 근처에서 선형 근사보다 더 정확함을 보장한다. 구체적으로, 다음을 만족하는 함수 h₂(x)가 존재한다.

$f(x) = P_2(x) + h_2(x)(x - a)^2, \quad \lim_{x \to a} h_2(x) = 0.$

여기서 나머지 항은

$R_2(x) = f(x) - P_2(x) = h_2(x)(x - a)^2$

이며, x가 a에 가까워질 때 $(x - a)^2$ 항보다 더 빠르게 0으로 접근한다.

360px

마찬가지로, 더 높은 차수의 다항식을 사용하여 함수 f를 근사할 수 있다. 기준점 a에서 f의 더 많은 미분값과 일치시킬수록 더 좋은 근사를 얻을 수 있다.

일반적으로, 함수 f가 점 a에서 k번 미분 가능하다면, k차 테일러 다항식은 다음과 같이 정의된다.

$P_k(x) = f(a) + f'(a)(x-a) + \frac{f$ (a)}{2!}(x-a)^2 + \cdots + \frac{f^{(k)}(a)}{k!}(x-a)^k = \sum_{i=0}^k \frac{f^{(i)}(a)}{i!}(x-a)^i

여기서

f^{(i)}(a)

는 f의 a에서의 i계 도함수를 나타내고,

0! = 1

이다.

테일러 정리에 따르면, k차 테일러 다항식

P_k(x)

와 원래 함수

f(x)

의 차이인 나머지 항

R_k(x)

는 다음과 같이 표현될 수 있다.

f(x) = P_k(x) + R_k(x)

이때 나머지 항

R_k(x)

는

R_k(x) = h_k(x)(x-a)^k

형태로 쓸 수 있으며,

\lim_{x\to a} h_k(x) = 0

을 만족한다. 이를 [[페아노]]의 나머지 항 형태라고 한다. 이는 x가 a로 접근할 때 나머지 항

R_k(x)

가

(x-a)^k

보다 더 빠르게 0으로 수렴한다는 것을 의미한다. 작은 o 표기법을 사용하면 다음과 같이 표현할 수 있다.

R_k(x) = o(|x-a|^{k}), \quad x\to a.

테일러 다항식

P_k(x)

는 주어진 조건을 만족하는 유일한 k차 다항식이다. 즉, 만약 어떤 k차 다항식 p(x)와 함수

h_k(x)

가 존재하여

f(x) = p(x) + h_k(x)(x-a)^k, \quad \lim_{x\to a}h_k(x)=0

을 만족한다면, 반드시 p(x) = P_k(x)이다. 이런 의미에서 테일러 다항식은 점 a 근방에서 함수 f를 가장 잘 근사하는 k차 다항식이라고 할 수 있다.

6.1.2. 작동 원리

실수 값을 갖는 함수

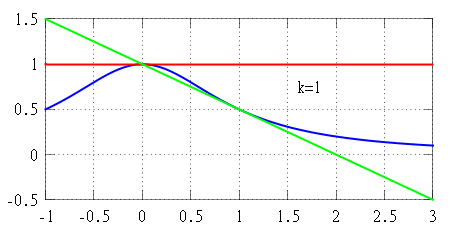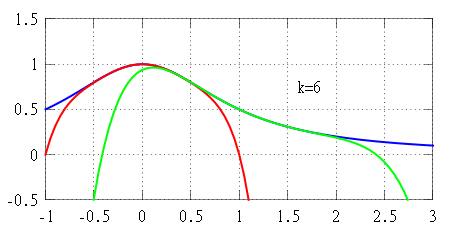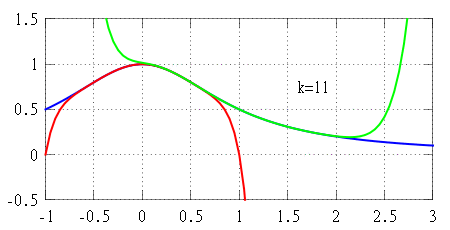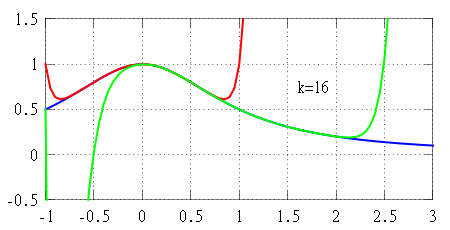
f(x)

가 점

x=a

에서 미분 가능하다면, 이 점 근처에서 선형 근사를 가질 수 있다. 이는 다음을 만족하는 함수

h_1(x)

가 존재한다는 것을 의미한다.

f(x) = f(a) + f'(a)(x - a) + h_1(x)(x - a), \quad \lim_{x \to a} h_1(x) = 0.

여기서

P_1(x) = f(a) + f'(a)(x - a)

는 점 a 근처의 x에 대한

f(x)

의 선형 근사이며, 그래프

y=P_1(x)

는 x = a에서 그래프

y=f(x)

에 대한 접선이다. 근사 오차는 다음과 같다.

R_1(x) = f(x) - P_1(x) = h_1(x)(x - a).

x가 a로 접근할 때, 이 오차는

f'(a)(x-a)

보다 훨씬 빠르게 0으로 접근하여

f(x)\approx P_1(x)

를 유용한 근사로 만든다.

f(x)

에 대한 더 나은 근사를 위해, 선형 함수 대신 2차 다항식을 사용할 수 있다.

P_2(x) = f(a) + f'(a)(x - a) + \frac{f

(a)}{2}(x - a)^2.

이 다항식은 $x=a$ 에서 $f(x)$ 의 함수값뿐만 아니라, 1계 및 2계 미분값까지 일치시킨다.

테일러 정리는 2차 근사가 $x=a$ 의 충분히 작은 이웃에서 선형 근사보다 더 정확함을 보장한다. 구체적으로,

$f(x) = P_2(x) + h_2(x)(x - a)^2, \quad \lim_{x \to a} h_2(x) = 0.$

여기서 근사 오차는

$R_2(x) = f(x) - P_2(x) = h_2(x)(x - a)^2$

이며, x가 a로 접근할 때 $(x - a)^2$ 보다 더 빠르게 0으로 접근한다.

마찬가지로, 더 높은 차수의 다항식을 사용하여 기준점에서 f의 더 많은 미분값과 일치시키면 f에 대한 더 나은 근사를 얻을 수 있다.

일반적으로, 차수 k의 다항식으로 함수를 근사할 때의 오차는 x가 a로 접근할 때 $(x-a)^k$ 보다 훨씬 빠르게 0으로 접근한다. 하지만, 근사 다항식의 차수를 높여도 근사 정확도가 향상되지 않는 함수도 존재하며, 심지어 무한히 미분 가능한 함수 중에서도 그러한 경우가 있다. 이런 함수는 x = a에서 해석적 함수가 아니라고 말하며, 이는 해당 점에서 함수의 미분값만으로는 함수를 국소적으로 완전히 결정할 수 없음을 의미한다.

테일러 정리는 기본적으로 점근적인 성질을 설명한다. 즉, $k$ 차 테일러 다항식 P_k로 근사할 때의 오차 $R_k$ 가 $x \to a$ 일 때 0이 아닌 $k$ 차 다항식보다 빠르게 0으로 접근한다는 사실만을 알려준다. 특정 이웃에서 오차가 실제로 얼마나 큰지에 대해서는 알려주지 않는다. 하지만 나머지 항에 대한 명시적인 공식을 사용하면 오차의 크기를 추정할 수 있으며, 이는 f가 추가적인 조건을 만족할 때 유효하다. 이러한 개선된 버전의 테일러 정리는 보통 전개 중심의 작은 이웃에서 근사 오차에 대한 균등 추정을 제공하지만, 함수 f가 해석적 함수라 할지라도 그 추정이 너무 큰 이웃에서는 성립하지 않을 수 있다. 이런 경우, 신뢰할 수 있는 테일러 근사를 얻기 위해 전개 중심이 다른 여러 테일러 다항식을 사용해야 할 수도 있다 (오른쪽 애니메이션 참조).

나머지 항을 활용하는 몇 가지 방법은 다음과 같다.

# 주어진 구간 (a – r, a + r)에서 $f(x)$ 를 추정하는 차수 k의 다항식 P_k(x)의 오차를 추정한다. (구간과 차수가 주어지면 오차를 찾음)
# 주어진 구간 (a − r, a + r)에서 다항식 P_k(x)가 $f(x)$ 를 주어진 오차 허용 범위 내에서 근사하는 가장 작은 차수 k를 찾는다. (구간과 오차 허용 범위가 주어지면 차수를 찾음)
# P_k(x)가 $f(x)$ 를 주어진 오차 허용 범위 내에서 근사하는 가장 큰 구간 (a − r, a + r)을 찾는다. (차수와 오차 허용 범위가 주어지면 구간을 찾음)

테일러 정리의 가장 기본적인 형태는 다음과 같이 기술된다.

테일러 정리
k ≥ 1을 정수라 하고, 함수 f: R → R가 점 a ∈ R에서 k번 미분 가능하다고 하자. 그러면 다음을 만족하는 함수 h_k: R → R가 존재한다.

$f(x) = f(a) + f'(a)(x-a) + \frac{f$ (a)}{2!}(x-a)^2 + \cdots + \frac{f^{(k)}(a)}{k!}(x-a)^k + h_k(x)(x-a)^k,

\lim_{x\to a}h_k(x)=0.

이때

h_k(x)(x-a)^k

항을 페아노의 나머지 항이라고 부른다.

테일러 정리에 나타나는 다항식

P_k(x) = f(a) + f'(a)(x-a) + \frac{f

(a)}{2!}(x-a)^2 + \cdots + \frac{f^{(k)}(a)}{k!}(x-a)^k
은 함수 f의 점 a에서의 $k$ 차 테일러 다항식이다. 테일러 다항식은 다음과 같은 의미에서 "점근적으로 가장 잘 맞는" 유일한 다항식이다. 즉, 어떤 함수 h_k: R → R와 k차 다항식 p에 대해
$f(x) = p(x) + h_k(x)(x-a)^k, \quad \lim_{x\to a}h_k(x)=0$
이 성립한다면, 반드시 p = P_k이다.

테일러 정리는 나머지 항
$R_k(x) = f(x) - P_k(x)$
의 점근적 거동을 설명한다. 이 나머지 항은 f''를 테일러 다항식으로 근사할 때의 근사 오차이다. 작은 o 표기법을 사용하면, 테일러 정리의 진술은 다음과 같이 쓸 수 있다.

R_k(x) = o(|x-a|^k), \quad x\to a.

6.2. 사회문화적 의의

테일러 정리는 복잡한 함수를 다루기 쉬운 다항 함수 형태로 근사하여 표현하는 데 주된 목적이 있다. 복잡한 함수는 직접 계산하기 어렵거나 컴퓨터를 이용하더라도 많은 시간이 소요될 수 있는데, 테일러 정리를 이용하면 이를 계산이 용이한 다항 함수로 바꾸어 문제를 해결할 수 있다. 다항 함수는 계산이 간편할 뿐만 아니라 미분과 적분도 상대적으로 쉽다는 장점을 가진다.

이러한 유용성 때문에 테일러 정리는 다양한 학문 및 기술 분야에서 중요한 도구로 활용된다. 예를 들어, 물리학에서는 복잡한 자연 현상을 수학적 모델로 설명하고 예측하는 데 테일러 정리가 사용된다. 공학 분야에서는 여러 시스템의 동작 방식을 분석하고 설계하는 과정에서 응용되며, 컴퓨터 과학에서는 알고리즘의 성능을 개선하고 최적화하는 데에도 기여한다.

7. 현대적 응용

테일러 정리는 함수의 값을 특정 지점 근처에서 다항식으로 근사하는 강력한 방법을 제공한다. 이 원리는 현대 과학과 공학의 다양한 분야에서 복잡한 문제를 해결하는 데 핵심적인 도구로 활용된다. 함수의 정확한 값을 계산하기 어렵거나 그 형태가 매우 복잡할 때, 테일러 전개를 이용하면 비교적 간단한 다항식 형태로 함수의 거동을 이해하고 예측할 수 있다. 예를 들어, 물리학에서는 복잡한 물리 현상을 모델링하고 분석하는 데 테일러 근사가 유용하게 사용된다. 또한, 수치 해석 분야에서는 미분 방정식의 해를 구하거나 함수의 최적값을 찾는 문제 등에서 테일러 정리가 중요한 역할을 한다. 구체적인 활용 사례는 아래 하위 섹션들에서 더 자세히 다룬다.

7.1. 물리학

테일러 정리는 함수를 특정 지점 근방에서 다항식으로 근사하는 방법을 제공하며, 이는 물리학을 포함한 다양한 과학 및 공학 분야에서 복잡한 함수를 다루는 데 유용하게 사용된다. 함수의 값을 직접 계산하기 어렵거나 함수의 형태가 복잡할 때, 테일러 다항식을 이용하여 비교적 간단한 형태로 함수의 거동을 이해하고 예측할 수 있다.

예를 들어, 지수 함수

f(x) = e^x

를 구간

[-1, 1]

에서 특정 오차 한계 내에서 근사해야 하는 경우를 생각해 보자. 테일러 정리에 따르면, x = 0을 중심으로 하는 이 함수의 k차 테일러 다항식

P_k(x)

는 다음과 같다.

:

P_k(x) = 1+x+\frac{x^2}{2!}+\cdots+\frac{x^k}{k!}

테일러 정리는 이 근사값과 실제 함수값 사이의 오차, 즉 나머지 항

R_{k+1}(x)

의 크기를 추정하는 방법도 제공한다.

:

R_{k+1}(x)=\frac{e^\xi}{(k+1)!}x^{k+1}

(여기서

\xi

는 0과 x 사이의 어떤 값)

함수

e^x

의 성질을 이용하여 나머지 항의 상한값을 계산하면, 구간

[-1, 1]

에서 오차의 절댓값을 다음과 같이 제한할 수 있다.

:

|R_{k+1}(x)| \leq \frac{4|x|^{k+1}}{(k+1)!} \leq \frac{4}{(k+1)!}

만약 오차를

10^{-5}

보다 작게 만들고 싶다면, 위 부등식을 만족하는 가장 작은 정수 k를 찾으면 된다. 계산 결과, k ≥ 9일 때, 즉 9차 이상의 테일러 다항식을 사용하면 원하는 정밀도를 얻을 수 있다. (계승 값

9! = 362,880

및

10! = 3,628,800

참고)

:

\frac{4}{(k+1)!} < 10^{-5} \quad \Leftrightarrow \quad (k+1)! > 400000 \quad \Leftrightarrow \quad k \geq 9

따라서 테일러 정리를 이용하면 다음과 같은 근사식을 얻을 수 있으며, 이 근사식의 오차는 구간

[-1, 1]

에서

10^{-5}

미만임이 보장된다.

:

e^x \approx 1+x+\frac{x^2}{2!} + \ldots + \frac{x^9}{9!}

이처럼 테일러 급수는 복잡한 함수의 값을 다항식 계산을 통해 원하는 정밀도로 근사할 수 있게 해주며, 이는 물리 현상을 수학적으로 모델링하고 분석하는 과정에서 중요한 도구가 된다.

8. 해석성과의 관계

함수가 해석적이라는 것은 국소적으로 수렴하는 멱급수로 표현될 수 있다는 의미이며, 이는 함수의 테일러 급수와 밀접한 관련을 가진다. 실수 변수 함수와 복소수 변수 함수에서 해석성과 테일러 급수의 관계는 약간의 차이를 보이는데, 자세한 내용은 하위 문단에서 설명한다.

8.1. 테일러 급수의 수렴성

R의 열린 구간인 I ⊂ R을 생각해 보자. 정의에 따르면, 함수 f : I → R는 수렴하는 멱급수로 국소적으로 정의되면 실해석적이다. 즉, 모든 a ∈ I에 대해 어떤 r > 0과 계수열 c_k ∈ R이 존재하여 (a − r, a + r) ⊂ I이고, 다음을 만족한다.

$f(x) = \sum_{k=0}^\infty c_k(x-a)^k = c_0 + c_1(x-a) + c_2(x-a)^2 + \cdots, \qquad |x-a|$

일반적으로, 멱급수의 수렴 반경은 코시-아다마르 공식으로부터 계산할 수 있다.

$\frac{1}{R} = \limsup_{k\to\infty}|c_k|^\frac{1}{k}.$

이 결과는 기하 급수와의 비교를 기반으로 하며, 동일한 방법으로 a를 중심으로 하는 멱급수가 R의 어떤 b ∈ R에 대해 수렴한다면, $r_b=\left\vert b-a \right\vert$ 인 닫힌 구간 $[a-r_b,a+r_b]$ 에서 균등 수렴해야 함을 보여준다. 여기서는 멱급수의 수렴만 고려하며, (a − R,a + R)가 f의 정의역 I를 벗어날 수도 있다.

a에서의 실해석적 함수 f의 테일러 다항식은 단순히 로컬 정의 멱급수의 유한 절단이다.

$P_k(x) = \sum_{j=0}^k c_j(x-a)^j, \qquad c_j = \frac{f^{(j)}(a)}{j!}$

해당 나머지 항은 로컬하게 해석적 함수로 주어진다.

$R_k(x) = \sum_{j=k+1}^\infty c_j(x-a)^j = (x-a)^k h_k(x), \qquad |x-a|$

여기서 함수

$\begin{align}& h_k:(a-r,a+r)\to \R \\[1ex]& h_k(x) = (x-a)\sum_{j=0}^\infty c_{k+1+j} \left(x - a\right)^j\end{align}$

또한 해석적인데, 그 이유는 정의 멱급수가 원래 급수와 동일한 수렴 반경을 가지기 때문이다. [a − r, a + r] ⊂ I이고 r < R이라고 가정하면, 이 모든 급수는 (a − r, a + r)에서 균등하게 수렴한다. 당연히 해석적 함수의 경우, 나머지 항 $R_k(x)$ 은 확장의 중심에서 도함수 f′(a)의 수열의 꼬리로 추정할 수 있다. 복소 해석학을 사용하면 다른 가능성이 발생하며, 이는 복소 해석학에서의 테일러 정리 섹션에서 설명한다.

함수 f의 테일러 급수는 모든 도함수가 유계이고 k가 무한대로 갈 때 너무 빠르게 증가하지 않는 어떤 구간에서 수렴할 것이다. (하지만 테일러 급수가 수렴하더라도, 아래에서 설명하듯이, f에 수렴하지 않을 수 있다. 이때 f는 비해석 함수라고 한다.)

무한히 미분 가능한 함수 f : R → R의 테일러 급수

$f(x) \approx \sum_{k=0}^\infty c_k(x-a)^k = c_0 + c_1(x-a) + c_2(x-a)^2 + \cdots$

는 a에서의 "무한 차수 테일러 다항식"으로 생각할 수 있다. 이제 나머지에 대한 추정은 만약 임의의 r에 대해, f의 도함수가 (a − r, a + r)에서 유계라고 알려져 있다면, 임의의 차수 k와 임의의 r > 0에 대해 다음을 만족하는 상수 M_k,r > 0가 존재함을 의미한다.

$|R_k(x)| \leq M_{k,r} \frac{|x-a|^{k+1}}{(k+1)!}$

이는 모든 x ∈ (a − r,a + r)에 대해 성립한다. 때로는 상수 M_k,r를 고정된 r과 모든 k에 대해 M_k,r가 위로 유계가 되도록 선택할 수 있다. 그러면 f의 테일러 급수는 어떤 해석 함수로 균등하게 수렴한다.

$\begin{align}& T_f:(a-r,a+r)\to\R \\& T_f(x) = \sum_{k=0}^\infty \frac{f^{(k)}(a)}{k!} \left(x-a\right)^k\end{align}$

(M_k,r가 위로 유계가 아니더라도, 충분히 천천히 증가하는 한 수렴을 얻는다.)

극한 함수 T_f는 정의에 의해 항상 해석적이지만, f가 무한히 미분 가능하더라도 원래 함수 f와 같을 필요는 없다. 이 경우, 우리는 f를 비해석 매끄러운 함수라고 부르며, 예를 들어 평평한 함수와 같다.

$\begin{align}& f:\R \to \R \\& f(x) = \begin{cases}e^{-\frac{1}{x^2}} & x>0 \\0 & x \leq 0 .\end{cases}\end{align}$

연쇄 법칙을 수학적 귀납법으로 반복적으로 사용하면, 임의의 차수 k에 대해,

$f^{(k)}(x) = \begin{cases}\frac{p_k(x)}{x^{3k}}\cdot e^{-\frac{1}{x^2}} & x>0 \\0 & x \leq 0\end{cases}$

는 2(k − 1)차 다항식 p_k에 대해 성립함을 보일 수 있다. 함수 $e^{-\frac{1}{x^2}}$ 는 $x \to 0$ 일 때 어떤 다항식보다 빠르게 0으로 수렴하므로, f는 무한히 미분 가능하며 모든 양의 정수 k에 대해 f^(k)(0) = 0이다. 위의 결과는 이 경우 모두 성립한다.

* f의 테일러 급수는 0 함수 T_f(x) = 0으로 균등하게 수렴하며, 이는 모든 계수가 0인 해석 함수이다.
* 함수 f는 이 테일러 급수와 같지 않으므로 비해석적이다.
* 임의의 차수 k ∈ N과 반지름 r > 0에 대해 위에서 언급한 나머지 경계를 만족하는 M_k,r > 0가 존재한다.

하지만, 고정된 r에 대해 k가 증가함에 따라, M_k,r의 값은 r^k보다 더 빠르게 증가하며, 오차는 0으로 수렴하지 않는다.

8.2. 복소 해석학에서의 테일러 정리

테일러 정리는 열린 부분 집합 U ⊂ C에서 복소 미분 가능한 함수 f : C → C로 일반화된다. 그러나 이 정리의 유용성은 복소해석학의 다른 일반적인 정리들에 의해 다소 가려지는데, 특히 코시 적분 공식을 사용하면 복소 미분 가능 함수 f : U → C에 대해 더 강력한 관련 결과를 추론할 수 있다.

닫힌 원판 B(z, r) ∪ S(z, r)가 U에 포함되도록 r > 0이라고 하자. 원 S(z, r)의 양의 매개변수화를 γ(t) = z + re^it ( $t \in [0,2 \pi]$ )라고 할 때, 코시 적분 공식은 다음과 같이 주어진다.

$f(z) = \frac{1}{2\pi i}\int_\gamma \frac{f(w)}{w-z}\,dw, \quad f'(z) = \frac{1}{2\pi i}\int_\gamma \frac{f(w)}{(w-z)^2} \, dw, \quad \ldots, \quad f^{(k)}(z) = \frac{k!}{2\pi i}\int_\gamma \frac{f(w)}{(w-z)^{k+1}} \, dw.$

여기서 모든 피적분 함수는 원 S(z, r)에서 연속이므로 적분 기호 아래에서 미분하는 것이 정당화된다. 중요한 결과 중 하나는, 함수 f가 열린 집합 U에서 한 번 복소 미분 가능하면 실제로는 U에서 무한히 여러 번 복소 미분 가능하다는 것이다. 즉, 복소 미분 가능한 함수는 자동으로 복소 해석적이다. 또한 코시 추정을 얻을 수 있다.

$|f^{(k)}(z)| \leq \frac{k!}{2\pi}\int_\gamma \frac{M_r}{|w-z|^{k+1}} \, dw = \frac{k!M_r}{r^k}, \quad \text{여기서 } M_r = \max_{|w-c|=r}|f(w)|$

이 부등식은 모든 z ∈ U와 B(z, r) ∪ S(c, r) ⊂ U인 r > 0에 대해 성립한다. 이 추정은 복소수 테일러 급수

$T_f(z) = \sum_{k=0}^\infty \frac{f^{(k)}(c)}{k!}(z-c)^k$

가 열린 원판 $B(c,r) \subset U$ (단, $S(c,r) \subset U$ )에서 함수 f로 균등 수렴함을 의미한다. 도함수 f^(k)(c)에 대한 적분 공식을 사용하고 기하급수를 이용하면 다음과 같이 T_f(z) = f(z)임을 보일 수 있다.

$\begin{align}T_f(z) &= \sum_{k=0}^\infty \frac{(z-c)^k}{2\pi i}\int_\gamma \frac{f(w)}{(w-c)^{k+1}} \, dw \\&= \frac{1}{2\pi i} \int_\gamma \frac{f(w)}{w-c} \sum_{k=0}^\infty \left(\frac{z-c}{w-c}\right)^k \, dw \\&= \frac{1}{2\pi i} \int_\gamma \frac{f(w)}{w-c}\left( \frac{1}{1-\frac{z-c}{w-c}} \right) \, dw \\&= \frac{1}{2\pi i} \int_\gamma \frac{f(w)}{w-z} \, dw \\&= f(z).\end{align}$

따라서 열린 집합 U ⊂ C에서 모든 복소 미분 가능 함수 f는 실제로 복소 해석적이며, 자신의 테일러 급수로 표현될 수 있다. 이는 실수 해석적 함수에 대한 테일러 정리의 성질들이 복소 해석 함수에도 유사하게 적용됨을 의미한다. 다만, 실수에서의 열린 구간 (a − r, a + r)은 복소수에서의 중심 c를 갖는 열린 원판 B(c, r)으로 대체된다. 테일러 전개는 다음과 같은 형태로 유지된다.

$f(z) = P_k(z) + R_k(z), \quad \text{여기서 } P_k(z) = \sum_{j=0}^k \frac{f^{(j)}(c)}{j!}(z-c)^j$

여기서 P_k(z)는 k차 테일러 다항식이고, 나머지 항 R_k(z)는 복소 해석적이다. 복소 해석학의 방법을 사용하면 테일러 전개에 관한 강력한 결과를 얻을 수 있다. 예를 들어, 영역 $W \subset U$ 의 경계 $\partial W \subset U$ 를 매개변수화하는 양의 방향으로 향한 요르단 곡선 $\gamma$ 에 대해 코시 적분 공식을 사용하면, 도함수 f^(j)(c)에 대한 표현식을 얻고, 위에서 T_f(z) = f(z)를 보인 계산을 약간 수정하여 나머지 항에 대한 정확한 공식을 유도할 수 있다.

$R_k(z) = \sum_{j=k+1}^\infty \frac{(z-c)^j}{2\pi i} \int_\gamma \frac{f(w)}{(w-c)^{j+1}} \, dw = \frac{(z-c)^{k+1}}{2\pi i} \int_\gamma \frac{f(w) \, dw}{(w-c)^{k+1}(w-z)} , \qquad z\in W.$

여기서 중요한 점은 영역 $W \subset U$ 에서 테일러 다항식에 의한 근사의 오차(나머지 항 R_k)는 경계 $\partial W \subset U$ 에서의 함수 f 값에 의해 제어된다는 것이다. 마찬가지로, 나머지 항에 대한 급수 표현에 코시 추정을 적용하면 다음과 같은 균등 추정을 얻을 수 있다.

$|R_k(z)|\leq \sum_{j=k+1}^\infty \frac{M_r |z-c|^j}{r^j}= \frac{M_r}{r^{k+1}} \frac{|z-c|^{k+1}}{1-\frac$

👆

좌우로 밀어서 보기

{r}}\leq \frac{M_r \beta^{k+1}}{1-\beta}, \qquad \text{단, } \frac

👆

좌우로 밀어서 보기

{r} \leq \beta < 1.

해석 함수는 테일러 급수로 나타낼 수 있기 때문에, 테일러 급수를 이용하여 함수의 국소적인 성질을 분석할 수 있다. 또한, 테일러 급수의 수렴 반경은 함수의 특이점과 밀접한 관련이 있어, 특이점을 분석하는 데 유용한 도구가 된다. 테일러 정리는 복소 해석학의 기본 정리 중 하나로, 여러 응용 분야에서 중요한 역할을 한다.

이름	테일러 정리
영어 이름	Taylor's theorem
분야	미적분학
설명	어떤 함수의 도함숫값을 이용하여 특정 점에서 함수값을 근사하는 방법

테일러 급수

정의	함수 f(x)의 a에서의 테일러 급수는 다음과 같이 정의된다.
급수 표현	f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!}(x-a)^n
중심	a는 테일러 급수의 중심이다.
나머지 항	테일러 급수는 무한 급수이므로, 실제로 계산할 때는 유한한 항까지만 계산하고 나머지는 오차항으로 처리한다. 이 오차항을 나머지 항이라고 한다.

활용

함수의 근사값 계산	테일러 정리를 이용하면 복잡한 함수의 값을 특정 점에서 근사적으로 계산할 수 있다.
함수의 성질 분석	테일러 급수를 이용하면 함수의 극값, 변곡점 등의 성질을 분석할 수 있다.
미분 방정식의 해 구하기	테일러 급수를 이용하여 미분 방정식의 해를 근사적으로 구할 수 있다.