분해계
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
분해계는 범주 C에서 두 사상의 집합 E와 M으로 구성되며, E와 M은 동형 사상을 포함하고 합성 연산에 닫혀 있다. 모든 사상 f는 m∘e로 분해 가능하며, 여기서 e는 E에, m은 M에 속한다. 분해는 함자적이며, 직교 사상과 약분해계 개념을 포함한다. 약분해계는 분해계보다 약한 조건을 만족하며, 모델 범주의 정의에 사용된다. 분해계는 쌍대 완비 범주에서 작은 대상 논법을 통해 구성될 수 있으며, 토포스, 작은 범주의 범주 등에서 예시를 찾을 수 있다. 분해계 개념은 1950년대 매클레인과 이스벨에 의해 연구되었다.
더 읽어볼만한 페이지
- 호모토피 이론 - 모노드로미
모노드로미는 연결 국소 연결 공간의 피복 공간에서 기본군의 작용으로 이해되는 개념으로, 모노드로미 작용에 대응하는 군 준동형의 상인 모노드로미 군을 통해 복소해석학, 리만 기하학, 미분방정식 등 다양한 분야에서 활용되며 갈루아 이론과도 관련된다. - 호모토피 이론 - 베유 대수
베유 대수는 체 K 위의 리 대수 g에 대하여 정의되는 미분 등급 대수이며, g의 쌍대 공간과 그 등급 이동으로 생성되는 외대수와 대칭 대수의 텐서곱으로 표현되고, 리 군의 분류 공간의 주다발의 무한소 형태를 나타내는 완전열과 관련이 있다. - 범주론 - 작은 범주
그로텐디크 전체 가 주어졌을 때, -작은 범주는 대상과 사상의 모임이 모두 의 원소인 범주를 의미하며, 이는 함자와 자연 변환과 함께 완비 범주이자 쌍대 완비 범주인 2-범주를 이룬다. - 범주론 - 토포스
토포스는 유한 완비 범주이자 데카르트 닫힌 범주이며 부분 대상 분류자를 갖는 특정한 조건을 만족하는 범주로서, 일계 논리 또는 일계 정의가 있는 대상의 부분 대상 개념을 갖는 데카르트 닫힌 범주로 이해될 수 있고, 위상 공간의 일반화이자 집합론에 대한 범주론적 일반화로서 수학의 공리적 기초를 제공한다.
2. 정의
'''분해계'''(''E'', ''M'')는 범주 '''C'''에 대해 다음과 같은 두 개의 사상의 집합 ''E''와 ''M''으로 구성된다.
# ''E''와 ''M''은 모두 '''C'''의 모든 동형 사상을 포함하고, 합성에 대해 닫혀있다.
# '''C'''의 모든 사상 ''f''는 로 분해될 수 있으며, 여기서 이고 이다.
# 분해는 ''함자적''이다. 즉, 와 가 몇몇 사상 와 에 대해 를 만족하는 두 사상이라면, 다음의 가환도를 가환하게 만드는 유일한 사상 가 존재한다.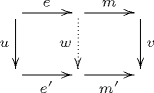
''참고:'' 는 화살표 범주에서 에서 로의 사상이다.
2. 1. 직교 사상
범주 에서, 두 사상 , 이 다음 조건을 만족시킨다고 하자.- 화살표 범주 속의 임의의 사상 (가환 사각형) 에 대하여, 이며 인 유일한 사상 가 존재한다.
- :
\begin{matrix}
\bullet&\xrightarrow{f}&\bullet\\
{\scriptstyle e}\downarrow&\exists! h\nearrow&\downarrow\scriptstyle m\\
\bullet&\xrightarrow{g}&\bullet
\end{matrix}
그렇다면, 이를 다음과 같이 표현한다.
- 와 이 서로 '''직교 사상'''(直交寫像, orthogonal morphisms|영어)이다.
- 가 에 대하여 '''왼쪽 유일 올림 성질'''(-唯一-性質, left unique lifting property|영어)을 만족시킨다.
- 이 에 대하여 '''오른쪽 유일 올림 성질'''(-唯一-性質, right unique lifting property|영어)을 만족시킨다.
이는 기호로 으로 나타낸다. 직교 관계는 대칭 관계가 아니다. 유일 올림 성질에 의하여 유일하게 존재하는 사상 를 '''올림'''이라고 한다.
사상의 모임 에 대하여, 사상 모임 및 를 다음과 같이 정의할 수 있다.
:
:
(간혹 를 로 표기하기도 한다.)
한편, 범주 에서 두 사상 , 이 다음 조건을 만족시키는 경우를 생각할 수 있다.
- 화살표 범주 속의 임의의 사상 (가환 사각형) 에 대하여, 이며 인 사상 가 존재한다. (그러나 이 사상은 유일할 필요가 없다.)
- :
\begin{matrix}
\bullet&\xrightarrow{f}&\bullet\\
{\scriptstyle e}\downarrow&\exists h\nearrow&\downarrow\scriptstyle m\\
\bullet&\xrightarrow{g}&\bullet
\end{matrix}
이 경우, 다음과 같이 표현한다.
- 가 에 대하여 '''왼쪽 올림 성질'''(-性質, left lifting property|영어)을 만족시킨다.
- 이 에 대하여 '''오른쪽 올림 성질'''(-性質, right lifting property|영어)을 만족시킨다.
이는 기호로 으로 나타낸다. 이 관계 역시 대칭 관계가 아니다. 올림 성질에 의하여 존재하는 (유일하지 않을 수 있는) 사상을 '''올림'''이라고 한다. 즉, 올림 성질은 유일 올림 성질에서 올림의 유일성 조건을 제외한 것이다.
사상의 모임 에 대하여, 사상 모임 및 를 다음과 같이 정의할 수 있다.
:
:
(간혹 를 또는 로, 를 또는 로 표기하기도 한다.)
2. 2. 분해계
범주 에서, 두 사상 , 이 서로 '''직교 사상'''(orthogonal morphisms영어), 기호 이라는 것은 다음 조건을 만족시키는 것을 의미한다:- 화살표 범주 속의 임의의 사상 (가환 사각형) 에 대하여, 이며 인 유일한 사상 가 존재한다.
- :
\begin{matrix}
\bullet&\xrightarrow{f}&\bullet\\
{\scriptstyle e}\downarrow&{\scriptstyle\exists! h}\nearrow&\downarrow\scriptstyle m\\
\bullet&\xrightarrow{g}&\bullet
\end{matrix}
이때 유일하게 존재하는 사상 를 '''올림'''이라고 한다. 는 에 대해 '''왼쪽 유일 올림 성질'''(left unique lifting property영어)을 만족시키고, 은 에 대해 '''오른쪽 유일 올림 성질'''(right unique lifting property영어)을 만족시킨다고도 한다. 직교 관계는 대칭 관계가 아니다.
사상의 모임 에 대하여, 다음과 같이 사상 모임을 정의한다:
:
:
(간혹 를 로 표기하기도 한다.)
범주 위의 '''분해계'''(factorization system영어) 는 다음 조건을 만족시키는 두 사상 모임 의 쌍이다:
1. 와 은 모두 의 모든 동형 사상을 포함한다.
2. 의 모든 사상 는 와 같이 이고 인 사상의 합성으로 표현(분해)될 수 있다 ().
3. 다음 조건들이 서로 동치이며, 이 중 하나 (따라서 모두)를 만족시킨다:
- 이며 이다. (직교성을 이용한 정의)
- 이며 이다.
- (함자성) 임의의 및 에 대하여, 화살표 범주 에서의 사상 (즉, 를 만족하는 )가 주어지면, 이고 를 만족하는 유일한 사상 가 존재한다.
- ::
\bullet&\xrightarrow{e}&\bullet&\xrightarrow{m}&\bullet\\
{\scriptstyle f'}\downarrow&{\scriptstyle\exists! g}\nearrow&{\scriptstyle e'}\downarrow&\nearrow{\scriptstyle m'}&{\scriptstyle f}\downarrow\\
\bullet&\xrightarrow{e'}&\bullet&\xrightarrow{m'}&\bullet
\end{matrix}
- ::
분해계가 주어졌을 때, 임의의 사상의 분해 는 동형 사상을 무시하면 유일하다.
위의 정의 조건 3은 다음 두 조건과 동치이다:
1. 의 모든 사상 는 로 분해될 수 있으며, 여기서 이고 이다.
2. 이고 이다. (여기서 은 와 같은 표기이다.)
2. 3. 약분해계
범주 에서, 두 사상 , 이 다음 조건을 만족시킨다고 하자.- 화살표 범주 속의 임의의 사상 (가환 사각형) 에 대하여, 이며 인 사상 가 존재한다. (그러나 이 사상은 유일할 필요가 없다.)
- :
\begin{matrix}
\bullet&\xrightarrow{f}&\bullet\\
{\scriptstyle e}\downarrow&{\scriptstyle\exists}\nearrow{\scriptstyle h}&\downarrow\scriptstyle m\\
\bullet&\xrightarrow{g}&\bullet
\end{matrix}
그렇다면, 이를 다음과 같이 쓴다.
- 가 에 대하여 '''왼쪽 올림 성질'''(-性質, left lifting property영어)을 만족시킨다.
- 이 에 대하여 '''오른쪽 올림 성질'''(-性質, right lifting property영어)을 만족시킨다.
이는 기호로 으로 쓴다. 이 역시 대칭 관계가 아니다. 올림 성질에 의하여 존재하는 (유일하지 않을 수 있는) 사상을 '''올림'''이라고 한다. 즉, 올림 성질은 유일 올림 성질에서 올림의 유일함을 생략한 것이다.
사상의 모임 에 대하여, 사상 모임 및 를 다음과 같이 정의하자.
:
:
(간혹 를 또는 로, 를 또는 로 표기하기도 한다.)
범주 위에 다음과 같은 데이터 가 주어졌다고 하자.
이 데이터가 다음 조건을 모두 만족시킨다면, '''약분해계'''(弱分解系, weak factorization system영어)라고 한다.[1]
- 이다. 즉, 는 의 모든 사상에 대해 왼쪽 올림 성질을 갖는 사상들의 모임이다.
- 이다. 즉, 은 의 모든 사상에 대해 오른쪽 올림 성질을 갖는 사상들의 모임이다.
- 의 모든 사상 는 로 인수분해될 수 있으며, 이때 이고 이다.
모든 분해계는 약분해계이지만, 그 역은 일반적으로 성립하지 않는다. 약분해계에서 주어진 사상의 분해는 유일하지 않을 수 있다.
약분해계는 모델 범주의 정의에 사용되는 중요한 개념이다. 모델 범주는 완비 및 공완비 범주 와 세 종류의 사상 모임(약한 동치 , 올림 , 코올림 )으로 구성되는데, 이때 와 는 약분해계를 이룬다.[2] 모델 범주에서 사상이 에 속하면 자명한 올림, 에 속하면 자명한 코올림이라고 한다. 객체 가 종착 객체로의 사상 이 올림이면 피브란트(fibrant)라고 하며, 시작 객체로부터의 사상 가 코올림이면 코피브란트(cofibrant)라고 한다.[3]
3. 성질
범주 위에 다음과 같은 데이터 가 주어졌다고 가정하자.
이 데이터에 대하여 다음 조건들은 서로 동치이며, 이 조건들을 만족시키는 데이터 를 '''분해계'''라고 한다.
- 이며 이다.
- 이며 이다.
- 함자성: 임의의 및 에 대하여, 화살표 범주 에서의 사상 이 존재한다면, 인 및 이 존재한다. 즉, 임의의 사상 및 및 에 대하여 라면, 이고 인 사상 가 유일하게 존재한다. 이는 다음 그림으로 나타낼 수 있다.
- :
\bullet&\twoheadrightarrow&\bullet&\hookrightarrow&\bullet\\
\downarrow&&\downarrow\scriptstyle\exists!&&\downarrow\\
\bullet&\twoheadrightarrow&\bullet&\hookrightarrow&\bullet
\end{matrix}
위 그림에서 의 원소는 로, 의 원소는 로 표기하였다.
분해계가 주어졌을 때, 임의의 사상의 분해는 동형 사상을 무시하면 유일하다는 성질을 가진다.
비슷한 개념으로 '''약분해계'''(weak factorization system영어)가 있다. 이는 다음 조건을 만족시키는 데이터 를 말한다.
- 이며 이다.
모든 분해계는 약분해계이지만, 그 역은 일반적으로 성립하지 않는다. 약분해계에서는 주어진 사상의 분해가 유일하지 않을 수 있다.
특정 조건 하에서는 분해계를 구성할 수 있다. 다음이 주어졌다고 하자.
- 쌍대 완비 범주
- 속의 사상들의 모임
또한, 다음이 성립한다고 가정하자.
- 임의의 사상 , 에 대하여, 의 정의역 가 -콤팩트 대상(compact object영어)이 되는 정칙 기수 가 존재한다.
이러한 조건이 만족되면, 는 분해계를 이룬다. 이를 '''작은 대상 논법'''(small object argument영어)이라고 한다. 이 논법은 특정 모임 이 주어졌을 때, 이로부터 분해계를 구성하는 방법을 제공한다.
4. 예
임의의 범주에서, 모든 사상의 모임을 왼쪽 모임으로, 동형 사상의 모임을 오른쪽 모임으로 잡는다면 이는 분해계를 이룬다. 반대로, 동형 사상의 모임을 왼쪽 모임으로, 모든 사상의 모임을 오른쪽 모임으로 잡는다면 이 역시 분해계를 이룬다. 이는 가장 기본적인 분해계의 예시이다.
모든 토포스에서는 전사 사상의 모임을 왼쪽 모임으로, 단사 사상의 모임을 오른쪽 모임으로 잡으면 분해계를 형성한다. 예를 들어, 집합의 토포스 에서 모든 함수는 그 치역으로의 전사 함수(전사 사상)와 치역에서 공역으로 가는 단사 함수(단사 사상)의 합성으로 유일하게 분해될 수 있다.
작은 범주의 범주 에서는 대상에 대해 전단사인 함자들의 모임을 왼쪽 모임으로, 충실충만한 함자들의 모임을 오른쪽 모임으로 하는 분해계가 존재한다.
모든 모형 범주 위에는 다음과 같은 두 약분해계가 자연스럽게 존재한다. 약분해계는 분해계의 조건을 약간 약화시킨 개념이다.
- 왼쪽 모임: (자명한 코파이버화), 오른쪽 모임: (파이버화)
- 왼쪽 모임: (코파이버화), 오른쪽 모임: (자명한 파이버화)
여기서 는 코파이버화(cofibration), 는 파이버화(fibration), 는 약한 동치(weak equivalence)의 모임을 나타낸다.
집합의 범주 위에서는 (선택 공리를 가정할 때) 정확히 6개의 약분해계가 존재하며[4], 이 중 4개는 분해계이다.
예를 들어, (단사, 전사) 약분해계에서 함수 의 분해는 다음과 같이 이루어진다.
:
여기서 는 단사 함수(포함 함수)를, 는 전사 함수를 나타낸다.
위상 공간의 범주 에서는 올뭉치와 관련된 분해계 개념을 찾아볼 수 있다. 모든 CW 복합체 에 대한 포함 사상 들의 모임을 라고 하자. 세르 올뭉치는 에 대해 오른쪽 올림 성질(right lifting property)을 만족시키는 연속 함수로 정의된다.
:
유사하게, 모든 위상 공간 에 대한 포함 사상 들의 모임을 라고 할 때, 후레비치 올뭉치는 에 대해 오른쪽 올림 성질을 만족시키는 연속 함수이다.
:
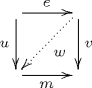
오른쪽 올림 성질은 다음 가환 그림으로 표현된다. 사상 와 이 있을 때, 모든 사상 에 대해 를 만족하면, 이고 를 만족하는 사상 (대각 사상)가 존재한다는 것이다.
이 대각 사상 는 일반적으로 유일하지 않을 수 있으며, 이는 분해계의 직교성(orthogonality)과의 차이점이다. 올뭉치의 경우, 이 대각 사상은 두 함수 사이의 호모토피를 나타낸다. 만약 올뭉치가 피복 공간이라면 올림은 유일하다.
대수기하학에서도 분해계와 관련된 개념이 사용된다. 스킴의 사상 중 일부는 특정 올림 성질을 통해 정의된다.
- 매끄러운 사상: 멱영 아이디얼 에 대한 몫 에 대해 오른쪽 올림 성질을 만족시키는 국소 유한 표시 사상이다.
- 에탈 사상: 매끄러운 사상의 조건에서 오른쪽 올림 성질을 오른쪽 유일 올림 성질로 강화한 것이다.
또한, 공역이 국소 뇌터 스킴인 유한형 사상에 대해, 모든 값매김환 의 분수체에 대한 사상 을 고려할 때,
이러한 조건을 '''valuative criterion|값매김 조건영어'''이라고 부른다.
5. 역사
분해계 개념의 시초는 손더스 매클레인의 1950년 논문[5]이다. 이 논문에서 매클레인이 정의한 ‘bicategory|바이캐터고리영어’라는 개념은 분해계를 갖춘 범주의 개념과 흡사하다. 이후 존 롤프 이스벨(John Rolfe Isbell영어)이 이 개념을 1950년대에 연구하였다.[6]
참조
[1]
기타
Riehl
2014
[2]
기타
Riehl
2014
[3]
문서
Valery Isaev - On fibrant objects in model categories
[4]
웹인용
The nine model category structures on the category of sets
https://web.archive.[...]
2016-02-12
[5]
논문
Duality for groups
1950
[6]
논문
Some remarks concerning categories and subspaces
1957
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com
