오일러 지표

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
3. 성질
4. 예시
5. 오일러 공식의 증명 (다면체)
- 5.1. 코시의 증명
- 5.2. 쌍대 그래프를 이용한 증명
6. 다른 불변량과의 관계
7. 일반화
참조

1. 개요

오일러 지표는 사슬 복합체, 위상 공간, CW 복합체 등 다양한 수학적 대상에 대해 정의되는 정수이다. 사슬 복합체의 오일러 지표는 호몰로지 군의 계수를 이용하여 계산하며, 위상 공간의 경우 특이 사슬 복합체의 오일러 지표로 정의된다. CW 복합체의 오일러 지표는 세포 사슬 복합체의 오일러 지표이며, 다면체의 경우 꼭짓점, 모서리, 면의 개수를 이용하여 계산할 수 있다. 오일러 지표는 위상 불변량이며, 분리 집합, 합집합, 곱공간 등 다양한 위상 공간 연산에 대해 성질을 갖는다. 또한, 곡면의 종수와 밀접한 관련이 있으며, 고차원 도형, 그래프, 오비폴드 등 다양한 대상에 대해 일반화되어 정의된다.

더 읽어볼만한 페이지

위상 그래프 이론 - 곡면 종수
곡면 종수는 곡면의 '구멍' 수를 나타내는 위상수학적 개념으로, 유향 곡면은 자를 수 있는 최대 횟수, 비가향 곡면은 구에 연결된 교차모의 수로 정의되며, 매듭, 손잡이 다양체, 그래프, 스킴 등 다양한 수학적 대상에 대해서도 정의된다.
위상 그래프 이론 - 베티 수
베티 수는 위상 공간의 연결성을 나타내는 위상수학적 불변량으로, 호몰로지 군의 계수로 정의되며 공간에 존재하는 "구멍"의 수를 나타내는 지표로 해석되고, 데이터 분석 등 다양한 분야에서 활용된다.
레온하르트 오일러 - 오일러-라그랑주 방정식
오일러-라그랑주 방정식은 변분법으로 범함수의 정류점을 찾는 편미분 방정식으로, 라그랑주 역학 등 다양한 분야에 활용되며 뉴턴 역학을 일반화한 것으로 여겨진다.
레온하르트 오일러 - 오일러-마스케로니 상수
오일러-마스케로니 상수 $\gamma$ 는 조화급수와 자연로그 함수의 차이의 극한으로 정의되는 수학 상수로, 감마 함수, 리만 제타 함수 등 다양한 수학적 개념과 관련되어 있으며 유리수인지 무리수인지 밝혀지지 않은 미해결 문제이다.
위상수학 - 뫼비우스의 띠
"상상력" 한가 아닌 답변을 바랍니다.
위상수학 - 공간
공간은 물체의 위치와 운동을 기술하는 배경으로, 시간과 함께 시공간을 구성하며, 학문 분야에 따라 정의와 관점이 다르지만, 현대 물리학에서는 고차원 공간을 가정하기도 한다.

오일러 지표

2. 정의

사슬 복합체 $(C_\bullet,\partial_\bullet)$ 의 호몰로지 $H_\bullet(C)$ 가 모두 유한 계수를 갖는다고 가정하고, $H_\bullet$ 이 어떤 최저·최고 차수 밖에서는 계수가 0이라고 할 때, 사슬 복합체의 '''오일러 지표''' $\chi(C_\bullet)\in\mathbb Z$ 는 다음과 같은 정수이다.

: $\chi(C_\bullet)=\sum_i(-1)^i\operatorname{rank}H_i(C)\in\mathbb Z$

단순 복합체의 '''오일러 지표'''는 다음과 같은 교대 합으로 나타낼 수 있다.

: $\chi = k_0 - k_1 + k_2 - k_3 + \cdots,$

여기서 ''k''_''n''은 복합체 내에서 ''n''-단순체의 수를 의미한다.

2. 1. 위상 공간

위상 공간

X

의 '''오일러 지표'''

\chi(X)

는 그 특이 사슬 복합체의 오일러 지표이다. 모든 위상 공간에 대해, ''n''번째 베티 수 ''b''_''n''을 ''n''번째 특이 호몰로지 군의 계수로 정의할 수 있다. 오일러 지표는 다음과 같은 교대 합으로 정의할 수 있다.

:

\chi = b_0 - b_1 + b_2 - b_3 + \cdots.

이 값은 베티 수가 모두 유한하고 특정 지수 ''n''₀를 넘어서 0인 경우 잘 정의된다.

위상 공간

X

의 오일러 지표

\chi(X)

는 다음과 같은 교대합으로 정의된다^[20].

:

\chi(X) = \sum_{n = 0}^{\infty} (-1)^n b_n

여기서

b_n

은 위상 공간

X

의

n

차원 베티 수이며, 이는 호몰로지 군

H_n(X)

의 아벨 군으로서의 계수이다.

2. 2. CW 복합체

유한 CW 복합체의 오일러 지표는 다음과 같은 교대 합으로 정의된다.

:

\chi = k_0 - k_1 + k_2 - k_3 + \cdots,

여기서

k_n

은 복합체 내에서

n

차원 세포의 수를 나타낸다.

2. 3. 사슬 복합체

사슬 복합체(Chain complex)

(C_\bullet,\partial_\bullet)

의 호몰로지(Homology)

H_\bullet(C)

가 모두 유한 계수를 가지며,

H_\bullet

이 어떤 최저·최고 차수 밖에서는 계수가 0이라고 가정한다. 그렇다면, 사슬 복합체

(C_\bullet,\partial_\bullet)

의 '''오일러 지표'''

\chi(C_\bullet)\in\mathbb Z

는 다음과 같은 정수이다.

:

\chi(C_\bullet)=\sum_i(-1)^i\operatorname{rank}H_i(C)\in\mathbb Z

위상 공간

X

의 '''오일러 지표'''

\chi(X)

는 그 특이 사슬 복합체의 오일러 지표이다. CW 복합체

X

의 '''오일러 지표'''는 세포 사슬 복합체의 오일러 지표이다. 특히, 그래프나 다면체는 자연스럽게 CW 복합체를 이루므로, 오일러 지표를 조합론적으로 계산할 수 있다.

더 일반적으로, 모든 위상 공간에 대해, ''n''번째 베티 수 ''b''_''n''을 ''n''번째 특이 호몰로지 군의 계수로 정의할 수 있다. '''오일러 지표'''는 다음과 같은 교대 합으로 정의할 수 있다.

:

\chi = b_0 - b_1 + b_2 - b_3 + \cdots.

이 값은 베티 수가 모두 유한하고 특정 지수 ''n''₀를 넘어서 0인 경우 잘 정의된다. 단순 복합체의 경우, 이는 이전 단락의 정의와 동일하지 않지만, 호몰로지 계산은 두 정의가

\chi

에 대해 동일한 값을 제공한다는 것을 보여준다.

2. 4. 다면체

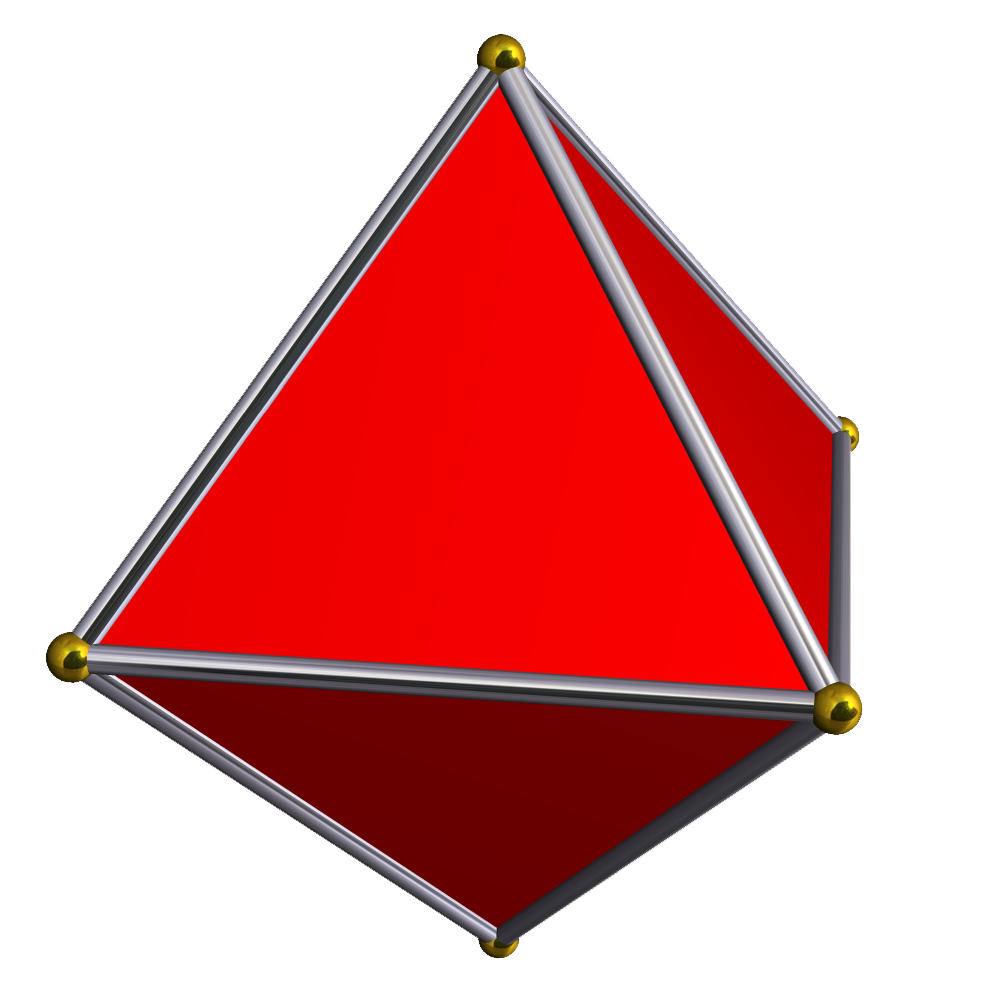
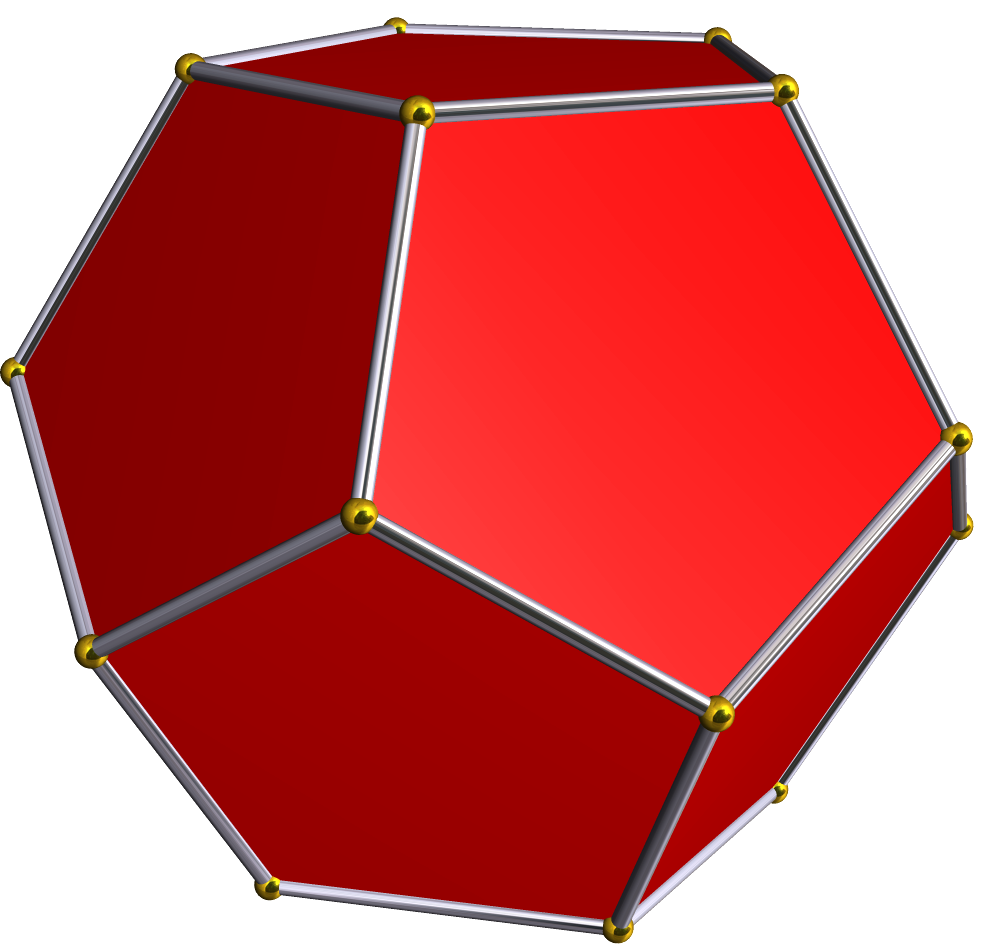
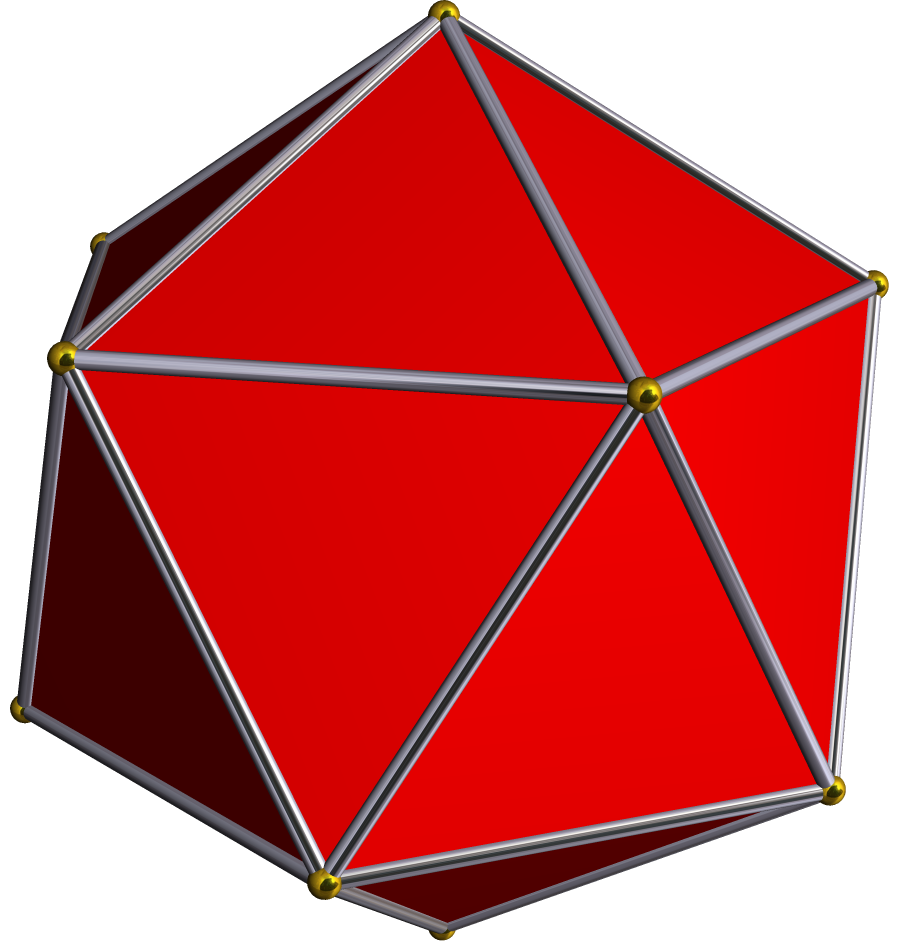
''v''를 꼭짓점, ''e''를 모서리, ''f''를 면의 수라고 할 때, 다면체의 오일러 지표

\chi

는 다음과 같이 정의된다.

:

\chi = v - e + f

오일러 지표는 위상수학적 불변량이고, 모든 다면체는 구와 위상동형이므로, 다면체의 오일러 지표의 값은 그 모양에 관계없이 항상 2이다.

이름	꼭짓점 v	모서리 e	면 f	오일러 지표: v - e + f
정사면체	4	6	4	2
정육면체	8	12	6	2
정팔면체	6	12	8	2
정십이면체	20	30	12	2
정이십면체	12	30	20	2

1758년 오일러가 제시한 이 방정식^[2]은 '''오일러의 다면체 공식'''으로 알려져 있다.^[3]

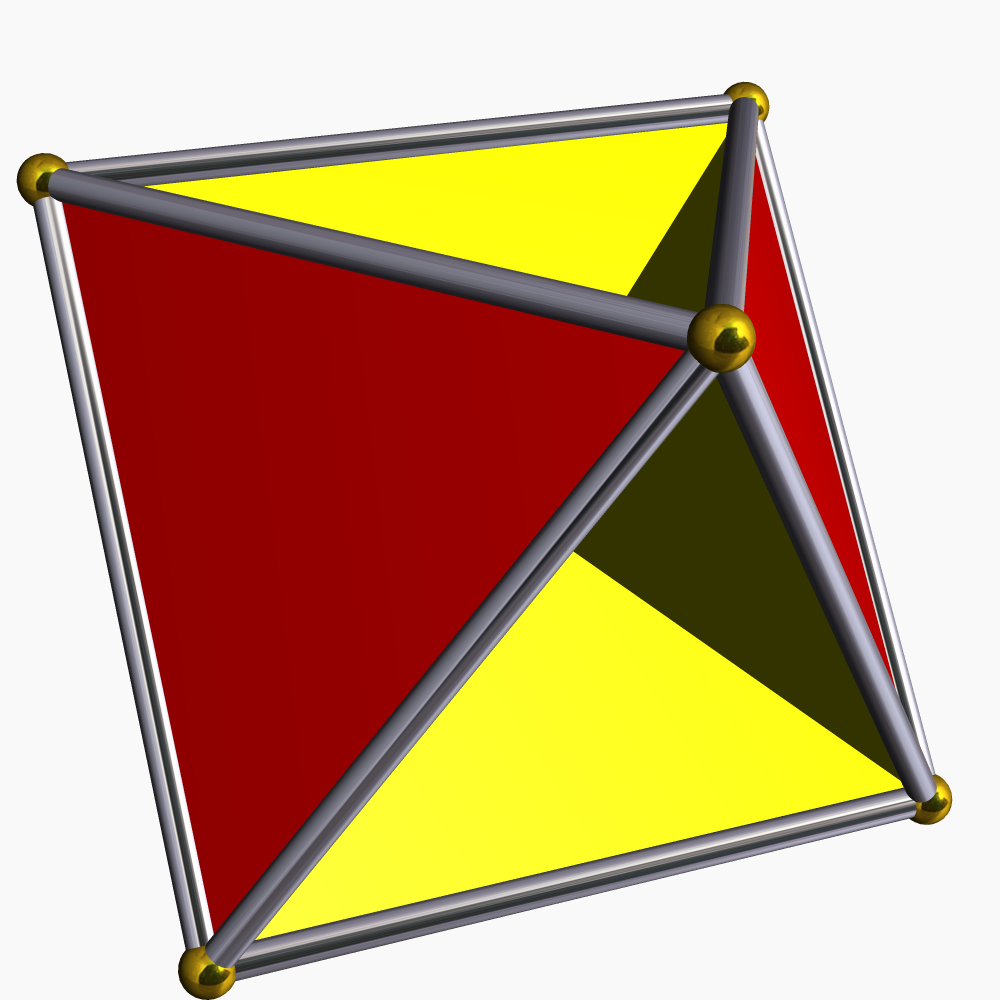
비볼록 다면체의 표면은 다양한 오일러 지표를 가질 수 있다.

이름	이미지	정점 v	모서리 e	면 f	오일러 지표: $\chi = v - e + f$
사반육면체		6	12	7	1
팔반팔면체		12	24	12	0
육반팔면체		12	24	10	-2
작은 별모양 십이면체	--	12	30	12	-6
큰 별모양 십이면체	--	20	30	12	2

정다면체의 경우, 아서 케일리는 밀도, 꼭짓점 도형 밀도 , 및 면 밀도를 사용하여 오일러 공식의 수정된 형태를 유도했다.

:

이 버전은 볼록 다면체(밀도가 모두 1임)와 비볼록 케플러-푸앵소 다면체 모두에 적용된다.

사영 다면체는 모두 실 사영 평면과 같이 오일러 지표가 1이고, 토로이드 다면체의 표면은 모두 원환면과 같이 오일러 지표가 0이다.

다면체인 경우, 꼭짓점의 수를 , 모서리의 수를 , 면의 수를 로 하여 오일러 지표는

:

로 쓸 수 있다. 볼록 다면체라면 이것은 항상 2와 같고, 이것을 오일러의 다면체 정리라고 한다.

2. 5. 그래프

오일러 지표는 연결된 평면 그래프에 대해 다면체 표면과 동일한

V - E + F

공식을 사용하여 정의할 수 있으며, 여기서

F

는 외부 면을 포함한 그래프의 면의 수이다.

어떤 평면 연결 그래프

G

의 오일러 지표는 2이다. 이는 기본 사례로 트리를 시작하여

G

에 의해 결정된 면의 수에 대한 귀납법으로 쉽게 증명할 수 있다. 트리의 경우,

E = V - 1

이고

F = 1

이다. 만약

G

가

C

개의 연결 요소(단절된 그래프)를 가지고 있다면,

F

에 대한 귀납법에 의한 동일한 논증은

V - E + F - C = 1

임을 보여준다.

스테레오 투영을 통해 평면은 2-구에 매핑되므로 연결된 그래프는 오일러 지표가 2인 구의 다각형 분해에 매핑된다.

유한 CW 복합체

K

에 포함된

n

차원 단체의 개수를

q_n

이라고 하면,

:

\chi(K) = \sum_{n = 0}^\infty (-1)^n q_n

이다^[21]。

특히

K

가 유한 연결 그래프인 경우, 꼭짓점의 수를

v

, 모서리의 수를

e

로 하여 오일러 지표는

\chi(K) = v - e

로 쓸 수 있다. 만약 그래프

K

가 사이클을 가지지 않는다면

\chi(K) = 1

이다.

3. 성질

오일러 지표는 위상 공간에 대한 여러 기본적인 연산에 대해 다음과 같은 성질을 갖는다.

오일러 지표는 호모토피 불변량이다. 즉, 호모토피 동치인 두 위상 공간은 같은 오일러 지표를 갖는다. 예를 들어, 모든 수축 가능 공간은 오일러 지표가 1이다. 모든 볼록 다면체는 3차원 공과 위상 동형이므로, 그 표면은 2차원 구와 위상 동형이며, 오일러 지표는 2이다.

두 위상 공간 ''M''과 ''N''의 분리 집합의 오일러 지표는 각 오일러 지표의 합과 같다.

: $\chi(M \sqcup N) = \chi(M) + \chi(N).$

''M''과 ''N''이 더 큰 공간 ''X''의 부분 공간이라면, 포함-배제 원리에 따라 다음이 성립한다.

: $\chi(M \cup N) = \chi(M) + \chi(N) - \chi(M \cap N).$

두 개의 연결된 닫힌 n-다양체 $M, N$ 의 연결합 $M \# N$ 의 오일러 지표는 다음과 같다.^[8]

: $\chi(M \# N) = \chi(M) + \chi(N) - \chi(S^n).$

두 위상 공간 ''M''과 ''N''의 곱공간 $M \times N$ 의 오일러 지표는 다음과 같다.

: $\chi(M \times N) = \chi(M) \cdot \chi(N).$

''k''-겹 덮개 공간 $\tilde{M} \to M$ 에 대해, 다음이 성립한다.

: $\chi(\tilde{M}) = k \cdot \chi(M).$

올뭉치 $p\colon E \to B$ (올 $F$ )에 대해, 특정 조건 하에서 다음이 성립한다.^[9]

: $\chi(E) = \chi(F)\cdot \chi(B).$

정다면체의 경우, 오일러 지표는 다음과 같이 계산된다.

정다면체의 오일러 지표
꼭짓점	모서리	면	오일러 지표
4	6	4	2
8	12	6	2
6	12	8	2
20	30	12	2
12	30	20	2

유한 CW 복합체 에 포함된 n 차원 단체의 개수를 $q_n$ 이라고 하면, 오일러 지표는 다음과 같이 계산된다.^[21]

: $\chi(K) = \sum_{n = 0}^\infty (-1)^n q_n$

특히, K가 유한 연결 그래프인 경우, 꼭짓점의 수를 v, 모서리의 수를 e로 하여 오일러 지표는 $\chi(K) = v - e$ 로 쓸 수 있다. 만약 그래프 K가 사이클을 가지지 않는다면 $\chi(K) = 1$ 이다. 또한 K가 다면체인 경우, 꼭짓점의 수를 v, 모서리의 수를 e, 면의 수를 f로 하여 오일러 지표는

: $\chi(K) = v - e + f$

로 쓸 수 있다. 볼록 다면체라면 이것은 항상 2와 같고, 이것을 오일러의 다면체 정리라고 한다.

4. 예시

다면체의 경우, 꼭짓점의 수를 , 모서리의 수를 , 면의 수를 로 하여 오일러 지표를 $\chi = v - e + f$ 로 계산할 수 있다. 볼록 다면체의 경우 이 값은 항상 2이며, 이를 오일러의 다면체 정리라고 한다. 오일러가 1758년에 제시한 이 공식^[2]은 '''오일러의 다면체 공식'''으로 알려져 있다.^[3]

이름	정점 ()	모서리 ()	면 ()	오일러 지표: $\ \chi = V - E + F\$
정사면체	4	6	4	2
정육면체	8	12	6	2
정팔면체	6	12	8	2
정십이면체	20	30	12	2
정이십면체	12	30	20	2

일반적인 곡면의 경우, 표면에 다각형을 그려 오일러 지표를 계산할 수 있다.

이름	그림	χ
구간	--	1
원		0
원판	--	1
구		2
토러스 (두 원의 곱)	--	0
이중 토러스	--	-2
삼중 토러스	--	-4
실수 사영 평면	--	1
뫼비우스 띠	--	0
클라인 병		0
두 개의 구 (연결되지 않음) (두 개의 구의 분리된 합집합)	200x200px	4
세 개의 구 (연결되지 않음) (세 개의 구의 분리된 합집합)		6
n 개의 구 (연결되지 않음) (n개의 구의 분리된 합집합)	. . .	2n

고차원 도형의 경우, $n$ 차원 구의 오일러 지표는 $\chi = 1 + (-1)^n$ 이다. 즉, $n$ 이 홀수이면 0이고, $n$ 이 짝수이면 2이다. $n$ 차원 실수 사영 공간의 오일러 지표는 0 또는 1이다. $n$ 차원 토러스와 모든 콤팩트 평행화 가능 다양체의 오일러 지표는 0이다.^[12] 닫힌 다양체의 오일러 지표는 차원이 홀수이면 0이다.^[13]

일반적인 축구공(깎은 정이십면체)은 오각형 12개와 육각형 20개로 이루어져 있으며, 오일러 지표는 2이다.^[11]

4. 1. 다면체

v를 꼭짓점, e를 모서리, f를 면의 수라고 할 때 오일러 지표

\chi

는 다음과 같다.

:

\chi = v - e + f

오일러 지표는 위상수학적 불변량이고, 모든 다면체는 구와 위상동형이므로, 다면체의 오일러 지표의 값은 그 모양에 관계 없이 항상 2이다.

오일러가 1758년에 제시한 이 방정식^[2]은 '''오일러의 다면체 공식'''으로 알려져 있다.^[3] 이 공식은 구의 오일러 지표(즉,

\ \chi = 2\

)에 해당하며, 구면 다면체에도 동일하게 적용된다.

이름	정점 ()	모서리 ()	면 ()	오일러 지표: $\ \chi = V - E + F\$
정사면체	4	6	4	2
정육면체	8	12	6	2
정팔면체	6	12	8	2
정십이면체	20	30	12	2
정이십면체	12	30	20	2

다면체의 경우, 꼭짓점의 수를 , 모서리의 수를 , 면의 수를 로 하여 오일러 지표는

: $\chi(K) = v - e + f$

로 쓸 수 있다. 볼록 다면체라면 이것은 항상 2와 같고, 이것을 오일러의 다면체 정리라고 한다.

4. 2. 곡면

일반적인 곡면의 오일러 지표는 표면에 다각형을 그려서 계산할 수 있다. 오일러 지표는 표면의 다각형화(즉, CW 복합체)를 찾아 위에서 정의한 공식을 사용하여 계산한다.

이름	그림	χ
구간	--	1
원		0
원판	--	1
구		2
토러스 (두 원의 곱)	--	0
이중 토러스	--	-2
삼중 토러스	--	-4
실수 사영 평면	--	1
뫼비우스 띠	--	0
클라인 병		0
두 개의 구 (연결되지 않음) (두 개의 구의 분리된 합집합)		4
세 개의 구 (연결되지 않음) (세 개의 구의 분리된 합집합)		6
n 개의 구 (연결되지 않음) (n개의 구의 분리된 합집합)	. . .	2n

4. 3. 고차원 도형

n

차원 구는 다음과 같은 특이 호몰로지 군을 갖는다.

:

H_k(\mathrm{S}^n) = \begin{cases} \mathbb{Z} ~& k = 0 ~~ \mathsf{ or } ~~ k = n \\ \{0\} & \mathsf{otherwise}\ , \end{cases}

따라서 0차원과

n

차원에서 베티 수 1을 가지며, 다른 모든 베티 수는 0이다. 그러면 오일러 지표는

\chi = 1 + (-1)^n

이다. 즉,

n

이 홀수이면 0이고,

n

이 짝수이면 2이다.

n

차원 실수 사영 공간은

n

차원 구를 대각사상으로 나눈 몫 공간이다. 따라서 오일러 지표는 해당 구의 절반, 즉 0 또는 1이다.

n

차원 토러스는

n

개의 원의 곱 공간이다. 곱의 성질에 의해 오일러 지표는 0이다. 더 일반적으로, 모든 콤팩트 평행화 가능 다양체, 예를 들어 모든 콤팩트 리 군은 오일러 지표가 0이다.^[12]

닫힌 다양체의 오일러 지표는 차원이 홀수이면 0이다.^[13] 가향 가능한 경우의 예는 푸앵카레 쌍대성의 따름정리이다. 이 성질은 모든 콤팩트 공간 위상적 층 공간에 더 일반적으로 적용되며, 모든 층이 홀수 차원을 갖는다. 또한 이중 덮개 가향 이중 덮개를 통해 닫힌 홀수 차원 비가향 다양체에도 적용된다.

4. 4. 축구공

일반적인 축구공(깎은 정이십면체)은 오각형 12개와 육각형 20개로 이루어져 있으며, 오일러 지표는 2이다.^[11] 축구공은 각 꼭짓점에서 세 개의 조각이 만나도록 오각형과 육각형 조각을 함께 꿰매어 만든다. (예: 아디다스 텔스타)^[11] 오각형이 ''P''개, 육각형이 ''H''개 사용되었다면, 면의 수는

F = P + H

, 꼭짓점의 수는

V = \tfrac{1}{3}(5P + 6H)

, 모서리의 수는

E = \tfrac{1}{2}(5P + 6H)

이다. 따라서 오일러 지표는 다음과 같이 계산된다.^[11]

:

V - E + F = \tfrac{1}{3}(5P + 6H) - \tfrac{1}{2}(5P + 6H) + P + H = \tfrac{1}{6}P

구의 오일러 지표가 2이므로,

P = 12

이다. 즉, 이러한 방식으로 제작된 축구공은 항상 오각형 12개를 가진다. 육각형의 수는 1을 제외한 어떤 음이 아닌 정수도 될 수 있다.^[11] 이 결과는 풀러렌과 골드버그 다면체에 적용될 수 있다.^[11]

5. 오일러 공식의 증명 (다면체)

코시의 증명 외에도 오일러 공식을 증명하는 다른 방법이 있다. 다면체의 한 면을 제거하고 남은 면들을 평면으로 펼치면, 다면체의 정점과 변의 관계를 나타내는 평면 그래프를 얻을 수 있다.

이 평면 그래프의 전역 트리와 그 쌍대를 생각하면, 전역 트리의 쌍대가 원래 그래프 쌍대의 전역 트리가 됨을 보일 수 있다.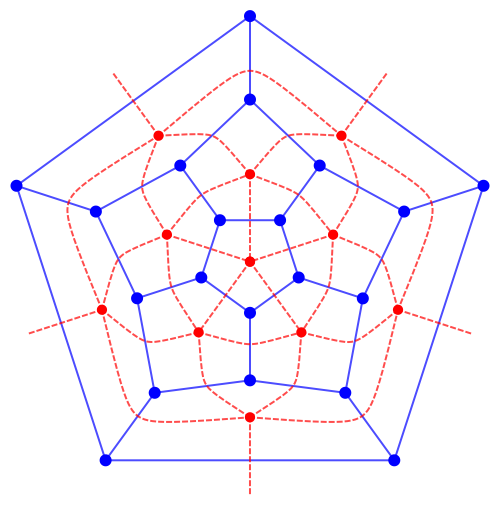

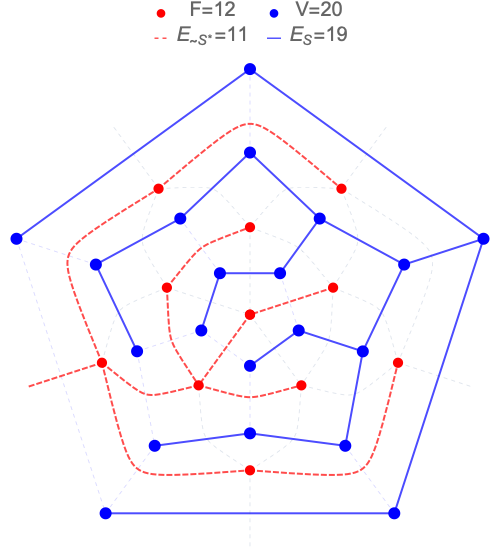
정십이면체 다면체 그래프(파란색)와 그 쌍대(빨간색). 쌍대 그래프의 정점 중 하나는 무한대에 존재한다.

정십이면체 다면체 그래프의 전역 트리(파란색)와 그 쌍대(빨간색). 그래프의 전역 트리와 그 쌍대가 갖는 관계로부터 오일러의 다면체 정리가 유도된다.

평면 그래프의 모든 변은 전역 트리와 그 쌍대 그래프의 전역 트리에 대응하는 변으로 분해할 수 있다.

트리 그래프의 정점의 수 ''v''와 변의 수 ''e''는 ''e'' = ''v'' - 1라는 관계를 갖는다.

그래프 G의 전역 트리 T의 변의 수를 e_T라 하면, e_T = v - 1 이다. G의 쌍대 G'의 변의 수를 e_T'라 하면, T'는 G'의 전역 트리이므로, G'의 정점의 수, 즉 G의 면의 수 f에 대해 e_T' = f - 1이다. G의 변의 수와 G'의 변의 수를 더하면 G의 변의 수와 같고, G'의 각 변은 G의 각 변에 일대일로 대응하므로,

:

e = (v - 1) + (f - 1)

이 성립하며, 이는 오일러 공식과 같다.

5. 1. 코시의 증명

코시는 1811년에 오일러 공식에 대한 증명을 제시했다. 이 증명은 모든 볼록 다면체뿐만 아니라, 경계가 위상적으로 구와 동등하고 면이 위상적으로 원반과 동등한 모든 다면체에 적용된다.

증명 과정은 다음과 같다.

1. 다면체 표면의 한 면을 제거한다.

2. 제거된 면의 모서리를 서로 당겨서 나머지 부분을 점과 곡선으로 이루어진 평면 그래프로 변형한다. 이때 제거된 면의 둘레는 얻어진 그래프를 외부에서 둘러싸도록 배치한다. 이는 정육면체의 특수한 경우에 대한 세 개의 그래프 중 첫 번째 그래프로 설명된다. (처음 다면체 표면이 구와 위상동형이라는 가정이 이를 가능하게 한다.)

3. 이러한 변형 후에는 정규 면이 더 이상 정규적이지 않다. 꼭짓점과 모서리의 수는 동일하게 유지되지만 면의 수는 1 감소한다. 따라서 다면체에 대한 오일러 공식을 증명하는 것은 이 변형된 평면 객체에 대해 ''V'' - ''E'' + ''F'' = 1임을 증명하는 것으로 축소된다.

frame

4. 세 변 이상을 가진 면이 있는 경우 대각선을 그린다. 즉, 아직 연결되지 않은 두 꼭짓점을 연결하는 면을 가로지르는 곡선이다. 각 새로운 대각선은 하나의 모서리와 하나의 면을 추가하고 꼭짓점의 수는 변경하지 않으므로 ''V'' - ''E'' + ''F''의 값을 변경하지 않는다. (모든 면이 원반이라는 가정은 요르단 곡선 정리를 통해 이 연산이 면의 수를 하나 증가시키는 것을 보여주기 위해 필요하다.) 모든 면이 삼각형이 될 때까지 이러한 방식으로 모서리를 계속 추가한다.

5. 다음 두 변환 중 하나를 반복적으로 적용하여 외부 경계가 항상 단순 사이클임을 유지한다.

외부에 인접한 모서리가 하나만 있는 삼각형을 제거한다. 이는 두 번째 그래프로 설명된다. 이렇게 하면 모서리와 면의 수가 각각 하나씩 감소하고 꼭짓점의 수는 변경되지 않으므로 ''V'' - ''E'' + ''F''를 보존한다.
네트워크의 외부에 의해 공유되는 두 개의 모서리가 있는 삼각형을 제거한다. 이는 세 번째 그래프로 설명된다. 각 삼각형 제거는 꼭짓점 하나, 모서리 두 개, 면 하나를 제거하므로 ''V'' - ''E'' + ''F''를 보존한다.

6. 이러한 변환은 결국 평면 그래프를 단일 삼각형으로 줄인다. (단순 사이클 불변성이 없으면 삼각형을 제거하면 나머지 삼각형이 분리되어 나머지 인수가 무효화될 수 있다. 유효한 제거 순서는 쉘링의 기본 예이다.)

이 시점에서 단독 삼각형은 ''V'' = 3, ''E'' = 3, 및 ''F'' = 1이므로 ''V'' - ''E'' + ''F'' = 1이다. 위의 두 변환 단계 각각이 이 양을 보존했으므로 변형된 평면 객체에 대해 ''V'' - ''E'' + ''F'' = 1을 보여주었고, 따라서 다면체에 대해 ''V'' - ''E'' + ''F'' = 2임을 증명했다.

추가 증명은 엡스타인 (2013)을 참조하라.^[4] 여러 증명, 결함 및 한계점을 포함하여 라카토스 (1976)의 ''증명과 반증''에서 예시로 사용된다.^[5]

5. 2. 쌍대 그래프를 이용한 증명

다면체의 정점과 변의 관계는 평면 그래프로 나타낼 수 있다. 먼저 다면체의 면 중 하나를 제거하고, 뚫린 구멍을 넓혀 나머지 면을 평면에 가깝게 한다. 이렇게 만들어진 그래프의 바깥쪽 영역을 처음에 제거한 면에 대응시키면, 다면체의 정점과 변의 관계를 갖는 평면 그래프를 얻을 수 있다.

다음으로, 평면 그래프의 전역 트리와 그 쌍대를 생각한다. 그래프의 전역 트리란 그래프의 모든 정점을 연결하고, 폐로를 포함하지 않는 그래프이다. 또한, 쌍대 그래프는 원래 그래프의 면에 대응하는 정점을 가지고, 원래 그래프의 면들을 잇는 변에 대응하는 변을 갖는 그래프이다. 전역 트리의 쌍대는 원래 그래프의 쌍대 중 전역 트리에 포함되지 않는 변에 대응하는 변을 포함하는 그래프이다. 전역 트리의 쌍대가 원래 그래프의 쌍대의 전역 트리가 된다.

이제, 평면 그래프 와 그 쌍대 를 생각한다. 의 전역 트리 ''''에 대해, 중 ''''에 포함되지 않는 그래프를 ''''로 한다. 또한, 중 ''''에 대응하는 그래프를 ''''로 한다. ''''는 폐로를 갖지 않으므로, 의 각 면을 둘러싸는 변 중 적어도 하나는 ''''에 포함된다. 이 사실을 쌍대의 세계에서 다시 말하면, 의 각 정점은 반드시 ''''가 갖는 변에 의해 연결된다는 것이다. 여기서 만약 ''''가 폐로를 갖는다면, 동일한 논의에 의해, 의 정점 중 적어도 하나가 ''''에 의해 연결되지 않게 된다. 그러나, 이것은 ''''가 전역 트리인 것과 모순되므로, ''''는 폐로를 갖지 않는다. 따라서, ''''는 의 모든 정점을 연결하고, 폐로를 갖지 않는다. 즉, ''''는 의 전역 트리이다.

이로부터, 평면 그래프의 모든 변은 전역 트리와 그래프의 쌍대의 전역 트리에 대응하는 변으로 분해할 수 있다.

트리 그래프는 하나의 정점에서 시작하여, 정점과 변을 각각 하나씩 그래프에 추가해 나감으로써 만들 수 있다. 이 때문에, 트리 그래프의 정점의 수 ''''와 변의 수 ''''는, 이라는 관계를 갖는다.

이제, 그래프 에 대해 그 전역 트리 가 주어졌다고 가정한다. 의 변의 수를 라고 하면, 가 성립한다. 또한 의 쌍대 ''''의 변의 수를 라고 하면, ''''는 ''''의 전역 트리이므로, ''''의 정점의 수, 즉 의 면의 수 ''''에 대해 유사한 관계 가 성립한다. 의 변의 수와 ''''의 변의 수를 더하면 의 변의 수와 같고, 또한 ''''의 각 변은 ''''의 각 변에 일대일로 대응하므로,

:

e = (v - 1) + (f - 1)

가 성립한다. 이것은 오일러 공식과 다름없다.

6. 다른 불변량과의 관계

닫힌 가향 곡면의 오일러 지표는 종수 $g$ (곡면의 연결합 분해에서 원환면의 수, 직관적으로 "손잡이"의 수)를 사용하여 다음과 같이 계산할 수 있다.

: $\chi = 2 - 2g ~.$

닫힌 비가향 곡면의 오일러 지표는 비가향 종수 $k$ (곡면의 연결합 분해에서 실사영평면의 수)를 사용하여 다음과 같이 계산할 수 있다.

: $\chi = 2 - k ~.$

닫힌 매끄러운 다양체의 경우 오일러 지표는 '''오일러 수'''와 일치한다. 즉, 다양체의 기본류에서 평가된 접다발의 오일러류이다. 오일러류는 차례로 모든 다른 특성류와 벡터 다발과 관련이 있다.

닫힌 리만 다양체의 경우 오일러 지표는 곡률을 적분하여 찾을 수도 있다. 2차원인 경우에는 가우스-보네 정리를, 일반적인 경우에는 일반화된 가우스-보네 정리를 참조하라.

가우스-보네 정리의 이산적 유사체는 데카르트의 정리로, 다면체의 "총 결함"은 완전한 원으로 측정되며, 이는 다면체의 오일러 지표이다.

하드위거 정리는 오일러 지표를 ℝⁿ 에서 콤팩트 볼록 다면체의 유한 합에서 정의된 "0차 균질"인 ( 스칼라 곱셈 까지) 병진 불변, 유한 가산, 반드시 비음수가 아닌 집합 함수로 특징짓는다.

7. 일반화

모든 조합론적 세포 복합체에 대해, 오일러 지표는 0-세포의 수에서 1-세포의 수를 빼고 2-세포의 수를 더하는 방식으로 정의된다. 특히, 유한 집합의 오일러 지표는 단순히 그 기수이며, 그래프의 오일러 지표는 정점의 수에서 모서리의 수를 뺀 것이다.^[14]

더 일반적으로, 모든 사슬 복합체의 오일러 지표는 이 사슬 복합체의 호몰로지 군의 계수의 교대 합으로 정의할 수 있다.^[15]

대수 기하학에서, scheme 위의 모든 coherent sheaf $\mathcal{F}$ 에 대해, 오일러 지표는 $\mathcal{F}$ 의 -번째 층 코호몰로지 군의 차원의 교대합으로 정의된다.

오비폴드는 모든 다양체가 정수 오일러 지표를 갖는 것과 달리, 분수 오일러 지표를 가질 수 있다.

축소된 호몰로지의 오일러 지표는 유계된 유한 poset의 오일러 지표로 일반화되기도 한다. 이러한 poset의 오일러 지표는 정수로 정의되며, 여기서 μ는 해당 poset의 뫼비우스 함수이다.

범주는 유리수 값을 갖는 오일러 지표를 정의함으로써 더욱 일반화될 수 있다.^[16]

참조

_[1] 서적 A History of Folding in Mathematics: Mathematizing the Margins Birkhäuser
_[2] 간행물 Elementa doctrinae solidorum https://scholarlycom[...]
_[3] 문서
_[4] acad. pers. wbs. Twenty-one proofs of Euler's formula: V − E + F = 2 http://www.ics.uci.e[...] 2022-05-27
_[5] 서적 Proofs and Refutations Cambridge Technology Press
_[6] 문서 Algebraic Topology Springer
_[7] 문서 Introduction to toric varieties Princeton University Press
_[8] 웹사이트 Homology of connected sum http://topospaces.su[...] 2016-07-13
_[9] 문서 Algebraic Topology https://books.google[...] Springer
_[10] 간행물 Fibre bundles and the Euler characteristic http://www.math.purd[...]
_[11] 서적 An Atlas of Fullerenes
_[12] 서적 Characteristic Classes Princeton University Press
_[13] 문서
_[14] 서적 Limits of graphs in group theory and computer science EPFL Press
_[15] 문서 Euler characteristic
_[16] 간행물 The Euler characteristic of a category http://www.math.uiuc[...]
_[17] 서적 Differential Topology Springer
_[18] 문서
_[19] 문서 Weisstein
_[20] 문서
_[21] 서적 Topology and Geometry Springer

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com