이등분

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

이등분은 기하학에서 대상(선분, 각, 다각형 등)을 두 개의 동일한 부분으로 나누는 것을 의미한다.

선분의 이등분선은 선분의 중점을 지나며, 특히 수직으로 만나는 경우 수직이등분선이라고 한다. 수직이등분선은 자와 컴퍼스를 사용하여 작도할 수 있으며, 선분 위의 모든 점에서 선분의 양 끝점까지의 거리가 같다.

각의 이등분선은 각을 두 개의 동일한 크기로 나누는 선이며, 자와 컴퍼스로 작도할 수 있다. 삼각형, 사각형과 같은 다각형의 이등분선은 면적, 둘레, 대각선 등을 이등분하는 데 사용된다. 삼각형의 면적 이등분선은 무한히 많으며, 중선을 포함한다. 사각형의 대각선은 서로를 이등분하며, 평행사변형의 대각선은 서로를 이등분한다. 사면체의 부피 이등분선은 사면체의 이중 중앙선을 포함하는 평면이다.

더 읽어볼만한 페이지

초등 기하학 - 대원
구면기하학에서 대원은 구의 중심을 지나는 평면과 구의 교선으로, 유클리드 공간의 직선에 대응하며, 서로 대극점이 아닌 두 점을 잇는 최단 거리인 대원 거리를 정의하고, 자오선이나 적도처럼 항해, 천문학 등 다양한 분야에서 응용된다.
초등 기하학 - 현 (기하학)
현은 원 둘레를 두 호로 나누는 선분으로, 원에 내접하는 정다각형의 변이 될 수 있으며, 원의 중심을 지나는 가장 긴 현은 지름이라고 한다.

이등분

2. 선분의 이등분선

어떤 선분의 이등분선은 그 선분의 중점을 지나는 선이다. 특히, 선분과 수직으로 만나는 이등분선을 '''수직이등분선'''이라고 한다.

브라마굽타의 정리에 따르면, 원에 내접하는 사각형의 대각선이 직각으로 교차하는 경우, 대각선의 교점에서 사각형의 한 변에 수선을 그어 만들어지는 직선은 해당 사각형의 대변을 이등분한다.

2. 1. 수직이등분선의 성질

선분의 수직 이등분선 위의 각 점은 대상 선분의 양쪽 끝점으로부터의 거리가 같다는 특징을 갖는다. 따라서, 보로노이 다이어그램에서 영역의 경계선은 각 모점의 이등분선의 일부가 된다.

선분 $AB$ 의 수직 이등분선은 또한 각 점 $X$ 가 선분 AB의 끝점으로부터 등거리에 있다는 속성을 갖는다.

'''(D)'''

\quad |XA| = |XB|

.

증명은

와 피타고라스 정리로부터 유도된다.

:

|XA|^2=|XM|^2+|MA|^2=|XM|^2+|MB|^2=|XB|^2 \; .

속성 '''(D)'''는 일반적으로 수직 이등분선의 작도에 사용된다.^[1]

고전 기하학에서, 이등분은 컴퍼스와 자 작도이며, 이는 동일한 반지름과 다른 중심을 가진 호를 그릴 수 있는 능력에 달려 있다.^[1]

선분

AB

는 반지름

r>\tfrac 1 2 |AB|

인 교차하는 원을 그림으로써 이등분되며, 이 원의 중심은 선분의 양 끝점이다. 두 원의 교차점에 의해 결정되는 선은 선분의 수직 이등분선이다. 이등분선의 작도는 선분의 중점

M

을 알지 못하는 상태에서 수행되므로, 이 작도는 이등분선과 선분의 교차점으로

M

을 결정하는 데 사용된다.^[1]

이 작도는 실제로 "주어진 점"

P

에서 ''주어진 선''

g

에 ''수직인 선''을 작도할 때 사용된다. 중심이

P

이고 선

g

와 두 점

A,B

에서 교차하는 원을 그리면, 작도될 수직선은 선분

AB

를 이등분하는 선이다.^[1]

자, 컴퍼스에 의한 작도가 가능하다. 선분의 양쪽 끝점을 중심으로 동일한 반지름의 원호를 그리고, 각 원호의 교점과 선분을 연결한다. 원호 위의 교점과 선분의 각 끝점에 의해 만들어지는 삼각형이 합동이므로, 원호 위의 교점을 연결하는 직선이 수직 이등분선이 된다. (그림 1.)

2. 2. 수직이등분선의 작도

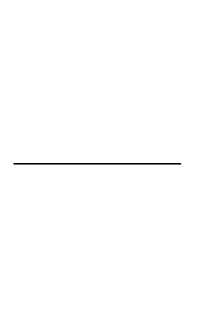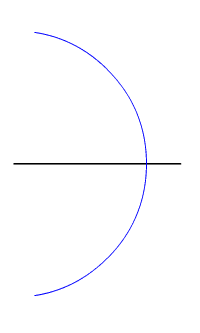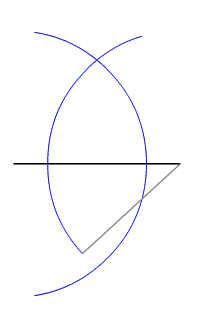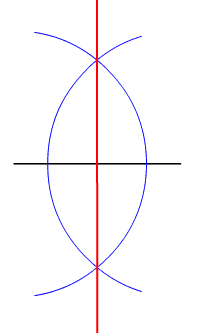
선분의 수직이등분선 작도 방법. 빨간색 직선은 검은색 선분의 수직이등분선이다.

선분의 수직이등분선을 작도하는 방법은 다음과 같다. 선분의 양 끝에서 반지름의 길이가 같은 원호를 두 개 그린다. 이때 호의 반지름은 선분의 길이의 반보다 커야 하며, 중심각은 두 호가 두 점에서 만날 수 있을 정도로 커야 한다. 두 호의 교점 둘을 잇는 직선이 선분의 수직이등분선이다.

고전 기하학에서, 이등분은 간단한 컴퍼스와 자 작도이며, 이는 동일한 반지름과 다른 중심을 가진 호를 그릴 수 있는 능력에 달려 있다.^[1]

선분

AB

는 반지름

r>\tfrac 1 2 |AB|

인 교차하는 원을 그림으로써 이등분되며, 이 원의 중심은 선분의 양 끝점이다. 두 원의 교차점에 의해 결정되는 선은 선분의 수직이등분선이다.^[1] 이등분선의 작도는 선분의 중점

M

을 알지 못하는 상태에서 수행되므로, 이 작도는 이등분선과 선분의 교차점으로

M

을 결정하는 데 사용된다.^[1]

이 작도는 실제로 "주어진 점"

P

에서 ''주어진 선''

g

에 ''수직인 선''을 작도할 때 사용된다. 중심이

P

이고 선

g

와 두 점

A,B

에서 교차하는 원을 그리면, 작도될 수직선은 선분

AB

를 이등분하는 선이다.^[1]

수직이등분선은 자, 컴퍼스에 의한 작도가 가능하다. 선분의 양쪽 끝점을 중심으로 동일한 반지름의 원호를 그리고, 각 원호의 교점과 선분을 연결한다. 원호 위의 교점과 선분의 각 끝점에 의해 만들어지는 삼각형이 합동이므로, 원호 위의 교점을 연결하는 직선이 수직이등분선이 된다.^[2]

2. 3. 수직이등분선의 방정식

선분

AB

의 수직 이등분선은 각 점

X

가 선분 AB의 끝점으로부터 등거리에 있다는 속성을 갖는다.

:(D)

\quad |XA| = |XB|

.

이는 피타고라스 정리로부터 유도된다.

:

|XA|^2=|XM|^2+|MA|^2=|XM|^2+|MB|^2=|XB|^2 \; .

속성 (D)는 일반적으로 수직 이등분선의 작도에 사용된다.

만약

\vec a,\vec b

가 두 점

A,B

의 위치 벡터라면, 그 중점은

M: \vec m=\tfrac{\vec a+\vec b}{2}

이고 벡터

\vec a -\vec b

는 수직 이등분선의 법선 벡터이다. 따라서 벡터 방정식은

(\vec x-\vec m)\cdot(\vec a-\vec b)=0

이다.

\vec m =\cdots

을 대입하고 방정식을 전개하면 다음의 벡터 방정식이 된다.

:(V)

\quad \vec x\cdot(\vec a-\vec b)=\tfrac 1 2 (\vec a^2-\vec b^2) .

A=(a_1,a_2),B=(b_1,b_2)

를 사용하면 좌표 형태의 방정식을 얻을 수 있다.

:(C)

\quad (a_1-b_1)x+(a_2-b_2)y=\tfrac 1 2 (a_1^2-b_1^2+a_2^2-b_2^2) \; .

또는 명시적으로 다음과 같이 표현할 수 있다.

:(E)

\quad y = m(x - x_0)  +y_0

,

여기서

\; m = - \tfrac{b_1 - a_1}{b_2 - a_2}

,

\;x_0 = \tfrac{1}{2}(a_1 + b_1)\;

, 그리고

\;y_0 = \tfrac{1}{2}(a_2 + b_2)\;

이다.

2. 4. 수직이등분선의 응용

수직 이등분선은 탈레스 원의 중심, 삼각형의 방심 중심을 찾거나 보로노이 다이어그램의 경계를 구성하는 등 다양한 기하학적 문제를 해결하는 데 사용된다.

수직 이등분선 위의 각 점은 대상 선분의 양 끝점에서 같은 거리에 있다. 따라서 보로노이 다이어그램에서 영역의 경계선은 각 모점의 이등분선의 일부가 된다. (그림 1.)

3. 각의 이등분선

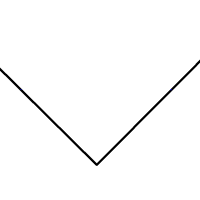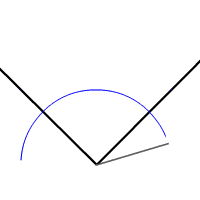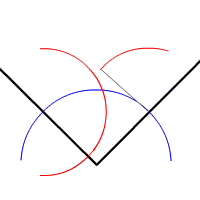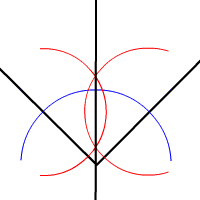
'''각의 이등분선'''은 각도를 같은 크기의 두 각으로 나누는 선이다. 각은 하나의 이등분선만 가진다.

각의 '내부 이등분선'(내각의 이등분)은 180° 미만의 각도를 두 개의 동일한 각도로 나누는 선, 반직선, 또는 선분이다. '외부 이등분선'(외각의 이등분)은 원래 각을 형성하는 한 변과 다른 변의 연장선으로 형성된 보각 (원래 각에서 180°를 뺀 값)을 두 개의 동일한 각도로 나누는 선이다.^[1]

자(도구)와 컴퍼스로 각을 이등분하려면, 꼭짓점을 중심으로 하는 원을 그린 후, 원이 각의 각 변에서 만나는 두 점을 중심으로 같은 크기의 원 두 개를 그린다. 이 두 원의 교차점(두 점)을 잇는 선이 각 이등분선이다.

이 구성의 정확성은 문제의 대칭에 의존하며 매우 직관적이다. 각의 삼등분 (각을 세 개의 동일한 부분으로 나누기)은 자와 컴퍼스만으로는 불가능하며, 이는 피에르 방첼이 처음 증명하였다.

3. 1. 각의 이등분선의 성질

'''각의 이등분선'''은 각도를 같은 크기의 두 각으로 나누는 선이다. 각은 하나의 이등분선만 가지며, 각의 이등분선 위의 모든 점은 각을 이루는 두 변에서 같은 거리에 있다.^[1]

각의 내부 이등분선과 외부 이등분선은 서로 수직이다.

자(도구)와 컴퍼스를 사용하여 각을 이등분하려면, 먼저 각의 꼭짓점을 중심으로 원을 그린다. 이 원은 각의 두 변과 각각 한 점에서 만나게 된다. 다음으로, 각 변과 원이 만나는 두 점을 중심으로 각각 같은 반지름의 원을 그린다. 이 두 원이 만나는 두 점을 지나는 직선이 바로 각의 이등분선이 된다.

3. 2. 각의 이등분선의 작도

자(도구)와 컴퍼스를 사용하여 각을 이등분하려면, 먼저 각의 꼭짓점을 중심으로 원을 그려 각의 두 변과 만나는 두 점을 찾는다. 이 두 점을 각각 중심으로 하고 반지름이 같은 두 원을 그리면, 두 원이 만나는 두 점을 지나는 직선이 각의 이등분선이 된다.^[1]

이 작도 방법은 문제의 대칭성에 기반하여 직관적으로 이해할 수 있다. 각의 삼등분은 자와 컴퍼스만으로는 불가능하며, 이는 피에르 방첼이 처음 증명하였다.

3. 3. 각의 이등분선의 방정식

두 직선의 방정식

l_1x+m_1y+n_1=0

과

l_2x+m_2y+n_2=0

으로 표현되는 각의 내부 및 외부 이등분선은 다음 두 방정식으로 주어진다.^[2]

:

\frac{l_1x+m_1y+n_1}{\sqrt{l_1^2+m_1^2}} = \pm \frac{l_2x+m_2y+n_2}{\sqrt{l_2^2+m_2^2}}.

3. 4. 각의 이등분선 정리

각의 이등분선 정리는 삼각형의 한 변이 반대 각을 이등분하는 선에 의해 나누어지는 두 선분의 상대적인 길이와 관련이 있다. 이 정리는 그들의 상대적인 길이를 삼각형의 다른 두 변의 상대적인 길이와 같다고 말한다.^[3]

삼각형의 변의 길이를

a,b,c

, 반둘레를

s=(a+b+c)/2

라 하고, A가 변

a

의 맞은편 각도라면, 각 A의 내각 이등분선의 길이는 다음과 같다.

:

\frac{2 \sqrt{bcs(s-a)}}{b+c},

또는 삼각법 용어로,^[4]

:

\frac{2bc}{b+c}\cos \frac{A}{2}.

삼각형 ABC에서 각 A의 내각 이등분선의 길이가

t_a

이고 이 이등분선이 A의 맞은편 변을 길이 ''m''과 ''n''의 두 부분으로 나눈다면,^[3]

:

t_a^2+mn = bc

여기서 ''b''와 ''c''는 꼭짓점 B와 C의 맞은편 변의 길이이고, A의 맞은편 변은 ''b'':''c''의 비율로 나뉜다.

각 A, B, C의 내각 이등분선의 길이가

t_a, t_b,

및

t_c

라면,^[5]

:

\frac{(b+c)^2}{bc}t_a^2+ \frac{(c+a)^2}{ca}t_b^2+\frac{(a+b)^2}{ab}t_c^2 = (a+b+c)^2.

두 개의 합동이 아닌 삼각형은 세 개의 내각 이등분선 길이의 동일한 집합을 공유하지 않는다.^[6]^[7]

4. 다각형의 이등분선

다각형의 변이나 각을 이등분하는 선에 대해 알아본다.

삼각형의 내각 이등분선은 내심에서 만나며, 외각 이등분선과 내각 이등분선도 한 점에서 만난다. 이와 관련된 점들은 특정 조건을 만족하면 한 직선 위에 존재한다.^[3] 삼각형의 중선은 꼭짓점과 마주보는 변의 중점을 연결하며 무게중심에서 만난다. 수직 이등분선은 변을 수직으로 이등분하며 외심에서 만난다.^[9]

사각형의 경우, 마주보는 변의 중점을 연결하는 두 선분은 각각 두 변을 이등분하며, "꼭짓점 무게중심"에서 만난다.^[10] 특히 마름모의 대각선은 서로 마주보는 각을 이등분한다.^[1]

4. 1. 삼각형

삼각형에서 두 외각의 이등분선과 다른 내각의 이등분선은 한 점에서 만난다.^[3]

각 외각 이등분선과 반대쪽 연장 변이 만나는 세 점은 공선점이다(서로 같은 선 위에 있다).^[3]

두 내각 이등분선과 반대쪽 변의 교점, 그리고 다른 외각 이등분선과 반대쪽 연장 변의 교점, 이렇게 세 교점은 한 직선 위에 있다.^[3]

4. 1. 1. 중선

삼각형의 세 중선은 각각 한 꼭짓점과 그 맞은편 변의 중점을 연결하는 선분이며, 그 변을 이등분한다. 세 중선은 무게중심이라는 한 점에서 만나는데, 이는 균일한 밀도를 가진 삼각형의 질량 중심이다. 따라서 삼각형의 무게중심과 꼭짓점을 지나는 모든 선은 맞은편 변을 이등분한다. 무게중심은 각 중선을 2:1로 나눈다.^[1]

4. 1. 2. 수직이등분선

삼각형 변의 내부에 있는 수직 이등분선은 그 변을 수직으로 이등분하는 선의 일부로, 삼각형 내부에 완전히 위치한다. 삼각형의 세 변의 수직 이등분선은 외심(세 꼭짓점을 지나는 원의 중심)에서 만난다.^[9] 따라서 삼각형의 외심을 지나고 한 변에 수직인 모든 선은 그 변을 이등분한다.

예각삼각형에서 외심은 두 개의 가장 짧은 변의 내부에 있는 수직 이등분선을 같은 비율로 나눈다. 둔각삼각형에서 두 개의 가장 짧은 변의 수직 이등분선 (외심까지 반대쪽 삼각형 변을 넘어 연장됨)은 각 교차하는 삼각형 변에 의해 같은 비율로 나뉜다.^[9]

임의의 삼각형에 대해, 내부에 있는 수직 이등분선은 ${\displaystyle p_{a}={\tfrac {2aT}{a^{2}+b^{2}-c^{2}}},}$ ${\displaystyle p_{b}={\tfrac {2bT}{a^{2}+b^{2}-c^{2}}},}$ 그리고 ${\displaystyle p_{c}={\tfrac {2cT}{a^{2}-b^{2}+c^{2}}},}$으로 주어지며, 여기서 변은 ${\displaystyle a\geq b\geq c}$이고 면적은 ${\displaystyle T.}$^[9]이다.

선분의 이등분선은 해당 선분의 중점을 통과한다. 특히 대상 선분과 수직으로 교차하는 경우, 해당 이등분선을 '''수직 이등분선'''이라고 한다. 수직 이등분선 위의 각 점은 대상 선분의 양쪽 끝점으로부터의 거리가 같다는 특징을 갖는다. 따라서, 보로노이 다이어그램에서 영역의 경계선은 각 모점의 이등분선의 일부가 된다.

수직 이등분선은 자와 컴퍼스로 작도할 수 있다. 선분의 양쪽 끝점을 중심으로 동일한 반지름의 원호를 그리고, 각 원호의 교점과 선분을 연결한다. 원호 위의 교점과 선분의 각 끝점에 의해 만들어지는 삼각형이 합동이므로, 원호 위의 교점을 연결하는 직선이 수직 이등분선이 된다.

브라마굽타의 정리에 따르면, 원에 내접하는 사각형의 대각선이 직각으로 교차하는 경우, 대각선의 교점에서 사각형의 한 변에 수선을 그어 만들어지는 직선은 해당 사각형의 대변을 이등분한다.

4. 2. 사각형

볼록 사각형의 마주보는 변의 중점을 연결하는 두 선분(이등분선)은 각각 두 변을 이등분한다. 두 이등분선과 대각선의 중점을 연결하는 선분은 "꼭짓점 무게중심"이라고 불리는 한 점에서 만나며, 이 점에 의해 모두 이등분된다.^[10]

4. 2. 1. 마름모

마름모의 각 대각선은 서로 마주보는 각을 이등분한다.^[1]

5. 면적 및 둘레 이등분선

평행사변형의 중점을 지나는 모든 직선은 넓이^[11]와 둘레를 이등분한다. 원 또는 타원의 중심을 지나는 모든 현은 면적과 둘레를 이등분하며, 원의 경우 이는 원의 지름이다.

5. 1. 삼각형

삼각형의 면적을 이등분하는 선은 무한히 많다. 그 중 세 개는 삼각형의 중선(변의 중점과 반대쪽 꼭짓점을 연결)이며, 이들은 삼각형의 무게중심에서 공점선이다. 실제로, 이들은 무게중심을 통과하는 유일한 면적 이등분선이다. 다른 세 개의 면적 이등분선은 삼각형의 변과 평행하며, 각각 다른 두 변과 교차하여 ratio|래시오^영어 1의 비율로 변을 분할한다.^[11] 이 여섯 개의 선은 세 개씩 공점선으로 만난다. 세 개의 중선이 공점선일 뿐만 아니라, 모든 중선은 두 개의 변과 평행한 면적 이등분선과 공점선이다.

무한히 많은 면적 이등분선의 포락선은 델토이드이다.^[11] 델토이드의 꼭짓점은 중선의 중점에 위치한다. 델토이드 내부의 모든 점은 세 개의 서로 다른 면적 이등분선 위에 있고, 외부의 모든 점은 단 하나의 면적 이등분선 위에 있다. 델토이드의 변은 삼각형의 연장된 변에 점근선인 쌍곡선의 호이다.^[11] 면적 이등분선의 포락선의 면적과 삼각형의 면적의 비율은 모든 삼각형에 대해 불변하며, 약 0.019860... (2% 미만)이다.

삼각형의 분할선은 삼각형의 둘레를 이등분하고 세 변 중 하나의 중점에 한 끝점을 갖는 선분이다. 세 개의 분할선은 스피커 원의 중심인 스피커 점에서 공점선이다. 이는 중심 삼각형의 내접원이다. 분할선은 각 이등분선과 평행하다.

5. 2. 평행사변형

평행사변형의 중점을 지나는 모든 직선은 넓이^[11]와 둘레를 이등분한다.

5. 3. 원과 타원

원 또는 타원의 중심을 지나는 모든 현은 면적과 둘레를 이등분한다. 원의 경우, 이는 원의 지름이다.

6. 대각선 이등분선

평행사변형의 대각선은 서로를 이등분한다.

6. 1. 평행사변형

평행사변형의 대각선은 서로를 이등분한다.

7. 부피 이등분선

사면체의 두 대변을 주어진 비율로 나누는 평면은 사면체의 부피도 같은 비율로 나눈다. 따라서 사면체의 이중 중앙선(마주보는 변의 중점을 연결하는 선)을 포함하는 모든 평면은 사면체의 부피를 이등분한다.^[13]^[14]

참조

_[1] 웹사이트 Exterior Angle Bisector http://mathworld.wol[...] Weisstein, Eric W.
_[2] 서적 Analytical Conics Dover Publications 2007
_[3] 서적 Advanced Euclidean Geometry Dover Publ. 2007
_[4] 논문 On the existence of triangles with given lengths of one side and two adjacent angle bisectors http://forumgeom.fau[...] 2004
_[5] 간행물 Mathematical Gazette 2009-03
_[6] 논문 The existence of a triangle with prescribed angle bisector lengths 1994
_[7] 웹사이트 A purely geometric proof of the uniqueness of a triangle with prescribed angle bisectors http://forumgeom.fau[...] 2008
_[8] 웹사이트 Quadrilateral http://mathworld.wol[...] Weisstein, Eric W.
_[9] 논문 Perpendicular Bisectors of Triangle Sides http://forumgeom.fau[...] 2013
_[10] 서적 College Geometry Dover Publ. 2007
_[11] 학술지 Halving a triangle 1972-05
_[12] 간행물 Triangle Equalizers 2010-04
_[13] 웹사이트 Tetrahedron http://mathworld.wol[...] Weisstein, Eric W.
_[14] 서적 The tetrahedron Chelsea 1979

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com