자전축의 세차운동

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

자전축의 세차운동은 지구 자전축이 팽이처럼 회전하는 현상으로, 태양과 달의 중력, 그리고 다른 천체들의 영향으로 발생한다. 이 운동은 약 25,772년의 주기를 가지며, 남극과 북극의 천구 극의 위치 변화, 춘분점 이동, 계절 변화 등 다양한 효과를 나타낸다. 자전축의 세차운동은 고대부터 관측되었으며, 히파르코스와 같은 천문학자들에 의해 연구되었다. 세차운동은 극점 항성의 변화를 가져오며, 춘분점의 이동은 별자리의 시대 변화를 초래한다. 세차운동의 원인은 지구의 적도 융기에 작용하는 태양과 달의 중력의 회전력이며, 그 값은 현대 천문학에서 정밀하게 계산되고 있다.

더 읽어볼만한 페이지

세차 운동 - 극운동
극운동은 지구 자전축의 불규칙한 운동으로 챈들러 요동, 연주기 진동, 불규칙적 표류로 구성되며 지구 핵-맨틀 운동, 해수면 재분포, 지각균형 재조정 등으로 발생하고 우주측지학 방법으로 관측되며 IERS에서 데이터를 제공한다.
세차 운동 - 자전축 기울기
자전축 기울기는 천체의 자전축이 궤도면에 수직인 방향에서 기울어진 각도로, 계절 변화와 기후에 영향을 미치며, 지구의 경우 황도 경사각이라고도 한다.

자전축의 세차운동
개요
현상	천체의 회전축 방향이 점진적으로 변하는 현상
원인	중력 조석력
관련 용어	장동 극운동
지구 자전축 세차운동
주기	약 26,000년
주요 영향	춘분점의 이동 별자리의 변화
현재 북극성	폴라리스
미래 북극성	베가 (약 11,000년 후)
설명	지구의 자전축이 팽이처럼 회전하면서 생기는 현상
관련 정보
서양 점성술	태양궁의 변화에 영향

2. 명칭

세차(歲差)라는 한자어는 지구에서 볼 때, 항성을 기준으로 한 하늘(항성년)과 절기를 만드는 태양을 기준으로 한 하늘(회귀년) 사이의 차이를 의미한다.^[45] 황도 좌표계에서 그 차이는 항성 황도대와 회귀 황도대 사이의 차이이다.^[46] 세차운동은 자전축이나 춘분점이 이동하는 현상을 일컫는 천문학 용어이다.^[47]

영어 단어 'precession'은 '먼저 오다'라는 뜻의 라틴어 ''praecedere''에서 유래했다. 지구에서 관찰되는 별들은 지구의 일주 운동 때문에 매일 동쪽에서 서쪽으로, 그리고 지구가 태양을 공전하기 때문에 매년 이동하는 것으로 보인다. 동시에 별들은 1년에 약 50각초의 속도로 이러한 움직임을 약간 앞지르는 것을 관찰할 수 있으며, 이는 "춘분점의 세차운동"으로 알려진 현상이다.

천문학자들은 이러한 운동을 설명할 때 일반적으로 이 용어를 단순히 "세차운동"으로 줄여서 사용한다. 물리학자들은 이 운동의 ''원인''을 설명할 때 "세차운동"이라는 용어를 사용해 왔는데, 이는 관찰 가능한 현상과 그 원인 사이의 혼란을 야기했다. 천문학에서 일부 세차운동은 실제적이고 다른 세차운동은 겉보기이기 때문에 이는 중요하다. 이 문제는 많은 천문학자들이 물리학자 또는 천체 물리학자라는 사실로 더욱 복잡해진다.

천문학에서 사용되는 "세차운동"이라는 용어는 일반적으로 관찰 가능한 춘분점의 세차운동(하늘을 가로질러 겉보기 역행 운동하는 별)을 설명하는 반면, 물리학에서 사용되는 "세차운동"이라는 용어는 일반적으로 기계적 과정을 설명한다.

3. 효과

지구 자전축의 세차운동은 여러 가지 관측 가능한 현상을 일으킨다.

첫째, 천구의 극이 움직인다. 현재 북극성인 폴라리스는 천구의 북극에 가깝지만, 세차운동으로 인해 시간이 지나면 다른 별이 북극성이 된다.^[42] 세페우스자리 감마는 약 3200년에 폴라리스를 이어 북극성이 될 것이다. 천구의 남극에는 현재 밝은 별이 없지만, 시간이 지나면 세차운동으로 인해 밝은 별이 남극성이 될 것이다.

둘째, 동지, 춘분 등 계절과 관련된 지구의 위치가 천천히 변한다.^[42] 세차운동의 효과 때문에 회귀년은 항성년보다 약 20분 더 짧다.

셋째, 춘분점이 황도를 따라 1년에 약 50.3 각초씩, 약 71.6년에 1도씩 서쪽으로 이동한다.^[42]

압세스(태양에 가장 가깝고 가장 멀리 접근하는 지점)와 달력 날짜(계절 표시)의 연간 주기의 일치는 20,000년의 허구적인 세차 운동 주기(지구의 실제 세차 운동 주기인 26,000년이 아님)의 네 개의 동일하게 간격을 둔 단계에서 나타난다. 계절 날짜는 북반구의 날짜이다. 허구적인 지구의 축의 기울기와 궤도의 이심률은 과장되어 있다. 근사 추정치. 표시된 단계에 대한 약한 행성 세차 운동의 효과는 무시된다.

3. 1. 천구 극의 이동

남쪽과 북쪽의 천구의 극은 공간에 고정된 항성 배경에 대하여 25,772 율리우스년(2000년 비율) 동안 한 번의 주기를 마치는 원을 그리며 이동하는 것으로 나타난다. 따라서, 오늘날 북극성인 폴라리스는 시간이 지남에 따라 변하게 될 것이며, 다른 항성이 북극성이 될 것이다.^[42] 대략 3200년에, 항성 세페우스자리 감마가 폴라리스에 이어 그 위치를 차지하게 될 것이다. 천구의 남극에는 현재 그 위치를 표시할 만한 밝은 행성이 없지만, 시간이 흐르면 세차 운동이 진행되어 밝은 항성을 남극성으로 만들 것이다. 천구의 극이 이동함에 따라서, 지구의 특정 위치에서 관측될 때 모든 별 시야의 외견상 방위에 있어서 상응하는 점진적인 이동이 있다.

3. 2. 계절 변화

지구의 자전축이 회전함에 따라 지구의 위치가 서서히 변한다.^[42] 예를 들어, 지구의 자전축 기울기가 태양을 가장 바로 향하고 있을 때, 지구의 궤도상 위치가 하지점을 나타낸다고 가정한다면, 한 차례의 완전한 주기 이후에 태양이 배경 항성을 기준으로 외견상 같은 위치에 복귀했을 때, 지구의 자전축 기울기는 태양을 가장 바로 향하고 있지 않다. 세차운동의 효과로 인하여, 그것이 약간 "뒤"에 있게 된다. 다른 한편으로는, 그 궤도 상의 하지점이 조금 이르게 나타난다. 그러므로, 계절의 주기를 (예를 들어, 하지부터 하지까지 또는 춘분부터 춘분까지를) 측정하는 회귀년은 항성에 대한 태양의 외견상 위치로 측정되는 항성년보다 약 20분 더 짧다.

3. 3. 춘분점 이동

춘분점은 황도를 따라 1년에 약 50.3 각초씩, 약 71.6년에 1도씩 서쪽으로 이동한다.^[42] 이러한 춘분점의 이동은 별자리의 시대 변화와 관련이 있다.

4. 역사

기원전 280년경 사모스의 아리스타르코스가 항성년과 회귀년의 값이 다르다는 논쟁의 여지가 있는 증거를 제시했지만, 일반적으로 세차운동의 발견은 로도스 또는 니케아의 그리스 천문학자 히파르코스(기원전 190~120년)의 업적으로 인정된다.^[48] 클라우디오스 프톨레마이오스의 ''알마게스트''에 따르면, 히파르코스는 스피카와 그 외의 밝은 항성들의 경도를 측정하고, 티모카리스(기원전 320~260년)와 아리스틸루스(기원전 ~280년)의 자료와 비교하여 스피카가 추분점에 대하여 2° 움직였다는 결론을 얻었다. 또한 회귀년과 항성년을 비교하여 근소한 차이를 발견했다. 히파르코스는 춘분점이 황도대를 통해 이동("세차운동")하며, 세차의 비율은 한 세기에 1° 보다 작지 않고, 36000년 보다 길지 않은 시간 안에 한 번의 완전한 주기를 완주한다는 결론을 내렸다.

히파르코스의 기록은 대부분 소실되었지만, 지구중심설에 따라 지구를 중심으로 천구가 공전하며 세차운동을 설명한 프톨레마이오스에 의해 언급되었다. 히파르코스는 프톨레마이오스와 마찬가지로 지구가 아닌 하늘이 움직인다는 지구중심설의 관점에서 세차운동을 생각했을 것으로 추정된다.

2세기의 프톨레마이오스는 히파르코스의 세차운동 연구를 이어나갔다. 그는 월식을 사용하지 않는 방법으로 레굴루스와 스피카 등의 밝은 항성들의 경도를 측정했다. 그는 히파르코스의 방식을 사용하고 달의 이동과 시차를 보정하여 계산했다.^[49] 프톨레마이오스는 자신의 관찰 결과와 히파르코스, 메넬라우스, 티모카리스, 아그리파의 값들을 비교했다. 그는 히파르코스와 자신의 시간 사이(약 265년)에 항성이 2°40', 즉 100년에 1°씩(1년에 36") 이동했음을 발견했는데, 이는 오늘날 밝혀진 비율인 1년에 약 50"(72년에 1°)와 차이가 있다. 그는 세차운동이 황도에 인접한 천체뿐만 아니라 모든 항성에 적용되며, 그 주기는 히파르코스가 계산한 값과 같은 36000년임을 확인했다.

히파르코스와 관계없이 세차운동을 발견했다는 다른 문화권들의 주장이 있지만, 일반적으로 옹호되지는 않는다.^[51] 알바타니에 따르면, 칼데아의 천문학자들은 회귀년과 항성년을 구별했으며, 기원전 330년경에 세차운동을 설명할 수 있는 위치에 있었을 것이라고 한다.

고대 이집트에서 히파르코스 시대 이전에 세차운동을 알고 있었다는 주장이 있지만, 논쟁의 여지가 있다. 카르나크 신전 단지의 일부 건물이 특정 항성이 뜨거나 지는 지점을 향해 건축되었고, 세차운동으로 인해 방향이 틀어지면 신전을 재건축했다는 주장이 있다.^[52] 그러나, 이러한 관찰이 이집트인들이 항성의 이동을 이해했다는 의미는 아니다. 하토르 신전의 항성 지도인 덴데라 황도대는 분점의 세차를 기록한 것으로 추정되기도 하지만,^[52] 고대 이집트인들이 세차운동을 알고 있었다 하더라도, 그 지식은 현재까지 남아있는 천문학 문헌에는 기록되어 있지 않다.

마이클 라이스는 고대 이집트인들이 밤하늘을 헌신적으로 관찰했기 때문에 세차운동의 효과를 간과할 수 없었을 것이라고 언급하며,^[53] 세차운동이 이집트 발전을 이해하는 기초가 된다고 보았다.^[53] 카를 구스타프 융에 따르면, 라이스는 기원전 제3천년기 (어쩌면 그 이전)에 이집트에서 매우 정밀한 천문 관찰이 이루어졌다는 증거가 명확하다고 주장한다.^[53]

메소아메리카의 장주기력이 세차운동에 대해 조정되었다는 추측이 있지만, 전문적인 마야 문명을 연구하는 학자들에게는 수용되지 않는다. 밀브레이스는 "플레이아데스를 포함하는 30,000년의 장주기년은 ... 춘분점의 세차운동을 계산하려는 노력이 되어왔을 수도 있다."고 전했다.^[55]

12세기 바스카라 2세는 《수리야싯단타》를 인용하여 세차운동과 관련된 값을 제시했다.^[56] 힌디어 주석서에 따르면, 세차 주기의 최종 값은 아야나의 회전수(+199669)와 삼파트의 회전수(-30000)를 더해 1칼파당 +169669로 계산된다. 문잘라는 아야나의 이동 주기를 21636년으로 보았는데, 이는 근일점 세차운동을 고려한 현대적 세차 값과 유사하다.^[57] 바스카라 2세는 삼파트의 주기를 144000년(1칼파에 30000번)으로 제시했다.^[57] 그는 아야나와 삼파트를 조합한 최종 용어를 명시하지 않았지만, 그가 제시한 값은 궤도상 근일점 세차를 고려한 세차운동을 계산한 것임을 보여준다.^[57]

우희(281~356)는 세차운동을 언급한 최초의 중국 천문학자이다. 그는 세차율을 50년에 1°로 추산했다.^[60]

중세 이슬람의 천문학에서, 마라게 천문대에서 편찬된 지즈이 일카니는 분점의 세차를 세 년당 51각초로 정했는데, 그 값은 현대의 값인 50.2각초와 매우 근접하다. 중세에, 이슬람과 라틴의 기독교 천문학자들은 그러한 "진동"을 세차가 더해지는 항성의 이동으로 간주했다. 니콜라우스 코페르니쿠스는 《천구의 회전에 관하여(''De revolutionibus orbium coelestium'')》(1543년)에서 세차를 지구 자전축의 이동의 결과로 확신한 최초의 문헌을 냈다.

한 세기가 지나고 세차운동은 아이작 뉴턴의 《자연철학의 수학적 원리(''Philosophiae Naturalis Principia Mathematica'')》(1687년)에서 중력의 결과라고 설명되었다.^[49]

4. 1. 헬레니즘 세계

히파르코스(기원전 190~120년)는 그리스의 천문학자로, 로도스 또는 니케아(이즈니크) 출신이며 일반적으로 세차운동의 발견자로 여겨진다. 프톨레마이오스의 ''알마게스트''에 따르면, 히파르코스는 스피카와 다른 밝은 별들의 경도를 측정했다. 그는 자신의 측정값을 선배 천문학자인 티모차리스(기원전 320~260년)와 아리스틸루스(기원전 ~280년)의 자료와 비교하여 스피카가 추분점에 대해 2° 이동했음을 알아냈다. 또한 절기년(태양이 분점으로 되돌아오는 데 걸리는 시간)과 항성년(태양이 고정된 별로 되돌아오는 데 걸리는 시간)의 길이를 비교하여 약간의 불일치를 발견했다. 히파르코스는 분점이 황도대를 통해 움직이고("세차운동"), 세차운동의 속도가 1세기 동안 1° 이상이며, 36,000년 이내에 완전한 주기를 완료한다고 결론 내렸다.^[6]

히파르코스의 거의 모든 저작은 세차운동에 관한 연구를 포함하여 유실되었다. 그의 저작은 프톨레마이오스에 의해 언급되었는데, 프톨레마이오스는 세차운동을 움직이지 않는 지구를 중심으로 하는 천구의 회전으로 설명했다. 히파르코스도 프톨레마이오스와 마찬가지로 세차운동을 지구의 움직임이 아닌 천체의 움직임으로, 즉 지구 중심설적인 관점에서 생각했다고 추정하는 것이 타당하다.

프톨레마이오스는 히파르코스의 연구를 이은 천문학자로 알려져 있다. 그는 레굴루스, 스피카 등 밝은 별들의 경도를 측정했는데, 월식 현상을 필요로 하지 않는 히파르코스의 달 방법의 변형을 사용했다. 그는 일몰 전에 달과 태양 사이의 경도 각도를 측정하고, 일몰 후에 달에서 별까지의 각도를 측정했다. 그는 히파르코스의 모델을 사용하여 태양의 경도를 계산하고, 달의 움직임과 시차에 대한 보정을 했다.^[7] 프톨레마이오스는 자신의 관측 결과를 히파르코스, 알렉산드리아의 메넬라오스, 티모차리스, 아그리파의 관측 결과와 비교했다. 그는 히파르코스의 시대와 자신의 시대 사이(약 265년)에 별들이 2°40', 즉 100년에 1°(1년에 36") 이동했다는 것을 발견했다(오늘날 받아들여지는 속도는 1년에 약 50" 또는 72년에 1°). 그러나 프톨레마이오스가 자신의 측정을 하는 대신 히파르코스의 수치를 단순히 신뢰했을 수도 있다. 그는 또한 세차 운동이 황도 근처의 별뿐만 아니라 모든 항성에도 영향을 미친다는 것을 확인했으며, 그의 주기는 히파르코스의 주기와 같은 36,000년이었다.^[6]

4. 1. 1. 히파르코스

기원전 2세기 그리스의 천문학자 히파르코스는 일반적으로 세차운동을 발견한 인물로 알려져 있다.^[48] 클라우디오스 프톨레마이오스의 ''알마게스트''에 따르면, 히파르코스는 스피카와 다른 밝은 별들의 경도를 측정했다. 그는 자신의 측정값을 티모카리스(기원전 320~260년)와 아리스틸루스(기원전 ~280년)의 자료와 비교하여 스피카가 추분점에 대해 2° 이동했음을 알아냈다. 또한 회귀년(태양이 춘분점으로 되돌아오는 데 걸리는 시간)과 항성년(태양이 고정된 별로 되돌아오는 데 걸리는 시간)의 길이를 비교하여 약간의 차이를 발견했다.^[6] 히파르코스는 춘분점이 황도대를 통해 이동("세차운동")하며, 세차의 비율은 한 세기에 1° 보다 작지 않다는, 즉 36000년 보다 길지 않은 시간 동안 한 번의 완전한 주기를 완주한다는 결론을 내렸다.

히파르코스의 기록은 세차운동에 대한 그의 업적을 포함해서 모두 소실되었다. 그의 기록은 지구중심설에 따라 정지한 지구를 중심으로 하는 천구의 공전으로 세차운동을 설명한 프톨레마이오스에 의해서 언급되었다.

히파르코스는 《지점과 분점의 이동에서(On the Displacement of the Solsticial and Equinoctial Points)》(알마게스트 3권 1장과 7권 2장에서 묘사됨)에서 그의 발견을 설명했다. 그는 월식 동안의 항성 스피카의 황도상 경도를 측정했고 그것이 추분점에서 서쪽으로 6° 쯤에 있음을 알았다. 그는 알렉산드리아의 티모카리스의 측정값과 자신의 것을 비교하여, 스피카의 경도가 약 150년 동안에 2°가량 감소했음을 알았다. 그는 다른 항성의 이동에도 주목했다. 그는 황도와 인접한 항성만이 시간이 흐르면서 이동한다고 추측했다.

히파르코스는 항성의 위치를 측정하는데 월식을 이용했다. 주야 평분점은 하늘에 표시되지 않았으므로, 그는 달을 참조점으로 사용했다. 히파르코스는 이미 어떤 순간의 태양의 경도를 계산할 수 있는 방법을 개발했었다. 달이 충에 있을 때, 보름달 동안에 월식이 일어난다. 식의 중간점 때에, 달은 태양으로부터 정확히 180°에 위치한다. 히파르코스는 그 때의 달로부터 스피카의 경도 차이를 측정했던 것이다. 그는 그 값에 달과의 경도 차인 180°를 더해서 계산된 태양의 경도값을 더했다. 그는 티모카리스의 자료와 같은 절차로 작업하지 않았다.^[49]

히파르코스는 《한 해의 길이(On the Length of the Year)》에서 세차운동을 연구하기도 했다. 회귀년은 지구로부터 보는 관점에서, 태양이 황도(천구의 항성들 사이에 있는 경로)를 따라 같은 위치로 복귀하는데 걸리는 시간의 길이이다. 항성년은 천구의 항성을 기준으로 태양이 같은 위치로 복귀하는데 걸리는 시간의 길이이다. 세차운동은 매년마다 항성의 경로를 약간씩 변하게 하므로, 항성년이 회귀년보다 길다. 히파르코스는 회귀년의 길이를 365+1/4−1/300일 또는 365.24667일로 계산했다.^[49] 그는 그 값을 항성년의 길이와 비교해서 세차의 비율을 1°보다 적지 않은 값으로 산정했다. 그 정보로부터 항성년의 값을 계산하면, 365+1/4+1/144일 또는 365.25694일 나온다.^[61]

그는 《윤달과 윤일에 대하여(On Intercalary Months and Days)》(현재 소실) 에 있는 메톤과 칼리포스의 달력을 수정하여 그의 회귀년과 근접한 태음태양력을 만들었는데, 그것은 프톨레마이오스에 의해 ''알마게스트'' 제3권 제1장에서 소개 되었다.^[62]

안티키테라 메커니즘에서 히파르코스의 수리적 특징을 확인할 수 있다. 그 메커니즘은 메톤 주기와, 칼리푸스 주기, 사로스 주기 그리고 엑셀리그모스 주기의 태양년을 기초로 한다. 안티키테라 메커니즘에 대한 연구는 고대인들이 하늘에서의 태양과 달의 이동에 관한 모든 위상에 기반하는 매우 정확한 달력을 사용하고 있었음을 증명한다.

4. 1. 2. 프톨레마이오스

프톨레마이오스는 히파르코스의 세차운동 연구를 이어나간 것으로 알려진 최초의 천문학자이다. 그는 월식을 이용하지 않고 레굴루스와 스피카 등 밝은 항성들의 경도를 측정했다.^[49] 일몰 전에 태양으로부터 멀어지는 달의 경도를 측정하고, 일몰 후에는 달부터 항성까지의 경도를 측정하는 방식이었다. 그는 히파르코스의 방식을 사용하여 태양의 경도를 계산하고 달의 이동과 시차를 보정했다.^[49]

프톨레마이오스는 자신의 관찰 결과를 히파르코스, 메넬라우스, 티모카리스, 아그리파의 값들과 비교했다. 그 결과 히파르코스와 자신의 시간 사이(약 265년)에 항성이 2°40', 즉 100년에 1° (1년에 36")씩 이동했음을 발견했다. 이는 오늘날 밝혀진 비율인 1년에 약 50"(72년에 1°)와 차이가 있다. 그는 세차운동이 황도에 인접한 천체 뿐만 아니라 모든 항성에 적용됨을 확인했으며, 그 주기는 히파르코스가 계산한 값과 같은 36,000년이었다.^[6]

4. 2. 기타 문화권

히파르코스 시대 이전에 고대 이집트에서 세차운동을 알고 있었다는 주장이 제기되었지만, 논란의 여지가 있다. 고대 이집트인들은 정확한 달력을 유지하고 사원 벽에 날짜를 기록했기 때문에 "대략적인" 세차율을 기록하는 것은 쉬운 일이었을 것이다.

덴데라의 하토르 사원 안에 있는 별자리 지도인 덴데라 황도대는 세차운동을 기록한 것으로 추정된다.^[10] 어쨌든, 고대 이집트인들이 세차운동을 알고 있었다면, 그들의 지식은 남아있는 천문학적 텍스트에 기록되어 있지 않다.

고대 이집트에 관한 대중적인 작가인 마이클 라이스는 고대 이집트인들이 세차운동을 관찰했음에 틀림없다고 썼으며,^[11] 이러한 인식이 그들의 문화에 심오한 영향을 미쳤다고 제안했다.^[12] 라이스는 이집트인들이 세차운동에 따라 연관된 별들의 위치 변화에 맞춰 사원의 방향을 재조정했다고 언급했다.^[13]

4. 2. 1. 바빌로니아

알바타니에 따르면, 칼데아의 천문학자들은 회귀년과 항성년을 구별했으며, 비록 부정확하지만 기원전 330년경에 이미 세차운동을 인지하고 있었을 것이라고 추정된다. 그러나 이러한 주장은 일반적으로 받아들여지지 않는다.^[51]

4. 2. 2. 고대 이집트

히파르코스 시대 이전에 고대 이집트에서 세차운동을 알고 있었다는 주장이 제기되었지만, 논쟁의 여지가 있다. 예를 들어, 카르나크 신전 단지의 일부 건물은 특정 항성이 뜨거나 지는 지점을 향해 건축되었고, 세차운동으로 인해 방향이 틀어지면 신전을 재건축했다는 주장이 있다.^[52] 그러나, 이러한 항성 정렬의 오차 관찰이 이집트인들이 항성이 황도를 따라 이동하는 것을 이해했다는 의미는 아니다. 그럼에도 불구하고, 그들은 정확한 달력을 보유하고 있었고, 신전 재건축 기간을 기록했다면 대략적인 세차운동 비율을 계산하는 것은 간단했을 것이다. 하토르 신전의 항성 지도인 덴데라 황도대는 분점의 세차를 기록한 것으로 추정되기도 한다.^[52] 그러나 고대 이집트인들이 세차운동에 대해 알고 있었다 하더라도, 그 지식은 현재까지 남아있는 천문학 문헌에는 기록되어 있지 않다.

마이클 라이스는 그의 저서 《이집트의 유산(Egypt's Legacy)》에서 고대인들이 세차운동의 역학을 알았는지는 불분명하지만, 밤하늘을 헌신적으로 관찰했기 때문에 그 효과를 간과할 수 없었을 것이라고 언급했다.^[53] 그는 세차운동이 이집트 발전을 이해하는 기초가 된다고 보았고,^[53] 심지어 국민국가로서의 이집트와 살아있는 신으로서의 이집트 왕은 이집트인들이 세차운동으로 인한 천체의 이동을 깨달은 결과라고 생각했다.^[53] 카를 구스타프 융에 따르면, 라이스는 기원전 제3천년기 (어쩌면 그 이전)에 이집트에서 매우 정밀한 천문 관찰이 이루어졌다는 증거가 명확하다고 주장한다.^[53] 라이스는 이집트인들이 세차운동으로 인해 항성의 위치가 이동하면 신전의 방향을 다시 조정했으며, 이러한 일이 새로운 왕조의 치세 동안 여러 차례 일어난 것으로 보인다고 언급했다.^[53]

로버트 보벌과 그레이엄 핸콕은 《창세의 수호신(Keeper of Genesis)》에서 고대 이집트의 기념물이 하늘의 지도로 기능했으며, 관련 제식은 천체의 사건에서 비롯된 현세의 활동이었다고 주장한다. 그들은 세차적 주기가 제프 테피("최초의 시간")로 알려진 먼 조상의 시대로 "되돌아 옴"을 상징하는 의식을 통해 기원전 10,500년경으로 계산했다.

4. 2. 3. 마야

메소아메리카의 장주기력이 세차운동에 대해 조정되었다는 추측이 있지만, 전문적인 마야 문명을 연구하는 학자들에게는 수용되지 않는다. 그러나, 밀브레이스는 "플레이아데스를 포함하는 30,000년의 장주기년은 ... 춘분점의 세차운동을 계산하려는 노력이 되어왔을 수도 있다."고 전했다.^[55]

4. 2. 4. 인도

바스카라 2세는 《수리야싯단타》를 인용하여 "43억 2천만 년의 1칼파 동안 삼파트는 30000번을 음회전하고, 아야나는 199669회 전진한다"고 기록했다.^[57] 힌디어 주석서에 따르면, 세차 주기의 최종 값은 아야나의 회전수(+199669)와 삼파트의 회전수(-30000)를 더해 1칼파당 +169669로 계산된다.^[57]

문잘라는 아야나의 이동 주기를 21636년으로 보았는데, 이는 근일점 세차운동을 고려한 현대적 세차 값과 유사하다.^[57] 바스카라 2세는 삼파트의 주기를 144000년(1칼파에 30000번)으로 제시했다.^[57] 그는 아야나와 삼파트를 조합한 최종 용어를 명시하지 않았지만, 그가 제시한 값은 궤도상 근일점 세차를 고려한 세차운동을 계산한 것임을 보여준다.^[57]

바스카라 2세는 《수리야싯단타》가 유효하지 않다고 언급했지만,^[58] 그의 설명은 다소 혼란스럽다.^[57] 그는 자신의 견해를 밝히지 않고, 《수리야싯단타》, 문잘라, 그리고 익명의 자료들을 인용했다.^[59]

1200년 이전 인도에는 세차운동에 대한 두 가지 이론, 즉 속도 유무와 관련된 이론 및 여러 세차운동 모델이 존재했다. 수리야 시단타에 묘사된 세차운동은 인도 달력에서 사용되는 별자리 시대인 아야남샤를 사용했다.^[14] ''수리야 시단타''의 춘분점은 별자리 시대를 기준으로 양쪽으로 27° 진동했으며, 주기는 54″/년 속도로 7200년이었다.^[15]^[16]

바라흐미히라는 세차운동을 한 방향으로 46°40′의 호를 그리고 시작점으로 돌아오는 것으로 설명했지만, 주기는 명시하지 않아 연간 속도는 알 수 없다.^[16]

여러 저자들은 세차운동을 4,320,000,000년의 칼파에서 약 200,000회전(60″/년)으로 묘사했다. 비스누찬드라는 189,411회전(56.8″/년), 바스카라 1세는 194,110회전(58.2″/년), 바스카라 2세는 199,699회전(59.9″/년)으로 제시했다.^[16]

4. 2. 5. 중국

우희(281~356)는 세차운동을 언급한 최초의 중국 천문학자이다. 그는 세차율을 50년에 1°로 추산했다.^[60]

4. 3. 중세와 르네상스

중세 이슬람의 천문학에서 세차 운동은 프톨레마이오스의 《알마게스트》를 기반으로 알려졌으며, 관측을 통해 그 값을 개선했다.

알바타니는 자신의 저서 《지즈 알 사비(Zij Al-Sabi)》에서 히파르코스의 세차 운동 계산과 프톨레마이오스의 100태양년에 1도의 값을 언급하며, 자신이 세차 운동을 측정하여 66태양년에 1도임을 발견했다고 말했다.^[18]

이후 알 수피는 자신의 《항성서》에서 프톨레마이오스의 세차 운동 값인 100태양년에 1도와 동일한 값을 언급했다. 그는 알 마문 치세 동안 만들어진 《지즈 알 뭄타한(Zij Al Mumtahan)》에서 66태양년에 1도라는 다른 값을 인용했다. 또한 알바타니의 《지즈 알 사비》에서 알바타니의 시대와 프톨레마이오스의 시대의 차이를 설명하기 위해 별의 좌표를 11도 10분으로 조정했다고 언급했다.^[19]

마라게 천문대에서 편찬된 《지즈-이 일칸(Zij-i Ilkhani)》는 춘분점의 세차 운동을 연간 51초로 정했는데, 이는 현대 값인 50.2초와 매우 가깝다.^[20]

중세 시대에 이슬람과 라틴 기독교 천문학자들은 "진동"을 세차 운동에 "추가해야" 하는 고정된 별의 운동으로 취급했다. 이 이론은 일반적으로 아랍 천문학자 타비트 이븐 쿠라의 것으로 여겨지지만, 현대에는 그 귀속에 이의가 제기되었다. 니콜라우스 코페르니쿠스는 《천체의 회전에 관하여》(1543)에서 진동에 대한 다른 설명을 발표했다. 이 저서는 세차 운동을 지구 축의 운동의 결과로 명확하게 언급한 최초의 사례이다. 코페르니쿠스는 세차 운동을 지구의 세 번째 운동으로 특징지었다.^[21]

4. 4. 현대

1세기 이상이 지난 후, 아이작 뉴턴은 프린키피아(1687)에서 세차 운동을 중력의 결과로 설명했다.^[22] 하지만, 뉴턴의 원래 세차 운동 방정식은 맞지 않아, 장 르 롱 달랑베르와 그 후의 과학자들에 의해 상당히 수정되었다.

5. 미트라교의 의문

미트라교 학자들 가운데 한 명인 데이빗 울란지는 미트라(''미트라스 솔 인빅투스'': 정복할 수 없는 태양)를 세차운동의 원인이 되는 제2의 태양이나 항성으로 해석했다.^[1] 그는 그 종교가 히파르코스의 세차운동 발견에 영감을 받아왔을 수도 있다고 제언했다.^[1] 그의 분석의 일부는 대부분의 미트라교 신전에서 발견되는 황소를 신성시하는 그 종교의 형상인 토럭터니에 근거한다.^[1] 울란지에 의하면, 토럭터니는 항성 차트이다.^[1] 미트라스는 두 번째 태양이나 초월-우주적 태양 그리고 또는 페르세우스자리 별자리이며, 황소는 황도대의 별자리인 황소자리이다.^[1] 보다 이른 점성술적 시대에는 태양이 황소자리에 있을 때가 춘분이었다.^[1] 그러한 이유로 토럭터니는 (춘분점에 기반하여 기원전 2000년경의 또는 추분점에 기인하면 기원전 11,500년경의) "황소자리의 시대" 을 끝마치는 미트라-페르세우스를 기념한다.^[1]

미트라교의 도상학은 황도대의 양 쪽에서 횃불을 든 두 명의 소년(카우테스와 카우토파테스)을 포함하기도 한다.^[1] 울란지와 월터 크루텐던은 그의 저서 《신화와 시간의 잃어버린 별(Lost Star of Myth and Time)》에서 그들이 우주적 세차의 근본 요소인 성장과 부패 또는 계몽과 무지의 시대를 의미한다고 해석했다.^[1] 그러므로, 미트라교는 대년(한 번의 완전한 분점의 세차운동을 뜻하는 플라톤식 기간)의 세차 주기 안에서 변화하는 시대와 관계있는 것을 지닌다고 여겨진다.^[1]

6. 극점 항성 변경

세차운동의 결과 중 하나는 극점 항성이 변경되는 것이다. 현재 지구의 북극을 가리키는 별은 폴라리스인데, 겉보기등급 2.1(변광성)로 적당히 밝고 천구의 북극에서 약 1도 떨어져 있어 북극성의 역할을 하기에 알맞다.^[64]

과거 기원전 3000년경 북극성은 용자리 용자리의 투반이었으나, 겉보기등급이 3.67로 폴라리스보다 훨씬 어두워 현대의 빛 공해가 심한 도시에서는 보기 어렵다. 거문고자리의 밝은 별 베가는 종종 최고의 북극성으로 꼽히기도 하는데, 기원전 12,000년경에 북극성이었고, 서기 14,000년경에 다시 북극성이 될 예정이지만, 천구의 북극에서 5° 이내로 접근하지는 않는다.^[42]

고유운동으로 인해, 폴라리스는 기원전 23,600년에는 현재보다 천구의 북극에 더 가까웠으며, 약 27,800년 후에 다시 북극성이 될 때는 현재보다 더 멀리 떨어져 있게 될 것이다.

현재 천구의 남극은 눈에 띄는 밝은 별이 없어 찾기 어렵다. 명목상 남극성은 팔분의자리 시그마인데, 겉보기등급이 5.5로 매우 어두워 이상적인 조건에서도 맨눈으로 보기 힘들다. 그러나 서기 80세기에서 90세기 사이에는 천구의 남극이 돛자리를 지나가면서 밝은 별들이 남극성이 될 것이다.

이러한 상황은 별자리 지도에서도 확인할 수 있다. 남극의 방향은 남십자자리 쪽으로 이동하고 있는데, 지난 2,000년 동안 남십자자리가 남극을 가리키는 역할을 해왔다. 그러나 고대 그리스 시대와 달리 현재는 아열대 북위도 지역에서 남십자자리를 관측하기 어려워졌다.

7. 극점의 이동과 분점의 이동

위의 그림들은 지구 자전축의 세차운동과 춘분점의 이동 사이의 관계를 설명한다. 이 그림들은 항성들의 실제 위치와는 상관 없이 지구에서 보는 그것들의 위치에 따라 그것들이 자리한 가상의 구(球)인 천구에서의 지구 자전축의 위치를 보여준다.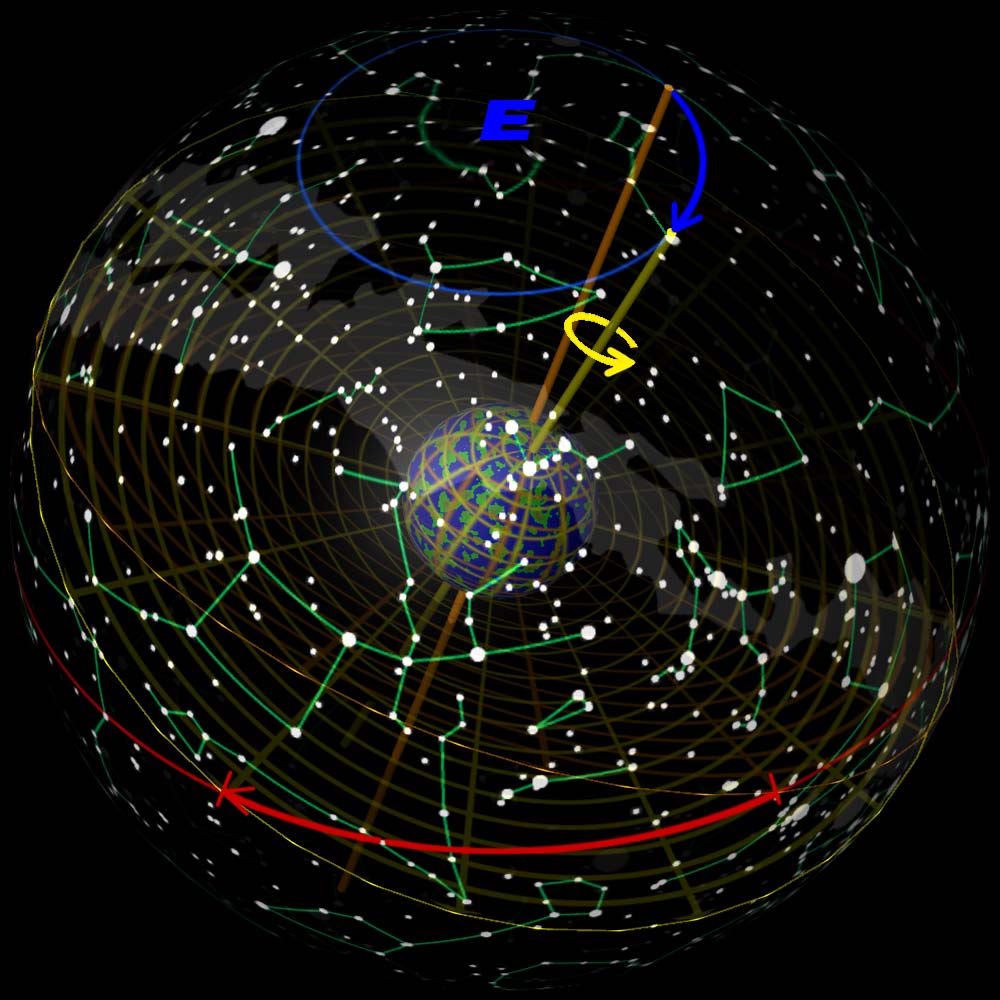

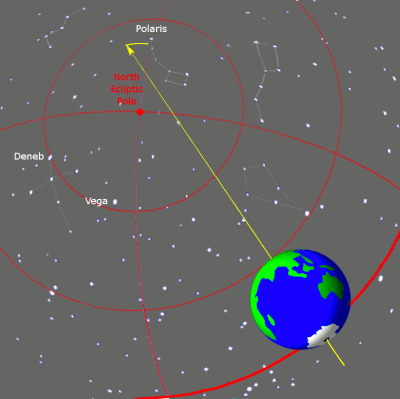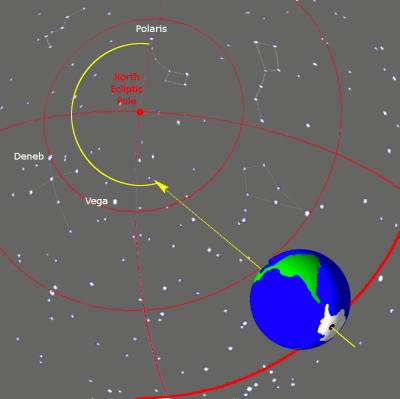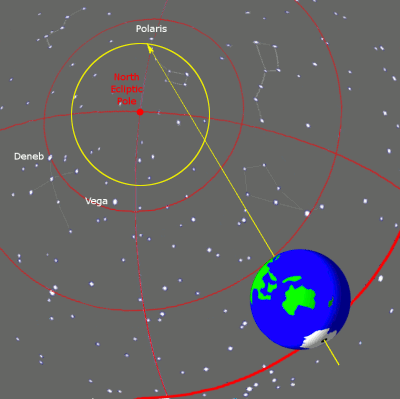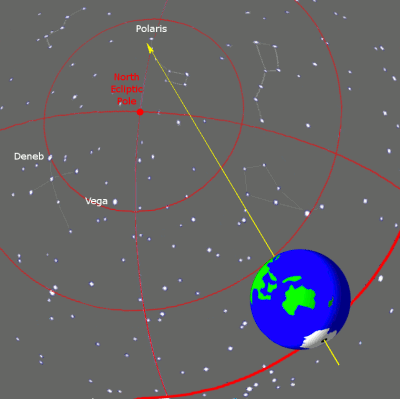
지구의 옆에서 보는 26,000년 세차운동의 원. 현재 북쪽의 극점 항성은 폴라리스(Polaris)이다. 약 8,000년 후에는 밝은 항성 데네브(Deneb)가 될 것이며, 약 12,000년에는 베가(Vega)가 될 것이다.

좌측 그림은 황도의 북극(파란색 E)을 중심으로, 황도경사각으로 알려진 약 23.4°의 각도 기울기를 가진, 항성들 사이에서의 25,700년의 한 주기 동안의 지구의 자전축이 묘사되어 있다. 세차운동의 방향은 지구의 일주운동 방향과는 반대이다. 주황색 축은 투반을 가리키고 있을 때인 5,000년 전의 지구 자전축이다. 폴라리스를 가리키고 있는 노란색 축은 현재의 자전축이다.

춘분점은 천구의 주야평분선이 황도(붉은선)를 가로지르는 데에서 나타나는데, 지구의 자전축이 태양과 지구를 연결하는 선과 수직을 이루는 곳이다. 자전축이 한 방향에서 다른 방향으로 세차운동할 때, (지구를 두르는 원형 격자로 표시되는) 지구의 적도면도 움직인다. 천구의 적도는 지구의 적도에서 천구로 투영되는데, 그러므로, 그것은 지구의 적도면과 동시에 움직이며, 황도와의 교차점도 마찬가지이다.

5,000년 전의 춘분점은 황소자리의 항성 알데바란에 가까웠다. 오늘날 춘분점은 (붉은색 화살표로 표시된 만큼) 물고기자리 성좌의 어딘가로 이동해오고 있다.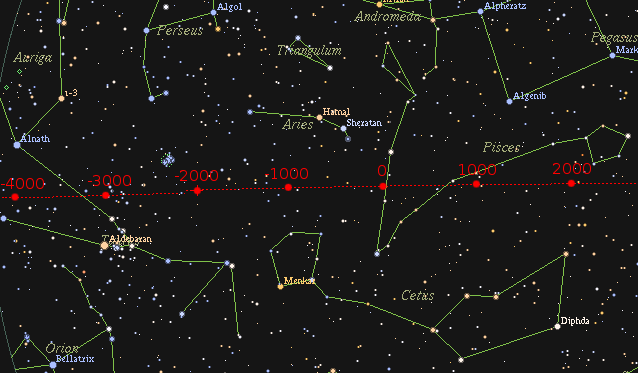

지난 6천년 동안의 항성들 사이에서 춘분점의 서쪽으로의 이동을 보여주는 그림

위의 그림들은 세차운동의 가변적 속도와 황도의 가변적 기울기, (현재 경도 174°.8764에 있는 축을 중심으로 하는 황도면의 느린 회전인) 행성 세차 그리고 항성의 고유 운동이 계산에 포함되지 않은 근사치일 뿐이다.

8. 원인

지구 세차운동의 원인은 태양과 달의 중력, 그리고 다른 천체들의 영향 때문이다. 이는 아이작 뉴턴 경이 처음으로 설명했다.^[66]

자전축 세차운동은 팽이의 세차운동과 유사하다. 두 경우 모두 중력이 작용한다. 팽이는 힘이 회전축과 거의 평행하게 작용하는 경향이 있지만, 지구는 태양과 달의 중력이 자전축에 거의 수직으로 작용한다.

지구는 완전한 구체가 아닌 편구체로, 적도 지름이 극 지름보다 약 43km 더 크다. 지구의 자전축 기울기 때문에 한 해의 대부분 동안 태양에 가까운 쪽은 북쪽이나 남쪽으로 중심에서 벗어나 있고, 먼 쪽은 반대쪽으로 벗어나 있다. 중력은 거리에 따라 감소하므로, 가까운 쪽에 더 강한 중력이 작용하여 태양이 지구의 한쪽 면을 더 강하게 끌어당긴다. 이로 인해 지구에 작은 회전력(토크)이 발생하며, 이 회전력의 축은 지구 자전축과 거의 수직이다. 만약 지구가 완전한 구체였다면 세차운동은 일어나지 않았을 것이다.

이러한 평균 회전력은 황도 극에서 기울어진 자전축 방향에 수직으로 작용하므로, 자전축 기울기 자체는 변하지 않는다. 태양(또는 달)으로부터의 회전력 크기는 지구 자전축에 대한 중력 작용 방향에 따라 달라지며, 그 각도가 직각에 가까울수록 0에 가까워진다.

위 설명은 태양을 중심으로 설명했지만, 황도를 따라 움직이는 대부분의 천체, 특히 달에게도 같다. 태양과 달의 결합된 작용은 일월세차라고 불린다. 이들은 위치 변화로 인해 안정된 점진적 이동(약 25,700년에 한 번의 완전한 주기) 외에도 간헐적인 작은 변화를 야기한다. 세차 속도와 자전축에서의 그러한 진동은 장동으로 알려져 있다. 가장 중요한 기간은 18.6년이며 20각초 이하의 진폭이다.

일월세차 외에도 태양계의 다른 행성들의 작용은 황도 전체를 현재 황경에서 측정된 약 174°에 있는 축을 중심으로 느리게 회전하게 만든다. 행성 세차라고 불리는 이 현상은 황도면을 1년에 0.47 각초(일월 세차보다 약 5백 배 더 작은)만큼씩 움직이게 한다. 이 두 세차운동의 합은 일반세차로 알려져 있다.

9. 방정식

지구에 미치는 기조력은 역제곱 법칙에 따라 계산되며, 섭동을 일으키는 천체(태양, 달, 행성)가 지구에서 가까운 쪽에 더 큰 중력을 미치기 때문에 발생한다. 지구 중심에 작용하는 섭동 천체의 중력을 지구 표면 전체에 작용하는 중력에서 빼면 기조력만 남는다. 이 기조력은 지구의 적도 융기에 작용하는 두 가지 힘으로 나타나는데, 이 힘들은 우력으로 분해되어 황도면에 대한 지구 자전축에 회전력 벡터를 생성한다.^[67]^[68]

이 회전력 벡터는 다음과 같이 표현된다.^[32]^[33]

: $\overrightarrow{T} = \frac{3Gm}{r^3}(C-A)\sin\delta\cos\delta\begin{pmatrix}\sin\alpha\\-\cos\alpha\\0\end{pmatrix}$

여기서,

''Gm''은 섭동 천체의 표준 중력 매개변수
''r''은 섭동 천체까지의 지구 중심 거리
''C''는 지구 자전축의 관성 모멘트
''A''는 지구 적도 지름의 관성 모멘트
''C'' - ''A''는 지구 적도 융기의 관성 모멘트 (''C'' > ''A'')
''δ''는 섭동 천체의 적위 (적도 북쪽 또는 남쪽)
''α''는 섭동 천체의 적경 (춘분점에서 동쪽)

지구 중심에서의 회전력에 대한 세 방향 단위 벡터는 '''x'''(황도면 내 춘분점 방향), '''y'''(황도면 내 하지점 방향), '''z'''(황도 북극 방향)이다.

태양에 대한 '''x''' 방향의 값은 사인 제곱 파형으로, 분점에서 0, 지점에서 최대 0.36495이다. '''y''' 방향의 값은 사인파로, 분점과 지점에서 0, 그 사이에서 최대 ±0.19364이다. 두 파형은 주기와 진폭이 비슷하다. '''z''' 방향 값은 0이다.

'''y''' 방향의 평균 회전력은 0이므로 세차 운동에 영향을 주지 않는다. 태양에 대한 '''x''' 방향의 평균 회전력은 다음과 같다.^[34]

:

T_x = \frac{3}{2}\frac{Gm}{a^3 (1-e^2)^{3/2}}(C-A)\sin\epsilon\cos\epsilon

여기서,

$a$ 는 지구 또는 달의 궤도 긴반지름
''e''는 지구 또는 달의 궤도 이심률
$\epsilon\,\!$ 은 적도면과 황도면 사이의 각도 (태양에 대한 ''δ''의 최대값, 달에 대한 평균 최대값)

세차 운동은 다음 식으로 계산된다.^[33]

:

\frac{d\psi}{dt} = \frac{T_x}{C\omega\sin\epsilon}

여기서 ''ω''는 지구의 각속도, ''Cω''는 지구의 각운동량이다. 따라서 태양에 의한 세차 운동의 1차 성분은 다음과 같다.^[33]

:

\frac{d\psi_S}{dt} = \frac{3}{2}\left[\frac{Gm}{a^3 (1-e^2)^{3/2}}\right]_S\left[\frac{(C-A)}{C}\frac{\cos\epsilon}{\omega}\right]_E

달에 의한 세차 운동은 다음과 같다.

:

\frac{d\psi_L}{dt} = \frac{3}{2}\left[\frac{Gm(1-1.5\sin^2 i)}{a^3 (1-e^2)^{3/2}}\right]_L\left[\frac{(C-A)}{C}\frac{\cos\epsilon}{\omega}\right]_E

여기서 ''i''는 달 궤도면과 황도면 사이의 각도이다. 태양, 달, 지구의 매개변수는 각각 S, L, E로 표시된 대괄호 안에 있다.

(1-1.5\sin^2 i)

는 황도에 대한 달 궤도 경사를 나타낸다. ''(C−A)/C''는 지구의 동역학적 타원율 또는 편평도이며, 지구 내부 구조가 명확하지 않아 관측된 세차에 맞춰 조정된다. 지구가 균질하다면, 이 값은 세 번째 제곱된 이심률과 같다.^[35]

:

e''^2 = \frac{\mathrm{a}^2 - \mathrm{c}^2}{\mathrm{a}^2 + \mathrm{c}^2}

여기서 a는 적도 반지름(6378137m), c는 극 반지름(6356752m)이며, 이다.

J2000.0에 대한 매개변수는 다음과 같다.^[36]^[37]

태양	달	지구
GM = 1.3271244E	GM = 4.902799E	(C − A)/C = 0.003273763
a = 1.4959802E	a = 3.833978E	ω = 7.292115E
e = 0.016708634	e = 0.05554553	$\epsilon\,\!$ = 23.43928°
	i = 5.156690°

이를 통해 계산된 태양과 달에 의한 세차 운동은 다음과 같다.

''dψ_S/dt'' = 2.450183E
''dψ_L/dt'' = 5.334529E

이 값들을 각초/년("/a)으로 변환하면 다음과 같다.

''dψ_S/dt'' = 15.948788″/a (윌리엄스의 값 15.948870″/a와 유사)^[33]
''dψ_L/dt'' = 34.723638″/a (윌리엄스의 값 34.457698″/a와 유사)

태양 방정식은 지구 궤도가 타원에 가깝기 때문에 비교적 정확하지만, 달 방정식은 달 궤도가 태양에 의해 크게 왜곡되어 정확도가 떨어진다.

10. 값

사이먼 뉴컴은 19세기 말 경도상의 일반세차(''p'')를 1회귀년 당 5,025.64각초로 계산했으며, 이는 인공위성의 더 정확한 관측 결과와 전자계산기의 정교한 모형이 나오기 전까지 널리 사용되었다. 1976년 제이 헨리 리스케는 ''p''값이 율리우스력의 1세기 당 5,029.0966 각초라는 개선된 이론을 제시했다. 초장기선 간섭 관측법(VLBI)과 달 레이저 거리 측정실험(LLR)과 같은 현대 기술은 더 정밀한 관측을 가능하게 했고, 국제천문연맹은 2000년에 세차운동에 대한 새로운 상수값을, 2003년과 2006년에 새로운 계산 기법과 다항식 표현을 채택했다.

누적된 세차운동 값은 다음과 같다.^[73]

:''p_A'' = 5,028.796195×''T'' + 1.1054348×''T''² + 섭동항

여기서 ''T''는 J2000 이후 율리우스 세기(36,525일)로 측정한 시간이다.

세차의 비율은 위 식의 도함수로 다음과 같다.:

:''p'' = 5,028.796195 + 2.2108696×''T'' + 섭동항

이 속도의 상수항(5,028.796195)은 25,772년의 한 번의 완전한 세차 주기에 해당한다.

세차운동의 비율은 일정하지 않고, ''T''의 일차항과 섭동항으로 표시되는 시간 동안 천천히 증가한다. 이 공식은 제한된 기간 동안만 유효하며, ''T''가 충분히 커지면 ''T''²항이 우세해져 ''p''값은 매우 커진다. 태양계의 수치모델에 대한 정교한 계산은 세차값의 상수들이 황도의 경사각과 같은 41,000년의 주기임을 보여준다.

''p'' = ''a'' + ''b'' sin (2π''T''/''P'') (여기서 ''P''는 410세기의 기간)

이론적 모델은 ''T''의 섭동력에 상응하는 타당한 정수(계수)들을 계산할 수 있지만, (제한된) 다항식을 간헐적인 함수와 일치시키는 것은 불가능하므로, 위와 같은 어림셈에서 발생하는 오류는 ''T'' 값의 증가 범위 없이 늘어나게 된다. 국제천문연맹은 최고로 발전된 가용 이론을 선택했으며, 수세기 동안의 과거와 미래에 관한 모든 공식은 큰 오차를 보이지 않지만, 수천년 동안의 과거와 미래에 대해서는 다소 정확성을 가지며, 그 이상의 연대에 대해서는 불일치가 매우 크다.

세차운동은 조수의 변속으로 인해 5억년 동안 59"/a에서 45"/a(년=율리우스년)로 장기간 감소한다. 단기간(수만년)의 변동이 평균내어진 이후, 장기간의 변동은 다음 다항식에 가깝다. (''T''는 율리우스년 십억년(Ga)):^[74]

:''p''^- = 50.475838 − 26.368583''T'' + 21.890862''T''²

:''p''⁺ = 50.475838 − 27.000654''T'' + 15.603265''T''²

세차값은 ''p''⁺보다 +0.135052"/a의 작은 값만큼 더 클 것이다.

워드에 따르면, 약 15억년 후 달과의 거리가 현재의 60.3 지구 반경에서 66.5 지구 반경으로 멀어지면, 행성의 작용으로부터 비롯된 공진은 세차를 49,000년으로 밀려있게 하고, 약 20억년경에 달과의 거리가 68 지구반경이 될 때는 69,000년이 밀려있을 것이다.

참조

_[1] 서적 World of earth science Thomson-Gale 2003
_[2] 간행물 "Celestial Reference Systems" in Seidelmann, P.K. (ed.) ''Explanatory Supplement to the Astronomical Almanac'' University Science Books
_[3] 웹사이트 Astro 101 – Precession of the Equinox http://www.wwu.edu/d[...] 2009-01-02
_[4] 서적 Practical and Spherical Astronomy https://archive.org/[...] Cambridge 1863
_[5] 웹사이트 IAU 2006 Resolution B1: Adoption of the P03 Precession Theory and Definition of the Ecliptic http://www.iau.org/s[...] 2009-02-28
_[6] 서적 Ptolemy's Almagest Princeton University Press
_[7] 문서
_[8] 논문 The Alleged Babylonian Discovery of the Precession of the Equinoxes
_[9] 문서 "Just How Precise is Maya Astronomy?" https://web.archive.[...] 2007-12
_[10] 문서
_[11] 문서 Egypt's Legacy
_[12] 문서
_[13] 문서
_[14] 서적 Report of the Calendar Reform Committee https://dspace.gipe.[...] Council of Scientific and Industrial Research
_[15] 서적 Translation of Surya Siddhanta: A Textbook of Hindu Astronomy https://archive.org/[...] University of Calcutta
_[16] 논문 Precession and trepidation in Indian astronomy before A.D. 1200
_[17] 문서
_[18] 웹사이트 Zij Al-Sabi' http://shamela.ws/br[...] 2017-09-30
_[19] 웹사이트 Book of Fixed Stars https://www.wdl.org/[...]
_[20] 논문 The Influence of Islamic Astronomy in Europe and the Far East 1939-05
_[21] 서적 The Edge of Objectivity: An Essay in the History of Scientific Ideas https://archive.org/[...] Princeton University Press
_[22] 문서
_[23] 문서
_[24] 문서
_[25] 문서
_[26] 문서
_[27] 웹사이트 HIP 11767 http://webviz.u-stra[...] 2011-03-01
_[28] 뉴스 Kochab http://stardate.org/[...] University of Texas McDonald Observatory 2015-06-14
_[29] Reprint The Ever-Changing Sky: A guide to the celestial sphere https://books.google[...] Cambridge University Press
_[30] 웹사이트 precession of the equinoxes | Infoplease https://www.infoplea[...]
_[31] 웹사이트 Basics of Space Flight, Chapter 2 http://www2.jpl.nasa[...] Jet Propulsion Laboratory/NASA 2013-10-29
_[32] 간행물 Spherical and practical astronomy as applied to geodesy Frederick Unger
_[33] 논문 Contribution to the Earth's Obliquity Rate, Precession, and Nutation https://articles.ads[...]
_[34] 논문 "Precession of a planet with a satellite"
_[35] 서적 Mathematical tracts on the lunar and planetary theories, the figure of the earth, precession and nutation, the calculus of variations, and the undulatory theory of optics https://archive.org/[...] 1842
_[36] 논문 Numerical expressions for precession formulae and mean elements for the Moon and the planets
_[37] 간행물 IERS Technical Note 13 – IERS Standards (1992) http://ilrs.gsfc.nas[...]
_[38] 간행물 N. Capitaine et al. 2003 http://syrte.obspm.f[...]
_[39] 논문 A long-term numerical solution for the insolation quantities of the Earth
_[40] 논문 Comments on the long-term stability of the earth's obliquity
_[41] 서적 Celestial Reference Systems University Science Books
_[42] 웹사이트 Astro 101 – Precession of the Equinox http://www.wwu.edu/d[...] 2013-02-27
_[43] 서적 Practical and Spherical Astronomy http://books.google.[...] Cambridge
_[44] 웹인용 IAU 2006 Resolution B1: Adoption of the P03 Precession Theory and Definition of the Ecliptic http://www.iau.org/s[...] 2013-03-04
_[45] 웹인용 세차(歲差) http://db.itkc.or.kr[...] 한국고전번역원 2013-02-08
_[46] 웹사이트 ayanamsa http://en.mimi.hu/as[...]
_[47] 웹인용 세차운동 http://astro.kasi.re[...] 천문우주지식정보(KASI) 2013-02-09
_[48] 간행물 Continued fraction decipherment: the Aristarchan ancestry of Hipparchos' yearlength & precession http://www.dioi.org/[...]
_[49] 서적 The History and Practice of Ancient Astronomy http://books.google.[...] Oxford University Press 1998-10-01
_[50] 서적 History of the planetary systems from Thales to Kepler A history of astrono[...] Dover Publications
_[51] 간행물 The Alleged Babylonian Discovery of the Precession of the Equinoxes 1950-01-01
_[52] 서적 Secrets of the Great Pyramid
_[53] 서적 Egypt's Legacy: The Archetypes of Western Civilization 3000-30 Bc http://books.google.[...]
_[54] 서적 The Prehistory of Egypt: From the First Egyptians to the First Kings Blackwell Publishers
_[55] 간행물 Just How Precise is Maya Astronomy? http://www.institute[...] 2007-12-01
_[56] 문서 Siddhānta-shiromani, Golādhyāya, section-VI, verses 17–19
_[57] 문서 Translation of the Surya Siddhānta by Pundit Bāpu Deva Sāstri and of the Siddhānta Siromani by the Late Lancelot Wilkinson revised by Pundit Bāpu Deva Sāstri, printed by C B Lewis at Baptist Mission Press, Calcutta, 1861; Siddhānta Shiromani Hindi commentary by Pt Satyadeva Sharmā, Chowkhambā Surbhārati Prakāshan, Varanasi, India.
_[58] 문서 Vāsanābhāshya commentary Siddhānta Shiromani (published by Chowkhamba)
_[59] 문서 cf. Suryasiddhanta, commentary by E. Burgess, ch.iii, verses 9-12.
_[60] 서적 A History of Astronomy http://books.google.[...]
_[61] 서적 Dictionary of Scientific Biography의 "Hipparchus"
_[62] 서적 Ptolemy's Almagest http://books.google.[...] Springer-Verlag
_[63] 저널 New precession expressions, valid for long time intervals https://www.aanda.or[...] 2011-10-01
_[64] 웹인용 HIP 11767 http://webviz.u-stra[...] 2011-03-01
_[65] 서적 The ever-changing sky: a guide to the celestial sphere http://books.google.[...] Cambridge University Press
_[66] 웹사이트 The Columbia Electronic Encyclopedia, 6th ed., 2007 http://www.infopleas[...]
_[67] 서적 Spherical and practical astronomy as applied to geodesy Frederick Unger
_[68] 간행물 Contributions to the Earth's obliquity rate, precession, and nutation http://adsabs.harvar[...]
_[69] 간행물 Precession of a planet with a satellite
_[70] 서적 Mathematical tracts on the lunar and planetary theories, the figure of the earth, precession and nutation, the calculus of variations, and the undulatory theory of optics http://books.google.[...]
_[71] 논문 Numerical expressions for precession formulae and mean elements for the Moon and the planets http://adsabs.harvar[...] 1994
_[72] 간행물 IERS Technical Note 13 – IERS Standards (1992) http://ilrs.gsfc.nas[...]
_[73] 논문 Expressions for IAU 2000 precession quantities http://syrte.obspm.f[...] 2003
_[74] 논문 A long-term numerical solution for the insolation quantities of the Earth http://www.aanda.org[...] 2004

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com