베셀 함수
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
베셀 함수는 특정 형태의 상미분 방정식인 베셀 방정식을 만족하는 함수들의 총칭이다. 이 방정식은 다양한 물리적 현상을 모델링하는 데 사용되며, 특히 원통 좌표계나 구면 좌표계에서 파동 전파 및 정적 전위 문제를 해결하는 데 중요한 역할을 한다. 베셀 함수에는 제1종 및 제2종 베셀 함수, 변형 베셀 함수, 한켈 함수, 구면 베셀 함수 등 여러 종류가 있으며, 각기 다른 형태와 성질을 가진다. 베셀 함수는 전자기파, 열전도, 진동, 양자역학, 신호 처리 등 다양한 분야에 응용된다.
더 읽어볼만한 페이지
- 특수 초기하함수 - 지수 함수
지수 함수는 양의 상수 *a*를 밑으로 하는 *y = ax* 형태의 함수이며, 특히 자연로그의 역함수인 *ex*는 다양한 정의와 응용을 가지며 복소수로 확장될 수 있다. - 특수 초기하함수 - 르장드르 다항식
르장드르 다항식은 르장드르 미분 방정식의 해로 정의되는 직교 다항식 계열로, 생성 함수, 로드리게스 공식, 또는 점화식을 통해 정의될 수 있으며, 물리학, 공학, 수치해석 등 다양한 분야에서 응용된다. - 푸리에 해석학 - 라플라스 변환
라플라스 변환은 함수 f(t)를 복소수 s를 사용하여 적분을 통해 다른 함수 F(s)로 변환하는 적분 변환이며, 선형성을 가지고 미분방정식 풀이 등 공학 분야에서 널리 사용된다. - 푸리에 해석학 - 푸리에 변환
푸리에 변환은 복소 함수를 주파수 성분으로 분해하는 적분 변환으로, 푸리에 급수의 확장 개념이며, 시간-주파수 영역 변환, 선형성, 컨볼루션 정리, 불확정성 원리 등의 성질을 가지며 다양한 분야에 활용된다. - 특수 함수 - 람베르트 W 함수
람베르트 W 함수는 we^w = z를 만족하는 w를 찾는 람베르트 이름을 딴 역함수 관계를 가지며, 여러 분야에서 지수 함수 방정식을 푸는 데 응용되는 무한히 많은 가지를 가진 함수이다. - 특수 함수 - 감마 함수
감마 함수는 양의 실수부를 갖는 복소수 z에 대해 오일러 적분으로 정의되고 해석적 연속을 통해 복소평면 전체로 확장된 팩토리얼 함수의 일반화로서, 수학, 물리학, 공학 등 다양한 분야에서 활용되며 여러 표현과 성질을 가진다.
2. 정의
베셀 함수는 다음과 같은 상미분 방정식으로 표현되는 함수이다.
:
여기서 는 임의의 복소수이며, 이 방정식을 차수의 '''베셀 방정식'''(Bessel equation영어)이라고 한다.
베셀 방정식은 2차 상미분 방정식이므로, 선형 독립인 두 해를 가진다. 일반해는 다음과 같다.
:
여기서 c1, c2는 임의의 상수, 는 제1종 베셀 함수, 는 제2종 베셀 함수이다.
상황에 따라 다양한 표현이 사용되며, 대표적인 해는 아래 표와 같다.
제2종 베셀 함수와 제2종 구면 베셀 함수는 때때로 및 대신 , 으로 표시된다.[2][17]
2. 1. 베셀 방정식 유도
베셀 방정식은 2차원 헬름홀츠 방정식:
을 극좌표계에서 변수분리하면서 등장한다.
먼저 헬름홀츠 방정식은 선형이므로 를 극좌표 에 대해
:
와 같이 변수분리할 수 있는데, 는 극좌표계 상에서 각도를 나타내므로 는 360° 회전변환에 불변하는 형태인
: 또는 ()
가 되고, 이를 헬름홀츠 방정식에 대입할 시 라플라스 연산자가 극좌표계에서
:
로 나타남에 따라 다음과 같은 베셀 방정식을 얻는다.
:
3. 베셀 함수의 종류
베셀 방정식의 해는 일반적으로 두 가지 종류로 나뉜다.
제2종 베셀 함수와 제2종 구면 베셀 함수는 때때로 및 대신 각각 및 으로 표시되기도 한다.[2][17]
3. 1. 제1종 베셀 함수 (Jα)
α가 임의의 복소수일 때, 베셀 방정식을 통해 나타나는 가장 기본적인 해를 '''제1종 베셀 함수''' Jα(x)라고 하며 다음과 같이 정의한다.[3]:
여기서 임의의 복소수에 대한 계승 를 의미한다. (는 감마 함수이다.)
만약 α가 정수가 아니라면, Jα(x)와 J-α(x)는 선형 독립이면서 베셀 방정식의 해가 된다. 따라서
:
(여기서 c1, c2는 상수)는 α가 정수가 아닐 때의 베셀 방정식의 일반해가 된다.
n이 정수인 베셀 함수에 대해선 다음과 같이 적분 표현을 사용해서 베셀 함수를 나타낼 수 있다.
:
이 형태는 프리드리히 베셀이 사용했던 접근법이며, 여기서 다른 몇몇 성질들을 유도해냈다.
또 다른 적분 형태의 정의로는 다음이 있다.
:

베셀 함수는 다음과 같이 일반화된 초기하 급수로 표현할 수 있다.[13]
:
이 식은 베셀 함수를 베셀-클리포드 함수로 전개하는 것과 관련이 있다.
라게르 다항식 Lk와 임의로 선택된 매개변수 t를 사용하여 베셀 함수는 다음과 같이 표현할 수 있다.[14]
:
3. 1. 1. 제1종 베셀 함수의 성질
제1종 베셀 함수(Bessel function of the first kind)는 다음과 같은 여러 가지 중요한 성질을 가진다.- (α가 정수일 때만 정의됨)
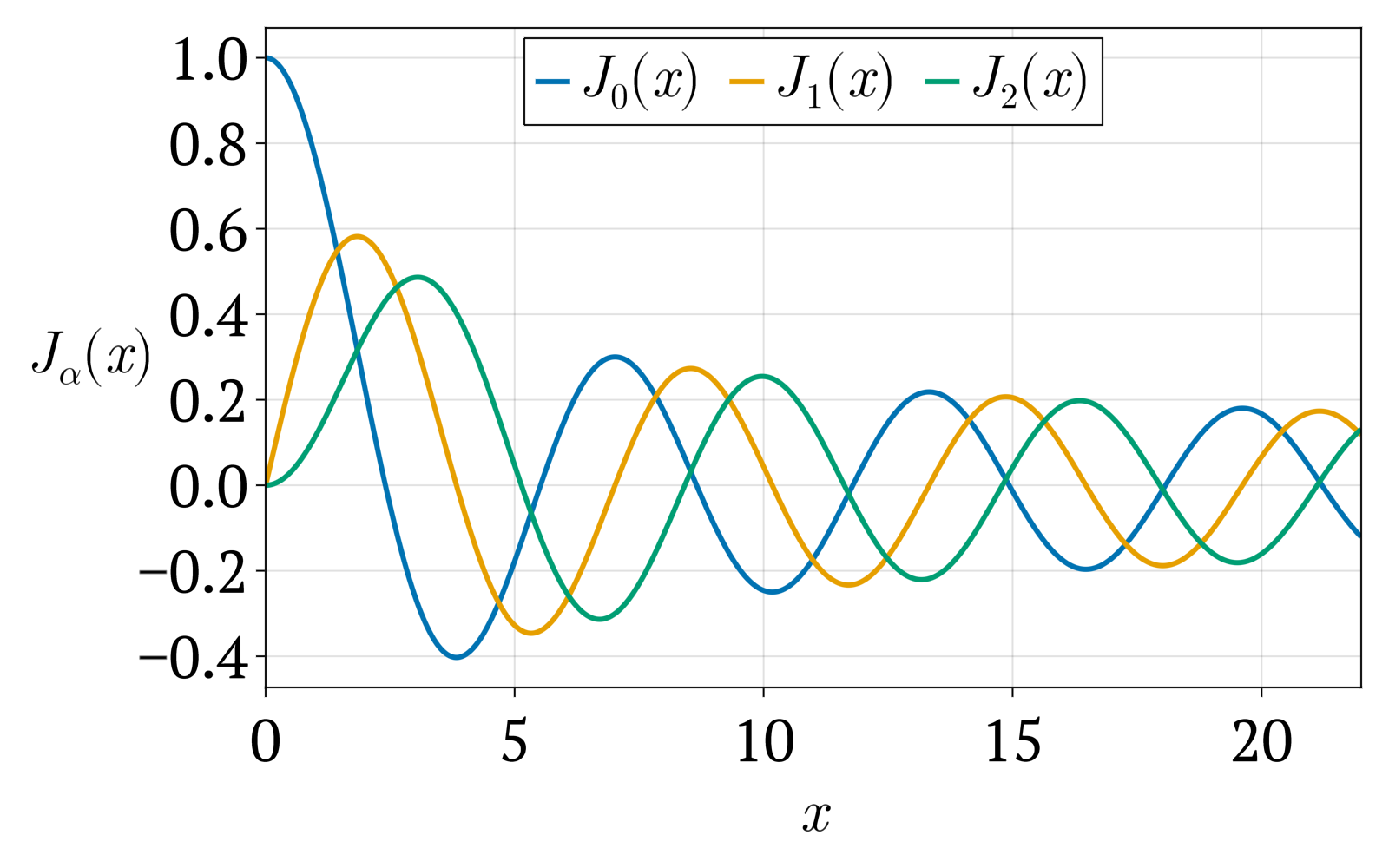
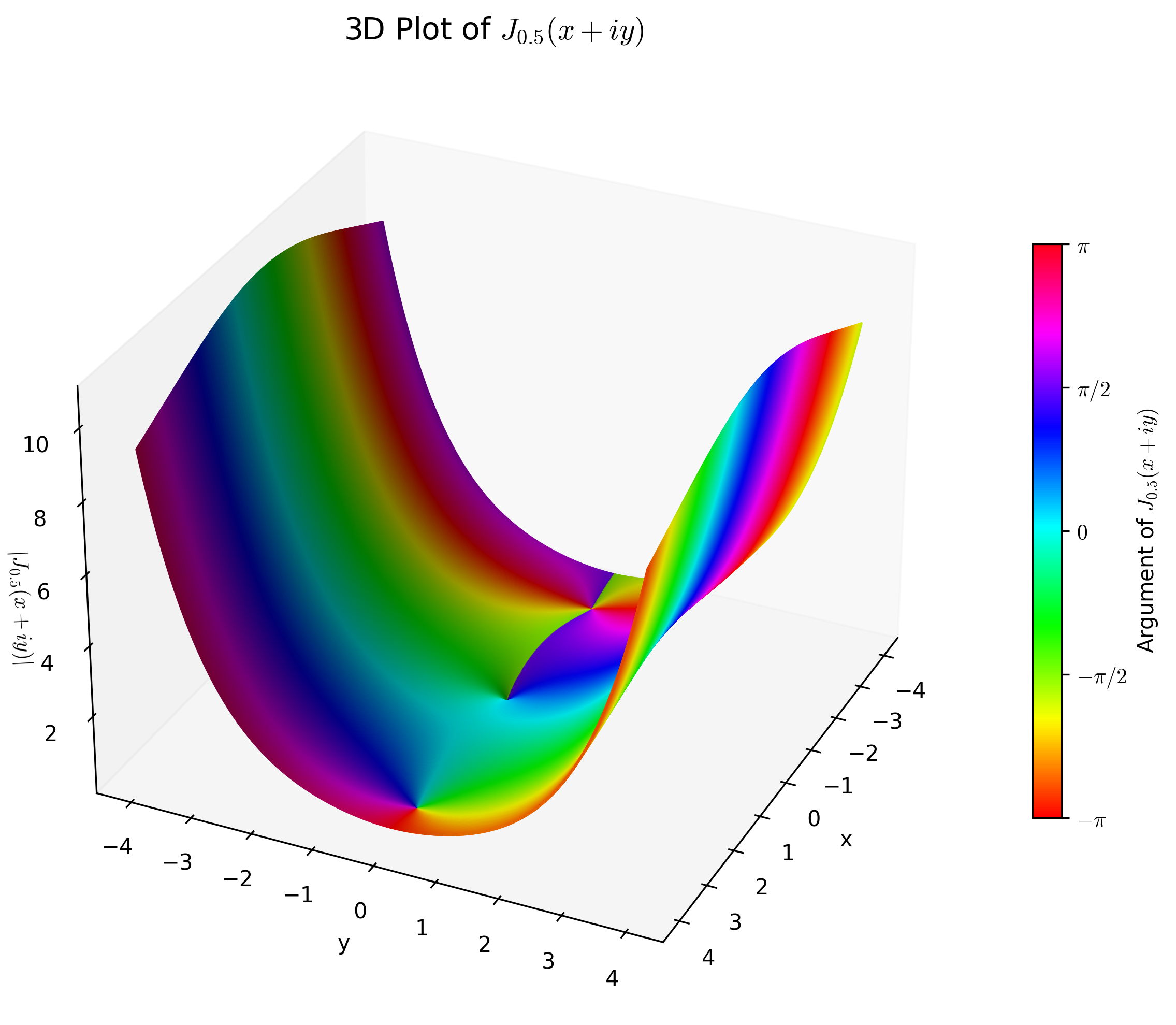
제1종 베셀 함수는 로 표시되며, 베셀 미분 방정식의 해이다. 정수 또는 양의 의 경우, 제1종 베셀 함수는 원점()에서 유한하며, 음의 비정수 의 경우, 제1종 베셀 함수는 가 0에 가까워질 때 발산한다. 제1종 베셀 함수는 매클로린 급수에 를 곱하여 정의할 수 있다 (가 정수일 필요는 없으며, 테일러 급수에서는 비정수 거듭제곱이 허용되지 않음에 유의). 이는 프로베니우스 방법을 베셀 방정식에 적용하여 찾을 수 있다.[3]
:
여기서 는 감마 함수이며, 비정수 값에 대한 팩토리얼 함수의 변형된 일반화이다. 제1종 베셀 함수는 가 정수이면 전체 함수이고, 그렇지 않으면 0에서 특이점을 갖는 다중값 함수이다. 베셀 함수의 그래프는 대략 에 비례하여 감소하는 진동하는 사인 함수 또는 코사인 함수와 유사하게 보이지만, 일반적으로 뿌리가 주기적이지 않으며, 큰 에 대해서는 점근적으로만 주기적이다.
비정수 의 경우, 함수 와 는 선형 독립이므로 미분 방정식의 두 해가 된다. 반면에, 정수 차수 의 경우, 다음 관계가 유효하다(감마 함수는 음수가 아닌 각 정수에서 단순 극을 갖는다):[5]
:
이는 두 해가 더 이상 선형 독립이 아니라는 것을 의미한다. 이 경우, 두 번째 선형 독립 해는 제2종 베셀 함수로 밝혀진다.
3. 2. 제2종 베셀 함수 (Yα)

베셀 방정식의 계수 가 정수이면 이므로 두 함수는 독립이 아니게 된다. 이 경우 나머지 한 해를 '''제2종 베셀 함수''' Yα(x)라고 하고, 다음과 같이 정의한다.
:.
가 정수가 아닐 경우에는 위 공식은 극한 없이 바로 사용할 수 있지만, 가 정수일 경우에는 극한을 취하여야만 한다.
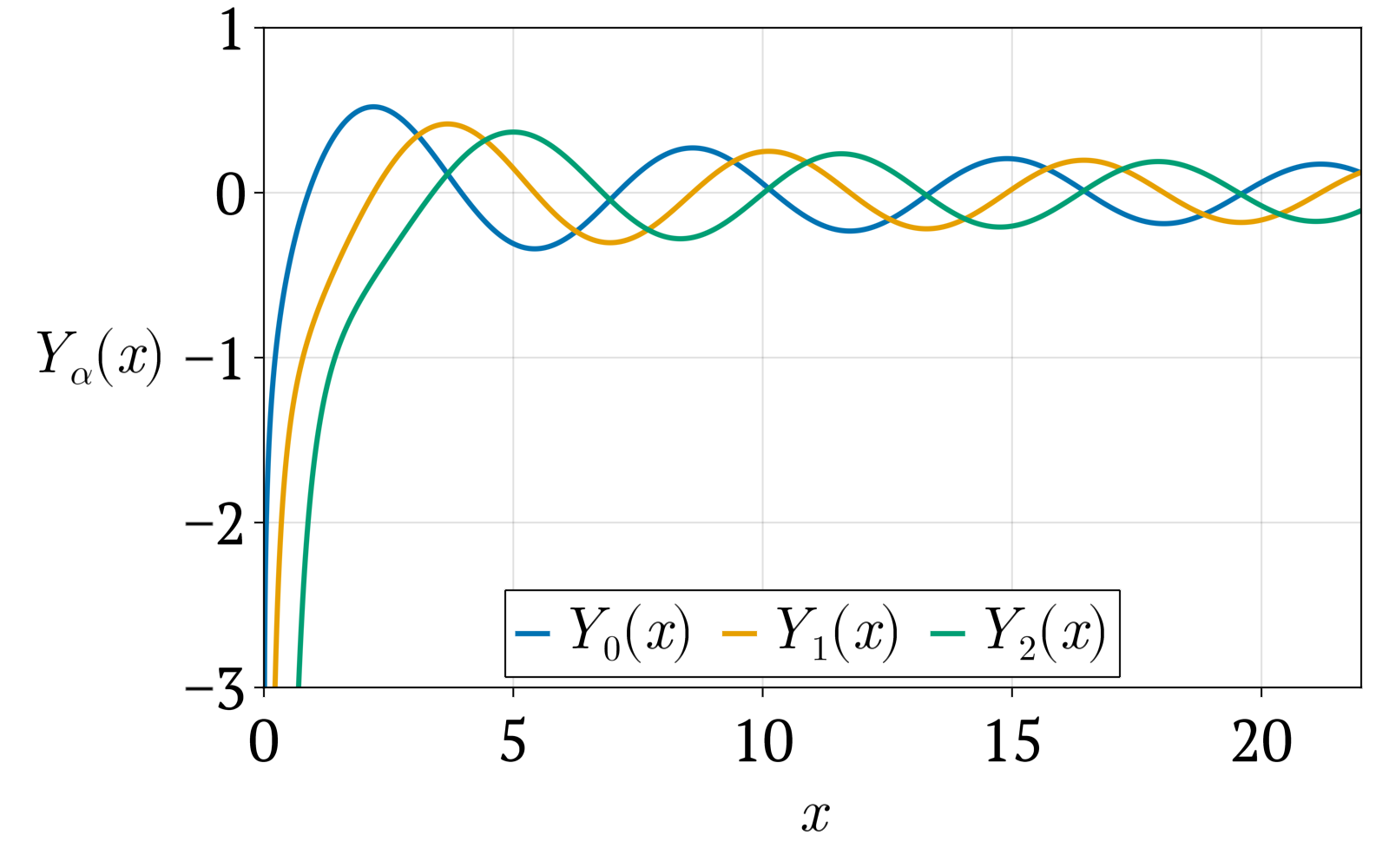
제2종 베셀 함수는 로 표기하며, 경우에 따라 로 표기하기도 한다. 카를 노이만에 따라 '''노이만 함수'''라고도 불린다.[15]
비정수 의 경우, 는 다음 식과 같이 와 관련이 있다.
:
정수 차수 의 경우, 이 함수는 비정수 가 으로 수렴하는 극한을 취하여 정의된다.
:
만약 이 음이 아닌 정수라면, 다음 급수를 얻는다.[16]
:
여기서 는 디감마 함수이며, 감마 함수의 로그 미분이다.[17]
다음과 같은 적분 공식도 있다 (에 대해):[18]
:
인 경우: (여기서 는 오일러 상수이다.)
:
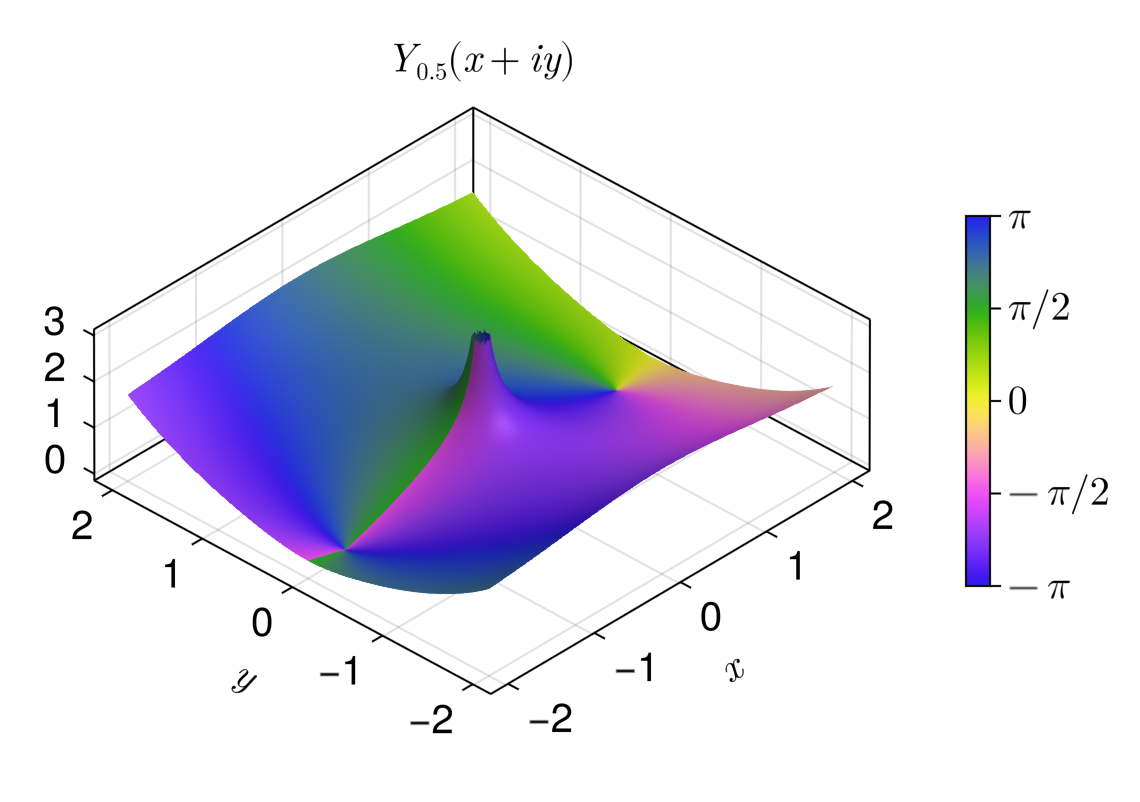
는 가 정수일 때 베셀 방정식의 두 번째 선형 독립 해로서 필요하다.
또한 가 정수일 때, 제1종 함수의 경우와 마찬가지로 다음 관계가 성립한다.
:
와 둘 다 음의 실수 축을 따라 잘린 복소 평면에서 의 정칙 함수이다. 가 정수일 때, 베셀 함수 는 의 전해석 함수이다. 만약 가 0이 아닌 값으로 고정되어 있다면, 베셀 함수는 의 전해석 함수이다.
3. 3. 변형 베셀 함수 (Iα, Kα)
변형 베셀 함수(Modified Bessel function)는 다음과 같은 변형 베셀 방정식의 해이다.:
제1종 변형 베셀 함수()와 제2종 변형 베셀 함수()로 나뉜다. 방정식의 특징 때문에 쌍곡 베셀 함수라고도 불린다.
베셀 함수는 복소수 인자 에 대해서도 유효하며, 순수한 허수 인자의 경우가 중요한 특별한 경우이다.
는 행켈 함수로 표현할 수 있다.
일반 베셀 함수 와 는 변형 베셀 함수를 통해 다음과 같이 표현할 수 있다. ( 인 경우)[24]
:
실수 인자의 함수로서 진동하는 일반 베셀 함수와 달리, 와 는 각각 지수 증가 및 지수 감소 함수이다. 일반 베셀 함수 와 마찬가지로, 함수 는 에서 에 대해 0으로 수렴하고, 에 대해 에서 유한하다. 마찬가지로, 는 에서 발산한다.[26]
변형 베셀 함수는 다음과 같은 성질을 가진다. 여기서 n은 양의 정수 또는 0이다.
:
:
3. 3. 1. 제1종 변형 베셀 함수 (Iα)

'''제1종 변형 베셀 함수''' Iα(x)는 변형 베셀 방정식의 기본적인 해이며, 다음과 같이 정의된다.[22]
:Iα(x)|Iα(x) = i-αJα(ix)영어
제1종 변형 베셀 함수는 급수 형태로 다음과 같이 표현된다.
:Iα(z)|Iα(z) = (1/2z)α Σk=0∞ (1/4z2)k / (k! Γ(α+k+1))영어
선적분을 이용하면 다음과 같이 표현할 수 있다.
:In(z)|In(z) = 1/2πi ∮e(z/2)(t+1/t)t-n-1dt영어
여기서 적분 경로는 원점을 반시계 방향으로 도는 임의의 고리이다.
다음과 같은 적분 표현법도 존재한다.
:Iα(z)|Iα(z)=1/π ∫0π ez cos θ cos (αθ) dθ - sin (απ)/π ∫0∞ e-z cosh t - αtdt영어
만약 α가 정수이면 위 식은 다음과 같이 간단해진다.
:In(z)|In(z)=1/π ∫0π ez cos θ cos (nθ) dθ영어
n = 0 에서의 제1종 변형 베셀 함수를 미분하면 다음과 같은 결과를 얻는다.[22]
:In(x)|In(x)=Tnd/dxI0(x)영어
여기서 Tn은 제1종 체비세프 다항식이다.
변형 베셀 함수는 복소수 인자에 대해서도 유효하며, 순수한 허수 인자의 경우가 중요한 특별한 경우이다. 이 경우, 베셀 방정식의 해를 '''변형 베셀 함수''' (또는 때때로 '''쌍곡선 베셀 함수''') '''제1종 및 제2종'''이라고 부른다.[22]
실수 인자의 함수로서 진동하는 일반 베셀 함수와 달리, Iα는 지수적 증가 함수이다. 일반 베셀 함수 Jα와 마찬가지로, 함수 Iα는 x = 0 에서 α > 0 에 대해 0으로 수렴하고, α = 0 에 대해 x = 0 에서 유한하다.[26]
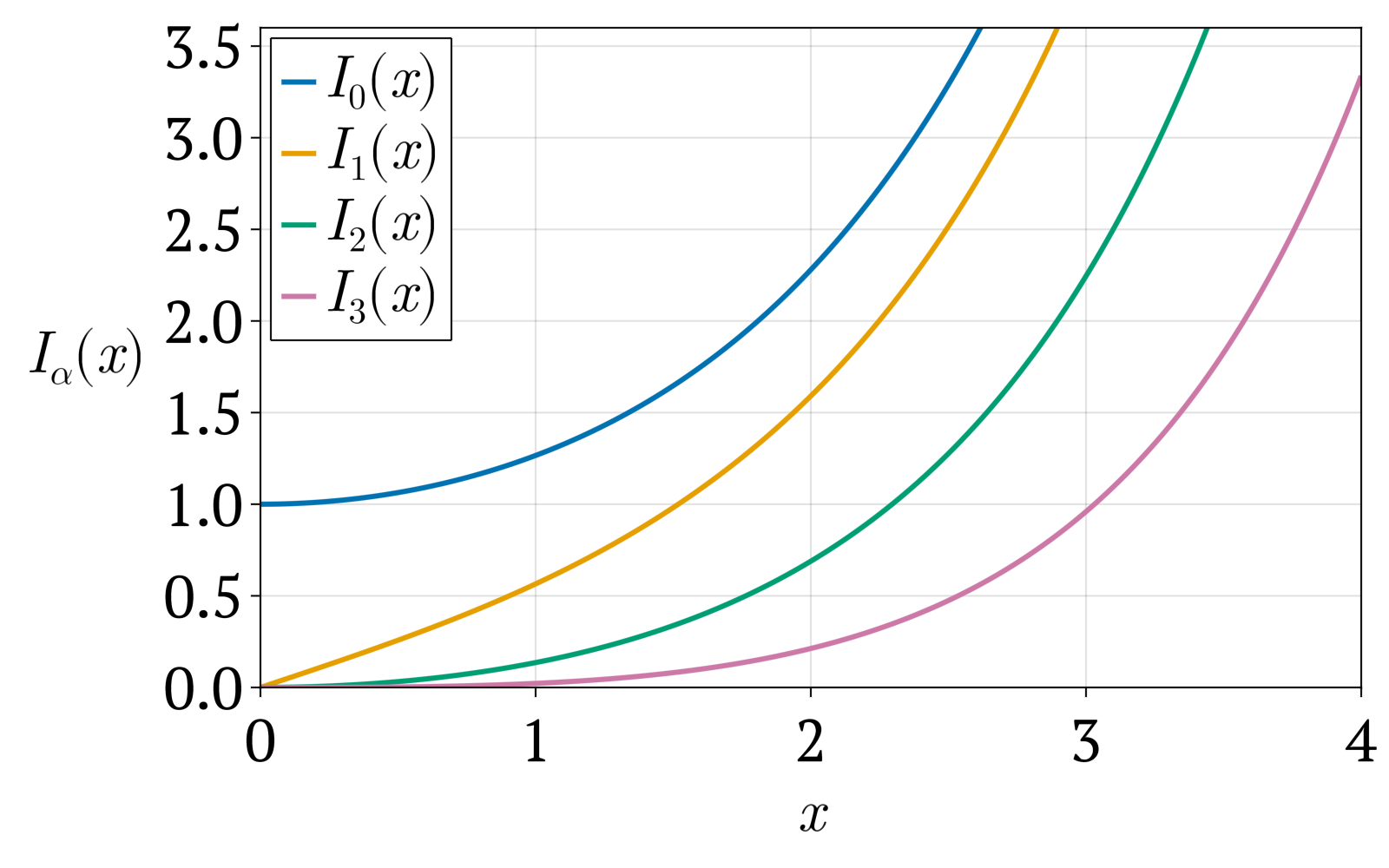
제1종 및 제2종 베셀 함수를 변형 베셀 함수로 표현할 수 있다(이는 -π < arg z ≤ π/2 인 경우 유효하다).[24]
:Jα(iz)|Jα(iz) = eαπi/2 Iα(z)영어
:Yα(iz)|Yα(iz) = e(α+1)πi/2Iα(z) - 2/π e-απi/2Kα(z)영어
Iα는 변형 베셀 방정식의 선형 독립 해이다.[25]
:x2 d2y/dx2 + x dy/dx - (x2 + α2)y = 0|x2 d2y/dx2 + x dy/dx - (x2 + α2)y = 0영어
변형 베셀 함수에 대한 두 가지 적분 공식은 (Re(x) > 0에 대해) 다음과 같다.[27]
:Iα(x)|Iα(x) = 1/π∫0π excos θ cos αθ dθ - sin απ/π∫0∞ e-xcosh t - αt dt영어
변형 베셀 함수는 다음과 같은 성질을 가진다. 여기서 n은 양의 정수 또는 0이다.
:I-n(x)|I-n(x) = In(x)영어
3. 3. 2. 제2종 변형 베셀 함수 (Kα)

제2종 변형 베셀 함수는 변형 베셀 방정식의 두 번째 선형 독립 해이다.[25] 이 함수는 다음과 같이 정의된다.[22]
:
α가 정수가 아닌 경우 위와 같이 정의되고, 정수인 경우 극한을 사용하여 정의한다.[22]
:
제2종 변형 베셀 함수는 실수 인자 x에 대해 실수값을 가지며,[22] 지수적으로 감소하는 형태를 띤다.[26]
제2종 변형 베셀 함수는 다음과 같은 이름으로도 불렸다.[28]
3. 4. 한켈 함수 (H(1)α, H(2)α)
베셀 미분 방정식에 대한 선형 독립적인 두 개의 해를 제공하는 표현식에는 한켈 함수 ''Hα''(1)(''x'')와 ''Hα''(2)(''x'')가 있으며, 정의식은 다음과 같다.:H|에이치영어α(1)(x) = J|제이영어α(x) + i Y|와이영어α(x)
:H|에이치영어α(2)(x) = J|제이영어α(x) - i Y|와이영어α(x)
여기서 는 허수 단위이다. J|제이영어α(x)와 Y|와이영어α(x)의 선형 결합으로 주어지는 이러한 해의 표현은 제3종 베셀 함수로 알려져 있다(한켈 함수는 원통파의 방정식에서 안쪽 혹은 바깥쪽으로의 원통파 전파 해를 표현한다).
3. 5. 구면 베셀 함수 (jn, yn)
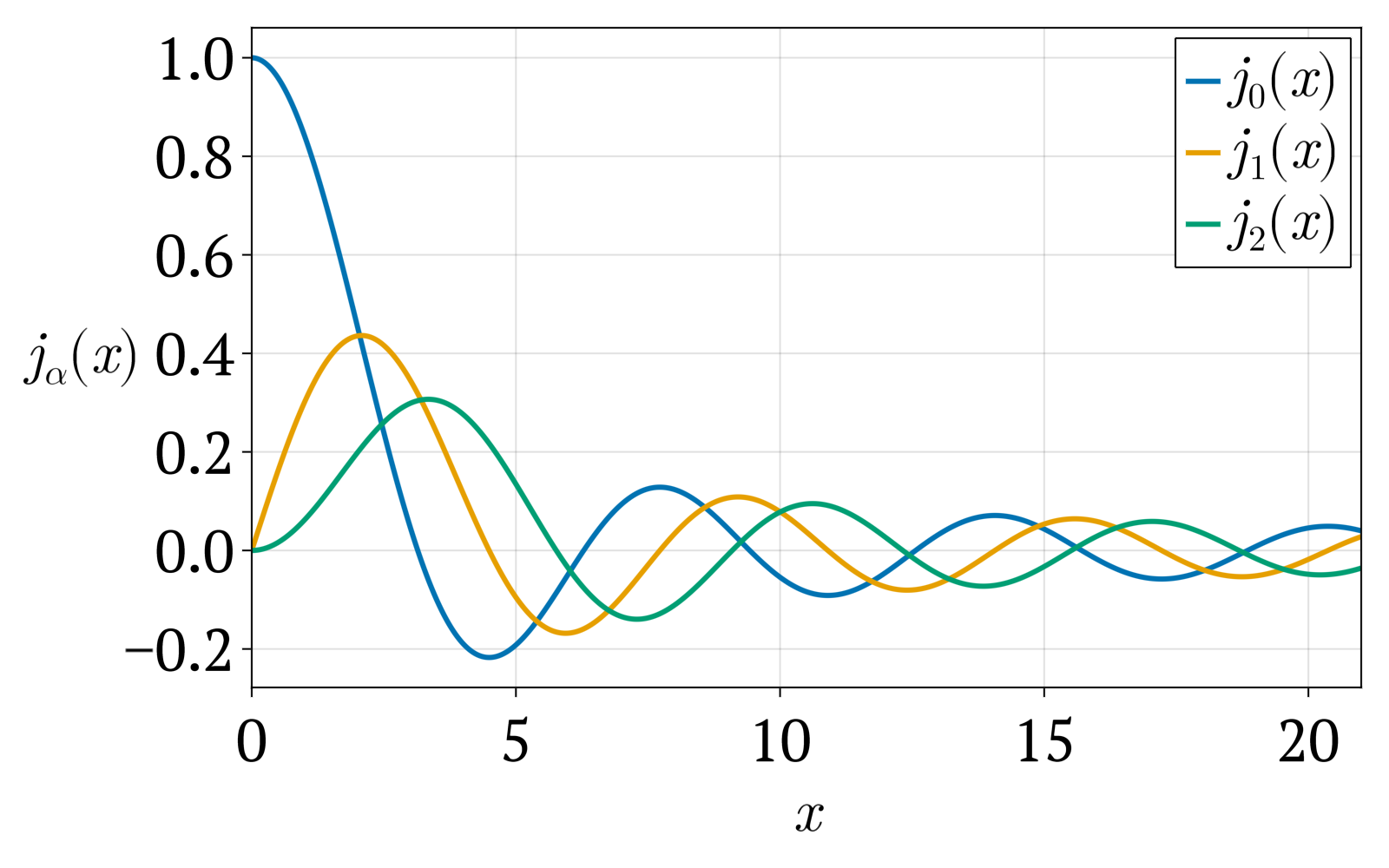
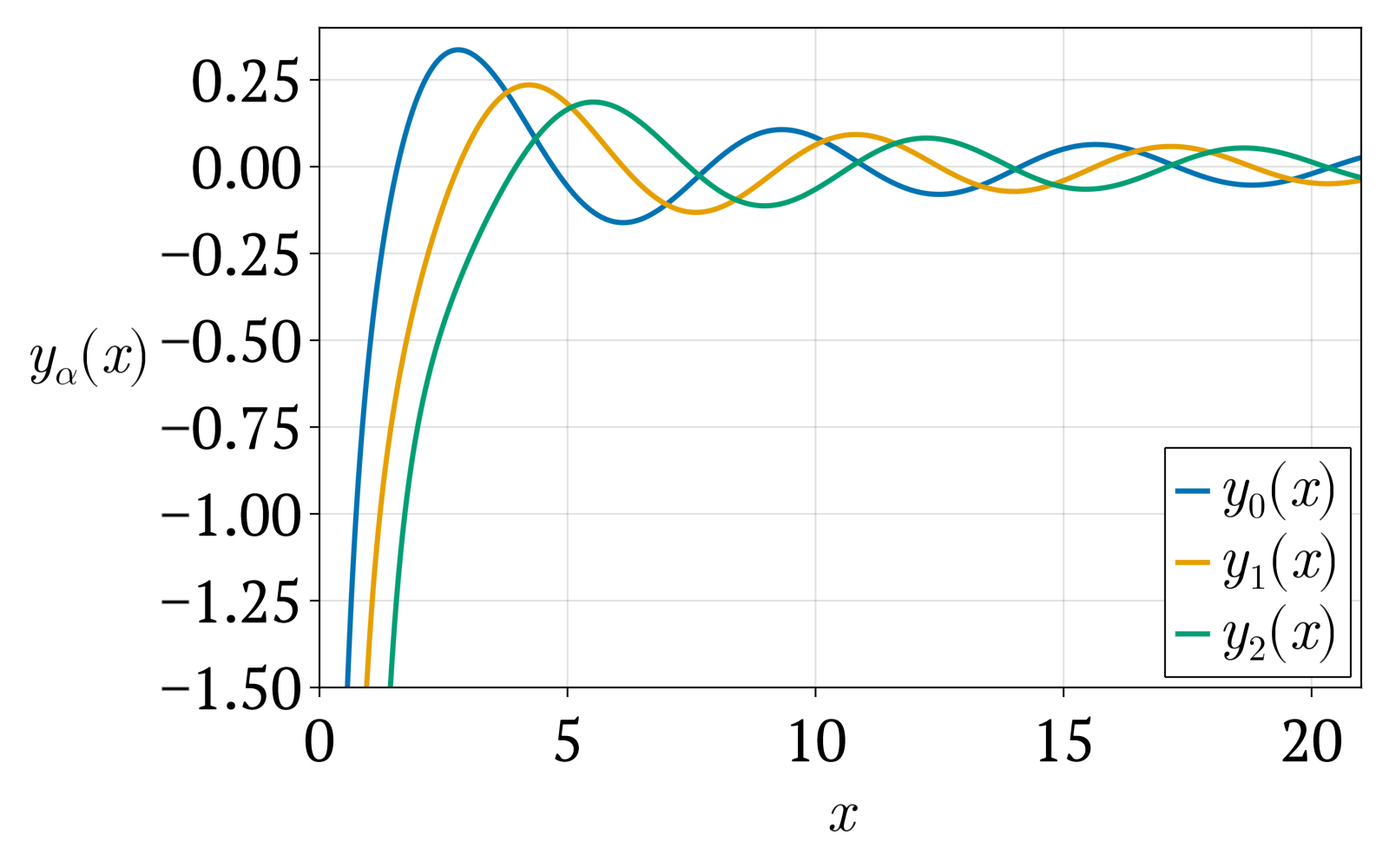
구면 베셀 함수는 구면 좌표계에서 헬름홀츠 방정식을 변수분리하여 풀 때 나타나는 방사형 방정식의 해이다. 이 방정식은 다음과 같다.[31]
이 방정식의 두 선형 독립 해는 '''구면 베셀 함수''' 및 이며, 일반 베셀 함수 및 과 다음과 같은 관계를 갖는다.
은 또는 으로도 표기되며, 일부 저자는 이 함수를 '''구면 노이만 함수'''라고 부른다.
일반 베셀 함수와의 관계로부터 다음을 알 수 있다.
구면 베셀 함수는 레일리 공식으로도 쓸 수 있다.[32]
0차 구면 베셀 함수 는 싱크 함수(비정규화)이다. 몇 가지 구면 베셀 함수는 다음과 같다.[33][34]
처음 몇 개 구면 베셀 함수의 0이 아닌 근은 다음과 같다.
정수 베셀 함수 , 와 달리, 구면 베셀 함수 , 는 유한 급수 표현을 갖는다.[36]
3. 5. 1. 구면 베셀 함수의 생성 함수
구면 베셀 함수는 다음과 같은 생성 함수를 갖는다.[35]3. 6. 리카티-베셀 함수 (Sn, Cn, ξn, ζn)
리카티-베셀 함수는 구면 베셀 함수와 약간의 차이만 보인다.
이 함수들은 다음과 같은 미분 방정식을 만족한다.
예를 들어, 이러한 종류의 미분 방정식은 가상적인 원통형 무한 포텐셜 장벽을 가진 양자역학에서 슈뢰딩거 방정식의 반경 방향 성분을 풀 때 나타난다.[38] 이 미분 방정식과 리카티-베셀 해는 또한 미(Mie, 1908)에 의해 처음 발표된 해로 알려진, 구에 의한 전자기파 산란 문제인 미 산란에서도 발생한다. 최근 개발과 참고 문헌에 대해서는 예를 들어 Du (2004)[39]를 참조하라.
데바이(1909)에 따라, Sn, Cn 대신 ψn, χn 표기가 사용되기도 한다.
4. 베셀 함수의 성질
베셀 함수는 다음과 같은 다양한 성질을 갖는다.
정수 차수 n의 경우, Jn은 생성 함수에 대한 로랑 급수를 통해 정의되기도 한다.
:
이는 1843년 P. A. Hansen이 사용한 방법이다.
형식의 베셀 함수의 무한 급수는 많은 물리 시스템에서 나타나며 Sung 급수로 닫힌 형식으로 정의된다.[45] 예를 들어 N=3 일때,
이다.
베셀 함수를 사용한 급수 전개 (Kapteyn 급수)는 다음과 같다.
:
정수 차수에 대한 중요한 관계는 야코비-앙거 전개이다.
:
:
이는 평면파를 원통형파의 합으로 전개하거나, 톤 변조된 FM 신호의 푸리에 급수를 찾는데 사용된다.
일반적으로, 급수
:
는 f의 Neumann 전개라고 불린다.
선택된 함수는 특별한 표현을 허용한다.
:
이때
:
직교 관계 때문이다.
:
베셀 함수를 정의하는 또 다른 방법은 푸아송 표현 공식과 Mehler-Sonine 공식이다.
:
여기서 ν > -1/2 이고 z ∈ C 이다.[48] 이 공식은 특히 푸리에 변환을 다룰 때 유용하다.
베셀 방정식이 x로 나누면 에르미트 (자기 수반)가 되기 때문에, 해는 적절한 경계 조건에 대해 직교 관계를 만족해야 한다. 특히, 다음과 같다.
:
여기서 α > -1, δm,n은 크로네커 델타이며, uα,m은 Jα(x)의 m번째 영점 이다.
만약 작은 매개변수 ε에 의존하는 x의 박스카 함수를 다음과 같이 정의하면,
:
(여기서 rect는 사각형 함수)의 한켈 변환(어떤 주어진 차수 α > -1/2), gε(k)는 어떤 주어진 k에 대해 ε가 0에 가까워질 때 Jα(k)에 접근한다.
:
이는 1 근처를 제외하고는 모든 곳에서 0이다. ε가 0에 가까워지면, 우변은 δ가 디랙 델타 함수인 δ(x - 1)에 접근한다. 이는 (분포의 의미에서) 다음과 같은 극한을 허용한다.
:
그런 다음 변수의 변경은 ''폐쇄 방정식''을 생성한다.[49]
:
(α > -1/2에 대해).
베셀 방정식의 또 다른 중요한 속성은 아벨의 항등식에서 파생되며, 해의 론스키 행렬식과 관련이 있다.
:
여기서 Aα와 Bα는 베셀 방정식의 두 해이며, Cα는 x에 독립적인 상수이다.
두 베셀 함수의 곱은 다음 합을 허용한다.
:
:
베셀 함수는 다음의 곱셈 정리를 따른다.
:
여기서 λ와 ν는 임의의 복소수로 간주할 수 있다.[54][55]
4. 1. 점화식
베셀 함수 (는 , , , 를 나타냄)는 다음의 점화 관계를 만족한다.[50]:
:
이 두 항등식은 더하거나 빼는 방식으로 결합하여 다른 관계를 생성할 수 있다. 이를 통해 낮은 차수(또는 낮은 도함수)의 값을 이용하여 더 높은 차수(또는 더 높은 도함수)의 베셀 함수를 계산할 수 있다. 특히 다음이 성립한다.[51]
:
수정된 베셀 함수 (는 또는 를 나타냄)도 다음과 같은 점화 관계를 따른다.
:
4. 2. 적분 표현
프리드리히 베셀|프리드리히 베셀한국어이 사용했던 접근법은 다음과 같은 적분 표현을 사용한다.[6]:
여기서 다른 몇몇 성질들을 유도해냈다.
또 다른 적분 형태의 정의는 다음과 같다.
:
이것은 한센-베셀 공식이라고도 불린다.[7]
경로적분법을 사용하면 베셀 함수를 다음과 같이 표현할 수 있다.[61]
:
여기서 적분 경로는 원점을 주변으로 반시계방향으로 도는 임의의 고리이다.
정수 n에 대한 베셀 함수의 또 다른 정의는 적분 표현을 사용하여 가능하다.[8]
:
Re(x) > 0 에 대해, Schläfli의 적분 중 하나를 사용하여 비정수 차수로 확장될 수 있다.[9][10][11][12]
:
Re(x) > 0 에 대해, 제2종 베셀함수의 적분 공식은 다음과 같다.[18]
:
n = 0 인 경우, (오일러 상수 에 대해)는 다음과 같다.[18]
:
베셀 함수의 적분 표현은 다음과 같다.[61]
한센의 적분 표현은 다음과 같다.[61]
푸아송의 적분 표현은 다음과 같다.[61]
슐레플리의 적분 표현은 다음과 같다.[62] 단, 복호는 위쪽이 , 아래쪽이
샤프하이트린의 적분 표현은 다음과 같다.[63] 단, 복호는 위쪽이 , 아래쪽이
하이네의 적분 표현은 다음과 같다.[63] 단, 복호는 위쪽이 , 아래쪽이
휘테커의 적분 표현은 다음과 같다.[64] 여기서 는 르장드르 다항식
4. 3. 생성 함수
베셀 함수는 생성 함수를 사용하여 표현할 수 있다. 다음 공식을 야코비와 카를 테오도어 앙거(Carl Theodor Angerde)의 이름을 따서 야코비-앙거 전개(Jacobi–Anger expansion)라고 한다.:.
구면 베셀 함수도 생성 함수로 표현할 수 있다. 이 공식을 레일리 전개(Rayleigh expansion)라고 한다.
:.
여기서 은 르장드르 다항식이다.
정수 차수의 경우, 생성 함수에 대한 로랑 급수를 통해 정의되기도 한다.
:
이는 1843년 P. A. Hansen이 사용한 접근 방식이다.
정수 차수에 대한 또 다른 중요한 관계는 ''야코비-앙거 전개''이다.
:
:
이는 평면파를 원통형파의 합으로 전개하거나, 톤 변조된 FM 신호의 푸리에 급수를 찾는데 사용된다.
4. 4. 점근 전개
x|x영어가 매우 클 때, 베셀 함수는 다음과 같은 점근적 형태를 가진다.[40]:
:[65]
:
:
행켈 함수의 점근적 형태는 다음과 같다.[40]
:
:[65]
:
:
구면 베셀 함수는 다음과 같은 점근적 형태를 가진다.
:
:
:
:
4. 5. 직교성
베셀 함수(Bessel function)의 영점에 대한 수치 연구는 Gil, Segura, Temme (2007), Kravanja, Ragos, Vrahatis, Zafiropoulos (1998) 및 Moler (2004)를 참조할 수 있다. J0의 첫 번째 영점(j0,1, j0,2 및 j0,3)은 각각 약 2.40483, 5.52008 및 8.65373에서 발생한다.[59]4. 6. 영점
카를 루트비히 지겔은 1929년에 베셀 함수의 영점에 대한 여러 성질을 증명하였다.[52] 와 그 도함수 는 ''ν''가 유리수이고 ''x''가 0이 아닌 대수적 수일 때 초월수이다.[52]베셀 자신은 음이 아닌 정수 에 대해 방정식 이 에서 무한히 많은 해를 갖는다는 것을 증명했다.[56] 하지만 함수들을 같은 그래프에 그리면 에서의 영점을 제외하고는 서로 다른 값에 대해 영점이 일치하지 않는 것처럼 보인다. 이러한 현상은 '''부르제 가설'''(Bourget's hypothesis)로 알려져 있는데, 임의의 정수 및 에 대해 함수 와 는 에서의 영점을 제외하고는 공통 영점을 갖지 않는다는 것이다.[57] 이 가설은 1929년에 카를 루드비히 지겔에 의해 증명되었다.[57]
지겔은 또한 ''ν''가 유리수일 때, 와 의 모든 0이 아닌 근과 의 모든 근이 초월수임을 증명했다.[58]
5. 베셀 함수의 응용
라플라스 방정식과 헬름홀츠 방정식의 분리 가능한 해를 원통 좌표계 또는 구면 좌표계에서 찾을 때 베셀 방정식이 나타난다. 따라서 베셀 함수는 파동 전파 및 정적 전위 문제 등 다양한 분야에 응용된다. 원통 좌표계에서는 정수 차수 베셀 함수를, 구면 좌표계에서는 반정수 차수 베셀 함수를 얻는다.
베셀 함수는 신호 처리 (예: 주파수 변조 합성, 카이저 윈도우, 베셀 필터) 등에도 활용된다.[1]
5. 1. 물리학
베셀 방정식은 라플라스 방정식과 헬름홀츠 방정식의 분리 가능한 해를 원통 좌표계 또는 구면 좌표계에서 찾을 때 나타난다. 따라서 베셀 함수는 파동 전파 및 정적 전위 문제에 특히 중요하다. 원통 좌표계에서는 정수 차수의 베셀 함수를, 구면 문제에서는 반정수 차수의 베셀 함수를 얻는다.베셀 함수는 다음과 같은 다양한 물리 현상을 기술하는 데 사용된다.
베셀 함수는 신호 처리(예: 주파수 변조 합성, 카이저 윈도우, 베셀 필터)와 같은 다른 문제에도 활용된다.[1]
5. 1. 1. 전자기파
원통형 도파관 내 전자기파[1]5. 1. 2. 열전도
베셀 함수는 원통형 물체의 열전도를 설명하는 데 사용된다.[1]5. 1. 3. 진동
얇은 원형 또는 환형 음향 막(드럼 헤드 또는 다른 막명악기 등)의 진동 모드를 분석할 때 베셀 함수가 사용된다.[1]5. 1. 4. 양자역학
베셀 함수는 자유 입자에 대한 슈뢰딩거 방정식의 반경 방향 해(구면 및 원통 좌표)를 구하는 데 사용된다.[1] 가상적인 원통형 무한 포텐셜 장벽을 가진 양자역학에서 슈뢰딩거 방정식의 반경 방향 성분을 풀 때, 다음과 같은 형태의 미분 방정식이 나타난다.[38]:
이 미분 방정식의 해는 리카티-베셀 함수로 나타낼 수 있으며, 이는 구면 베셀 함수와 약간의 차이만 보인다. 리카티-베셀 함수는 미 산란 문제에도 나타난다.[39]
5. 2. 신호 처리
베셀 함수는 신호 처리에서 유용한 특성을 가지며, FM 합성, 카이저 윈도우, 베셀 필터 등에 사용된다.[1]5. 3. 기타 응용
베셀 함수는 라플라스 방정식과 헬름홀츠 방정식의 분리 가능한 해를 원통 좌표계 또는 구면 좌표계에서 찾을 때 나타난다. 따라서 베셀 함수는 파동 전파 및 정적 전위 문제에 중요하다. 원통 좌표계에서는 정수 차수 베셀 함수(integer order Bessel functions영어)를, 구면 문제에서는 반정수 차수(half-integer order Bessel functions영어)를 얻는다.베셀 함수는 다음과 같은 다양한 분야에 응용된다.
- 원통형 도파관 내 전자기파
- 비점성 유동 회전 흐름의 압력 진폭
- 원통형 물체의 열전도
- 얇은 원형 또는 환형 음향 막(예: 드럼 헤드 또는 다른 막명악기)의 진동 모드
- 격자에서의 확산 문제
- 자유 입자에 대한 슈뢰딩거 방정식의 반경 방향 해 (구면 및 원통 좌표)
- 양자장론에서 페르미 전파자의 위치 공간 표현
- 음향 방사 패턴 해결
- 원형 파이프라인의 주파수 의존 마찰
- 부유체의 역학
- 각도 분해능
- DNA를 포함한 나선형 물체로부터의 회절
- 두 개의 정규 분포된 확률 변수의 곱의 확률 밀도 함수[1]
- 지구물리학 및 지진학에서 미소 진동에 의해 생성된 표면파 분석
베셀 함수는 신호 처리(예: 주파수 변조 합성, 카이저 윈도우, 베셀 필터) 등에도 사용된다.
6. 역사
참조
[1]
논문
Why and when to expect Gaussian error distributions in epoch of reionization 21-cm power spectrum measurements
2023-06
[2]
웹사이트
Spherical Bessel Function of the Second Kind
[3]
문서
p. 360, 9.1.10
https://personal.mat[...]
Abramowitz and Stegun
[4]
서적
A Course of Modern Analysis
Cambridge University Press
1927
[5]
문서
p. 358, 9.1.5
https://personal.mat[...]
Abramowitz and Stegun
[6]
서적
Special Functions: An introduction to the classical functions of mathematical physics
Wiley
[7]
웹사이트
Hansen-Bessel Formula
[8]
문서
The relevant integral is an unnumbered equation between equations 28 and 29. Note that Bessel's would today be written .
Bessel, F.
1824
[9]
문서
p. 176
https://books.google[...]
Watson
[10]
웹사이트
Properties of Hankel and Bessel Functions
http://www.math.ohio[...]
2010-10-18
[11]
웹사이트
Integral representations of the Bessel function
https://www.nbi.dk/~[...]
2018-03-25
[12]
문서
exercise 11.1.17
Arfken & Weber
[13]
문서
p. 362, 9.1.69
https://personal.mat[...]
Abramowitz and Stegun
[14]
서적
Orthogonal Polynomials
AMS
1975
[15]
웹사이트
Bessel Functions of the First and Second Kind
http://www.mhtlab.uw[...]
2022-05-24
[16]
웹사이트
NIST Digital Library of Mathematical Functions
https://dlmf.nist.go[...]
2016-10-25
[17]
웹사이트
Bessel Function of the Second Kind
[18]
문서
p. 178
https://books.google[...]
Watson
[19]
문서
p. 358, 9.1.3, 9.1.4
https://personal.mat[...]
Abramowitz and Stegun
[20]
문서
p. 358, 9.1.6
https://personal.mat[...]
Abramowitz and Stegun
[21]
문서
p. 360, 9.1.25
https://personal.mat[...]
Abramowitz and Stegun
[22]
문서
p. 375, 9.6.2, 9.6.10, 9.6.11
https://personal.mat[...]
Abramowitz and Stegun
[23]
논문
A direct proof of Nicholson's integral
1930
[24]
문서
p. 375, 9.6.3, 9.6.5
https://personal.mat[...]
Abramowitz and Stegun
[25]
문서
p. 374, 9.6.1
https://personal.mat[...]
Abramowitz and Stegun
[26]
서적
Quantum Electrodynamics
Springer
2009
[27]
문서
p. 181
https://books.google[...]
Watson
[28]
웹사이트
Modified Bessel Functions §10.32 Integral Representations
http://dlmf.nist.gov[...]
NIST
2024-11-20
[29]
논문
Cascade Processes of Energy Loss by Emission of Hard Photons
2004
[30]
논문
The Mixture of Normal Distributions with Different Variances
https://dml.cz/bitst[...]
1957
[31]
문서
p. 437, 10.1.1
https://personal.mat[...]
Abramowitz and Stegun
[32]
문서
p. 439, 10.1.25, 10.1.26
https://personal.mat[...]
Abramowitz and Stegun
[33]
문서
p. 438, 10.1.11
https://personal.mat[...]
Abramowitz and Stegun
[34]
문서
p. 438, 10.1.12
https://personal.mat[...]
Abramowitz and Stegun
[35]
문서
p. 439, 10.1.39
https://personal.mat[...]
Abramowitz and Stegun
[36]
논문
Algorithms for computing Bessel functions of half-integer order with complex arguments
https://www.scienced[...]
[37]
서적
https://personal.mat[...]
[38]
서적
Introduction to Quantum Mechanics
[39]
학술지
Mie-scattering calculation
2004
[40]
서적
https://personal.mat[...]
[41]
간행물
Digital Library of Mathematical Functions
https://dlmf.nist.go[...]
NIST
[42]
서적
https://personal.mat[...]
[43]
서적
https://personal.mat[...]
[44]
논문
Fröhlich and Spencer 1981 Appendix B
https://projecteucli[...]
[45]
arXiv
On Infinite Series of Bessel functions of the First Kind
[46]
서적
https://personal.mat[...]
[47]
서적
A Treatise on the Theory of Bessel Functions
https://books.google[...]
Cambridge University Press
2018-03-25
[48]
서적
Table of Integrals, Series, and Products
Academic Press, Inc.
2015
[49]
문서
[50]
서적
https://personal.mat[...]
[51]
서적
https://personal.mat[...]
[52]
서적
On Some Applications of Diophantine Approximations: a translation of Carl Ludwig Siegel's Über einige Anwendungen diophantischer Approximationen by Clemens Fuchs, with a commentary and the article Integral points on curves: Siegel's theorem after Siegel's proof by Clemens Fuchs and Umberto Zannier
Scuola Normale Superiore
2014
[53]
학술지
Review: Carl Ludwig Siegel, Transcendental numbers
https://projecteucli[...]
1950-11
[54]
서적
https://personal.mat[...]
[55]
학술지
On the Addition and Multiplication Theorems for the Special Functions
1950
[56]
문서
1824
[57]
문서
[58]
학술지
Transcendentality of zeros of higher dereivatives of functions involving Bessel functions
1995
[59]
서적
[60]
웹사이트
Bessel function
https://www.britanni[...]
Britannica
2021-03-20
[61]
문서
岩波数学公式
[62]
문서
岩波数学公式
[63]
문서
岩波数学公式
[64]
문서
岩波数学公式
[65]
문서
岩波数学公式
[66]
저널
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com

