순환소수
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
순환소수는 소수점 아래 숫자가 무한히 반복되는 소수를 의미한다. 순환마디는 반복되는 숫자 묶음을, 순환마디가 소수점 바로 아래부터 시작하면 순순환소수, 그렇지 않으면 혼순환소수라고 한다. 순환소수는 점, 괄호, 빈쿨룸 등 다양한 표기법으로 나타낼 수 있으며, 무한등비급수의 합을 이용하여 분수로 변환할 수 있다. 모든 유리수는 유한소수 또는 순환소수로 표현 가능하며, 10진법에서 분모가 2와 5 이외의 소인수를 가질 때 순환소수가 된다. 순환마디의 길이는 분모와 관련된 곱셈 순서에 따라 결정되며, 소수의 역수는 순환소수가 된다. 순환소수는 암호학, 오류 정정 코딩 등 다양한 분야에 응용되며, 다른 기수법에서도 나타날 수 있다.
더 읽어볼만한 페이지
- 유리수 - 1/2
1/2는 0과 1의 산술 평균이자 1을 2로 나눈 값으로, 0.5로 표현되며 수학적 성질과 다양한 분야에서 활용된다. - 유리수 - 반정수
반정수는 정수에 1/2을 더한 수로 표현되며, 정수와 함께 덧셈 연산에 대해 군을 형성하지만 환은 형성하지 않고, 양자역학, 페르미온의 스핀, 4차원 격자 포장 등 다양한 분야에 응용된다. - 기수법 - 이진법
이진법은 0과 1 두 개의 숫자를 사용하는 밑이 2인 위치 기수법으로, 컴퓨터 과학의 기초가 되었으며 현대 컴퓨터에서 데이터를 저장하고 처리하는 데 사용된다. - 기수법 - 구진법
구진법은 9를 밑으로 하는 위치 기수법으로 0부터 8까지의 숫자를 사용하여 수를 나타내며, 3의 배수 표현이 간결하고 3의 역수는 유한소수로 표현되는 특징이 있다.
2. 용어
- 순순환소수: 소수점 바로 아래부터 순환마디가 반복되는 소수이다. 예를 들어 1/3 = 0.333... 과 같다.
- 혼순환소수: 소수점 아래 순환마디가 바로 시작되지 않지만, 일정 부분에서 순환마디가 반복되는 소수이다. 예를 들어 1/6 = 0.1666... 과 같다.
- 순환마디: 순환소수에서 일정하게 되풀이되는 가장 짧은 한 부분이다. 예를 들어 0.333...의 순환마디는 3이다.
3. 표기법
순환소수는 순환마디 양 끝에 위치한 숫자들 위에 점을 찍어 나타낸다. 예를 들어, 1/7 = 0.142857142857... = 0.142857 과 같이 표현할 수 있다.[4]
순환소수를 나타내는 방법은 여러 가지가 있으며, 보편적으로 사용되는 표기법은 없다. 다음은 다양한 표기법과 예시이다.
- 빈쿨룸: 미국, 캐나다, 인도, 프랑스, 독일, 이탈리아, 스위스, 체코, 슬로바키아, 슬로베니아, 칠레, 터키 등에서 사용.[4]
- 점: 대한민국, 일본, 중화인민공화국, 영국, 뉴질랜드, 오스트레일리아, 남아프리카 공화국, 싱가포르, 태국, 말레이시아, 모로코, 파키스탄, 튀니지, 이란, 알제리, 이집트 등에서 사용.
- 괄호: 오스트리아, 덴마크, 핀란드, 네덜란드, 노르웨이, 폴란드, 러시아, 우크라이나, 베트남, 이스라엘 등 일부 유럽 지역에서 사용.
- 아크: 스페인, 아르헨티나, 브라질, 멕시코 등 일부 라틴 아메리카 국가에서 사용.
- 줄임표: 비공식적으로 사용되며, 어떤 숫자가 반복되는지, 반복되는지 여부 등에 대한 불확실성을 야기할 수 있다.
순환절을 나타내는 방법으로, 순환절의 시작과 끝 숫자 위에 점을 찍거나, 순환절 전체에 윗줄을 긋거나, 밑줄을 긋거나, 괄호로 묶는 방법이 자주 사용된다.
4. 순환소수를 분수로 변환하기
순환소수는 무한등비급수의 합으로 나타낼 수 있으며, 이를 통해 유리수(분수)로 바꿀 수 있다. 방정식, 단축 표기법 등 다양한 방법이 사용된다.
각 순환 소수는 정수 계수를 갖는 선형 방정식을 만족하며, 그 해는 유리수이다. 예를 들어 ''α'' = 5.8144144144...는 다음 방정식을 만족한다.
순환소수를 분수로 바꾸는 방법은 다음과 같다.
- 방정식 활용:
예시 1:
예시 2:
- 단축 표기법: 반복되는 숫자가 ''n''개이고, 마지막 숫자 하나를 제외한 모든 숫자가 0이고 마지막 숫자가 1인 경우, 분수는 이다. (분모는 ''n''개의 9)
일반적인 순환 소수를 분수로 표현하는 공식::''x'' = 0.a1 a2 … an
:10n ''x'' = a1 a2 … an.a1 a2 … an
:(10n - 1)''x'' = 99 … 99''x'' = a1 a2 … an
:''x'' = =
예시:
- 0.444444... = (반복 블록: 4, 1자리)
- 0.565656... = (반복 블록: 56, 2자리)
- 0.012012... = = (반복 블록: 012, 3자리)
- 0.999999... = = 1 (반복 블록: 9, 1자리)
소수점과 반복 블록 사이에 ''k''개의 0이 있으면, 분모에 ''n''개의 9 뒤에 ''k''개의 0을 추가한다.
예시:
- 0.000444... = (반복 블록: 4, 0이 3개)
- 0.005656... = (반복 블록: 56, 0이 2개)
- 0.00012012... = = (반복 블록: 012, 0이 2개)
다른 유형의 순환 소수: 유한 소수와 위 유형 중 하나의 순환 소수 합으로 표현 가능.
예시:
- 1.23444... = 1.23 + 0.00444... = + =
더 빠른 방법: 소수점을 무시하고 계산.
- 1.23444... = = (분모: 9 한 개, 0 두 개)
- 0.3789789... = = (분모: 9 세 개, 0 한 개)
주기가 ''n''이고 소수점 뒤 반복되지 않는 자리가 ''k''개인 순환 소수는 분자 분모가 (10''n'' - 1)10''k''인 분수로 표현 가능.
분수 의 순환 소수 주기는 10''n'' - 1이 ''d''로 나누어지는 가장 작은 ''n''이다.
생성 규칙을 이용한 방법
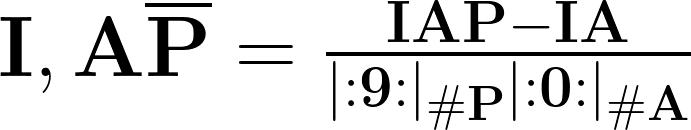
- : 정수 부분
- : 비순환마디
- : 비순환마디 길이
- : 순환마디 (0이 아닌 반복되는 숫자)
- : 순환마디 길이
생성된 분수에서 숫자 9는 번, 숫자 0은 번 반복.
예시:{| class="wikitable"
|-
| 3.254444…
| = 3.25
| =
| =
| =
|-
|-
| 0.512512…
| = 0.
| =
| =
| =
|-
|-
| 1.09191…
| = 1.0
| =
| =
| =
|-
|-
| 1.333…
| = 1.
| =
| =
| =
| =
|-
|-
| 0.3789789…
| = 0.3
| =
| =
| =
| =
|}
- 무한 급수 활용: 순환 소수는 무한히 많은 유리수의 합(무한 등비 급수)으로 표현 가능.
예시:
- 0.1 = + + + … =
- 0.142857 = + + … = =
무한등비급수: 첫째 항이 ''a''이고 공비가 ''r''인 등비 급수의 합은 (|r| < 1)
엄밀한 정의: 무한소수는 극한으로 정의. 순환소수는 무한등비급수의 합의 극한으로, 유리수이다.
예시:
- 2.423 = 2 + + + … =
일반화:
- ''a'': 순환하지 않는 유한 소수 부분
- ''b'': 순환절 부분만 떼어낸 소수 부분
- ''n'': 순환절의 길이
: a + b()
5. 분수 표현과의 관계
유리수를 소수 형태로 나타내기 위해서는 나눗셈을 사용한다. 예를 들어, 를 소수로 나타내면 다음과 같다.
0.0
74 ) 5.00000
4.44
560
518
420
370
500
위의 나눗셈에서 나머지 50에 도달하여 "0"을 내리면, 500을 74로 나누는 문제가 발생한다. 이는 처음에 시작했던 문제와 같으므로 소수는 0.0675675675…와 같이 반복된다.
어떤 정수 분수 에서, k 단계에서의 나머지는 ''A'' × 10''k'' (modulo ''B'')이다. 주어진 제수(除數)에 대해 가능한 나머지는 유한 개이다. 위의 예에서 가능한 나머지는 0, 1, 2, ..., 73이다. 나눗셈 과정에서 나머지가 0이 되면 소수는 그 지점에서 종료된다. 나머지가 0이 되지 않으면 나눗셈은 영원히 계속되고, 결국 이전에 나타났던 나머지가 다시 나타난다. 그러면 그 다음 단계는 이전과 같은 나머지가 나타났을 때와 같은 결과를 반복한다. 이렇게 반복되는 숫자들을 "순환마디"라고 하며, 이는 0보다 큰 특정 길이를 가지며, "주기"라고도 한다.[5]
십진법에서 분수를 기약분수로 나타냈을 때, 분모가 2나 5 이외의 소인수를 가지면 순환소수가 된다. 즉, 분모가 2''m'' 5''n'' (''m'', ''n''은 음이 아닌 정수)으로 표현될 수 없으면 순환소수가 된다.
각 순환 소수는 정수 계수를 갖는 선형 방정식을 만족하며, 그 고유한 해는 유리수이다. 예를 들어, ''α'' = 5.8144144144...는 다음 방정식을 만족한다.
이러한 정수 계수를 찾는 방법은 아래에 설명되어 있다.
주어진 순환 소수 에서, , , 는 숫자 그룹이며, 는 의 자릿수를 나타낸다. 을 곱하면 순환 그룹과 종결 그룹이 분리된다.
만약 소수가 종결되면() 증명이 완료된다.[6] 이고 개의 자릿수가 있는 경우, 로 나타내며, 여기서 는 종결되는 숫자 그룹이다. 그러면,
여기서 는 ''i''번째 ''숫자''를 나타내고,
이므로,[7]
는 정수()와 유리수()의 합이므로 도 유리수이다.[8]
순환소수의 '''순환마디'''는 소수 부분의 주기적인 수열 중에서 최소 길이를 말한다. 예를 들어 = 0.3333…}}은 순환마디가 3이다. 순환마디의 마지막은 0이 될 수 있다. 예를 들어, = 2.370370… 의 순환마디는 370이다. 순환마디의 시작은 소수 둘째 자리 이후에 나타날 수 있다. 예를 들어, 십진법 = 0.04629629… 의 순환마디는 소수 셋째 자리부터인 629이다.
어떤 수가 유한소수로 나타낼 수 있는지는 기수에 따라 다르며, 기약분수의 분모가 기수의 거듭제곱을 나눌 수 있는 경우에만 해당 수는 유한소수로 나타낼 수 있다. 따라서 어떤 기약분수가 순환소수로 표시되는지도 기수에 따라 달라진다. 예를 들어 는 십진법에서는 유한소수 0.2로 나타내지만, 이진법에서는 순환소수 0.00110011…으로 나타낸다.
유한소수는 마지막 자릿수 뒤에 0을 무한히 나열한다고 보면 형식적으로 순환소수로 간주할 수 있다. 마찬가지로, 0.999... 등의 수열을 이용하여 유한소수를 순환소수로 고쳐 쓸 수도 있다.
순환 소수(무한 소수)의 순환마디가 "0" 또는 "9"인 경우, 둘 다 실질적으로는 유한 소수가 된다. 일반적으로 양의 실수에 대해 유한 소수는 두 종류의 순환 소수로 나타낼 수 있으며, 반대로 두 가지 방법으로 소수 표시가 가능한 것은 그 중 하나가 유한 소수인 경우에 한한다.
예를 들어, 1은 1.0000…으로 나타낼 수 있으며, 이는 순환마디가 0인 순환 소수이다. 한편, 끝자리의 1을 1 줄여 0으로 하고, 그 다음을 모두 9로 한 0.999...와 같다고도 생각할 수 있다. 이는 순환마디가 9인 순환 소수가 된다.
0.9999… = 1은 다음과 같이 증명할 수 있다.
:로 한다.
:
:
:
: 1}}
마찬가지로, 십이진법의 은 소수 표시가 0.4이지만, 이는 0.4000…이라는 것이며, 순환마디가 0인 순환 소수이다. 한편, 0.3BBB…라고도 생각할 수 있으며, 이는 순환마디가 B(11)인 순환 소수가 된다.
마찬가지로, 이십진법의 도 보통 0.4로 나타내지만, 이는 0.4000…이라는 것이며, 순환마디가 0인 순환 소수이다. 한편, 0.3JJJ…라고도 생각할 수 있으며, 이는 순환마디가 J(19)인 순환 소수가 된다.
유리수가 유한 소수 표기를 갖는 것은, 십진법 표기라면, 분모의 소인수가 2, 5 뿐일 때 에 한한다. 일반적인 진법 표기에서는, 분모의 소인수가 의 소인수가 되어야 한다. 예를 들어, 십팔진법이라면 분모의 소인수가 2, 3 뿐일 때이다.
순환소수로 표시되는 수는 정수의 분수로도 나타낼 수 있으며, 유리수에 포함된다. 반면, 유한하지 않은 비순환 소수로 표시되는 수가 존재하며, 이는 유리수에 포함되지 않는다. 실수 중 유리수에 포함되지 않는 수를 무리수라고 한다。무리수의 예로는 2의 제곱근이나 원주율이 있다. 앞서 언급했듯이 유한소수도 순환소수로 나타낼 수 있으며, 유리수는 모두 순환소수로 나타낼 수 있지만, 반대로 순환소수로 나타낼 수 있는 실수는 유리수에 한정된다。
6. 순환마디의 길이
어떤 정수 분수 에 대해, 나눗셈 과정에서 나머지가 0이 되지 않으면, 나눗셈은 영원히 계속된다. 결국에는 이전에 나타났던 나머지가 다시 나타나게 되는데, 이때부터 같은 몫과 나머지가 반복된다. 이렇게 반복되는 일련의 숫자들을 "순환마디"라고 부르며, 이는 0보다 큰 특정 길이를 가지며, "주기"라고도 한다.[5]
10진법에서 분수는 기약분수로 나타냈을 때, 분모가 2나 5 이외의 소인수를 가지면 순환소수를 가진다.
다음은 분수 (''n'' = 1, 2, 3, ...)의 십진법 반복절의 길이 ''ℓ''10(''n'')을 나타낸 표이다.
분수 , ''n'' = 1, 2, 3, ...의 십진법 반복절의 길이 ''ℓ''10(''n'')은 다음과 같다.
: 0, 0, 1, 0, 0, 1, 6, 0, 1, 0, 2, 1, 6, 6, 1, 0, 16, 1, 18, 0, 6, 2, 22, 1, 0, 6, 3, 6, 28, 1, 15, 0, 2, 16, 6, 1, 3, 18, 6, 0, 5, 6, 21, 2, 1, 22, 46, 1, 42, 0, 16, 6, 13, 3, 2, 6, 18, 28, 58, 1, 60, 15, 6, 0, 6, 2, 33, 16, 22, 6, 35, 1, 8, 3, 1, 18, 6, 6, 13, 0, 9, 5, 41, 6, 16, 21, 28, 2, 44, 1, 6, 22, 15, 46, 18, 1, 96, 42, 2, 0... .
자연수의 역수의 순환절 길이에 대해, 특정 길이가 되는 최소의 자연수를 순환절 길이 0부터 작은 순서대로 나열하면 다음과 같다.
: 1, 3, 11, 27, 101, 41, 7, 239, 73, 81, 451, 21649, 707, 53, 2629, 31, 17, 2071723, 19, 1111111111111111111, 3541, 43, 23, 11111111111111111111111, 511, 21401, 583, 243, 29, 3191, 211, 2791, 353, 67, 103, 71, 1919, 2028119, 909090909090909091, …
2와 5[19] 이외의 소수 의 역수의 순환 마디 길이는 의 약수이다. 유한 소수의 순환 마디 길이를 1로 한다면, 2와 5도 이 조건을 만족한다.
일반적으로, 분모가 2 또는 5가 아닌 소수인 (즉, 10과 서로소인) 기약 분수는 항상 순환 소수를 생성한다.[19]
미첼(Mitchell)[13]과 딕슨(Dickson)[14]은 순환소수의 다양한 성질을 제시하였다. 그 중 순환마디의 길이에 관한 성질은 다음과 같다.
- 정수 ''k''에 대한 의 순환마디의 길이는 항상 ≤ ''k'' − 1이다.
- 만약 ''p''가 소수라면, 의 순환마디는 ''p'' − 1을 나눈다.
- 만약 ''k''가 합성수라면, 의 순환마디는 엄밀하게 ''k'' − 1보다 작다.
- ''k''와 상대 소수인 ''c''에 대한 의 순환마디는 의 순환마디와 같다.
- 만약 ''k'' = 2''a''·5''b''·''n''이고, 여기서 ''n'' > 1이며, ''n''이 2나 5로 나누어 떨어지지 않는다면, 의 과도항의 길이는 max(''a'', ''b'')이고, 순환마디는 ''r''과 같은데, 여기서 ''r''은 10 mod n의 곱셈 차수이며, 이는 을 만족하는 가장 작은 정수이다.
- 만약 ''p'', ''p′'', ''p″'',...가 서로 다른 소수라면, 의 순환마디는 , , ,....의 순환마디의 최소공배수와 같다.
- 만약 ''k''와 ''k′''이 2 또는 5 이외의 공통 소인수를 갖지 않는다면, 의 순환마디는 와 의 순환마디의 최소공배수와 같다.
- 만약 소수 ''p''에 대해,
::
:가 어떤 ''m''에 대해 성립하지만,
::
:이라면, ''c'' ≥ 0에 대해,
::
6. 1. 소수의 역수
2와 5를 제외한 소수의 역수는 순환소수가 된다. 예를 들어, 1/7 = 0.142857이고, 1/17 = 0.0588235294117647이다. 이처럼 반복되는 부분을 순환마디라고 한다.(p는 소수)의 순환마디의 길이는 10 모듈로 ''p''의 곱셈 순서와 같다. 10이 모듈로 ''p''의 원시근이라면 순환마디의 길이는 ''p'' − 1과 같고, 그렇지 않다면 ''p'' − 1의 약수이다. 이는 페르마의 소정리에서 임을 통해 추론할 수 있다.[9]
만약 소수 ''p''에 대한 의 순환마디의 길이가 ''p'' − 1과 같다면, 그 순환마디는 '''순환수'''라고 불린다. 예를 들어 다음 분수들이 순환수에 속한다.
- = 0.142857 (6자리 반복)
- = 0.0588235294117647 (16자리 반복)
- = 0.052631578947368421 (18자리 반복)
순환수의 모든 "진분수" 배수(즉, 같은 자릿수를 갖는 배수)는 순환 순열이다. 예를 들어,
- = 1 × 0.142857 = 0.142857
- = 2 × 0.142857 = 0.285714
- = 3 × 0.142857 = 0.428571
의 나눗셈을 실행하면 순차적인 나머지는 순환 수열 가 된다.
순환 소수는 9의 보수 형태로 두 개의 수열로 나뉘는 짝수 길이의 순환 소수를 갖는다. 예를 들어 는 '142'로 시작하고 '857'이 뒤따르며, (순환에 의해)은 '857'로 시작하여 ''그것의'' 9의 보수 '142'가 뒤따른다.
일반적으로, 분모가 2 또는 5가 아닌 소수인 (즉, 10과 서로소인) 기약 분수는 항상 순환 소수를 생성한다.[19]
6. 2. 합성수의 역수
10과 서로소인 합성수의 역수는 순환소수가 되며, 순환마디의 길이는 카마이클 함수 등을 이용하여 계산할 수 있다.분모가 2 또는 5가 아닌 소수인 (즉, 10과 서로소인) 기약 분수는 항상 순환 소수를 생성한다. 1/''p''의 순환마디의 길이(반복되는 소수 부분의 주기)는 10 모듈로 ''p''의 곱셈 순서와 같다. 만약 10이 모듈로 ''p''의 원시근이라면, 순환마디의 길이는 ''p'' − 1과 같고, 그렇지 않다면 순환마디의 길이는 ''p'' − 1의 약수이다. 이 결과는 10''p''−1 ≡ 1 (mod ''p'')임을 나타내는 페르마의 소정리에서 추론할 수 있다.[5]
만약 ''p''가 2 또는 5가 아닌 소수라면, 분수 1/''p''2의 소수 표현은 순환 소수가 된다.
:1/'''49''' = 0.020408163265306122448979591836734693877551.
주기(반복 길이) ''L''(49)는 ''λ''(49) = 42의 약수여야 한다. 여기서 ''λ''(''n'')은 카마이클 함수라고 알려져 있다. 이는 정수 ''n''이 양수일 때
:am ≡ 1 (mod n)
''n''과 상호소수인 모든 정수 ''a''에 대해 이 조건을 만족하는 가장 작은 정수 ''m''이 ''λ''(''n'')이라는 카마이클 정리에서 비롯된다.
1/''p''2의 주기는 일반적으로 ''pT''''p''이며, 여기서 ''T''''p''는 1/''p''의 주기이다. 이것이 참이 아닌 세 개의 알려진 소수가 있으며, 이 경우 1/''p''2의 주기는 1/''p''의 주기와 같다. 이는 ''p''2이 10''p''−1−1을 나누기 때문입니다. 이 세 소수는 3, 487, 56598313이다.[12]
마찬가지로, 1/''p''''k''의 주기는 일반적으로 ''p''''k''–1''T''''p''이다.
만약 ''p''와 ''q''가 2 또는 5가 아닌 소수라면, 분수 1/''pq''의 소수 표현은 순환 소수가 된다. 예시는 1/119이다.
:'''119''' = 7 × 17
:''λ''(7 × 17) = LCM(''λ''(7), ''λ''(17)) = LCM(6, 16) = 48,
여기서 LCM은 최소공배수를 나타낸다.
1/''pq''의 주기 ''T''는 ''λ''(''pq'')의 약수이며, 이 경우 48이다.
:1/119 = 0.008403361344537815126050420168067226890756302521.
1/''pq''의 주기 ''T''는 LCM(''T''''p'', ''T''''q'')이며, 여기서 ''T''''p''는 1/''p''의 주기이고 ''T''''q''는 1/''q''의 주기이다.
만약 ''p'', ''q'', ''r'' 등이 2 또는 5가 아닌 소수이고, ''k'', ''ℓ'', ''m'' 등이 양의 정수라면,
:
는 주기가
:
인 순환 소수이며, 여기서 ''Tpk'', ''Tqℓ'', ''Trm'',...는 위에서 정의된 바와 같이 각각 순환 소수 1/''pk'', 1/''qℓ'', 1/''rm'',...의 주기이다.
6. 3. 10과 서로소가 아닌 수의 역수
10과 서로소가 아니지만 2나 5 이외의 소인수를 갖는 정수의 역수는 혼순환소수가 된다. 이러한 수는 다음과 같이 표현할 수 있다.[5]:
여기서 ''a''와 ''b''는 둘 다 0이 아니고, ''p'', ''q'' 등은 2나 5가 아닌 소수이다.
이 분수는 또한 다음과 같이 표현할 수 있다.
: (''a'' > ''b''인 경우)
: (''b'' > ''a''인 경우)
: (''a'' = ''b''인 경우)
이러한 소수는 다음과 같은 특징을 갖는다.
- 소수점 뒤에 최대 max(''a'', ''b'') 자릿수의 초기 비반복 구간(과도 상태)이 나타난다. 이 구간의 일부 또는 모든 숫자는 0일 수 있다.
- 이후 분수와 동일한 순환마디가 반복된다.
예를 들어, = 0.03에서
- ''a'' = 2, ''b'' = 0, 나머지 인수 이다.
- 03은 2개의 초기 비반복 숫자이다.
- 571428은 6개의 반복 숫자이며, 이는 }의 순환마디와 같다.
다음은 분수와 그 값, 순환마디의 길이를 나타낸 표이다.
7. 다른 기수법
분수로 표현된 유리수는 십진법뿐만 아니라 이진법, 십이진법 등 다른 기수법에서도 순환소수로 나타낼 수 있다. 어떤 수가 유한소수로 나타낼 수 있는지는 기수에 따라 다르며, 기약분수의 분모가 기수의 거듭제곱으로 나누어 떨어지는 경우에만 해당 수는 유한소수로 나타낼 수 있다. 따라서 어떤 기약분수가 순환소수로 표시되는지도 기수에 따라 달라진다. 예를 들어 1/5는 십진법에서는 유한소수 0.2로 나타내지만, 이진법에서는 순환소수 0.00110011…으로 나타낸다.
순환마디의 길이는 기수에 따라 달라지는데, 예를 들어 십이진법에서 1/5 = 0.24972497…는 순환마디가 4이고, 1/7 = 0.186A35186A35…는 순환마디가 6이다.
; 반드시 순환 소수가 되는 예
- N진법 표기에서 1/(N-1)의 소수는 반드시 0.1111…이 된다. 구진법의 경우 1/8 = 0.1111…이 되고, 십진법의 경우 1/9 = 0.1111…이 된다.
- 곱셈표의 마지막에 오는 (10-1)²의 역수는 정수 두 번째 자리에 오는 수가 빠지고, (10-1)자리의 순환 소수가 된다. 예를 들어, 육진법의 경우 5²의 역수는 1/41 = 0.0123501235…가 되어, 4가 빠지고 순환마디는 5자리가 된다. 구진법의 경우 8²의 역수는 1/71 = 0.0123456801234568…이 되어, 7이 빠지고 순환마디는 8자리가 된다.
- 여러 자리수로 일의 자리가 1인 수를 역수로 하면 순환 소수가 된다. 예를 들어, 십이진법의 경우 1/31 = 0.03A85232B03A85232B…가 되고, 십육진법의 경우 1/21 = 0.07C1F07C1F…가 된다.
; 순환마디가 짧아지는 예
순환마디의 길이는 10-1 및 10n-1을 소인수 분해했을 때 어떤 수가 오느냐에 따라 결정된다.
8. 응용
순환소수는 암호학 및 오류 정정 코딩 분야에서 활용될 수 있다.[16] 이러한 응용 분야에서는 일반적으로 2를 밑으로 하는 순환소수가 사용되며, 이는 이진 시퀀스를 생성한다. ''p''가 소수이고 2가 ''p''의 원시근일 때, 최대 길이 이진 시퀀스(Maximum Length Binary Sequence)는 다음과 같다.[17]
:
주기 ''p'' − 1의 이러한 시퀀스는 이동에 대해 -1의 음의 피크를 갖는 자기 상관 함수를 갖는다. 이러한 시퀀스의 무작위성은 다이하드 테스트에 의해 조사되었다.[18]
9. 기타
곱셈에서 순환소수의 순환적 거동은 특정 숫자로 곱할 때 순환 순열되는 정수의 구성으로도 이어진다. 예를 들어 102564 × 4 = 410256이다. 102564는 4/39의 반복절이고 410256은 16/39의 반복절이다.[13][14]
순환소수의 다양한 성질은 다음과 같다.
- 정수 ''k''에 대한 1/''k''의 순환마디의 길이는 항상 ''k'' − 1보다 작거나 같다.
- 만약 ''p''가 소수라면, 1/''p''의 순환마디는 ''p'' − 1을 나눈다.
- 만약 ''k''가 합성수라면, 1/''k''의 순환마디는 ''k'' − 1보다 작다.
- ''k''와 상대 소수인 ''c''에 대한 ''c''/''k''의 순환마디는 1/''k''의 순환마디와 같다.
- 만약 ''k'' = 2''a''·5''b''·''n''이고, 여기서 ''n'' > 1이며, ''n''이 2나 5로 나누어 떨어지지 않는다면, 1/''k''의 과도항의 길이는 max(''a'', ''b'')이고, 순환마디는 ''r''과 같은데, 여기서 ''r''은 10 mod n의 곱셈 차수이며, 이는 10''r'' ≡ 1 (mod ''n'')을 만족하는 가장 작은 정수이다.
- 만약 ''p'', ''p′'', ''p″'',...가 서로 다른 소수라면, 1/(''p'' ''p′'' ''p″'' ⋯)의 순환마디는 1/''p'', 1/''p′'', 1/''p″'',....의 순환마디의 최소공배수와 같다.
- 만약 ''k''와 ''k′''이 2 또는 5 이외의 공통 소인수를 갖지 않는다면, 1/(''k k′'')의 순환마디는 1/''k''와 1/''k′''의 순환마디의 최소공배수와 같다.
- 만약 소수 ''p''에 대해,
::
:가 어떤 ''m''에 대해 성립하지만,
::
:이라면, ''c'' ≥ 0에 대해,
::
- 만약 ''p''가 1로 끝나는 '''적절한 소수'''라면, 즉 1/''p''의 순환마디가 길이 ''p'' − 1의 순환수이고, ''p'' = 10''h'' + 1인 경우, 여기서 ''h''는 각 숫자 0, 1, ..., 9가 순환마디에 정확히 ''h'' = (''p'' − 1)/10번 나타난다.
순환마디의 다른 성질에 대해서는 다음 자료를 참고할 수 있다.[15]
참조
[1]
서적
What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed.
Oxford University Press
[2]
논문
Why Does 0.999... = 1?: A Perennial Question and Number Sense
[3]
웹사이트
Lambert's Original Proof that π is irrational.
https://math.stackex[...]
2023-12-19
[4]
간행물
Aide-mémoire
LEP
[5]
문서
For a base b and a divisor n, in terms of group theory this length divides
[6]
웹사이트
Rational numbers have repeating decimal expansions
https://www.aapelivu[...]
2023-12-23
[7]
웹사이트
The Sets of Repeating Decimals
https://www.sjsu.edu[...]
2023-12-23
[8]
웹사이트
Prove that every repeating decimal represents a rational number
https://www.stumblin[...]
2023-12-23
[9]
논문
Digital roots and reciprocals of primes
2000-03
[10]
서적
History of the Theory of Numbers
Chelsea Publishing Co.
[11]
논문
Some Properties of Repetends
1887-08
[12]
서적
Recreations in the Theory of Numbers
[13]
논문
A nonlinear random number generator with known, long cycle length
1993-01
[14]
서적
History of the Theory of Numbers
Chelsea Publ. Co.
[15]
논문
Some properties of repetends
2003-11
[16]
논문
On decimal sequences
1981-09
[17]
논문
Encryption and error-correction using d-sequences
[18]
논문
Randomness of D sequences via diehard testing
[19]
웹사이트
循環節
http://math.sakura.n[...]
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com
