맨위로가기

오일러 공식

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

오일러 공식은 1740년경 레온하르트 오일러가 유도한 공식으로, 지수 함수와 삼각 함수 간의 관계를 나타낸다. 이 공식은 복소 평면에서 복소수를 표현하고, 삼각 함수를 지수 함수로 표현하는 데 사용되며, 복소수의 로그를 정의하는 데에도 활용된다. 오일러 공식은 다양한 유도 방법이 존재하며, 복소수 이론, 삼각법, 위상수학, 전기 공학 등 여러 분야에 응용된다. 오일러 공식에 x = π를 대입하면 오일러 등식 e^(iπ) + 1 = 0이 도출되는데, 이는 수학의 아름다움을 나타내는 공식으로 여겨진다.

더 읽어볼만한 페이지

  • 항등식 - 피어츠 항등식
    피어츠 항등식은 디랙 스피너와 바일 스피너의 곱셈 결과를 나타내는 관계식으로, 디랙 스피너는 스칼라, 벡터, 텐서, 축벡터, 유사스칼라 간의 곱셈 결과를 표로 나타내며, 바일 스피너는 반가환성을 만족하는 특정 형태를 가진다.
  • 항등식 - 삼각 함수 항등식
    삼각 함수 항등식은 삼각함수들의 정의, 주기성, 대칭성, 이동, 피타고라스 정리, 덧셈 정리 등을 포함하는 삼각함수들 사이의 관계를 나타내는 등식이다.
  • 레온하르트 오일러 - 오일러-라그랑주 방정식
    오일러-라그랑주 방정식은 변분법으로 범함수의 정류점을 찾는 편미분 방정식으로, 라그랑주 역학 등 다양한 분야에 활용되며 뉴턴 역학을 일반화한 것으로 여겨진다.
  • 레온하르트 오일러 - 오일러-마스케로니 상수
    오일러-마스케로니 상수 \gamma는 조화급수와 자연로그 함수의 차이의 극한으로 정의되는 수학 상수로, 감마 함수, 리만 제타 함수 등 다양한 수학적 개념과 관련되어 있으며 유리수인지 무리수인지 밝혀지지 않은 미해결 문제이다.
  • 초등대수학 - 이차 방정식
    이차 방정식은 최고차항이 2차인 대수 방정식으로, ax^2 + bx + c = 0 형태로 표현되며 근의 공식으로 해를 구하고 판별식에 따라 실근 또는 허근을 가지며 여러 분야에 응용된다.
  • 초등대수학 - 방정식
    방정식은 수학에서 두 식이 등호로 연결된 형태로, 미지수의 값을 구하는 것을 목표로 하며, 다양한 종류로 분류되어 여러 수학 및 과학 분야에서 활용된다.
오일러 공식
설명
유형수학 공식
분야수학, 물리학
명명자레온하르트 오일러
형태
공식e^(ix) = cos(x) + i sin(x)
설명e: 자연 상수
i: 허수 단위
cos: 코사인 함수
sin: 사인 함수
x: 실수
특수한 경우
x = πe^(iπ) + 1 = 0 (오일러 등식)
활용
응용 분야복소 해석학
푸리에 해석
삼각 함수 간략화

2. 역사

1714년 로저 코츠가 다음과 같은 형태의 공식을 처음 발견하였다.[28]

: \ln(\cos x + i\sin x) \,=\, ix

1740년경 레온하르트 오일러는 지수 함수와 삼각 함수 표현의 급수 전개를 비교하여 현재와 같은 형태의 오일러 공식을 유도했다.[6][4] 이 공식은 1748년 그의 저서 ''무한소 해석 입문''에서 처음 출판되었다.[7]

그러나 로저 코츠와 오일러 모두 이 공식이 지닌 '복소수를 복소평면 위의 하나의 점으로 볼 수 있다'는 기하학적 의미를 인지하지 못했고, 이는 약 50년 후 카스파르 베셀에 의해 설명되었다.[28]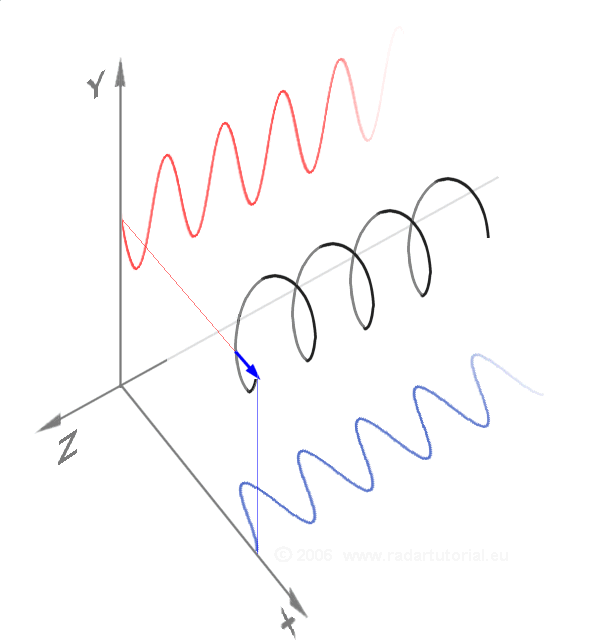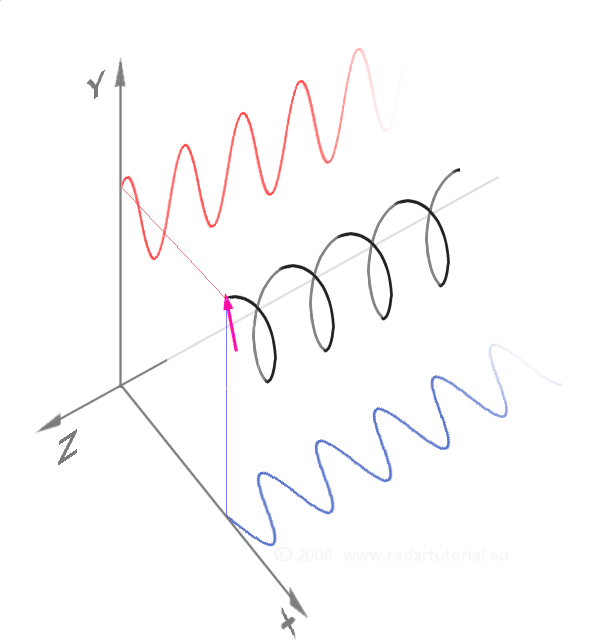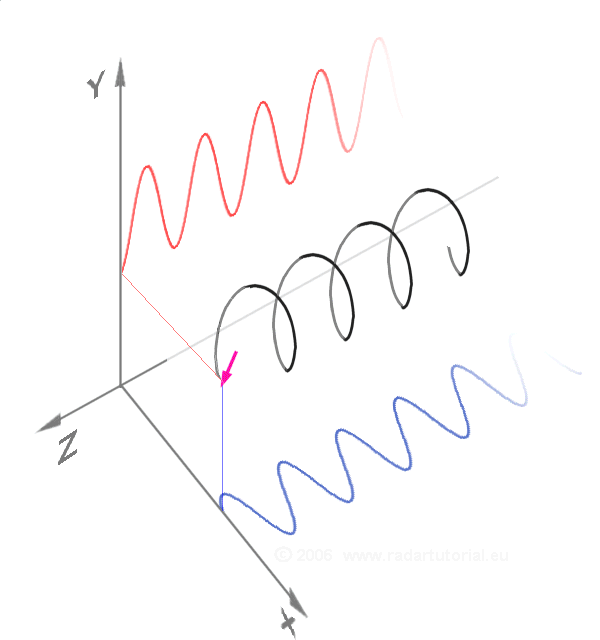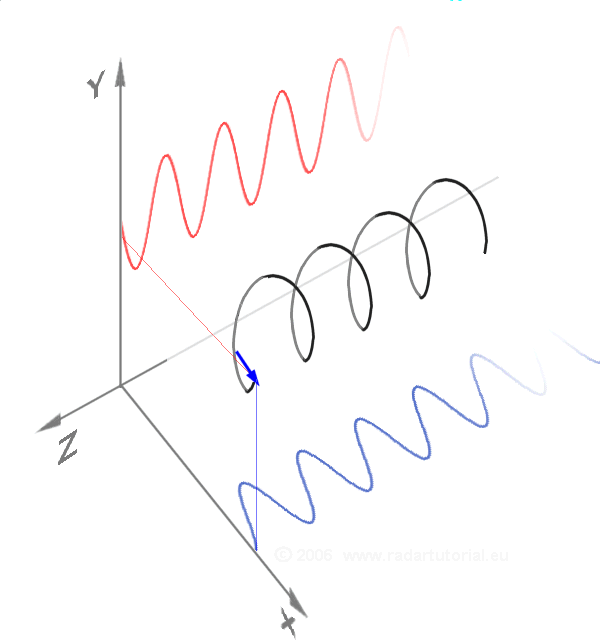

3차원 공간에서 오일러 공식을 나선형으로 시각화한 그림.

3. 공식 유도

지수 함수와 삼각 함수를 매클로린 급수로 전개하거나, 드 무아브르의 정리를 이용하거나, 미분 계산 또는 미분방정식을 이용하여 오일러 공식을 유도할 수 있다.


  • '''테일러 급수를 이용한 방법'''은 하위 섹션에서 상세히 다룬다.

  • '''드 무아브르의 정리를 이용한 방법''': 드 무아브르의 정리에 의해 다음이 성립한다.

:\begin{align}

\cos n\theta+i\sin n\theta

&=(\cos \theta+i\sin \theta)^n,\\

\cos n\theta-i\sin n\theta

&=(\cos \theta-i\sin \theta)^n.

\end{align}

양변을 더하면

:2\cos n\theta = (\cos \theta+i\sin \theta)^n+(\cos \theta-i\sin \theta)^n.

을 얻고, 우변의 두 항을 이항 정리에 따라 전개하여 정리하면,

:\cos n\theta

=\sum_{k=0}^{\left[\tfrac{n}{2}\right]} (-1)^k\binom{n}{2k}\ (\cos \theta)^{n-2k}(\sin \theta)^{2k}

=\sum_{k=0}^{\left[\tfrac{n}{2}\right]} (-1)^k\binom{n}{2k}\ (\cos \theta)^n (\tan \theta)^{2k}

을 얻는다. 여기서 n\theta = x로 치환하고, n \rightarrow \infty의 극한을 취하면 오일러 공식을 얻을 수 있다.

  • '''미분 계산을 이용한 방법''': 함수 f(x) = e^{-ix}(\cos x + i\sin x)를 정의하고 x에 대해 미분하면 f'(x) = 0을 얻는다. 따라서 f(x)는 상수함수이고, f(0) = 1이므로 f(x) = 1이다. 이를 정리하면 오일러 공식을 얻는다.[9][10]

  • '''미적분을 이용한 방법''': 복소수 z = \cos x + i\sin x를 x에 대해 미분하고, i^2 = -1임을 이용하여 정리하면 \frac{dz}{dx}=iz를 얻는다. 변수를 분리하여 적분하면 \ln z = ix + C (C는 적분 상수)를 얻고, 초기 조건 x=0을 대입하면 C=0임을 알 수 있다. 따라서 z = e^{ix}이고, 이를 정리하면 오일러 공식을 얻는다.[12]

  • '''미분방정식을 이용한 방법''': 함수 g(x) = e^{ix}의 도함수와 이계도함수를 구하면 g''(x) + g(x) = 0 이라는 2차 선형 미분방정식을 얻는다. 이 미분방정식의 일반해는 g(x) = A \cos x + B \sin x (A, B는 상수)이고, 초기 조건 g(0) = 1 과 g'(0) = i를 대입하면 A = 1, B = i를 얻는다. 따라서 g(x) = e^{ix} = \cos x + i \sin x이다.[20][26]

3. 1. 테일러 급수를 이용한 방법

테일러 급수에 따라 실수 범위에서 다음 식이 성립한다.[11][16][17][18][23][24][27][29]

:e^x = \sum^{\infin}_{n=0}{\frac{x^n}{n!}}

:\cos x = \sum^{\infin}_{n=0}{\frac{(-1)^n}{(2n)!}}x^{2n}

:\sin x = \sum^{\infin}_{n=0} \frac{(-1)^n}{(2n+1)!} x^{2n+1}

이때 x가 복소수일 때에 앞의 무한급수를 각각의 함수로 정의한다. 그러면

:

\begin{align}

e^{iz} &{}= 1 + iz + \frac{(iz)^2}{2!} + \frac{(iz)^3}{3!} + \frac{(iz)^4}{4!} + \frac{(iz)^5}{5!} + \frac{(iz)^6}{6!} + \frac{(iz)^7}{7!} + \frac{(iz)^8}{8!} + \cdots \\

&{}= 1 + iz - \frac{z^2}{2!} - \frac{iz^3}{3!} + \frac{z^4}{4!} + \frac{iz^5}{5!} - \frac{z^6}{6!} - \frac{iz^7}{7!} + \frac{z^8}{8!} + \cdots \\

&{}= \left( 1 - \frac{z^2}{2!} + \frac{z^4}{4!} - \frac{z^6}{6!} + \frac{z^8}{8!} - \cdots \right) + i\left( z - \frac{z^3}{3!} + \frac{z^5}{5!} - \frac{z^7}{7!} + \cdots \right) \\

&{}= \cos z + i\sin z

\end{align}



가 된다.

이 공식을 이해하기 위해서는 멱급수가 무엇인지 알고 있어야 한다. 멱급수란 하나의 수의 지수를 증가시키며 모두 더한 값을 말하며, 지수함수의 멱급수는 다음과 같다.

:e^x=1+x+\frac{x^2}{2}+\frac{x^3}{3\times2}+\frac{x^4}{4\times3\times2}+\cdot\cdot\cdot



이 멱급수의 지수 x에 iz(복소수에 임의의 수 z를 곱한 값)을 추가하면, i\sin z에 \cos z를 더한 값과 완벽하게 일치한다.

즉, e^{iz} \,=\, \cos z + i\sin z가 성립하는 것이다.

의 테일러 급수의 처음 몇 개 항의 플롯 .


의 거듭제곱에 대한 기본적인 사실뿐만 아니라 멱급수 전개를 사용하여 오일러 공식을 증명할 수 있다.

위에서 제시된 멱급수 정의를 사용하여 x의 실수 값에 대해 다음과 같이 전개할 수 있다.

:\begin{align}

e^{ix} &= 1 + ix + \frac{(ix)^2}{2!} + \frac{(ix)^3}{3!} + \frac{(ix)^4}{4!} + \frac{(ix)^5}{5!} + \frac{(ix)^6}{6!} + \frac{(ix)^7}{7!} + \frac{(ix)^8}{8!} + \cdots \\[8pt]

&= 1 + ix - \frac{x^2}{2!} - \frac{ix^3}{3!} + \frac{x^4}{4!} + \frac{ix^5}{5!} - \frac{x^6}{6!} - \frac{ix^7}{7!} + \frac{x^8}{8!} + \cdots \\[8pt]

&= \left( 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \frac{x^8}{8!} - \cdots \right) + i\left( x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots \right) \\[8pt]

&= \cos x + i\sin x ,

\end{align}

마지막 단계에서 두 항이 \cos x와 \sin x의 매클로린 급수임을 알 수 있다. 각 급수가 절대 수렴하기 때문에 항의 재배열이 가능하다.

실함수로서의 지수 함수 e^x, 삼각 함수 \cos x, \sin x를 각각 매클로린 급수로 전개하면 다음과 같다.

:e^x = \textstyle\sum\limits_{n=0}^{\infin} \dfrac{x^n}{n!} \quad (x \in \mathbb{R} )

:\cos x = \textstyle\sum\limits_{n=0}^{\infin} \dfrac{(-1)^n}{(2n)!} \, x^{2n} \quad (x \in \mathbb{R} )

:\sin x = \textstyle\sum\limits_{n=0}^{\infin} \dfrac{(-1)^n}{(2n+1)!} \, x^{2n+1} \quad (x \in \mathbb{R} )

이들 멱급수의 수렴 반경이 무한대(\infty)임은 달랑베르의 비율 판정법에 의해 확인할 수 있다. 따라서 이들 급수는 변수 x를 복소수 전체로 확장할 수 있으며, 광의 균등 수렴한다. 즉, 이들 급수로 표시되는 함수는 정함수이다. 해석적 연속하면, 일치 정리에 의해 복소수 전체에서의 정칙 함수로서의 확장은 유일하며, 이 수렴 멱급수로 표시된다.

여기서 e^x의 x를 ix로 바꾸고, e^{ix}의 멱급수가 절대 수렴하므로 급수의 항의 순서는 임의로 교환 가능하다는 점을 고려하면 다음과 같다.

:\begin{align}

e^{ix}

&= \textstyle\sum\limits^{\infin}_{n=0} \dfrac{i^n}{n!} x^n \\

&= \textstyle\sum\limits^{\infin}_{n=0} \dfrac{i^{2n}}{(2n)!}x^{2n} + \sum\limits_{n=0}^{\infin} \dfrac{i^{2n+1}}{(2n+1)!} x^{2n+1} \\

&= \textstyle\sum\limits_{n=0}^{\infin} \dfrac{(-1)^n}{(2n)!} x^{2n} + i \sum\limits_{n=0}^{\infin} \dfrac{(-1)^n}{(2n+1)!} x^{2n+1} \\

&= \cos x + i\sin x

\end{align}

드 무아브르의 정리를 이용한 증명은 다음과 같다.

드 무아브르의 정리에 의해

:\begin{align}

\cos n\theta+i\sin n\theta

&=(\cos \theta+i\sin \theta)^n,\\

\cos n\theta-i\sin n\theta

&=(\cos \theta-i\sin \theta)^n.

\end{align}

양변을 더하면

:2\cos n\theta = (\cos \theta+i\sin \theta)^n+(\cos \theta-i\sin \theta)^n.

우변의 두 항을 이항 정리에 따라 전개하면, i의 홀수 제곱 항은 상쇄되고, i의 짝수 제곱 항만 이중으로 더해지므로

:\begin{align}

\cos n\theta

&=\sum_{k=0}^{\left[\tfrac{n}{2}\right]} (-1)^k\binom{n}{2k}\ (\cos \theta)^{n-2k}(\sin \theta)^{2k}\\

&=\sum_{k=0}^{\left[\tfrac{n}{2}\right]} (-1)^k\binom{n}{2k}\ (\cos \theta)^n (\tan \theta)^{2k}

\end{align}

을 얻는다. 이것은 \cos \theta의 n 배각 공식의 닫힌 표시식이다([s]는 s의 정수 부분).

이 식에서 n\theta = x로 치환하면

:\cos x = \sum_{k=0}^{\infty} (-1)^k\binom{n}{2k}

\left(\cos \frac{x}{n}\right)^n \left(\tan \frac{x}{n}\right)^{2k}.

합의 상한을 \infty로 다시 썼지만, k > n/2일 때 이항 계수 부분이 0이 되므로 이는 n/2까지의 합과 같다.

n \rightarrow \infty의 극한에서는

:\cos \frac{x}{n} \sim 1\ ,\ \sin \frac{x}{n} \sim \frac{x}{n}\ ,\ \tan \frac{x}{n} \sim \frac{x}{n}

이 되어, 각 항에서 점근적으로 같다는 것을 확인할 수 있다.

따라서

:\binom{n}{2k} \sim \frac{n^{2k}}{(2k)!}\ ,\ \left(\cos \frac{x}{n}\right)^n \sim 1\ ,\ \left(\tan \frac{x}{n}\right)^{2k} \sim \frac{x^{2k}}{n^{2k}}

이 된다. 따라서

:\cos x = \sum^{\infin}_{k=0} \frac{(-1)^k}{(2k)!} x^{2k}

을 얻을 수 있다.

마찬가지로 \sin x에 대해 생각하면

:

\sin x = \sum_{k=0}^{\infty} (-1)^k\binom{n}{2k+1}

\left (\cos \frac{x}{n}\right)^n \left (\tan \frac{x}{n} \right)^{2k+1}



에서

:\sin x = \sum^{\infin}_{k=0} \frac{(-1)^k}{(2k+1)!} x^{2k+1}

을 얻는다.

여기서, n \rightarrow \infty의 극한을 취할 때 오차항의 거동을 고려한다.

:\cos \frac{x}{n} = 1+a_n

이라고 하면

:\begin{align}

\left(\cos \frac{x}{n} \right)^n

&= \left(1+a_{n} \right)^n\\

&= 1+na_n +\binom{n}{2} {a_n}^2+ \dotsb

\end{align}

이므로, a_n이 작을 때, n제곱하면 오차는 대략 n배 되지만, a_n이 1/n보다 빠르게 0에 가까워질 때에는 극한에 영향을 미치지 않는다.

본 논의에서

:\begin{align}

a_n &=\cos \frac{x}{n}-1\\

&=-2\sin^2 \frac{x}{2n}

\end{align}

이므로

:a_n \sim -\frac{x^2}{2n^2}

이 된다.

따라서, O-표기법을 이용하여 점근 거동을 나타내면

:\cos \frac{x}{n}=1+O\left(\frac{1}{n^2}\right).

따라서

:\lim_{n\rightarrow \infty}\left(\cos \frac{x}{n} \right)^n=1.

여기서, 드 무아브르의 정리에 되돌아가

:\cos n\theta+i\sin n\theta = (\cos \theta+i\sin \theta)^n.

위 식에서 n\theta = x로 놓으면

:\cos x+i\sin x = \left(\cos \frac{x}{n}+i\sin \frac{x}{n}\right)^n.

여기서, n \rightarrow \infty의 극한을 취했을 때

:\cos \frac{x}{n}+i\sin \frac{x}{n}=1+\frac{ix}{n}+O\left(\frac{1}{n^2}\right)

이므로

:\lim_{n\rightarrow \infty}\left(\cos \frac{x}{n}+i\sin \frac{x}{n}\right)^n

= \lim_{n\rightarrow \infty}\left(1+\frac{ix}{n}\right)^n = e^{ix}.

따라서

:e^{ix} = \cos x + i\sin x

을 얻을 수 있다.

3. 2. 미분 계산을 이용한 증명

함수 f(x) = e^{-ix}(\cos x + i\sin x)를 정의하고, x에 대해 미분하면 다음과 같다.

: \frac {d}{dx} f(x) = -ie^{-ix}(\cos x + i\sin x)+e^{-ix}(-\sin x + i\cos x) = e^{-ix}(-i \cos x + \sin x -\sin x + i\cos x) =0

따라서 f(x) = C (단, C는 상수)이다.

x=0 을 대입하면 f(0) = 1 이므로, C=1이다.

그러므로 e^{-ix}(\cos x + i\sin x) = 1 이고, 양변에 e^{ix}를 곱하면 오일러 공식 e^{ix} = (\cos x + i\sin x) 를 얻는다.[9][10]

이 증명은 삼각 함수와 지수 함수의 몫이 상수 함수 1임을 보여주며, 따라서 두 함수는 같아야 한다. (지수 함수는 0이 아니므로, 이것이 허용된다.)

다른 증명으로, 실수 변수 x의 함수 f(x) := (\cos x+i\sin x)\cdot e^{-ix}를 정의하고 x에 대해 미분하면 다음과 같다.

:

\begin{align}

f'(x)&= (\cos x+i\sin x)'\cdot e^{-ix} +(\cos x+i\sin x)\cdot (e^{-ix})' \\

&= (-\sin x+i\cos x)\cdot e^{-ix} -(\cos x+i\sin x)\cdot ie^{-ix} \\

&= (-\sin x+i\cos x-i\cos x+\sin x)\cdot e^{-ix} \qquad (i^2 = -1)\\

&= 0.

\end{align}

따라서 f(x)는 상수함수이고, f(0) = 1이므로, 모든 실수 x에 대해 f(x) = 1이다. 이를 식에 대입하고 정리하면 오일러 공식 e^{ix} =\cos x+i\sin x을 얻는다.[27]

3. 3. 미적분을 이용한 방법

복소수 z = \cos x + i\sin x를 생각하자.[12] 양변을 x에 대해 미분하면 \frac{dz}{dx} = -\sin x + i\cos x 이다. i^2 = -1이므로, \frac{dz}{dx}=i^2\sin x + i\cos x=i(\cos x + i\sin x)=iz이다.

z를 이항한 후 양변을 적분하면 다음과 같다.

:

\begin{align}

\frac{1}{z}\,\frac{dz}{dx}&= i \\

\int\frac{1}{z}\,dz&=\int i\,dx \\

\ln z&=ix + C

\end{align}



여기서 C는 적분 상수이다.

x=0일 때를 계산하면 \ln z = C 이고, z = \cos x + i\sin x = \cos 0 + i \sin 0 = 1이다. 따라서 \ln 1 = C 이므로, C = 0이다.

그러므로 다음 식이 성립한다.

:

\begin{align}

\ln z &= ix \\

z &= e^{ix} \\

e^{ix} &= \cos x + i\sin x

\end{align}


3. 4. 미분방정식을 이용한 방법

함수 g(x)를 g(x) = e^{ix}로 정의하면, 이 함수의 도함수와 이계도함수는 다음과 같다.

:

\begin{align}

g'(x) &= i e^{ix} \\

g''(x) &= i^2 e^{ix} = -e^{ix}

\end{align}



여기서 g''(x) = -g(x) 또는 g''(x) + g(x) = 0 이라는 2차 선형 미분방정식이 만들어진다. 이 미분방정식은 일차 독립인 두 해를 가진다.

:

\begin{align}

g_1(x) &= \cos x \\

g_2(x) &= \sin x

\end{align}



차수가 같은 미분방정식의 선형 결합도 해가 되므로, 위 미분방정식의 일반적인 해는 다음과 같다.

:

\begin{align}

g(x)

&= A g_1(x) + B g_2(x)\\

&= A \cos x + B \sin x\\

g'(x)

&=-A \sin x + B \cos x

\end{align}



여기서 A와 B는 상수이다.

함수 g(x)의 초기 조건 g(0) = e^{i0} = 1 과 g'(0) = i e^{i0} = i를 대입하면,

:

\begin{align}

g(0) &= A \cos 0 + B \sin 0 &= A \\

g'(0) &= -A \sin 0 + B \cos 0 &= B

\end{align}



즉, g(0) = A = 1 이고 g'(0) = B = i 이므로,

:g(x) \,=\, e^{ix} = \cos x + i \sin x이다.[20][26]

4. 응용

오일러 공식을 이용하면 복소수를 극형식으로 간소하게 표현할 수 있다. 복소수 는 로 나타낼 수 있으며, 특히 일 때 유도되는 는 '''오일러의 등식'''이라고 불린다.

오일러 공식을 통해 코사인 함수와 사인 함수를 쌍곡선 함수로 변환할 수 있다.[15]

:\cos \theta = \cosh i \theta

:\sin \theta = \tfrac{1}{i} \sinh i \theta

미분 방정식이나 푸리에 급수 등을 쉽게 다루기 위해 삼각 함수를 복소 지수 함수로 바꾸어 사용하기도 한다.[15]

전기 공학, 신호 처리 등에서는 주기적으로 변하는 신호를 분석하고 처리하는 데 오일러 공식을 활용한다. 푸리에 해석에서는 신호를 사인파 함수의 조합으로 설명하며, 오일러 공식을 통해 허수 지수를 갖는 지수 함수의 합으로 표현할 수 있다. 페이저 해석에서도 커패시터나 인덕터의 임피던스를 나타낼 때 오일러 공식을 사용한다.[15]

4. 1. 복소수 이론

오일러 공식은 복소수를 극형식으로 표현하고, 복소수의 곱셈, 거듭제곱 연산을 간편하게 수행할 수 있게 해준다.[29] 복소 평면에서 오일러 공식은 함수가 가 실수 전체에서 변함에 따라 복소 평면에서 단위 원을 그린다는 것을 보여준다. 여기서 는 원점과 단위 원 위의 점을 연결하는 선이 양의 실수 축과 이루는 각도로, 반시계 방향으로, 라디안으로 측정된다.

오일러 공식은 데카르트 좌표와 극좌표계 간의 변환 수단을 제공하며, 극좌표 형식은 복소수의 곱셈이나 거듭제곱에 사용될 때 수학을 단순화한다. 모든 복소수 와 켤레 복소수 는 다음과 같이 쓸 수 있다.

\begin{align}

z &= x + iy = |z| (\cos \varphi + i\sin \varphi) = r e^{i \varphi}, \\

\bar{z} &= x - iy = |z| (\cos \varphi - i\sin \varphi) = r e^{-i \varphi},

\end{align}

여기서

  • 는 실수 부분,
  • 는 허수 부분,
  • 는 의 크기,
  • 이다.


는 의 인수이며, 즉, 라디안으로 반시계 방향으로 측정된 ''x''축과 벡터 ''z'' 사이의 각도이며, 이는 의 덧셈까지 정의된다.

오일러 공식을 통해 복소수의 로그를 정의할 수 있다. 이를 위해 다음의 로그 정의와 지수 법칙을 사용한다.

a = e^{\ln a},

e^a e^b = e^{a + b},

위 식들은 모든 복소수 와 에 유효하다. 따라서 다음을 쓸 수 있다.

z = \left|z\right| e^{i \varphi} = e^{\ln\left|z\right|} e^{i \varphi} = e^{\ln\left|z\right| + i \varphi}

모든 에 대해. 양변에 로그를 취하면 다음이 나타난다.

\ln z = \ln \left|z\right| + i \varphi,

이것은 복소 로그의 정의로 사용될 수 있다. 복소수의 로그는 가 다중 값이기 때문에 다중값 함수이다.

마지막으로, 오일러 공식은 여러 삼각 항등식과 드 무아브르 공식을 유도하는데 사용된다.

4. 2. 삼각법

오일러 공식을 이용하면 삼각 함수와 쌍곡선 함수 사이의 관계를 파악할 수 있다. 오일러 공식, 삼각 함수의 정의, 그리고 지수 함수의 항등식을 통해 대부분의 삼각 항등식을 쉽게 유도할 수 있다.[13] 이는 해석학과 삼각법을 연결하며, 사인 함수와 코사인 함수를 지수 함수의 가중 합으로 해석할 수 있게 해준다.

:\cos x = \operatorname{Re} \left(e^{ix}\right) =\frac{e^{ix} + e^{-ix}}{2}, \\

:\sin x = \operatorname{Im} \left(e^{ix}\right) =\frac{e^{ix} - e^{-ix}}{2i}.

위의 두 방정식은 오일러 공식을 더하거나 빼고, 코사인이나 사인에 대해 풀어서 얻을 수 있다.

:e^{ix} = \cos x + i \sin x,

:e^{-ix} = \cos(- x) + i \sin(- x) = \cos x - i \sin x

이 공식들은 복소수 인자 x에 대한 삼각 함수의 정의로 사용될 수 있다. 예를 들어, x = iy로 놓으면 다음과 같다.

:\cos iy = \frac{e^{-y} + e^y}{2} = \cosh y,

:\sin iy = \frac{e^{-y} - e^y}{2i} = \frac{e^y - e^{-y}}{2}i = i\sinh y.

또한 다음이 성립한다.

:\cosh ix = \frac{e^{ix} + e^{-ix}}{2} = \cos x,

:\sinh ix = \frac{e^{ix} - e^{-ix}}{2} = i\sin x.

복소 지수 함수는 사인 및 코사인 성분보다 다루기 쉽기 때문에, 복소 지수 함수를 이용하면 삼각 함수 계산을 단순화할 수 있다.[13] 예를 들어 사인과 코사인을 지수 함수와 관련된 표현으로 변환하여 문제를 해결할 수 있다.

4. 3. 위상수학

위상수학에서 오일러 공식은 허수 지수 함수 t \mapsto e^{it}가 실수선 \mathbb R에서 단위 원 \mathbb S^1으로 가는 전사 사상이라고 해석할 수 있다. 이는 \mathbb R을 \mathbb S^1의 덮개 공간으로 나타낸다. 오일러 항등식은 이 사상의 커널이 \tau \mathbb Z (\tau = 2\pi)임을 나타낸다.

오일러 공식과 항등식을 결합한 가환도표

4. 4. 기타 응용

전기 공학, 신호 처리 등에서 주기적으로 변하는 신호를 분석하고 처리하는 데 오일러 공식을 활용한다. 예를 들어 푸리에 해석에서는 신호를 사인파 함수의 조합으로 설명하며, 오일러 공식을 통해 허수 지수를 갖는 지수 함수의 합으로 표현할 수 있다. 페이저 해석에서도 오일러 공식을 사용하여 커패시터나 인덕터의 임피던스를 나타낸다.[15]

미분 방정식을 풀 때, 최종 해가 사인과 코사인을 포함하는 실수 함수이더라도, 지수 함수 가 미분 연산의 고유 함수이기 때문에 오일러 공식을 써서 해를 단순화하기도 한다. 즉, 미분 방정식이나 푸리에 급수 등을 쉽게 다루기 위해 삼각 함수를 복소 지수 함수로 바꾸어 사용한다.

5. 오일러 등식

오일러 공식에서 x|x영어 = π 를 대입하면, eiπ + 1 = 0 이라는 오일러 등식을 얻을 수 있다. 오일러 등식은 수학에서 가장 아름다운 공식 중 하나로 여겨지며, 5개의 기본적인 수학 상수(0, 1, e, i, π)와 3개의 기본적인 수학 연산(덧셈, 곱셈, 거듭제곱)을 모두 포함한다. 소설 "박사가 사랑한 수식"에서 오일러 등식이 중요한 모티브로 사용되었다.[15]

참조

[1] 서적 A Course in Complex Analysis in One Variable https://books.google[...] World Scientific Publishing Co.
[2] 서적 The Feynman Lectures on Physics, vol. I https://feynmanlectu[...] Addison-Wesley
[3] 문서
[4] 서적 Mathematics and Its History https://books.google[...] Springer
[5] 서적 Euler's Greatest Hits https://books.google[...] Mathematical Association of America
[6] 문서 Chapter 8: On transcending quantities arising from the circle http://www.17century[...] Introduction to the Analysis of the Infinite
[7] 문서
[8] 간행물 Solution d'un problème concernant le calcul intégral, avec quelques abrégés par rapport à ce calcul 1702
[9] 서적 Mathematical Analysis Pearson 1974
[10] 웹사이트 How to prove Euler's formula: $e^{i\varphi}=\cos(\varphi) +i\sin(\varphi)$? https://math.stackex[...] 2018-06-25
[11] 서적 A Modern Introduction to Differential Equations https://books.google[...] Elsevier Science 2016-03-23
[12] 서적 Calculus http://ocw.mit.edu/r[...] Wellesley-Cambridge
[13] 웹사이트 Complex Sinusoids https://ccrma.stanfo[...] 2024-09-10
[14] 웹사이트 The Tau Manifesto http://tauday.com/ta[...] 2013-09-14
[15] 서적 Mathematics and Its History https://books.google[...] Springer
[16] 문서
[17] 문서
[18] 문서
[19] 문서
[20] 문서
[21] 문서
[22] 웹사이트 2階微分方程式 http://www.is.oit.ac[...]
[23] 문서
[24] 웹사이트 オイラーの数学から — 『無限解析序説』への招待 － 野海 正俊 http://www.sci.kobe-[...]
[25] 웹사이트 複素数の取り扱いとオイラーの公式 https://web.archive.[...]
[26] 웹사이트 "{{math|e{{sup|π''i''}} + 1 =\n{{#invoke:documentation|main|_content={{ {{#invoke:documentation|contentTitle}}}}}} 0}}" http://sci-tech.ksc.[...]
[27] 웹사이트 複素関数を学ぶ人のために － 山口大学 理学部 物理・情報科学科 - 芦田 正巳 http://collie.low-te[...]
[28] 문서
[29] 서적 수학 100


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com