분할복소수

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

분할복소수는 실수 x, y와 쌍곡 단위 j (j² = +1)로 구성된 수 z = x + jy로 정의된다. 이는 복소수와 유사하지만, 허수 단위 i (i² = -1) 대신 쌍곡 단위를 사용하며, 덧셈과 곱셈 연산이 정의된다. 분할복소수는 2차원 실수 가환 결합 대수를 이루며, 두 실수체의 직접곱과 환 동형이다. 분할복소수는 영인자를 가지며, 기하학적으로는 민코프스키 평면의 기하학을 설명하는 데 사용된다. 분할복소수의 절댓값은 쌍곡선을 정의하며, 곱셈은 쌍곡선 회전(로렌츠 부스트)을 나타낸다. 제임스 코클은 분할복소수와 유사한 대수를 처음 사용했으며, 윌리엄 클리퍼드는 이를 모터라고 불렀다. 분할복소수는 시공간 평면의 로렌츠 부스트를 표현하는 데 활용된다.

더 읽어볼만한 페이지

합성 대수 - 복소수
복소수는 실수와 허수 단위를 사용하여 a + bi 형태로 나타내며, 복소 평면에서 표현되고 덧셈, 뺄셈, 곱셈, 나눗셈 연산이 가능하며, 다양한 수학 및 과학 분야에 활용된다.
합성 대수 - 팔원수
팔원수는 실수체 위의 8차원 노름 나눗셈 대수로서, 사원수 대수에 케일리-딕슨 구성을 적용하여 얻어지며, 교환 및 결합 법칙은 만족하지 않으나 교대 대수의 성질을 갖고, 수학 및 물리학 분야에서 활용된다.
다원수 - 팔원수
팔원수는 실수체 위의 8차원 노름 나눗셈 대수로서, 사원수 대수에 케일리-딕슨 구성을 적용하여 얻어지며, 교환 및 결합 법칙은 만족하지 않으나 교대 대수의 성질을 갖고, 수학 및 물리학 분야에서 활용된다.
다원수 - 사원수
사원수는 윌리엄 로언 해밀턴이 도입한 수 체계로, 덧셈과 곱셈 연산이 정의되며 3차원 공간 회전을 표현하는 데 유용한 실수, 복소수의 일반화된 4차원 벡터 공간이다.
가환대수학 - 매개계
매개계는 뇌터 국소 가환환과 유한 생성 가군을 사용하여 정의되며, 가군의 길이와 크룰 차원을 활용하여 정칙 국소환에서 정칙 매개계의 성질을 규명하고, 추상대수기하학에서 기하학적 대상의 분류와 연구에 중요한 역할을 한다.
가환대수학 - 크룰 차원
크룰 차원은 환 내의 소수 아이디얼 체인의 길이를 이용하여 정의되며, 환론 및 대수기하학에서 중요한 역할을 하고 다양한 개념으로 확장되어 사용된다.

분할복소수
개요
종류	쌍곡 복소수
다른 이름	분할 복소수 쌍곡수 쿼터니온의 실수 부분환
기호	D
대수 구조	실수 위의 2차원 결합 대수
곱셈	(x + yj)(w + zj) = (xw + yz) + (xz + yw)j
켤레	(x + yj)* = x - yj
노름	N(z) = x² - y²
성질
항등원	1
영인자	존재 (예: (1 + j)(1 - j) = 0)
가역원	x² - y² ≠ 0인 모든 원소
나눗셈 대수	아님
순서환	아님
체	아님
정역	아님
유클리드 정역	아님
표현
행렬 표현	(x, y) → xI + yJ =
평면에서의 표현	실수 평면 ℝ 유사 유클리드 공간 ℝ

2. 정의

분할복소수는 다음과 같은 형식으로 표기되는 수이다.

: ''z'' = ''x'' + ''jy''

여기서 ''x''와 ''y''는 실수이고, 쌍곡 단위^[1] ''j''는 다음을 만족한다.

: ''j''² = +1

복소수의 체에서 허수 단위 ''i''는 $i^2 = -1$ 을 만족한다. 부호의 차이는 분할복소수를 일반 복소수와 구별해준다. 쌍곡 단위 ''j''는 실수가 아니라 독립적인 양이다.

이러한 모든 ''z''의 집합을 '''분할복소 평면'''이라고 한다. 분할복소수의 덧셈과 곱셈은 다음과 같이 정의된다.

: (''x'' + ''jy'') + (''u'' + ''jv'') = (''x'' + ''u'') + ''j''(''y'' + ''v'')

: (''x'' + ''jy'')(''u'' + ''jv'') = (''xu'' + ''yv'') + ''j''(''xv'' + ''yu'')

이 곱셈은 교환 법칙, 결합 법칙을 만족하며 덧셈에 대해 분배 법칙이 성립한다.

이원수도 참조

2. 1. 직접적 정의

분할복소수는 실수 가환 결합 대수를 이루며, 2차원 실수 벡터 공간으로 표현할 수 있다. 이 공간의 기저는

\{1,\mathrm j\}

이다. 이 기저에서 분할복소수의 곱셈은 다음과 같이 정의된다.

:

(a,b) \cdot (c, d) = (ac + bd, bc + ad)

즉,

:

(a+b\mathrm j)(c+d\mathrm j) = (ac+bd) + (bc+ad)\mathrm j

이다.

추상대수학 용어로, 분할복소수는 다항식환 \R[x]를

x^2-1

다항식에 의해 생성된 아이디얼로 나눈 몫으로 설명할 수 있다.

:

\mathbb{R}[x]/(x^2 - 1)

이 몫에서 x의 이미지는 "허수" 단위 j이다. 분할복소수는 체가 아니며, 모든 영이 아닌 영원소는 영인자이다. 덧셈과 곱셈은 평면의 일반적인 위상에 대해 연속적인 연산이므로, 분할복소수는 위상환을 형성한다.

분할복소수의 대수는 임의의 수 z와 w에 대해

:

\lVert zw \rVert = \lVert z \rVert \lVert w \rVert ~

이므로 합성 대수를 형성한다.

정의로부터 분할복소수의 환은 실수 ℝ에 대한 순환군 C₂의 군환 ℝ[C₂]와 동형임을 알 수 있다. 분할 복소수 전체의 환은 클리퍼드 대수의 특별한 경우이며, '''양의 정부호 이차 형식'''을 갖춘 일차원 벡터 공간 위의 클리퍼드 대수가 된다.

2. 2. 두 실수체의 직합

실수체

\mathbb R

의, 스스로와의 직접곱을 생각하면, 그 위의 곱셈은 다음과 같다.

:

(a,b)(c,d) = (ac,bd)\qquad\forall a,b,c,d\in\mathbb R

이는 실수 가환 결합 대수로서 분할복소수의 대수와 동형이다. 구체적으로, 이 경우

1_{\mathbb R\oplus\mathbb R} = (1,1)

이므로,

\mathrm j = (1,-1)

를 정의하면,

\mathrm j^2 = 1

이 되어,

\mathbb R\oplus\mathbb R\cong\mathbb R[\mathrm j]/(\mathrm j^2 - 1)

임을 알 수 있다. 물리학적으로, 이 정의는 빛원뿔 좌표계를 사용하는 것에 해당한다.

분할 복소수는 덧셈과 곱셈이 쌍별로 정의된 직접 합 과 환 동형이다.

e=\tfrac{1}{2}(1-j)

및

e^* = \tfrac{1}{2}(1+j)

와 같은 두 개의 자명하지 않은 멱등원이 존재한다. 멱등원은

ee=e

및

e^*e^*=e^*

임을 만족한다. 이 두 원소는 모두 널(null)이며,

\lVert e \rVert = \lVert e^* \rVert = e^* e = 0 ~.

이다. 와 ^∗를 분할 복소 평면의 다른 기저로 사용하는 것이 편리하며, 이 기저는 '''대각 기저''' 또는 '''널 기저'''라고 불린다.

작용은 쌍곡선 버서

e^{bj} \!

의 경우, 이 선형 변환 하에서 압착 사상에 해당한다.

\sigma: (u, v) \mapsto \left(ru, \frac{v}{r}\right),\quad r = e^b ~.

2. 3. 행렬을 통한 정의

분할복소수의 대수

\tilde{\mathbb C}

는 2차원 표현을 가지므로, 2×2 실수 행렬로 정의될 수 있다.^[3] 항등원의 스칼라배가 아니지만 제곱이 1인 임의의 2×2 실수 행렬

\mathrm j

를 잡으면, 이는 분할복소수의 행렬 표현을 정의한다.

분할 복소수

z = x + jy

는 행렬

z \mapsto \begin{pmatrix}x & y \\ y & x\end{pmatrix}

로 나타낼 수 있다. 분할복소수의 덧셈과 곱셈은 행렬의 덧셈과 곱셈으로 주어지며,

z

의 제곱된 모듈러스는 해당 행렬의 행렬식으로 주어진다.

2x2 실수 행렬의 4차원 환에는 분할 복소 평면을 나타내는 방법이 여러가지가 있다. 예를 들어 ''a'' = 0일 때, (''b,c'')는 표준 쌍곡선 위의 점이 된다.

3. 연산

복소수와 마찬가지로, 분할 복소 켤레수의 개념을 정의할 수 있다. 만약

: $z = x + jy ~,$

이면, z의 켤레 복소수는 다음과 같이 정의된다.

: $z^* = x - jy ~.$

켤레 복소수는 대합이며, 복소 켤레수와 유사한 속성을 만족한다. 즉,

: $\begin{align}(z + w)^* &= z^* + w^* \\(zw)^* &= z^* w^* \\\left(z^*\right)^* &= z.\end{align}$

분할 복소수 $z=x+jy$ 의 제곱 절댓값은 등방성 이차 형식으로 주어진다.

: $\lVert z \rVert^2 = z z^* = z^* z = x^2 - y^2 ~.$

이것은 합성 대수 속성을 갖는다.

: $\lVert z w \rVert = \lVert z \rVert \lVert w \rVert ~.$

그러나, 이 이차 형식은 양의 정부호가 아니라, 부호수 (1, −1)를 갖기 때문에, 절댓값은 노름이 ''아니다''.

관련된 쌍선형 형식은 다음과 같다.

: $\langle z, w \rangle = \operatorname\mathrm{Re}\left(zw^*\right) = \operatorname\mathrm{Re} \left(z^* w\right) = xu - yv ~,$

여기서 $z=x+jy$ 이고 $w=u+jv$ 이다. 여기서, ''실수 부분''은 $\operatorname\mathrm{Re}(z) = \tfrac{1}{2}(z + z^*) = x$ 로 정의된다. 제곱 절댓값의 또 다른 표현은 다음과 같다.

: $\lVert z \rVert^2 = \langle z, z \rangle ~.$

양의 정부호가 아니기 때문에, 이 쌍선형 형식은 내적이 아니다. 그럼에도 불구하고 쌍선형 형식은 종종 ''부정 내적''이라고 불린다. 절댓값을 노름이라고 부르는 것과 유사한 용어 남용이 있다.

분할 복소수는 절댓값이 0이 아닌 경우, 즉 $x \pm j x$ 형태의 수는 역수를 갖지 않는다. 가역 원소의 곱셈 역원은 다음과 같다.

: $z^{-1} = \frac{z^*}{ {\lVert z \rVert}^2} ~.$

가역적이지 않은 분할 복소수는 영 벡터라고 불린다. 이것들은 실수 a에 대해 $(a \pm j a)$ 형태를 갖는다.

3. 1. 켤레

분할복소수 z^영어 = a + bj의 켤레는 z* = a - bj로 정의된다. 이는 실수 선형 변환이자 환 준동형이다.

분할 복소 켤레수는 대합이며, 다음과 같은 복소 켤레수와 유사한 속성을 만족한다.

$(z + w)^* = z^* + w^*$
$(zw)^* = z^* w^*$
$\left(z^*\right)^* = z$

3. 2. 절댓값

분할복소수의 실수 벡터 공간 위에는 다음과 같은 비퇴화 이차 형식이 존재한다.

:

|z|^2 = z \bar z \in \mathbb R\qquad\forall z\in\tilde{\mathbb C}

즉,

:

|a+b\mathrm j|^2 = a^2 - b^2 \in \mathbb R\qquad\forall a,b\in\mathbb R

이다. 이는 다음과 같이 곱셈을 보존한다.

:

|xy|^2 = |x|^2|y|^2\qquad\forall x,y\in\tilde{\mathbb C}

이는 양의 정부호가 아니라 부정부호이다. 즉, 음의 값을 가질 수 있다. 복소수와 마찬가지로, 분할 복소 켤레수의 개념을 정의할 수 있다. 만약

z = x + jy ~,

이면, 의 켤레 복소수는 다음과 같이 정의된다.

z^* = x - jy ~.

켤레 복소수는 대합이며, 복소 켤레수와 유사한 속성을 만족한다. 즉,

\begin{align}(z + w)^* &= z^* + w^* \\(zw)^* &= z^* w^* \\\left(z^*\right)^* &= z.\end{align}

분할 복소수

z=x+jy

의 제곱 절댓값은 등방성 이차 형식으로 주어진다.

:

\lVert z \rVert^2 = z z^* = z^* z = x^2 - y^2 ~.

이것은 합성 대수 속성을 갖는다.

:

\lVert z w \rVert = \lVert z \rVert \lVert w \rVert ~.

그러나, 이 이차 형식은 양의 정부호가 아니라, 부호수 (1, −1)를 갖기 때문에, 절댓값은 노름이 아니다.

관련된 쌍선형 형식은 다음과 같다.

:

\langle z, w \rangle = \operatorname\mathrm{Re}\left(zw^*\right) = \operatorname\mathrm{Re} \left(z^* w\right) = xu - yv ~,

여기서

z=x+jy

이고

w=u+jv

이다. 여기서, 실수 부분은

\operatorname\mathrm{Re}(z) = \tfrac{1}{2}(z + z^*) = x

로 정의된다. 제곱 절댓값의 또 다른 표현은 다음과 같다.

:

\lVert z \rVert^2 = \langle z, z \rangle ~.

양의 정부호가 아니기 때문에, 이 쌍선형 형식은 내적이 아니다. 그럼에도 불구하고 쌍선형 형식은 종종 부정 내적이라고 불린다. 절댓값을 노름이라고 부르는 것과 유사한 용어 남용이 있다.

분할 복소수는 절댓값이 0이 아닌 경우, 즉 형태의 수는 역수를 갖지 않는다. 가역 원소의 곱셈 역원은 다음과 같다.

:

z^{-1} = \frac{z^*}{ {\lVert z \rVert}^2} ~.

가역적이지 않은 분할 복소수는 영 벡터라고 불린다. 이것들은 실수 에 대해 형태를 갖는다.

3. 3. 지수 함수

분할복소수에 대하여, 지수 함수는 다음과 같이 정의된다.

:exp(a + bj) = exp(a)(cosh b + (sinh b)j) (a, b는 실수)

이는 다음 성질을 만족시킨다.

:exp(x+y) = exp(x)exp(y) (x, y는 분할복소수)

또한, 이를 실수체에 제한할 경우, 이는 실수의 지수 함수와 일치한다.

분할복소수의 2×2 행렬 표현에서, 이는 행렬 지수 함수와 일치한다.

4. 성질

분할복소수는 가환 결합 대수이지만, 영인자를 가지므로 정역은 아니다.

:(1 + j)(1 - j) = 0

사실, |xy|² = |x|²|y|²이므로, 분할복소수가 영인자일 필요충분조건은 그 제곱 절댓값이 0인 것이다.

분할복소수는 다항식환 \R[x]를 x² - 1 다항식에 의해 생성된 아이디얼로 나눈 몫으로 설명할 수 있다.

:R[x]/(x² - 1).

몫에서 x의 이미지는 "허수" 단위 j이다. 이 설명에서 분할복소수가 실수에 대한 가환대수를 형성한다는 것을 알 수 있다. 이 대수는 영원소가 가역적이지 않기 때문에 체가 아니다. 모든 영이 아닌 영원소는 영인자이다.

덧셈과 곱셈은 평면의 일반적인 위상에 대해 연속적인 연산이므로, 분할복소수는 위상환을 형성한다.

분할복소수의 대수는 임의의 수 z와 w에 대해

:|| zw || = || z || || w ||

이므로 합성 대수를 형성한다.

정의로부터 분할복소수의 환은 실수 R에 대한 순환군 C₂의 군환 R[C₂]와 동형임을 알 수 있다.

4. 1. 영인자

분할복소수의 대수는 2차원 실수 가환 결합 대수이다. 이는 정역이 아니며, (1 + j)(1 - j) = 0과 같이 0이 아닌 두 분할복소수의 곱이 0이 될 수 있으므로 영인자를 갖는다. 사실, |xy|² = |x|²|y|²이므로, 분할복소수가 영인자일 필요충분조건은 그 제곱 절댓값이 0인 것이다.

4. 2. 환의 스펙트럼

분할복소수의 대수는 2차원 실수 가환 결합 대수이다. 이는 정역이 아니며, 예를 들어 다음과 같이 영인자를 갖는다.

:(1+j)(1-j) = 0

사실, |xy|²=|x|²|y|²이므로, 분할복소수가 영인자일 필요 충분 조건은 그 제곱 절댓값이 0인 것이다.

분할복소수의 환의 스펙트럼은 두 실수 0차원 아핀 공간의 분리합집합이다.

:

\operatorname{Spec}(\mathbb R) = \mathbb A^0_{\mathbb R}\sqcup\mathbb A^0_{\mathbb R}

5. 기하학적 의미

[[파일:null|섬네일|

단위 쌍곡선:

공액 쌍곡선:

점근선: ]]

실수 2차원 벡터 공간에 민코프스키 내적을 부여한 -차원 민코프스키 공간은 }로 표기한다. 유클리드 평면 의 기하학이 복소수로 설명될 수 있는 것처럼, 민코프스키 평면 }의 기하학은 분할 복소수로 설명될 수 있다.

0이 아닌 모든 실수 에 대해, 점의 집합

: $\left\{ z : \lVert z \rVert^2 = a^2 \right\}$

은 쌍곡선이다. 이 쌍곡선은 와 을 통과하는 오른쪽 및 왼쪽 가지로 구성된다. 인 경우를 단위 쌍곡선이라고 한다. 공액 쌍곡선은 다음과 같이 주어진다.

: $\left\{ z : \lVert z \rVert^2 = -a^2 \right\}$

와 를 통과하는 위쪽과 아래쪽 가지로 구성된다. 쌍곡선과 공액 쌍곡선은 널 요소의 집합을 형성하는 두 개의 대각선 점근선에 의해 분리된다.

: $\left\{ z : \lVert z \rVert = 0 \right\}.$

이 두 개의 선(때로는 널 콘)은 에서 수직이며 기울기는 ±1이다.

분할 복소수 와 는 이면 쌍곡선 직교라고 한다. 일반적인 직교성과 유사하지만, 특히 일반적인 복소수 산술에서 알려진 것처럼 이 조건은 더 미묘하다. 이는 시공간에서 동시 초평면 개념의 기초를 형성한다.

분할 복소수에 대한 오일러 공식의 유사체는

: $\exp(j\theta) = \cosh(\theta) + j\sinh(\theta).$

이다. 이 공식은 거듭제곱 급수 확장에서 cosh은 짝수 거듭제곱만 갖는 반면 sinh은 홀수 거듭제곱을 갖는다는 사실을 사용하여 도출할 수 있다.^[2] 쌍곡 각도 의 모든 실수 값에 대해 분할 복소수 는 노름 1을 가지며 단위 쌍곡선의 오른쪽 가지에 놓인다. 와 같은 숫자는 쌍곡선 versor라고 불려왔다.

는 절댓값이 1이므로, 어떤 분할 복소수 에 를 곱하면 의 절댓값이 유지되며 ''쌍곡선 회전''(또는 로렌츠 부스트 또는 압착 매핑)을 나타낸다. 를 곱하면 기하학적 구조가 유지되어 쌍곡선을 자신으로, 널 콘을 자신으로 가져온다.

절댓값(또는 등가적으로, 내적)을 보존하는 분할 복소 평면의 모든 변환 집합은 군을 형성하며, 이를 일반화된 직교군 이라고 한다. 이 군은 SO(1, 1)로 표시되는 부분군을 형성하는 쌍곡선 회전과,

: $z \mapsto \pm z$ and $z \mapsto \pm z^*.$

로 주어진 네 개의 이산 반사로 구성된다.

지수 맵

: $\exp\colon (\R, +) \to \mathrm{SO}^{+}(1, 1)$

은 를 에 의한 회전으로 보내는 것으로, 일반적인 지수 공식이 적용되므로 군 동형 사상이다.

: $e^{j(\theta + \phi)} = e^{j\theta}e^{j\phi}.$

5. 1. 단위 쌍곡선

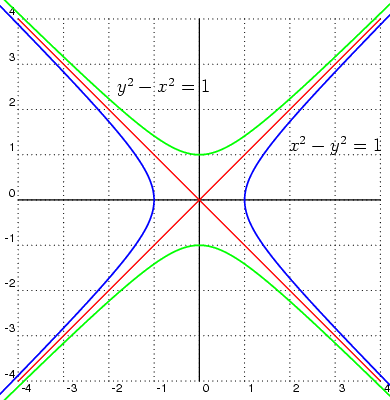
절댓값이 1인 분할복소수 집합은 단위 쌍곡선을 이룬다. 0이 아닌 임의의 실수 a에 대해, 점 집합 { z : ||z|| = a² }는 쌍곡선을 이루며, a = 1인 경우가 단위 쌍곡선이다. 단위 쌍곡선은 좌우로 (1, 0)과 (-1, 0)을 통과하는 두 개의 가지를 갖는다. 켤레 쌍곡선은 { z : ||z|| = -a² }으로 주어지며, 상하로 (0, a)와 (0, -a)를 통과하는 두 개의 가지를 갖는다. 이 쌍곡선과 켤레 쌍곡선은 널 원뿔(null cone)이라 불리는 두 개의 점근선에 의해 분리되며, 이 점근선은 기울기가 ±1이고, ℝ²에서 직교한다.

분할복소수 z, w가 = 0을 만족할 때, 쌍곡적 직교성(Hyperbolic orthogonality)이라고 한다. 이는 시공간에서의 동시 초평면(simultaneous hyperplane) 개념의 근간을 이룬다.

분할복소수에서의 오일러 공식 유사물은 exp(jθ) = cosh(θ) + jsinh(θ)이다. 임의의 실수 쌍곡 각 θ에 대해, 분할복소수 λ = exp(jθ)는 노름이 1이고 단위 쌍곡선의 오른쪽 가지 위에 있으며, 쌍곡 벨솔이라 불린다.

λ는 절댓값이 1이므로, 임의의 분할복소수 z에 λ를 곱하는 연산은 z의 절댓값을 유지하며, 쌍곡적 회전(로렌츠 변환, 축소 사상)을 표현한다. λ를 곱하는 연산은 쌍곡선을 자신에게, 널 원뿔을 자신에게 사상하는 기하학적 구조를 유지한다.

분할복소 평면상 절댓값(내적)을 보존하는 변환 전체 집합은 부정 직교군 O(1, 1)이라는 군을 이룬다. 이 군은 쌍곡적 회전과 z ↦ ±z 및 z ↦ ±z* 로 주어지는 4개의 이산적 반사 변환의 조합으로 이루어진다. 쌍곡적 회전 전체는 SO⁺(1, 1)로 표시되는 O(1, 1)의 부분군을 이룬다.

쌍곡 각 θ를 쌍곡 회전 exp(jθ)로 사상하는 지수 사상 exp:(ℝ, +) → SO⁺(1,1)는 군 동형이다.

5. 2. 쌍곡선 직교

두 분할복소수 에 대해 = 0}}이면 두 분할복소수는 쌍곡적 직교성(Hyperbolic orthogonality)이라고 한다. 이는 일반적인 복소수 연산에서의 직교성과 유사하지만, 시공간에서의 동시 초평면(simultaneous hyperplane) 개념의 근간을 이룬다는 점에서 더 심오한 의미를 갖는다.

분할복소수에서의 오일러 공식은 와 같다. 쌍곡 각(Hyperbolic angle) θ에 대해, 분할복소수 는 노름이 1이고 단위 쌍곡선의 오른쪽 가지 위에 있으며, '''쌍곡 벨솔'''이라고 불린다.

를 곱하는 연산은 쌍곡선을 자신에게, 널 원뿔을 자신에게 사상하는 기하학적 구조를 유지하며, 이는 부정 직교군(Indefinite orthogonal group) 군의 작용으로 설명된다. 이 군은 쌍곡적 회전과 이산적 반사 변환의 조합으로 이루어진다. 쌍곡 각 θ를 쌍곡 회전 로 사상하는 지수 사상은 군 동형이다.

5. 3. 쌍곡선 회전

절댓값이 1인 분할복소수를 곱하는 것은 쌍곡선 회전을 나타낸다. 임의의 실수를 취하는 쌍곡 각(Hyperbolic angle) θ에 대해, 분할복소수 λ ≡ exp(jθ)는 노름이 1이고 단위 쌍곡선의 오른쪽 가지 위에 있다. 이러한 수 λ는 쌍곡 벨솔이라고 불린다. λ는 절댓값이 1이므로, 임의의 분해형 복소수 z에 λ를 곱하는 연산은 z의 절댓값을 유지하며, 쌍곡적 회전(좁은 의미의 로렌츠 변환, 축소 사상이라고도 함)을 표현한다. λ를 곱하는 연산은, 쌍곡선을 자신에게 사상하고 널 원뿔을 자신에게 사상한다는 의미에서, 기하학적 구조를 유지한다.

분해형 복소 평면상의 절댓값을 보존하는 변환 전체가 이루는 집합은 부정 직교군(Indefinite orthogonal group) O(1, 1)라고 불리는 군을 이룬다. 이 군은 쌍곡적 회전과 z ↦ ±z 및 z ↦ ±z*로 주어지는 4개의 이산적반사 변환의 조합으로 이루어진다. 쌍곡 각 θ를 쌍곡 회전 exp(jθ)로 사상하는 지수 사상

exp : (ℝ, +) → SO+(1,1)

는, 일반적인 지수 법칙을 사용하면

e^{j(θ+∮)} = e^{jθ}e^{j∮}

가 성립하므로, 군 동형이다.

6. 역사

제임스 코클(James Cockle^영어, 1819~1895)은 1848년에 분할복소수에 해당하는 대수 체계를 최초로 사용하였다.^[22] 코클은 이를 "실수 테사린"(real tessarine^영어)이라고 불렀으며, 원소

\mathrm j

를 “불가능성”(impossibility^영어)을 나타내는 것으로 해석하였다.^[4]^[20] 그는 "불가능성을 나타내는 기호는 적절할 뿐만 아니라, 대수 연구의 다양한 주제를 정확하게 분류하고, 실재하지 않는 값과 존재 불가능한 값들을 구별하려면, 사실 불가결하다."라고 언급했다. 코클은

0' = 1 + \sqrt j

라는 식에서

+\sqrt j = -1

를 유도하고, 최종적으로

j^2 = 1

임을 보였다.^[22] 그는 이 기호(''j'')의 성질이 "순수한 불가능성 — 동시에 양수이자 음수인 값 — 의 제곱은 가능한 값으로 취급되어야 한다. 모순은 제곱을 하면 사라진다"라고 설명했다.^[22]

윌리엄 클리퍼드는 분할복소수를 "모터"(motor^영어)라고 불렀으며, 스핀의 합을 나타내는 데 사용했다.^[4] 클리퍼드는 분할복소수를 지금은 분할-사원수라고 불리는 사원수 대수의 계수로 사용하는 것을 도입했다. 그는 그 요소들을 "모터"라고 불렀는데, 이는 일반적인 복소수의 원환군에서 가져온 "로터"의 동작과 유사한 용어였다.^[4]

20세기 후반부터, 분할복소수 곱셈은 시공간 평면의 로렌츠 부스트로 여겨져 왔다.^[5]^[6]^[7]^[8]^[9]^[10] 이 모델에서,

z = x + y j

는 시공간 평면에서 사건을 나타내며, 여기서 ''x''는 초 단위로, ''y''는 광초 단위로 측정된다. 분할복소수 방정식

e^{aj} \ e^{bj} = e^{(a + b)j}

는 단위 쌍곡선에서 곱셈을 표현하며, 공선 속도에 대한 속도의 가산성을 보여준다.

1941년 E.F. 알렌은 분할복소수 기하 산술을 사용하여

zz^* = 1

에 내접하는 삼각형의 9점 쌍곡선을 설정했다.^[14]

6. 1. 제임스 코클

제임스 코클(James Cockle^영어, 1819~1895)은 1848년에 분할복소수에 해당하는 대수 체계를 최초로 사용하였다.^[22] 코클은 이를 "실수 테사린"(real tessarine^영어)이라고 불렀으며, 원소

\mathrm j

를 “불가능성”(impossibility^영어)을 나타내는 것으로 해석하였다.^[4]^[20] 그는 "불가능성을 나타내는 기호는 적절할 뿐만 아니라, 대수 연구의 다양한 주제를 정확하게 분류하고, 실재하지 않는 값과 존재 불가능한 값들을 구별하려면, 사실 불가결하다."라고 언급했다. 코클은

0' = 1 + \sqrt j

라는 식에서

+\sqrt j = -1

를 유도하고, 최종적으로

j^2 = 1

임을 보였다.^[22] 그는 이 기호(''j'')의 성질이 "순수한 불가능성 — 동시에 양수이자 음수인 값 — 의 제곱은 가능한 값으로 취급되어야 한다. 모순은 제곱을 하면 사라진다"라고 설명했다.^[22]

윌리엄 킹던 클리퍼드도 이러한 대수 체계를 사용하였으며,^[23] "모터"(motor^영어)라고 불렀다.^[4]

6. 2. 윌리엄 킹던 클리퍼드

윌리엄 킹던 클리퍼드는 분할복소수를 "모터"라고 불렀으며, 스핀의 합을 나타내는 데 사용했다.^[4] 클리퍼드는 분할복소수를 지금은 분할-사원수라고 불리는 사원수 대수의 계수로 사용하는 것을 도입했다. 그는 그 요소들을 "모터"라고 불렀는데, 이는 일반적인 복소수의 원환군에서 가져온 "로터"의 동작과 유사한 용어였다.^[4] 1941년 E.F. 알렌은 분할복소수 기하 산술을 사용하여 = 1}}에 내접하는 삼각형의 9점 쌍곡선을 설정했다.^[14]

6. 3. 현대 물리학에서의 응용

20세기 후반부터, 분할복소수 곱셈은 시공간 평면의 로렌츠 부스트로 여겨져 왔다.^[5]^[6]^[7]^[8]^[9]^[10] 이 모델에서, 숫자 는 시공간 평면에서 사건을 나타내며, 여기서 ''x''는 초 단위로, 는 광초 단위로 측정된다. 분할복소수 방정식

e^{aj} \ e^{bj} = e^{(a + b)j}

는 단위 쌍곡선에서 곱셈을 표현하며, 공선 속도에 대한 속도의 가산성을 보여준다.

7. 대한민국에서의 분할복소수

7. 1. 교육

7. 2. 연구

8. 같이 보기

8. 1. 관련 개념

8. 2. 응용 분야

참조

_[1] 서적 Geometry of Mobius Transformations: Elliptic, Parabolic, and Hyperbolic actions of SL(2,R) Imperial College Press 2012
_[2] 논문 On a New Imaginary in Algebra https://www.biodiver[...] 1848
_[3] Wiki Abstract Algebra/2x2 real matrices
_[4] 논문 On a New Imaginary in Algebra https://www.biodiver[...] 1849
_[5] 간행물 Semi-complex analysis and mathematical physics https://arxiv.org/ab[...] 1994
_[6] 서적 The Mathematics of Minkowski Space-Time Birkhäuser Verlag 2008
_[7] 서적 Geometry of Minkowski Space-Time Springer Science & Business Media 2011
_[8] 논문 Extending special relativity via the perplex numbers 1986
_[9] 간행물 Transformations in Special Relativity 1985
_[10] 간행물 Hyperbolic Number Plane http://garretstar.co[...] 1995
_[11] 간행물 On Generalized Cayley-Dickson Algebras http://projecteuclid[...] 1967
_[12] 간행물 Review of "Quadratic forms permitting composition" by A.A. Albert 1942
_[13] 간행물 Sobre el numero complejo hiperbolico y su relacion con la geometria de Borel Universidad Nacional de la Plata, Republica Argentina 1935
_[14] 간행물 On a Triangle Inscribed in a Rectangular Hyperbola 1941
_[15] 웹사이트 Calculus of Approximations http://www.cs.utep.e[...] 1956
_[16] 학위논문 The Number Theory of a System of Hyperbolic Complex Numbers https://escholarship[...] McGill University 1949
_[17] 학위논문 Introduction to Hyperbolic Number Theory https://escholarship[...] McGill University 1949
_[18] 논문 Gaussian, parabolic, and hyperbolic numbers 1968
_[19] 서적 Geometry of Lie Groups Kluwer Academic Publishers 1997
_[20] 간행물 Mr. J. Cockle on a New Imaginary in Algebra https://www.biodiver[...] 1849
_[21] 간행물 On a Triangle Inscribed in a Rectangular Hyperbola American Mathematical Monthly 1941
_[22] 저널 On a New Imaginary in Algebra https://www.biodiver[...] 1849
_[23] 저널 Further notes on biquaternions

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com