복소수

3. 표기

복소수는 직교 형식, 극형식, 지수 형식 등 다양한 방법으로 표현될 수 있다.

• '''직교 형식''': 복소수 $z$는 실수 $x$, $y$를 사용하여 $z\; =\; x\; +\; iy$와 같이 나타낼 수 있다. 여기서 $x$는 실수부, $y$는 허수부라고 하며, 복소수의 덧셈과 뺄셈에서 편리하게 쓰인다.

• '''극형식''': 복소 평면 상의 점을 원점으로부터의 거리와 각도를 이용하여 나타내는 방식이다. 복소수 $z$는 $z\; =\; r(\backslash cos\backslash theta\; +\; i\backslash sin\backslash theta)$와 같이 표현된다. 여기서 $r$은 절댓값, $\backslash theta$는 편각이라고 하며, 복소수의 곱셈과 나눗셈에서 편리하게 쓰인다.

• '''지수 형식''': 오일러 공식 $e^\{i\backslash theta\}=\backslash cos\backslash theta+i\backslash sin\backslash theta$에 따라, 복소수 $z$는 $z\; =\; re^\{i\backslash theta\}$와 같이 표현된다. 복소수의 곱셈과 나눗셈에서 편리하게 쓰인다.

• 실수부: $\backslash operatorname\{Re\}z=x=r\backslash cos\backslash theta\backslash in\backslash mathbb\; R$
• 허수부: $\backslash operatorname\{Im\}z=y=r\backslash sin\backslash theta\backslash in\backslash mathbb\; R$
• 절댓값: $|z|=\backslash sqrt\{x^2+y^2\}=r\backslash in[0,\backslash infty)$
• 편각: $\backslash operatorname\{arg\}z=\backslash operatorname\{atan2\}(y,x)=\backslash theta\backslash ,\backslash operatorname\{mod\}\backslash ,2\backslash pi\backslash in(-\backslash pi,\backslash pi]$
• 켤레 복소수 ($z\backslash ne0$): $\backslash bar\; z=x-iy=re^\{-i\backslash theta\}\backslash in\backslash mathbb\; C$

3. 1. 복소평면

3. 2. 직교 형식

3. 3. 극형식

3. 4. 지수 형식

3. 5. 실수부, 허수부, 절댓값, 편각, 켤레 복소수

• $z$의 실수부는 실수 단위 1에 붙는 계수이다.
• : $\backslash operatorname\{Re\}z=x=r\backslash cos\backslash theta\backslash in\backslash mathbb\; R$
• $z$의 허수부는 허수 단위 $i$에 붙는 계수이다.
• : $\backslash operatorname\{Im\}z=y=r\backslash sin\backslash theta\backslash in\backslash mathbb\; R$
• $z$의 절댓값은 원점까지의 거리이며, 피타고라스 정리에 따라 다음과 같다.
• : $|z|=\backslash sqrt\{x^2+y^2\}=r\backslash in[0,\backslash infty)$
• $z$의 편각은 가로축과의 사잇각이다.
• : $\backslash operatorname\{arg\}z=\backslash operatorname\{atan2\}(y,x)=\backslash theta\backslash ,\backslash operatorname\{mod\}\backslash ,2\backslash pi\backslash in(-\backslash pi,\backslash pi]$
• $z\backslash ne0$의 켤레 복소수는 가로축에 대해 반사하여 얻는 복소수이다.
• : $\backslash bar\; z=x-iy=re^\{-i\backslash theta\}\backslash in\backslash mathbb\; C\backslash qquad\; z\backslash ne0$

• $\backslash operatorname\{Re\}(z\backslash pm\; w)=\backslash operatorname\{Re\}z\backslash pm\backslash operatorname\{Re\}w$
• $\backslash operatorname\{Im\}(z\backslash pm\; w)=\backslash operatorname\{Im\}z\backslash pm\backslash operatorname\{Im\}w$
• $\backslash operatorname\{Re\}(zw)=\backslash operatorname\{Re\}z\backslash operatorname\{Re\}w-\backslash operatorname\{Im\}z\backslash operatorname\{Im\}w$
• $\backslash operatorname\{Im\}(zw)=\backslash operatorname\{Re\}z\backslash operatorname\{Im\}w+\backslash operatorname\{Im\}z\backslash operatorname\{Re\}w$

• $|z|\backslash ge0$
• $|z|=0\backslash iff\; z=0$
• $|z+w|\backslash le|z|+|w|$
• $|z+w|=|z|+|w|\backslash iff\; z\backslash bar\; w\backslash in[0,\backslash infty)$
• $|zw|=|z||w|$
• $\backslash left|\backslash frac\; zw\backslash right|=\backslash frac$

  
  
  복소수의 편각은 다음과 같이 나타낼 수 있다.
  
  :$\backslash operatorname\{arg\}z=\backslash operatorname\{atan2\}(\backslash operatorname\{Im\}z,\backslash operatorname\{Re\}z)=\backslash frac1\{2i\}\backslash ln\backslash frac\; z\backslash bar\; z$
  
  복소수의 편각에 대해 다음 성질들이 성립한다.

  
  
  • $\backslash operatorname\{arg\}(zw)\backslash equiv\backslash operatorname\{arg\}z+\backslash operatorname\{arg\}w\backslash pmod\{2\backslash pi\}$
  • $\backslash operatorname\{arg\}\backslash frac\; zw\backslash equiv\backslash operatorname\{arg\}z-\backslash operatorname\{arg\}w\backslash pmod\{2\backslash pi\}$

  
  
  켤레 복소수는 다음과 같이 나타낼 수 있다.
  
  :$\backslash bar\; z=\backslash operatorname\{Re\}z-i\backslash operatorname\{Im\}z=|z|e^\{-i\backslash operatorname\{arg\}z\}$
  
  켤레 복소수 $\backslash bar\{\}\backslash colon\backslash mathbb\; C\backslash to\backslash mathbb\; C$는 대합 노름 대수 자기 동형을 이루며, 다음 성질들이 성립한다.

  
  
  • $\backslash bar\backslash bar\; z=z$
  • $|\backslash bar\; z|=|z|$
  • $\backslash overline\{z+w\}=\backslash bar\; z+\backslash bar\; w$
  • $\backslash overline\{z-w\}=\backslash bar\; z-\backslash bar\; w$
  • $\backslash overline\{zw\}=\backslash bar\; z\backslash bar\; w$
  • $\backslash overline\backslash frac\; zw=\backslash frac\backslash bar\; z\backslash bar\; w$

  4. 연산

  복소수는 덧셈, 뺄셈, 곱셈, 나눗셈에 대해 닫혀 있다. 복소수의 집합은 체를 이루는데, 이는 복소수 연산이 교환 법칙, 결합 법칙, 분배 법칙을 만족시키기 때문이다.
  
  

  

  
  

  4. 1. 동일성

  두 복소수가 서로 같을 필요충분조건은 실수부와 허수부가 서로 같은 것이다.
  
  :$a+bi=c+di\backslash iff\; a=c\backslash land\; b=d\backslash qquad\; a,b,c,d\backslash in\backslash mathbb\; R$
  
  다르게 표현하면, 두 복소수가 '''같다'''는 것은 그들의 실수부 및 허수부가 각각 같다는 것이다.
  
  :$z\_1\; =\; z\_2\; \backslash iff\; (\; \backslash operatorname\{Re\}\; z\_1\; =\; \backslash operatorname\{Re\}\; z\_2\; )\; \backslash land\; (\; \backslash operatorname\{Im\}\; z\_1\; =\; \backslash operatorname\{Im\}\; z\_2\; )$
  

  4. 2. 덧셈과 뺄셈

  두 복소수의 덧셈은 실수부와 허수부를 각각 더하여 계산한다. 즉, 다음과 같다.
  
  :$(a+bi)+(c+di)=(a+c)+(b+d)i$
  
  뺄셈도 마찬가지로 실수부와 허수부를 각각 빼서 계산한다.
  
  :$(a+bi)-(c+di)=(a-c)+(b-d)i$
  
  특히, 복소수의 덧셈에 대한 역원은 다음과 같다.
  
  :$-(a+bi)=(-a)+(-b)i$
  
  복소수의 덧셈은 교환 법칙과 결합 법칙을 만족시킨다.
  
  두 복소수의 덧셈은 기하학적으로 나타낼 수 있다. 복소 평면에서 두 복소수 a와 b의 합은 O와 a, b를 세 꼭짓점으로 하는 평행사변형을 그려서 구할 수 있다. (단, 세 점이 한 직선 위에 있지 않아야 한다)
  

  4. 3. 곱셈과 나눗셈

  두 복소수의 곱셈은 다음과 같다.
  
  :$(a+bi)(c+di)=(ac-bd)+(ad+bc)i$
  
  두 복소수의 나눗셈은 분모의 켤레 복소수를 분모와 분자에 각각 곱해 구한다. (나누는 수가 0이 아니어야 한다.)
  
  :$\backslash frac\{a+bi\}\{c+di\}=\backslash frac\{ac+bd\}\{c^2+d^2\}+\backslash frac\{-ad+bc\}\{c^2+d^2\}i\backslash qquad\; c+di\backslash ne0$
  
  특히, 0이 아닌 복소수의 곱셈 역원은 다음과 같다.
  
  :$\backslash frac1\{a+bi\}=\backslash frac\; a\{a^2+b^2\}-\backslash frac\; b\{a^2+b^2\}i\backslash qquad\; a+bi\backslash ne0$
  
  극형식으로 나타낸 복소수
  
  :$z=r(\backslash cos\backslash theta+i\backslash sin\backslash theta)$
  
  :$w=s(\backslash cos\backslash varphi+i\backslash sin\backslash varphi)$
  
  에 대하여 쓰면 다음과 같다.
  
  :$zw=rs(\backslash cos(\backslash theta+\backslash varphi)+i\backslash sin(\backslash theta+\backslash varphi))$
  
  :$\backslash frac\; zw=\backslash frac\; rs(\backslash cos(\backslash theta-\backslash varphi)+i\backslash sin(\backslash theta-\backslash varphi))\backslash qquad\; w\backslash ne0$
  
  :$\backslash frac1z=\backslash frac\; 1r(\backslash cos\backslash theta-i\backslash sin\backslash theta)\backslash qquad\; z\backslash ne0$
  
  마찬가지로, 지수 형식으로 나타낸 복소수
  
  :$z=re^\{i\backslash theta\}$
  
  :$w=se^\{i\backslash varphi\}$
  
  에 대하여 쓰면 다음과 같다.
  
  :$zw=rse^\{i(\backslash theta+\backslash varphi)\}$
  
  :$\backslash frac\; zw=\backslash frac\; rse^\{i(\backslash theta-\backslash varphi)\}\backslash qquad\; w\backslash ne0$
  
  :$\backslash frac\; 1z=\backslash frac\; 1re^\{-i\backslash theta\}\backslash qquad\; z\backslash ne0$
  
  복소수의 곱셈은 교환 법칙과 결합 법칙을 만족시키며, 덧셈에 대한 분배 법칙을 만족시킨다.
  

  4. 4. 순서체의 실패

  복소수체 위에는 순서체의 구조를 줄 수 없다. 즉, 다음을 만족시키는 전순서 $\backslash le\; \backslash subseteq\; \backslash mathbb\; C\; \backslash times\; \backslash mathbb\; C$가 존재하지 않는다.^[62][66]

  
  
  • 임의의 $z,\; w\; \backslash in\; \backslash mathbb\; C$에 대하여, $z,\; w\; >\; 0$이라면, $z\; +\; w\; >\; 0$이며 $zw\; >\; 0$이다.

  
  
  귀류법을 사용하여, 복소수체가 순서체가 되게 하는 전순서 $\backslash le\; \backslash subseteq\; \backslash mathbb\; C\; \backslash times\; \backslash mathbb\; C$가 존재한다고 가정하자. 그렇다면,
  
  :
  
  이거나
  
  :
  
  이다. 따라서,
  
  :
  
  이며,
  
  :
  
  이며,
  
  :
  
  이다. 이는 모순이다.
  
  물론, $\backslash mathbb\; C$ 위의 순서 관계는 얼마든지 존재한다. 예를 들어, 다음과 같다.

  
  
  • (사전식 순서: 전순서)
  • (직접곱: 부분 순서) $z\; \backslash le\; w\; \backslash iff\; \backslash operatorname\{Re\}\; z\; \backslash le\; \backslash operatorname\{Re\}\; w\; \backslash land\; \backslash operatorname\{Im\}\; z\; \backslash le\; \backslash operatorname\{Im\}\; w\; \backslash qquad\; z,\; w\; \backslash in\; \backslash mathbb\; C$
  • (절댓값의 크기 비교: 원전순서) $z\; \backslash le\; w\; \backslash iff\; |z|\; \backslash le\; |w|\; \backslash qquad\; z,\; w\; \backslash in\; \backslash mathbb\; C$

  
  
  이는 제곱하면 음수가 되는 수(예: 허수 단위)가 존재하기 때문이다.
  

  4. 5. 실수부와 허수부 (연산)

  복소수 $z$는 다음과 같이 표현할 수 있다.
  
  :$z\; =\; x\; +\; iy$ (여기서 $x$, $y$는 실수)
  
  이때,

  
  
  • $x$를 $z$의 실수부 (real part^영어)라고 하며, \(\operatorname{Re} z = x\)로 나타낸다.
  • $y$를 $z$의 허수부 (imaginary part^영어)라고 하며, \(\operatorname{Im} z = y\)로 나타낸다.

  
  
  복소수의 덧셈과 뺄셈은 실수부와 허수부를 각각 더하고 빼서 계산한다.
  
  :$(a\; +\; bi)\; +\; (c\; +\; di)\; =\; (a\; +\; c)\; +\; (b\; +\; d)i$
  
  :$(a\; +\; bi)\; -\; (c\; +\; di)\; =\; (a\; -\; c)\; +\; (b\; -\; d)i$
  
  특히, 복소수의 덧셈에 대한 역원은 다음과 같다.
  
  :$-(a+bi)=(-a)+(-b)i$
  
  복소수의 덧셈은 교환 법칙과 결합 법칙을 만족시킨다.
  
  복소수 $z\; =\; a\; +\; bi$ (여기서 $a$, $b$는 실수)의 켤레 복소수 (complex conjugate^영어)는 허수부의 부호를 바꾼 복소수 $a\; -\; bi$이며, $\backslash bar\{z\}$ 또는 $z^*$로 나타낸다^[66]. 즉,
  
  :$\backslash bar\; z\; =\; a\; -\; bi\; =\; \backslash operatorname\{Re\}\; z\; -\; i\backslash operatorname\{Im\}\; z$
  
  켤레 복소수는 다음과 같은 성질을 갖는다.

  
  
  • $\backslash bar\backslash bar\; z=z$
  • $|\backslash bar\; z|=|z|$
  • $\backslash overline\{z+w\}=\backslash bar\; z+\backslash bar\; w$
  • $\backslash overline\{z-w\}=\backslash bar\; z-\backslash bar\; w$
  • $\backslash overline\{zw\}=\backslash bar\; z\backslash bar\; w$
  • $\backslash overline\backslash frac\; zw=\backslash frac\backslash bar\; z\backslash bar\; w$

  
  
  또한, 켤레 복소수는 정칙 함수가 아니다.
  

  4. 6. 절댓값과 편각 (연산)

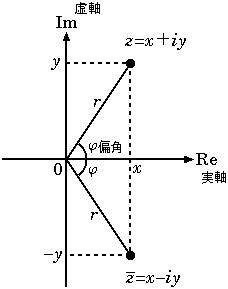
  복소수를 실수부와 허수부로 나타내는 것과는 별개로, 복소 평면상의 점 를 원점 으로부터의 거리와, 과 선분 가 이루는 각을 반시계 방향으로 측정한 쌍(의 극좌표)으로 나타내는 방법이 있다. 이를 통해 복소수의 극형식 개념이 도입된다.
  
  복소수 (는 실수)의 절댓값은
  
  :$|z|\; =\; \backslash sqrt\{x^2\; +\; y^2\}$
  
  로 정의된다. 이는 이상의 실수이다. 가 실수 (즉 )일 때 는 실수의 절댓값 와 일치한다.
  
  복소수의 절댓값은 피타고라스 정리에 의해 복소 평면에서 원점 과의 유클리드 거리와 같다. 그리고 다음이 성립한다.

  
  
  • 비퇴화성:
  • 삼각 부등식: (반가법성이라고도 함)
  • 곱셈성:

  
  반대로, 복소수의 절댓값은 실수의 절댓값을 복소수로 확장한 노름 대수로서 특징지어진다.
  
  복소수 의 절댓값 는 를 극형식으로 표시할 때:
  
  :
  
  동경 과 같다.
  
  켤레 복소수와 자신의 곱은 절댓값의 제곱과 같다. 즉 복소수 에 대해
  
  :$|z|^2\; =\; z\backslash overline\{z\}\; =\; x^2\; +\; y^2$
  
  가 성립한다.
  
  복소수 의 편각(응용의 장면에서는 종종 "위상"이라고도 불린다) 는 복소 평면상에서 양의 실수축에서 측정한 동경 의 각도이다. 편각 의 값은 라디안으로 나타낸다.
  
  각에 의 임의의 정수 배를 더해도 그것이 나타내는 동경, 복소수는 같으므로 편각을 주는 함수는 다중 함수이다.
  
  그래서 편각 를 일가 함수로 정의하기 위해, '''주값'''을 구간 로 하는 경우, 역탄젠트 함수로부터 다음과 같이 정의된다^[68](계산기 언어에서는 의 역탄젠트 함수를 두 개의 인수 에 대한 atan2로 구현하는 경우가 많다):
  
  :$\backslash arg\; z\; =\; \backslash begin\{cases\}$
  
  \arctan \dfrac{y}{x} &\text{if } x > 0 \\
  
  \arctan \dfrac{y}{x} + \pi &\text{if } x < 0 \text{ and } y \ge 0 \\
  
  \arctan \dfrac{y}{x} - \pi &\text{if } x < 0 \text{ and } y < 0 \\
  
  \dfrac{\pi}{2} &\text{if } x = 0 \text{ and } y > 0 \\

  
  
  • \dfrac{\pi}{2} &\text{if } x = 0 \text{ and } y < 0 \\

  
  \text{indeterminate} &\text{if } x = y = 0
  
  \end{cases}
  
  복소수가 일 때만 편각은 부정(indeterminate)이 된다.
  
  위의 정의에서 음수가 되는 편각의 값에 대해 를 더하면 주값은 가 된다.
  
  복소수 가 주값의 끝 값의 근방을 연속적으로 변화한다면, 편각의 값도 또한 그 근방에서 연속적으로 변화하도록 가지를 취하는 것으로, 그것을 단순히 와 같이 쓴다.
  
  복소수의 곱셈, 나눗셈, 거듭제곱은 극형식으로 나타낸 다음 계산하는 것이 직교 좌표 형식보다 더 낫다. 두 복소수의 극형식을 다음과 같이 나타내면
  
  :,
  
  :
  
  곱 는 삼각 함수의 덧셈 정리:
  
  :$\backslash cos\; \backslash alpha\; \backslash cos\; \backslash beta\; -\; \backslash sin\; \backslash alpha\; \backslash sin\; \backslash beta\; =\; \backslash cos\; (\; \backslash alpha\; +\; \backslash beta\; ),$
  
  :$\backslash cos\; \backslash alpha\; \backslash sin\; \backslash beta\; +\; \backslash sin\; \backslash alpha\; \backslash cos\; \backslash beta\; =\; \backslash sin\; (\; \backslash alpha\; +\; \backslash beta\; )$
  
  에 의해
  
  :$z\_1\; z\_2\; =\; r\_1\; r\_2\; (\; \backslash cos\; (\; \backslash varphi\_1\; +\; \backslash varphi\_2\; )\; +\; i\; \backslash sin\; (\; \backslash varphi\_1\; +\; \backslash varphi\_2\; ))$
  
  가 된다. 즉, 곱의 절대값은 절대값의 곱이고, 곱의 편각은 편각의 합이다.
  
  에서 허수 단위 를 곱하는 것 (작용)은 복소 평면상에서 원점을 중심으로 시계 반대 방향으로 직각 회전시키는 것이다. 따라서 허수 단위 는 복소 평면상에서 직교 좌표로 의 위치에 있다.
  
  마찬가지로 몫은
  
  :$\backslash frac\{z\_1\}\{z\_2\}\; =\; \backslash frac\{r\_1\}\{r\_2\}\; \backslash left(\; \backslash cos\; (\; \backslash varphi\_1\; -\; \backslash varphi\_2\; )\; +\; i\; \backslash sin(\; \backslash varphi\_1\; -\; \backslash varphi\_2\; )\; \backslash right)$
  
  가 된다.
  

  4. 7. 켤레 복소수 (연산)

  복소수 의 ''켤레 복소수''는 와 같이 정의된다.^[8] 기하학적으로, 는 실수 축에 대한 의 반사이다. 두 번 켤레 복소수를 취하면 원래의 복소수가 된다: . 복소수가 자신의 켤레 복소수와 같을 때에만 실수이다.
  
  모든 복소수 에 대해, 곱
  
  :
  
  는 ''음이 아닌 실수''이다. 이를 통해 ''z''의 ''절댓값''(또는 ''크기'')을 제곱근으로 정의할 수 있다.
  
  :}.
  
  켤레 복소수를 사용하여, 0이 아닌 복소수 의 역수는 다음과 같이 계산할 수 있다.
  
  :{z\bar{z}}
  
  = \frac{\bar{z}}{|z|^2}
  
  = \frac{x - yi}{x^2 + y^2}
  
  = \frac{x}{x^2 + y^2} - \frac{y}{x^2 + y^2}i.}}
  
  더 일반적으로, 임의의 복소수 를 0이 아닌 복소수 로 나누면 다음과 같다.
  
  :
  

  5. 종류

  복소수는 실수부와 허수부의 값에 따라 실수, 허수, 순허수 등으로 분류할 수 있다. 또한, 어떤 다항식의 근이 될 수 있는지에 따라 대수적 수와 초월수로 분류할 수 있다.
  

  5. 1. 실수와 허수

  복소수 $z$는 실수부와 허수부가 0인지에 따라 다음과 같이 분류된다.

  
  
  • $\backslash operatorname\{Im\}z=0$이면, $z$를 '''실수'''라고 한다.
  • $\backslash operatorname\{Im\}z\backslash ne0$이면, $z$를 '''허수'''라고 한다.
  • $\backslash operatorname\{Im\}z\backslash ne0$이고 $\backslash operatorname\{Re\}z=0$이면, $z$를 '''순허수'''라고 한다.

  
  
  복소수 $z$에 대하여, 다음 조건들은 서로 동치이다.

  
  
  • $z$는 실수이다.
  • $\backslash operatorname\{Im\}z=0$
  • $z=0$이거나, $\backslash operatorname\{arg\}z=0,\backslash pi$
  • $z=\backslash bar\; z$

  
  
  또한, 다음 조건들은 서로 동치이다.

  
  
  • $z$는 순허수이다.
  • $\backslash operatorname\{Re\}z=0\backslash ne\backslash operatorname\{Im\}z$
  • $\backslash operatorname\{arg\}z=\backslash pm\backslash frac\backslash pi2$
  • $z=-\backslash bar\; z\backslash ne0$

  
  
  예를 들어, $-1,1/3,\backslash sqrt[3]2,\backslash pi$는 실수이며, $1+i,-2i,2+\backslash sqrt3i$는 허수이며, 이들 가운데 $-2i$는 순허수이다.
  

  5. 2. 대수적 수와 초월수

  복소수 $z$는 어떤 다항식의 근이 될 수 있는지에 따라 다음과 같이 분류된다.

  
  
  • 만약 $f(z)=0$인 복소수 계수 다항식 $f(x)\backslash ne0$가 존재한다면, $z$를 '''대수적 수'''라고 한다.
  • 만약 $f(z)=0$인 복소수 계수 다항식 $f(x)\backslash ne0$가 존재하지 않는다면, $z$를 '''초월수'''라고 한다.

  
  
  예를 들어, $\backslash sqrt[3]2,(1+i)/\backslash sqrt2$는 대수적 수이며, $e,\backslash pi$는 초월수이다.
  

  6. 확장

  복소수체는 대수적으로 닫힌 체이지만, 다른 수 체계로 확장될 수 있다.
  
  복소수에 포함되지 않는 다른 수가 존재하지 않는다는 의미는 아니다. 수는 인간의 자유로운 상상력을 기반으로 얼마든지 만들 수 있기 때문이다.^[79] 예를 들어, $\backslash sqrt\{x\}\; =\; -1$을 만족하는 $x$는 복소수가 아니며, 이러한 수를 새로 정의할 수 있다. 초월 확대를 사용하면 복소수체를 더 큰 체로 확장할 수 있다. 또한, 복소수체를 사원수(쿼터니언)라는 더 큰 나눗셈 대수로 확장할 수 있다. 그러나 3차원 이상의 $\backslash mathbb\; R$-대수는 체가 될 수 없다.
  
  실수체 $\backslash mathbb\; R$을 $\backslash mathbb\; C$로 확장하는 과정은 '케일리-딕슨 구성'의 한 예시이다. 이 구성을 $\backslash C$에 반복적으로 적용하면 사원수, 팔원수(옥토니언),^[55] 십육원수(세데니언) 등이 생성된다. 이 구성은 관련된 수 체계의 구조적 속성을 약화시킨다. 예를 들어, 복소수에서 사원수로 넘어가면 교환 법칙이 성립하지 않으며, 팔원수는 결합 법칙도 성립하지 않는다.
  
  실수와 달리, $\backslash Complex$는 순서체가 아니다. 즉, 덧셈과 곱셈과 호환되는 관계를 정의할 수 없다. 실제로, 모든 순서체에서 임의의 원소의 제곱은 필연적으로 양수이므로 $\backslash Complex$에 대한 순서는 존재할 수 없다.
  
  초복소수는 $\backslash mathbb\; R,$ $\backslash mathbb\; C,$ 등을 일반화한다. 예를 들어, 이 개념에는 분할 복소수가 포함된다.
  
  p-진수의 체 $\backslash mathbb\; Q\_p$는 유리수체에 대한 거리 선택에 따라 생성된다. 오스트로프스키의 정리에 의해, $\backslash mathbb\; Q$를 완비하는 비자명한 다른 방법은 $\backslash mathbb\; R$과 $\backslash mathbb\; Q\_p$ 뿐이다.
  
  체 및 이들의 유한 차원 확대체는 모두 국소체이다.
  

  6. 1. 대수적 폐포

  대수학의 기본 정리에 따르면, 복소수 계수 다항식의 근은 모두 복소수이다.^[79] 예를 들어,
  
  :$\backslash pm\backslash sqrt\; i=\backslash pm\backslash frac\{1+i\}\backslash sqrt2$
  
  는 여전히 복소수이다. 따라서, 복소수는 다항식의 가상의 근을 새로운 원소로 추가하는 방식으로는 더 이상 확장되지 않는다. 추상대수학의 용어를 사용하면, 복소수체는 대수적으로 닫힌 체이다.
  
  대수학의 기본 정리에 따르면 복소수를 계수로 하는 대수 방정식의 해는 존재하며 또한 복소수가 된다. 즉,
  
  :$a\_n\; z^n\; +\; \backslash cdots\; +\; a\_1\; z\; +\; a\_0\; \backslash quad\; (\; \backslash ,\; a\_r\; \backslash in\; \backslash mathbb\{C\}\; ,\; \backslash \; a\_n\; \backslash neq\; 0\; \backslash ,\; )$
  
  은 적어도 하나의 복소근을 갖는다.
  
  위의 다항식의 복소근 중 하나를 $\backslash alpha\_1$로 하고, 인수 정리를 귀납적으로 사용하면, 위의 다항식은
  
  :$\backslash textstyle\; \backslash sum\backslash limits\_\{r=0\}^n\; a\_r\; z^r\; =\; a\_n\; \backslash prod\backslash limits\_\{k=1\}^n\; (z-\; \backslash alpha\_k\; )\; \backslash quad\; (\; \backslash ,\; \backslash alpha\_k\; \backslash in\; \backslash mathbb\{C\}\; \backslash ,\; )$
  
  과 같이 복소수 범위에서 인수 분해된다. 이것은 복소수가 대수 방정식에 의한 수의 확장의 최대임을 의미한다. 즉, 복소수 집합은 대수적 폐체이다.
  
  이 사실에 의해 "임의의 대수적 폐체에 대해 성립하는 정리"를 복소수 집합에도 적용할 수 있다. 예를 들어, 임의의 공집합이 아닌 복소 정사각 행렬은 적어도 하나의 복소 고유값을 갖는다.
  
  체는 다음 세 가지 성질을 만족한다.

  
  
  • 대수적 폐체이다.

  6. 2. 사원수 및 기타 확장

  대수학의 기본 정리에 따르면, 복소수 계수를 가지는 다항식의 근은 모두 복소수이다. 예를 들어,
  
  :$\backslash pm\backslash sqrt\; i=\backslash pm\backslash frac\{1+i\}\backslash sqrt2$
  
  는 여전히 복소수이다. 따라서 복소수는 다항식의 가상의 근을 새로운 원소로 추가하여 확장되지 않는다. 추상대수학 용어로, 복소수체는 대수적으로 닫힌 체이다.
  
  하지만 복소수에 포함되지 않는 다른 수가 존재하지 않는다는 의미는 아니다. 수는 인간의 자유로운 상상력을 기반으로 얼마든지 만들 수 있기 때문이다.^[79] 예를 들어, $\backslash sqrt\{x\}\; =\; -1$ 을 만족하는 $x$는 복소수가 아니며, 이러한 수를 새로 정의할 수 있다. 초월 확대를 사용하면 복소수체를 더 큰 체로 확장할 수 있다. 또한, 복소수체를 사원수(쿼터니언)라는 더 큰 나눗셈 대수로 확장할 수 있다. 그러나 3차원 이상의 $\backslash mathbb\; R$-대수는 체가 될 수 없다.
  
  실수체 $\backslash mathbb\; R$을 $\backslash mathbb\; C$로 확장하는 과정은 ''케일리-딕슨 구성''의 한 예시이다. 이 구성을 $\backslash C$에 반복적으로 적용하면 사원수, 팔원수(옥토니언),^[55] 십육원수(세데니언), 트리진타듀오니언이 생성된다. 이 구성은 관련된 수 체계의 구조적 속성을 약화시킨다.
  
  

  수 체계

  	유리수 $\backslash Q$	실수 $\backslash R$	복소수 $\backslash C$	사원수 $\backslash mathbb\; H$	팔원수 $\backslash mathbb\; O$	십육원수 $\backslash mathbb\; S$
  완비	아니오	예	예	예	예	예
  $\backslash R$-차원	[해당 없음]	1	2	4	8	16
  순서	예	예	아니오	아니오	아니오	아니오
  곱셈 교환	예	예	예	아니오	아니오	아니오
  곱셈 결합	예	예	예	예	아니오	아니오
  노름 나눗셈 대수	[해당 없음]	예	예	예	예	아니오

  
  
  실수와 달리, $\backslash Complex$는 순서체가 아니다. 즉, 덧셈과 곱셈과 호환되는 관계를 정의할 수 없다. 실제로, 모든 순서체에서 임의의 원소의 제곱은 필연적으로 양수이므로 $\backslash Complex$에 대한 순서의 존재를 배제한다. $\backslash C$에서 사원수 $\backslash mathbb\; H$로 넘어가면 교환 법칙이 성립하지 않으며, 팔원수는 (교환 법칙이 성립하지 않는 것 외에도) 결합 법칙도 성립하지 않는다. 실수, 복소수, 사원수 및 팔원수는 모두 $\backslash mathbb\; R$ 위의 노름 나눗셈 대수이다. Hurwitz의 정리에 따르면, 이것이 유일하며, 케일리-딕슨 구성의 다음 단계인 십육원수는 이러한 구조를 갖지 못한다.
  
  초복소수는 $\backslash mathbb\; R,$ $\backslash mathbb\; C,$ $\backslash mathbb\; H,$ 및 $\backslash mathbb\{O\}$을 일반화한다. 예를 들어, 이 개념에는 분할 복소수가 포함되며, 이는 링 $\backslash mathbb\; R[x]/(x^2-1)$의 원소이다(복소수의 경우 $\backslash mathbb\; R[x]/(x^2+1)$과 반대). 이 링에서 방정식은 4개의 해를 갖는다.
  
  복소수는 실수체 위의 실수 단위, 허수 단위의 선형 결합이지만, 여기에 새로운 단위를 유한 개 더하여 가환체(일반적인 사칙 연산이 가능한 수의 체계)를 만들 수 없다.^[75][76] 실수체에서 확장하여 를 얻는 과정은 케일리-딕슨 구성법이라고 불린다. 이 과정을 밀고 나가면, 더 고차원의 사원수체, 팔원수체를 얻을 수 있다. 이들의 실수체 위의 선형 공간으로서의 차원은 각각이다. 이 문맥에서 복소수는 "이원수"(''binarions'')라고도 불린다.^[77]
  
  주의해야 할 점은, 실수체에 케일리-딕슨 구성을 적용함으로써 순서에 관한 성질이 상실된다는 것이다. 더 고차원으로 진행하면 실수나 복소수에 관해 잘 알려진 성질이 상실될 것이다. 사원수는 유일한 비가환체이며^[75][76](즉, 어떤 두 사원수에 대해 가 된다), 팔원수에서는 (비가환일 뿐만 아니라) 곱셈에 관한 결합 법칙도 상실된다(즉, 어떤 팔원수에 대해 가 된다). 일반적으로, 실수체 상의 노름多元體는 동형에 의한 차이를 제외하고, 실수체, 복소수체, 사원수체, 팔원수체의 4 종류밖에 없다.^[78] 케일리-딕슨 구성의 다음 단계에서 얻어지는 십육원수 환에서는 이 구조가 사라진다.
  
  체, 및 이들의 유한 차원 확대체는 모두 국소체이다.
  

7. 성질

복소수체는 체의 공리, 대수적 폐체 등 중요한 성질들을 만족한다.

복소수 의 켤레 복소수는 다음과 같이 정의된다.

:$\backslash overline\; z\; =\; x-yi.$^[8]

기하학적으로, 는 실수 축에 대한 의 반사이다. 두 번 켤레 복소수를 취하면 원래의 복소수가 된다. 즉, $\backslash overline\{\backslash overline\{z\}\}=z.$이다. 복소수가 자신의 켤레 복소수와 같을 때에만 실수이다.

모든 복소수 에 대해, 곱

:$z\; \backslash cdot\; \backslash overline\; z\; =\; (x+iy)(x-iy)\; =\; x^2\; +\; y^2$

는 음이 아닌 실수이다. 이를 통해 ''z''의 절댓값(또는 크기)을 제곱근으로 정의할 수 있다.

:$$|z|=\backslash sqrt\{x^2+y^2\}.$$

피타고라스 정리에 의해, $|z|$는 복소 평면에서 복소수 ''z''를 나타내는 점에서 원점까지의 거리이다.

켤레 복소수를 사용하여, 0이 아닌 복소수 $z\; =\; x\; +\; yi$의 역수는 다음과 같이 계산할 수 있다.

:$$$$

\frac{1}{z}

= \frac{\bar{z}}{z\bar{z}}

= \frac{\bar{z}}

7. 1. 체 구조

• 닫힘: 임의의 두 복소수의 합과 곱은 다시 복소수가 된다.
• 역원의 존재: 임의의 복소수 ''z''에 덧셈 역원 -''z''가 존재하며, 그것 또한 복소수이다.
• 역수의 존재: 임의의 0이 아닌 복소수에 대해 곱셈 역원 1/''z''가 존재한다.
• 추가로 몇 가지 법칙을 만족한다. 복소수 ''z''₁, ''z''₂, ''z''₃에 대해
• * 합의 교환 법칙: ''z''₁ + ''z''₂ = ''z''₂ + ''z''₁
• * 합의 결합 법칙: (''z''₁ + ''z''₂) + ''z''₃ = ''z''₁ + (''z''₂ + ''z''₃)
• * 곱의 교환 법칙: ''z''₁''z''₂ = ''z''₂''z''₁
• * 곱의 결합 법칙: (''z''₁''z''₂)''z''₃ = ''z''₁(''z''₂''z''₃)
• * 분배 법칙: ''z''₁(''z''₂ + ''z''₃) = ''z''₁''z''₂ + ''z''₁''z''₃

7. 2. 위상적 특징

• 는 덧셈, 곱셈 및 역원에 대해 닫혀 있다.
• 와 가 의 서로 다른 원소이면 또는 가 에 속한다.
• 가 의 공집합이 아닌 임의의 부분 집합이면, 이며, 여기서 는 $\backslash Complex$에 속한다.

8. 복소함수

복소수를 변수로 하는 함수는 복소해석학의 주요 연구 대상이다.

일반적으로 2차원 그래프로 표현되는 실수 함수와 달리, 복소 함수는 4차원 그래프를 가지며, 이를 표현하기 위해 여러 방법이 사용된다. 예를 들어 3차원 그래프에 색을 추가하여 4차원을 나타내거나, 복소 평면에서 복소 함수의 동적 변환을 애니메이션으로 만들기도 한다.

복소해석학은 실수해석학에서는 볼 수 없는 몇 가지 특징을 보인다. 예를 들어, 두 정칙 함수가 복소 평면의 매우 작은 일부에서만 일치하더라도, 전체에서 일치하는 경우가 있다. (항등 정리)^[49]

8. 1. 복소해석학

일반적으로 2차원 그래프로 표현되는 실수 함수와 달리, 복소 함수는 4차원 그래프를 가지며, 4차원을 암시하기 위해 3차원 그래프를 색상 코딩하거나 복소 평면의 복소 함수의 동적 변환을 애니메이션화하여 유용하게 표현할 수 있다.

8. 2. 수렴

복소수열은 실수부와 허수부가 모두 수렴할 때 수렴한다고 한다. 이는 실수의 절댓값을 복소수의 절댓값으로 대체하는 (ε, δ)-극한의 정의와 동등하다. 더 추상적인 관점에서, 거리를 갖는 $\backslash mathbb\{C\}$는 다음과 같다.

$$\backslash operatorname\{d\}(z\_1,\; z\_2)\; =\; |z\_1\; -\; z\_2|$$

이는 완비 거리 공간이며, 특히 두 복소수 $z\_1$와 $z\_2$에 대해 삼각 부등식이 성립한다.

$$|z\_1\; +\; z\_2|\; \backslash le\; |z\_1|\; +\; |z\_2|$$

8. 3. 복소 지수 함수

복소 지수 함수 또는 는 급수

:$\backslash exp\; z:=\; \backslash textstyle\backslash sum\backslash limits\_\{n=0\}^\{\backslash infty\}\; \backslash displaystyle\; \backslash frac\{z^n\}\{n!\}\; =\; 1\; +\; z\; +\; \backslash frac\{z^2\}\{2\}\; +\; \backslash frac\{z^3\}\{6\}\; +\; \backslash cdots$

로 정의된다. 이 급수의 수렴 반경은 이므로, 복소 지수 함수는 상의 정칙 함수(전체 함수)이다.

임의의 실수 에 대해 다음 등식이 성립한다.

:$\backslash exp\; i\backslash varphi\; =\; \backslash cos\; \backslash varphi\; +\; i\backslash sin\; \backslash varphi$ (오일러 공식)

일반적인 복소 변수 로 확장한 코사인 함수 , 사인 함수 는 다음 식으로 정의할 수 있다.

:$\backslash begin\{align\}$

\cos z &= \frac{e^{iz} + e^{-iz}}{2} \\

\sin z &= \frac{e^{iz} - e^{-iz}}{2i}

\end{align}

코사인 함수, 사인 함수는 전체 함수이다. 전체 함수인 확장의 방법은, 일치 정리에 의해 유일하다.

, 등의 쌍곡선 함수도 마찬가지로 복소 지수 함수에 의해 정의할 수 있다.

물리학에서 진동이나 파동 등 서로 밀접한 관련이 있는 두 개의 실수 물리량을 복소수의 형태로 조합하여 표현하는 것이 편리한 경우가 많아 자주 사용된다.

8. 4. 복소 로그 함수

자연 로그는 역함수로 정의되어, 임의의 양의 실수 ''t''에 대해 $\backslash exp(x)\; =\; t$를 만족하는 고유한 실수 ''x''가 존재한다. 즉,

:$\backslash ln\; \backslash colon\; \backslash R^+\; \backslash to\; \backslash R\; ;\; x\; \backslash mapsto\; \backslash ln\; x$는 지수 함수의 역함수이다. 복소수의 경우에는 상황이 다른데, 함수 방정식과 오일러 항등식에 의해

:$\backslash exp(z+2\backslash pi\; i)\; =\; \backslash exp\; z\; \backslash exp\; (2\; \backslash pi\; i)\; =\; \backslash exp\; z$

가 성립하기 때문이다. 예를 들어, $e^\{i\backslash pi\}\; =\; e^\{3i\backslash pi\}\; =\; -1$이므로, $i\backslash pi$와 $3i\backslash pi$ 모두 $-1$의 복소 로그 값이 될 수 있다.

일반적으로 0이 아닌 임의의 복소수 ''w''에 대해, 방정식

:$\backslash exp\; z\; =\; w$

를 만족하는 임의의 수 ''z''를 ''w''의 복소 로그라 하고, $\backslash log\; w$로 표시한다. 이 ''z''는

:$z\; =\; \backslash log\; w\; =\; \backslash ln|w|\; +\; i\backslash arg\; w$

로 나타낼 수 있다. 여기서 $\backslash arg$는 인수로 위에서 정의되었고, $\backslash ln$은 (실수) 자연 로그이다. $\backslash arg$는 다중값 함수이므로 $2\backslash pi$의 배수까지 고유하며, $\backslash log$도 다중값이다. $\backslash log$의 주요 값은 허수 부분을 구간 $(-\backslash pi,\; \backslash pi]$로 제한하여 취하며, 이는 복소 로그가 $\backslash R^+\; +\; \backslash ;\; i\; \backslash ,\; \backslash left(-\backslash pi,\; \backslash pi\backslash right]$(그림에서 $S\_0$로 표시됨)의 값을 갖는 전단사 함수가 되도록 한다.

:$\backslash ln\; \backslash colon\; \backslash ;\; \backslash Complex^\backslash times\; \backslash ;\; \backslash to\; \backslash ;\; \backslash ;\; \backslash ;\; \backslash R^+\; +\; \backslash ;\; i\; \backslash ,\; \backslash left(-\backslash pi,\; \backslash pi\backslash right]$

$z\; \backslash in\; \backslash Complex\; \backslash setminus\; \backslash left(\; -\backslash R\_\{\backslash ge\; 0\}\; \backslash right)$, 즉 $z$가 음이 아닌 실수(양수 또는 비실수)인 경우, 복소 로그의 주요 값은 로 얻어진다. 이는 음의 실수를 제외하고 해석 함수이지만, 주요 값이 $\backslash ln\; z\; =\; \backslash ln(-z)\; +\; i\backslash pi$인 음의 실수 $z\; \backslash in\; -\backslash R^+$에서는 연속인 함수로 확장될 수 없다.

복소 지수 $z^\backslash omega$는

:$z^\backslash omega\; =\; \backslash exp(\backslash omega\; \backslash ln\; z)$

로 정의되며, $\backslash omega$가 정수가 아닌 경우 다중값을 갖는다. $\backslash omega\; =\; 1/n$ (단, $n$은 자연수)인 경우, 앞서 언급한 $n$제곱근의 비고유성이 나타난다. $z\; >\; 0$가 실수이고 $\backslash omega$가 임의의 복소수일 때, 실수 로그 $\backslash ln\; x$를 사용하여 선호하는 지수 함수를 정의할 수 있다.

복소수는 실수와 달리 수정되지 않은 거듭제곱 및 로그 항등식을 일반적으로 만족하지 않는데, 이는 단일 값 함수로 단순하게 취급할 때 특히 그렇다. 거듭제곱 및 로그 항등식의 실패를 참고하면, 예를 들어

:$a^\{bc\}\; =\; \backslash left(a^b\backslash right)^c$

는 성립하지 않는다. 이 방정식의 양변은 복소 지수의 정의에 의해 다중값이며, 좌변의 값은 우변의 값의 부분집합이다.

실함수와 달리, 복소수 $z$에 관한 방정식

:$\backslash exp\; z\; =\; w$

는 임의의 0이 아닌 복소수 $w$에 대해 무한 개의 복소수 해를 갖는다. 이러한 해 $z$, 즉 $w$의 복소대수함수 $\backslash log\; w$는

:$\backslash log\; w\; =\; \backslash ln|w|\; +\; i\backslash arg\; w$

로 나타낼 수 있다. 여기서 $\backslash ln$은 실함수로서의 자연로그이고, $\backslash arg$는 앞서 설명한 편각이다. 이 값은 편각과 마찬가지로 $2\backslash pi$의 정수배만큼의 차이를 제외하고 유일하므로, 복소대수함수 또한 다중가함수이다. 따라서 주치를 사용하며, 허수부 $\backslash arg\; w$를 구간 $(-\backslash pi,\; \backslash pi]$로 하는 경우가 많다.

8. 5. 복소수의 복소수 거듭제곱

복소 로그 함수를 통해 정의되며, 다가 함수이다.^[55] 복소수의 복소수 거듭제곱 $z^\omega$는 다음과 같이 정의된다.

:$z^\backslash omega\; =\; \backslash exp(\backslash omega\; \backslash log\; z)$

로그 함수는 다가 함수이므로, 복소수의 복소수 거듭제곱도 일반적으로 다가 함수가 된다. 특히 $\omega = \frac{1}{n}$ (n은 자연수) 형태일 때는, 복소수 $z$의 $n$제곱근 $\sqrt[n]{z}$를 나타내며, 값은 유일하게 정해지지 않는다.

로그 함수의 적절한 가지를 택하여 일가 함수로 취급할 때, 실수의 실수 거듭제곱에 대해 성립했던 지수 법칙이나 로그 법칙은 복소수의 복소수 거듭제곱에서는 일반적으로 성립하지 않는다. 예를 들어,

:$a^\{bc\}\; =\; (a^b)^c$

는 $a$, $b$, $c$가 복소수인 경우에는 일반적으로 성립하지 않는다. 이 식의 양변을 다가 값을 갖는 것으로 간주하는 경우, 좌변 값의 전체는 우변 값의 전체가 이루는 집합의 부분 집합이 된다.

8. 6. 정칙 함수

복소해석학에서, '''정칙 함수'''(正則函數, holomorphic function^영어)는 복소수 평면의 열린 집합에서 정의된 복소 미분 가능한 함수를 말한다.^[49] 복소 미분 가능성은 실수 미분 가능성보다 훨씬 강력한 조건인데, 이는 여러 방향으로 $z\_0$에 접근할 수 있는 자유가 있기 때문이다.

예를 들어, 함수

:$f(z)\; =\; \backslash overline\; z$

는 $\backslash R^2\; \backslash to\; \backslash R^2$ 함수로 미분 가능하지만 복소 미분 가능하지는 ''않다''.^[49]

실수 미분 가능한 함수는 코시-리만 방정식을 만족하는 경우에만 복소 미분 가능하다. 이는 때때로 다음과 같이 요약된다.^[49]

:$\backslash frac\{\backslash partial\; f\}\{\backslash partial\; \backslash overline\; z\}\; =\; 0.$

복소해석은 실수해석에서는 나타나지 않는 몇 가지 특징을 보여준다. 예를 들어, 항등 정리는 두 개의 정칙 함수와 가 $\backslash mathbb\{C\}$의 임의로 작은 열린 부분 집합에서 일치하면 서로 일치한다고 주장한다.^[49] 유형 함수는 정칙 함수를 사용하여 $f(z)/(z\; -\; z\_0)^n$로 지역적으로 쓸 수 있는 함수이며, 여전히 정칙 함수의 일부 특징을 공유한다. 다른 함수는 $z\; =\; 0$인 $\backslash sin(1/z)$와 같이 본질적 특이점을 갖는다.^[49]

9. 응용

복소수는 신호 처리, 제어 이론, 전자기학, 유체 역학, 양자역학, 지도 제작, 진동 분석 등 다양한 과학 분야에서 응용된다.^[74]

• '''신호 처리''': 주기적으로 변하는 신호를 편리하게 설명하기 위해 사용된다. 실수 신호를 주기 함수의 합으로 표현하는 푸리에 분석에서 주기 함수는 복소수 함수 형태로 표현된다.
• '''제어 이론''': 라플라스 변환을 사용하여 시스템을 시간 영역에서 복소 주파수 영역으로 변환하여 분석한다. 근궤적, 나이퀴스트 선도, 니콜스 선도 기법 등에서 복소 평면이 활용된다.
• '''전자기학''': 전기 공학에서 푸리에 변환을 사용하여 전압과 전류를 분석한다. 저항, 축전기, 인덕터를 임피던스라는 단일 복소수로 결합하여 회로를 분석하는 페이저 미적분이 사용된다.
• '''유체 역학''': 2차원 포텐셜 흐름을 설명하는 데 복소 함수가 사용된다.^[3]
• '''양자 역학''': 양자역학의 수학적 공식화에서 복소 힐베르트 공간이 사용되며, 슈뢰딩거 방정식과 하이젠베르크의 행렬역학 등 기본 공식에 복소수가 사용된다.
• '''상대성 이론''': 시공간에 대한 계량 텐서의 일부 공식에서 시간 성분을 허수로 간주하면 공식이 간단해진다. 텐서의 일반화인 스피너에도 복소수가 필수적이다.

9. 1. 기하학

• 만델브로 집합
• 마든 정리

9. 1. 1. 도형

9. 1. 2. 프랙탈 기하학

9. 1. 3. 삼각형

9. 2. 대수적 수론

9. 3. 해석적 정수론

9. 4. 이상 적분

9. 5. 동역학 방정식

9. 6. 선형대수학

9. 7. 제어 이론

• 오른쪽 반평면에 있으면 불안정하다.
• 모두 왼쪽 반평면에 있으면 안정하다.
• 허수 축에 있으면 한계 안정성을 갖는다.

9. 8. 신호 분석

9. 9. 물리학

10. 역사

복소수의 개념은 16세기 타르탈리아, 제롤라모 카르다노와 같은 이탈리아 수학자들이 삼차 방정식과 사차 방정식의 근에 대한 공식을 발견하면서 처음 나타났다. 당시 수학자들은 실수해를 구하려 했지만, 이 과정에서 음수의 제곱근을 다루는 것이 필요함을 알게 되었다. 그러나 당시에는 음수에 대한 이해도 부족했기에 복소수는 수로 인정받지 못했다.^[71]

17세기에 르네 데카르트가 "허수"라는 용어를 처음 사용했다. 18세기 아브라함 드무아브르와 레온하르트 오일러는 복소수에 대한 연구를 진행했다. 드무아브르의 공식과 오일러의 공식이 그들의 업적을 보여준다.

1799년 카스파르 베셀이 복소수를 기하학적으로 표현하면서 복소수의 존재성이 완전히 받아들여졌다. 카를 프리드리히 가우스는 베셀의 발견을 널리 알렸고, 복소수는 중요한 수의 확장으로 인정받게 되었다. 그러나 복소수의 기하학적 표현은 1685년 존 월리스의 저서에도 이미 나타나 있었다.^[72]

16세기 이탈리아 수학자 카르다노와 봄벨리는 삼차 방정식 해의 공식을 연구하면서 음수의 제곱근을 취해야 할 필요성을 알게 되었다.

17세기 르네 데카르트는 '허'(imaginary)라는 단어를 사용해 허수라 칭했고, 허수에 대한 부정적 시각을 강화했다. 이후 존 월리스가 기하학적 해석을 시도했고, 요한 베르누이, 오일러, 달랑베르 등에 의해 허수를 사용한 해석학, 물리학 연구가 이루어졌다.

복소 평면은 1797년 노르웨이 수학자 카스파르 베셀(Caspar Wessel)의 논문에서 처음 등장했다고 알려졌으나, 덴마크어로 쓰여 1895년에야 발견되었다. 1806년 장-로베르 아르강(Jean-Robert Argand)의 복소 평면 팜플렛은 르장드르를 통해 퍼졌지만, 곧 잊혀졌다.

1814년 코시가 복소 해석을 시작하여, 복소수를 변수로 하는 해석 함수와 복소선 적분을 다루었다.^[71]

1831년 가우스가 복소 평면을 발표하며, '가우스 평면'으로 알려지게 되었다.^[72] 이로써 허수에 대한 부정적 시각은 사라지고 복소수가 수용되었다. 가우스는 1796년 이전에 이미 복소 평면 개념에 도달했으며, 1799년 학위 논문에서 대수학의 기본 정리를 증명하며 복소수의 중요 특징을 보였으나, 개념을 명확히 드러내지는 않았다.^[73]

10. 1. 초기 역사

참조

_[1] 서적 Elements of the History of Mathematics Springer
_[2] 간행물 https://books.google[...]
_[3] 서적 College algebra https://archive.org/[...] Wiley
_[4] 서적 Complex Variables McGraw Hill 2009-04-14
_[5] 간행물
_[6] 서적 Geometry: A comprehensive course Dover
_[7] 웹사이트 Complex Number https://mathworld.wo[...] 2020-08-12
_[8] 간행물
_[9] 서적 Numerical Linear Algebra with Applications: Using MATLAB and Octave https://books.google[...] Academic Press
_[10] 서적 Precalculus with Calculus Previews: Expanded Volume https://books.google[...] Jones & Bartlett Learning
_[11] 간행물
_[12] 서적 Complex Variables: Theory And Applications PHI Learning Pvt. Ltd
_[13] 서적 Electric circuits Prentice Hall
_[14] 서적 Modular Forms: A Classical And Computational Introduction https://books.google[...] World Scientific Publishing Company
_[15] 간행물
_[16] 서적 A history of mathematical thought, volume 1
_[17] 서적 Tristan Needham, Visual Complex Analysis, Oxford University Press Inc., New York, 1998, 592 strani http://worldcat.org/[...]
_[18] 문서 Girolamo Cardano 2016
_[19] 문서 An Imaginary Tale: The Story of √−1 Princeton University Press 1998
_[20] 서적 A History of Mathematics, Brief Version Addison-Wesley
_[21] 저널 On a new species of imaginary quantities connected with a theory of quaternions https://babel.hathit[...] 1844
_[22] 서적 Trigonometry https://books.google[...] John Wiley & Sons
_[23] 서적 An Imaginary Tale: The Story of √−1 http://mathforum.org[...] Princeton University Press 2011-04-20
_[24] 서적 The Unattainable Attempt to Avoid the Casus Irreducibilis for Cubic Equations: Gerolamo Cardano's De Regula Aliza Springer
_[25] 서적 La Géométrie {{pipe}} The Geometry of René Descartes with a facsimile of the first edition https://archive.org/[...] Dover Publications 2011-04-20
_[26] 서적 Enlightening Symbols: A Short History of Mathematical Notation and Its Hidden Powers https://books.google[...] Princeton University Press
_[27] 서적 Mathematical Fallacies and Paradoxes https://books.google[...] Courier Corporation
_[28] 서적 Introductio in Analysin Infinitorum https://books.google[...] Marc Michel Bosquet & Co. 1748
_[29] 저널 Om Directionens analytiske Betegning, et Forsog, anvendt fornemmelig til plane og sphæriske Polygoners Oplosning https://babel.hathit[...] 1799
_[30] 서적 A Treatise of Algebra, Both Historical and Practical ... https://echo.mpiwg-b[...] printed by John Playford, for Richard Davis 1685
_[31] 서적 Essai sur une manière de représenter les quantités imaginaires dans les constructions géométriques http://www.bibnum.ed[...] Madame Veuve Blanc 1806
_[32] 문서 Demonstratio nova theorematis omnem functionem algebraicam rationalem integram unius variabilis in factores reales primi vel secundi gradus resolvi posse https://books.google[...] 1799
_[33] 서적 From Kant to Hilbert: A Source Book in the Foundations of Mathematics https://books.google[...] Oxford University Press 2020-03-18
_[34] 웹사이트 Adrien Quentin Buée (1745–1845): MacTutor https://mathshistory[...]
_[35] 저널 Mémoire sur les quantités imaginaires https://royalsociety[...] 1806
_[36] 서적 La vraies théore des quantités négatives et des quantités prétendues imaginaires https://archive.org/[...] Mallet-Bachelier 1861
_[37] 서적 A Treatise on the Geometrical Representation of the Square Roots of Negative Quantities https://archive.org/[...] Cambridge University Press 1828
_[38] 간행물 Consideration of the objections raised against the geometrical representation of the square roots of negative quantities 1829
_[39] 간행물 On the geometrical representation of the powers of quantities, whose indices involve the square roots of negative numbers 1829
_[40] 간행물 Nouveaux principes de géométrie de position, et interprétation géométrique des symboles imaginaires https://babel.hathit[...] 1813
_[41] 서적 Two Cultures https://books.google[...] Birkhäuser
_[42] 서적 An Introduction to the Theory of Numbers OUP Oxford
_[43] 웹사이트 MODULUS http://members.aol.c[...] 1999-09-21
_[44] 서적 Cours d'analyse de l'École royale polytechnique https://archive.org/[...] L'Imprimerie Royale 1821
_[45] 서적 1831
_[46] 서적 1831
_[47] 서적 1831
_[48] 서적 Vorlesungen über die complexen Zahlen und ihre Functionen https://books.google[...] Leopold Voss 1867
_[49] 서적 1998
_[50] 간행물 Triangles I: Shapes
_[51] 간행물 An Elementary Proof of Marden's Theorem http://mathdl.maa.or[...] 2012-01-01
_[52] 간행물 The Most Marvelous Theorem in Mathematics http://mathdl.maa.or[...] 2012-01-01
_[53] 서적 Electromagnetism Manchester Physics Series
_[54] 서적 Model theory of fields Springer-Verlag
_[55] 서적 A Taste of Jordan Algebras Springer
_[56] 간행물 Cisoidal oscillations https://ia800708.us.[...] American Institute of Electrical Engineers 2023-06-24
_[57] 서적 Complex variables and applications McGraw-Hill 1996
_[58] 웹사이트 なぜ虚数単位iの2乗は-1になるのか?#6.3.3. 複素数の由来 https://xseek-qm.net[...]
_[59] PDF 複素数 2006/10/05 http://www.cc.miyaza[...]
_[60] PDF 複素平面の基本概念 http://edupa.info/pd[...]
_[61] 서적 数学用語と記号ものがたり 裳華房 2003-08-25
_[62] 서적 NEW ACTION LEGEND数学2+B―思考と戦略 数列・ベクトル 東京書籍 2019-02-01
_[63] 웹사이트 Complex Number
_[64] 서적 複素解析 オーム社 1995-05
_[65] 서적 College Algebra and Trigonometry https://books.google[...] Cengage Learning
_[66] 서적 1988
_[67] 웹사이트 四元数と三次元空間における回転
_[68] 서적 Complex Variables: Theory And Applications https://books.google[...] PHI Learning Pvt. Ltd
_[69] 서적 Electric circuits https://books.google[...] Prentice Hall
_[70] 문서 解析概論
_[71] 서적
_[72] 서적
_[73] 서적
_[74] 문서
_[75] 서적
_[76] 서적
_[77] 서적 A Taste of Jordan Algebras Springer
_[78] 서적
_[79] 웹사이트 수학산책 : 복소수와 제곱근 http://navercast.nav[...] 2010-10-11