벡터 다발

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

벡터 다발은 위상 공간 위에 정의되는 수학적 구조로, 각 점마다 유한 차원 벡터 공간인 올(fiber)을 갖는 일종의 공간이다. 국소적으로는 밑 공간과 벡터 공간의 곱으로 나타낼 수 있으며, 이를 국소 자명화라고 한다. 벡터 다발은 올의 차원이 모든 점에서 같으면 계수를 갖는다고 하며, 계수가 1인 벡터 다발은 선 다발이라고 한다.

벡터 다발은 직합, 텐서곱, 쌍대 다발 등의 연산을 통해 새로운 벡터 다발을 생성할 수 있으며, 이러한 연산은 벡터 공간 연산을 섬유별로 수행하여 정의된다. 매끄러운 다양체 위에서는 매끄러운 함수를 기반으로 하는 매끄러운 벡터 다발을 정의할 수 있으며, 접다발, 연관 벡터 다발 등이 그 예시이다.

벡터 다발은 위상 K-이론과 같은 이론을 통해 분류되며, 이는 복소 벡터 다발의 동형류를 이용하여 정의되는 아벨 군이다. 또한, 벡터 다발은 계량, 복소 구조 등 추가적인 구조를 가질 수 있으며, 바나흐 공간을 올로 갖는 바나흐 다발이나, 더 일반적인 섬유 다발로 확장될 수 있다.

더 읽어볼만한 페이지

벡터 다발 - 법다발
법다발은 다양체 $M$에 매장된 다양체 $N$의 접다발을 $M$의 접다발로 확장한 몫다발로, 리만 다양체에서는 법선 공간들의 모임으로 정의되며 여법선 다발과 관련이 깊다.
벡터 다발 - 접다발
접다발은 매끄러운 다양체 위의 각 점에 접하는 벡터 공간들을 모아놓은 공간으로, 국소 좌표계를 사용하여 정의되며, 사영 사상을 통해 매끄러운 벡터 다발을 이루고, 다양체의 미분 구조 연구에 중요한 역할을 한다.

벡터 다발

2. 정의

벡터 다발은 위상 공간 $X$ 의 각 점 $x$ 에 벡터 공간 $V_x$ 를 대응시키되, 이 벡터 공간들이 "국소적으로는" $X$ 와 고정된 벡터 공간의 데카르트 곱처럼 보이도록 "잘 붙여놓은" 구조를 말한다.

가장 간단한 예는 자명한 다발(trivial bundle|트리비얼 번들^영어)이다. 이는 밑공간 $X$ 와 고정된 $k$ 차원 벡터 공간 $\mathbb{R}^k$ 의 곱공간 $E = X \times \mathbb{R}^k$ 로 정의된다. 이때 다발 사영 $\pi: E \to X$ 는 단순히 $(x, v) \mapsto x$ 로 주어진다. 모든 점 $x \in X$ 에서 올 $\pi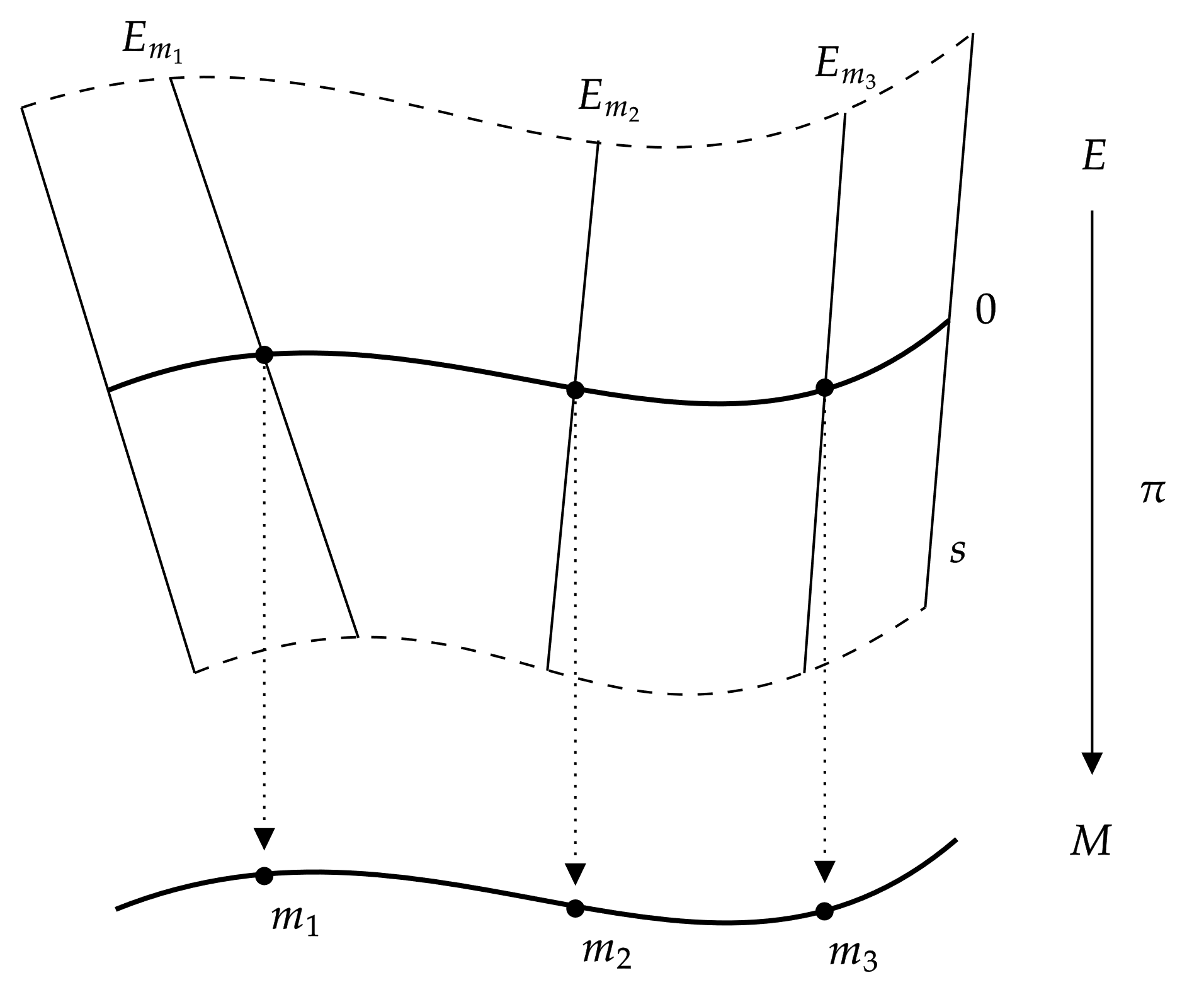^{-1}(x) = \{x\} \times \mathbb{R}^k$ 는 $\mathbb{R}^k$ 와 동형이다.

일반적으로 벡터 다발은 자명하지 않을 수 있다. 대표적인 예로 미분 가능 다양체

M

의 접다발

TM

이 있다. 이는

M

의 각 점

x

에 그 점에서의 접공간

T_x M

을 대응시킨 것이다. 예를 들어, 2차원 구의 접다발은 털 뭉치 정리에 의해 자명하지 않다.

정식으로 실수 벡터 다발은 다음 요소들로 구성된다.

# 위상 공간

X

(밑공간 또는 기저 공간) 및 위상 공간

E

(전체 공간)

# 연속 함수인 전사 함수

\pi: E \to X

(다발 사영 또는 사영)

#

X

의 모든 점

x

에 대해, 올

E_x = \pi^{-1}(x)

에 주어진 유한 차원 실수 벡터 공간 구조

이 요소들은 다음 국소 자명화(local trivialization) 조건을 만족해야 한다.

X

의 모든 점

x

에 대해,

x

를 포함하는 열린 근방

U \subseteq X

, 자연수

k

, 그리고 위상동형사상

:

\phi\colon U \times \mathbb{R}^{k} \to \pi^{-1}(U)

가 존재하여, 모든

y \in U

에 대해 다음 두 조건이 성립한다.

모든 벡터 $v \in \mathbb{R}^k$ 에 대해 $(\pi \circ \phi)(y, v) = y$ 이다. (즉, $\phi$ 는 올을 보존한다.)
사상 $v \mapsto \phi(y, v)$ 는 두 벡터 공간 $\mathbb{R}^k$ 와 올 $E_y = \pi^{-1}(y)$ 사이의 선형 동형사상이다.

국소 자명화 조건은 벡터 다발이 국소적으로는 밑공간과 벡터 공간의 곱, 즉 자명한 다발처럼 보인다는 것을 의미한다.

각 올

E_x

는 유한 차원 벡터 공간이므로 차원

k_x

를 가진다. 국소 자명화 조건에 의해 함수

x \mapsto k_x

는 국소 상수 함수이며, 따라서

X

의 각 연결 성분 위에서 상수 값을 갖는다. 만약 모든

x \in X

에 대해

k_x

가 동일한 상수

k

와 같다면,

k

를 벡터 다발의 계수(rank|랭크^영어)라고 부르며,

E

를 계수 $k$ 의 벡터 다발이라고 한다. 계수가 1인 벡터 다발은 선다발(line bundle|라인 번들^영어)이라고 한다.

2. 1. 가군 다발

다음 데이터가 주어졌다고 가정하자.

위상 공간 $X$
위상환 $K$
$K$ 위의 위상 왼쪽 가군 $_KV$
올다발 $\pi\colon E\twoheadrightarrow X$
각 $x\in X$ 에 대하여, 올 $E_x=\pi^{-1}(x)$ 위의 $K$ -위상 왼쪽 가군 구조

만약

X

가 다음과 같은 호환 조건을 만족시키는 열린 덮개

(U_i)_{i\in I}

및 위상 동형 사상들의 족

:

\left(\phi_i\colon U_i\times V\to\pi^{-1}(U_i)\right)_{i\in I}

를 가질 수 있다면, 올다발

(X,E,\pi)

를 올

V

의 왼쪽 가군 다발(-加群-, left module bundle^영어)이라 한다.

여기서 임의의

i\in I

및

x\in U_i

에 대하여

\phi_i(x,-)\colon v\mapsto\phi_i(x,v)

는

V

와 올

E_x

사이의

K

-위상 왼쪽 가군 동형을 정의한다. 위와 같은 구조

(U_i,\phi_i)_{i\in I}

를

E

의 국소 자명화(局所自明化, local trivialization^영어)라고 한다. 그러나 국소 자명화의 구조는 가군 다발을 정의하는 데이터에 포함되지 않는다.

마찬가지로 오른쪽 가군 다발(-加群-, right module bundle^영어)을 정의할 수 있다. 만약

K

가 가환 위상환이라면 왼쪽 가군 다발과 오른쪽 가군 다발을 구별할 필요가 없다.

가군 다발은 벡터 다발의 일반화된 개념으로 볼 수 있다. 만약 위상환

K

가 위상체일 경우, 이에 대한 가군 다발은 벡터 다발이라 한다.

특별한 경우로, 만약

K

가 위상체이며

V=K

일 경우, 올이

K

인 벡터 다발을 선다발(線다발, line bundle^영어)이라고 한다.

또한, 만약

V

가 바나흐 공간일 경우 올이

V

인 벡터 다발을 바나흐 다발(Banach bundle^영어)이라고 한다. 이와 비슷하게 힐베르트 공간 올을 갖는 힐베르트 다발(Hilbert bundle^영어)이나 국소 볼록 공간 올을 갖는 국소 볼록 벡터 다발(locally convex vector bundle^영어)을 정의할 수 있다.

2. 2. 벡터 다발

위상체

K

위의 가군 다발을 '''벡터 다발'''이라고 한다.^[1] 벡터 다발은 위상수학, 미분기하학, 대수기하학 등 다양한 수학 분야에서 중요한 개념이다. 공간

X

위의 벡터 다발은

X

의 각 점

x

에 벡터 공간

V_x

를 대응시키되, 이 벡터 공간들이 "매끄럽게" 또는 "연속적으로" 변하도록 붙여놓은 구조를 의미한다.

구체적으로, '''실수 벡터 다발'''은 다음 요소들로 구성된다.^[2]

위상 공간 $X$ ('''밑공간''' 또는 '''기저 공간''')와 $E$ ('''전체 공간''')
연속 함수인 전사 함수 $\pi: E \to X$ ('''다발 사영''' 또는 '''사영''')
$X$ 의 모든 점 $x$ 에 대해, 올 $\pi^{-1}(x)$ 에 주어진 실수 벡터 공간 구조

이 요소들은 다음 호환성 조건을 만족해야 한다:

X

의 모든 점

x

에 대해,

x

를 포함하는 열린 근방

U \subseteq X

, 자연수

k

, 그리고 위상동형사상

:

\phi\colon U \times \mathbb{R}^{k} \to \pi^{-1}(U)

가 존재하여, 모든

y \in U

에 대해 다음 두 조건이 성립한다.

모든 벡터 $v \in \mathbb{R}^k$ 에 대해 $(\pi \circ \phi)(y, v) = y$ 이다.
사상 $v \mapsto \phi(y, v)$ 는 두 벡터 공간 $\mathbb{R}^k$ 와 $\pi^{-1}(y)$ 사이의 선형 동형사상이다.

위 조건을 만족하는

(U, \phi)

를 벡터 다발의 '''국소 자명화'''(local trivialization^eng)라고 부른다.^[3] 국소 자명화는 다발 사영

\pi

가 국소적으로는 곱공간

U \times \mathbb{R}^k

에서

U

로의 사영처럼 보인다는 것을 의미한다. 즉, 벡터 다발은 국소적으로는 밑공간과 벡터 공간의 데카르트 곱처럼 보인다.

모든 올

\pi^{-1}(x)

는 유한 차원 실수 벡터 공간이므로 차원

k_x

를 가진다. 국소 자명화 조건에 의해 함수

x \mapsto k_x

는 국소 상수 함수이며, 따라서

X

의 각 연결 성분 위에서 상수 값을 갖는다. 만약 모든

x \in X

에 대해

k_x

가 동일한 상수

k

와 같다면,

k

를 벡터 다발의 '''계수'''(rank^eng)라고 부르며,

E

를 '''계수

k

의 벡터 다발'''이라고 한다. 종종 벡터 다발의 정의에는 계수가 잘 정의되도록

k_x

가 상수라는 조건이 포함되기도 한다.^[2] 계수가 1인 벡터 다발은 '''선다발'''(line bundle^eng)이라고 한다. 이는 위상체

K

에 대해 올이

K

자체인 벡터 다발, 즉 계수가 1인 벡터 다발에 해당한다.^[1]

데카르트 곱

X \times \mathbb{R}^k

에 사영

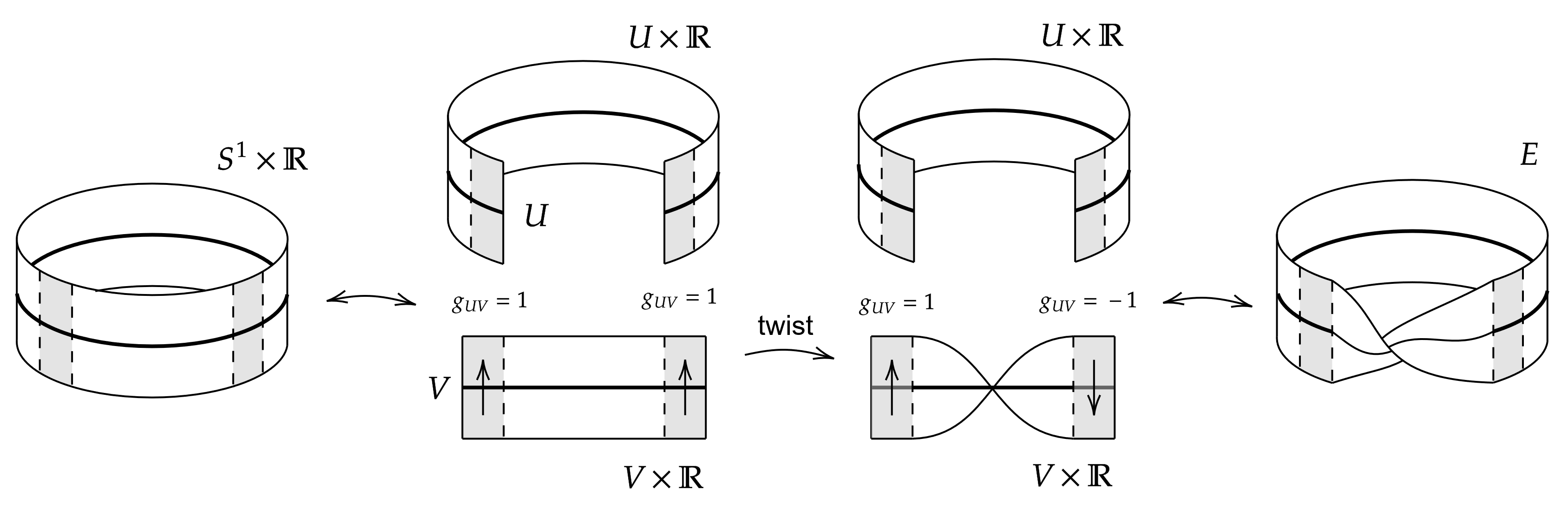
\pi: X \times \mathbb{R}^k \to X, (x, v) \mapsto x

를 부여하면 벡터 다발 구조를 가지며, 이를

X

위의 '''계수

k

의 자명한 다발'''(trivial bundle^eng)이라고 한다.^[3] 국소 자명화는 벡터 다발이 국소적으로는 자명한 다발과 동형임을 의미한다. 하지만 전체적으로는 자명하지 않을 수 있는데, 대표적인 예가 뫼비우스 띠이다.

벡터 다발의 정의에서 올이 되는 유한 차원 실수 벡터 공간

\mathbb{R}^k

대신 다른 종류의 위상 벡터 공간을 사용할 수도 있다. 예를 들어, 올이 바나흐 공간인 경우 '''바나흐 다발'''(Banach bundle^eng), 힐베르트 공간인 경우 '''힐베르트 다발'''(Hilbert bundle^eng), 국소 볼록 공간인 경우 '''국소 볼록 벡터 다발'''(locally convex vector bundle^eng) 등을 정의할 수 있다.^[1] 실수 벡터 다발 대신 복소수 벡터 공간을 올로 사용하면 '''복소 벡터 다발'''을 정의할 수 있다.

벡터 다발

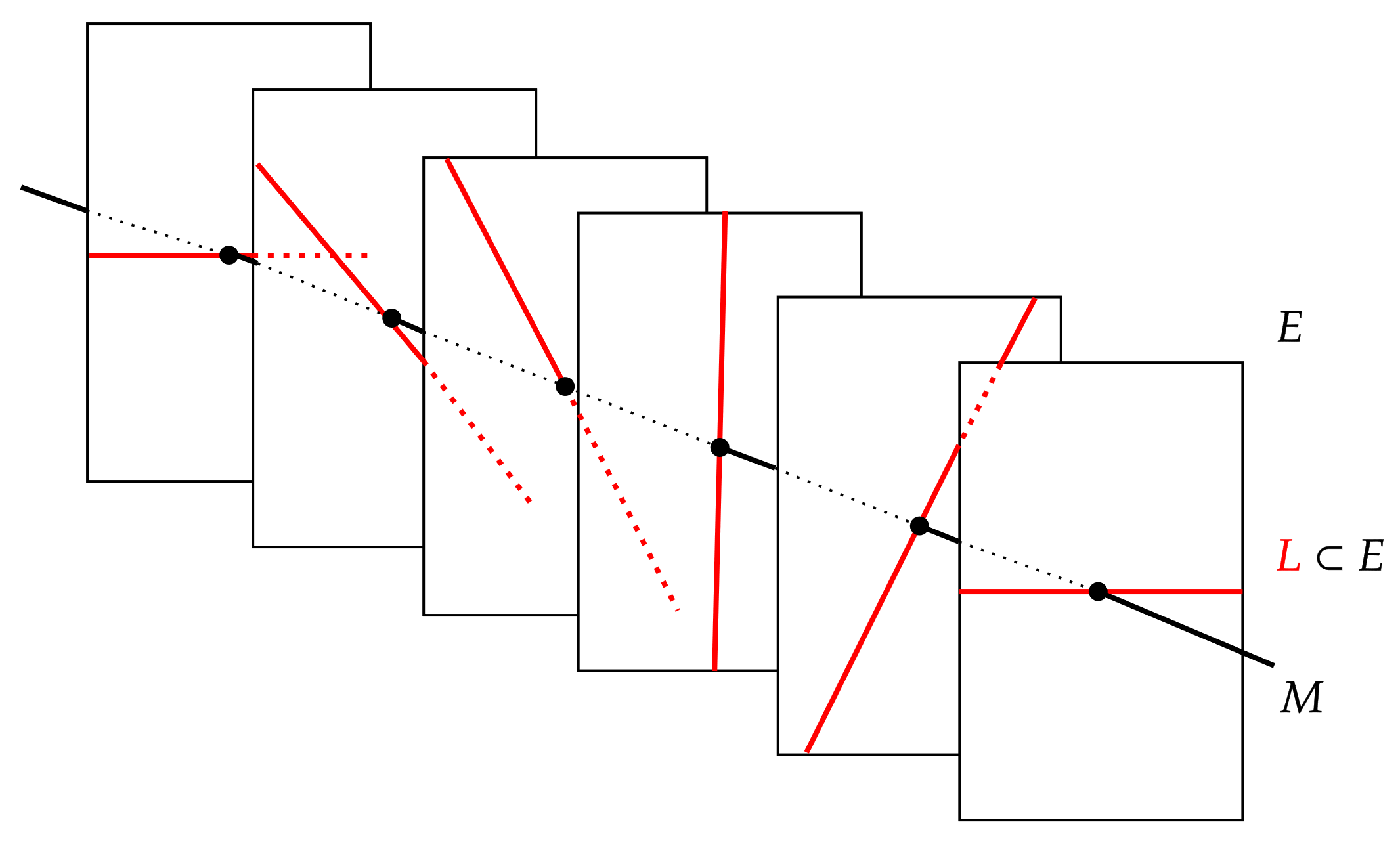
\pi: E \to X

가 주어졌을 때, 전체 공간

E

의 부분 집합

F \subseteq E

가 다음 조건을 만족하면 '''부분 다발'''(subbundle^eng)이라고 한다:

$\pi|_F : F \to X$ (사영 $\pi$ 를 $F$ 에 제한한 함수) 또한 벡터 다발 구조를 이룬다.
모든 $x \in X$ 에 대해, 올 $F_x = F \cap E_x$ 는 $E_x$ 의 벡터 부분 공간이다.

자명한 다발의 부분 다발이 항상 자명한 것은 아니다. 예를 들어, 원

S^1

위의 자명하지 않은 선다발인 뫼비우스 띠는 원 위의 자명한 계수 2 벡터 다발

S^1 \times \mathbb{R}^2

의 부분 다발로 구현될 수 있다.^[4] 콤팩트 공간 위의 모든 실수 벡터 다발은 충분히 높은 계수의 자명한 다발의 부분 다발로 나타낼 수 있다.^[4]

2. 3. 매끄러운 벡터 다발

미분기하학을 전개하기 위해서는 연속 함수 대신 매끄러운 함수를 사용해야 한다. 이를 바탕으로 매끄러운 벡터 다발을 정의할 수 있다. 다음과 같은 데이터가 주어졌다고 가정하자.

매끄러운 다양체 $X$
유클리드 공간 $\mathbb{R}^n$
매끄러운 올다발 $\pi\colon E\twoheadrightarrow X$
각 $x\in X$ 에 대하여, 올(fiber) $E_x = \pi^{-1}(x)$ 위의 $n$ 차원 실수 벡터 공간 구조

만약

X

가 다음 호환 조건을 만족시키는 열린 덮개

(U_i)_{i\in I}

및 미분 동형 사상들의 족(family)

:

\left(\phi_i\colon U_i\times\mathbb{R}^n\to\pi^{-1}(U_i)\right)_{i\in I}

를 가질 수 있다면, 올다발

(E, \pi, X)

를

n

차원 '''매끄러운 벡터 다발'''(smooth vector bundle^영어)이라고 한다. 여기서 각

\phi_i

를 국소 자명화(local trivialization)라고 부른다.

이때 임의의

i\in I

및

x\in U_i

에 대하여, 사상

\phi_i(x, -)\colon v\mapsto\phi_i(x,v)

는 표준 올

\mathbb{R}^n

과 특정 올

E_x

사이의 실수 벡터 공간 동형 사상을 정의한다. 이 정의에서 전체 공간

E

와 밑공간

X

는 매끄러운 다양체이고, 사영 사상

\pi: E \to X

는 매끄러운 함수이며, 국소 자명화

\phi_i

는 미분 동형 사상이다. 따라서 매끄러운 벡터 다발의 스칼라체는 실수체이고 벡터 공간의 차원은 유한해야 한다.

두 개의 자명한 벡터 다발이 열린 집합 $U_\alpha$ 와 $U_\beta$ 에서 접착될 수 있다. 이는 올(fiber)에 선형 변환을 적용한 후 음영 처리된 회색 영역을 함께 붙이는 데 사용되는 변환 함수 $g_{\alpha \beta}$ 를 통해서 이루어진다(파란색 사변형이 $g_{\alpha\beta}$ 의 영향을 받는 것을 참고). 변환 함수를 다르게 선택하면 접착 후 자명하지 않은 서로 다른 벡터 다발이 생성될 수 있다.

계수(rank)

k

인 벡터 다발

E\to X

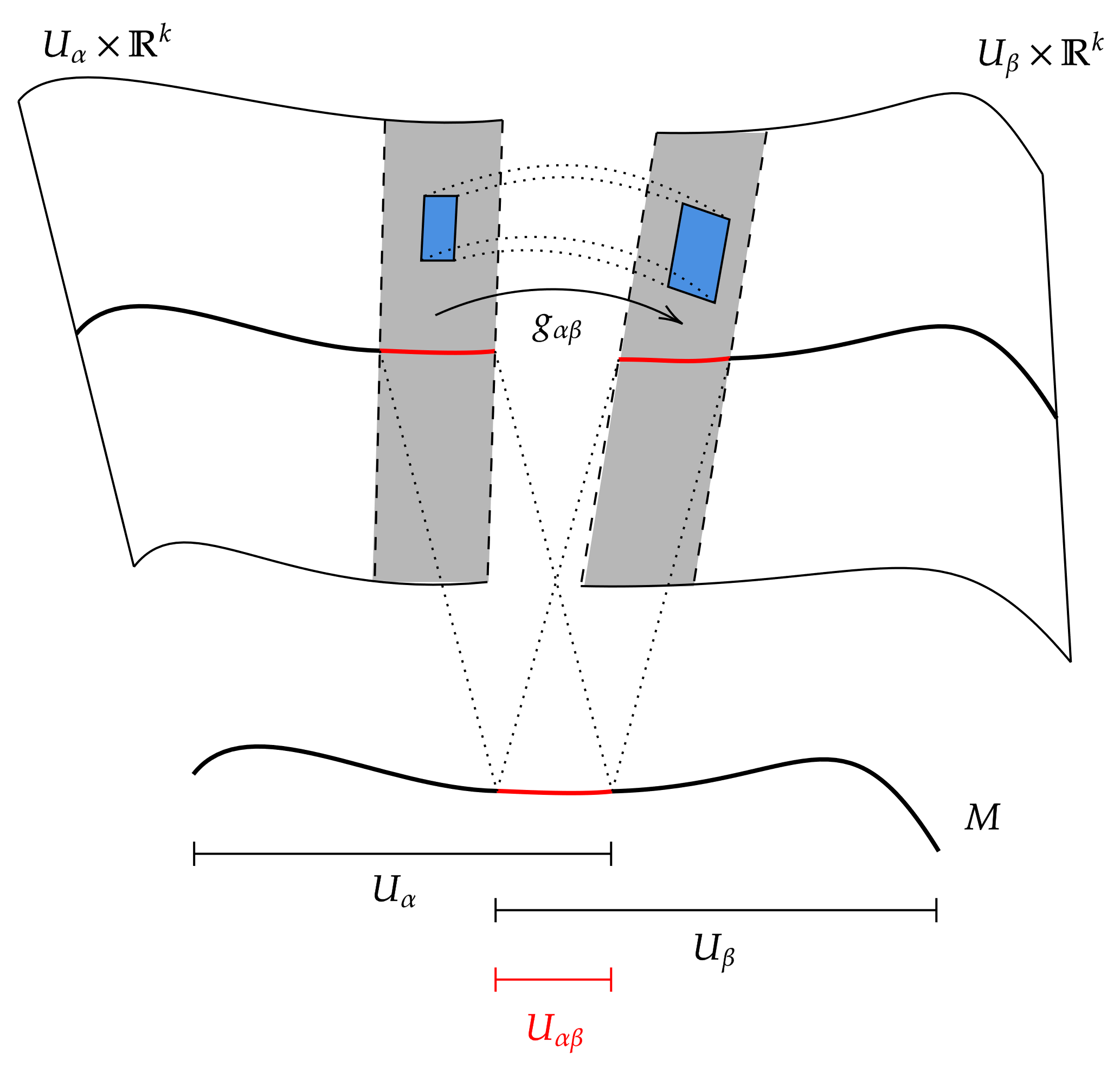
와, 다발이 자명해지는 두 개의 열린 이웃(neighborhood)

U

와

V

가 주어졌다고 하자. 즉, 다음과 같은 국소 자명화 사상이 존재한다.

:

\begin{align}\varphi_U\colon U\times \mathbb{R}^k &\mathrel{\xrightarrow{\cong}} \pi^{-1}(U), \\\varphi_V\colon V\times \mathbb{R}^k &\mathrel{\xrightarrow{\cong}} \pi^{-1}(V)\end{align}

이때 합성 함수

:

\varphi_U^{-1}\circ\varphi_V \colon (U\cap V)\times\mathbb{R}^k\to (U\cap V)\times\mathbb{R}^k

는 겹치는 영역

U\cap V

에서 잘 정의되며, 어떤 일반선형군

\operatorname{GL}(k, \mathbb{R})

-값을 갖는 매끄러운 함수

g_{UV}\colon U\cap V\to \operatorname{GL}(k, \mathbb{R})

에 대해 다음을 만족한다.

:

\varphi_U^{-1}\circ\varphi_V (x,v) = \left (x,g_{UV}(x)v \right)

이 함수들

g_{UV}

를 벡터 다발의 '''변환 함수'''(transition function) 또는 '''좌표 변환'''(coordinate transformation)이라고 부른다. 매끄러운 벡터 다발은 이 변환 함수

g_{UV}

가 리 군인

\operatorname{GL}(k,\mathbb{R})

로 가는 매끄러운 함수라는 사실로 특징지을 수 있다.

변환 함수들의 집합은 다음 코사이클 조건(cocycle condition)을 만족시킨다.

:

g_{UU}(x) = I \quad (\text{identity matrix})

:

g_{UV}(x)g_{VW}(x)g_{WU}(x) = I \quad \text{for all } x \in U\cap V\cap W

이는 다발이 자명해지는 모든

U,V,W

에 대해

U\cap V\cap W\neq \emptyset

일 때 성립한다. 이 조건은 국소 자명화들이 겹치는 영역에서 서로 호환됨을 보장한다. 데이터

(E, X, \pi, \mathbb{R}^k)

는 올다발을 정의하며, 추가 데이터인 변환 함수

g_{UV}

는 올에 대한 군 작용이

\operatorname{GL}(k, \mathbb{R})

의 표준 작용인

\operatorname{GL}(k, \mathbb{R})

구조군을 지정한다.

반대로, 올

\mathbb{R}^k

에 표준 방식으로 작용하는

\operatorname{GL}(k, \mathbb{R})

코사이클(즉, 위의 코사이클 조건을 만족하는 변환 함수들의 집합)을 가진 올다발

(E, X, \pi, \mathbb{R}^k)

가 주어지면, 연관 다발(associated bundle)로서 벡터 다발이 존재한다. 이것은 벡터 다발에 대한 올다발 구성 정리의 한 예이며, 벡터 다발의 대안적인 정의로 간주될 수 있다.

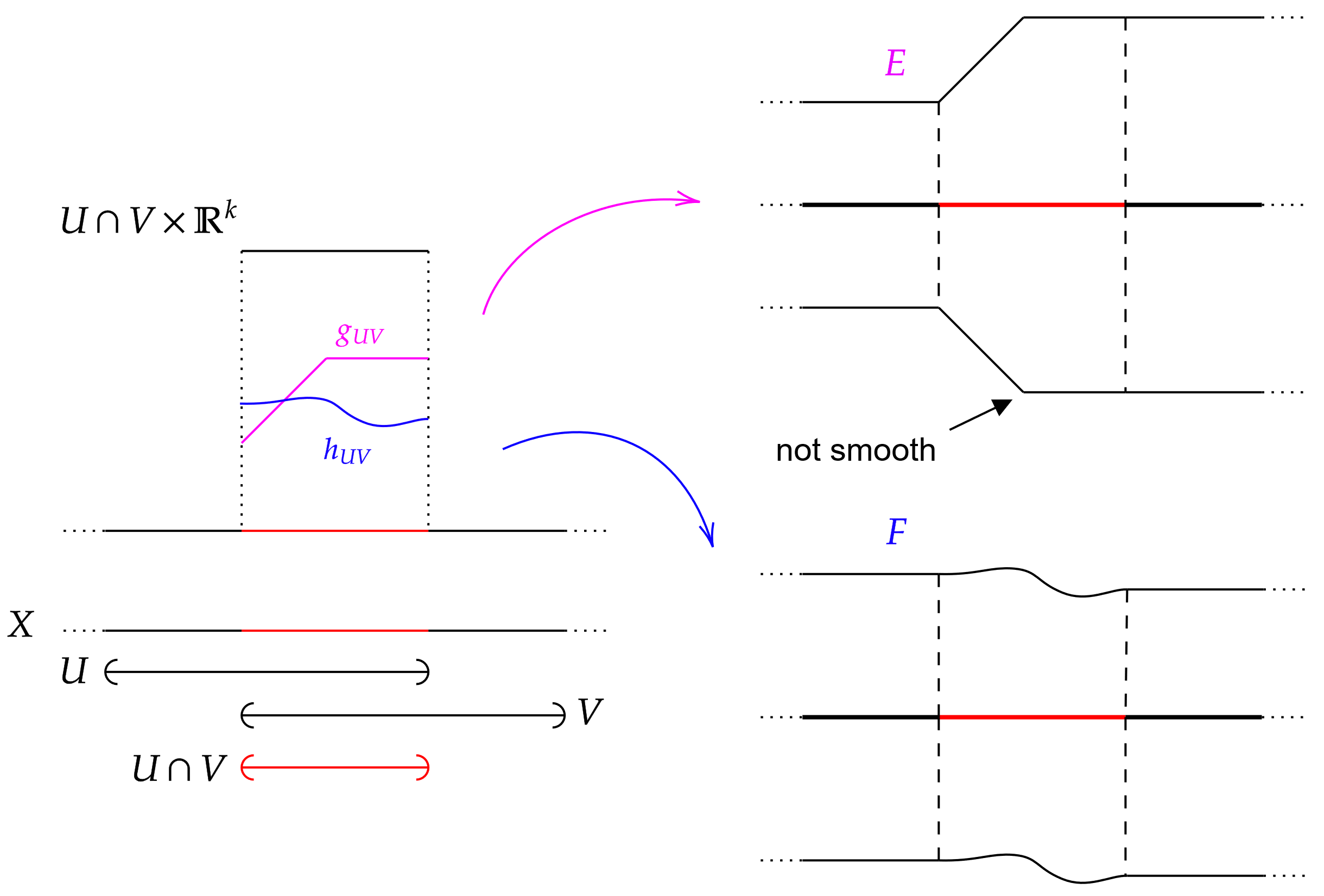
벡터 다발을 설명하는 변환 함수의 규칙성은 벡터 다발의 유형을 결정한다. 연속 변환 함수 $g_{UV}$ 가 사용되면, 결과 벡터 다발 $E$ 는 연속적일 뿐 매끄럽지는 않다. 매끄러운 변환 함수 $h_{UV}$ 가 사용되면, 결과 벡터 다발 $F$ 는 매끄러운 벡터 다발이다.

요구되는 매끄러움의 정도에 따라 다양한 종류의 벡터 다발을 정의할 수 있다. 변환 함수

g_{UV}

가 다음과 같은 성질을 가질 때 벡터 다발은 각각 다음과 같이 불린다.

''C^r'' 함수이면 ''' $C^r$ 벡터 다발'''
''C''^∞'' 함수이면 ''' $C^\infty$ 벡터 다발''' (또는 단순히 '''매끄러운 벡터 다발''')
실해석적 함수이면 '''실해석적 벡터 다발''' ( $C^\omega$ 벡터 다발) (이 경우 $\operatorname{GL}(k, \mathbb{R})$ 은 실해석적 구조를 가짐)
정칙 함수이면 '''정칙 벡터 다발''' (밑공간 $X$ 가 복소다양체이고, $\operatorname{GL}(k, \mathbb{C})$ 가 복소 리 군임)
대수적 함수이면 '''대수 벡터 다발''' (밑공간 $X$ 가 대수다양체이고, $\operatorname{GL}(k)$ 가 대수군임)

여기서는 주로

C^\infty

-벡터 다발, 즉 매끄러운 벡터 다발을 다룬다.

C^\infty

-다양체

M

의 접다발

(TM, \pi_{TM}, M)

은 매끄러운 벡터 다발의 가장 중요한 예이다.

C^\infty

-벡터 다발

(E, p, M)

은 일반적인

C^\infty

-올다발이 가지지 않는 중요한 속성을 가진다. 즉, 임의의

v \in E_x

에서의 접공간

T_v(E_x)

는 올

E_x

자체와 자연스럽게 동일시될 수 있다. 이 동일시는 다음과 같이 정의된 '''수직 올림'''(vertical lift^영어)

\operatorname{vl}_v: E_x \to T_v(E_x)

을 통해 얻어진다.

:

\operatorname{vl}_vw[f] := \left.\frac{d}{dt}\right|_{t=0}f(v + tw), \quad \text{for } w \in E_x, f\in C^\infty(E_x).

수직 올림은 또한 자연스러운

C^\infty

-벡터 다발 동형 사상

p^*E \to VE

로 볼 수 있다. 여기서

(p^*E, p^*p, E)

는

p: E \to M

을 통해

E

위에

(E, p, M)

의 당김 다발이고,

VE := \ker(p_*) \subset TE

는 '''수직 접다발'''(vertical tangent bundle^영어)이며, 이는 전체 공간

E

의 접다발

(TE, \pi_{TE}, E)

의 자연스러운 벡터 부분 다발이다.

임의의 매끄러운 벡터 다발의 전체 공간

E

는

V_v := \operatorname{vl}_v v

로 정의되는 자연스러운 벡터장

V

를 가지며, 이를 '''표준 벡터장'''(canonical vector field^영어)이라 한다. 더 공식적으로,

V

는 접다발

(TE, \pi_{TE}, E)

의 매끄러운 단면이며, 올별 스칼라 곱셈에 의해 주어지는 리 군 작용

(t,v) \mapsto e^t v

(여기서

v \in E \setminus \{0\}

)의 무한소 생성자로 정의될 수도 있다. 표준 벡터장

V

는 매끄러운 벡터 다발 구조를 완전히 특징짓는다.

X

가 매끄러운 다양체

M

위의 매끄러운 벡터장이고

X_x = 0

인

x \in M

일 때, 선형 사상

:

C_x(X): T_x M \to T_x M; \quad C_x(X) Y = (\nabla_Y X)_x

는

M

위의 선형 공변 미분

\nabla

의 선택에 의존하지 않는다. 표준 벡터장

V

는 다음 공리들을 만족한다.

#

V

의 흐름(flow)

(t, v) \mapsto \Phi^t_V(v)

는 전역적으로 정의된다.

# 각

v \in E

에 대해 극한

\lim_{t\to\infty} \Phi^t_V(v)

가

E

안에 유일하게 존재한다. (이는 영단면 위의 점이다.)

#

V_v = 0

일 때마다

C_v(V) \circ C_v(V) = C_v(V)

가 성립한다. (

C_v(V)

는 사영 작용소이다.)

#

V

의 영점 집합(zero set)은

E

의 매끄러운 부분 다양체(영단면)이며, 그 여차원은

C_v(V)

의 계수(rank)와 같다.

반대로,

E

가 임의의 매끄러운 다양체이고

V

가 위 1-4 공리를 만족하는

E

위의 매끄러운 벡터장이라면, 표준 벡터장이

V

인

E

위의 유일한 벡터 다발 구조가 존재한다.

임의의 매끄러운 벡터 다발

(E, p, M)

에 대해, 그 접다발

(TE, \pi_{TE}, E)

의 전체 공간

TE

는 자연스러운 '''2차 벡터 다발 구조'''

(TE, p_*, TM)

를 가진다. 여기서

p_*

는 표준 사영

p: E \to M

의 푸시포워드(pushforward)이다. 이 2차 벡터 다발 구조의 벡터 다발 연산(덧셈과 스칼라 곱셈)은 원래 벡터 다발의 덧셈

+: E \times_M E \to E

및 스칼라 곱셈

\lambda: \mathbb{R} \times E \to E

연산의 푸시포워드

+_{*}: T(E \times_M E) \to TE

및

\lambda_{*}: T(\mathbb{R} \times E) \to TE

로부터 유도된다.

벡터 다발

\pi: E \to X

와

X

의 열린 집합

U

가 주어졌을 때,

\pi

의

U

위의 '''절단'''(section^영어)을 생각할 수 있다. 매끄러운 벡터 다발의 맥락에서는 '''매끄러운 절단'''을 주로 다루는데, 이는

\pi \circ s = \operatorname{id}_U

를 만족하는 매끄러운 사상

s: U \to E

를 말한다. 이는 본질적으로

U

의 각 점

x

에, 그 점 위의 올

E_x

에 속하는 벡터

s(x)

를 매끄럽게 대응시키는 것이다. 예를 들어, 미분 가능 다양체의 접다발의 매끄러운 절단은 그 다양체 위의 벡터장과 같다.

\Gamma(U, E)

또는

F(U)

를

U

위의 매끄러운 절단 전체의 집합으로 표기하자.

F(U)

는 항상 최소한 하나의 원소, 즉 '''영 절단'''(zero section)을 포함한다. 이는

U

의 모든 점

x

를 벡터 공간

E_x = \pi^{-1}(x)

의 영벡터

0_x

에 대응시키는 절단

s_0(x) = 0_x

이다. 각 점에서의 절단의 덧셈과 스칼라 곱셈 연산(즉,

(s_1+s_2)(x) = s_1(x)+s_2(x)

,

(\alpha s)(x) = \alpha(x) s(x)

여기서

\alpha: U \to \mathbb{R}

는 매끄러운 함수)에 의해,

F(U)

는 그 자체가 실수 벡터 공간이 되며, 또한

U

위에서 정의된 매끄러운 실수값 함수들의 환

C^\infty(U)

위의 가군이 된다. 이러한 벡터 공간/가군들의 모임(열린 집합

U

에 따라 변함)은

X

위의 벡터 공간들의 층 또는

C^\infty_X

-가군의 층을 이룬다. (

C^\infty_X

는

X

위의 매끄러운 함수들의 구조층).

모든

C^\infty_X

-가군의 층이 매끄러운 벡터 다발의 절단 층으로 표현되는 것은 아니며, 국소적으로 자유이고 유한 생성인 경우에만 해당한다. 이는 국소적으로 벡터 다발이

U \times \mathbb{R}^k \to U

형태이고, 그 절단은 정확히 매끄러운 사상

U \to \mathbb{R}^k

(즉, 매끄러운 함수

U \to \mathbb{R}

의

k

-튜플)에 대응하기 때문이다.

더 나아가,

X

위의 매끄러운 실수 벡터 다발의 범주는, 국소적으로 자유이고 유한 생성인

C^\infty_X

-가군의 층의 범주와 범주 동치이다. 이는 벡터 다발과 관련된 대수적 구조(절단 가군)를 통해 벡터 다발을 연구할 수 있게 해준다.

n

-계수 벡터 다발이 자명하다는 것(즉,

X \times \mathbb{R}^n

과 동형이라는 것)은 그 다발이

n

개의 선형 독립적인 전역 절단(global section,

U=X

인 경우의 절단)을 갖는다는 것과 동치이다.

2. 4. 벡터 다발 사상

벡터 다발

\pi_1: E_1 \to X_1

에서 벡터 다발

\pi_2: E_2 \to X_2

로의 '''사상'''은 연속 함수인

f: E_1 \to E_2

와

g: X_1 \to X_2

의 쌍으로 구성되며, 다음 두 조건을 만족시킨다.

다음 가환 다이어그램이 가환한다. 즉, $g \circ \pi_1 = \pi_2 \circ f$ 이다.
*
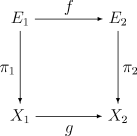
벡터 다발 사상의 가환성
모든 $x \in X_1$ 에 대해, $f$ 가 유도하는 사상 $\pi_1^{-1}(x) \to \pi_2^{-1}(g(x))$ 는 벡터 공간 사이의 선형 사상이다. 여기서 $\pi_1^{-1}(x)$ 는 $x$ 위의 올 (벡터 공간)을 의미한다.

사상

g

는

f

에 의해 유일하게 결정되는데, 이를 "

f

가

g

를 덮는다"고 표현한다.

만약

E_1, E_2, X_1, X_2

가 모두 매끄러운 다양체이고

f, g, \pi_1, \pi_2

가 모두 매끄러운 함수이면, 이 사상을 '''매끄러운 벡터 다발 사상'''(smooth vector bundle morphism^영어)이라고 부른다.

모든 벡터 다발과 그 사이의 벡터 다발 사상들은 하나의 범주를 형성한다. 마찬가지로, 매끄러운 벡터 다발과 매끄러운 벡터 다발 사상들은 매끄러운 벡터 다발의 범주를 형성한다. 벡터 다발 사상은 올다발 사이의 다발 사상의 특별한 경우이며, 때로는 '''(벡터) 다발 준동형사상'''(vector bundle homomorphism^영어)이라고도 불린다.

벡터 다발 사상

f: E_1 \to E_2

가 역함수

f^{-1}: E_2 \to E_1

을 가지며 이 역사상 또한 벡터 다발 사상이 될 때,

f

를 '''(벡터) 다발 동형사상'''(vector bundle isomorphism^영어)이라고 한다. 이 경우 두 벡터 다발

E_1

과

E_2

는 서로 '''동형'''(isomorphic^영어)이라고 말한다.

어떤 벡터 다발

E

가 자명한 다발 (즉, 곱공간

X \times \mathbb{R}^k

형태의 다발)과 동형일 때, 그 동형사상을

E

의 '''자명화'''(trivialization^영어)라고 하며,

E

를 '''자명하다'''(trivial^영어) 또는 '''자명화 가능하다'''(trivializable^영어)고 한다. 모든 벡터 다발은 국소적으로는 자명하다. 즉, 각 점 주변의 작은 영역에서는 자명한 다발과 동형이다.

기저 공간

X

를 고정하고, 이

X

위의 벡터 다발들만 생각할 수도 있다. 이 경우 사상은 기저 공간 사이의 사상

g

가 항등 함수

\mathrm{id}_X

인 벡터 다발 사상, 즉

g = \mathrm{id}_X

인 경우만을 고려한다. 이는 다음 다이어그램이 가환하는 사상을 의미한다.

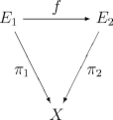
고정된 기저 공간 X 위의 벡터 다발 사상

이러한 벡터 다발들과

X-사상들 역시 범주를 이루지만, 이 범주는 아벨 범주 가 아니다. 일반적으로 벡터 다발 사상의 핵을 자연스럽게 벡터 다발로 만들기 어렵기 때문이다.벡터 다발 사상 f: E_1 \to E_2 가 기저 공간 사상 g: X_1 \to X_2 를 덮을 때, 이 사상은 X_1 위의 벡터 다발 E_1 에서 당김 다발 g^*E_2 로 가는 벡터 다발 사상으로도 해석될 수 있다.

3. 연산

위상 벡터 공간에 적용 가능한 직합, 텐서곱, 연속 쌍대 공간 구하기 등의 연산은 벡터 다발에도 각 올별로 적용하여 정의할 수 있다. 즉, 벡터 공간에 대한 대부분의 연산은 올별 연산을 통해 벡터 다발의 연산으로 자연스럽게 확장된다.

주요 연산의 예시는 다음과 같다.

'''쌍대 다발'''(dual bundle^eng) $E^*$ : 각 올 $E_x$ 의 쌍대 벡터 공간 $(E_x)^*$ 를 올로 갖는 다발이다. 쌍대 다발은 국소적으로 자명하며, 이는 쌍대 벡터 공간을 취하는 연산이 함자이기 때문이다.
'''휘트니 합'''(Whitney sum^eng) 또는 '''직합 다발'''(direct sum bundle^eng) $E \oplus F$ : 각 올이 두 벡터 공간 $E_x$ 와 $F_x$ 의 직합 $E_x \oplus F_x$ 인 벡터 다발이다.
'''텐서 곱 다발'''(tensor product bundle^eng) $E \otimes F$ : 각 올이 두 벡터 공간 $E_x$ 와 $F_x$ 의 텐서 곱 $E_x \otimes F_x$ 인 벡터 다발이다.
'''준동형 다발'''(Hom-bundle^eng) $\operatorname{Hom}(E, F)$ : 각 올이 $E_x$ 에서 $F_x$ 로 가는 선형 사상들의 공간( $\operatorname{Hom}(E_x, F_x)$ )인 벡터 다발이다. 이 다발의 단면은 $E$ 에서 $F$ 로 가는 벡터 다발 준동형 사상과 일대일 대응된다. 쌍대 다발은 $\operatorname{Hom}(E, \mathbb{R} \times X)$ 와 같으며, 자연스러운 동형 사상 $\operatorname{Hom}(E,F) \cong E^*\otimes F$ 가 존재한다.
'''고유 다발'''(eigenbundle^eng): 자기 준동형 다발 $\operatorname{Hom}(E, E)$ 의 단면 $s$ 와 함수 $f: X \to \mathbb{R}$ 가 주어졌을 때, 각 점 $x \in X$ 에서의 올을 선형 사상 $s(x): E_x \to E_x$ 의 $f(x)$ -고유 공간으로 정의하여 구성할 수 있다.

이러한 연산들은 대부분 함자적인 성질을 가지며, 이는 벡터 공간의 범주에서의 연산이 벡터 다발의 범주에서도 의미 있게 정의될 수 있음을 보여준다.

또 다른 중요한 연산으로 '''당김 다발'''(pull-back bundle^eng) 구성이 있다. 벡터 다발

E \to Y

와 연속 함수

f: X \to Y

가 주어지면,

Y

위의 벡터 다발

E

를 함수

f

를 통해

X

위의 벡터 다발

f^*E

로 "당겨올" 수 있다. 이때

X

의 점

x

위의 올은 기본적으로

Y

의 점

f(x)

위의 올과 같다. 예를 들어, 휘트니 합

E \oplus F

는

X \times X

위의 다발

E \times F

를 대각 사상

X \to X \times X

를 통해 당겨온 것으로 볼 수도 있다.

3. 1. 직합

위상 공간

X

위의 같은 위상환

K

에 대한 두 왼쪽 가군 다발

E, E' \twoheadrightarrow X

가 주어졌다고 하자. 이 두 벡터 다발의 '''직합'''(direct sum)

E \oplus E'

을 정의할 수 있다. 각 점

x \in X

에서 직합 다발

E \oplus E'

의 올(fiber)은 각 다발의 올들의 직합으로 정의된다.

:

(E \oplus E')_x = E_x \oplus E'_x

만약

X

가 매끄러운 다양체이고

E

와

E'

이 매끄러운 벡터 다발이라면, 그 직합

E \oplus E'

역시 매끄러운 벡터 다발이 된다.

벡터 다발의 직합은 하슬러 휘트니의 이름을 따서 '''휘트니 합'''(Whitney sum)이라고도 불린다.

벡터 공간에 적용할 수 있는 많은 연산들은 각 올에 해당 연산을 적용하는 방식으로 벡터 다발로 확장될 수 있다. 직합 외에도 쌍대 다발, 텐서 곱 다발, Hom-다발 등이 이러한 방식으로 정의된다. 예를 들어, 두 벡터 다발

E

,

F

가 주어졌을 때, 각 올

E_x

,

F_x

의 텐서 곱

E_x \otimes F_x

을 올로 가지는 '''텐서 곱 다발'''

E \otimes F

를 정의할 수 있다.

3. 2. 텐서곱

위상 공간

X

위의, 같은 가환 위상환

K

에 대한 가군 다발

E, E'

이 주어졌다고 하자. 그렇다면 두 가군 다발의 '''텐서곱'''

E \otimes_K E'

을 정의할 수 있다. 각 점

x \in X

에서

E \otimes_K E'

의 섬유(fiber)는 각 섬유의

K

-텐서곱으로 정의된다.

:

(E \otimes_K E')_x = E_x \otimes_K E'_x

만약

X

가 매끄러운 다양체이고,

E

와

E'

이 실수체

\mathbb{R}

위의 매끄러운 벡터 다발이라면, 이들의 텐서곱

E \otimes_{\mathbb R} E'

역시 매끄러운 벡터 다발이다. 이는 벡터 공간에 대한 텐서곱 연산을 각 섬유별로 적용하여 벡터 다발의 연산으로 확장한 것이다.

일반적으로, 같은 체 위의 벡터 공간 쌍에 대해 수행할 수 있는 많은 함자적 연산은, 위상 공간

X

위의 벡터 다발 쌍

E, F

에 대해서도 섬유별 연산을 통해 확장될 수 있다. '''텐서곱 다발'''(tensor product bundle^eng)

E \otimes F

는 이러한 방식으로 정의된다.

텐서곱 다발은 다른 벡터 다발 연산과도 관련이 있다. 예를 들어, 쌍대 다발

E^*

와 벡터 다발

F

의 텐서곱

E^* \otimes F

는 준동형 다발

\operatorname{Hom}(E, F)

와 자연스럽게 동형이다. 즉, 다음과 같은 벡터 다발의 동형 사상이 존재한다.

:

\operatorname{Hom}(E,F) \cong E^*\otimes F

3. 3. 쌍대 벡터 다발

위상 공간

X

위의, 위상체

K

에 대한 벡터 다발

E

의 '''쌍대 벡터 다발'''(dual vector bundle^영어)

E^*

는 각 올(fiber)이

E

의 해당 올의 연속 쌍대 공간인 벡터 다발이다. 즉, 점

x \in X

에서의 올은 다음과 같이 정의된다.

:

E^*_x=(E_x)^*

만약

X

가 매끄러운 다양체이고

E

가 매끄러운 벡터 다발이라면, 그 쌍대 벡터 다발

E^*

역시 매끄러운 벡터 다발이 된다.

쌍대 벡터 다발

E^*

는

x \in X

이고

\phi \in (E_x)^*

인 쌍

(x, \phi)

들의 집합으로도 정의할 수 있다. 여기서

(E_x)^*

는 점

x

에서의 올

E_x

의 쌍대 벡터 공간을 나타낸다.

쌍대 다발은 국소적으로 자명하다. 이는 원래 벡터 다발

E

의 국소 자명화에 대해 그 쌍대 공간을 취하는 연산을 적용하면, 이것이 쌍대 다발

E^*

의 국소 자명화가 되기 때문이다. 이러한 성질은 쌍대 벡터 공간을 취하는 연산이 함자이기 때문에 성립한다.

쌍대 벡터 다발

E^*

는

E

에서 자명한 다발

\mathbb{R} \times X

로 가는 선형 사상들의 모임인 Hom-다발

\operatorname{Hom}(E, \mathbb{R} \times X)

와 자연스럽게 동형이다. 또한, 임의의 두 벡터 다발

E

,

F

에 대해 다음과 같은 표준적인 벡터 다발 동형 사상이 존재한다.

:

\operatorname{Hom}(E,F) \cong E^*\otimes F

여기서

\otimes

는 텐서 곱 다발을 의미한다.

4. 성질

위상 공간 $X$ 위의, 위상체 $K$ 에 대한 벡터 다발들의 범주는 가법 범주를 이루지만, 일반적으로 핵과 여핵을 갖지 못해 아벨 범주를 이루지 못한다. (이 문제를 해결하기 위해, 대수기하학에서는 보통 연접층을 대신 사용한다.)

벡터 다발 위에는 벡터 다발 구조와 호환되는 에레스만 접속인 '''코쥘 접속'''이라는 구조를 정의할 수 있다.

각 점에 법선을 대응시키는 맵은 곡면에서 단면으로 생각할 수 있다. 곡면은 공간 $X$ 이고, 각 점 $x$ 에는 $x$ 에 부착된 벡터 공간의 벡터가 있다.

벡터 다발

\pi: E \to X

와

X

의 열린 부분 집합

U

가 주어지면,

U

에서

\pi

의 '''단면'''을 고려할 수 있다. 단면이란, 합성

\pi \circ s = \mathrm{id}_U

(즉, 모든

u \in U

에 대해

(\pi \circ s)(u) = u

)를 만족하는 연속 함수

s: U \to E

이다. 본질적으로 단면은

U

의 모든 점에 해당 점 위의 올(벡터 공간)에 속하는 벡터를 연속적으로 대응시키는 것을 의미한다. 예를 들어, 미분 가능 다양체의 접다발의 단면은 해당 다양체 위의 벡터장과 같다.

F(U)

를

U

위의 모든 단면의 집합이라고 하자.

F(U)

는 항상 최소한 하나의 원소, 즉 '''영 단면'''을 포함한다. 영 단면은

U

의 모든 원소

x

를 벡터 공간

\pi^{-1}(\{x\})

의 영 벡터에 대응시키는 함수

s

이다. 단면들의 점별 덧셈과 스칼라 곱셈을 통해

F(U)

는 그 자체가 실수 벡터 공간이 된다. 이러한 벡터 공간들의 모음은

X

위의 벡터 공간들의 층을 이룬다.

s

가

F(U)

의 원소이고

\alpha: U \to \mathbb{R}

이 연속 함수이면, 점별 스칼라 곱으로 정의된

\alpha s

는 다시

F(U)

에 속한다. 따라서

F(U)

는

U

위의 연속 실수 값 함수들의 환에 대한 가군으로 볼 수 있다. 또한,

X

위의 연속 실수 값 함수들의 구조 층을

\mathcal{O}_X

라고 하면, 단면들의 층

\mathcal{F}

는

\mathcal{O}_X

-가군의 층이 된다.

모든

\mathcal{O}_X

-가군의 층이 벡터 다발에서 이러한 방식으로 발생하는 것은 아니며, 국소 자유 층만이 그렇다. (이유: 국소적으로 우리는 사영

U \times \mathbb{R}^k \to U

의 단면을 찾고 있는데, 이는 정확히 연속 함수

U \to \mathbb{R}^k

이며, 이는 연속 함수

U \to \mathbb{R}

의

k

-튜플이다.)

더욱이,

X

위의 실수 벡터 다발의 범주는 국소 자유이고 유한 생성인

\mathcal{O}_X

-가군의 층의 범주와 동치이다. 따라서 우리는

X

위의 실수 벡터 다발의 범주를

\mathcal{O}_X

-가군의 층의 범주 안에 있는 것으로 생각할 수 있다. 이 후자의 범주는 아벨 범주이므로, 여기서 벡터 다발 사상의 핵과 여핵을 계산할 수 있다.

랭크

n

벡터 다발이 자명하다는 것은

n

개의 선형 독립적인 전역 단면을 갖는다는 것과 필요충분 조건이다.

5. 분류

위상 공간 위의 유한 차원 실수 또는 복소수 벡터 다발들은 '''위상 K이론'''이라는 환으로 분류된다.

6. 예

공간 $X$ 위의 벡터 다발이란, $X$ 의 각 점 $x$ 에 벡터 공간 $V(x)$ 를 대응시켜(붙여), 그것들이 "잘 붙여져" 원래의 $X$ 와 같은 종류의 공간(예: 위상 공간, 다양체, 대수다양체)을 이루는 것을 말한다.

가장 단순한 예는 모든 점 $x \in X$ 에 대해 동일한 고정된 벡터 공간 $V$ 를 붙이는 경우이다. 즉, $V(x) = V$ 이다. 이렇게 만들어진 벡터 다발 $X \times V$ 를 자명한 벡터 다발이라고 부른다.

더 복잡하고 중요한 예시 중 하나는 매끄러운 다양체 $M$ 의 접다발이다. 이는 다양체 $M$ 의 각 점 $x \in M$ 에 그 점에서의 접벡터 공간 $T_x M$ 을 대응시킨 것이다. 접다발은 일반적으로 자명한 다발이 아니다. 예를 들어, 2차원 구면의 접다발은 털 뭉치 정리에 의해 자명하지 않다. 어떤 다양체의 접다발이 자명할 경우, 그 다양체를 평행화 가능parallelizable^eng하다고 한다.

6. 1. 자명한 벡터 다발

임의의 위상 공간

X

와 위상 벡터 공간

V

가 주어졌을 때, 데카르트 곱

X \times V

는 자연스러운 사영

\pi: X \times V \to X

,

\pi(x, v) = x

와 함께 벡터 다발 구조를 가진다. 이러한 벡터 다발을 자명한 벡터 다발이라고 부른다.

이는 가장 단순한 형태의 벡터 다발로, 기저 공간

X

의 모든 점

x

에 대응하는 올

\pi^{-1}(x)

이 모두 동일한 벡터 공간

V

와 동형이다. 즉, 벡터 다발 전체가 기저 공간과 하나의 고정된 벡터 공간의 곱 공간으로 표현된다. 예를 들어,

X \times \mathbb{R}^k

는 사영

(x, v) \mapsto x

와 함께

X

위의 계수

k

인 자명한 다발이다.

만약

X

가 매끄러운 다양체이고

V = \mathbb{R}^k

(k차원 유클리드 공간)이라면,

X \times \mathbb{R}^k

는 매끄러운 벡터 다발을 이룬다.

자명한 벡터 다발은 벡터 다발의 국소 자명화가 전체 기저 공간

X

에 대해 하나로 주어지는 특별한 경우로 볼 수 있다.

6. 2. 접다발

임의의 매끄러운 다양체

M

위에는 접다발(

TM

)이라는 중요한 매끄러운 벡터 다발이 존재한다. 접다발은 다양체

M

의 각 점

x \in M

에 그 점에서의 접공간

T_x M

을 대응시켜 만든 구조이다. 접다발

TM

의 차원은 원래 다양체

M

의 차원과 같다.

접다발은 벡터 다발의 중요한 예시이지만, 일반적으로 자명한 다발은 아니다. 예를 들어, 2차원 구면의 접다발은 털 뭉치 정리에 의해 자명하지 않음이 알려져 있다. 어떤 다양체의 접다발이 자명할 경우, 그 다양체를 평행화 가능parallelizable^eng하다고 부른다.

매끄러운 다양체

M

의 접다발

TM

은 매끄러운 벡터 다발의 대표적인 예이다. 또한, 접다발의 절단은 다양체

M

위의 벡터장과 동일한 개념이다.

6. 3. 연관 벡터 다발

위상 공간

X

위의 주다발과, 주다발의 구조 위상군의 연속 표현이 주어졌을 때,

X

위에 '''연관 벡터 다발'''이라는 벡터 다발을 구성할 수 있다.

6. 4. 이산 공간

한원소 공간

\{\bullet\}

위의

K

-벡터 다발의 개념은

K

-위상 벡터 공간의 개념과 동치이며, 한원소 공간

\{\bullet\}

위의 매끄러운 벡터 다발의 개념은 유한 차원 실수 벡터 공간의 개념과 동치이다.

7. 추가 구조 및 일반화

벡터 다발은 종종 추가적인 구조를 가지기도 한다. 예를 들어, 벡터 다발에 벡터 다발 계량을 부여할 수 있다. 일반적으로 이 계량은 양의 정부호여야 하며, 이 경우 벡터 다발 ''E''의 각 올(fiber)은 유클리드 공간이 된다. 또한, 복소 구조를 갖춘 실수 벡터 다발은 복소 벡터 다발에 해당한다. 이는 벡터 다발의 정의에서 실수 벡터 공간과 실수 선형 사상을 각각 복소 벡터 공간과 복소 선형 사상으로 바꾸어 정의할 수도 있다. 더 일반적으로, 벡터 다발에 부가된 추가 구조는 구조군 축소를 통해 이해할 수 있다. 실수체나 복소수체 외에 더 일반적인 위상체 위의 벡터 다발도 정의하여 사용할 수 있다.

벡터 다발의 개념을 일반화하여, 올 ''F''를 유한 차원 벡터 공간 대신 바나흐 공간으로 사용하는 '''바나흐 다발'''을 정의할 수 있다.^[1] 이 경우, 국소 자명화는 단순히 선형 동형사상이 아니라 바나흐 공간의 동형사상이어야 하며, 좌표 변환 사상

: $g_{UV} \colon U\cap V \to \operatorname{GL}(F)$

는 바나흐 다양체 사이의 연속 사상이어야 한다. 만약 C^''p''-급 다발을 다룬다면, 관련된 모든 사상 역시 C^''p''-급이어야 한다.

벡터 다발은 올이 벡터 공간이고 코사이클(cocycle)이 벡터 공간 구조를 보존하는 특별한 종류의 섬유 다발이다. 더 일반적인 섬유 다발은 올이 벡터 공간이 아닌 다른 구조를 가질 수 있도록 구성된다. 예를 들어, 올이 구인 섬유 다발은 구 다발이라고 불린다.

8. K-이론

위상 공간 위의 유한 차원 실수 또는 복소수 벡터 다발들은 '''위상 K이론'''이라는 환으로 분류된다. 콤팩트 하우스도르프 공간 $X$ 의 K-이론 군 $K(X)$ 는 $X$ 위의 복소 벡터 다발 $E$ 의 동형 사상류 $[''E'']$ 를 생성원으로 하는 아벨 군으로 정의된다.^[2] 이때, 벡터 다발의 짧은 완전열

$0 \to A \to B \to C \to 0$

이 주어지면, K-이론에서는 다음의 관계가 성립한다.

$[B] = [A] + [C]$

복소 벡터 다발 대신 실수 벡터 다발을 사용하여 유사하게 구성한 것을 KO-이론이라고 한다. 또한 콤팩트 지지를 갖는 K-이론이나 고차 K-이론 군 등도 정의할 수 있다.

라울 보트의 유명한 보트 주기성 정리는 임의의 위상 공간 $X$ 의 K-이론이 $X$ 의 이중 현수(suspension)인 $S^2X$ 의 K-이론과 동형임을 나타낸다. (다른 표현으로는 $X$ 와 2차원 구면 $S^2$ 의 곱공간 $X \times S^2$ 의 K-이론과 동형이라고도 한다.)

대수 기하학에서는 스키마 $X$ 위의 벡터 다발에 위와 같은 동치 관계를 부여하여 정의된 K-이론 군뿐만 아니라, 스키마 위의 코히어런트 층으로 구성된 K-이론 군도 고려한다. 만약 기저 스키마가 매끄럽다면 이 두 구성은 자연스럽게 같은 군을 정의한다.

참조

_[1] 서적 Differential and Riemannian manifolds Springer-Verlag
_[2] 문서 この群は[[グロタンディーク群]]と呼ばれる。
_[3] 서적 벡터 속 이론 http://minumsa.minum[...] 민음사 1989-01-01
_[4] 서적 Vector bundles and their applications Kluwer 1998
_[5] 서적 Векторные расслоения и их применения Наука 1984

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com