산 해리 상수
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
산 해리 상수(pKa)는 용액 내 산-염기 평형을 정량적으로 나타내는 척도이다. 아레니우스, 브뢴스테드-로우리, 루이스의 산-염기 정의에 따라 산의 해리 반응을 설명하며, 산의 세기를 나타낸다. pKa는 산의 분자 구조, 용매, 온도 등에 따라 달라지며, 헨더슨-하셀바흐 방정식을 통해 pH와 산, 짝염기의 관계를 나타낸다. 강산은 낮은 pKa 값을, 약산은 높은 pKa 값을 가지며, 다염기산은 여러 단계로 해리되어 각 단계별 pKa 값을 갖는다. pKa 값은 화학, 생화학, 약학, 환경 과학 등 다양한 분야에서 활용되며, 특히 완충 용액 설계, 약물 개발, 환경 문제 해결 등에 중요한 역할을 한다.
더 읽어볼만한 페이지
- 염기 - 수산화물
수산화물은 수산화 이온을 포함하는 화합물로, 브뢴스테드-로우리 염기 및 루이스 염기로 작용하며, 다양한 무기 및 유기 반응에서 중요한 역할을 한다. - 염기 - 강염기
강염기는 수용액에서 수산화 이온을 많이 생성하는 염기로, 알칼리 금속, 알칼리 토류 금속 등의 수산화물과 초염기를 포함한다. - 산 (화학) - 왕수
왕수는 진한 질산과 염산을 1:3 몰 비율로 혼합한 것으로, 금이나 백금 같은 귀금속을 녹일 수 있는 강력한 산화력을 가진 용액이며, 염화 금산 제조, 식각, 분석화학 등에 사용된다. - 산 (화학) - 질산
질산은 강산이자 강력한 산화력을 지닌 무색 액체로, 비료, 폭발물, 나일론 생산 등 산업에 널리 쓰이지만 부식성과 테러 악용 위험성도 있으며, 현재는 주로 암모니아 산화법으로 생산된다. - 평형화학 - 헤모글로빈
헤모글로빈은 척추동물 혈액에서 산소를 운반하는 주요 단백질로, 헴과 글로빈이 결합된 4개의 소단위체로 구성된 사량체 구조를 가지며, 헴의 철 성분이 산소와 결합하여 폐에서 조직으로 산소를, 조직에서 이산화탄소와 양성자를 운반하고, 산소 결합은 여러 요인에 의해 영향을 받으며, 유전자 돌연변이는 헤모글로빈병증을 유발하고, 농도와 기능은 질병 진단에 활용되며, 다양한 생물종에서 발견된다. - 평형화학 - 해리 (화학)
해리는 분자, 복합체, 또는 이온이 더 작은 구성 요소로 분리되는 과정을 의미하며, 해리 상수는 화학 평형 상태에서 반응의 정도를 측정하는 데 사용된다.
2. 정의
아레니우스의 초기 분자 정의에 따르면, 산은 수용액에서 해리되어 수소 이온(양성자)을 방출하는 물질이다.[5]
:
이 해리 반응의 평형 상수는 해리 상수로 알려져 있다.
브뢴스테드와 로우리는 이를 양성자 교환 반응으로 더 일반화했다.[6][7][8]
:
산은 양성자를 잃어 짝염기를 남기고, 양성자는 염기에 전달되어 짝산을 생성한다.
용액 화학에서는 용매에 관계없이 용매화된 수소 이온의 약어로 를 사용하는 것이 일반적이다. 수용액에서 는 양성자가 아닌 용매화된 히드로늄 이온을 나타낸다.[9][10]
산 해리의 더 넓은 정의에는 물 분자의 분열에 의해 양성자가 생성되는 가수분해가 포함된다. 예를 들어, 붕산()은 마치 양성자 주개인 것처럼 를 생성하지만, 라만 분광법에 의해 이것이 가수분해 평형 때문임이 확인되었다.[11]
:
마찬가지로, 금속 이온 가수분해는 와 같은 이온이 약산으로 작용하게 한다.[12]
:
루이스의 초기 정의에 따르면, 산은 전자쌍을 받아들여 배위 공유 결합을 형성하는 물질이다.[13]
산의 일반식을 '''HA'''로, 용매를 '''Hsol'''로 하면, 해리 평형 반응은 다음과 같다.
:
이때, 산 해리 상수 '''Ka'''는 용매의 농도 '''[Hsol]'''를 상수 안에 포함하여 다음과 같이 나타낼 수 있다.
:
여기서 활동도 는 농도로 근사한다. Ka는 용매의 종류와 온도에 따라 달라지는 평형 상수이다.
Ka는 물질에 따라 크게 다르고, 경우에 따라서는 자릿수가 매우 크거나 작아 취급하기 불편하므로, 음의 상용로그 '''p''K''a = −log10''K''a'''로 나타내는 경우가 많다. 염기의 경우, 마찬가지로 '''염기 해리 상수'''(p''K''b)를 사용한다.
어떤 물질에서 수소 이온 하나가 떨어져 나간 화학종을 그 물질의 공액 염기라고 하며, 반대로 어떤 물질에 수소 이온 하나가 붙은 화학종을 그 물질의 공액 산이라고 한다. 예를 들어, 물()의 공액 염기는 수산화물 이온(), 공액 산은 옥소늄 이온()이다.
산 해리 상수와 염기 해리 상수는 용매의 자체 이온화 상수를 통해 서로 변환 가능하므로, 문헌에는 산 해리 상수만 제시되는 경우가 많다. 염기의 산 해리 상수 값은 그 염기의 공액 산의 산 해리 상수 값이다.
2. 1. 평형 상수
Thermodynamic equilibrium constant|열역학적 평형 상수영어 는 다음과 같이 정의된다.[14]:
여기서 는 평형 상태에서 화학종 X의 활동도를 나타낸다. 는 무차원이다. 해리 생성물의 활동도는 분자에, 반응물의 활동도는 분모에 배치된다.
활동도는 농도와 활동도 계수 (''γ'')의 곱이므로, 다음과 같이 쓸 수도 있다.
:
여기서 는 HA의 농도를 나타내고 는 활동도 계수의 몫이다.
이러한 복잡성을 피하기 위해, 높은 이온 강도의 매질에서 결정하여 가 항상 일정하다고 가정한다.[14] 예를 들어, 0.1 M 질산나트륨 또는 3 M 과염소산칼륨 용액을 사용한다. 그러면,
:
:
을 얻는다.
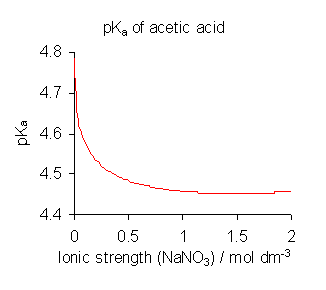
발표된 해리 상수 값은 특정 이온 매질을 참조하며, 조건에 따라 다른 값이 얻어질 수 있다. 아세트산의 경우, 이온 강도에 따라 p''K''a 값이 달라진다.
일반식
:
에서, ''K''a는 차원이 농도인 것처럼 보이지만, 이므로, 평형 상수 는 물리적 차원을 가질 수 없다. 이러한 모순은 여러 가지 방법으로 해결할 수 있다.
- 활동도 계수의 몫이 1이라고 가정.
- 각 농도 값을 c/c0의 비율로 표현 (c0는 [가상의] 표준 상태의 농도, 1).[18]
- 농도를 몰분율 척도로 표현 (몰분율은 차원이 없음).
생화학에서는 "''K''a = 30 mM"과 같이 차원이 있는 값을 인용하여 계산에 사용된 농도 값의 척도인 밀리몰(mM) 또는 마이크로몰(μM)을 나타내는 것이 일반적이다.
산의 일반식을 '''HA'''로, 용매를 '''Hsol'''로 하면, 해리 평형 반응은 다음과 같다.
:
이때, 산 해리 상수 '''Ka'''는 용매의 농도 '''[Hsol]'''를 상수 안에 포함하여 다음과 같이 나타낼 수 있다.
:
여기서는 활동도 를 농도로 근사하고 있다. Ka는 용매와 온도에 따라 달라진다.
Ka는 물질에 따라 크게 다르므로, 음의 상용로그 '''p''K''a = −log10''K''a'''로 나타내는 경우가 많다.
염기의 경우, '''염기 해리 상수'''(p''K''b)를 사용한다. 염기의 일반식을 '''B'''로, 용매를 '''Hsol'''로 하면, 염기가 수소 이온을 받는 반응은 다음과 같다.
:
따라서, 염기 해리 상수 '''K''b'''는 다음과 같이 나타낼 수 있다.
:
''K''b도 ''K''a와 마찬가지로, '''p''K''b'''로 나타낸다. p''K''b가 작을수록 염기성이 강하다.
어떤 물질에서 수소 이온이 떨어져 나간 화학종은 공액 염기, 수소 이온이 붙은 화학종은 공액 산이다. 물()의 공액 염기는 수산화물 이온(), 공액 산은 옥소늄 이온()이다.
산 해리 상수와 염기 해리 상수의 정의에서, 산 HA의 산 해리 상수 Ka와 그 공액 염기 A-의 염기 해리 상수 Kb는 다음 식이 성립한다.
:
즉, Ka와 Kb의 곱은 용매의 자체 이온화 상수와 같다. 수용액 중에서는 물의 이온곱 (25℃에서 10-14)과 같으므로, 상용로그 표기에서는 pKa + pKb = 14가 성립한다.
산 해리 상수와 염기 해리 상수는 용매의 자체 이온화 상수를 통해 서로 변환 가능하므로, 문헌에는 산 해리 상수만 제시되는 경우가 많다.
염기의 산 해리 상수 값은 그 염기의 공액 산의 산 해리 상수 값이다.
2. 2. 단계별 해리 상수
다양성자산은 한 개 이상의 양성자를 잃을 수 있는 화합물이다. 단계별 해리 상수는 각각 단일 양성자의 손실에 대해 정의된다. 첫 번째 양성자의 해리에 대한 상수는 ''K''a1로 표시될 수 있으며, 연속적인 양성자의 해리에 대한 상수는 ''K''a2 등으로 표시된다. 인산(Phosphoric acid)은 세 개의 양성자를 잃을 수 있기 때문에 다양성자산의 예이다.[25]
위의 표에서처럼 연속적인 p''K'' 값의 차이가 약 4 이상일 때, 각 종은 자체적으로 산으로 간주될 수 있다.[26] 사실 H2PO4-의 염은 pH를 약 5.5로 조절하여 용액에서 결정화될 수 있으며, HPO42-의 염은 pH를 약 10으로 조절하여 용액에서 결정화될 수 있다. 종 분포도는 두 이온의 농도가 pH 5.5와 10에서 최대임을 보여준다.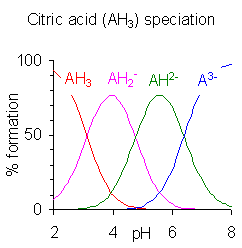
연속적인 p''K'' 값의 차이가 약 4 미만이면 평형 상태에 있는 종의 존재 pH 범위가 겹친다. 차이가 작을수록 겹침이 많아진다. 오른쪽에 구연산의 경우가 나와 있는데, 구연산 용액은 pH 2.5~7.5의 전체 범위에서 완충된다.
폴링의 첫 번째 법칙에 따르면, 주어진 산의 연속적인 p''K'' 값은 증가한다(p''K''a2 > p''K''a1).[27] 같은 원자에 이온화될 수 있는 수소를 두 개 이상 가진 옥시산의 경우, p''K''a 값은 제거되는 각 양성자에 대해 약 5단위 증가하는 경우가 많다.[28][29]
위 표에서 두 번째 양성자는 음전하를 띤 종에서 제거된다는 것을 알 수 있다. 양성자는 양전하를 띠기 때문에 제거하는 데 추가적인 에너지가 필요하며, 이것이 p''K''a2가 p''K''a1보다 큰 이유이다. p''K''a3는 p''K''a2보다 크며, 더 큰 전하 분리가 있기 때문이다. 폴링의 법칙에 대한 예외가 발견되면 구조의 주요 변화도 일어나고 있음을 나타낸다. VO2+(aq)의 경우, 바나듐은 팔면체, 6배위인 반면, 바나딘산은 사면체, 4배위이다. 즉, 첫 번째 해리에서는 네 개의 "입자"가 방출되지만, 다른 해리에서는 두 개의 "입자"만 방출되므로, 첫 번째 반응에 대한 표준 깁스 자유 에너지 변화에 대한 엔트로피 기여가 다른 반응보다 훨씬 크다.
2. 3. 염기 해리 상수
Base dissociation constant영어 ''K''b는 염기 B가 양성자화되어 짝산 HB+를 형성하는 ''결합'' 상수로 정의된다.:
:
:
''K''b는 짝산의 ''K''a와 관련이 있다. 물에서 수산화 이온(OH-)의 농도는 수소 이온의 농도와 ''K''w = [H+][OH-]에 의해 관련되어 있으므로,[16]
:
[OH-]에 대한 식을 ''K''b에 대한 식에 대입하면
:
''K''a, ''K''b 및 ''K''w가 동일한 온도 및 이온 강도 조건에서 결정될 때, 코로그리즘을 취하면 p''K''b = p''K''w - p''K''a가 된다.[30] 25 °C의 수용액에서 p''K''w는 13.9965이므로,
:
가 성립한다.
염기의 경우, 마찬가지로 '''염기 해리 상수'''(p''K''b)를 사용한다. 염기의 일반식을 '''B'''로, 용매를 '''Hsol'''로 하면, 염기가 수소 이온을 받는 반응은 다음과 같다.
:
따라서, 염기 해리 상수 '''K''b'''는 용매의 농도 '''[Hsol]'''을 상수에 포함하여 다음과 같이 나타낼 수 있다.
:
''K''b도 ''K''a와 마찬가지로, 음의 상용로그로 나타낸 '''p''K''b'''로 다루는 경우가 많다. p''K''b가 작을수록 염기성이 강해진다.
어떤 물질에서 수소 이온 하나가 떨어져 나간 화학종을 그 물질의 공액 염기라고 부른다. 반대로, 어떤 물질에 수소 이온 하나가 붙은 화학종을 그 물질의 공액 산이라고 한다. 예를 들어, 물(H2O)의 공액 염기는 수산화물 이온(OH-), 공액 산은 옥소늄 이온(H3O+)이다.
산 해리 상수와 염기 해리 상수의 정의에서, 어떤 산 HA의 산 해리 상수 Ka와 그 공액 염기 A-의 염기 해리 상수 Kb 사이에는 다음 식이 성립한다.
:
즉, 어떤 용매 중에서 ''K''a와 ''K''b의 곱은 그 용매의 자체 이온화 상수와 같다. 특히 수용액 중에서는 물의 이온곱(25℃에서 )과 같아지므로, 상용로그 표기에서는 p''K''a + p''K''b = 14가 성립한다.[88]
3. 이론적 배경
산 해리 상수는 기저 화학 열역학 반응의 직접적인 결과이며, p''K''a 값은 반응의 표준 깁스 자유 에너지 변화에 정비례한다. p''K''a 값은 온도에 따라 변하며, 르 샤틀리에의 원리에 따라 반응이 흡열 반응일 때 온도가 증가하면 ''K''a는 증가하고 p''K''a는 감소한다. 발열 반응의 경우는 그 반대이다.[3][4]
p''K''a 값은 산의 분자 구조에도 영향을 받는다. 폴링은 다양성자산의 연속적인 p''K''a 규칙과 =O 및 −OH기의 수에 따라 산화물의 p''K''a를 추정하는 규칙을 제안했다. 산 해리 상수의 크기에 영향을 미치는 다른 구조적 요인으로는 유도 효과, 공명 효과, 수소 결합이 있다. 함메트 방정식은 p''K''a 추정에 자주 사용되었다.[3][4]
평형 상수는 반응의 표준 깁스 자유 에너지 변화와 관련이 있으며, 산 해리 상수의 경우 다음과 같다.
:.
여기서 ''R''은 기체 상수이고 ''T''는 절대 온도이다. 25 °C에서 kJ·mol−1 단위의 Δ''G'' ≈ 5.708 p''K''a (1 kJ·mol−1 = 1000 줄/몰)이다. 자유 에너지는 엔탈피 항과 엔트로피 항으로 구성된다.[56]
:
표준 엔탈피 변화는 열량 측정법 또는 반트호프 방정식을 사용하여 결정할 수 있지만, 열량 측정법이 더 선호된다. 표준 엔탈피 변화와 산 해리 상수를 모두 결정하면 위의 방정식을 사용하여 표준 엔트로피 변화를 쉽게 계산할 수 있다.
다음 표는 p''K''a 및 Δ''H''의 실험값으로 계산된 엔트로피 항을 나타낸다. 데이터는 신중하게 선택되었으며 25 °C 및 이온 강도 0의 물을 기준으로 한다.[56]
p''K''a가 양수이면 해리 반응에 대한 표준 자유 에너지 변화도 양수이다. 일부 반응은 발열 반응이고 일부는 흡열 반응이지만, Δ''H''가 음수이면 ''T''ΔS가 Δ''G''가 양수임을 결정하는 주요 요소이다. 이러한 반응에서는 엔트로피 기여가 항상 불리하다. 수용액의 이온은 주변 물 분자를 배향시키는 경향이 있으며, 이는 용액을 정렬하고 엔트로피를 감소시킨다. 이온이 엔트로피에 기여하는 것은 종종 음수인, 특히 작거나 고도로 하전된 이온에 대해 편몰 엔트로피이다.[57] 중성 산의 이온화에는 두 개의 이온이 형성되므로 엔트로피가 감소한다. 같은 산의 두 번째 이온화에서 이온이 3개가 되고 음이온은 전하를 띠므로 엔트로피가 다시 감소한다.
반응에 대한 ''표준'' 자유 에너지 변화는 표준 상태의 반응물에서 표준 상태의 생성물로의 변화이며 평형 상태에서의 자유 에너지 변화는 0이다.
묽은 용액에서 일양성자산 HA의 해리는 다음과 같이 나타낼 수 있다.
:HA ⇄ A- + H+
열역학적 평형 상수 K⊖는 다음과 같이 정의된다.[14]
:K⊖ = {A-}{H+} / {HA}
여기서 {X}는 평형 상태에서 화학종 X의 활동도를 나타낸다.
활동도는 농도와 활동도 계수 (''γ'')의 곱이므로, 정의는 다음과 같이 쓸 수도 있다.
:K⊖ = ([A-][H+]/[HA])Γ, Γ = (γA- * γH+) / γHA
여기서 [HA]는 HA의 농도를 나타내고 Γ는 활동도 계수의 몫이다.
이러한 복잡성을 피하기 위해, 해리 상수는 높은 이온 강도의 매질에서 결정된다.[14] 예를 들어, 매질은 0.1 몰 (M) 질산나트륨 또는 3 M 과염소산칼륨 용액일 수 있다. 이 가정을 사용하면,
:Ka = K⊖/Γ = [A-][H+]/[HA]
:pKa = -log10([A-][H+]/[HA]) = log10([HA]/[A-][H+])
을 얻는다.
발표된 해리 상수 값은 특정 이온 매질을 참조하며, 아세트산에서 보여주는 것처럼 다른 조건에서는 다른 값이 얻어진다는 점에 유의해야 한다. 발표된 상수가 특정 응용에 필요한 것과 다른 이온 강도를 참조하는 경우, 특이 이온 이론(SIT) 및 기타 이론을 사용하여 조정할 수 있다.[15]
모든 평형 상수는 반트호프 방정식에 따라 온도에 따라 변화한다.[17]:
:dln(K)/dT = ΔH⊖/RT2
R은 기체 상수이고 T는 절대 온도(켈빈)이다. 따라서 발열 반응의 경우 표준 엔탈피 변화 ΔH⊖는 음수이고 ''K''는 온도가 증가함에 따라 감소한다. 흡열 반응의 경우 ΔH⊖는 양수이고 ''K''는 온도가 증가함에 따라 증가한다.
반응에 대한 표준 엔탈피 변화는 키르히호프의 열화학 법칙에 따라 온도의 함수이기도 하다.:
:(∂ΔH/∂T)p = ΔCp
여기서 ΔCp는 일정 압력에서의 열용량 변화이다. 실제로는 ΔH⊖는 작은 온도 범위에서 일정하다고 볼 수 있다.
4. 강산과 약산
아레니우스의 정의에 따르면, 강산은 수용액에서 거의 완전히 해리되어 수소 이온()을 방출하는 물질이다.[5] 이때 p''K''a 값은 0보다 작다.[19] 용매 준평 효과에 의해 강산은 물에서 거의 동일한 산도를 갖는다.[20][21] 이는 해리되지 않은 산의 양이 검출 한계 미만이기 때문이다. 질산(p''K''a ≈ -1.7)은 pH가 1보다 큰 수용액에서 강산으로 작용하며,[22] 수용액 HCl의 p''K''a 값은 -9.3으로 추정된다.[23]
약산은 수용액에서 부분적으로만 해리되는 산으로, p''K''a 값이 상대적으로 크다. 아세트산은 약산의 예시로, 물에 양성자를 기증하여 아세테이트 이온과 히드로늄 이온을 생성한다.
5. 단일 양성자산
''K''a를 정의하는 식을 재배열하고, pH = -log10[H+]를 대입하면[24]
:
이것은 헨더슨-하셀바흐 방정식이며, 다음과 같은 결론을 도출할 수 있다.
- 중화 반응이 절반 진행되었을 때, [A-]/[HA] = 1이다. log(1) = 0이므로, 중화 반응 절반 지점에서의 pH는 수치적으로 p''K''a와 같다. 반대로, pH = p''K''a일 때, HA의 농도는 A-의 농도와 같다.
- 완충 영역은 p''K''a ± 2의 범위에 걸쳐 있다. p''K''a ± 1 범위를 벗어나면 완충 작용은 약해진다. pH ≤ p''K''a - 2이면 물질은 완전히 양성자화된 것으로 간주되고, pH ≥ p''K''a + 2이면 완전히 해리(탈양성자화)된 것으로 간주된다.
- pH를 알면 [A-]/[HA] 비율을 계산할 수 있다. 이 비율은 산의 분석적 농도와 무관하다.
물에서 측정 가능한 p''K''a 값은 강산의 경우 약 -2부터 매우 약한 산(또는 강염기)의 경우 약 12까지 범위를 가진다.
원하는 pH의 완충 용액은 약산과 그 짝염기의 혼합물로 만들 수 있다. 실제로, 이 혼합물은 산을 물에 녹이고 필요한 양의 강산 또는 강염기를 첨가하여 만들 수 있다. 산의 p''K''a와 분석적 농도를 알면, ICE 테이블을 사용하여 일양성자산 용액의 해리 정도와 pH를 쉽게 계산할 수 있다.
어떤 물질에서 수소 이온 하나가 떨어져 나간 화학종을 그 물질의 짝염기라고 부른다. 반대로, 어떤 물질에 수소 이온 하나가 붙은 화학종을 그 물질의 짝산이라고 한다. 예를 들어, 물(H2O)의 짝염기는 수산화 이온(OH-), 짝산은 옥소늄 이온(H3O+)이다.
산 해리 상수와 염기 해리 상수의 정의에서, 어떤 산 HA의 산 해리 상수 Ka와 그 짝염기 A-의 염기 해리 상수 Kb 사이에는 다음 식이 성립한다.
:
즉, 어떤 용매 중에서 Ka와 Kb의 곱은 그 용매의 자체 이온화 상수와 같다. 특히 수용액 중에서는 물의 이온곱 (25℃에서 10-14 M2)과 같아지므로, 상용로그 표기에서는 pKa + pKb = 14가 성립한다.
산 해리 상수와 염기 해리 상수는 용매의 자체 이온화 상수를 매개로 하여 서로 변환 가능하기 때문에, 문헌 등에는 산 해리 상수만이 제시되는 경우가 많다.
참고로, 염기의 산 해리 상수 값은 그 염기의 짝산의 산 해리 상수 값이다.
6. 다양성자산
다양성자산은 하나 이상의 양성자를 잃을 수 있는 화합물이다. 각 양성자의 손실은 단계별로 일어나며, 각각의 해리 상수(''K''a1, ''K''a2 등)로 정의된다. 예를 들어, 인산(H3PO4)은 세 개의 양성자를 잃을 수 있는 다양성자산이다.
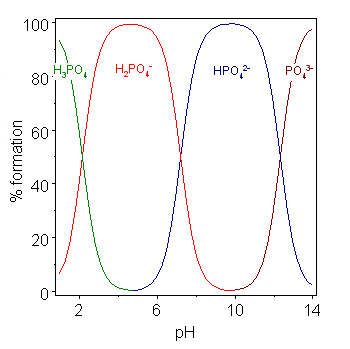
위 표에서 볼 수 있듯이, 연속적인 p''K'' 값의 차이가 약 4 이상이면 각 종은 독립적인 산으로 간주될 수 있다.[26] 예를 들어, H2PO4-의 염은 pH를 약 5.5로 조절하여 결정화할 수 있고, HPO42-의 염은 pH를 약 10으로 조절하여 결정화할 수 있다.
연속적인 p''K'' 값의 차이가 약 4 미만이면, 평형 상태에 있는 종들의 pH 범위가 겹치게 된다. 차이가 작을수록 겹침은 더 커진다. 구연산의 경우, pH 2.5~7.5 범위에서 여러 종이 함께 존재하며 용액은 완충 작용을 한다.
폴링의 첫 번째 법칙에 따르면, 동일한 산에서 연속적인 p''K'' 값은 증가한다(p''K''a2 > p''K''a1).[27] 이는 양성자를 제거할수록 음전하가 증가하여 추가적인 양성자 제거가 어려워지기 때문이다.[28][29]
어떤 물질에서 수소 이온() 하나가 떨어져 나간 화학종을 그 물질의 공액 염기라고 한다. 반대로, 어떤 물질에 수소 이온이 하나 붙은 화학종을 그 물질의 공액 산이라고 한다. 예를 들어, 물(H2O)의 공액 염기는 수산화 이온(OH-)이고, 공액 산은 옥소늄 이온(H3O+)이다.
산 해리 상수(Ka)와 염기 해리 상수(Kb)는 다음 관계를 갖는다.
:
즉, Ka와 Kb의 곱은 용매의 자체 이온화 상수와 같다. 수용액에서는 물의 이온곱(25℃에서 10-14 M2)과 같으므로, pKa + pKb = 14가 성립한다. 따라서, 산 해리 상수 값만 주어져도 염기 해리 상수를 알 수 있다.
6. 1. 등전점
용액 내 물질의 경우, 등전점(pI)은 양전하 종의 농도 합(전하 값으로 가중 평균)이 음전하 종의 농도 합(전하 값으로 가중 평균)과 같아지는 pH로 정의된다. 각 유형의 종이 하나씩 있는 경우, 등전점은 pK 값으로부터 직접 구할 수 있다. 글리신(AH로 정의)의 예를 들어 보자. 고려해야 할 두 가지 해리 평형이 있다.:
:
두 번째 방정식에서 [AH]에 대한 식을 첫 번째 방정식에 대입하면
:
등전점에서 양전하 종(
:
따라서, 로그를 취하면 pH는 다음과 같이 주어진다.
:
아미노산의 pI 값은 단백질 생성 아미노산에 나열되어 있다. 두 개 이상의 하전 종이 서로 평형 상태에 있는 경우, 완전한 종 분포 계산이 필요할 수 있다.
7. 염기도
염기도는 염기의 세기를 나타내는 척도로, 염기 해리 상수(p''K''b) 또는 짝산의 산 해리 상수(p''K''aH)로 표현할 수 있다. 강염기는 p''K''b 값이 작거나 p''K''aH 값이 크다.
염기의 평형 상수 ''K''b는 일반적으로 염기 B가 양성자화되어 짝산 를 형성하는 ''결합'' 상수로 정의된다.
:
:[30]
''K''b는 짝산의 ''K''a와 관련이 있다. 물에서 수산화 이온 의 농도는 수소 이온의 농도와 에 의해 관련되어 있으므로, 에 대한 식을 ''K''b에 대한 식에 대입하면
:
가 된다. ''K''a, ''K''b 및 ''K''w가 동일한 온도 및 이온 강도 조건에서 결정될 때, 코로그리즘을 취하면 p''K''b = p''K''w − p''K''a가 된다. 25 °C의 수용액에서 p''K''w는 13.9965이므로,
:
이다. 이는 대부분의 실제 목적에 충분한 정확도를 가지고 있다. 사실상 p''K''a와 별도로 p''K''b를 정의할 필요는 없지만, 오래된 문헌에서 p''K''b 값만 찾을 수 있는 경우가 많기 때문에 여기서 정의한다.[31]
유기화학과 같은 화학의 하위 분야에서는 p''K''b를 염기도의 척도로 사용하지 않고, 짝산의 p''K''a 값(p''K''aH로 표시)을 사용한다. 평형 상태에 있는 염기 B와 그 짝산 에 대해, 이는 다음과 같이 정의된다.
:
p''K''aH 값이 높을수록 더 강한 염기임을 나타낸다. 예를 들어, 및 값은 (트리에틸아민)이 (피리딘)보다 더 강한 염기임을 나타낸다.
염기의 경우, 마찬가지로 '''염기 해리 상수'''(p''K''b)를 사용한다. 염기의 일반식을 '''B'''로, 용매를 '''Hsol'''로 하면, 염기가 수소 이온을 받는 반응은 다음과 같다.
:
따라서, 염기 해리 상수 '''K''b'''는 용매의 농도 '''[Hsol]'''을 상수에 포함하여 다음과 같이 나타낼 수 있다.
:
''K''b도 ''K''a와 마찬가지로, 음의 상용로그 표시로 한 '''p''K''b'''로 다루는 경우가 많다. p''K''b가 작을수록 염기성이 강해진다.
어떤 물질에서 수소 이온 하나가 떨어져 나간 화학종을 그 물질의 공액 염기라고 부른다. 반대로, 어떤 물질에 수소 이온 하나가 붙은 화학종을 그 물질의 공액 산이라고 한다. 예를 들어, 물()의 공액 염기는 수산화물 이온(), 공액 산은 옥소늄 이온()이다.
산 해리 상수와 염기 해리 상수의 정의에서, 어떤 산 HA의 산 해리 상수 Ka와 그 공액 염기 A-의 염기 해리 상수 Kb 사이에는 다음 식이 성립한다.
:
즉, 어떤 용매 중에서 Ka와 Kb의 곱은 그 용매의 자체 이온화 상수와 같다. 특히 수용액 중에서는 물의 이온곱 (25℃에서 10-14 M2)과 같아지므로, 상용로그 표기에서는 pKa + pKb = 14가 성립한다.
산 해리 상수와 염기 해리 상수는 용매의 자체 이온화 상수를 매개로 하여 서로 변환 가능하기 때문에, 문헌 등에는 산 해리 상수만이 제시되는 경우가 많다.
참고로, 염기의 산 해리 상수 값은 그 염기의 공액 산의 산 해리 상수 값이다.
8. 양쪽성 물질
양쪽성 물질은 pH에 따라 산 또는 염기로 작용할 수 있는 물질이다. 물은 대표적인 양쪽성 물질이다. 이 외에도 중탄산 이온(HCO3-)은 탄산(H2CO3) 분자의 짝염기이자 탄산 이온(CO32-)의 짝산으로, 다음과 같은 평형을 이룬다.[30]
:
:
탄산 평형은 인체의 산염기 균형에 중요한 역할을 한다.
아미노산 또한 양쪽성 물질인데, 중성 분자가 내부 산-염기 평형의 영향을 받는다는 특징이 있다. 염기성 아미노기는 산성 카르복실기에서 양성자를 끌어당겨 결합하여 쯔비터이온을 형성한다.[30]
:
pH가 약 5 미만이면 카르복실기와 아미노기 모두 양성자화되며, pH가 증가함에 따라 다음과 같이 산이 해리된다.
:
높은 pH에서는 아미노기가 탈양성자화되는 두 번째 해리가 일어날 수 있다.
:
이처럼 아미노산 분자는 양성자화되거나 탈양성자화될 수 있기 때문에 양쪽성을 띤다.
8. 1. 물의 자동 이온화
물 분자는 양성자(H+)를 얻거나 잃을 수 있는 양쪽성 물질이다. 물의 이온화 평형은 다음과 같이 나타낼 수 있다.:
여기서 H+는 용매화된 양성자를 나타내며, 히드로늄 이온(H3O+)으로 쓰이기도 하지만, 실제로는 H5O2+, H7O3+, H9O4+ 등 여러 물 분자에 의한 용매화가 존재하므로 정확한 표현은 아니다.[32]
일반적으로 물의 농도는 일정하다고 가정하여, 물의 이온화 상수 *K*w는 다음과 같이 정의된다.
:
- K*w는 자동이온화 상수이자 산 해리 상수의 특수한 경우이며, p*K*a와 유사하게 로그 형태로도 정의할 수 있다.
:
p*K*w 값은 온도에 따라 변하며, 순수한 물에서의 p*K*w 값은 다음 표와 같다.[33]
이 데이터는 포물선으로 모델링할 수 있으며, 해당 방정식에 따르면 p*K*w = 14는 24.87 °C에서 얻어진다. 이 온도에서 수소 이온(H+)과 수산화 이온(OH-) 농도는 각각 10−7 M이다.
어떤 물질에서 수소 이온 하나가 떨어져 나간 화학종을 그 물질의 공액 염기라 하고, 반대로 수소 이온 하나가 붙은 화학종을 그 물질의 공액 산이라 한다. 예를 들어, 물(H2O)의 공액 염기는 수산화물 이온(OH-)이고, 공액 산은 옥소늄 이온(H3O+)이다.
산 해리 상수와 염기 해리 상수의 정의에 따르면, 어떤 산 HA의 산 해리 상수 *K*a와 그 공액 염기 A-의 염기 해리 상수 *K*b의 곱은 용매의 자체 이온화 상수와 같다. 특히 수용액에서는 물의 이온곱(25℃에서 10-14 M2)과 같으므로, 상용로그 표기에서는 p*K*a + p*K*b = 14가 성립한다.
9. 비수용액에서의 산도
비수용액에서 산 해리 상수(p''K''a)는 용매의 성질에 큰 영향을 받는다. 용매가 이온화를 촉진하는 경우는 다음과 같다.[34]
- 양성자성 용매: 수소 결합을 형성할 수 있다.
- 높은 주개 수: 강한 루이스 염기이다.
- 높은 유전 상수: 이온 종에 좋은 용매이다.
유기 화합물의 p''K''a 값은 비양성자성 용매인 디메틸 설폭사이드(DMSO)[34]와 아세토니트릴(ACN)[35]을 사용하여 얻는 경우가 많다.
디메틸 설폭사이드(DMSO)는 물보다 유전 상수가 낮고 극성이 덜하여 비극성, 소수성 물질을 더 쉽게 용해시키기 때문에 물의 대안으로 널리 사용된다. DMSO는 약 1에서 30까지 측정 가능한 p''K''a 범위를 갖는다. 아세토니트릴은 DMSO보다 염기성이 약하기 때문에, 일반적으로 이 용매에서 산은 더 약하고 염기는 더 강하다. 아세토니트릴(ACN)[36][37][38] 및 디메틸 설폭사이드(DMSO)[39]에 대한 25 °C에서의 일부 p''K''a 값은 다음 표에 나와 있다. 비교를 위해 물에 대한 값도 포함되어 있다.
산의 이온화는 물보다 산성 용매에서 더 적다. 예를 들어, 염화수소는 아세트산에 용해될 때 약산이다. 이는 아세트산이 물보다 훨씬 약한 염기이기 때문이다.
:
: 
비양성자성 용매에서는 수소 결합에 의해 올리고머(예: 아세트산 이량체)가 형성될 수 있다. 산은 짝염기에 수소 결합을 형성할 수도 있는데, 이를 동족회합이라고 한다. 동족회합은 짝염기를 안정화시켜 산의 산도를 높이고 유효 p''K''a 값을 낮춘다. 동족회합은 아세토니트릴 용액에서 파라-톨루엔술폰산의 양성자 주개 능력을 거의 800배나 향상시킨다.[43]
수용액에서는 물이 산보다 짝염기에 더 강한 수소 결합을 형성하기 때문에 동족회합이 발생하지 않는다.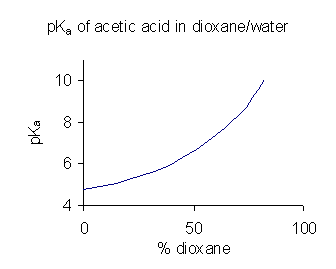
화합물의 물에 대한 용해도가 제한적인 경우, 물/디옥산 또는 물/메탄올과 같은 용매 혼합물에서 p''K''a 값을 결정하기도 한다. 혼합물의 유전 상수가 감소함에 따라 p''K''a 값은 증가한다.
혼합 용매에서 얻은 p''K''a 값은 수용액에 직접 사용할 수 없다. 용매가 표준 상태에 있을 때 활동도가 1로 정의되기 때문이다. 수용액에 사용할 p''K''a 값을 얻으려면 다양한 공용매 혼합물에서 얻은 값으로부터 공용매 농도가 0이 되도록 외삽해야 한다.
특정 혼합 용매에서 얻은 p''K''a 값은 서로 비교하여 상대적인 산의 세기를 알 수 있다. 디메틸 설폭사이드(DMSO)와 같은 특정 비수 용매에서 얻은 p''K''a 값도 마찬가지이다.
두 가지 다른 용매의 표준 상태를 비교할 수 있는 방법이 없기 때문에, 산 해리 상수에 대한 보편적이고 용매에 독립적인 척도는 개발되지 않았다.
10. p''K''a 값에 영향을 미치는 요인
폴링의 두 번째 법칙에 따르면, 옥소산의 p''K''a 값은 주로 옥소기(=O)의 수에 의존하며, 하이드록시기(-OH)의 수나 중심 원자에는 거의 영향을 받지 않는다. p''K''a 값은 옥소기가 없을 때(m=0) 약 8, 1개일 때(m=1) 약 2, 2개일 때(m=2) 약 -3, 3개 이상일 때(m=3) -10보다 작다.[27] 옥소기의 수가 증가하면 중심 원자의 산화 상태가 높아지고, 이는 짝염기의 음전하를 비편재화시켜 안정화시키므로 산성도가 강해진다.[46] 예를 들어, HClO의 p''K''a는 7.2, HClO2는 2.0, HClO3는 -1이며, HClO4는 강산이다().[7]
유도 효과와 공명 효과도 p''K''a 값에 영향을 미친다. 예를 들어, 아세트산의 수소 원자를 전기음성도가 더 큰 염소 원자로 치환하면 이온화가 더 쉬워져 p''K''a 값이 감소한다. 염소 원자의 수가 증가함에 따라 p''K''a 값은 순서대로 4.7, 2.8, 1.4, 0.7로 감소한다.[48]
함메트 방정식은 치환기가 p''K''a 값에 미치는 영향을 정량적으로 나타내는 선형 자유 에너지 관계의 일종이다.[49]
: log(''K''a) = log(''K'') + ρσ
여기서 ''K''a는 치환된 화합물의 해리 상수, ''K''는 치환기가 수소일 때의 해리 상수, ρ는 치환되지 않은 화합물의 특성 값, σ는 각 치환기의 특성 값이다.
알코올은 일반적으로 물에서 산으로 작용하지 않지만, OH기에 인접한 이중 결합이 있으면 케토-에놀 토토머화에 의해 p''K''a가 감소할 수 있다. 아스코르브산이 대표적인 예이다.
분자내 수소 결합도 p''K''a 값에 영향을 줄 수 있다. 푸마르산과 말레산의 p''K''a 값 차이가 대표적인 예이다. 말레산은 ''시스'' 이성질체로, 분자 내 수소 결합을 형성하여 첫 번째 양성자 제거를 촉진하고 두 번째 양성자 제거를 억제한다. 반면, 푸마르산은 ''트랜스'' 이성질체로, 분자 내 수소 결합을 형성하지 않아 두 p''K''a 값의 차이가 크지 않다.[53]
프로톤 스펀지는 강한 염기성을 띠는 화합물로, 양성자화 과정에서 분자 내 변형이 완화되고 강한 내부 수소 결합이 형성되어 p''K''a 값이 12.1에 달한다.[54][55]
용매와 용매화 효과도 p''K''a 값에 영향을 미친다. 예를 들어, 메틸아민의 염기성 순서는 기체 상태에서는 Me3N > Me2NH > MeNH2 > NH3 순이지만, 물에서는 Me2NH > MeNH2 > Me3N > NH3 순으로 바뀐다. 이는 물 분자와의 수소 결합 및 용매화 효과 차이 때문이다.[4]
10. 1. 열역학
산 해리 상수는 반응의 표준 깁스 자유 에너지 변화에 정비례하며, 이는 반응의 표준 깁스 자유 에너지 변화와 관련이 있다.:.
여기서 ''R''은 기체 상수이고 ''T''는 절대 온도이다. 25 °C에서 kJ·mol−1 단위의 Δ''G'' ≈ 5.708 p''K''a (1 kJ·mol−1 = 1000 줄/몰)이다. 자유 에너지는 엔탈피 항과 엔트로피 항으로 구성된다.[56]
:
표준 엔탈피 변화()는 반트호프 방정식에 따라 온도에 따라 변하며, p''K''a 값의 온도 의존성을 설명할 수 있다.
:
은 기체 상수이고 는 절대 온도(켈빈)이다. 따라서 흡열 반응일 때, 온도가 증가함에 따라 ''K''a는 증가하고 p''K''a는 감소한다. 발열 반응의 경우는 그 반대이다.
표준 엔탈피 변화와 표준 엔트로피 변화 ()를 통해 p''K''a 값의 온도 의존성을 설명할 수 있다.
다음은 25 °C 및 이온 강도 0의 물을 기준으로 하는 엔트로피 항을 나타낸 표이다.[56]
11. 실험적 측정
p''K''a 값은 일반적으로 전위차(pH) 적정을 통해 실험적으로 결정되지만, p''K''a 값이 약 2 미만이거나 11 초과인 경우에는 pH 측정의 실질적인 어려움 때문에 분광 광도법 또는 NMR 측정이 필요할 수 있다.[58]
일반적인 절차는 다음과 같다. 먼저 높은 이온 강도를 가진 매질 내 화합물 용액을 강산을 사용하여 화합물이 완전히 양성자화될 때까지 산성화한다. 그 후, 강염기를 사용하여 모든 양성자가 제거될 때까지 용액을 적정한다. 적정 과정의 각 지점에서 유리 전극과 pH 미터를 사용하여 pH를 측정하고, 최소 제곱법을 사용하여 계산된 pH 값을 관찰된 값에 맞춤으로써 평형 상수를 구한다.[59]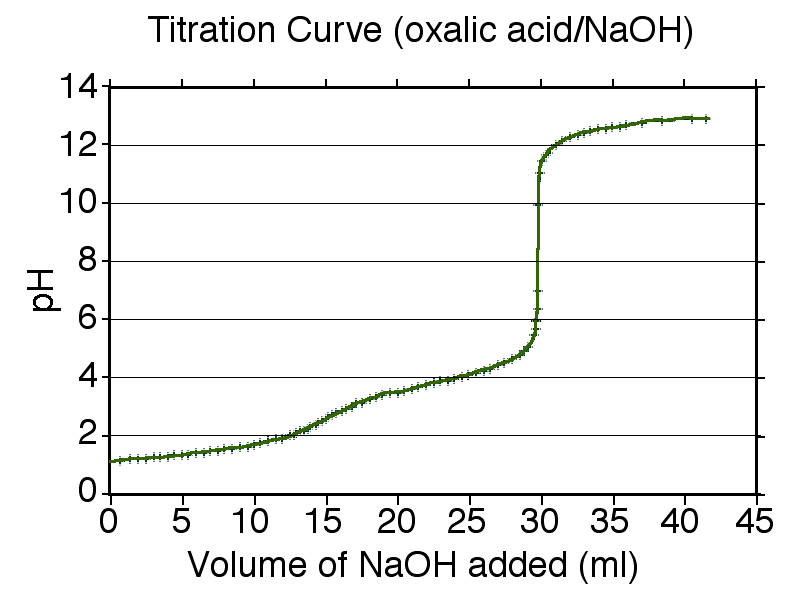
이온 강도를 거의 일정하게 유지하기 위해, 첨가되는 강염기의 총 부피는 초기 적정 대상 용액의 부피에 비해 작아야 한다. 이를 통해 적정 중 p''K''a가 일정하게 유지된다. 오른쪽 그림은 옥살산의 계산된 적정 곡선을 보여준다. 옥살산의 p''K''a 값은 1.27과 4.27이며, 따라서 완충 영역은 pH 약 1.3과 pH 약 4.3을 중심으로 형성된다. 이 완충 영역은 산과 짝염기의 농도 변화에 따라 p''K''a 값을 얻는 데 필요한 정보를 제공한다.
두 완충 영역 사이에는 pH 약 3에서 종말점 또는 당량점이 나타나는데, 이 종말점은 날카롭지 않다. 이는 완충 영역이 약간 겹치는 이양성자산의 전형적인 특징이며, 이 예시에서는 p''K''a2 − p''K''a1 값이 약 3이다. (만약 p''K'' 값의 차이가 약 2 이하라면 종말점은 눈에 띄지 않는다.) 두 번째 종말점은 pH 약 6.3에서 시작되며 날카로운데, 이는 모든 양성자가 제거되었음을 의미한다. 이 경우 용액은 완충되지 않으며, 소량의 강염기를 첨가하면 pH가 급격히 상승한다. 그러나 pH는 무한정 상승하지 않고, pH 약 11 (p''K''w − 3)에서 새로운 완충 영역이 시작되는데, 이는 물의 자체 이온화가 중요해지는 지점이다.
유리 전극으로 수용액의 pH 값을 2 미만으로 측정하는 것은 매우 어렵다. 네른스트 방정식이 그러한 낮은 pH 값에서는 적용되지 않기 때문이다. 따라서 p''K'' 값이 2 미만이거나 11 초과인 경우에는 분광 광도법[60][61] 또는 NMR[62][63] 측정을 pH 측정 대신 사용하거나, pH 측정과 함께 사용한다.
유리 전극을 사용할 수 없는 비수용액의 경우에는 흡광도 또는 형광 측정을 포함하는 분광 광도법을 주로 사용한다.[37] 이때 측정되는 양은 각 광활성 종의 기여도의 합에 비례하는 것으로 가정하며, 흡광도 측정의 경우에는 비어-람베르트 법칙이 적용되는 것으로 가정한다.
등온 적정 열량측정법(ITC)을 사용하면 p''K'' 값과 더불어 산 해리에 대한 표준 엔탈피도 함께 결정할 수 있다.[64] 간단한 시스템의 경우에는 기기 제조업체에서 제공하는 소프트웨어를 통해 계산을 수행한다.
일반적인 물을 포함하는 수용액은 1H NMR 측정에 사용할 수 없고, 대신 중수()를 사용해야 한다. 그러나 13C NMR 데이터는 일반적인 물과 함께 사용할 수 있으며, 1H NMR 스펙트럼은 비수용액 매질과 함께 사용할 수 있다. NMR로 측정되는 양은 양성자 교환이 NMR 시간 척도에서 빠르기 때문에 시간 평균 화학적 이동을 나타낸다. 31P와 같이 다른 화학적 이동도 측정할 수 있다.
11. 1. 미시 상수
아미노산 시스테인의 탈양성자화에서 거시상수는 두 개의 미시상수의 합으로 나타낼 수 있다. 여기서 미시상수는 황 또는 질소에서의 탈양성자화를 나타내며, 거시상수 합은 산 해리 상수이다.[66]
스퍼민과 같은 염기는 양성자화가 여러 부위에서 발생할 수 있다. 예를 들어, 단일 양성자화는 말단 기 또는 내부 기에서 발생할 수 있다. 이때 측정된 ''K''b 값은 미시반응에 대한 K 값의 합으로, 다음과 같이 나타낼 수 있다.[67]
:

반응물이 연속적으로 두 개의 반응을 거칠 때, 결합된 반응에 대한 거시상수는 두 단계에 대한 미시상수의 곱이다. 예를 들어, 시스테인 양쪽성 이온은 황과 질소에서 각각 하나의 양성자를 잃을 수 있으며, 두 개의 양성자를 잃는 전체 거시상수는 두 개의 해리 상수의 곱이다.[66]
12. 응용 및 중요성
산 해리 상수(p''K''a) 값은 용액 내 산-염기 평형을 이해하고 정량적으로 처리하는 데 필수적이며, 다양한 분야에 응용된다.
생화학:
- 효소 활성 및 단백질 안정성은 단백질과 아미노산 곁사슬의 p''K''a 값에 크게 영향을 받는다.[68] 단백질 p''K''a 값은 직접 측정하기 어려울 때 이론적 방법을 통해 계산할 수 있다.
- 생화학 반응 연구에 사용되는 완충 용액은 생리적 pH 또는 그 근처의 용액을 제공하며, 구성 요소의 p''K''a 값을 알아야 설계할 수 있다.[69] MOPS와 트리스는 중요한 완충 용액의 예시이다.[70][71]
- 완충 작용은 산-염기 항상성과 같은 산-염기 생리학의 필수적인 부분이며,[72] 산-염기 장애를 이해하는 데 중요하다.[73][74][75]
- 분자마다 다른 등전점(pI)을 가지며, 이는 p''K''a 값의 함수이다. 이를 이용하여 2차원 겔 전기영동(2-D 겔 폴리아크릴아마이드 겔 전기영동)과 같은 기술로 단백질을 분리할 수 있다.[76]
분석화학:
- 완충 용액은 용액의 pH를 특정 값으로 고정하는 데 사용되며, 완충 용량은 pH = p''K''a일 때 가장 크다.[77]
- 산-염기 추출에서 화합물을 유기상으로 효율적으로 추출하기 위해 적절한 완충액을 사용하여 수상의 pH를 최적화할 수 있다. 최적 pH에서는 전기적으로 중성인 종의 농도가 최대화되어 유기 용매에 더 잘 녹는다.[78]
약학:
- 화합물의 이온화는 용해도 및 친유성과 같은 물리적 거동 및 거시적 특성을 변화시킨다. 약물 개발 과정에서 이온화 가능한 그룹의 p''K''a를 조절하여 혈액 내 화합물의 농도를 조절할 수 있다.[79]
배위화학:
- 금속 이온(루이스 산)과 리간드(루이스 염기) 사이의 배위 착물 형성을 이해하려면 리간드의 양성자화 반응과 금속 이온의 가수분해 반응에 대한 p''K''a 값을 알아야 한다.[80]
환경과학 및 화학 해양학:
- 산-염기 평형은 호수와 강에서 중요하며,[82][83][84] 부식산은 천연수의 주요 구성 요소 중 하나이다.
- 화학 해양학에서 해수 내 철(III)의 용해도를 정량화하기 위해 철(III) 가수분해 생성물의 p''K''a 값과 수산화철의 용해도곱을 사용한다.[86]
위험 평가:
- 산이나 염기와 관련된 위험을 평가할 때 p''K''a 값에 대한 지식이 필요할 수 있다.[81] 예를 들어, 사이안화 수소는 매우 독성이 강한 기체인데, 수용액에서는 p''K''a가 약 9인 약산이다. pH에 따라 사이안화 수소의 위험성이 달라진다.
13. 일반적인 물질의 p''K''a 값
p''K''a영어 값은 화합물의 산성도를 나타내는 중요한 지표이며, 다양한 분야에서 활용된다. 아래 표는 25°C 물에서 측정된 일반적인 물질의 p''K''a영어 값이다.[7][87]
더 많은 p''K''a영어 값은 열역학 섹션에서 확인할 수 있으며, DMSO에서 측정된 탄소산의 p''K''a영어 값은 카르바니온 페이지에서 확인할 수 있다.
참고:
- 식품: 김치, 된장, 고추장 등 한국 전통 발효 식품에서 젖산균, 초산균 등이 생성하는 유기산의 p''K''a영어는 발효 과정 및 제품의 맛과 보존성에 영향을 미친다.
- 환경: 한국의 산성비 문제에서 황산, 질산 등의 p''K''a영어는 산성비 강도와 생태계 영향 평가에 중요 지표가 된다.
- 의약품: 한국 제약 산업에서 신약 개발 시 약물의 p''K''a영어는 용해도, 흡수율, 생체 이용률 등에 영향을 미치는 중요 고려 사항이다.
- 학계: 더불어민주당 등 진보 진영은 환경 문제와 사회적 약자에 대한 관심을 바탕으로 p''K''a영어 관련 연구 (환경 오염 물질, 약물 내성 문제 해결 등)에 영향을 줄 수 있다.
참조
[1]
서적
General Chemistry
https://archive.org/[...]
Saunders College Publishing
1992
[2]
서적
General Chemistry
https://archive.org/[...]
Prentice Hall
2002
[3]
서적
pKa Prediction for Organic Acids and Bases
Chapman & Hall
[4]
백과사전
Reference Module in Chemistry, Molecular Sciences and Chemical Engineering
Elsevier
[5]
서적
Inorganic Chemistry
Prentice Hall
[6]
서적
The Proton in Chemistry
https://archive.org/[...]
Chapman & Hall
[7]
서적
Inorganic Chemistry
Oxford University Press
[8]
서적
(Housecroft3rd)
[9]
학술지
Spectral Signatures of Hydrated Proton Vibrations in Water Clusters
[10]
학술지
Proton hydration in aqueous solution: Fourier transform infrared studies of HDO spectra
[11]
서적
Modern Inorganic Chemistry
https://archive.org/[...]
McGraw-Hill
[12]
서적
Metal Ions in Solution
Ellis Horwood
[13]
서적
General Chemistry
https://archive.org/[...]
Prentice Hall
[14]
서적
The Determination of Stability Constants
McGraw–Hill
[15]
웹사이트
Project: Ionic Strength Corrections for Stability Constants
https://iupac.org/pr[...]
International Union of Pure and Applied Chemistry
2019-03-28
[16]
서적
The determination of stability constants : and other equilibrium constants in solution
https://books.google[...]
McGraw-Hill
[17]
서적
Physical Chemistry
Oxford University Press
[18]
서적
General chemistry: principles and modern applications
https://archive.org/[...]
Prentice Hall
2002
[19]
서적
Inorganic Chemistry
Oxford University Press
[20]
서적
Inorganic Chemistry
Addison-Wesley
[21]
서적
Inorganic Chemistry
Oxford University Press
[22]
학술지
Dissociation constant of nitric acid
[23]
학술지
Acidity of Strong Acids in Water and Dimethyl Sulfoxide
[24]
웹사이트
Henderson–Hasselbalch Equation: Derivation of pKa and pKb
http://pharmaxchange[...]
2012-10-22
[25]
학술지
Chemical speciation of environmentally significant heavy metals with inorganic ligands. Part 1: The Hg2+ – Cl−, OH−, CO32-, SO42-, and PO43- aqueous systems
2005
[26]
서적
Chemistry: The Central Science
Prentice-Hall
[27]
서적
Chemistry of the Elements
Butterworth-Heinemann
[28]
서적
Inorganic Chemistry
Prentice Hall
[29]
서적
Inorganic Chemistry
Harper & Row
[30]
서적
CRC Handbook of Chemistry and Physics, Student Edition
CRC Press
[31]
서적
Fundamentals of Analytical Chemistry
Brooks/Cole
2014
[32]
서적
(Housecroft2nd)
[33]
서적
The Physical Chemistry of Electrolytic Solutions
https://archive.org/[...]
Reinhold Publishing Corp.
[34]
서적
Organic Chemistry
Oxford University Press
[35]
서적
Advanced Organic Chemistry
John Wiley & Sons
[36]
논문
Pentakis(trifluoromethyl)phenyl, a Sterically Crowded and Electron-withdrawing Group: Synthesis and Acidity of Pentakis(trifluoromethyl)benzene, -toluene, -phenol, and -aniline
[37]
논문
A Comprehensive Self-Consistent Spectrophotometric Acidity Scale of Neutral Brønsted Acids in Acetonitrile
[38]
논문
Extension of the Self-Consistent Spectrophotometric Basicity Scale in Acetonitrile to a Full Span of 28 pKa Units: Unification of Different Basicity Scales
[39]
웹사이트
Bordwell pKa Table (Acidity in DMSO)
http://www.chem.wisc[...]
2008-11-02
[40]
서적
Housecroft3rd
[41]
서적
Acidity Functions
Academic Press
[42]
서적
Superacids
Wiley Interscience
[43]
논문
Proton Acceptor Power and Homoconjugation of Mono- and Diamines
[44]
서적
Organic chemistry
McGraw–Hill
[45]
논문
Physicochemical Properties of a New Multicomponent Cosolvent System for the pKa Determination of Poorly Soluble Pharmaceutical Compounds
[46]
서적
Inorganic chemistry
Pearson Prentice Hall
2005
[47]
서적
Concepts and Models of Inorganic Chemistry
Wiley
[48]
서적
The nature of the chemical bond and the structure of molecules and crystals; an introduction to modern structural chemistry
https://archive.org/[...]
Cornell University Press
[49]
서적
Organic Chemistry
McGraw–Hill
[50]
논문
The Effect of Structure upon the Reactions of Organic Compounds. Benzene Derivatives
[51]
논문
A Survey of Hammett Substituent Constants and Resonance and Field Parameters
[52]
논문
Compilation and critical evaluation of structure-reactivity parameters and equations: Part 2. Extension of the Hammett σ scale through data for the ionization of substituted benzoic acids in aqueous solvents at 25 °C (Technical Report)
[53]
서적
Organic chemistry
McGraw–Hill
[54]
논문
The Remarkable Basicity of 1,8-bis(dimethylamino)naphthalene
[55]
논문
Strain Effects on Amine Basicities
[56]
논문
Thermodynamic Quantities for the Ionization Reactions of Buffers
https://www.nist.gov[...]
[57]
서적
Atkins' physical chemistry.
https://archive.org/[...]
W H Freeman
2006
[58]
서적
Determination and Use of Stability Constants
Wiley
[59]
서적
Computational Methods for the Determination of Formation Constants
Plenum
[60]
논문
Multiwavelength Spectrophotometric Determination of Acid Dissociation Constants of Ionizable Drugs
[61]
논문
The Chemistry of Multi-Protic Drugs Part 1: A Potentiometric, Multi-Wavelength UV and NMR pH Titrimetric Study of the Micro-Speciation of SKI-606
[62]
논문
Guidelines for NMR easurements for Determination of High and Low pKa Values
http://media.iupac.o[...]
[63]
논문
Accurate Determination of Low p''K'' Values by 1H NMR Titration
[64]
논문
Methods in Enzymology
Elsevier
2016
[65]
백과사전
Reference Module in Chemistry, Molecular Sciences and Chemical Engineering
Elsevier
[66]
논문
The spectrum of a dissociation intermediate of cysteine: a biophysical chemistry experiment
1988-02-01
[67]
논문
Determination of Protonation Constants of Some Fluorinated Polyamines by Means of 13C NMR Data Processed by the New Computer Program HypNMR2000. Protonation Sequence in Polyamines.
[68]
논문
A Novel View of pH Titration in Biomolecules
[69]
논문
Hydrogen Ion Buffers for Biological Research
[70]
서적
Gel Electrophoresis: Proteins
https://archive.org/[...]
Bios Scientific Publishers
[71]
서적
Gel Electrophoresis: Nucleic Acids
Bios Scientific Publishers
[72]
서적
Acid–Base and Potassium Homeostasis
https://archive.org/[...]
Churchill Livingstone
[73]
서적
Fundamentals of Acids, Bases, Buffers & Their Application to Biochemical Systems
Kendall/Hunt Pub. Co.
[74]
서적
Buffer Solutions: The Basics
https://archive.org/[...]
Oxford University Press
[75]
서적
Buffers for pH and Metal Ion Control
Chapman & Hall
[76]
서적
Handbook of Isoelectric Focusing and Proteomics
Elsevier
[77]
서적
Reactions of Acids and Bases in Analytical Chemistry
Horwood
[78]
학술지
Acid Extraction by Acid–Base-Coupled Extractants
[79]
서적
Absorption and Drug Development: Solubility, Permeability, and Charge State
Wiley
[80]
서적
Chemistry of Complex Equilibria
Horwood
[81]
서적
Risk Assessment of Chemicals: An Introduction
Springer
[82]
서적
Fundamentals of Analytical Chemistry
Thomson Brooks/Cole
[83]
서적
Water Chemistry
https://archive.org/[...]
Wiley
[84]
서적
Aquatic Chemistry: Chemical Equilibria and Rates in Natural Waters
Wiley
[85]
서적
Chemical Oceanography
Taylor and Francis
[86]
학술지
The Solubility of Iron in Seawater
[87]
서적
Lange's Handbook of Chemistry
https://archive.org/[...]
McGraw–Hill
[88]
서적
化学便覧
日本化学会
[89]
문서
수소 이온은 용액에 그대로 존재하지 않는다.
[90]
서적
General Chemistry
https://archive.org/[...]
Saunders College Publishing
1992
[91]
문서
K값보다 pK값을 인용하는 것이 일반적이다.
[92]
문서
활동도 계수의 지수
[93]
서적
General Chemistry
https://archive.org/[...]
Prentice Hall
2002
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com
