맨위로가기

근계

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

근계는 유한 차원 실수 내적 공간의 부분 집합으로, 특정 조건들을 만족하는 경우를 말한다. 근계는 근이 공간을 생성하고, 근의 스칼라 배수는 특정 값만을 가지며, 반사에 닫혀 있고, 정수성 조건을 만족해야 한다. 이러한 조건들을 통해 근계는 다양한 성질을 가지며, 특히 두 근 사이의 각도는 제한된다.

근계는 딘킨 다이어그램을 통해 분류되며, 기약 근계는 고전 근계(An, Bn, Cn, Dn)와 예외 근계(G₂, F₄, E₆, E₇, E₈)로 나뉜다. 근계는 양근과 단순근, 근 격자, 무게 격자 등의 구성 요소를 가지며, 바일 군과 카르탕 행렬과 같은 개념과도 관련된다.

근계는 반단순 리 대수의 표현론에서 유래되었으며, 리 대수의 구조를 분석하고 표현을 분류하는 데 중요한 도구로 사용된다. 근계의 개념은 19세기 후반 빌헬름 킬링에 의해 처음 도입되었으며, 엘리 카르탕과 예브게니 딘킨에 의해 발전되었다.

더 읽어볼만한 페이지

  • 유클리드 기하학 - 결정계
    결정계는 결정 구조의 대칭성에 따라 7가지(삼사, 단사, 사방, 정방, 삼방, 육방, 입방)로 분류되며, 각 결정계는 고유한 대칭 요소와 점군의 대칭성을 갖는다.
  • 유클리드 기하학 - 퐁슬레-슈타이너 정리
    퐁슬레-슈타이너 정리는 자와 주어진 원(중심 포함)만 사용하여 자와 컴퍼스로 작도 가능한 모든 것을 작도할 수 있다는 기하학적 정리이다.
  • 리 대수 - 베유 대수
    베유 대수는 체 K 위의 리 대수 g에 대하여 정의되는 미분 등급 대수이며, g의 쌍대 공간과 그 등급 이동으로 생성되는 외대수와 대칭 대수의 텐서곱으로 표현되고, 리 군의 분류 공간의 주다발의 무한소 형태를 나타내는 완전열과 관련이 있다.
  • 리 대수 - 아핀 리 대수
    아핀 리 대수는 카츠-무디 대수의 특수한 경우로, 유한 차원 단순 리 대수에 대응하는 루프 대수의 중심 확장으로 구성되며, 딘킨 도표를 통해 분류되고, 끈 이론과 2차원 등각장론 등 다양한 분야에 응용된다.
  • 리 군 - 리 대수
    리 대수는 가환환 위의 가군과 리 괄호 연산으로 구성되며 쌍선형성, 교대성, 야코비 항등식을 만족하고, 리 군 연구와 분류, 표현 이론에 중요한 역할을 한다.
  • 리 군 - 보렐-베유-보트 정리
    보렐-베유-보트 정리는 복소수 반단순 리 군의 표현론에서 층 코호몰로지를 사용하여 리 군의 기약 표현을 설명하며, 보렐-베유 정리와 보트의 일반화를 포함한다.
근계
개요
분야수학, 리 이론
정의유클리드 공간에서 특정 조건을 만족하는 벡터들의 집합
관련 개념리 대수, 바일 군
역사
기원리 대수의 분류에서 비롯
발전리 이론 및 관련 분야에서 중요한 도구로 발전
성질
기저루트계는 유클리드 공간의 기저를 이룬다.
정수 계수루트들의 선형 결합은 정수 계수를 가진다.
반사 대칭루트에 대한 반사는 다른 루트를 보존한다.
분류
단순근루트계를 생성하는 기본적인 루트들의 집합
딘킨 다이어그램루트계의 구조를 시각적으로 표현하는 그래프
기약 루트계더 작은 루트계로 분해될 수 없는 루트계
유형Aₙ, n ≥ 1
Bₙ, n ≥ 2
Cₙ, n ≥ 3
Dₙ, n ≥ 4
E₆, E₇, E₈
F₄
G₂
응용
리 대수리 대수의 분류 및 표현론
리 군리 군의 구조 및 표현론
대칭 공간대칭 공간의 연구
특이점 이론특이점 이론에서의 응용

2. 정의

'''근계'''(root system)는 유한 차원 실수 내적 공간에서 정의되는 특별한 벡터들의 집합이다. 이 집합은 다음 성질들을 만족해야 한다.

# 근들은 공간 전체를 생성한다. 즉, 공간 내의 모든 벡터는 근들의 선형 결합으로 표현될 수 있다.

# 어떤 근의 스칼라 배가 다시 근이 되는 경우는 그 근 자신과 그 근에 -1을 곱한 경우뿐이다.

# 임의의 근에 대해 수직인 초평면에 대한 반사를 생각했을 때, 다른 근을 반사시켜도 여전히 근계에 속하는 근이 된다.

# 임의의 두 근에 대해, 한 근을 다른 근 방향으로 사영했을 때, 그 결과는 원래 근의 정수배 또는 반정수배가 된다.

이 조건들을 수식으로 표현하면 다음과 같다.


  • 모든 두 근 \alpha, \beta \in \Phi에 대해, \Phi는 \sigma_\alpha(\beta) := \beta - 2 \frac{(\alpha, \beta)}{(\alpha, \alpha)}\alpha를 포함한다.
  • 모든 두 근 \alpha, \beta \in \Phi에 대해, \langle \beta, \alpha \rangle := 2\frac{(\alpha, \beta)}{(\alpha, \alpha)}는 정수이다.


여기서 (\cdot, \cdot)은 내적을, \langle \cdot, \cdot \rangle은 특별한 연산을 나타낸다.

정수성 조건을 제외하고 정의하는 경우도 있는데, 이때 정수성 조건까지 만족하는 근계를 '결정 근계'라고 부른다.[5]

A2 근계


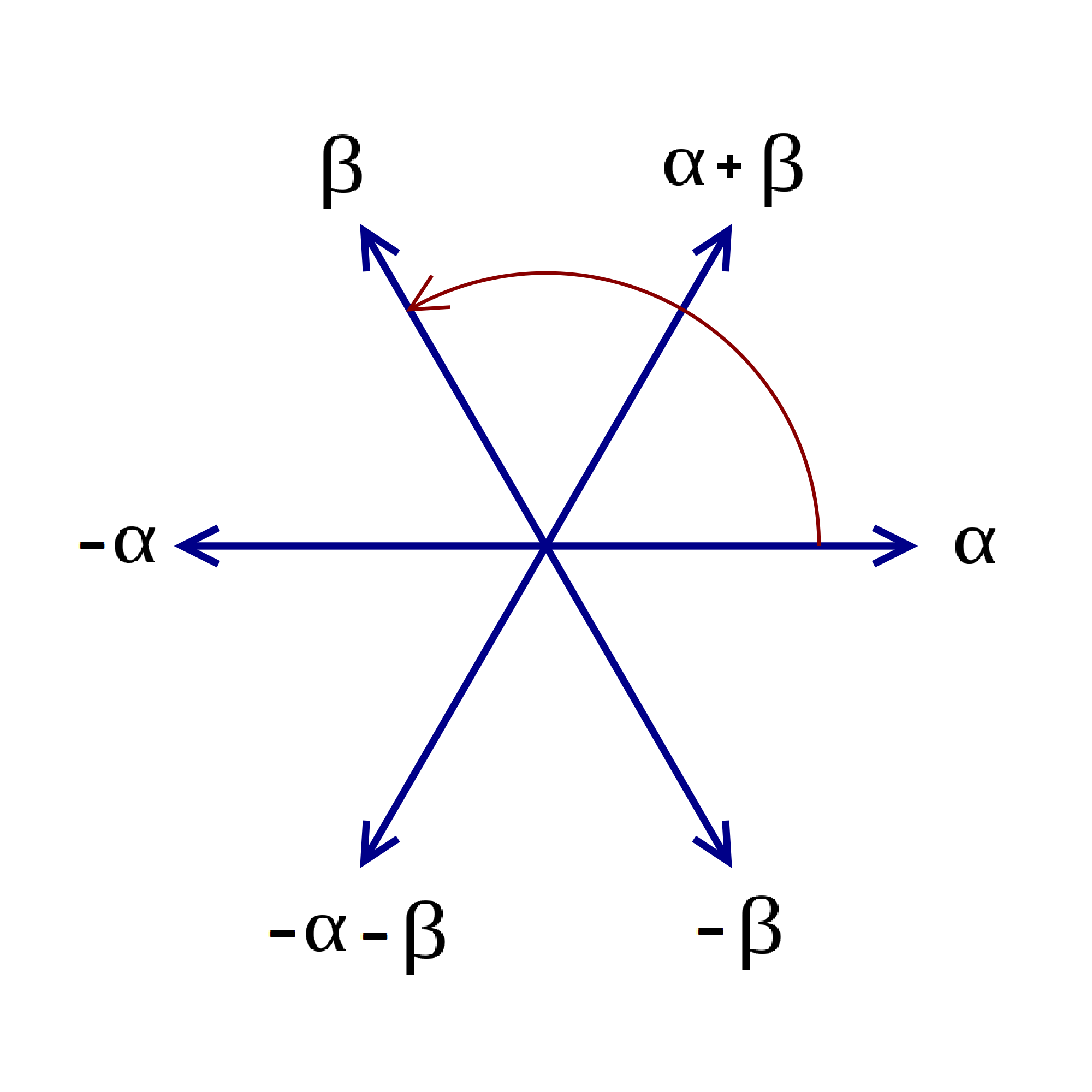
예를 들어, 오른쪽 그림과 같이 2차원 유클리드 공간에 있는 여섯 개의 벡터를 보자. 이 벡터들은 전체 공간을 생성하며, 한 벡터에 수직인 선에 대해 반사 변환을 하면 다른 벡터가 다시 원래 벡터 집합에 속하게 된다. 또한, 반사된 벡터는 원래 벡터와 다른 벡터의 정수배만큼 차이가 난다. 이 조건을 모두 만족하므로, 이 벡터들은 근계를 이룬다. 이 근계는 A2라고 불린다.

2. 1. 동형

두 실수 내적 공간 V, V' 및 그 속의 근계 \Phi\subseteq V, \Phi'\subseteq V'에 대하여, f(\Phi)=\Phi'가 되는 전단사 실수 선형 변환 f\colon V\to V'이 존재하며, 또한

:\frac{(f(\alpha),f(\beta))_{V'}}{(f(\alpha),f(\alpha))_{V'}}=\frac{(\alpha,\beta)_V}{(\alpha,\alpha)_V}\qquad\forall\alpha,\beta\in \Phi

라면, (V,\Phi)와 (V',\Phi')를 서로 '''동형'''이라고 한다.

특히, 동형이 등거리 변환일 필요는 없다. 예를 들어, 항등 함수 (V,(-,-))\to(V,2(-,-)) 역시 허용된다. 이 때문에, 통상적으로, 근계에서 가장 긴 근의 노름을 \sqrt2로 놓는다. (이에 따라, 더 짧은 근의 노름은 1 또는 \sqrt{2/3}이다.)

두 근계 (''E''1, Φ1)와 (''E''2, Φ2)는 각 근 쌍에 대해 숫자 \langle x, y \rangle가 보존되도록 Φ1을 Φ2로 보내는 가역 선형 변환 ''E''1 → ''E''2가 있는 경우 '''동형'''이라고 한다.[7]

2. 2. 표기

근계는 유한 차원 실수 내적 공간 (V,(\cdot,\cdot))에서 다음 다섯 조건을 모두 만족시키는 부분 집합 \Phi\subseteq V이다.

# V의 모든 원소는 \Phi의 원소들의 선형 결합으로 나타낼 수 있다.

# \alpha\in\Phi이면, -\alpha\in\Phi이고, 그 밖의 다른 스칼라배 t\Phi (t\in\mathbb R)는 \Phi의 원소가 아니다.

# 임의의 \alpha,\beta\in\Phi에 대하여, \alpha에 대하여 수직인 초평면에 대한 \beta의 반사\beta-2\alpha(\alpha,\beta)/(\alpha,\alpha)도 \Phi의 원소다.

# 0\not\in\Phi이며, \forall \alpha,\beta\in\Phi\colon 2(\alpha,\beta)/(\alpha,\alpha)\in\mathbb Z

# 유한 집합이다.

근계의 원소는 '''근'''이라고 부른다. 근계의 '''계수'''(階數, rank영어)는 V의 차원이다.

두 실수 내적 공간 V, V' 및 그 속의 근계 \Phi\subseteq V, \Phi'\subseteq V'에 대하여, 만약 f(\Phi)=\Phi'가 되는 전단사 실수 선형 변환 f\colon V\to V'이 존재하며,

:\frac{(f(\alpha),f(\beta))_{V'}}{(f(\alpha),f(\alpha))_{V'}}=\frac{(\alpha,\beta)_V}{(\alpha,\alpha)_V}\qquad\forall\alpha,\beta\in \Phi

라면, (V,\Phi)와 (V',\Phi')를 서로 '''동형'''이라고 한다.

통상적으로, 다음과 같은 표기를 사용한다.

:\langle\alpha,\beta\rangle=\frac{2(\alpha,\beta)}{(\alpha,\alpha)}

'''근계''' \Phi는 다음 조건을 만족하는 0이 아닌 유한 개의 벡터('''근'''이라고 함) 집합이다.[2][3]

# 근은 ''E''를 생성한다.

# \Phi에 속하는 근 \alpha의 스칼라 배수는 \alpha와 -\alpha뿐이다.

# 모든 근 \alpha\in\Phi에 대해, 집합 \Phi는 \alpha에 수직인 초평면에 대한 반사에 닫혀 있다.

# ('''정수성''') 만약 \alpha와 \beta가 \Phi의 근이라면, \alpha를 지나는 선에 대한 \beta의 투영은 \alpha의 ''정수 또는 반정수'' 배이다.

조건 3과 4를 각각 다르게 표현하면 다음과 같다.

# 모든 두 근 \alpha,\beta \in \Phi 에 대해, 집합 \Phi는 원소 \sigma_\alpha(\beta):=\beta-2\frac{(\alpha,\beta)}{(\alpha,\alpha)}\alpha를 포함한다.

# 모든 두 근 \alpha,\beta\in\Phi에 대해, 숫자 \langle \beta, \alpha \rangle := 2 \frac{(\alpha,\beta)}{(\alpha,\alpha)}는 정수이다.

어떤 저자들은 근계의 정의에 조건 1~3만 포함시키기도 한다.[4] 이러한 맥락에서, 정수성 조건도 만족하는 근계를 '''결정 근계'''라고 한다.[5]

3. 성질

근계는 다음과 같은 성질을 갖는다.


  • 두 근 사이의 각은 특정 값으로 제한된다. 두 근 $\alpha$, $\beta$ 사이의 각을 $\theta$라고 하면, $2\cos(\theta)$는 -2에서 2 사이의 정수이다.
  • $\cos\theta=0, \pm \tfrac12, \pm\tfrac{\sqrt2}2, \pm\tfrac{\sqrt3}2, \pm1$이다. 즉, $\theta$는 90°, 60° 또는 120°, 45° 또는 135°, 30° 또는 150°, 0° 또는 180°이다.
  • 0° 또는 180°는 근이 될 수 있는 조건에 의해 제외된다.
  • 각 근 쌍에 대한 가능한 경우는 다음과 같다.[13]
  • 90도: 길이 비율은 제한 없음.
  • 60도 또는 120도: 길이 비율은 1.
  • 45도 또는 135도: 길이 비율은 $\sqrt 2$.
  • 30도 또는 150도: 길이 비율은 $\sqrt 3$.


정수성 공리에 따라, 두 근 사이의 각은 $\pi/2$, $\pi/3$, $\pi/4$, $\pi/6$ 또는 이들의 여각이다.


정수성 공리에 따라, 두 근 사이 각의 코사인은 정수의 제곱근의 반이어야 한다.

::\mathbb Z\ni 2 \frac{(\alpha,\beta)}{(\alpha,\alpha)} \cdot 2 \frac{(\alpha,\beta)}{(\beta,\beta)} = 4 \frac{(\alpha,\beta)^2}{\vert \alpha \vert^2 \vert \beta \vert^2} = 4 \cos^2(\theta) = (2\cos(\theta))^2.

$E$를 표준 유클리드 벡터 공간으로 하고, $(\cdot,\cdot)$로 나타내는 내적을 갖는 유한 차원 유클리드 벡터 공간이라고 할 때, 근계 $\Phi$는 다음 조건을 만족하는 0이 아닌 유한 개의 벡터(근) 집합이다.[2][3]

1. 근은 $E$를 생성한다.

2. $\Phi$에 속하는 근 $\alpha$의 스칼라 배수는 $\alpha$와 $-\alpha$뿐이다.

3. 모든 근 $\alpha\in\Phi$에 대해, 집합 $\Phi$는 $\alpha$에 수직인 초평면에 대한 반사에 닫혀 있다.

4. ('''정수성''') 만약 $\alpha$와 $\beta$가 $\Phi$의 근이라면, $\alpha$를 지나는 선에 대한 $\beta$의 투영은 $\alpha$의 ''정수 또는 반정수'' 배이다.

조건 3과 4는 다음과 같이 표현할 수 있다.

1. 모든 두 근 $\alpha,\beta \in \Phi $에 대해, 집합 $\Phi$는 원소 $\sigma_\alpha(\beta):=\beta-2\frac{(\alpha,\beta)}{(\alpha,\alpha)}\alpha$를 포함한다.

2. 모든 두 근 $\alpha,\beta\in\Phi$에 대해, 숫자 $ \langle \beta, \alpha \rangle := 2 \frac{(\alpha,\beta)}{(\alpha,\alpha)}$는 정수이다.

어떤 저자들은 근계의 정의에 조건 1~3만 포함시키기도 한다.[4] 이러한 맥락에서, 정수성 조건도 만족하는 근계를 '''결정 근계'''라고 한다.[5] 다른 저자들은 조건 2를 생략하기도 하는데, 이 경우 조건 2를 만족하는 근계를 '''축소된''' 근계라고 한다.[6]

3. 1. 연산

근계 $(V,\Phi)$와 임의의 실수 $t\in\mathbb R\setminus\{0\}$, 그리고 임의의 직교 행렬 $M\in\operatorname O(V;\mathbb R)$에 대하여, $(V,tM\Phi)$ 역시 근계를 이루며, 이는 원래 근계 $(V,\Phi)$와 동형이다.

두 근계 $(V,\Phi)$, $(V',\Phi')$가 주어졌을 때, 그 '''직합''' $\Phi\oplus\Phi'$은 다음과 같다.

:$\Phi\oplus\Phi'=\iota(\Phi)\cup\iota'(\Phi')$

:$V\xrightarrow\iota V\oplus V'\xleftarrow{\iota'}V'$

여기서 $\iota$와 $\iota'$은 직합의 정의에 등장하는 표준 포함 사상이다.

'''기약 근계'''(旣約根系, irreducible root system영어)는 두 (자명하지 않은) 근계의 합이 아닌, 자명하지 않은 근계다. 모든 근계는 기약 근계의 합으로 유일하게 나타낼 수 있다.

기약 근계의 근은 모두 길이가 같거나, 두 가지 길이가 있다. 길이가 두 가지인 경우 긴 것은 '''긴 근'''(long root영어), 짧은 것은 '''짧은 근'''(short root영어)으로 분류한다. 만약 길이가 모두 같다면, 모든 근이 긴 근이다. 이 경우, 긴 근과 짧은 근의 노름의 비는 $\sqrt2$이다. 통상적으로 긴 근의 노름은 $\sqrt2$로, 짧은 근의 노름은 (만약 존재한다면) $1$로 잡는다.[2][3]

근계 $(V,\Phi)$의 '''쌍대 근계'''(雙對根系, dual root system영어)는 다음과 같다.

  • $V^\vee$는 $V$의 (대수적) 쌍대 공간이다. 물론, 내적을 사용하여 표준적인 동형 사상 $V\to V^\vee$이 존재한다.
  • $\Phi^\vee=\{\alpha^\vee\colon\alpha\in\Phi\}$
  • 임의의 $u,v\in V$에 대하여, $u^\vee\in V^*$, $u^\vee(v)=\langle u,v\rangle=2(u,v)/(u,u)$

그렇다면 $(V^\vee,\Phi^\vee)$ 역시 근계를 이룬다.

임의의 근계 $(V,\Phi)$는 그 이중 쌍대 근계 $(V^{\vee\vee},\Phi^{\vee\vee})$와 표준적으로 동형이다.

단순 근계 가운데, $B_n$의 쌍대 근계는 $C_n$이다. 다른 단순 근계들($A_n$, $D_n$, $E_6,E_7,E_8,F_4,G_2$)은 스스로의 쌍대 근계이다.

''E''를 표준 유클리드 벡터 공간으로 하고, $(\cdot,\cdot)$로 나타내는 내적을 갖는 유한 차원 유클리드 벡터 공간이라고 하자. '''근계''' $\Phi$는 다음 조건을 만족하는 0이 아닌 유한 개의 벡터('''근'''이라고 함) 집합이다.

# 모든 두 근 $\alpha,\beta \in \Phi $에 대해, 집합 $\Phi$는 원소 $\sigma_\alpha(\beta):=\beta-2\frac{(\alpha,\beta)}{(\alpha,\alpha)}\alpha$를 포함한다.

# 모든 두 근 $\alpha,\beta\in\Phi$에 대해, 숫자 $ \langle \beta, \alpha \rangle := 2 \frac{(\alpha,\beta)}{(\alpha,\alpha)}$는 정수이다.

어떤 저자들은 근계의 정의에 조건 1~3만 포함시키기도 한다.[4] 이러한 맥락에서, 정수성 조건도 만족하는 근계를 '''결정 근계'''라고 한다.[5] 다른 저자들은 조건 2를 생략하기도 하는데, 이 경우 조건 2를 만족하는 근계를 '''축소된''' 근계라고 한다.[6]

두 근계 ($E$1, Φ1)와 ($E$2, Φ2)는 각 근 쌍에 대해 숫자 $ \langle x, y \rangle$가 보존되도록 Φ1을 Φ2로 보내는 가역 선형 변환 $E$1 → $E$2가 있는 경우 '''동형'''이라고 한다.[7]

두 루트 사이 각도의 코사인은 정수 제곱근의 반정수 배로 제한된다. 왜냐하면, $ \langle \beta, \alpha \rangle$와$ \langle \alpha, \beta \rangle$는 모두 가정에 의해 정수이고,

:$\begin{align}

\langle \beta, \alpha \rangle \langle \alpha, \beta \rangle

&= 2 \frac{(\alpha,\beta)}{(\alpha,\alpha)} \cdot 2 \frac{(\alpha,\beta)}{(\beta,\beta)}

= 4 \frac{(\alpha,\beta)^2}{\vert \alpha \vert^2 \vert \beta \vert^2} \\

&= 4 \cos^2(\theta) = (2\cos(\theta))^2 \in \mathbb{Z}

\end{align}$

이기 때문이다.

루트 $\Phi$가 $V$의 루트계일 때, 루트 $\alpha$의 '''코루트''' $\alpha^\vee$는

:$\alpha^\vee= {2\over (\alpha,\alpha)}\, \alpha$

로 정의된다. 코루트의 집합도 $V$의 루트계 $\Phi^\vee$를 이루며, '''쌍대 루트계''' (또는 때로는 *역 루트계*)라고 불린다.

4. 분류

기약 근계는 고전 근계와 예외 근계로 분류된다. 고전 근계는 고전군(직교군, 특수 유니터리 군, 심플렉틱 군)의 리 대수(의 복소화)의 근계인 반면, 예외 근계는 그렇지 않다.


  • 고전 근계: $A_n$, $B_n$, $C_n$, $D_n$의 네 가지 족으로 나뉜다.
  • 예외 근계: $G_2, F_4, E_6, E_7, E_8$의 다섯 가지가 있다.


근계는 두 개의 진부분 집합 \Phi=\Phi_1\cup\Phi_2의 합집합으로 분할될 수 없을 때 기약적이다. 여기서 모든 \alpha\in\Phi_1 및 \beta\in\Phi_2에 대해 (\alpha,\beta)=0이다. 기약 근계는 예브게니 딩킨의 이름을 딴 '''딘킨 도표'''라는 그래프와 대응한다.[36]

주어진 근계는 하나 이상의 가능한 단순근 집합을 가지지만, 바일 군은 그러한 선택에 대해 추이적으로 작용한다.[19] 결과적으로, 딘킨 도표는 단순근의 선택에 의존하지 않으며, 근계 자체에 의해 결정된다. 반대로, 동일한 딘킨 도표를 가진 두 개의 근계가 주어지면, 기저에 있는 근을 시작으로 근을 일치시켜 시스템이 실제로 동일함을 보일 수 있다.[20] 따라서 근계를 분류하는 문제는 가능한 딘킨 도표를 분류하는 문제로 축소되며, 근계는 딘킨 도표가 연결되어 있을 때에만 기약적이다.[21]

4. 1. 기약 근계의 목록

기약 근계는 고전 근계와 예외 근계로 분류된다. 고전 근계는 $A_n$, $B_n$, $C_n$, $D_n$의 네 가지 족으로 나뉘며, 예외 근계는 $G_2, F_4, E_6, E_7, E_8$의 다섯 가지가 있다. 아래첨자는 근계의 계수를 나타낸다. 고전 근계는 고전군(직교군, 특수 유니터리 군, 심플렉틱 군)의 리 대수(의 복소화)의 근계이나, 예외 근계는 그렇지 않다. 다음 표에서는 긴 근의 길이를 $\sqrt2$로 정규화하였다.[36]

근계근의 수짧은 근 수긴 근 부분격자의 지표카르탕 행렬식바일 군의 크기콕서터 수 $h$이중 콕서터 수 $h^\vee$딘킨 도표콕서터 라벨[37]이중 콕서터 라벨[37]
$A_n$ ($n \ge 1$)$n(n+1)$$n+1$$(n+1)!$$n+1$\bullet-\bullet-\cdots-\bullet$1-1-\cdots-1$
$B_n$ ($n \ge 2$)$2n^2$$2n$22$2^n n!$$2n$$2n-1$\bullet-\bullet-\cdots-\bullet\Rightarrow\bullet$1-2-\cdots-2\Rightarrow2$$1-2-\cdots-2\Rightarrow1$
$C_n$ ($n \ge 3$)$2n^2$$2n(n-1)$22$2^n n!$$2n$$n+1$\bullet-\bullet-\cdots-\bullet\Leftarrow\bullet$2-2-\cdots-2\Leftarrow1$$1-1-\cdots-1\Leftarrow1$
$D_n$ ($n \ge 4$)$2n(n-1)$4$2^{n-1} n!$$2n-2$\bullet-\bullet-\cdots-\bullet<{\bullet\atop\bullet}$1-2-\cdots-2<{1\atop1}
E6723$2^7 \times 3^4 \times 5$12{\bullet-\bullet\atop\bullet-\bullet}>\bullet-\bullet$1-2 \atop 1-2 >3-2$
E71262$2^{10} \times 3^4 \times 5 \times 7$18{\bullet\atop{}}{-\atop{}}{\bullet\atop\bullet}>\bullet-\bullet-\bullet-\bullet$2 \atop {} - \atop {} 3 \atop 2 >4-3-2-1$
E82401$2^{14} \times 3^5 \times 5^2 \times 7$30{\bullet\atop{}}{-\atop{}}{\bullet\atop\bullet}>\bullet-\bullet-\bullet-\bullet-\bullet$2 \atop {} - \atop {} 4 \atop 3 >6-5-4-3-2$
F4482441$2^7 \times 3^2$129\bullet-\bullet\Rightarrow\bullet-\bullet$2-3\Rightarrow4-2$$2-3\Rightarrow2-1$
G212631$2^2 \times 3$64\bullet\Rrightarrow\bullet$2\Rrightarrow3$$2\Rrightarrow1$



$A_n$형 근계의 단순근은 다음과 같다. (편의상 $\mathbb R^{n+1}$의 원소로 표기하였다.)


  • $\alpha^1=(1,-1,0,\dots,0,0)$
  • $\alpha^2=(0,1,-1,\dots,0,0)$
  • $\vdots$
  • $\alpha^n=(0,0,\dots,1,-1)$


$B_n$형 근계의 단순근은 다음과 같다.

  • $\alpha^1=(1,-1,0,\dots,0,0)$
  • $\alpha^2=(0,1,-1,\dots,0,0)$
  • $\vdots$
  • $\alpha^{n-1}=(0,0,\dots,1,-1)$
  • $\alpha^n=(0,0,\dots,0,1)$


$C_n$형 근계의 단순근은 다음과 같다.

  • $\alpha^1=(1,-1,0,\dots,0,0)$
  • $\alpha^2=(0,1,-1,\dots,0,0)$
  • $\vdots$
  • $\alpha^{n-1}=(0,0,\dots,1,-1)$
  • $\alpha^n=(0,0,\dots,0,2)$


$D_n$형 근계의 단순근은 다음과 같다.

  • $\alpha^1=(1,-1,0,\dots,0,0)$
  • $\alpha^2=(0,1,-1,\dots,0,0)$
  • $\vdots$
  • $\alpha^{n-1}=(0,0,\dots,1,-1)$
  • $\alpha^n=(0,0,\dots,1,1)$


예외적 기약 근계는 E₆, E₇, E₈, F₄, G₂의 총 5개가 있다. 이들의 단순근들은 다음과 같다.

E8
1-1000000
01-100000
001-10000
0001-1000
00001-100
000001-10
00000110
-½-½-½-½-½-½-½-½



F4
1-100
01-10
0010
-½-½-½-½



G2
$\sqrt{2/3}$0
$-\sqrt{3/2}$$1/\sqrt2$


4. 2. 딘킨 도표

기약근계의 딘킨 도표


각 근계 (V,\Phi)에 대하여, '''딘킨 도표'''(Дынкин圖表, Dynkin diagram영어)는 일종의 유향 그래프이다. 딘킨 도표는 다음과 같이 구성된다.

  • 각 단순근에 대응하는 꼭짓점을 갖는다.
  • 두 꼭짓점 사이에는 0개, 1개, 2개, 또는 3개의 변이 존재할 수 있다.
  • 변이 2개 또는 3개인 경우, 변은 방향을 가지며, 더 짧은 단순근을 가리킨다.
  • 두 꼭짓점 사이의 변의 수는 두 단순근 사이의 각도에 대응된다.


근 사이 각 (라디안)근 사이 각 (°)변의 종류
\pi/290°변 없음
2\pi/3120°하나의 변
3\pi/4135°두 개의 변 + 화살표
5\pi/6150°세 개의 변 + 화살표



딘킨 도표는 단순근의 선택에 관계없이 동일하다.[19]

기약 근계의 딘킨 도표는 연결 그래프이다. 딘킨 도표의 연결 성분 분해는 근계의 기약 근계들로의 직합 분해와 같다.[21]

4. 3. 카르탕 행렬

근계 \Phi와 그 위에 순서가 매겨진 단순근의 열 \alpha_1,\dots,\alpha_r이 주어졌다고 하자. 그렇다면, 이에 대응하는 '''카르탕 행렬'''(Cartan matrix영어) M은 다음과 같은 r\times r 정사각 행렬이다.

:M=(M_{ij})_{i,j=1,\dots,r}

:M_{ij}=2\frac{(\alpha_i,\alpha_j)}{(\alpha_i,\alpha_i)}

정의에 따라, 카르탕 행렬의 대각선 성분 값은 모두 2이다.

카르탕 행렬이 주어지면, 이에 대응하는 근계 (및 복소수 반단순 리 대수)를 재구성할 수 있다.

4. 4. 바일 군

A_2 근계의 바일 군은 정삼각형의 대칭군이다.


Φ의 근과 관련된 초평면에 대한 반사에 의해 생성된 ''E''의 등거리 변환 군을 Φ의 바일 군이라고 한다. 바일 군은 유한 집합 Φ에 충실한 작용을 하므로 항상 유한하다. 아래 그림에서 A_2에 대해 점선으로 표시된 근에 수직인 초평면이 반사 평면이다. 바일 군은 6개의 원소를 가진 정삼각형의 대칭군이다. 이 경우 바일 군은 근계의 전체 대칭군은 아니다 (예: 60도 회전은 근계의 대칭이지만 바일 군의 원소는 아니다).

만약 Φ가 ''E''에서의 근계라면, 근 α의 '''코근''' α∨는 다음과 같이 정의된다.

\alpha^\vee= {2\over (\alpha,\alpha)}\, \alpha.

코근들의 집합은 ''E''에서 근계 Φ∨를 이루며, 이를 '''쌍대 근계''' (또는 ''역 근계'')라고 부른다.[17] 정의에 따라 α∨ ∨ = α이므로, Φ는 Φ∨의 쌍대 근계이다. Φ∨에 의해 생성된 ''E''에서의 격자는 '''코근 격자'''라고 불린다. Φ와 Φ∨는 모두 같은 바일 군 ''W''을 가지며, ''W''의 ''s''에 대해 다음이 성립한다.

(s\alpha)^\vee= s(\alpha^\vee).

Δ가 Φ의 단순근 집합이라면, Δ∨는 Φ∨의 단순근 집합이다.[17]

아래에 설명된 분류에서, A_n과 D_n 형의 근계와 예외적인 근계 E_6,E_7,E_8,F_4,G_2는 모두 자기 쌍대적이다. 즉, 쌍대 근계가 원래의 근계와 동형이다. 반면에 B_n과 C_n 근계는 서로 쌍대적이지만, 동형은 아니다 (단, n=2인 경우는 예외).

색칠된 영역은 기저 \{\alpha_1,\alpha_2\}에 대한 기본 바일 방이다.


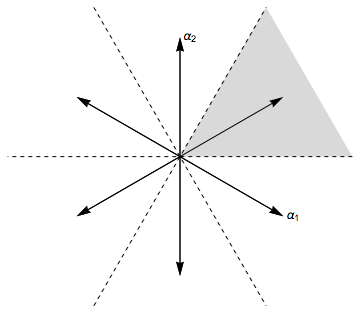
\Phi\subset E가 근계인 경우, 각 근 \alpha에 수직인 초평면을 고려할 수 있다. \sigma_\alpha가 초평면에 대한 반사를 나타내고, 바일 군은 모든 \sigma_\alpha에 의해 생성된 E의 변환 군임을 상기하자. 초평면 집합의 여집합은 분리되어 있으며, 각 연결 성분은 '''바일 방'''이라고 한다. 단순 근의 특정 집합 Δ를 고정했다면, Δ와 관련된 '''기본 바일 방'''을 모든 \alpha\in\Delta에 대해 (\alpha,v)>0인 점 v\in E의 집합으로 정의할 수 있다.

반사 \sigma_\alpha,\,\alpha\in\Phi는 \Phi를 보존하므로, 근에 수직인 초평면 집합도 보존한다. 따라서 각 바일 군 요소는 바일 방을 순열한다.

이 그림은 A_2 근계의 경우를 보여준다. 근에 직교하는 "초평면" (이 경우 1차원)은 점선으로 표시된다. 60도의 여섯 개 구역은 바일 방이며, 색칠된 영역은 표시된 기저와 관련된 기본 바일 방이다.

바일 방에 대한 기본적인 일반 정리는 다음과 같다.

:'''정리''': 바일 군은 바일 방에 자유롭고 추이적으로 작용한다. 따라서 바일 군의 차수는 바일 방의 수와 같다.

예를 들어 A_2의 경우, 바일 군은 여섯 개의 원소를 가지며 여섯 개의 바일 방이 있다.

관련된 결과는 다음과 같다.

:'''정리''': 바일 방 C를 고정한다. 그러면 모든 v\in E에 대해, v의 바일 궤도는 C의 폐포 \bar C에 정확히 하나의 점을 포함한다.

루트계가 기약이라는 것은, 두 개의 진부분집합의 합집합 \Phi = \Phi_1 \cup \Phi_2 로, 모든 \alpha \in \Phi_1 과 \beta \in \Phi_2 에 대해 (\alpha, \beta) = 0이 되는 것으로 분할될 수 없음을 말한다.

기약 루트계는 Eugene Dynkin|예브게니 딘킨영어의 이름을 딴 '''딘킨 도형'''이라는 그래프와 대응한다. 이러한 그래프의 분류는 단순한 조합론이며, 기약 루트계의 분류를 가져온다.

루트계가 주어졌을 때, 앞 절에서처럼 단순 루트의 집합 \Delta를 선택한다. 부속된 딘킨 도형의 꼭짓점은 \Delta의 벡터에 대응한다. 벡터의 직교하지 않는 각 쌍 사이에 변이 그려진다. 이루는 각이 2\pi/3 라디안일 때는 무방향의 단일 변이며, 3\pi/4일 때는 유향 이중 변이며, 5\pi/6일 때는 유향 삼중 변이다. "유향 변"이라는 용어는 이중·삼중 변은 짧은 쪽의 벡터를 가리키는 기호가 붙는다는 것을 의미한다.

주어진 루트계의 단순 루트의 집합의 가능성은 하나가 아니지만, 바일 군은 그러한 선택에 추이적으로 작용한다.[33] 따라서 딘킨 도형은 단순 루트들의 선택에 의존하지 않고, 루트계 자체에 의해 결정된다. 반대로, 같은 딘킨 도형을 가진 두 개의 루트계가 주어지면, 기저의 루트에서부터 맞추기 시작하여, 두 개가 사실은 같다는 것을 보일 수 있다.

따라서 루트계의 분류 문제는 가능한 딘킨 도형의 분류 문제로 귀결된다. 루트계가 기약인 것과 그 딘킨 도형이 연결되어 있는 것은 동치이다. 딘킨 도형은 기저 \Delta의 말로 E의 내적 정보를 가지고 있으며, 이 내적이 정부호여야 한다는 조건은 원하는 분류를 얻는 데 필요한 모든 것임이 판명된다.

실제 연결 도형은 다음과 같다. 하첨자는 도형의 꼭짓점의 개수(따라서 대응하는 기약 루트계의 계수)를 나타낸다.

ΦΦ|Φ<|IDW|
An (n ≥ 1)n(n + 1)n + 1(n + 1)!
Bn (n ≥ 2)2n22n222n n!
Cn (n ≥ 3)2n22n(n - 1)2n-122n n!
Dn (n ≥ 4)2n(n - 1)42n-1 n!
E6 (mathematics)|E6영어72351840
E7 (mathematics)|E7영어12622903040
E8 (mathematics)|E8영어2401696729600
F4 (mathematics)|F4영어4824411152
G2 (mathematics)|G2영어1263112



기약 루트계는 대응하는 연결된 딘킨 도형에 따라 명명된다. 4개의 무한족(A''n'', B''n'', C''n'', D''n''이며, '''고전적 루트계'''라고 불린다)과 5개의 예외적인 경우('''예외형 루트계''')가 존재한다.[34] 하첨자는 루트계의 계수를 의미한다.

기약 루트계에서 길이 (\alpha, \alpha)^{1/2}의 값은 많아야 2 종류이며, '''짧은''' 루트와 '''긴''' 루트이다. 모든 루트가 같은 길이를 가질 때는 길다고 정의하며, 루트계는 '''simply laced'''라고 불린다. 이것은 A, D, E의 경우에 일어난다. 같은 길이의 임의의 두 루트는 바일 군의 같은 궤도에 들어간다. Simply laced가 아닌 경우 B, C, G, F에서는 루트 격자는 짧은 루트에 의해 생성되며, 긴 루트는 부분 격자를 생성하며, 이것은 바일 군으로 불변이며, 코루트 격자의 r^2/2 배에 등가이며, 여기서 r은 긴 루트의 길이이다.

첨부된 표에서, |\Phi^<|는 짧은 루트의 개수를 나타내며, I는 긴 루트에 의해 생성되는 부분 격자의 루트 격자에서의 지수를 나타내며, D는 카르탕 행렬의 행렬식을 나타내며, |W|는 바일 군의 차수를 나타낸다.

5. 구성 요소

근계의 구성 요소는 다음과 같다.


  • 단순근(單純根, simple root영어): 어떤 양근의 집합이 주어졌을 때, 두 양근의 합으로 나타낼 수 없는 근이다. 단순근들의 집합은 기저를 이룬다.[14] 단순근은 다음과 같은 속성을 갖는다.[15]
  • 모든 근은 단순근의 정수 계수 선형 결합으로 표현된다.
  • 각 근에 대한 선형 결합 계수는 모두 음이 아니거나 모두 음수이다.
  • 주어진 근계에 대해 단순근 집합을 선택하는 방법은 여러 가지이지만, 바일 군의 작용에 의해 달라진다.[16]
  • 근 격자: 근계에 의해 생성된 '''Z'''-부분 모듈이다. 격자의 일종이다.[7]
  • 무게 격자: 주어진 근계와 관련된 격자로, 반단순 리 대수의 표현론에서 유래되었다. 각 코루트와의 내적이 정수인 벡터를 적분 벡터라고 하며, 이들의 집합을 무게 격자라고 한다. 근은 항상 적분 벡터이므로, 근의 정수 선형 조합도 적분 벡터이다. 하지만 일반적으로 무게 격자는 근 격자와 일치하지 않는다. 즉, 근의 정수 조합이 아닌 적분 벡터가 존재한다.[18]

5. 1. 양근과 단순근

어떤 양근의 집합이 주어졌을 때, 단순근(單純根, simple root영어)은 두 양근의 합으로 나타낼 수 없는 근이다. 단순근들의 집합은 V의 기저를 이룬다.[14]

\Phi^+의 원소는 두 \Phi^+ 원소의 합으로 쓸 수 없을 경우 단순근(또는 "기본 근")이라고 한다. (단순근의 집합은 \Phi의 기저라고도 한다.) 단순근의 집합 \Delta는 다음과 같은 추가적인 특별한 속성을 가진 E의 기저이다.[15]

  • 모든 근 \alpha\in\Phi는 *정수* 계수를 갖는 \Delta 원소의 선형 결합이다.
  • 각 \alpha\in\Phi에 대해, 앞의 내용에서의 계수는 모두 음이 아니거나 모두 음수이다.


각 근계 \Phi에 대해 양의 근 집합, 즉 단순근 집합을 선택하는 방법은 다양하지만, 두 양의 근 집합은 바일 군의 작용에 의해 달라진다.[16]

5. 2. 근 격자

근계 Φ의 '''근 격자'''는 Φ에 의해 생성된 ''E''의 '''Z'''-부분 모듈이다. 이는 ''E''의 격자이다.[7]

5. 3. 무게 격자

'''무게 격자'''(weight lattice)는 주어진 근계와 관련된 격자로, 반단순 리 대수의 표현론에서 유래된 용어이다.

''E'' 안의 벡터 \lambda가 각 코루트와의 내적이 정수일 경우, 즉

2\frac{(\lambda,\alpha)}{(\alpha,\alpha)}\in\mathbb Z,\quad\alpha\in\Phi.[18]

를 만족하면 '''적분'''이라고 한다.

\alpha\in\Delta인 \alpha^\vee 의 집합이 쌍대 근계의 기저를 형성하므로, \lambda가 적분인지 확인하려면 \alpha\in\Delta에 대해 위의 조건을 확인하는 것으로 충분하다.

적분 요소의 집합을 '''무게 격자'''라고 부른다.

근계의 정의는 근 자체가 적분 요소임을 보장한다. 따라서 근의 모든 정수 선형 조합도 적분이다. 그러나 대부분의 경우, 근의 정수 조합이 아닌 적분 요소가 존재한다. 즉, 일반적으로 무게 격자는 근 격자와 일치하지 않는다.

6. 예시



그림과 같이 2차원 유클리드 공간 '''R'''2에 있는 여섯 개의 벡터를 '''루트'''라고 부르자. 이 벡터들은 공간 전체를 생성한다. 어떤 루트 ''β''에 수직인 선을 생각하면, 그 선에 대한 '''R'''2의 반사는 다른 루트 ''α''를 또 다른 루트로 보낸다. 보내진 루트는 ''α'' + ''nβ''와 같으며, 여기서 ''n''은 정수이다 (이 경우 ''n'' = 1). 이 여섯 개의 벡터는 정의를 만족하며, 루트 시스템 ''A''2를 형성한다.[8]

6. 1. 낮은 차원의 근계

0차원 근계는 자명하게 하나 밖에 없다.

1차원 근계는 하나 밖에 없으며, \{-\sqrt2,\sqrt2\}\subset\mathbb R이다.

2차원 근계는 총 4개가 있으며, 이들 가운데 3개는 기약 근계이다. (B_2와 C_2는 서로 동형이며, A_1\times A_1과 D_2 역시 서로 동형이다.)

Root system A1 + A1
Root system A2
Root system B2
A_1 \times A_1A_2B_2
Root system C2
Root system D2
--
C_2D_2G_2



랭크 1의 근계는 단 하나뿐이며, 두 개의 영이 아닌 벡터 \{\alpha, -\alpha\}로 구성된다. 이 근계를 A_1이라 부른다.[8]

랭크 2에는 \sigma_\alpha(\beta) = \beta + n\alpha에 해당하는 네 가지 가능성이 있으며, 여기서 n = 0, 1, 2, 3이다.[8] A_1\times A_1는 D_2와 동형이고 B_2는 C_2와 동형이다.

근계는 생성하는 격자에 의해 결정되지 않는다. A_1 \times A_1과 B_2는 둘 다 정사각형 격자를 생성하는 반면, A_2와 G_2는 둘 다 육각형 격자를 생성한다.

Φ가 ''E''의 근계이고, ''S''가 Ψ = Φ ∩ ''S''에 의해 span되는 ''E''의 부분 공간일 때마다 Ψ는 ''S''의 근계이다. 따라서 랭크 2의 네 가지 근계의 전체 목록은 임의의 랭크의 근계에서 선택된 두 개의 루트에 대한 기하학적 가능성을 보여준다. 특히, 그러한 두 개의 루트는 0, 30, 45, 60, 90, 120, 135, 150 또는 180도의 각도에서 만나야 한다.

6. 2. 반단순 리 대수에 대응되는 근계

복소수체 위의 반단순 리 대수 \mathfrak g 및 그 카르탕 부분 대수 \mathfrak h\subseteq\mathfrak g가 주어졌다고 하자. \mathfrak h는 \mathfrak g의 킬링 형식을 통해 자연스럽게 유한 차원 실수 내적 공간을 이룬다.

그렇다면, \mathfrak g의 딸림표현에 대응하는 \mathfrak h-무게들

:\Phi=\{\alpha\in \mathfrak h^\vee\colon \mathfrak g_\alpha\ne0\}\subseteq\mathfrak h^\vee

을 생각하자. 그렇다면, (\mathfrak h^\vee,\Phi)는 근계를 이룬다. 또한, 다음이 성립한다.

  • \mathfrak g의 단순 리 대수들로의 직합 분해는 (\mathfrak h^\vee,\Phi)의 기약 근계들로의 직합 분해와 대응한다.
  • 특히, 단순 리 대수에 대응하는 근계는 기약 근계이다.
  • 두 반단순 리 대수가 서로 동형일 필요충분조건은 그 대응하는 근계가 서로 동형인 것이다.


반단순 리 대수의 근계

만약 \mathfrak{g}가 복소수 반단순 리 대수이고 \mathfrak{h}가 카르탕 부분대수라면, 다음과 같이 근계를 구성할 수 있다. \alpha\in\mathfrak{h}^*가 \alpha\neq 0이고, 모든 H\in\mathfrak{h}에 대해 다음을 만족하는 X\neq 0\in\mathfrak{g}가 존재하면, \alpha를 \mathfrak{h}에 대한 \mathfrak{g}의 '''근'''이라고 한다.

[H,X]=\alpha(H)X

내적을 통해 근의 집합이 근계를 형성한다는 것을 보일 수 있다.[9] \mathfrak{g}의 근계는 \mathfrak{g}의 구조를 분석하고 표현을 분류하는 데 기본적인 도구이다.

7. 역사

근계의 이론은 복소수 반단순 리 대수의 표현론에서 비롯되었다. 각 반단순 리 대수에는 근계를 대응시킬 수 있으며, 단순 리 대수에 대응되는 근계는 기약 근계이다.

엘리 카르탕은 카르탕 행렬의 개념을 도입하였고, 예브게니 딘킨은 딘킨 도표의 개념을 도입하였다.

만약 \mathfrak{g}가 복소수 반단순 리 대수이고 \mathfrak{h}가 카르탕 부분대수라면, 다음과 같이 근계를 구성할 수 있다. \alpha\in\mathfrak{h}^*가 \alpha\neq 0이고, 모든 H\in\mathfrak{h}에 대해 다음을 만족하는 X\neq 0\in\mathfrak{g}가 존재하면, \alpha를 \mathfrak{h}에 대한 \mathfrak{g}의 '''근'''이라고 한다.

[H,X]=\alpha(H)X

내적을 통해 근의 집합이 근계를 형성한다는 것을 보일 수 있다.[9] \mathfrak{g}의 근계는 \mathfrak{g}의 구조를 분석하고 표현을 분류하는 데 기본적인 도구이다.

1889년경 빌헬름 킬링이 근계 개념을 처음으로 도입했다.[10][11] 그는 이를 사용하여 복소수 체 상의 모든 단순 리 대수를 분류하려고 시도했다. 킬링은 원래 분류 과정에서 실수를 범하여 두 개의 예외적인 랭크 4 근계를 나열했지만, 실제로는 F4로 알려진 근계가 하나만 존재한다. 카르탕은 킬링의 두 근계가 동형임을 보여주면서 이 실수를 나중에 수정했다.[12]

킬링은 현재 카르탕 부분 대수 \mathfrak{h}라고 불리는 것을 고려하여 리 대수 L의 구조를 연구했다. 그 다음, 그는 x \in \mathfrak{h}인 경우, 특성 다항식 \det (\operatorname{ad}_L x - t)의 근을 연구했다. 여기서 "근"은 \mathfrak{h}의 함수로, 또는 실제로 쌍대 벡터 공간 \mathfrak{h}^*의 원소로 간주된다. 이러한 근의 집합은 위에서 정의된 대로 \mathfrak{h}^* 내에서 근계를 형성하며, 여기서 내적은 킬링 형식이다.[11]

참조

[1] 논문 Graphs with least eigenvalue −2; a historical survey and recent developments in maximal exceptional graphs
[2] 서적 Bourbaki, Ch.VI, Section 1
[3] 서적
[4] 서적
[5] 서적
[6] 서적
[7] 서적
[8] 서적 Proposition 8.8
[9] 서적
[10] 서적
[11] 서적
[12] 서적
[13] 서적 Proposition 8.6
[14] 서적
[15] 서적
[16] 서적
[17] 서적
[18] 서적
[19] 서적
[20] 서적
[21] 서적
[22] 서적
[23] 서적
[24] 서적
[25] 서적 Theorem 7.35
[26] 서적
[27] 서적
[28] 서적 Section 18.3 and Theorem 18.4
[29] 서적 Sphere Packings, Lattices and Groups https://books.google[...] Springer 1998
[30] 서적 Section 8.9
[31] 서적
[32] 논문 Graphs with least eigenvalue −2; a historical survey and recent developments in maximal exceptional graphs http://www.sciencedi[...]
[33] 서적 Proposition 8.23
[34] 서적 Lie Groups, Lie Algebras, and Representations: An Elementary Introduction Springer
[35] 서적 Sphere packings, lattices, and groups Springer
[36] 서적 String theory. Volume 2
[37] 서적 Affine Lie algebras and quantum groups: an introduction with applications in conformal field theory http://www.cambridge[...] Cambridge University Press 1995-03


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com