쿠르트 괴델
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
쿠르트 괴델은 20세기 가장 영향력 있는 논리학자이자 수학자 중 한 명으로, 1906년 체코 브르노에서 태어나 1978년 미국 프린스턴에서 사망했다. 그는 빈 대학교에서 수학과 물리학을 공부하며 수리논리학에 관심을 갖게 되었고, 1930년 제1차 술어 논리의 완전성 정리를 증명하여 박사 학위를 받았다. 1931년에는 20세기 수학기초론과 논리학에서 가장 중요한 발견으로 평가받는 불완전성 정리를 발표하여 힐베르트 프로그램에 큰 타격을 주었다. 1938년에는 구성 가능 전체 개념을 도입하여 선택 공리와 연속체 가설이 체르멜로-프렝켈 집합론과 무모순임을 증명했다. 나치 독일의 오스트리아 병합 이후 미국으로 이주하여 프린스턴 고등연구소 교수로 재직하며 알베르트 아인슈타인과 교류했다. 괴델은 불완전성 정리, 완전성 정리, 구성 가능성 개념 등 다양한 분야에서 중요한 업적을 남겼으며, 앨버트 아인슈타인 상, 미국 국가 과학상 등을 수상했다.
더 읽어볼만한 페이지
- 체코의 논리학자 - 베르나르트 볼차노
베르나르트 볼차노는 프라하 출신의 수학자이자 철학자로, 엄밀한 수학적 증명을 추구하고 객관주의적 논리학을 정립하려 했으며, 수학에서는 중간값 정리와 볼차노-바이어슈트라스 정리로, 철학에서는 『지식학』에서의 '명제 자체' 등의 개념으로 유명하고 후설 등에게 영향을 미쳤다. - 쿠르트 괴델 - 괴델, 에셔, 바흐
더글러스 호프스태터의 책 "괴델, 에셔, 바흐"는 괴델의 불완전성 정리, 에셔의 미술, 바흐의 음악을 통해 재귀, 자기 참조, 지능과 의식의 본질을 탐구하며, 다양한 분야를 넘나드는 사유를 제공하여 퓰리처상을 수상하는 등 큰 반향을 일으켰다. - 쿠르트 괴델 - 괴델상
괴델상은 이론 컴퓨터 과학 분야의 뛰어난 업적을 기리기 위해 1993년부터 매년 수여되는 상이다. - 오스트리아의 논리학자 - 루트비히 비트겐슈타인
루트비히 비트겐슈타인은 20세기 중요한 철학자 중 한 명으로, 『논리철학논고』를 통해 초기 논리실증주의를 대표하고 『철학적 탐구』로 후기 일상언어철학의 기초를 세웠으며, 언어 게임 개념을 제시하여 현대 철학에 큰 영향을 미쳤다. - 오스트리아의 논리학자 - 루트비히 폰 미제스
오스트리아 학파의 대표적인 학자인 루트비히 폰 미제스는 실천론을 정립하여 사회주의 경제 체제의 불가능성을 주장하고 자유방임주의를 옹호하며 통화, 경기변동 등 다양한 경제학 분야에 기여했다.
| 쿠르트 괴델 - [인물]에 관한 문서 | |
|---|---|
| 기본 정보 | |
 | |
| 출생 이름 | 쿠르트 프리드리히 괴델 |
| 출생일 | 1906년 4월 28일 |
| 출생지 | 브르노, 오스트리아-헝가리 제국 (현재 체코) |
| 사망일 | 1978년 1월 14일 |
| 사망지 | 미국 뉴저지주 프린스턴 |
| 국적 | 오스트리아, 체코슬로바키아, 독일, 미국 |
| 분야 | 수학, 수리논리학, 물리학 |
| 근무 기관 | 프린스턴 고등연구소 |
| 모교 | 빈 대학교 (PhD, 1930) |
| 박사 학위 논문 제목 | 논리 계산의 완전성에 관하여 (Über die Vollständigkeit des Logikkalküls) |
| 박사 학위 논문 발표 연도 | 1929년 |
| 박사 지도 교수 | 한스 한 |
| 배우자 | 아델레 님부르스키 (1938년 결혼) |
 | |
| 주요 업적 | |
| 업적 | 괴델의 불완전성 정리 괴델의 완전성 정리 괴델의 구성 가능 전체 괴델 계량 (닫힌 시간꼴 곡선) 괴델 논리 괴델-두메트 논리 괴델의 β 함수 괴델의 맹점 괴델 수 괴델 연산 괴델의 속도 향상 정리 괴델의 존재론적 증명 괴델-겐첸 변환 괴델-매킨지-타르스키 변환 폰 노이만-베르나이스-괴델 집합론 ω-무모순 이론 ZFC와의 연속체 가설의 무모순성 구성 가능성 공리 콤팩트성 정리 응축 보조정리 대각 보조정리 변증법적 해석 순서수 정의 가능 집합 새총 논증 |
| 수상 | |
| 수상 내역 | 알베르트 아인슈타인 상 (1951년) 왕립 학회 회원 (1968년) 미국 국가 과학 훈장 (1974년) |
| 철학적 성향 | |
| 철학 분야 | 분석 철학 |
| 철학 시대 | 20세기 철학 |
| 철학 지역 | 서양 철학 |
| 주요 관심사 | 논리 철학 수학 철학 종교 철학 일반 상대성 이론 |
2. 생애
유복한 시민계급 가정에서 태어났으며, 어려서부터 건강이 좋지 않았지만 학업 성적이 우수했다. 1912년 사립 시민학교에 입학했고, 이후 김나지움을 거쳐 1924년 빈 대학 물리학과에 입학했다. 대학에서 모리츠 슐리크가 이끌던 빈 학파의 세미나에 참여하며 수리 논리학에 깊은 관심을 갖게 되었다. 1928년에는 훗날 아내가 된 아델 포르케르트(Adele Porkert, 1899~1981)를 만났다.
카를 멩거의 수학 콜로퀴움에 참여했으며, 1929년 《제1단 술어논리의 완전성 정리》를 제출하여 1930년 박사 학위를 받았다. 이듬해인 1931년에는 20세기 수학기초론과 논리학 분야에서 가장 중요한 발견 중 하나로 꼽히는 불완전성 정리를 발표했다. 이 정리는 수학의 무모순성을 증명하려던 다비트 힐베르트의 힐베르트 프로그램에 큰 영향을 주었으며, 존 폰 노이만 등 당대 학자들로부터 "인간 이성의 한계를 보여주었다"는 평가를 받았다. 1938년에는 구성 가능 전체 개념을 도입하여 선택 공리와 연속체 가설이 체르멜로-프렝켈 집합론과 무모순임을 증명했다.
빈 대학 강사로 활동했으나, 1940년경 나치 독일의 영향력이 커지자 아내와 함께 미국으로 이주하여 프린스턴 고등연구소 교수가 되었다. 이곳에서 알베르트 아인슈타인과 매우 가깝게 지내며 물리학, 철학 등으로 연구 분야를 넓혔다. 아인슈타인 방정식의 해인 괴델 우주를 제시하고, 고트프리트 라이프니츠 철학 연구 및 신의 존재 증명을 시도하기도 했다.
말년에는 극심한 건강염려증과 피해망상에 시달렸으며, 특히 독살에 대한 공포로 부인이 주는 음식 외에는 거부했다. 부인이 병원에 입원하자 식사를 거부하여 결국 영양실조 및 쇠약으로 사망했다.
2. 1. 유년기 및 교육
1906년 4월 28일, 당시 오스트리아-헝가리 제국의 브륀(현재 체코 브르노)에서 유복한 독일어 사용 시민 가정에서 태어났다.[6] 그의 아버지는 주요 섬유 회사의 임원이자 공동 소유주였던 루돌프 괴델(1874–1929)이었고, 어머니는 마리안 괴델(결혼 전 성씨 한슈, 1879–1966)이었다.[6] 아버지는 가톨릭 신자였고 어머니는 개신교 신자였으며, 자녀들은 개신교 신자로 양육되었다. 괴델의 조상들은 브륀의 문화계에서 활동하기도 했는데, 예를 들어 할아버지 요제프 괴델은 당시 유명한 성악가였으며 몇 년 동안 Brünner Männergesangverein|브륀 남성 합창단de의 멤버였다.[8]어린 시절 괴델은 끝없는 호기심 때문에 가족들 사이에서 Herr Warum|헤르 바룸de("왜 씨")이라는 별명으로 불렸다. 여섯 살 또는 일곱 살 무렵 류마티스열을 앓았는데, 완전히 회복했음에도 평생 심장에 영구적인 손상을 입었다고 믿었다.[12] 네 살 때부터 시작된 잦은 건강 문제는 평생 동안 이어졌다.[12]
제1차 세계 대전 패배로 오스트리아-헝가리 제국이 해체된 후, 12세의 괴델은 자동으로 체코슬로바키아 시민이 되었다. 그는 자신을 항상 오스트리아인으로 여겼으며, 체코슬로바키아에서는 망명자처럼 느꼈다고 전해진다.[9] 1929년 2월 체코슬로바키아 시민권을 포기하고, 같은 해 4월 오스트리아 시민권을 취득했다.[10] 이후 1938년 나치 독일의 오스트리아 병합으로 독일 시민이 되었고, 제2차 세계 대전 후인 1948년에는 미국 시민권을 얻었다.[11]
1912년부터 1916년까지 브륀의 루터교 학교인 Evangelische Volksschule|에반겔리셰 폴크슐레de에 다녔고, 1916년부터 1924년까지는 Deutsches Staats-Realgymnasium|도이체스 슈타츠-레알김나지움de(김나지움)에 재학했다. 그는 모든 과목에서 우수한 성적을 거두었으며, 특히 수학, 언어, 종교 과목에서 두각을 나타냈다. 처음에는 언어에 뛰어났으나 점차 역사와 수학에 더 큰 관심을 보였다. 십대 시절에는 가벨스베르거 속기법,[13] 아이작 뉴턴에 대한 비판, 임마누엘 칸트의 저작 등을 공부했다.[14]
1924년, 18세의 나이로 형 루돌프가 의학을 공부하고 있던 빈 대학교에 입학했다. 이미 대학 수준의 수학 실력을 갖추고 있었으며,[15] 처음에는 이론 물리학을 공부하려 했으나 수학과 철학 강의도 수강했다.[16] 이 시기에 그는 수학적 실재론을 받아들였고, 칸트의 저작을 읽었다. 모리츠 슐리크, 한스 한, 루돌프 카르납 등이 참여하는 빈 학파의 세미나에 참여하면서 수리 논리학에 깊은 관심을 갖게 되었다. 특히 모리츠 슐리크가 진행한 버트런드 러셀의 《수학 철학 입문》에 대한 세미나가 큰 영향을 미쳤다. 괴델은 수리 논리학을 "모든 과학에 기초가 되는 아이디어와 원리를 담고 있는, 다른 모든 과학보다 우선하는 과학"으로 여겼다.[17] 1928년에는 훗날 아내가 된 아델 포르케르트(Adele Porkert, 1899–1981)를 만났다.
볼로냐에서 열린 다비트 힐베르트의 강의를 듣고 수학 체계의 완전성과 일관성 문제에 대해 알게 된 것도 그의 학문적 방향 설정에 영향을 주었을 수 있다. 1928년 힐베르트와 빌헬름 아커만이 출판한 《수학 논리의 원리》(Grundzüge der theoretischen Logik|그룬트취게 데어 테오레티셴 로기크de)에서 제기된 일계 논리의 완전성 문제를 접하고 이를 박사 논문 주제로 삼았다.[18] 1929년, 23세의 나이로 한스 한의 지도 아래 박사 논문 《제1단 술어논리의 완전성 정리》를 완성하여 일계 논리에 대한 완전성 정리를 증명했다.[18] 1930년 2월 6일 박사 학위를 받았으며,[18] 그의 논문은 추가 연구 내용과 함께 비엔나 과학 아카데미에서 출판되었다.
2. 2. 빈 대학교 시절
18세에 괴델은 형과 함께 비엔나 대학교에 입학했다. 그는 이미 대학 수준의 수학을 마스터한 상태였다.[15] 처음에는 이론 물리학을 공부할 의도였으나, 수학과 철학 수업에도 참여했다.[16] 이 시기에 그는 수학적 실재론 사상을 받아들였다. 칸트의 자연과학의 형이상학적 기초de를 읽었으며, 모리츠 슐리크가 주도하던 빈 학파(Wiener Kreis)의 세미나에 참여하면서 수리 논리학에 관심을 가지게 되었다.[17] 괴델에 따르면, 수리 논리학은 "모든 과학에 기초가 되는 아이디어와 원리를 담고 있는, 다른 모든 과학보다 우선하는 과학"이었다.[17] 그는 모리츠 슐리크, 한스 한, 루돌프 카르납과 함께 빈 학파 활동에 참여했으며, 슐리크가 진행한 버트런드 러셀의 저서 ''수학 철학 입문'' 세미나를 통해 수리 논리학에 대한 관심이 깊어졌다.1928년에는 훗날 아내가 된 아델 포르케르트(Adele Porkert, 1899~1981)를 만났다. 같은 해 다비트 힐베르트와 빌헬름 아커만이 출판한 Grundzüge der theoretischen Logikde (''수학 논리의 원리'')는 일계 논리의 완전성 문제를 제기했는데, 이는 괴델의 연구 방향에 영향을 주었을 수 있다.[18] 그는 카를 멩거의 수학 콜로퀴움에 참석했으며, 완전성 문제를 박사 논문 주제로 선택했다.[18]
1929년, 23세의 나이로 한스 한의 지도 아래 박사 논문을 완성했다.[18] 이 논문에서 그는 일계 논리에 대한 완전성 정리를 증명했다.[18] 그는 1930년 2월 6일 박사 학위를 받았고,[18] 그의 논문은 빈 과학 아카데미에서 출판되었다.
다음 해인 1931년에는 20세기 수학기초론 및 논리학에서 가장 중요한 발견 중 하나로 평가받는 불완전성 정리를 발표했다. 이 정리는 다비트 힐베르트가 수학의 무모순성을 증명하려 했던 힐베르트 프로그램에 큰 타격을 주었다. 불완전성 정리는 존 폰 노이만 등 당대의 주요 학자들로부터 "인간 이성의 한계를 보여주었다"는 평가를 받으며 격찬을 받았다.
1938년에는 구성 가능 전체라는 개념을 도입하여, 선택 공리와 연속체 가설이 체르멜로-프렝켈 집합론과 무모순 관계에 있음을 증명하였다.
2. 3. 미국 이민과 프린스턴 고등연구소
1933년 아돌프 히틀러가 독일에서 권력을 잡은 후 몇 년 동안 나치는 오스트리아에서 영향력을 키워나갔다. 1938년 나치 독일이 오스트리아를 병합하자, 빈 대학 강사로 있던 괴델은 1940년경 아내 아델레와 함께 나치 독일을 피해 미국으로 이주했다.[59]미국으로 이주한 괴델은 프린스턴 고등연구소의 교수가 되었다.[60] 그는 이미 1933년 미국 방문 당시 프린스턴 고등연구소에서 알베르트 아인슈타인을 만났으며[26], 이주 후 연구소에서 아인슈타인과 매우 가까운 사이가 되어 가족처럼 친밀하게 교류했다. 두 사람은 함께 산책하며 물리학, 철학 등 다양한 주제에 대해 깊은 대화를 나누었다. 이러한 교류는 괴델의 연구에도 영향을 미쳐, 1949년에는 아인슈타인 방정식의 한 해인 괴델 우주를 발표하기도 했다. 이 해는 기존의 우주 모델과는 다른 독특한 성질을 가지고 있어 아인슈타인 자신도 자신의 이론에 대해 다시 생각하게 만들었다고 전해진다.
1948년, 괴델은 미국 시민권을 취득했다.[60] 이때 그의 보증인 중 한 명이 아인슈타인이었다. 당시 미국 시민권을 얻기 위해서는 미국 헌법에 관한 면접 시험을 통과해야 했다. 괴델은 시험을 준비하며 미국 헌법을 깊이 연구했고, 그 과정에서 헌법 조항을 통해 합법적으로 독재 체제로 이행할 수 있는 논리적 허점을 발견했다고 주장했다. 면접 당일, 괴델은 이 발견에 대해 이야기하려 했으나 아인슈타인 등 동행인들이 그를 만류했다. 면접을 진행한 판사가 "당신은 독재 국가(나치 독일에 병합된 오스트리아)에서 오셨군요. 미국에서는 그런 일이 일어나지 않으니 안심하십시오."라고 말하자, 괴델은 "그렇기는커녕, 저는 어떻게 그런 일이 일어날 수 있는지를 증명할 수 있습니다."라고 즉시 반박하려 했다. 이에 아인슈타인 등이 당황하며 상황을 수습하는 일이 있었다.[61] 이 일화는 '괴델의 루프홀'로 알려져 있다.
2. 4. 말년
프린스턴 고등연구소 시절, 괴델은 알베르트 아인슈타인과 가족처럼 가깝게 지냈으며, 관심사를 물리학, 철학 등으로 넓혔다. 이 시기 그는 아인슈타인 방정식의 해인 괴델 우주를 제시하고, 고트프리트 라이프니츠의 철학을 연구하며 신의 존재에 대한 증명을 시도하기도 했다.말년에 괴델은 정신적 불안정과 질병으로 고통받았다. 특히 절친한 친구였던 모리츠 슐릭이 암살된 이후,[42] 독살에 대한 강박적인 공포로 인해 부인 아델이 직접 준비한 음식 외에는 아무것도 먹지 않았다.
1977년 말, 아델이 병원에 입원하여 곁을 비우자 괴델은 식사를 거부하기 시작했다.[43] 결국 그는 1978년 1월 14일 프린스턴 병원에서 "성격 장애로 인한 영양실조 및 쇠약"으로 사망했다. 사망 당시 그의 몸무게는 약 29.48kg에 불과했다.[44]
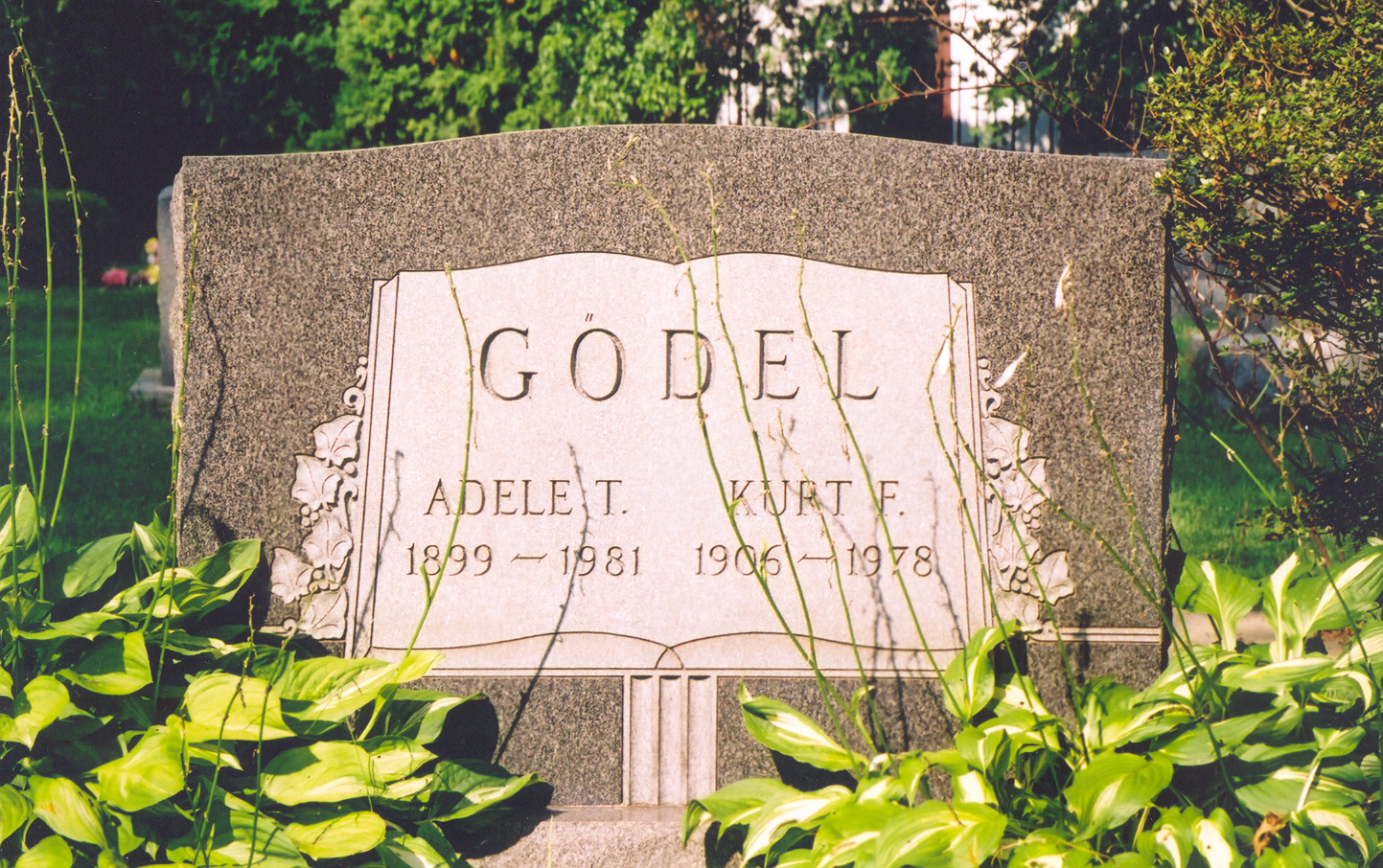
괴델은 프린스턴 묘지에 묻혔으며, 부인 아델은 1981년에 사망했다.[45]
3. 주요 업적
존 폰 노이만은 괴델의 업적을 현대 논리학에서 독보적이고 기념비적이며, 논리학의 본질과 가능성을 완전히 바꾸었다고 높이 평가했다.[19]
1930년 9월, 괴델은 쾨니히스베르크에서 열린 제2차 정확한 과학의 인식론에 관한 회의에 참석하여 제1차 술어 논리의 완전성 정리를 발표했다. 강연 말미에는 이 결과가 고차 논리로는 일반화되지 않는다고 언급하며 그의 가장 유명한 업적인 불완전성 정리를 암시했다.[20]
이듬해 괴델은 논문 Über formal unentscheidbare Sätze der 프린키피아 마테마티카와 관련된 시스템의 형식적으로 결정 불가능한 명제에 관하여/Principia Mathematicade und verwandter Systeme}}la에서 불완전성 정리를 공식적으로 발표했다. 이 정리는 페아노 공리와 같은 기본적인 산술 체계를 포함하는 충분히 강력하고 무모순적인 형식 체계는 필연적으로 불완전하며, 자신의 무모순성을 스스로 증명할 수 없다는 것을 보였다. 이는 수학 전체를 하나의 완전하고 무모순적인 공리 체계로 만들려 했던 힐베르트의 프로그램에 큰 영향을 주었다.[21] 괴델은 이 증명을 위해 명제, 증명 등을 숫자로 표현하는 괴델 넘버링 기법을 고안했다.[22]
1932년에는 짧은 논문 Zum intuitionistischen Aussagenkalkülde을 통해 직관주의 논리가 유한한 값만으로는 결정될 수 없음을 보였고, 이 과정에서 괴델-더밋 중간 논리(또는 괴델 퍼지 논리)로 알려진 체계를 암묵적으로 사용했다.[23] 1938년에는 구성 가능 전체 개념을 도입하여 선택 공리와 일반화된 연속체 가설이 ZF 집합론 공리들과 모순되지 않음을 증명했다.
1938년 안슐루스 이후 나치 독일 치하의 오스트리아에서 학문적 활동이 어려워지고 징집 위기에 처하자, 괴델은 1939년 말 아내와 함께 미국으로 망명했다. 시베리아 횡단 철도와 배편을 이용해 1940년 3월 프린스턴에 도착하여[29] 고등 연구소(IAS)에서 활동을 시작했다.[31]
프린스턴에서 괴델은 알베르트 아인슈타인과 깊은 우정을 나누었으며, 두 사람은 연구소에서 함께 산책하며 대화하는 모습으로 잘 알려졌다. 경제학자 오스카 모르겐슈테른은 아인슈타인이 말년에 괴델과 함께 집으로 걸어가는 특권을 누리기 위해 연구소에 다닌다고 말했다고 전했다.[32]
1947년 미국 시민권 시험에서 괴델은 미국 헌법 내에 독재를 가능하게 하는 논리적 허점(괴델의 루프홀)을 발견했다고 주장하여 동행한 아인슈타인과 모르겐슈테른을 당황하게 했으나, 심사관의 재치로 무사히 시민권을 취득했다.[33][34]
괴델은 1946년 고등 연구소 정회원이 되었고, 1953년 정교수, 1976년 명예 교수가 되었다.[35] 이 시기 그의 관심은 철학과 물리학으로 확장되었다. 1949년에는 일반 상대성 이론의 아인슈타인 방정식에 대한 해로서 닫힌 시간꼴 곡선을 포함하는 회전하는 우주 모델(괴델 우주)을 발표하여 이론적으로 시간 여행의 가능성을 제시했다.[36][37] 또한 고트프리트 라이프니츠, 임마누엘 칸트, 에드문트 후설 등의 철학을 연구했으며, 1970년대 초에는 라이프니츠의 아이디어를 현대 양상 논리로 형식화한 괴델의 존재론적 증명을 발표했다.
3. 1. 불완전성 정리
존 폰 노이만은 괴델의 업적에 대해 "현대 논리학에서 쿠르트 괴델의 업적은 독보적이고 기념비적입니다. 실제로 기념비 그 이상입니다. 이는 공간과 시간 속에서 오랫동안 보일 랜드마크입니다. ... 논리학은 괴델의 업적으로 인해 그 본질과 가능성이 완전히 바뀌었습니다."라고 평가했다.[19]
1930년 9월, 괴델은 쾨니히스베르크에서 열린 제2차 정확한 과학의 인식론에 관한 회의에 참석하여 1차 논리의 완전성 정리를 발표했다. 이때 그는 이 결과가 고차 논리로는 일반화되지 않는다고 언급하며 그의 불완전성 정리를 처음으로 암시했다.[20]
괴델은 1931년 발표한 논문 Über formal unentscheidbare Sätze der 프린키피아 마테마티카와 관련된 시스템의 형식적으로 결정 불가능한 명제에 관하여/Principia Mathematicade und verwandter Systeme}}la에서 불완전성 정리를 공식적으로 발표했다. 이 논문에서 그는 자연수의 산술(예: 페아노 공리 또는 체르멜로-프렝켈 집합론)을 포함할 만큼 강력한 계산 가능한 공리적 시스템은 다음과 같은 특징을 갖는다는 것을 증명했다.
# 만약 어떤 형식적 체계가 오메가-무모순적이라면, 그 체계는 구문적으로 완전할 수 없다. 즉, 참이지만 그 체계 내에서는 증명할 수 없는 명제가 반드시 존재한다.
# 어떤 체계의 무모순성은 그 체계 자체 내에서는 증명될 수 없다.
이 정리는 고틀로프 프레게의 연구에서 시작되어 화이트헤드와 버트런드 러셀의 Principia Mathematica|프린키피아 마테마티카la를 거쳐 힐베르트의 프로그램으로 이어진, 수학 전체의 기초가 될 수 있는 무모순적인 공리 체계를 찾으려는 반세기 동안의 노력을 사실상 종결시켰다.[21] 힐베르트 프로그램은 수학의 모든 문제가 유한한 단계 안에서 해결될 수 있음을 보이려 했으나, 괴델은 수학 체계 내에 증명 불가능한 참 명제가 존재하며, 수학 스스로 자신의 무모순성을 증명할 수 없음을 보임으로써 이 프로그램에 큰 타격을 주었다.
괴델은 증명을 위해 주어진 형식 체계 내에서는 증명할 수 없다고 주장하는 특별한 공식을 구성했다. 만약 이 공식이 그 체계 내에서 증명 가능하다면, 그 공식은 거짓이 되어 모순이 발생한다. 따라서 참이면서도 증명 불가능한 명제가 항상 존재할 수밖에 없다. 이를 위해 괴델은 수학적 명제, 증명, 증명 가능성 등의 개념을 자연수로 표현(인코딩)하는 독창적인 방법을 고안했는데, 이것이 바로 괴델 넘버링이다.[22]
또한 괴델은 1932년 발표한 짧은 논문 Zum intuitionistischen Aussagenkalkülde에서 직관주의 논리가 유한한 값만으로는 표현될 수 없음을 증명했다. 이 과정에서 그는 나중에 괴델-더밋 중간 논리 또는 괴델 퍼지 논리로 알려지게 되는 논리 체계를 암묵적으로 사용했다.[23]
3. 2. 완전성 정리
괴델은 제1차 술어 논리의 완전성 정리를 증명했다. 이 정리는 어떤 형식 체계의 공리들이 그 체계의 모든 모델에서 참인 모든 명제를 유도하기에 충분하다는 것을 의미한다. 그는 1930년 9월 쾨니히스베르크에서 열린 제2차 정확한 과학의 인식론에 관한 회의에서 이 정리를 공식적으로 발표했다. 또한 강연 말미에 이 결과가 고차 논리로는 일반화되지 않는다고 언급하며, 그의 불완전성 정리를 암시하기도 했다.[20]3. 3. 구성 가능 전체
1937년, 괴델은 선택 공리와 연속체 가설의 일관성을 증명하는 연구를 시작했다. 그는 이 가설들이 집합론의 일반적인 공리계 내에서 반증될 수 없음을 보이는 것을 목표로 삼았다.1938년 가을, 미국 프린스턴 고등연구소에서 연구하며 현대 수학의 고전으로 평가받는 ''집합론의 공리들과 선택 공리 및 일반화된 연속체 가설의 일관성''[27]을 출판했다. 이 논문에서 그는 구성 가능 전체(Constructible universe)라는 중요한 개념을 도입했다. 구성 가능 전체는 집합론의 하나의 모형으로, 존재하는 모든 집합이 더 단순하고 기본적인 집합들로부터 단계적으로 구성될 수 있는 것들만으로 이루어져 있다고 가정하는 세계이다.
괴델은 이 구성 가능 전체 안에서는 선택 공리(AC)와 일반화된 연속체 가설(GCH)이 모두 참이라는 것을 증명했다. 이는 AC와 GCH가 집합론의 표준 공리계인 체르멜로-프렝켈 공리계(ZF)와 모순되지 않음을 의미하는 중요한 결과였다. 이 증명은 당시 수학자들에게 큰 영향을 미쳤는데, 예를 들어 한-바나흐 정리와 같은 여러 수학적 정리를 증명할 때 선택 공리를 자유롭게 가정하고 사용할 수 있는 이론적 근거를 마련해주었기 때문이다.
이후 폴 코헨은 선택 공리와 일반화된 연속체 가설이 거짓이 되는 ZF 집합론의 모형을 구성함으로써, 이 두 공리가 ZF 공리계로부터 독립적임을 증명했다. 즉, ZF 공리만으로는 선택 공리와 연속체 가설을 증명할 수도, 반증할 수도 없다는 사실이 밝혀졌다. 이는 괴델의 무모순성 증명과 함께 집합론의 기초에 대한 이해를 심화시키는 데 크게 기여했다.
3. 4. 괴델 우주
1949년, 괴델은 일반 상대성 이론의 아인슈타인 방정식에 대한 하나의 해(解)를 발견했는데, 이 해는 닫힌 시간꼴 곡선(closed timelike curve)을 포함하고 있었다.[36] 괴델은 이 연구 결과를 그의 친구이자 동료였던 알베르트 아인슈타인의 70번째 생일 선물로 제공했다고 전해진다.[37]'회전하는 우주'라고도 불리는 이 해는 이론적으로 과거로의 시간 여행이 가능함을 시사했으며, 이는 아인슈타인으로 하여금 자신의 이론에 대해 다시 생각하게 만드는 계기가 되었다. 괴델이 발견한 이 특수한 해는 괴델 계량(Gödel metric)으로 알려져 있다.
3. 5. 괴델의 존재론적 증명
1970년대 초, 괴델은 라이프니츠가 제시한 존재론적 증명의 한 버전을 친구들에게 공개했다. 이 증명은 캔터베리의 안셀름의 아이디어에 기반한 것으로, 괴델은 이를 현대적인 양상 논리를 사용하여 더욱 엄밀하게 형식화했다. 이 작업은 오늘날 '괴델의 존재론적 증명'으로 알려져 있으며, 신의 존재에 대한 철학적 논의에 영향을 미쳤다.4. 기타

괴델의 철학 노트[54]는 베를린-브란덴부르크 과학 인문학 아카데미의 쿠르트 괴델 연구 센터에서 편집되고 있다.[55] 괴델의 전집 5권이 출판되었는데, 처음 두 권은 그의 출판물, 세 번째 권은 그의 유고에 포함된 미발표 원고, 마지막 두 권은 서신으로 구성되어 있다.
더글러스 호프스태터는 1979년에 괴델, M. C. 에셔, 요한 제바스티안 바흐의 업적과 사상을 기리기 위해 괴델, 에셔, 바흐라는 책을 썼다. 이 책은 괴델의 불완전성 정리가 튜링 완전 계산 시스템, 즉 인간의 뇌에도 적용될 수 있다는 사실의 파급 효과를 부분적으로 탐구한다. 2005년, 존 도슨은 전기 ''논리적 딜레마: 쿠르트 괴델의 삶과 업적''을 출판했다.[50] 스티븐 부디안스키의 괴델 생애에 관한 책, ''이성의 가장자리로의 여행: 쿠르트 괴델의 삶''[51]은 ''뉴욕 타임스'' 비평가들이 선정한 2021년 최고의 책 중 하나였다.[52] 괴델은 데이비드 말론의 2008년 BBC 다큐멘터리 ''위험한 지식''에서 다뤄진 네 명의 수학자 중 한 명이었다.[53]
1994년 영화 ''아이큐''에서는 루 자코비가 괴델 역을 맡았으며, 2023년 영화 ''오펜하이머''에서는 제임스 어바니악이 연기한 괴델이 아인슈타인과 함께 프린스턴 정원의 산책길에 잠시 등장한다.
1987년에 설립된 쿠르트 괴델 학회는 논리, 철학 및 수학사 연구를 장려하는 국제 기구이다. 빈 대학교는 쿠르트 괴델 수학 논리 연구 센터를 운영하고 있다. 기호 논리학회는 1990년부터 매년 괴델 강연을 개최하고 있으며, 괴델 상은 이론 컴퓨터 과학 분야의 뛰어난 논문에 매년 수여된다.
《괴델의 불완전성 정리 - "이성의 한계"의 발견》(블루백스 B-947)에서는 마리안느가 17세에 쿠르트를 낳았다고 되어 있지만, 이는 게오르크 크라이젤의 1982년 문헌 자체의 오류를 그대로 인용한 오정보이다.
5. 저서
- 독일어 원본
- 1930, "논리적 함수 미적분학의 공리의 완전성." ''Monatshefte für Mathematik und Physik'' '''37''': 349–60.
- 1931, "''프린키피아 마테마티카'' 및 관련 시스템의 형식적으로 결정 불가능한 명제에 관하여, I." ''Monatshefte für Mathematik und Physik'' '''38''': 173–98.
- 1932, "직관주의적 명제 미적분학에 관하여", ''Anzeiger Akademie der Wissenschaften Wien'' '''69''': 65–66.
- 영어 원본
- 1940. ''선택 공리와 일반화된 연속체 가설이 집합론의 공리와 일치함''. 프린스턴 대학교 출판부.
- 1947. "칸토어의 연속체 문제는 무엇인가?" ''The American Mathematical Monthly 54'': 515–25. 폴 베나세라프와 힐러리 퍼트넘 편집, ''수학 철학: 선별된 읽기''(1964, 1984 개정판), 케임브리지 대학교 출판부: 470–85에 재수록.
- 1950, "일반 상대성 이론의 회전하는 우주." ''케임브리지 국제 수학자 회의록,'' Vol. 1, pp. 175–81.
- 영어 번역본
- 쿠르트 괴델, ''Principia Mathematica 및 관련 시스템의 형식적으로 결정 불가능한 명제에 관하여'', B. Meltzer 역, 리처드 브레이스웨이트 서문 포함. 도버 출판사 (1962년 기본 서적판 재인쇄), 1992.
- 쿠르트 괴델, ''Principia Mathematica 및 관련 시스템의 형식적으로 결정 불가능한 명제에 관하여'', 마틴 히르젤 역, 2000.[56]
- 장 반 하이예누르트 편집, ''수학 논리학 소스북, 1879–1931''. 하버드 대학교 출판부, 1967.
- 1930. "논리적 함수 미적분학의 공리의 완전성," 582–91.
- 1930. "완전성과 일관성에 대한 몇 가지 메타수학적 결과," 595–96. (1931년 논문의 초록)
- 1931. ''Principia Mathematica'' 및 관련 시스템의 형식적으로 결정 불가능한 명제에 관하여, 596–616.
- 1931a. "완전성과 일관성에 관하여," 616–17.
- 일본어 번역본
- 『수학 기초론 - 선택 공리 및 일반 연속 가설의 집합론 공리와의 무모순성』 곤도 요이치 번역, 이토 서점, 1946년 4월.
- 전집 (Collected Works): 옥스퍼드 대학교 출판부: 뉴욕. 편집장: 솔로몬 페퍼만.
- 제1권: 출판물 1929–1936
- 제2권: 출판물 1938–1974
- 제3권: 미발표 에세이 및 강연
- 제4권: 서신, A–G
- 제5권: 서신, H–Z
- 철학적 노트 (Philosophical Notebooks): 데 그루이터: 베를린/뮌헨/보스턴. 편집자: Eva-Maria Engelen.
- 제1권: 철학 I 격언 0 / Philosophy I Maxims 0
- 제2권: 시간 관리 (격언) I 및 II / Time Management (Maxims) I and II
- 제3권: 격언 III / Maxims III
- 제4권: 격언 IV / Maxims IV
- 제5권: 격언 V / Maxims V
- 제6권: 격언 VI / Maxims VI
참조
[1]
간행물
Kurt Godel. 28 April 1906–14 January 1978
[2]
웹사이트
Gödel
[3]
웹사이트
Principia Mathematica
http://plato.stanfor[...]
[4]
서적
Gödel's Incompleteness Theorems
Oxford University Press
[5]
서적
Gödel's Incompleteness Theorems
Oxford University Press
[6]
문서
[7]
문서
[8]
문서
[9]
문서
[10]
서적
Collected works
https://books.google[...]
[11]
웹사이트
Kurt Godel
https://school.eb.co[...]
Encyclopædia Britannica, Inc.
2019-06-03
[12]
서적
Johann Friedrich Herbart
http://plato.stanfor[...]
Metaphysics Research Lab, Stanford University
2015-01-01
[13]
웹사이트
Gabelsberger stenography | Gödel Enigma | University of Helsinki
https://www.helsinki[...]
[14]
간행물
Gödel and philosophical idealism
[15]
문서
[16]
서적
Kurt Kurt Gödel: Das Album
https://books.google[...]
Springer-Verlag
[17]
문서
The Information: A History, a Theory, a Flood
Fourth Estate
[18]
학회자료
In the Scope of Logic, Methodology and Philosophy of Science
[19]
간행물
The Legend of von Neumann
1973-04
[20]
서적
The Vienna Circle: Studies in the Origins, Development, and Influence of Logical Empiricism
https://books.google[...]
Springer
2015
[21]
서적
Gödel's Proof
New York University Press
[22]
서적
Gödel's Incompleteness Theorems
https://plato.stanfo[...]
Stanford Encyclopedia of Philosophy
2015
[23]
서적
Constructivism in Mathematics: An Introduction
North-Holland
[24]
서적
Godel: A Life Of Logic, The Mind, And Mathematics
Basic Books
[25]
문서
[26]
문서
Hutchinson Encyclopedia
[27]
간행물
The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis
1938-11-09
[28]
웹사이트
Kurt Gödel at Notre Dame
https://math.nd.edu/[...]
[29]
간행물
Max Dehn, Kurt Gödel, and the Trans-Siberian Escape Route
https://www.ams.org/[...]
2002-10
[30]
간행물
The spy who flunked it: Kurt Gödel's forgotten part in the atom-bomb story
2024-03
[31]
웹사이트
Kurt Gödel
https://www.ias.edu/[...]
2019-12-09
[32]
문서
https://books.google[...]
[33]
문서
[34]
웹사이트
History of the Naturalization of Kurt Gödel
https://robert.accet[...]
1971-09-13
[35]
웹사이트
Kurt Gödel – Institute for Advanced Study
https://www.ias.edu/[...]
2015-12-01
[36]
논문
An Example of a New Type of Cosmological Solutions of Einstein's Field Equations of Gravitation
1949-07-01
[37]
뉴스
Das Genie & der Wahnsinn
http://www.tagesspie[...]
2008-01-13
[38]
서적
Logical Dilemmas: The Life and Work of Kurt Gödel.
https://books.google[...]
A K Peters
[39]
웹사이트
The President's National Medal of Science: Recipient Details {{!}} NSF – National Science Foundation
https://www.nsf.gov/[...]
2016-09-17
[40]
웹사이트
APS Member History
https://search.amphi[...]
2021-01-28
[41]
서적
"In:" Proceedings of the International Congress of Mathematicians, Cambridge, Massachusetts, August 30–September 6, 1950
2017-12-04
[42]
웹사이트
Tragic deaths in science: Kurt Gödel - looking over the edge of reason - Paperpile
https://paperpile.co[...]
[43]
논문
Gödel's universe
2005-05-04
[44]
서적
Obsessive Compulsive Disorder: Practical Tried-and-Tested Strategies to Overcome OCD
Class Publishing
[45]
웹사이트
Gödel and the limits of logic
https://plus.maths.o[...]
University of Cambridge
2006-06-01
[46]
서적
A to Z of Mathematicians
https://archive.org/[...]
Infobase Publishing
[47]
문서
[48]
서적
Kurt Gödel: Collected Works: Volume IV
OUP Oxford
[49]
문서
[50]
간행물
A. K. Peters
Wellesley, MA
[51]
간행물
W. W. Norton & Company
New York City
[52]
웹사이트
Times Critics' Top Books of 2021
https://www.nytimes.[...]
2022-07-05
[53]
웹사이트
Dangerous Knowledge
https://www.bbc.co.u[...]
2009-10-06
[54]
웹사이트
Kurt-Gödel-Forschungsstelle: die "Philosophischen Bemerkungen" Kurt Gödels (Kurt Gödel Research Centre: The 'Philosophical Remarks' of Kurt Gödel) – Berlin-Brandenburg Academy of Sciences and Humanities
https://www.bbaw.de/[...]
[55]
웹사이트
The Academy – Berlin-Brandenburg Academy of Sciences and Humanities
https://www.bbaw.de/[...]
[56]
논문
Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme, I
http://www.research.[...]
[57]
웹사이트
Gödel’s Incompleteness Theorem
https://link.springe[...]
Springerlink
2020-11-30
[58]
문서
The Consistency of the Continuum Hypothesis
1940
[59]
문서
[60]
문서
[61]
문서
[62]
문서
[63]
문서
[64]
문서
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com