적분

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사
3. 표기와 계산
4. 적분의 여러 형식
5. 성질
6. 응용
참조

1. 개요

적분은 아르키메데스가 고안하고 앙리 르베그가 완성한 미적분학의 핵심 개념이다. 도형의 면적과 부피를 구하는 데 사용되었으며, 미분과 역의 관계를 갖는다. 고대 그리스 시대부터 현대에 이르기까지 다양한 방식으로 정의되고 발전해왔으며, 리만 적분, 르베그 적분 등이 대표적이다. 적분은 선형성을 가지며, 상계와 하계, 함수 사이의 부등식 등 여러 성질을 만족한다. 확률, 넓이, 부피 계산, 운동학, 열역학, 인공지능 등 다양한 분야에서 활용된다.

더 읽어볼만한 페이지

수학 사이드바 - 추론 규칙
추론 규칙은 전제가 참일 때 결론이 필연적으로 참임을 보이는 논리적 도출 과정을 형식적으로 표현한 규칙으로, 다양한 유형이 존재하며 명제 논리와 술어 논리에서 기본적인 추론을 수행하는 데 사용되고, 형식 체계의 핵심 요소이다.
수학 사이드바 - 벡터 공간
벡터 공간은 체 위의 가군으로 정의되는 대수적 구조로, 벡터 덧셈과 스칼라 곱셈 연산을 가지며 특정 공리들을 만족하고, 기저, 차원, 선형 사상 등의 개념을 통해 수학과 물리학 등 다양한 분야에서 활용된다.
적분 - 가우스 적분
가우스 적분은 특정한 정적분의 값으로 정의되며, 확률론, 통계학, 물리학 등 여러 분야에서 중요한 역할을 수행하고 정규분포와 관련된 계산에서 핵심적인 역할을 한다.
적분 - 적분표
적분표는 다양한 함수들의 부정적분과 정적분 예시를 모아 놓은 목록으로, 유리 함수, 무리 함수, 삼각 함수, 지수 함수, 로그 함수 등 여러 함수와 닫힌 형식으로 표현되지 않는 함수의 정적분 값, 절댓값 함수, 곱으로 이루어진 함수를 포함하며, 마이어 히르슈의 적분 목록집에서 시작하여 그라드슈테인과 르지크의 표로 발전했다.
함수와 사상 - 지수 함수
지수 함수는 양의 상수 *a*를 밑으로 하는 *y = a^x* 형태의 함수이며, 특히 자연로그의 역함수인 *e^x*는 다양한 정의와 응용을 가지며 복소수로 확장될 수 있다.
함수와 사상 - 음함수와 양함수
음함수와 양함수는 함수의 표현 방식에 따른 분류로, 독립변수와 종속변수의 관계가 명시적으로 나타나는 경우를 양함수, 관계식이 한 식 안에 포함된 경우를 음함수라 하며, 음함수는 양함수로 표현하기 어렵거나 불가능한 경우가 있고, 음함수 미분법, 음함수 정리 등을 통해 여러 분야에서 활용된다.

적분
미적분
개념	미분법 적분법
주요 내용	함수의 극한 연속 함수 미분 적분 급수 벡터 미적분학 다변수 미적분학
적분법
정의	부정적분 정적분 이상적분 리만 적분 르베그 적분
적분법	부분적분 디스크 방법 원통셸 방법 치환적분 부분분수 적분법 적분 순서 적분의 점화식
적분 종류	선적분 면적분 삼중적분 경로적분
적분의 종류
정의	부정적분 정적분
다른 정의	리만 적분 르베그 적분 선적분 면적분 중적분 경로적분
특수한 적분	이상적분
적분법	부분적분 치환적분 삼각치환 부분분수 분해 적분 순서 변경 점화식
활용
면적	곡선 아래 면적 계산
부피	회전체의 부피 계산
추가 개념
관련 개념	미분 급수 벡터 미적분학 다변수 미적분학 확률미적분학 분수계 미적분학 말리아빈 미적분 변분법

2. 역사

아르키메데스가 적분의 아이디어를 처음 생각해내었고 앙리 르베그가 적분론을 완성하였다.^[64]

고대 그리스 시대 시라쿠사의 수학자 아르키메데스는 도형의 면적이나 부피를 구하는데 오늘날의 적분과 유사한 방법을 사용하였다. 아르키메데스는 구적법을 이용하여 원, 구, 포물선의 일부 등에 대한 면적과 부피를 구하는 증명을 제시하였다.^[65] 구적법 문제는 이후 오랫동안 별다른 진전을 보이지 못하였다가 르네상스 시기에 이르러 보나벤투라 카발리에리가 무한의 개념을 도입하면서 진전이 있었다. 1622년 카발리에리는 곡선으로 둘러싸인 도형의 면적을 매우 폭이 좁은 직사각형들의 면적을 합한 것으로 이해할 수 있다는 착상을 내놓았다. 이후 블레즈 파스칼은 지금의 적분 기호를 사용한 것은 아니지만 곡선의 면적은 모든 가로 선분의 합인 $\sum_{0 \le k < na } f\left(\frac{k}{n}\right)$ 의 단위, 즉 n에 대한 비와 같다는 것을 파악하고 있었다.^[66]

카발리에리 이후 유럽에서는 도형을 당시의 표현을 빌리자면 불가분량이라고 부르는 아주 작은 양으로 나누어 넓이나 부피를 구하는 방법이 지속적으로 연구되었다. 케플러는 케플러의 행성운동법칙에서 지구의 공전 궤도가 타원을 이루며 같은 시간 동안 지구가 지나가는 황도면의 넓이는 같다고 주장하였다. 그는 타원의 넓이를 계산하기 위해 카빌리에리 이후 알려진 불가분량을 이용하였다. 또한, 케플러는 포도주통의 내측 부피를 구하기 위해 포도주통을 이루는 입체도형을 얇은 막들의 집합으로 파악하여 합산하였다. 이러한 발상은 케플러가 적분의 발견에 매우 근접하였다는 것을 보여준다.^[67]^[68]

한편, 데카르트가 제시한 좌표 평면과 해석기하학의 출현은 미적분학이 발전하는 중요한 밑거름이 되었다.^[69] 아이작 뉴턴과 고트프리트 빌헬름 라이프니츠는 각자 독자적으로 미적분학을 수립하였으며 적분은 결국 미분의 역산으로 역도함수를 구하는 것과 같다는 점을 발견하였다. 이를 미적분학의 기본정리라고 한다.^[73]

19세기에 이르러 베른하르트 리만은 적분에 대해 수학적으로 엄밀한 정의를 내렸다. 1823년 오귀스탱 루이 코시는 모든 연속함수는 적분 가능함을 증명하였고, 리만은 이를 확장하여 연속 함수 f(x)의 적분은 해당 구간에서 리만 합의 극한과 같다는 점을 증명하였다. 이렇게 정의된 적분을 흔히 리만 적분이라 한다.^[71] 리만 적분은 이후 토마스 요아너스 스틸티어스에 의해 보다 간단히 정리되었다.^[70]

1902년 앙리 르베그는 연속된 함수의 유계 구간에 대해 내측도와 외측도의 개념을 정립하고 이를 덮개로 파악하여 계측하는 르베그 측도를 이용한 르베그 적분을 발표하였다. 르베그 적분은 n차원의 일반적인 함수에 대해 리만 적분을 확장하여 적용한 것이다. 르베그 적분은 특정 함수에 대해 리만 적분이 존재할 때에는 리만 적분과 일치하지만, 그렇지 않은 경우에도 적분 가능한 함수들을 만들어 낸다.^[71]

미적분학, 특히 적분은 수학의 역사에서 비교적 최근에 발전한 학문으로 꾸준히 확장되고 있다.^[71]

2. 1. 고대

고대 그리스 시대 시라쿠사의 수학자 아르키메데스는 도형의 면적이나 부피를 구하는데 오늘날의 적분과 유사한 방법인 '구적법'을 사용하였다.^[65] 아르키메데스는 구적법을 이용하여 원, 구, 포물선의 일부 등에 대한 면적과 부피를 구하는 증명을 제시하였다.^[65] 아르키메데스가 사용한 구적법은 크니도스의 에우독소스와 데모크리토스가 체계화한 소진법을 더욱 발전시킨 것이다.^[2]^[3]

기원후 3세기경 중국에서 유휘가 독자적으로 원의 넓이를 구하는 데 비슷한 방법을 사용하였다.^[4] 이 방법은 나중에 5세기에 중국 부자 수학자인 조충지와 조충이 구의 부피를 구하는 데 사용했다.^[4]

2. 2. 중세 및 근대

르네상스 시기 보나벤투라 카발리에리는 무한의 개념을 도입하여 곡선으로 둘러싸인 도형의 면적을 매우 폭이 좁은 직사각형들의 면적을 합한 것으로 이해할 수 있다는 착상을 내놓았다.^[66] 요하네스 케플러는 케플러의 행성운동법칙에서 지구의 공전 궤도가 타원을 이루며 같은 시간 동안 지구가 지나가는 황도면의 넓이는 같다고 주장하며, 타원의 넓이를 계산하기 위해 불가분량을 이용하였다.^[67]^[68]

중동에서는 라틴어로 알하젠(c. 965-1040년 AD)으로 알려진 이븐 알하이삼이 4제곱의 합에 대한 공식을 유도했다.^[5] 알하젠은 이 결과를 사용하여 포물면의 부피를 계산했다.^[7]

르네 데카르트가 제시한 좌표 평면과 해석기하학의 출현은 미적분학이 발전하는 중요한 밑거름이 되었다.^[69] 아이작 뉴턴과 고트프리트 빌헬름 라이프니츠는 각자 독자적으로 미적분학을 수립하였으며, 적분은 미분의 역산, 즉 미적분학의 기본정리를 발견하였다.^[73]

2. 3. 현대

19세기에 이르러 베른하르트 리만은 적분에 대해 수학적으로 엄밀한 정의를 내렸다.^[71]^[14] 1823년 오귀스탱 루이 코시는 모든 연속함수는 적분 가능함을 증명하였고, 리만은 이를 확장하여 연속 함수 f(x)의 적분은 해당 구간에서 리만 합의 극한과 같다는 점을 증명하였다. 이렇게 정의된 적분을 흔히 리만 적분이라 한다.^[71] 리만 적분은 이후 토마스 요아너스 스틸티어스에 의해 보다 간단히 정리되었다.^[70]

1902년 앙리 르베그는 연속된 함수의 유계 구간에 대해 내측도와 외측도의 개념을 정립하고 이를 덮개로 파악하여 계측하는 르베그 측도를 이용한 르베그 적분을 발표하였다.^[71] 르베그 적분은 n차원의 일반적인 함수에 대해 리만 적분을 확장하여 적용한 것이다. 르베그 적분은 특정 함수에 대해 리만 적분이 존재할 때에는 리만 적분과 일치하지만, 그렇지 않은 경우에도 적분 가능한 함수들을 만들어 낸다.^[71]

아이작 뉴턴과 고트프리트 빌헬름 라이프니츠는 적분에 대한 체계적인 접근법을 제시했지만, 그들의 작업에는 상당한 수준의 엄밀성이 부족했다. 버클리 주교는 뉴턴이 사용한 무한소량을 "사라진 양의 유령"이라고 부르며 기억에 남는 비판을 가했다.^[13]

2. 4. 어원

‘적분(積分)’이란 번역어를 근대에 처음 쓴 문헌은 엘리어스 루미스/Elias Loomis^영어의 《Analytical Geometry and of the Differential and Integral Calculus》(1835)를 1859년 알렉산더 와일리/Alexander Wylie (missionary)^영어와 이선란이 번역한 《대미적습급(代微積拾級)》이다.^[72] 조지프 니덤은 《중국의 과학과 문명/Science and Civilisation in China^영어》에서 11세기 중국에서 이미 ‘적분’이라는 번역어를 사용했었다고 주장했다.^[72]

3. 표기와 계산

오늘날 일반적으로 사용되는 적분을 나타내는 표기 $\int$ 은 라이프니츠가 제안한 것이다.^[73] 적분 가능한 함수 f(x)가 있을 때 적분의 표기는 다음과 같다.^[74]

: $\int_{a}^{b} f(x) dx$ (구간 $[a, b]$ 에 대한 함수 $f(x)=x$ 의 적분)

미적분학의 기본정리에 따라 적분은 미분의 역연산이다. 즉, 함수 $f(x)$ 를 도함수로 하는 원시함수 $F(x)$ 가 존재한다. 원시함수를 구하는 과정을 '''부정적분'''(不定積分)이라 한다.^[75]

함수 f(x)의 구간 [a, b]에 대한 적분은 시작점과 끝점이 있는 유계의 변화량을 뜻하며 이를 '''정적분'''(定積分)이라 한다. 리만 합의 극한으로서 정적분을 정의하는 것을 리만 적분이라고 하며, 별다른 설명이 없을 경우 적분은 흔히 리만 적분을 가리킨다.^[78]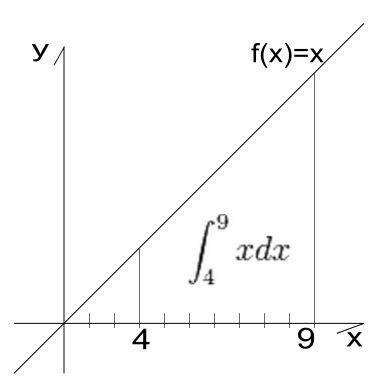

예를 들어

f(x)=x

의 구간 [4, 9] 에 대한 적분을 계산하면, 다음과 같다.

:

\int_{4}^{9} x dx = F(9) - F(4) = \left(\frac{1}{2} \cdot 9^2 + C \right) - \left( \frac{1}{2} \cdot 4^2 + C \right)

::

= \frac{9^2}{2} - \frac{4^2}{2} = \frac{81-16}{2} = \frac{65}{2} = 32.5

삼각함수 역시 미분적분의 기본정리를 이용하여 원시 함수를 구한 후 정적분을 계산한다. 예를 들어

f(x) = \sin{x} \

의 원시 함수는

F(x)= - \cos{x} + C \

가 되므로, 구간 [a,b]의 정적분은

:

\int_{a}^{b} \sin{x} dx = - \cos{b} + \cos{a} = \cos{a} - \cos{b}

와 같이 계산할 수 있다.

부정적분의 기호는 1675년 고트프리트 빌헬름 라이프니츠(Gottfried Wilhelm Leibniz)에 의해 도입되었다.^[15] 그는 "합"(sum) 또는 "총계"(total)를 의미하는 라틴어 ''summa''(summa로 표기)를 나타내는 ''ſ''(장음 s) 문자에서 적분 기호 '''∫'''를 차용하였다. 적분 기호 위아래에 극한값을 표시하는 현대적인 정적분 표기법은 1819년에서 1820년경 프랑스 아카데미의 ''Mémoires''에서 조제프 푸리에(Joseph Fourier)가 처음 사용했으며, 그의 1822년 저서에도 재인쇄되었다.^[16]

4. 적분의 여러 형식

적분은 여러 가지 형식으로 구분된다. 적분 계산에 대한 정의 방식이 달라 서로 다른 형식으로 분류되는 것이 대부분이지만, 교육적인 목적때문에 구분한 경우도 있다. 가장 일반적으로 널리 쓰이는 적분은 리만 적분과 르베그 적분이다.

적분을 정의하는 방법은 여러 가지가 있으며, 모두 동등한 것은 아니다. 서로 다른 정의가 사용되는 것은 대부분 다른 정의로는 적분이 정의되지 않는 특별한 경우에 다른 처리를 하기 위해서이지만, 그것뿐만 아니라 때로는 교육적인 이유가 개입하기도 한다. 가장 널리 사용되는 적분법은 리만 적분과 르베그 적분이다.

리만 적분과 르베그 적분을 확장한 리만-스틸티어스 적분, 르베그-스틸티어스 적분 등 여러 가지 확장이 존재한다.

다르부 적분: 다르부 합(제한된 리만 합)으로 정의되지만 리만 적분과 동등하다. 함수가 다르부 적분 가능한 것과 리만 적분 가능한 것은 동치이다. 다르부 적분은 리만 적분보다 정의하기가 더 쉽다는 장점이 있다.
리만-스틸체스 적분: 변수가 아닌 함수에 대해 적분하는 리만 적분의 확장이다.
르베그-스틸체스 적분: 요한 라돈이 더욱 발전시킨 것으로, 리만-스틸체스 적분과 르베그 적분을 일반화한다.
다니엘 적분: 측도에 의존하지 않고 르베그 적분과 르베그-스틸체스 적분을 포함한다.
하르 적분: 1933년 알프레드 하르가 도입한 국소적으로 컴팩트한 위상군에서의 적분에 사용된다.
헨스톡-쿠르츠바일 적분: 아르노 덩주, 오스카 페롱과 (가장 우아하게, 게이지 적분으로) 야로슬라프 쿠르츠바일에 의해 다양하게 정의되었고, 랄프 헨스톡에 의해 개발되었다.
킨친 적분: 알렉산드르 킨친의 이름을 따서 명명되었다.
이토 적분과 스트라토노비치 적분: 브라운 운동과 같은 반마팅게일에 대한 적분을 정의한다.
영 적분: 무한 변분의 특정 함수에 대한 일종의 리만-스틸체스 적분이다.
거친 경로 적분: 일부 추가적인 "거친 경로" 구조를 갖춘 함수에 대해 정의되며, 반마팅게일과 분수 브라운 운동과 같은 과정에 대한 확률적 적분을 일반화한다.
슈케 적분: 프랑스 수학자 Gustave Choquet이 1953년에 만든 부가적 또는 초가적 적분이다.
보흐너 적분: 바나흐 공간에서 값을 가지는 함수에 대한 르베그 적분의 일반화이다.

리만-스틸체스 적분은 유계 변동 함수 φ를 사용한 리만 적분의 확장이다.

:

\int_{a}^{b} f(x) d\varphi(x) = \lim \sum f(\xi)\delta\varphi

φ(x) = x일 때는 일반적인 리만 적분이며, φ가 미분 가능하고 φ'가 연속이면, 밀도를 갖는 리만 적분

:

\int_{a}^{b} f(x)d\varphi(x) = \int_{a}^{b} f(x)\varphi'(x)dx

의 형태가 된다.

르벡-스틸체스 적분은 르벡 적분과 리만-스틸체스 적분의 확장이다. 가법 집합 함수의 변동이 결정하는 측도에 관한 르벡 방식의 적분

:

\int_X f(x)\,d\Phi(x)

이며, 요한 라돈이 자세히 연구했다.

다니엘 적분은 적분을 선형 작용소로 정의한다. 이것은 측도의 개념을 반드시 필요로 하지 않으면서도 르벡 적분과 르벡-스틸체스 적분을 포함하는 광범위한 적분 개념을 제공한다.

일반적인 리만 적분은 적분 구간의 분할의 폭을 균일하게 0으로 가까이 할 때의 해당 리만 합의 극한으로 정의되지만, 리만 합의 취하는 방법이나 분할의 폭의 줄이는 방법을 바꿈으로써 다양한 적분을 정의할 수 있으며, 이와 같이 정의되는 적분을 리만형 적분이라고 한다. 예를 들어, 맥신 적분, 헨스톡-쿠르츠바일 적분과 같은 게이지 적분이 리만형 적분이다.

영 적분은 리만-스틸체스 적분의 일반화로, 유계 변동 함수를 사용하는 대신 무한한 변동의 함수를 사용한 것이다.

이토 적분이나 스트라토노비치 적분과 같은 브라운 운동을 수반하는 확률 과정에 대한 적분을 확률 적분이라고 한다.

정수론이나 표현론의 주변 분야에서 자주 사용되는, 국소 콤팩트 군 위에서 정의되는 불변 측도(하르 측도)에 관한 르벡 방식의 적분을 불변 적분이라 한다. 르벡 적분은 실수 전체가 가법에 관해 이루는 국소 콤팩트 아벨 군 '''R''' 위의 불변 측도로서 르벡 측도를 취한 불변 적분이다(이 경우의 불변은 평행 이동 불변성을 가리켜 말한다).

4. 1. 리만 적분

리만 적분은 주어진 구간에서 리만 합의 극한으로 적분을 정의한다.^[22] 폐구간 [a,b]는

a = x_0 \leqq t_1 \leqq x_1 \leqq t_2 \leqq x_2 \leqq \cdots \leqq x_{n-1} \leqq t_n \leqq x_n = b . \,\!

와 같이 더 작은 구간으로 분할될 수 있다.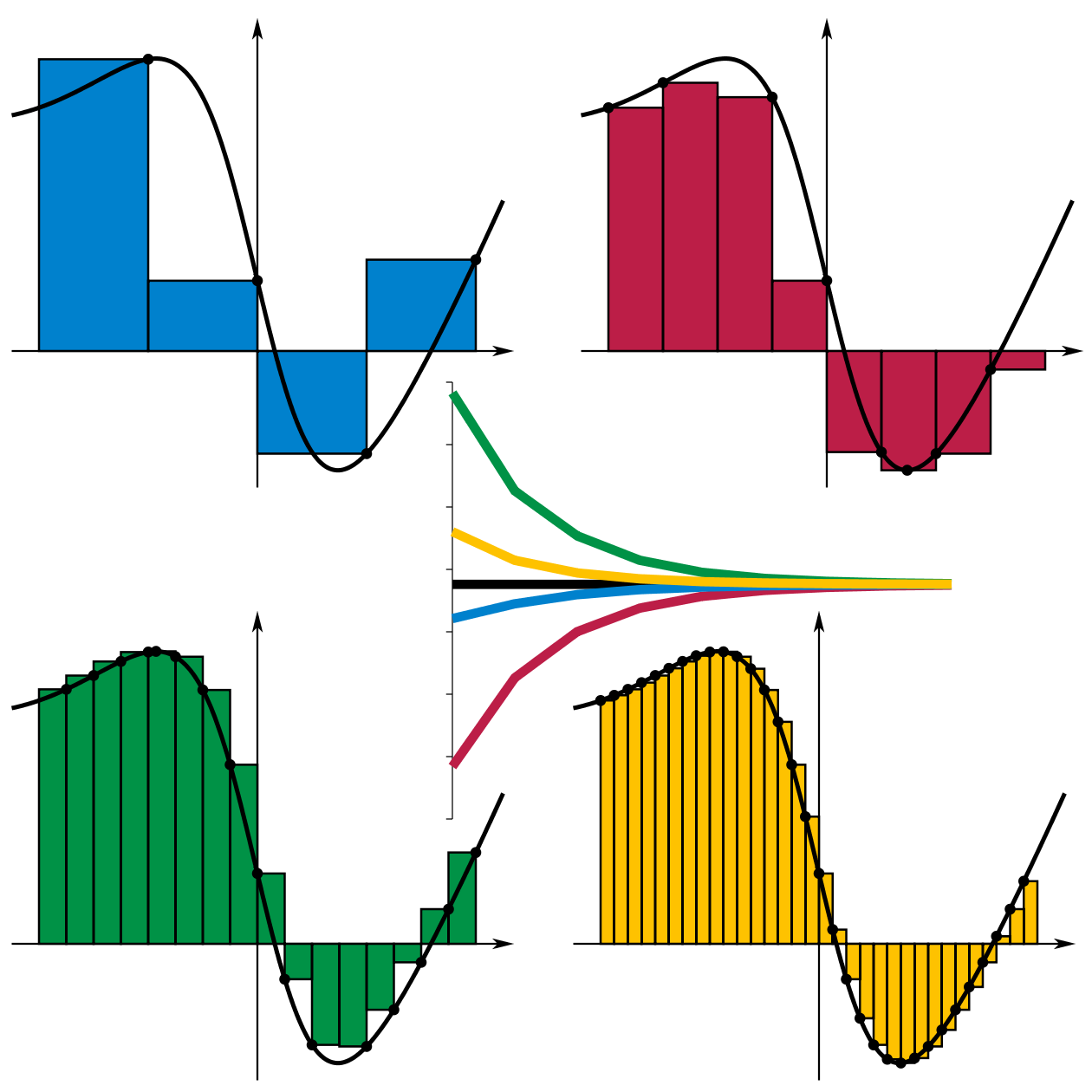

구간 [a,b]를 n 개의 하위 구간으로 분할하는 경우, 하위 구간들은 [''x''_''i''−1, ''x''_''i'']와 같이 ''i''에 의해 표기될 수 있다. 분할된 각각의 하위 구간의 표시는, ''t''_''i'' ∈ [''x''_''i''−1, ''x''_''i'']와 같이 지정할 수 있다. 함수 f(x)의 특정 구간 [a, b]를 n 개의 하위 구간으로 분할 할 때 리만 합은

\sum_{i=1}^{n} f(t_i) \Delta_i ;

와 같이 정의된다.

각각의 하위 구간들은 사각형을 구성하게 된다. 이때 곡선과 만나는 어느 지점을 사각형의 높이로 삼을 것인지에 따라 사각형의 크기가 달라지게 된다. 예를 들어 하위 구간의 시작점을 기준으로 한다면 왼쪽 리만 합, 끝점을 기준으로 한다면 오른쪽 리만 합, 가운데 지점을 기준으로 하는 가운데 리만 합, 하위 구간에서 곡선의 가장 높은 곳을 기준으로 하는 최댓값 리만 합 등을 만들 수 있다.^[79]^[77]

구간 [a,b]에 대하여 ''k''를 간격으로 하여 ''n'' 개로 분할된 하위 구간의 변량을 Δ_''k'' = ''x''_''k''−''x''_''k''−1 라 하면, 전체 구간 [a,b]는 분할 된 각각의 하위 구간들의 합으로 생각할 수 있다. 리만 적분은 구간 [a.b]에서 리만 합의 극한을 구하는 것과 같다. 이를 식으로 나타내면 다음과 같다.^[79]^[77]

:

\int_{a}^{b} f(x)dx=\lim_{n \to \infty}  \sum_{k=1}^{n}f(x_k) \Delta x \quad \left( x_{k} = a + k \Delta x,\ \Delta x =\frac {b-a} {n} \right)

선택된 태그가 각 구간에서 함수의 최댓값(또는 최솟값)인 경우, 리만 합은 상위(또는 하위) 다르부 합이 되어 리만 적분과 다르부 적분 사이의 밀접한 관계를 보여준다.

4. 2. 르베그 적분

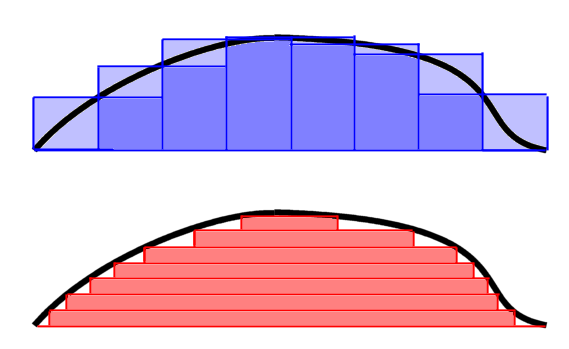
르베그 적분은 리만 적분에 비해 보다 광범위하게 적용할 수 있는 적분이다.^[80] 예를 들어 리만 적분으로는 철골의 질량을 쉽게 계산할 수 있지만, 철구의 질량은 계산하기 어렵다. 반면 르베그 적분은 형태에 제약 없이 사용할 수 있어 하중 계산 등에 흔히 쓰인다.

르베그 적분은 리만 적분의 확장으로 볼 수 있다.^[80] 리만 적분이 함수의 정의역을 분할하여 접근하는 반면, 르베그 적분은 함수의 치역을 분할하여 적분을 정의한다.^[26]

르베그 적분의 정의는 측도 μ를 정의하는 것에서 시작한다. 가장 간단한 경우, 구간 ''A'' = [''a'',''b'']의 르베그 측도 μ(''A'')는 구간의 폭 ''b'' - ''a''로 정의된다. 이 경우 르베그 적분과 리만 적분은 같은 값을 갖는다.^[27]

일반적인 접근법은 우선 측도 ''A''의 지시 함수의 적분을 다음과 같이 정의하는 것이다.

:

\int 1_A d\mu = \mu(A)

.

측정 가능한 단순 함수 ''s''를 0 이상의 자연수인 n개의 구역으로 분할하면,

:

\begin{align}\int s \, d\mu &{}= \int\left(\sum_{i=1}^{n} a_i 1_{A_i}\right) d\mu \\&{}= \sum_{i=1}^{n} a_i\int 1_{A_i} \, d\mu \\&{}= \sum_{i=1}^{n} a_i \, \mu(A_i)\end{align}

이 때, 단순 함수 ''s''에 의한 측도 ''A''_''i'' 에 포함되는 값 ''a''_''i''가 존재한다. 한편, 측정 가능한 ''E''를 다음과 같이 정의한다.

:

\int_E s \, d\mu = \sum_{i=1}^{n} a_i \, \mu(A_i \cap E) .

따라서, 함수 f의 르베그 적분은

:

\int_E f \, d\mu = \sup \left \{ \int_E s \, d\mu\, \colon 0 \leqq s\leqq f  \right \}

; (''s''는 단순 함수)

과 같이 되고, 음이 아닌 측정가능한 함수 f의 상한은 다음과 같이 표현할 수 있다.

:

\begin{align}f^+(x) &{}= \begin{cases}f(x), & \text{if } f(x) > 0 \\0, & \text{otherwise}\end{cases} \\f^-(x) &{}= \begin{cases}

f(x), & \text{if } f(x) < 0 \\

0, & \text{otherwise}\end{cases}\end{align}

결국, ''f''의 르베그 적분은

:

\int_E |f| \, d\mu < \infty , \,\!

일때

:

\int_E f \, d\mu = \int_E f^+ \, d\mu - \int_E f^- \, d\mu . \,\!

로 정의된다.

앙리 르베그는 폴 몽텔에게 보낸 편지에서 자신의 적분을 다음과 같이 설명했다.^[25]

4. 3. 기타 적분

적분은 여러 가지 형식으로 구분된다. 가장 일반적으로 널리 쓰이는 적분은 리만 적분과 르베그 적분이다. 리만 적분과 르베그 적분을 확장한 리만-스틸티어스 적분, 르베그-스틸티어스 적분 등 여러 가지 확장이 존재한다.

다르부 적분: 다르부 합(제한된 리만 합)으로 정의되지만 리만 적분과 동등하다. 함수가 다르부 적분 가능한 것과 리만 적분 가능한 것은 동치이다. 다르부 적분은 리만 적분보다 정의하기가 더 쉽다는 장점이 있다.
리만-스틸체스 적분: 변수가 아닌 함수에 대해 적분하는 리만 적분의 확장이다.
르베그-스틸체스 적분: 요한 라돈이 더욱 발전시킨 것으로, 리만-스틸체스 적분과 르베그 적분을 일반화한다.
다니엘 적분: 측도에 의존하지 않고 르베그 적분과 르베그-스틸체스 적분을 포함한다.
하르 적분: 1933년 알프레드 하르가 도입한 국소적으로 컴팩트한 위상군에서의 적분에 사용된다.
헨스톡-쿠르츠바일 적분: 아르노 덩주, 오스카 페롱과 (가장 우아하게, 게이지 적분으로) 야로슬라프 쿠르츠바일에 의해 다양하게 정의되었고, 랄프 헨스톡에 의해 개발되었다.
킨친 적분: 알렉산드르 킨친의 이름을 따서 명명되었다.
이토 적분과 스트라토노비치 적분: 브라운 운동과 같은 반마팅게일에 대한 적분을 정의한다.
영 적분: 무한 변분의 특정 함수에 대한 일종의 리만-스틸체스 적분이다.
거친 경로 적분: 일부 추가적인 "거친 경로" 구조를 갖춘 함수에 대해 정의되며, 반마팅게일과 분수 브라운 운동과 같은 과정에 대한 확률적 적분을 일반화한다.
슈케 적분: 프랑스 수학자 Gustave Choquet이 1953년에 만든 부가적 또는 초가적 적분이다.
보흐너 적분: 바나흐 공간에서 값을 가지는 함수에 대한 르베그 적분의 일반화이다.

리만-스틸체스 적분은 유계 변동 함수 φ를 사용한 리만 적분의 확장이다.

:

\int_{a}^{b} f(x) d\varphi(x) = \lim \sum f(\xi)\delta\varphi

φ(x) = x일 때는 일반적인 리만 적분이며, φ가 미분 가능하고 φ'가 연속이면, 밀도를 갖는 리만 적분

:

\int_{a}^{b} f(x)d\varphi(x) = \int_{a}^{b} f(x)\varphi'(x)dx

의 형태가 된다.

르벡-스틸체스 적분은 르벡 적분과 리만-스틸체스 적분의 확장이다. 가법 집합 함수의 변동이 결정하는 측도에 관한 르벡 방식의 적분

:

\int_X f(x)\,d\Phi(x)

이며, 요한 라돈이 자세히 연구했다.

다니엘 적분은 적분을 선형 작용소로 정의한다. 이것은 측도의 개념을 반드시 필요로 하지 않으면서도 르벡 적분과 르벡-스틸체스 적분을 포함하는 광범위한 적분 개념을 제공한다.

일반적인 리만 적분은 적분 구간의 분할의 폭을 균일하게 0으로 가까이 할 때의 해당 리만 합의 극한으로 정의되지만, 리만 합의 취하는 방법이나 분할의 폭의 줄이는 방법을 바꿈으로써 다양한 적분을 정의할 수 있으며, 이와 같이 정의되는 적분을 리만형 적분이라고 한다. 예를 들어, 맥신 적분, 헨스톡-쿠르츠바일 적분과 같은 게이지 적분이 리만형 적분이다.

영 적분은 리만-스틸체스 적분의 일반화로, 유계 변동 함수를 사용하는 대신 무한한 변동의 함수를 사용한 것이다.

이토 적분이나 스트라토노비치 적분과 같은 브라운 운동을 수반하는 확률 과정에 대한 적분을 확률 적분이라고 한다.

정수론이나 표현론의 주변 분야에서 자주 사용되는, 국소 콤팩트 군 위에서 정의되는 불변 측도(하르 측도)에 관한 르벡 방식의 적분을 불변 적분이라 한다. 르벡 적분은 실수 전체가 가법에 관해 이루는 국소 콤팩트 아벨 군 '''R''' 위의 불변 측도로서 르벡 측도를 취한 불변 적분이다(이 경우의 불변은 평행 이동 불변성을 가리켜 말한다).

5. 성질

5. 1. 피적분 함수에 대한 선형성

닫힌 구간 $[a, b]$에서 리만 적분 가능한 함수들의 집합은 점별 덧셈과 스칼라 곱 연산에 대해 벡터 공간을 이루며, 적분 연산

:

f \mapsto \int_a^b f(x) \; dx

은 이 벡터 공간 위의 선형 함수이다.^[31] 따라서 적분 가능한 함수들의 집합은 선형 결합에 대해 닫혀 있으며, 선형 결합의 적분은 적분들의 선형 결합이다.

:

\int_a^b (\alpha f + \beta g)(x) \, dx = \alpha \int_a^b f(x) \,dx + \beta \int_a^b g(x) \, dx. \,

마찬가지로, 주어진 측도 공간 $E$와 측도 $\mu$에 대한 실수 값 레베그 적분 가능 함수들의 집합은 선형 결합에 대해 닫혀 있으므로 벡터 공간을 이루며, 레베그 적분

:

f\mapsto \int_E f \, d\mu

은 이 벡터 공간 위의 선형 함수이므로 다음이 성립한다.^[30]

:

\int_E (\alpha f + \beta g) \, d\mu = \alpha \int_E f \, d\mu + \beta \int_E g \, d\mu.

더 일반적으로, 국소적으로 컴팩트한 위상체 K 위의 국소적으로 컴팩트한 완비 위상선형공간 V에 값을 갖는 가측함수들의 벡터 공간을 생각할때, 추상적분을 정의할 수 있다. 이 경우, 선형성은 적분이 V의 원소인 함수의 부분 공간에 대해 성립한다. 가장 중요한 특수한 경우는 K가 실수체, 복소수체, p-adic number체 또는 그의 유한 확장이고, V가 유한차원 벡터 공간일 때와, K가 복소수체이고, V가 복소 힐베르트 공간일 때 발생한다.^[32]

선형성과 어떤 자연스러운 연속성, 그리고 특정 종류의 "단순한" 함수에 대한 정규화는 적분의 대안적인 정의를 제공하는 데 사용될 수 있다. 다니엘 적분과 부르바키에의해 일반화된 경우가 이에 해당한다.

5. 2. 적분 부등식

닫힌 유계 구간 \[a, b\]에서 정의된 리만 적분 가능 함수에 대해 여러 부등식들이 성립하며, 이는 르벡 적분과 다니엘 적분으로 일반화될 수 있다.

상계와 하계: 닫힌 구간 \[a, b\]에서 적분 가능한 함수 f는 그 구간에서 반드시 유계이다. 모든 x ∈ \[a, b\]에 대해 m ≤ f(x) ≤ M을 만족하는 실수 m과 M이 존재한다. 따라서 다음이 성립한다.

:

m(b - a) \leq \int_a^b f(x) \, dx \leq M(b - a).

함수 사이의 부등식: 각 x ∈ \[a, b\]에 대해 f(x) ≤ g(x)이면 다음이 성립한다.

:

\int_a^b f(x) \, dx \leq \int_a^b g(x) \, dx.

:또한, 함수 사이의 부등식이 엄격하면 적분 사이의 부등식도 엄격하다. 즉, 각 x ∈ \[a, b\]에 대해 f(x) < g(x)이면 다음이 성립한다.

:

\int_a^b f(x) \, dx < \int_a^b g(x) \, dx.

부분 구간: \[c, d\]가 \[a, b\]의 부분 구간이고 모든 x에 대해 f(x) ≥ 0이면 다음이 성립한다.

:

\int_c^d f(x) \, dx \leq \int_a^b f(x) \, dx.

함수의 곱과 절댓값: f가 닫힌 구간 \[a, b\]에서 리만 적분 가능하면 |f|도 리만 적분 가능하며 다음이 성립한다.

:

\left| \int_a^b f(x) \, dx \right| \leq \int_a^b | f(x) | \, dx.

:또한, f와 g가 모두 리만 적분 가능하면 fg도 리만 적분 가능하며 다음이 성립한다.

:

\left( \int_a^b (fg)(x) \, dx \right)^2 \leq \left( \int_a^b f(x)^2 \, dx \right) \left( \int_a^b g(x)^2 \, dx \right).

:이 부등식은 코시-슈바르츠 부등식으로 알려져 있으며, 힐베르트 공간 이론에서 중요한 역할을 한다.

'''홀더 부등식''': p와 q가 $1 = \frac{1}{p} + \frac{1}{q} = 1$ 인 두 실수이고, f와 g가 두 리만 적분 가능 함수라고 하자. 그러면 |f|^p와 |g|^q도 적분 가능하며 다음 홀더 부등식이 성립한다.

:

\left|\int f(x)g(x)\,dx\right| \leq\left(\int \left|f(x)\right|^p\,dx \right)^{1/p} \left(\int\left|g(x)\right|^q\,dx\right)^{1/q}.

:p = q = 2일 때, 홀더 부등식은 코시-슈바르츠 부등식이 된다.

'''민코프스키 부등식''': p ≥ 1인 실수이고 f와 g가 리만 적분 가능 함수라고 하자. 그러면 |f|^p, |g|^p, 그리고 |f + g|^p도 리만 적분 가능하며 다음 민코프스키 부등식이 성립한다.

:

\left(\int \left|f(x)+g(x)\right|^p\,dx \right)^{1/p} \leq\left(\int \left|f(x)\right|^p\,dx \right)^{1/p} +\left(\int \left|g(x)\right|^p\,dx \right)^{1/p}.

:이 부등식의 유사체는 L^p 공간의 구성에 사용된다.

평균값 정리, 피적분 함수에 대한 적분의 단조성, 적분 구간에 대한 적분의 단조성 등이 성립한다.

5. 3. 기타 성질

[''a'', ''b'']/f}}가 실수 값을 가지는 리만 적분 가능 함수일 때, 구간 {{math^영어에 대한 적분은 a < b 인 경우에 정의된다. 이때 a > b 인 경우에도 적분을 정의할 수 있으며, 다음과 같다.^[19]

:

\int_a^b f(x) \, dx = - \int_b^a f(x) \, dx.

만약 a = b 이면, 다음이 성립한다.

:

\int_a^a f(x) \, dx = 0.

구간 에서 의 적분 가능성은 임의의 부분 구간 에서 의 적분 가능성을 의미하며, 특히 적분은 c가 의 임의의 원소인 경우 다음과 같은 성질을 갖는다.^[31]

:

\int_a^b f(x) \, dx = \int_a^c f(x) \, dx + \int_c^b f(x) \, dx.

따라서, a, b, c의 순환 순열에 대하여 다음 관계식이 잘 정의된다.

:

\begin{align}\int_a^c f(x) \, dx &{}= \int_a^b f(x) \, dx - \int_c^b f(x) \, dx \\&{} = \int_a^b f(x) \, dx + \int_b^c f(x) \, dx\end{align}

적분을 계산하는 가장 기본적인 기법은 미적분의 기본 정리에 기반하며, 피적분 함수와 적분이 적분 경로에 특이점이 없으면, 미적분의 기본 정리에 의해

:

\int_a^b f(x)\,dx=F(b)-F(a).

가 된다. 때로는 적분을 계산하기 위해 치환 적분법, 부분 적분법, 삼각 치환 적분법, 부분 분수를 이용한 적분법과 같은 기법을 사용해야 한다.

; 적분 구간에 대한 가법성

:

\int_{a}^{\xi}f(x)\,dx + \int_{\xi}^{b}f(x)\,dx = \int_{a}^{b}f(x)\,dx

; 치환 적분법

: (a = x(α), b = x(β)라는 조건 하에)

:

\int_{a}^{b} f(x)dx = \int_{\alpha}^{\beta} f(x(t)) {dx \over dt} dt.

; 부분 적분법

:

\int_{a}^{b} f'(x)g(x) dx = [f(x)g(x)]_{a}^{b} - \int_{a}^{b} f(x)g'(x) dx.

6. 응용

적분은 여러 분야에서 광범위하게 사용된다. 예를 들어, 확률론에서 적분은 특정 범위 내에 특정 확률변수가 들어갈 확률을 결정하는 데 사용된다.^[48] 또한, 전체 확률밀도함수 아래의 적분은 반드시 1이 되어야 한다.^[49]

적분은 곡선 경계를 가진 2차원 영역의 넓이를 계산하거나, 3차원 물체의 부피를 계산하는 데 사용된다.^[50] 원판이나 와셔와 같은 3차원 물체의 부피는 원판 적분을 통해 계산할 수 있다.^[51]

운동학에서 변위, 시간, 속도와 같은 양을 구하는 데에도 사용된다. 예를 들어, 직선 운동에서 시간 간격 $[a,b]$ 에 대한 물체의 변위는 다음과 같다.

: $x(b)-x(a) = \int_a^b v(t) \,dt,$

여기서 $v(t)$ 는 시간의 함수로 표현된 속도이다.^[52] 초기 위치 $A$ 에서 최종 위치 $B$ 까지 힘 $F(x)$ 가 하는 일은 다음과 같다.^[53]

: $W_{A\rightarrow B} = \int_A^B F(x)\,dx.$

적분은 열역학에서도 사용되며, 열역학적 적분은 두 주어진 상태 간의 자유 에너지 차이를 계산하는 데 사용된다.

4차 산업혁명 시대에 중요성이 커지고 있는 인공지능, 빅데이터 등의 분야에서도 핵심적인 개념으로 사용된다.

참조

_[1] 서적 Integral calculus 1967, 2016
_[2] 서적 2011
_[3] 서적 2002
_[4] 서적 2009
_[5] 서적 2009
_[6] 논문 Intervals and the Origins of Calculus https://doi.org/10.1[...] 1998-05-01
_[7] 서적 2009
_[8] 서적 2009
_[9] 서적 1986
_[10] 서적 2009
_[11] 서적 2011
_[12] 서적 1989
_[13] 서적 2009
_[14] 서적 2009
_[15] 서적 2011, 1899
_[16] 서적 1929, 1822
_[17] 서적 1929
_[18] 서적 1929
_[19] 서적 1967
_[20] 서적 2016
_[21] 서적 1967
_[22] 서적 2016
_[23] 서적 1991
_[24] 서적 1987
_[25] 서적 2008
_[26] 서적 1999
_[27] 서적 2004
_[28] 서적 2001
_[29] 서적 1999
_[30] 서적 1987
_[31] 서적 1967
_[32] 서적 1987
_[33] 서적 1967
_[34] 서적 1987
_[35] 서적 1967
_[36] 서적
_[37] 서적
_[38] 서적
_[39] 서적
_[40] 서적
_[41] 서적
_[42] 서적
_[43] 서적
_[44] 서적
_[45] 서적
_[46] 서적
_[47] 서적
_[48] 서적
_[49] 서적
_[50] 서적
_[51] 서적
_[52] 서적
_[53] 서적
_[54] 서적
_[55] 서적
_[56] 서적
_[57] 서적
_[58] 서적
_[59] 서적
_[60] 서적 なっとくする数学記号講談社
_[61] 서적 A Course in Real Analysis https://books.google[...]
_[62] 서적 解析教程 https://books.google[...] シュプリンガー・ジャパン
_[63] 서적 대학수학 청문각
_[64] 서적 르베그 적분 전남대학교 출판부
_[65] 서적 수학을 만든 사람들(상) 미래사
_[66] 서적 르베그 적분 전남대학교 출판부
_[67] 서적 오일러가 사랑한 수 e 경문사
_[68] 문서 케플러가 적용한 방법은 엄밀하지는 않지만 본질적으로 리만 적분의 방법과 동일한 것이다.
_[69] 서적 수학을 만든 사람들(상) 미래사
_[70] 웹사이트 Thomas Jan Stieltjes http://www-history.m[...]
_[71] 서적 미분적분학 학문사 1998
_[72] 서적 근대 중국의 언어와 역사 소명출판 2005
_[73] 서적 수학자들의 전쟁 프로네시스 2007
_[74] 서적 전기 수학 기전연구사 2009
_[75] 서적 이공수학개요 학문사 1996
_[76] 서적 현대토목수학 동화기술 2010
_[77] 서적 쉬운 미분·적분학 숭실대학교출판부 2008
_[78] 서적 대학수학 청문각 1998
_[79] 서적 대학수학 청문각 1998
_[80] 서적 Real Analysis: Modern Techniques and Their Applications John Wiley & Sons 1984

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com