대수기하학

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사
3. 주요 개념
4. 세부 분야
5. 다른 분야와의 관계
6. 주요 연구자
참조

1. 개요

대수기하학은 대수방정식의 해의 자취로 표현되는 대수다양체를 연구하는 기하학의 한 분야이다. 고대 그리스 시대부터 연구가 시작되었으며, 20세기 중반 알렉산더 그로텐디크에 의해 스킴이 도입되면서 정수론 등 다양한 분야에 적용되는 기본 도구가 되었다. 주요 개념으로는 아핀 대수다양체, 정칙 함수, 사영 대수다양체 등이 있으며, 고전적 대수기하학, 불변량 이론, 교차 이론, 산술기하학, 실수 대수기하학, 특이점 이론, 계산 대수기하학, 비가환 대수기하학 등의 세부 분야로 나뉜다. 통계학, 제어 이론, 로봇 공학 등 다양한 분야에 응용되며, 수리물리학, 기계 학습 등과의 관계 연구도 활발히 진행되고 있다.

더 읽어볼만한 페이지

대수기하학 - 타원곡선
타원곡선은 체 위에서 정의되고 특이점이 없으며 종수가 1인 사영 대수 곡선으로, 유리점을 가지며, 특정 형태의 방정식으로 표현되고, 실수체 위에서는 연결 성분 개수가 판별식에 따라 달라지며, 복소수체 위에서는 원환면과 위상적으로 동형이고, 점들 간에 군 연산이 정의되어 암호학 및 정수론에 활용된다.
대수기하학 - 매끄러운 함수
매끄러운 함수는 함수의 미분 가능성을 나타내는 척도로, k번 미분 가능하고 그 미분 함수가 연속일 경우 C^k로 표기하며, 무한히 미분 가능한 함수를 의미하고, 곡선의 부드러움을 측정하는 데 활용된다.
수학 - 회귀 분석
회귀 분석은 종속 변수와 하나 이상의 독립 변수 간의 관계를 모델링하고 분석하는 통계적 기법으로, 최소 제곱법 개발 이후 골턴의 연구로 '회귀' 용어가 도입되어 다양한 분야에서 예측 및 인과 관계 분석에 활용된다.
수학 - 수학적 최적화
수학적 최적화는 주어진 집합에서 실수 또는 정수 변수를 갖는 함수의 최댓값이나 최솟값을 찾는 문제로, 변수 종류, 제약 조건, 목적 함수 개수에 따라 다양한 분야로 나뉘며 여러 학문 분야에서 활용된다.

대수기하학

2. 역사

대수기하학은 초기에는 데카르트 좌표계 위에 유한개의 대수방정식들을 만족하는 해들의 자취로 표현되는 대상, 이른바 대수다양체를 연구하는 기하학 분야였다.

고대 그리스의 수학자들은 원뿔 곡선 및 이차 곡면과 같은, 간단한 실수 대수다양체들을 연구하였다. 또한, 고대의 수학은 대수학 대신 기하학에 중점을 두었으므로, 대수적인 문제들을 기하학적인 문제로 변환시켜 푸는 경우가 많았다. 예를 들어, 10세기 수학자 이븐 알 하이삼^[35]과 11세기 수학자 오마르 하이얌^[35]은 3차 방정식을 곡선의 교차점을 사용하여 풀었다.

대수기하학의 몇몇 기원은 기원전 5세기 헬레니즘 그리스의 연구로 거슬러 올라간다. 예를 들어 델로스 문제는 주어진 변 ''a''와 ''b''에 대해 변 ''x''의 세제곱이 직육면체 ''a''²''b''와 같은 부피를 갖도록 길이 ''x''를 구성하는 것이었다. 메나이크모스는 평면 원뿔 곡선 쌍 ''ay'' = ''x''²와 ''xy'' = ''ab''의 교차를 통해 이 문제를 기하학적으로 고려했다.^[2] 기원전 3세기 아르키메데스와 아폴로니우스는 좌표를 사용하여 원뿔 곡선에 대한 추가적인 문제를 체계적으로 연구했다.^[2] 아폴로니우스는 그의 저서 『원뿔 곡선』에서 해석 기하학과 매우 유사한 방법을 개발했는데, 그의 연구는 때때로 데카르트의 연구를 약 1800년 앞선 것으로 여겨진다.^[3]

중세 시대의 오마르 하이얌, 피사의 레오나르도, 게르소니데스, 니콜 오렘을 포함한 중세 수학자들은 순전히 대수적인 방법으로 특정 3차 및 2차 방정식을 풀고 결과를 기하학적으로 해석했다. 페르시아 수학자 오마르 하이얌은 산술, 대수, 기하학 사이에 관계가 있다고 믿었다.

19세기 중반에, 베른하르트 리만이 아벨 함수론 안에서 쌍유리 동치 등 대수기하학의 중심 개념을 만들어냈고, 19세기 후반에는, 이탈리아의 직관적인 대수기하학이 발전했다(대수기하학의 이탈리아 학파). 20세기 전반에는, 앙드레 베유, 오스카 자리스키에 의해 추상적인 대수기하학 연구가 진행되었고, 1950년대 이후 그로텐디크의 스킴론에 의해 대수기하학 전체가 크게 개편되었다.

2. 1. 근대 이전

르네 데카르트와 피에르 드 페르마는 좌표계를 사용하여 기하학적인 문제들을 대수적인 문제로 변환하는 방법을 제시하였다.^[3] 블레즈 파스칼과 지라르 데자르그는 사영기하학을 순수 기하학적인 방법으로 발전시켰다. 그러나 18세기에 미적분학이 발견되고 해석적 방법들이 도입되면서, 기하학의 대수적 접근에 대한 관심은 18세기까지 크게 줄어들었다.^[2]

2. 2. 19세기 ~ 20세기 초

19세기에는 비유클리드 기하학과 아벨 함수의 발견으로 잊혀졌던 대수적 기법들이 다시 중요해졌다. 아서 케일리는 사영 공간 위의 이차 형식을 연구하였고, 펠릭스 클라인은 에를랑겐 프로그램의 일환으로 사영기하학을 체계적으로 연구하였고, 쌍유리 변환의 개념을 정의하였다. 또한, 아벨 적분의 발견으로 베른하르트 리만은 리만 곡면을 정의하였고, 리만-로흐 정리를 증명하였다.^[25]

이 시기, 대수기하학의 기반이 되는 가환대수학이 발전하였다. 다비트 힐베르트는 힐베르트 영점 정리 및 힐베르트 기저 정리를 증명하였고, 프랜시스 매콜리는 소거 이론을 개발하였다. 이는 오랫동안 잊혀져 있다가, 이후 최근 특이점 이론의 기반으로 부활하게 되었다.

귀도 카스텔누오보, 페데리고 엔리퀘스, 자코모 알바네세, 파스콸레 델 페초, 프란체스코 세베리, 주세페 베로네세 등으로 구성된 이탈리아 학파는 대수다양체들을 쌍유리 동치 아래 분류하는 것을 목표로 삼았고, 이들은 모든 대수 곡면들을 분류하는 데 성공하였다 (엔리퀘스-고다이라 분류). 그러나 이들의 업적은 공리적으로 엄밀하지 못했고, 상당 부분은 훗날 오류로 밝혀졌으나 다른 부분들은 후대에 엄밀하게 재증명되었다.

2. 3. 20세기 중반 이후

B. L. 판 데르 바르덴, 오스카 자리스키, 앙드레 베유는 가환대수학, 평가론, 아이디얼 이론 등 현대 가환대수학에 기반하여 대수기하학의 기초를 개발했다.^[25] 이들은 이탈리아 대수기하학 학파의 결과를 증명하기 위한 엄격한 틀을 제공하는 것을 목표로 했다.^[25]

1950년대와 1960년대에 장 피에르 세르와 알렉산더 그로텐디크는 층 이론을 이용하여 기초를 재구성했다.^[25] 이후 1960년대부터 그로텐디크를 중심으로 스킴 개념이 호몰로지 기법과 함께 매우 정교하게 연구되었다.^[25] 10년간의 급속한 발전을 거쳐 1970년대에 이 분야는 안정되었고, 수론, 대수 다양체에 대한 고전적 기하학 문제, 특이점, 모듈, 형식 모듈 등에 새롭게 응용되었다.^[25]

아벨 다양체는 점들이 아벨 군을 이루는 투영 다양체로, 정의 방정식을 통해 쉽게 이해하기 어려운 중요한 다양체 부류이다.^[25] 타원 곡선은 풍부한 이론을 가진 아벨 다양체의 전형적인 예시이다.^[25] 이들은 페르마의 마지막 정리 증명에 중요한 역할을 했으며, 타원 곡선 암호에도 사용된다.^[25]

대수기하학은 다양체에 대한 일반적인 명제에 관심을 가지는 추상적인 경향과 함께, 주어진 다양체를 효과적으로 계산하는 방법도 개발하여 계산 대수기하학이라는 새로운 분야로 이어졌다.^[25] 이 분야의 창립 방법 중 하나는 1965년 브루노 부흐베르거가 도입한 그뢰브너 기저 이론이다.^[25] 또 다른 창립 방법은 1973년 조지 E. 콜린스가 도입한 원통형 대수 분해로, 특히 실 대수기하학에 전념한다.^[25]

계산 대수 기하학의 시작은 1979년 6월 프랑스 마르세유에서 열린 EUROSAM '79 (International Symposium on Symbolic and Algebraic Manipulation)로 추정할 수 있다. 이 회의에서 다음과 같은 주요 발표가 있었다.

데니스 아논(Dennis S. Arnon)은 조지 E. 콜린스의 원통형 대수 분해|Cylindrical algebraic decomposition|CAD^영어가 반대수적 집합(semi-algebraic set)의 위상 계산을 가능하게 함을 보였다.
브루노 부흐베르거는 그뢰브너 기저와 이를 계산하는 알고리즘을 제시했다.
다니엘 라자드는 동차 다항식 방정식 계를 풀기 위한 새로운 알고리즘을 제시했는데, 이는 예상되는 해의 수에서 본질적으로 다항적이며, 미지수의 수에서 단순 지수적인 계산 복잡성|computational complexity^영어을 가진다. 이 알고리즘은 매콜리|Francis Sowerby Macaulay^영어의 다변수 결정식과 깊이 관련되어 있다.

지난 수십 년 동안 기호적 방법을 보완하는 수치 대수 기하학|numerical algebraic geometry^영어이라는 수학적 이론이 발전해 왔다. 주요 전산 방법은 호모토피 연속|homotopy continuation^영어이며, 이는 대수 기하학 문제를 풀기 위한 부동 소수점 전산 모델을 뒷받침한다.

3. 주요 개념

체 ''k''에서 시작하여 고전 대수기하학을 전개한다. 이때 체 ''k''는 보통 복소수 '''C'''를 사용하지만, 체 ''k''가 대수적으로 닫혀있음을 가정하여도 동일한 결과를 얻을 수 있다. ''k''에 대한 ''n''차원 아핀 공간을 '''A'''ⁿ(''k'')로 표기하며, 좌표계를 고정하면 '''A'''ⁿ(''k'')를 ''k''^''n''으로 식별할 수 있다. 여기서 ''k''ⁿ을 사용하지 않는 이유는 ''k''ⁿ이 갖는 벡터 공간 구조를 "잊어버린다"는 것을 강조하기 위함이다.^[25]

함수 ''f'' : '''A'''^''n'' → '''A'''¹이 다항식으로 쓸 수 있다면, 즉 ''k''[''x''₁,...,''x''_''n'']에 다항식 ''p''가 있어 모든 점 ''M''의 좌표가 (''t''₁,...,''t''_''n'')일 때 ''f''(''M'') = ''p''(''t''₁,...,''t''_''n'')이 성립한다면, 이를 ''다항식''(또는 ''정칙'')이라고 한다. 함수가 다항식(또는 정칙)인 속성은 '''A'''^''n''에서 좌표계를 선택하는 것에 의존하지 않는다.^[25]

좌표계가 선택되면 아핀 ''n''-공간에 대한 정칙 함수는 ''k''에 대한 ''n'' 변수의 다항식 함수의 링으로 식별될 수 있다. 따라서 '''A'''^''n''에 대한 정칙 함수의 집합은 링이며, 이를 ''k''['''A'''^''n'']으로 표기한다.^[25]

다항식이 한 점에서 그 값을 평가했을 때 0이 되면 그 점에서 ''소멸''된다고 한다. ''k''['''A'''ⁿ]에 있는 다항식의 집합 ''S''의 ''소멸 집합''은 ''S''의 모든 다항식이 소멸되는 '''A'''^''n''의 모든 점의 집합 ''V''(''S'')이다. 이를 기호로 나타내면 다음과 같다.^[25]

: $V(S) = \{(t_1,\dots,t_n) \mid p(t_1,\dots,t_n) = 0 \text{ for all } p \in S\}.\,$

'''A'''^''n''의 부분 집합이 ''V''(''S'')인 경우, 이를 ''대수적 집합''이라고 한다. ''V''는 대수다양체를 의미한다.^[25]

'''A'''^''n''의 부분 집합 ''U''가 주어지면, 이를 생성하는 다항식의 집합을 정의할 수 있는데, ''I''(''U'')를 소멸 집합이 ''U''를 포함하는 모든 다항식의 집합으로 정의한다. ''I''는 아이디얼을 의미한다. ''I''(''U'')는 항상 다항식 링 ''k''['''A'''^''n'']의 아이디얼이다.^[25]

여기서 두 가지 질문이 발생한다.^[25]

'''A'''^''n''의 부분 집합 ''U''가 주어졌을 때, ''U'' = ''V''(''I''(''U''))는 언제 성립하는가?
다항식의 집합 ''S''가 주어졌을 때, ''S'' = ''I''(''V''(''S''))는 언제 성립하는가?

첫 번째 질문에 대한 답은 '''A'''^''n''에 대한 자리스키 위상을 도입함으로써 제공된다. 이 위상의 닫힌 집합은 대수적 집합이고, ''k''['''A'''^''n'']의 대수적 구조를 직접 반영한다. ''U'' = ''V''(''I''(''U''))는 ''U''가 대수적 집합이거나 자리스키 닫힌 집합인 경우에만 성립한다. 두 번째 질문에 대한 답은 힐베르트 영점 정리에 의해 주어진다. 이 정리의 한 형태는, ''I''(''V''(''S''))가 ''S''에 의해 생성된 아이디얼의 근기라고 말한다.^[25]

힐베르트 기저 정리는 ''k''['''A'''^''n'']의 아이디얼이 항상 유한하게 생성된다는 것을 의미한다.^[25]

대수적 집합은 두 개의 더 작은 대수적 집합의 합집합으로 쓸 수 없는 경우 ''기약적''이라고 한다. 모든 대수적 집합은 기약적 대수적 집합의 유한 합집합이며, 이 분해는 유일하다. 따라서 그 요소들은 대수적 집합의 ''기약 성분''이라고 불린다. 기약적 대수적 집합은 ''대수다양체''라고도 한다. 대수적 집합이 소 아이디얼의 다항식 링의 소멸 집합으로 정의될 수 있는 경우에만 다양체이다.^[25]

연속 함수가 위상 공간에 대한 자연스러운 사상이고, 매끄러운 함수가 미분 다양체에 대한 자연스러운 사상인 것처럼, 대수적 집합에 대한 자연스러운 함수 클래스가 있는데, 이를 ''정칙 함수'' 또는 ''다항 함수''라고 한다. '''A'''^''n''에 포함된 대수적 집합 ''V''에 대한 정칙 함수는 '''A'''^''n''에 대한 정칙 함수의 ''V''로의 제한이다.^[25]

''V''에 대한 정칙 함수는 환을 형성하며, ''k''[''V'']로 표기한다. 이 환을 ''V''의 ''좌표 환''이라고 한다. ''k''[''V'']는 ''k''['''A'''^''n'']/''I''(''V'')와 동일시될 수 있다.^[25]

3. 1. 다항식의 영점

고전 대수기하학의 주요 관심사는 여러 다항식들의 공통 영점을 기하학적으로 연구하는 것이었다. 즉, 모든 다항식들의 값이 0이 되는 집합이 어떤 기하학적 성질을 갖는지 연구했다. 예를 들어, 2차원 구는 3차원 유클리드 공간

\mathbb R^3

에서 다음 식을 만족시키는 점

(x, y, z)

들의 집합으로 정의할 수 있다.

:

x^2\ +\ y^2\ +\ z^2-1\ =\ 0

비슷하게,

\mathbb R^3

에서 다음 두 식

:

\begin{array}{lllllll}x^2 &+& y^2 &+& z^2-1 &=& 0 \\x   &+& y   &+& z     &=& 0\end{array}

을 모두 만족시키는 점들의 집합은 원이 된다.

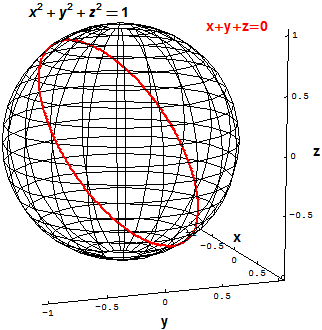
3차원 유클리드 공간 '''R'''³에서 반지름이 1인 2차원 구는 다음 식을 만족하는 모든 점

(x, y, z)

의 집합으로 정의할 수 있다.

:

x^2+y^2+z^2-1=0.\,

'''R'''³에서 "기울어진" 원은 다음 두 개의 다항식 방정식을 만족하는 모든 점

(x, y, z)

의 집합으로 정의할 수 있다.

:

x^2+y^2+z^2-1=0,\,

:

x+y+z=0.\,

3. 2. 아핀 대수다양체

체 ''k''에 대해, ''k'' 상의 ''n''차원 아핀 공간에서 다항식들의 영점 집합으로 정의되는 대수적 집합을 아핀 대수다양체라고 한다.

k[x_1,\cdots,x_n]

에 속하는 다항식

p

가 있어서

\mathbb A^n

에 속하는 임의의 점

(t_1,\cdots,t_n)

에 대해

f(t_1,\cdots,t_n) = p(t_1,\cdots,t_n)

이 성립하는 경우 함수

f: \mathbb A^n \to \mathbb A^1

를 정칙함수라고 한다.

n

차원 아핀 공간 상의 정칙 함수는

k

상의

n

변수 다항식과 동일하며,

k[\mathbb A^n]

로 쓴다.

S

가

k[\mathbb A^n]

의 부분집합일 때,

S

에 속하는 모든 다항식들이 0이 되는 점을

V(S)

로 쓰고, '

S

의 영점'이라고 하며 다음과 같이 정의한다.

:

V(S) = \{(t_1,\cdots,t_n) \in\mathbb A^n | \forall p \in S, p(t_1,\cdots,t_n) = 0\}

\mathbb A^n

의 부분 집합이 적당한

S

에 대해

V(S)

와 일치할 경우, 이를 대수적 집합이라 한다.

V

는 대수다양체(variety)의 첫 글자를 딴 것이다.

자리스키 위상은

\mathbb A^n

상에 정의되는,

k[\mathbb A^n]

의 대수적 구조가 반영된 위상이다. 이때 자리스키 위상은 아핀 공간 상의 대수적 집합을 닫힌 집합으로 하는 위상이다. 힐베르트 영점 정리는 다항식 집합과 그 영점 집합 사이의 관계를 설명한다.

힐베르트 기저 정리에 따르면

k[\mathbb A^n]

의 모든 아이디얼은 유한 생성된다.

그보다 작은 두 대수 집합의 합집합으로 나타낼 수 없는 대수 집합을 기약 대수 집합이라 하며, 이를 또한 대수다양체라고도 부른다. 대수 집합이 대수다양체가 될 필요충분조건은 그 집합을 정의하는 다항식들의 집합이 다항식환 내에서 소 아이디얼을 생성한다는 것이다.

대수적으로 닫힌 체 ''k''의 경우, 다음과 같은 대응 관계가 성립한다.

다항식환 $k[\mathbb A^n]$ 의 대수적 성질	아핀 공간 $\mathbb A^n(k)$ 의 기하학적 대상
아이디얼 $\mathfrak a$	아핀 대수 집합 $V(\mathfrak a)=\bigcap_{a\in\mathfrak a}a^{-1}(0)\subset\mathbb A^n$ (자리스키 위상에서 닫힌 부분 집합)
환의 원소 $f\in k[\mathbb A^n]$	아핀 공간 위의 정칙함수 $f\colon \mathbb A^n\to k$
극대 아이디얼 $(x_1-a_1,x_2-a_2,\dots,x_n-a_n)$	아핀 공간의 점 $(a_1,a_2,\dots,a_n)\in\mathbb A^n$ (스킴에서의 닫힌 점)
소 아이디얼 $\mathfrak p$	(기약) 아핀 대수다양체 $V(\mathfrak p)=\bigcap_{p\in\mathfrak p}p^{-1}(0)\subset\mathbb A^n$ (스킴에서의 닫히지 않은 점)
(유한 개의) 아이디얼의 곱 $\mathfrak a\mathfrak b$	대수 집합의 합집합 $V(\mathfrak a)\cup V(\mathfrak b)$
(임의의 개수의) 아이디얼의 합 $\sum_{\alpha\in I}\mathfrak a_\alpha$	대수 집합의 교집합 $\bigcap_{\alpha\in I}V(\mathfrak a_\alpha)$
소근기 $\sqrt{\mathfrak a}$	자리스키 위상에서의 폐포 $\operatorname{cl}(V(\mathfrak a))$
영 아이디얼 $\{0\}\subset k[\mathbb A^n]$	아핀 공간 전체 $\mathbb A^n$
단위 아이디얼 $k[\mathbb A^n]$	공집합 $\varnothing\subset\mathbb A^n$
아이디얼에 대한 몫환 $k[\mathbb A^n]/\mathfrak a$	대수 집합 위 정칙함수(regular function) $V(\mathfrak a)\to k$ 들의 환 $I(V(\mathfrak a))$
몫환에서의 동치류 $f+\mathfrak a\in k[\mathbb A^n]/\mathfrak a$	정칙함수의 $V(\mathfrak a)$ 에 대한 제한
소 아이디얼에 대한 몫환의 분수체 $\operatorname{Frac}(k[\mathbb A^n]/\mathfrak p)$	대수다양체 $V(\mathfrak p)$ 위 유리 함수체
소 아이디얼에 대한 몫환의 크룰 차원 (=몫환의 분수체의 초월 차수(transcendence degree))	대수다양체의 차원

3. 3. 정칙 함수

체 ''k''에 대한 ''n''차원 아핀 공간에 포함된 대수적 집합 ''V''에 대한 정칙 함수는 '''A'''^''n''에 대한 정칙 함수의 ''V''로의 제한으로 정의된다.

''V''에 대한 정칙 함수는 환을 형성하며, ''k''[''V'']로 표기한다. 이 환을 ''V''의 좌표 환이라고 한다. ''k''[''V'']는 ''k''['''A'''^''n'']/''I''(''V'')와 동일시될 수 있다.

3. 4. 사영 대수다양체

2차, 3차, 4차 다항식의 근을 구하는 공식은 실수를 대수적으로 더 완전한 복소수로 확장하는 것을 보여준다. 이와 유사하게, 대수적 다양체의 많은 성질은 아핀 공간을 기하학적으로 더 완전한 사영 공간으로 확장하는 것에서 나온다. 복소수가 다항식의 근인 ''i''를 추가하여 얻어지는 것처럼, 사영 공간은 평행선이 만나는 "무한대" 점들을 추가하여 만들어진다.

예를 들어, 다양체 (포물선)를 생각해보자. ''x''가 양의 무한대로 갈 때, 원점에서 점 (''x'', ''x''²)까지의 선의 기울기도 양의 무한대로 간다. ''x''가 음의 무한대로 갈 때, 같은 선의 기울기는 음의 무한대로 간다.

반면, 다양체 (삼차 곡선)의 경우, ''x''가 양의 무한대로 갈 때 원점에서 점 (''x'', ''x''³)까지의 선의 기울기는 양의 무한대로 가지만, ''x''가 음의 무한대로 갈 때도 기울기는 양의 무한대로 간다. 즉, 의 "무한대에서"의 거동은 과 다르다.

두 곡선의 ''사영 완비화''( 사영 평면에서 "무한대에서의" 연장)를 통해 이러한 차이를 알 수 있다. 포물선의 무한대 점은 정칙점이고, 그 접선은 무한대 직선이다. 반면 삼차 곡선의 무한대 점은 첨점이다. 두 곡선 모두 ''x''로 매개변수화되므로 유리 곡선이며, 리만-로크 정리에 의해 삼차 곡선은 아핀 공간에서 정칙점이므로 무한대에 특이점을 가져야 한다.

대수적 다양체의 많은 성질(birational 동치, 위상적 성질 등)은 "무한대에서"의 거동에 달려있어 사영 공간에서 다양체를 연구하는 것은 자연스럽다. 사영 기법은 대수 기하학의 많은 정리를 더 단순하고 명확하게 만들었으며, 베주 정리는 사영 공간에서만 가장 정확하게 표현된다.

오늘날, 차원 ''n''의 ''사영 공간'' '''P'''^''n''은 차원의 아핀 공간에서 원점을 지나는 직선들의 집합, 또는 차원의 벡터 공간에서 벡터 직선들의 집합으로 정의된다. 차원 공간에 좌표계를 선택하면, 직선의 모든 점은 ''k''의 원소로 곱해지는 것을 제외하고 동일한 좌표 집합을 갖는다. 이는 '''P'''^''n'' 점의 제차 좌표를 ''k''의 개 원소의 시퀀스로 정의하며, 0이 아닌 ''k''의 원소로 곱해지는 것은 무시한다(전체 시퀀스에 대해 동일).

개 변수에 대한 다항식은 원점을 지나는 직선의 모든 점에서 0이 되려면 동차 다항식이어야 한다. 이 경우, 다항식이 '''P'''^''n''의 해당 점에서 "소멸한다"고 한다. 이를 통해 '''P'''^''n''에서 유한 집합의 동차 다항식이 소멸하는 집합로 ''사영 대수적 집합''을 정의한다. 아핀 대수적 집합처럼, 사영 대수적 집합과 이를 정의하는 기약 동차 아이디얼 사이에는 전단사가 존재한다. ''사영 다양체''는 정의하는 아이디얼이 소수인 사영 대수적 집합이다. 즉, 사영 다양체는 동차 좌표환이 정역인 사영 대수적 집합이며, ''사영 좌표환''은 다양체를 정의하는 동차(기약) 아이디얼로 나눈 개 변수에 대한 다항식의 등급환의 몫이다. 모든 사영 대수적 집합은 사영 다양체의 유한한 합으로 고유하게 분해될 수 있다.

사영 다양체에서 정의될 수 있는 유일한 정칙 함수는 상수 함수이므로, 이 개념은 사영 상황에서 사용되지 않는다. 반면, ''유리 함수체'' 또는 ''함수체''는 아핀 경우처럼, 동차 좌표환에서 같은 차수의 두 동차 원소의 몫의 집합으로 정의되어 유용하다.

4. 세부 분야

'''고전적 대수기하학'''은 복소수와 같은 대수적으로 닫힌 체에서의 대수다양체의 분류를 목표로 한다. 주어진 차원에서 대수다양체의 쌍유리 동치에 대한 동치류를 열거하고, 주어진 대수다양체 속에서 부분다양체로 존재하는 대수다양체들의 동치류를 분류한다.
'''불변량 이론'''(invariant theory^영어)은 군의 대수다양체 위의 작용을 연구한다. 현대 대수기하학에서, 이는 데이비드 멈퍼드의 '''기하 불변량 이론'''(geometric invariant theory^영어)으로, 스킴의 언어로 재정의되었다.
'''교차 이론'''(intersection theory^영어)은 대수기하학 위에, 대수적 위상수학의 호몰로지와 유사한 구조들을 정의하는 이론이다.
'''산술기하학'''은 유리수체나 대수적 수체 위의 스킴을 다룬다. 예를 들어, 디오판토스 방정식은 이러한 스킴을 정의한다. 이 경우, 수론적인 문제를 기하학적인 문제로 재해석하여, 기하학적 기법을 적용할 수 있다.
'''실수 대수기하학'''(real algebraic geometry^영어)은 복소수 대신 실수 위의 초곡면들을 다룬다. 실수가 대수적으로 닫힌 체가 아니기 때문에 복소수의 경우 등장하지 않는 여러 현상들이 존재한다.
'''특이점 이론'''(singularity theory^영어)에서는 대수다양체의 특이점을 분류·연구한다.
'''계산 대수기하학'''(computational algebraic geometry^영어)에서는 주어진 대수다양체의 성질들을 계산하는 알고리즘을 다룬다.
'''비가환 대수기하학'''(noncommutative algebraic geometry^영어)은 스킴이 국소적으로 가환환인 것과 반대로, 비가환 대수적 구조들을 기하학적 기법들로 다룬다. 이는 (해석적) 비가환 기하학에 대응한다.

5. 다른 분야와의 관계

현대 대수기하학은 여러 분야와 깊게 연관되어 있다. 통계학,^[12] 제어 이론,^[13]^[14] 로봇 공학,^[15] 오류 정정 부호,^[16] 계산 계통 발생학,^[17] 기하 모델링,^[18] 끈 이론,^[19] 게임 이론,^[20] 그래프 매칭,^[21] 솔리톤,^[22] 정수 계획법^[23] 등이 그 예시이다. 특히, 수리물리학,^[26]^[27] 가적분계,^[28]^[29]^[30]^[31]^[32] 기계 학습^[33]^[34]과의 관계 및 응용이 연구되고 있다.

6. 주요 연구자

고바야시 구니히코
모리 시게후미: 1988년에 3차원 다양체의 극소 모델 존재 정리를 증명하였고, 이후 "모리의 프로그램"^[25]이라고 불리는 프로그램에 따라 분류가 강력하게 추진되고 있다.
히로나카 헤이스케
우메무라 히로시
이다카 시게루
사이토 슈지

참조

_[1] 웹사이트 Complexity of Algorithms https://www.cs.sfu.c[...] 2022-07-12
_[2] Q
_[3] 간행물 Shifting the foundations: Descartes's transformation of ancient geometry 1976-02-01
_[4] 웹사이트 Apollonius - Biography https://mathshistory[...] 2022-11-11
_[5] 간행물 Apollonius of Perga: Treatise on Conic Sections https://www.nature.c[...] 1896-08-01
_[6] 간행물 A Very Early Acquaintance with Apollonius of Perga's Treatise on Conic Sections in the Latin West https://cris.tau.ac.[...] 1976-06-01
_[7] 웹사이트 Omar Khayyam http://www-history.m[...] School of Mathematics and Statistics, University of St Andrews
_[8] 서적 The Development Of Arabic Mathematics Between Arithmetic And Algebra https://archive.org/[...] Springer 1994
_[9] 간행물 Excavating the errors in the "Mathematics" chapter of 1001 Inventions https://www.academia[...] 2016-01-01
_[10] 간행물 Géométrie algébrique et géométrie analytique http://www.numdam.or[...]
_[11] 웹사이트 Several approaches to non-archimedean geometry https://virtualmath1[...] 2024-07-13
_[12] 서적 Lectures on Algebraic Statistics https://books.google[...] Springer
_[13] 서적 Methods of Algebraic Geometry in Control Theory Part II Multivariable Linear Systems and Projective Algebraic Geometry https://books.google[...] Springer
_[14] 서적 Invariance and Systems Theory: Algebraic and Geometric Aspects Springer-Verlag 1982
_[15] 서적 Geometric Fundamentals of Robotics https://books.google[...] Springer
_[16] 서적 Algebraic Geometric Codes Basic Notions https://books.google[...] American Mathematical Soc.
_[17] 간행물 Algebraic Geometers See Ideal Approach to Biology http://siam.org/pdf/[...] 2007
_[18] 서적 Geometric Modeling and Algebraic Geometry https://books.google[...] Springer
_[19] 서적 Mirror Symmetry and Algebraic Geometry https://books.google[...] American Mathematical Soc.
_[20] 간행물 The algebraic geometry of perfect and sequential equilibrium
_[21] arXiv Dimers and Amoebae
_[22] 서적 Soliton Theory A Survey of Results https://books.google[...] Manchester University Press
_[23] 서적 Applications of Computational Algebraic Geometry https://books.google[...] American Mathematical Soc.
_[24] 웹사이트 Algebraic Geometry http://mathworld.wol[...]
_[25] 웹사이트 双有理幾何学 https://www.iwanami.[...] 岩波書店 2020-06-14
_[26] 문서 数理物理学の観点からの代数幾何学の新展開 https://kaken.nii.ac[...]
_[27] 문서 数理物理と代数幾何 http://pantodon.shin[...]
_[28] 문서 可積分系と代数幾何学の入り口 http://www.nara-wu.a[...]
_[29] 문서 代数幾何と可積分系の融合 - 理論の深化と数学・数理物理学における新展開 - https://kaken.nii.ac[...]
_[30] 서적 Integrable systems in the realm of algebraic geometry Springer Science & Business Media 2001
_[31] 문서 Integrable Systems and Algebraic Geometry, Proceedings of the Taniguchi Symposium 1997, Rokko Oriental Hotel, Kobe, 30 June – 4 July 1997 https://doi.org/10.1[...] 1998-10-01
_[32] 서적 Integrable Systems and Algebraic Geometry Cambridge University Press
_[33] 서적 代数幾何と学習理論森北出版 2006
_[34] 서적 Algebraic geometry and statistical learning theory Cambridge University Press 2009
_[35] 서적 Mathematical Thought from Ancient to Modern Times Oxford University Press 1972

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com