스킴 (수학)
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
스킴은 대수 기하학의 기본 개념으로, 가환환의 스펙트럼과 동형인 국소환 달린 공간이며, 국소적으로 아핀 스킴과 동형인 공간을 의미한다. 스킴 이론은 대수적 다양체의 개념을 일반화하여, 다양한 체와 환 위에서 기하학적 연구를 가능하게 한다. 스킴은 위상 공간, 사상, 가환층 등의 개념을 포함하며, 유한 극한과 섬유 곱을 가지는 범주를 형성한다. 스킴의 개념은 대수다양체, 사상, 족, 부분 스킴 등의 다양한 종류로 분류되며, 위상수학적, 범주론적, 대수적 성질을 갖는다. 스킴은 대수 기하학의 발전에 중요한 역할을 했으며, 대수적 공간, 스택 등으로 일반화되어 현대 수학의 다양한 분야에서 활용된다.
더 읽어볼만한 페이지
2. 정의
아핀 스킴은 국소적으로 아핀 스킴과 동형인 "공간"이다. 스킴은 다음과 같이 정의할 수 있다.
스킴은 범주를 형성하며, 그 사상은 국소환 달린 공간의 사상으로 정의된다. (참조: 스킴 사상.) 스킴 ''Y''에 대해, ''Y'' '''위의''' 스킴 ''X''(또는 ''Y''-'''스킴''')은 스킴 사이의 사상 ''X'' → ''Y''를 의미한다. 가환환 ''R'' '''위의''' 스킴 ''X''는 사상 ''X'' → Spec(''R'')을 의미한다.
체 ''k'' 위의 대수적 다양체는 특정 성질을 가진 ''k'' 위의 스킴으로 정의할 수 있다. 어떤 스킴을 다양체라고 불러야 하는지에 대해서는 다양한 관습이 있다. 표준적인 선택은 ''k'' 위의 '''다양체'''가 정수 분리된 스킴이며 ''k'' 위에 유한 타입인 것이다.[3]
스킴 사이의 사상 ''f'': ''X'' → ''Y''는 정칙 함수 환에 대한 '''당김 준동형 사상''', ''f''*: ''O''(''Y'') → ''O''(''X'')을 결정한다. 아핀 스킴의 경우, 이 구조는 스킴 사이의 사상 Spec(''A'') → Spec(''B'')와 환 준동형 사상 ''B'' → ''A'' 사이의 일대일 대응을 제공한다.[13] 이러한 의미에서 스킴 이론은 가환환 이론을 완전히 포함한다.
'''Z'''는 가환환의 범주에서 초기 대상이므로, 스킴의 범주는 Spec('''Z''')를 종결 대상으로 가진다.
가환환 ''R'' 위의 스킴 ''X''에 대해, ''X''의 ''R''-'''점'''은 사상 ''X'' → Spec(''R'')의 단면을 의미한다. ''X''(''R'')은 ''X''의 ''R''-점들의 집합을 나타낸다. 예시에서 이 정의는 ''R'' 값을 갖는 ''X''의 정의 방정식의 해 집합에 대한 이전의 개념을 재구성한다. ''R''이 체 ''k''일 때, ''X''(''k'')는 ''X''의 ''k''-유리점 집합이라고도 불린다.
더 일반적으로, 가환환 ''R'' 위의 스킴 ''X''와 임의의 가환 ''R''-대수 ''S''에 대해, ''X''의 ''S''-'''점'''은 ''R'' 위의 사상 Spec(''S'') → ''X''를 의미한다. ''X''(''S'')는 ''X''의 ''S''-점들의 집합을 나타낸다. (이것은 체 ''k'' 위의 방정식이 주어지면, ''k''의 임의의 체 확대 ''E''에서 방정식의 해 집합을 고려할 수 있다는 관찰을 일반화한다.) ''R'' 위의 스킴 ''X''에 대해, 할당 ''S'' ↦ ''X''(''S'')는 가환 ''R''-대수에서 집합으로 가는 함자이다. ''R'' 위의 스킴 ''X''가 이 점의 함자에 의해 결정된다는 것은 중요한 관찰이다.[6]
스킴의 섬유 곱은 항상 존재한다. 즉, 스킴 ''Y''로의 사상이 있는 임의의 스킴 ''X''와 ''Z''에 대해, 범주론적 섬유 곱 가 스킴의 범주에서 존재한다. ''X''와 ''Z''가 체 ''k'' 위의 스킴이면, Spec(''k'') 위의 섬유 곱은 ''k''-스킴의 범주에서 '''곱''' ''X'' × ''Z''라고 부를 수 있다. 예를 들어, ''k'' 위의 아핀 공간 과 의 곱은 ''k'' 위의 아핀 공간 이다.
스킴의 범주는 섬유 곱과 종결 대상 Spec('''Z''')를 가지므로, 모든 유한 극한을 가진다.
2. 1. 국소환 달린 공간을 통한 정의
'''아핀 스킴'''(affine scheme영어)은 (1이 있는) 어떤 가환환의 스펙트럼과 동형인 국소환 달린 공간이다.'''스킴'''은 국소적으로 아핀 스킴과 동형인 국소환 달린 공간이다. 국소환 달린 공간 가 열린 덮개 를 가져, 각 가 아핀 스킴을 이루는 경우 를 스킴이라고 한다.[13][6][15] '''스킴의 범주''' 는 스킴으로 구성된, 국소환 달린 공간의 범주 의 충만한 부분 범주이다.
'''아핀 스킴'''은 가환환 의 스펙트럼 과 동형인 국소 환 달린 공간이다. '''스킴'''은 열린 집합 로 덮히는 국소 환 달린 공간 이며, 각 (국소 환 달린 공간으로서)는 아핀 스킴이다. 에는 각 열린 부분 집합 에 '''상의 정칙 함수 환'''이라고 불리는 가환환 을 할당하는 층 가 있다. 스킴은 아핀 스킴인 "좌표 차트"로 덮여 있다고 생각할 수 있다. 정의는 스킴이 자리스키 위상을 사용하여 아핀 스킴을 붙여서 얻어진다는 것을 정확히 의미한다.
초창기에는 이것을 ''준스킴''이라고 불렀으며, 스킴은 분리된 준스킴으로 정의되었다. 준스킴이라는 용어는 사용되지 않지만, 그로텐디크의 "Éléments de géométrie algébrique" 및 멈포드의 "Red Book"과 같은 오래된 책에서 여전히 찾을 수 있다. 의 층 속성은 그 요소가 반드시 함수는 아니지만, 함수와 동일한 방식으로 제한으로부터 함께 연결될 수 있음을 의미한다.
2. 2. 점함자를 통한 정의
아핀 스킴의 범주 위에, 자리스키 위상에 대한 그로텐디크 위상을 주면 는 위치를 이룬다. 이 위치 위의 (집합 값을 갖는) 층의 범주 를 생각하자. 이는 토포스를 이룬다. 이 그로텐디크 위상은 준표준 위상이다. 즉, 임의의 가환환 에 대하여, 준층:
은 층을 이룬다. 이를 통해 포함 함자
:
:
를 정의할 수 있으며, 가환환을 층으로 여길 수 있다.
가환환 와 그 속의 아이디얼 이 주어졌을 때, 층 의 다음과 같은 부분층을 정의할 수 있다.[7]
:
준층 의 '''열린 부분층'''은 다음 조건을 만족시키는 부분층 이다.[7]
- 임의의 가환환 및 층 사상 에 대하여, 의 부분층 는 가 되는 아이디얼 가 존재한다.
층 가 다음 조건을 갖는 표현 가능 열린 부분층 들을 갖는다고 하자.
- 임의의 체 에 대하여, 이다.
그렇다면 이 조건들을 만족시키는, 의 충만한 부분 범주를 정의할 수 있다. 이 범주를 '''스킴의 범주''' 로 정의하며, 스킴은 이 범주의 원소이다.[7]
이 두 정의는 서로 동치이다. 구체적으로, 국소환 달린 공간으로서의 스킴 가 주어지면, 다음과 같은 준층을 정의할 수 있다.
:
:
즉, 이는 에 대하여, 의 -점들의 집합을 대응시킨다. 이를 '''점함자'''(functor of points영어)라고 한다. 이 준층은 자리스키 위상에 대하여 층을 이루며, 위 조건에 따라 스킴이 되는 것을 보일 수 있다.
3. 스킴의 사상
스킴 사상 는 다음 세 가지 관점으로 해석할 수 있다.
- ''' 위의 스킴 정의''': 는 위의 스킴을 정의한다. 이는 가 체(의 스펙트럼)인 경우의 일반화이다.
- '''의 -점 정의''': 는 의 -점을 정의한다. 이는 가 체(의 스펙트럼)인 경우의 일반화이다.
- '''에 의해 매개되는 족 정의''': 는 에 의해 매개되는 족을 정의한다. 이는 와 둘 다 유한 차원이며, 인 경우의 일반화이다.
스킴의 사상 ''f'': ''X'' → ''Y''는 정칙 함수의 환에 대한 '''당김 준동형 사상''' ''f''*: ''O''(''Y'') → ''O''(''X'')을 결정한다. 아핀 스킴의 경우, 이 구조는 스킴의 사상 Spec(''A'') → Spec(''B'')와 환 준동형 사상 ''B'' → ''A'' 사이의 일대일 대응을 제공한다.[13] 이러한 의미에서 스킴 이론은 가환환 이론을 완전히 포함한다.
'''Z'''는 가환환의 범주에서 초기 대상이므로, 스킴의 범주는 Spec('''Z''')를 종결 대상으로 가진다.
스킴의 섬유 곱은 항상 존재한다. 즉, 스킴 ''Y''로의 사상이 있는 임의의 스킴 ''X''와 ''Z''에 대해, 범주론적 섬유 곱 가 스킴의 범주에서 존재한다. ''X''와 ''Z''가 체 ''k'' 위의 스킴이면, Spec(''k'') 위의 섬유 곱은 ''k''-스킴의 범주에서 '''곱''' ''X'' × ''Z''라고 부를 수 있다. 예를 들어, ''k'' 위의 아핀 공간 과 의 곱은 ''k'' 위의 아핀 공간 이다.
스킴의 범주는 섬유 곱과 종결 대상 Spec('''Z''')를 가지므로, 모든 유한 극한을 가진다.
3. 1. ''S'' 위의 스킴
'''S 위의 스킴'''(''S''-scheme영어 또는 scheme over ''S''영어)은 스킴 에 대한 조각 범주의 대상이다. 즉, ''S'' 위의 스킴 은 스킴 와 스킴 사상 의 순서쌍이다.[13] 가 체나 가환환이라면, ''' 위의 스킴'''은 위의 스킴과 같다. 는 스킴의 범주의 끝 대상이므로, " 위의 스킴"은 "스킴"과 같은 뜻이다.스킴 ''Y'' '''위의''' 스킴 ''X''(또는 ''Y''-'''스킴''')은 스킴의 사상 ''X'' → ''Y''를 의미한다.
3. 2. 점
스킴 는 위상 공간이므로, 위상 공간으로서의 점을 정의할 수 있다. 스킴은 일반적으로 T1 공간이 아니므로, 닫힌 점과 닫히지 않은 점을 구분할 수 있다. 스킴의 닫히지 않은 점은 '''일반점'''이라고 한다. 닫힌 점은 대수다양체의 실제 "점"에 대응하며, 닫히지 않은 점은 (그 폐포를 취하면) 닫힌 부분 스킴에 대응한다.보다 일반적으로, 임의의 스킴 에 대하여, 의 '''-점'''(S-point영어)은 스킴 사상 를 뜻한다. 고전적으로는 가 어떤 체 의 스펙트럼인 경우를 다루며, 이 경우 는 를 체 위에서 정의하였을 때의 점에 대응한다.
의 '''기하학적 점'''(幾何學的點, geometric point영어)은 어떤 대수적으로 닫힌 체 에 대한 -점이다.
가환환 위의 스킴 에 대해, 의 -'''점'''은 사상 의 단면을 의미한다. 은 의 -점들의 집합을 나타낸다. 예시에서 이 정의는 값을 갖는 의 정의 방정식의 해 집합에 대한 이전의 개념을 재구성한다. 이 체 일 때, 는 또한 의 -유리점 집합이라고도 불린다.
더 일반적으로, 가환환 위의 스킴 와 임의의 가환 -대수 에 대해, 의 -'''점'''은 위의 사상 를 의미한다. 는 의 -점들의 집합을 나타낸다.
3. 3. 족
스킴의 족(family of schemes영어)은 스킴의 사상 이다.[8] 스킴의 족 의, 점 에서의 올(fiber영어)은 에서의 줄기인 국소환 의 잉여류체 에 대한 올곱:
이다.[13] 는 위상 공간으로서 원상 와 위상 동형이다.[13] 따라서, 스킴 사상 은 체 위의 스킴들의 족으로 해석할 수 있다.
스킴의 족은 매우 일반적인 개념이므로, 보통 평탄 사상을 이루는 평탄한 족(flat family영어), 매끄러운 사상을 이루는 매끄러운 족(smooth family영어) 등이 쓰인다.
3. 4. 몰입과 부분 스킴
두 국소환 달린 공간 , 사이의 사상 가 다음 두 조건을 만족시킨다면, '''열린 몰입'''(open immersion영어)이라고 한다.두 국소환 달린 공간 , 사이의 사상 가 다음 두 조건을 만족시킨다면, '''닫힌 몰입'''(closed immersion영어)이라고 한다.
스킴 의 '''열린 부분 스킴'''(open subscheme영어)은 위상 공간으로서 의 열린집합 이며, 위의 구조층은 층의 역상 이다.[13] 이에 따라, 열린 몰입 가 존재한다.
스킴 위에, 준연접층인 아이디얼 층 가 주어졌을 때, 에 대응하는 '''닫힌 부분 스킴'''(closed subscheme영어)은 집합으로서 닫힌집합 이며, 그 위의 구조층은 이다.[13] 이에 따라, 닫힌 몰입 가 존재한다. 스킴의 열린 부분 집합이 주어지면 이에 대응하는 열린 부분 스킴이 유일하게 결정되지만, 스킴의 닫힌 부분 집합이 주어지면 이에 대응하는 닫힌 부분 스킴은 유일하지 않을 수 있다.
스킴 의 '''부분 스킴'''(部分scheme, subscheme영어, sous-schéma프랑스어)은 열린 부분 스킴의 닫힌 부분 스킴이다.[15] 의 부분 스킴 의 부분 스킴 가 주어졌을 때, 는 의 부분 스킴이다.[15]
4. 성질
모든 스킴은 위상 공간으로서 차분한 공간이며 따라서 콜모고로프 공간이다. 또한, 모든 스킴은 국소 콤팩트 공간이다. 그러나 스킴은 일반적으로 T1 공간이지 않을 수 있다.[9]
구체적으로, 위상 공간 에 대하여, 다음 세 조건이 서로 동치이며, 이를 만족시키는 위상 공간을 '''스펙트럼 공간'''(spectral space영어)이라고 한다.
- 인 가환환 가 존재한다.
- 는 유한 콜모고로프 공간들의 역극한이다.
- 는 콤팩트 콜모고로프 차분한 공간이며, 의 콤팩트 열린집합들의 모임은 의 기저를 이루며, 의 두 콤팩트 열린집합 에 대하여, 역시 콤팩트 집합이다.
임의의 위상 공간 에 대하여, 다음 두 조건이 서로 동치이다.
- 위상 공간으로서 와 위상 동형인 스킴 가 존재한다.
- 모든 에 대하여, 스펙트럼 공간을 이루는 열린 근방 가 존재한다.
또한, 임의의 위상 공간 에 대하여, 다음 조건들이 서로 동치이다.
- 위상 공간으로서 와 위상 동형인 분리 스킴 가 존재한다.
- 는 어떤 스펙트럼 공간의 열린 부분 공간이다.
- 는 어떤 아핀 스킴의 열린 부분 스킴과 위상 동형이다.
스킴의 범주 는 유한 완비 범주이지만, 완비 범주도, 쌍대 완비 범주도, 심지어 유한 쌍대 완비 범주도 아니다.
스킴의 범주에서는 다음과 같은 (쌍대) 극한들이 존재한다.
- 모든 유한 극한이 존재한다.
- 유한 곱 이 존재한다. 다만, 일반적으로 스킴의 곱은 위상 공간으로서의 곱과 다르다.
- 끝 대상이 존재하며, 이다. 이는 가 가환환의 범주 의 시작 대상이기 때문이다.
- 올곱 가 존재한다. 로 놓으면 이는 일반적인 곱이 된다. 스킴의 올곱은 '''밑 변환'''(-變換, base change영어)이라고 한다. 이는 위의 스킴 를 위의 스킴 으로의 밑 변환이다.
- 임의의 (작은) 쌍대곱 이 존재한다. 이는 스킴의 분리합집합이다.
- 시작 대상이 존재하며, (자명환 의 스펙트럼)이다. 이는 자명환 이 가환환의 범주 의 끝 대상이기 때문이다. 위상 공간으로서 이는 공집합이다.
하지만 스킴의 범주에서는 다음과 같은 (쌍대) 극한들이 존재하지 않는다.
- 스킴들의 무한 곱은 일반적으로 존재하지 않는다. (다만, 아핀 스킴들의 무한 곱은 가환환의 무한 쌍대곱이므로 존재한다.)
- 스킴들의 밂은 일반적으로 존재하지 않는다.
- 두 스킴 및 열린 몰입 , 이 존재하였을 때 는 존재한다. 즉, 스킴을 열린 부분 스킴을 통해 이어붙일 수 있다.
- 두 스킴 및 닫힌 몰입 , 이 존재하였을 때 는 존재한다. 즉, 스킴을 닫힌 부분 스킴을 통해 이어붙일 수 있다.[10]
4. 1. 위상수학적 성질
스킴 는 위상 공간이므로, 위상 공간으로서의 점을 정의할 수 있다. 스킴은 일반적으로 T1 공간이 아니므로, 닫힌 점과 닫히지 않은 점을 구분할 수 있다. 스킴의 닫히지 않은 점은 '''일반점'''이라고 한다. 닫힌 점은 대수다양체의 실제 "점"에 대응하며, 닫히지 않은 점은 (그 폐포를 취하면) 닫힌 부분 스킴에 대응한다.보다 일반적으로, 임의의 스킴 에 대하여, 의 '''-점'''(-point영어)은 스킴 사상 를 뜻한다. 고전적으로는 가 어떤 체 의 스펙트럼인 경우를 다루며, 이 경우 는 를 체 위에서 정의하였을 때의 점에 대응한다.
의 '''기하학적 점'''(幾何學的點, geometric point영어)은 어떤 대수적으로 닫힌 체 에 대한 -점이다. 모든 스킴은 위상 공간으로서 차분한 공간이며 따라서 콜모고로프 공간이다. 또한, 모든 스킴은 국소 콤팩트 공간이다. 그러나 스킴은 일반적으로 T1 공간이지 않을 수 있다.
구체적으로, 위상 공간 에 대하여, 다음 세 조건이 서로 동치이며, 이를 만족시키는 위상 공간을 '''스펙트럼 공간'''(spectral space영어)이라고 한다.[9]
- 인 가환환 가 존재한다.
- 는 유한 콜모고로프 공간들의 역극한이다.
- 는 콤팩트 콜모고로프 차분한 공간이며, 의 콤팩트 열린집합들의 모임은 의 기저를 이루며, 의 두 콤팩트 열린집합 에 대하여, 역시 콤팩트 집합이다.
그렇다면 임의의 위상 공간 에 대하여, 다음 두 조건이 서로 동치이다.[9]
- 위상 공간으로서 와 위상 동형인 스킴 가 존재한다.
- 모든 에 대하여, 스펙트럼 공간을 이루는 열린 근방 가 존재한다.
또한, 임의의 위상 공간 에 대하여, 다음 조건들이 서로 동치이다.[9]
- 위상 공간으로서 와 위상 동형인 분리 스킴 가 존재한다.
- 는 어떤 스펙트럼 공간의 열린 부분 공간이다.
- 는 어떤 아핀 스킴의 열린 부분 스킴과 위상 동형이다.
4. 2. 범주론적 성질
스킴의 범주 는 유한 완비 범주이지만, 완비 범주도, 쌍대 완비 범주도, 심지어 유한 쌍대 완비 범주도 아니다.스킴의 범주에서는 다음과 같은 (쌍대) 극한들이 존재한다.
- 모든 유한 극한이 존재한다.
- 유한 곱 이 존재한다. 다만, 일반적으로 스킴의 곱은 위상 공간으로서의 곱과 다르다.
- 끝 대상이 존재하며, 이다. 이는 가 가환환의 범주 의 시작 대상이기 때문이다.
- 올곱 가 존재한다. 로 놓으면 이는 일반적인 곱이 된다. 스킴의 올곱은 '''밑 변환'''(-變換, base change영어)이라고 한다. 이는 위의 스킴 를 위의 스킴 으로의 밑 변환이다.
- 임의의 (작은) 쌍대곱 이 존재한다. 이는 스킴의 분리합집합이다.
- 시작 대상이 존재하며, (자명환 의 스펙트럼)이다. 이는 자명환 이 가환환의 범주 의 끝 대상이기 때문이다. 위상 공간으로서 이는 공집합이다.
하지만 스킴의 범주에서는 다음과 같은 (쌍대) 극한들이 존재하지 않는다.
- 스킴들의 무한 곱은 일반적으로 존재하지 않는다. (다만, 아핀 스킴들의 무한 곱은 가환환의 무한 쌍대곱이므로 존재한다.)
- 스킴들의 밂은 일반적으로 존재하지 않는다.
- 두 스킴 및 열린 몰입 , 이 존재하였을 때 는 존재한다. 즉, 스킴을 열린 부분 스킴을 통해 이어붙일 수 있다.
- 두 스킴 및 닫힌 몰입 , 이 존재하였을 때 는 존재한다. 즉, 스킴을 닫힌 부분 스킴을 통해 이어붙일 수 있다.[10]
스킴은 범주를 형성하며, 사상은 국소 환 달린 공간의 사상으로 정의된다. (참조: 스킴 사상.) 스킴 ''Y''에 대해, ''Y'' '''위의''' 스킴 ''X''(또는 ''Y''-'''스킴''')은 스킴의 사상 ''X'' → ''Y''를 의미한다. 가환환 ''R'' '''위의''' 스킴 ''X''는 사상 ''X'' → Spec(''R'')을 의미한다.
체 ''k'' 위의 대수적 다양체는 특정 속성을 가진 ''k'' 위의 스킴으로 정의될 수 있다. 정확히 어떤 스킴을 다양체라고 불러야 하는지에 대해 다양한 관습이 있다. 한 가지 표준적인 선택은 ''k'' 위의 '''다양체'''가 정수 분리된 스킴이며 ''k'' 위에 유한 타입인 것을 의미한다.[3]
스킴의 사상 ''f'': ''X'' → ''Y''는 정칙 함수의 환에 대한 '''당김 준동형 사상''', ''f''*: ''O''(''Y'') → ''O''(''X'')을 결정한다. 아핀 스킴의 경우, 이 구조는 스킴의 사상 Spec(''A'') → Spec(''B'')와 환 준동형 사상 ''B'' → ''A'' 사이의 일대일 대응을 제공한다. 이러한 의미에서 스킴 이론은 가환환 이론을 완전히 포함한다.
'''Z'''는 가환환의 범주에서 초기 대상이므로, 스킴의 범주는 Spec('''Z''')를 종결 대상으로 가진다.
가환환 ''R'' 위의 스킴 ''X''에 대해, ''X''의 ''R''-'''점'''은 사상 ''X'' → Spec(''R'')의 단면을 의미한다. ''X''(''R'')은 ''X''의 ''R''-점들의 집합을 나타낸다. ''R''이 체 ''k''일 때, ''X''(''k'')는 또한 ''X''의 ''k''-유리점 집합이라고도 불린다.
더 일반적으로, 가환환 ''R'' 위의 스킴 ''X''와 임의의 가환 ''R''-대수 ''S''에 대해, ''X''의 ''S''-'''점'''은 ''R'' 위의 사상 Spec(''S'') → ''X''를 의미한다. ''X''(''S'')는 ''X''의 ''S''-점들의 집합을 나타낸다. ''R'' 위의 스킴 ''X''에 대해, 할당 ''S'' ↦ ''X''(''S'')는 가환 ''R''-대수에서 집합으로 가는 함자이다. ''R'' 위의 스킴 ''X''가 이 점의 함자에 의해 결정된다는 것은 중요한 관찰이다.
스킴의 섬유 곱은 항상 존재한다. 즉, 스킴 ''Y''로의 사상이 있는 임의의 스킴 ''X''와 ''Z''에 대해, 범주론적 섬유 곱 가 스킴의 범주에서 존재한다. ''X''와 ''Z''가 체 ''k'' 위의 스킴이면, Spec(''k'') 위의 섬유 곱은 ''k''-스킴의 범주에서 '''곱''' ''X'' × ''Z''라고 부를 수 있다. 예를 들어, ''k'' 위의 아핀 공간 과 의 곱은 ''k'' 위의 아핀 공간 이다.
스킴의 범주는 섬유 곱과 종결 대상 Spec('''Z''')를 가지므로, 모든 유한 극한을 가진다.
4. 2. 1. 아핀 스킴과의 관계
아핀 스킴의 범주 는 스킴 범주 의 반사 부분 범주이다. 포함 함자 의 왼쪽 수반 함자는 구조층의 대역적 단면환의 스펙트럼이다.:
:
:
즉, 아핀 스킴의 극한은 스킴의 극한과 일치한다. 반대로, 스킴의 쌍대극한은 (만약 존재한다면) 아핀 스킴의 쌍대극한과 일반적으로 일치하지 않지만, 스킴의 쌍대극한에 함자를 가하면 이는 아핀 스킴의 쌍대극한과 일치한다.
4. 2. 2. 국소환 달린 공간과의 관계
스킴은 국소적으로 아핀 스킴과 동형인 국소환 달린 공간이며, 스킴의 범주 는 국소환 달린 공간의 범주 의 충만한 부분 범주이다. 즉, 국소환 달린 공간 가 열린 덮개 를 가져, 각 가 아핀 스킴을 이루는 경우 를 스킴이라고 한다.[13][6][15]모든 국소환 달린 공간의 범주 는 완비 범주이자 쌍대 완비 범주이다.[11]
포함 함자 에 따라, 스킴의 범주는 국소환 달린 공간의 범주의 충만한 부분 범주를 이룬다. 이 포함 함자는 쌍대극한을 보존하지 않으며, 일반적 극한도 보존하지 않는다. 그러나 이는 유한 극한을 보존한다.[11]
4. 3. 그로텐디크 위상
스킴의 범주 위에는 다양한 그로텐디크 준위상들이 존재한다.[7] 이들은 공통적으로 다음과 같은 형태로 정의된다.어떤 스킴 사상들의 모임 이 주어졌을 때, 의 덮개는 다음 조건을 만족시키는 사상들의 집합 이다.
- 집합으로서, 이다.
이에 따라, 다음과 같은 위상들을 정의할 수 있다.
이 밖에도 다음과 같은 위상들이 존재한다.
- '''fpqc 위상''': 충실하게 평탄한(fidèlement plate프랑스어) 준콤팩트(quasi-compacte프랑스어) 사상. 흔히 사용되는 위상 가운데 가장 섬세하다.
- '''니스네비치 위상'''(Nisnevich topology영어). 이는 예브세이 니스네비치(Евсей А. Нисневичru)가 도입하였으며, 대수적 K이론, 호모토피 이론, 모티브 이론에서 쓰인다.
- '''신토믹 위상'''(syntomic topology영어).[12] 이는 일부 경우 평탄 위상보다 더 계산하기 쉬우며, 주로 수론에서 쓰인다.
이 위상들은 다음과 같이 섬세함에 대하여 전순서 집합을 이룬다. (여기서 오른쪽으로 갈수록 더 섬세한 위상이다.)
: 비이산 위상 → 자리스키 위상 → 니스네비치 위상 → 에탈 위상 → fppf 위상 → fpqc 위상 → 표준 위상 → 이산 위상
fpqc 위상은 흔히 사용되는 가장 섬세한 그로텐디크 위상이므로, 흔히 사용되는 모든 그로텐디크 위상들은 준표준 위상이다. 즉, 표현 가능 준층은 항상 층을 이룬다.
5. 종류
스킴 이론에서는 여러 기술적인 용어들이 사용된다. 위상 공간의 성질을 스킴에 적용할 수 있는데, 예를 들어 다음과 같다.
- '''기약 스킴'''은 위상 공간으로서 기약 공간인 스킴이다.
- '''(준)콤팩트 스킴'''((quasi-)compact scheme영어)은 위상 공간으로서 콤팩트 공간인 스킴이다. 대수기하학에서는 "콤팩트" 대신 "준콤팩트"(quasicompact영어)를, "콤팩트 하우스도르프" 대신 "콤팩트"를 사용하는 경우가 많다. 스킴은 거의 항상 하우스도르프 공간이 아니다.
- '''연결 스킴'''(connected scheme영어)은 위상 공간으로서 연결 공간인 스킴이다.
- 스킴의 '''(크룰) 차원'''((Krull) dimension영어)은 위상 공간으로서의 크룰 차원이다.
가환환의 성질을 스킴으로 일반화할 수도 있다.
- '''축소 스킴'''은 모든 열린 집합 에서 구조층 이 축소환(0이 아닌 멱영원을 갖지 않는 환)인 스킴 이다.
- '''뇌터 스킴'''은 뇌터 환의 스펙트럼으로 구성된 유한 열린 덮개가 존재하는 스킴이다.
- '''정칙 스킴'''은 특이점을 갖지 않는 스킴이다. 즉, 모든 줄기가 정칙 국소환을 이루는 스킴이다.
이 밖에도 다음과 같은 용어들이 사용된다.
일반적으로, 체 가 주어졌을 때, 위의 스킴의 성질 가 다음 조건을 만족시킨다면, 를 '''기하학적 성질'''(幾何學的性質, geometric property영어)이라고 한다.
- 임의의 위의 스킴 및 임의의 체의 확대 에 대하여, 만약 가 를 만족시킨다면, 올곱 역시 ( 위의 스킴으로서) 를 만족시킨다.
스킴의 성질 가 다음 조건을 만족시킨다면, 를 '''국소적 성질'''(局所的性質, local property영어)이라고 한다.
- 스킴 가 를 만족시킬 필요충분조건은 임의의 열린 부분 스킴으로 구성된 열린 덮개 에 대하여 모든 가 를 만족시키는 것이다.
5. 1. 대수다양체
대수적으로 닫힌 체 위의 대수다양체의 범주를 라고 하고, 위의 스킴의 범주를 라고 하자. 그렇다면 함자 가 존재하며, 이에 따라 는 의 충만한 부분 범주를 이룬다.[13]대수다양체 에 대하여, 를 의 자리스키 위상 아래 닫힌 집합들의 집합이라고 하자. 위에 위상을, 닫힌 집합의 에 대한 상들이 닫힌 것으로 정의하면, 함수 는 연속 함수이다. 가 위의 다항식함수들의 층이라고 하면, 층의 상(image영어) 는 위의 환의 층 구조를 이룬다. 이에 따라 는 국소환 달린 공간의 구조를 갖춘다. 이 사상에 따라, 아핀 다양체의 상이 아핀 스킴임을 보일 수 있다. 대수다양체는 국소적으로 아핀 대수다양체인 공간이고, 스킴은 국소적으로 아핀 스킴인 공간이므로, 가 대수다양체에서 스킴으로의 함자임을 보일 수 있다. 또한, 이 스킴 의 경우, 상수함수로 인하여 정의되는 사상 가 존재한다. 따라서 는 위의 스킴이다. 이 함자는 충실충만한 함자이다.[13] 이 함자의 상은 유한형 정역 분리 스킴이다.[13]
관련된 용어로서, '''대수적 스킴'''(代數的scheme, algebraic scheme영어)은 체 위의 유한형 분리 스킴이다. 즉, 대수다양체는 정역 대수적 스킴이다.
5. 2. 사상의 종류
스킴 사상 는 다음 세 가지로 해석할 수 있으며, 이에 따라 서로 다른 용어로 불린다.- ''' 위의 스킴''' 정의: 가 체(의 스펙트럼)인 경우의 일반화이다.
- 의 '''-점''' 정의: 가 체(의 스펙트럼)인 경우의 일반화이다.
- '''에 의해 매개되는 족''' 정의: 와 둘 다 유한 차원이며, 인 경우의 일반화이다.
스킴 사이의 사상에는 여러 형용사가 적용된다. 스킴은 보통 계수체/환이 주어져 있는 스킴으로 여길 수 있으므로, 이러한 형용사는 스킴에도 적용된다. 예를 들어, 유한형 ''k'' 위의 스킴 는 그 사상 이 유한형인 스킴이다.
- '''유한형 사상''': 대략 "유한 여차원"을 뜻한다.
- '''유한 사상''': 대략 "여차원 0"을 뜻한다.
- '''평탄 사상''': 대략 "올이 연속적으로 변하는 족을 이루는 사상"이다. 즉, 일부 특수한 점에서 올이 퇴화할 수 있으나, 이 "퇴화"가 "연속적"으로 일어나며, 이러한 특수한 점은 "측도 0"이어야 한다.
- '''에탈 사상''': 대략 "국소 위상 동형"에 해당한다. 즉, 매끄러운 사상 가운데 여차원이 0인 것이다.
- '''매끄러운 사상''': 대략 평탄 사상 가운데, "특수한" (올이 퇴화하는) 점이 없는 것을 뜻한다.
- '''우세 사상'''(dominant morphism영어)은 상이 조밀 집합인 스킴 사상이다.
이 밖에도, 일반위상수학에서 사용되는 연속 함수의 다음과 같은 성질들이 사용된다.
(그러나 스킴의 고유 사상은 일반위상수학의 고유 함수와 관계없다.)
스킴의 사상의 성질 가 다음 조건을 만족시킨다면, '''밑 변환에 대하여 안정적인 성질'''(property stable under base change영어)이라고 한다.[13]
- 스킴의 사상 가 를 만족시킨다면, 임의의 스킴 및 사상 에 대하여, 역시 를 만족시킨다.
예를 들어, 유한형 사상은 밑 변환에 대하여 안정적이다. 밑 변환에 대하여 안정적이지 않은 성질 에 대하여, '''보편 사상'''(universally morphism영어)은 다음과 같은 사상 이다.
- 임의의 사상 에 대하여, 밑 변환 은 항상 사상이다.
6. 예시
체가 아닌 축소환의 스펙트럼은 한원소 공간이 아니다. 예를 들어 정수환 에 대한 텐서곱 는 2개 이상의 소 아이디얼을 가지므로 한원소 공간이 아니다.
를 대수적으로 닫힌 체라고 할 때, 아핀 공간 는 좌표가 에 있는 모든 점 의 대수적 다양체이며, 좌표환은 다항식환 이다. 이에 해당하는 스킴 은 자리스키 위상을 가진 위상 공간이며, 닫힌 점은 최대 아이디얼 이며, 이는 에서 사라지는 다항식 집합이다. 스킴은 또한 각 비최대 소 아이디얼 에 대해 닫히지 않은 점을 포함하며, 해당 소 아이디얼의 소멸은 기약적인 부분 다양체 를 정의한다. 스킴 점 의 위상적 폐포는 부분 스킴 이며, 부분 다양체의 모든 닫힌 점, 즉 또는 동등하게 를 만족하는 를 포함한다.
스킴 는 초평면의 여집합에 의해 주어진 열린 부분 집합의 기저를 갖는다.
여기서 는 기약 다항식이다. 이 집합은 정칙 함수의 좌표환으로 부여되며,
이는 주어진 열린 집합 에서 정칙인 일반적인 유리 함수환을 제공하는 고유한 층 를 유도한다.
각 환 요소 , 즉 상의 다항식 함수는 스킴 의 점에 대한 함수를 정의하며, 그 값은 몫환 에 있다. 를 자연 사상 아래의 의 이미지로 정의한다. 최대 아이디얼 는 ''잉여 필드'' 를 제공하며, 자연 동형 사상 를 통해 는 원래 값 에 해당한다.
다항식 의 소멸 궤적은 아핀 공간 의 초평면 부분 다양체 이며, 주 아이디얼 에 해당한다. 해당하는 스킴은 이며, 아핀 공간의 닫힌 부분 스킴이다. 예를 들어, 를 복소수 또는 실수로 취하면, 방정식 은 아핀 평면 에서 결절 3차 곡선을 정의하며, 이는 스킴 에 해당한다.
정수환 는 스킴 의 좌표환으로 간주될 수 있다. 자리스키 위상은 소수 의 주 이상 인 닫힌 점과, 전체 스킴의 폐포인 영 이상 인 일반 점을 갖는다. 닫힌 집합은 유한 집합이고 열린 집합은 그 여집합, 즉 여유한 집합이다; 점의 무한 집합은 조밀하다.
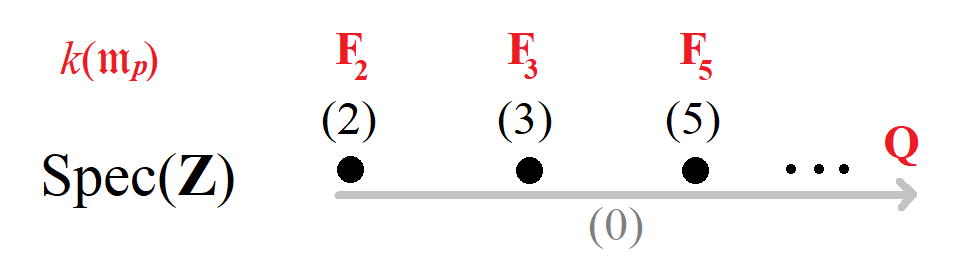
기약 원소 에 해당하는 기저 열린 집합은 이며, 좌표환은 이다. 열린 집합 에 대해, 이는 을 유도한다.
수 는 스킴 위의 함수에 해당하며, 에서의 값이 잉여체 에 있는 함수, 즉 를 법으로 하는 정수의 유한체에 해당한다. 이 함수는 로 정의되며, 일반 잉여환 에서 으로 정의된다. 함수 은 점에서의 값에 의해서만 결정되므로, 을 를 만족하는 임의의 함수 중 매우 특별한 형태인 닫힌 점에 대한 일종의 "정칙 함수"로 생각할 수 있다.
점 는 함수 의 영점 집합, 즉 잉여체에서 의 값이 0과 같은 점이다. 위의 "유리 함수"의 체는 일반 잉여환의 분수체, 즉 이다. 분수 는 분모의 소인수에 해당하는 점 에서 "극점"을 갖는다.
이것은 정수 이 공통 소인수를 갖지 않으면, 을 만족하는 정수 가 존재한다는 베주 항등식의 기하학적 해석을 제공한다. 기하학적으로, 이것은 스킴 에 대한 약한 힐베르트 영점 정리의 한 형태이다: 함수 이 에서 공통 영점 를 갖지 않으면, 이들은 좌표환 에서 단위 이상 을 생성한다. 실제로, 항을 열린 집합 에 의한 의 덮개에 종속적인 일종의 분할된 단위체로 간주할 수 있다.
아핀 공간 은 정수 계수를 갖는 다항식인 좌표환 를 갖는 대수다양체이다. 이에 해당하는 스킴은 이며, 그 점은 소 아이디얼 이다. 닫힌 점은 형태의 극대 아이디얼이며, 여기서 는 소수이고, 는 정수 인수를 갖지 않고, 를 법으로 하여 기약인 상수항이 아닌 다항식이다. 따라서 를 2차원으로, 좌표로 측정되는 "특성 방향"과 좌표를 갖는 "공간 방향"으로 묘사할 수 있다.
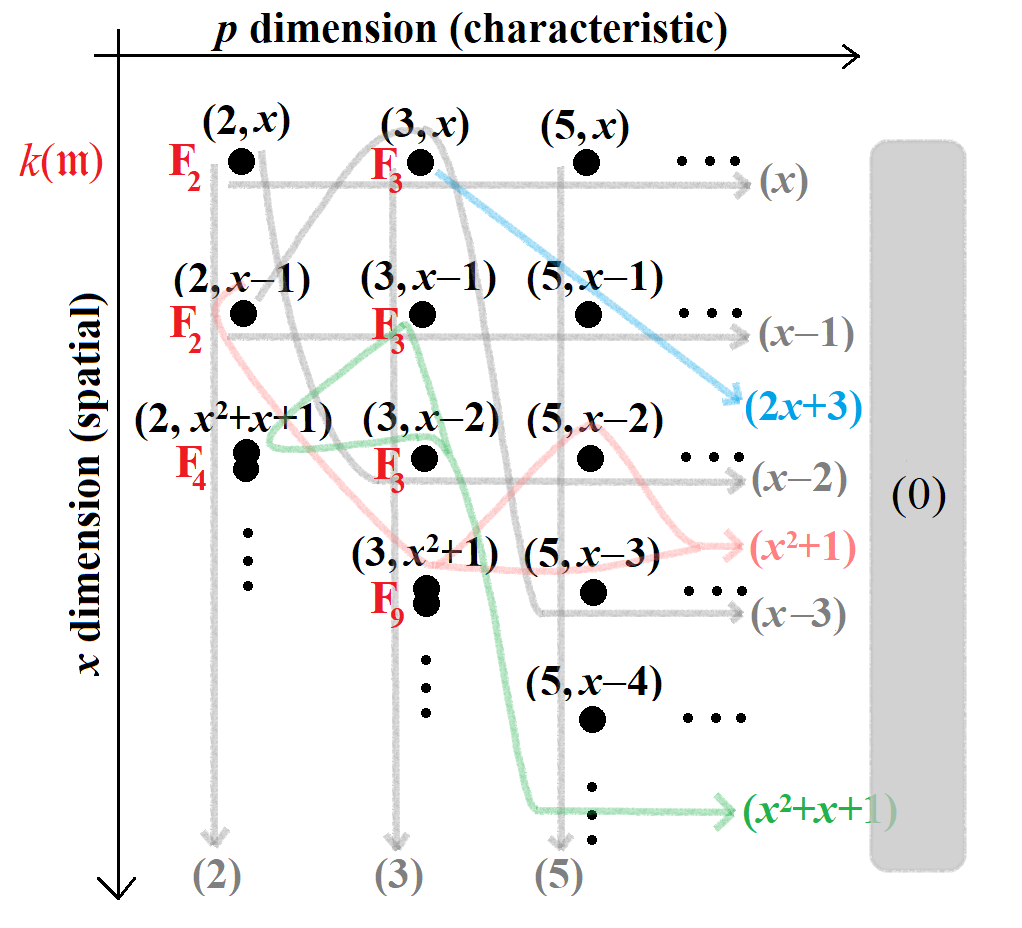
주어진 소수 는 소 아이디얼 의 부분 스킴인 "수직선" 를 정의한다. 이는 모든 에 대해 을 포함하며, 스킴의 "특성 점"이다. -좌표를 고정하면 "수평선" , 소 아이디얼 의 부분 스킴 를 얻는다. 또한 유리 좌표 에 해당하는 선 이 있으며, 이는 를 나누는 에 대해 와 교차하지 않는다.
과 같은 고차 "수평" 부분 스킴은 의 근인 -값, 즉 에 해당한다. 이는 서로 다른 -좌표에서 다르게 동작한다. 에서 의 두 점을 얻는데, 이는 이기 때문이다. 에서 한 개의 분기된 이중점 을 얻는데, 이는 이기 때문이다. 그리고 에서 는 의 확장 필드에서 에 해당하는 소 아이디얼이다. 이러한 값들을 구별할 수 없으므로(갈루아 군에 대해 대칭이므로), 을 두 개의 융합된 점으로 묘사해야 한다. 전반적으로, 은 두 개의 갈루아 대칭 수평선의 일종의 융합이며, 차수가 2인 곡선이다.
에서의 잉여 필드는 이며, 의 근 를 추가하는 의 필드 확장이다. 이는 개의 원소를 갖는 유한 필드이며, 이다. 다항식 는 스킴 에서 값 을 갖는 함수에 해당하며, 즉 이다. 다시 말해 각 는 닫힌 점에서의 값 에 의해 결정된다. 는 상수 다항식 의 소멸 궤적이며, 는 대수적 폐포 에서 의 근의 갈루아 궤도에 해당하는 각 특성 의 점을 포함한다.
스킴 는 고유하지 않으므로, 곡선 쌍이 예상된 중복도로 교차하지 못할 수 있다. 이는 디오판토스 방정식을 기하학적 도구로 분석하는 데 주요한 장애물이다. Arakelov 이론은 아핀 산술 스킴을 콤팩트화하여 이러한 장애물을 극복하고, 평가에 해당하는 무한대 점을 추가한다.
다항식 를 고려하면 아핀 스킴 는 로의 표준 사상을 가지며, 이를 산술 곡면이라고 한다. 섬유 는 유한체 위에서의 대수 곡선이다. 만약 가 타원 곡선이라면, 판별식 궤적 위에서의 섬유는 모두 특이 스킴이다.[4] 예를 들어, 가 소수이고 이면, 그 판별식은 이다. 이 곡선은 소수 위에서 특이하다.
임의의 가환환 ''R''과 자연수 ''n''에 대해, '''사영 공간''' 은 아핀 ''n''-공간의 ''n'' + 1개의 복사본을 열린 부분 집합을 따라 붙여서 스킴으로 구성할 수 있다. 이것은 아핀 스킴을 넘어가는 동기를 부여하는 기본적인 예시이다. 사영 공간이 아핀 공간보다 갖는 주요 장점은 이 ''R'' 위에서 고유 사상이라는 것이다; 이는 콤팩트성의 대수 기하학적 버전이다. 실제로, 복소 사영 공간 는 고전적 위상에서 콤팩트 공간인 반면, 은 그렇지 않다.
다항식 환 에서 양의 차수를 갖는 동차 다항식 ''f''는 의 닫힌 부분 스킴 을 결정하며, 이를 사영 초곡면이라고 한다. Proj 구성의 관점에서, 이 부분 스킴은 로 쓸 수 있다. 예를 들어, 의 닫힌 부분 스킴 는 유리수 위의 타원 곡선이다.
'''두 개의 원점을 갖는 직선''' (체 ''k'' 위에서)은 ''k'' 위 아핀 직선의 두 개의 복사본에서 시작하여, 항등 사상으로 두 개의 열린 부분 집합 A1 − 0을 접착하여 정의되는 스킴이다. 이는 분리되지 않은 스킴의 간단한 예시이다. 특히, 이는 아핀 스킴이 아니다.
아핀 스킴을 넘어가는 간단한 이유는 아핀 스킴의 열린 부분 집합이 아핀 스킴일 필요가 없다는 것이다. 예를 들어, 라고 하고, 복소수 위에서 생각해 보자; 그러면 ''n'' ≥ 2일 때 ''X''는 아핀 스킴이 아니다. (하지만, 원점을 제외한 아핀 직선은 아핀 스킴 과 동형이다. ''X''가 아핀 스킴이 아님을 보이기 위해, ''n'' ≥ 2일 때 ''X''의 모든 정칙 함수가 의 정칙 함수로 확장된다는 것을 계산한다: 이는 Hartogs의 보조정리와 유사하지만, 증명하기가 더 쉽다. 즉, 포함 사상 은 에서 로의 동형 사상을 유도한다. 만약 ''X''가 아핀 스킴이라면, ''f''가 동형 사상이라는 결론이 나오지만, ''f''는 전사 사상이 아니므로 동형 사상이 아니다. 그러므로, 스킴 ''X''는 아핀 스킴이 아니다.
''k''를 체라고 하자. 그러면 스킴 는 위상 공간이 양의 정수의 스톤-체흐 콤팩트화 (이산 위상으로)인 아핀 스킴이다. 실제로, 이 환의 소 아이디얼은 양의 정수에 대한 초여과기와 일대일 대응을 이루며, 아이디얼 는 양의 정수 ''n''과 관련된 주 초여과기에 해당한다. 이 위상 공간은 크룰 차원이 0차원이며, 특히, 각 점은 기약 성분이다. 아핀 스킴은 준콤팩트이므로, 이는 무한히 많은 기약 성분을 갖는 비-뇌터 준콤팩트 스킴의 예시이다. (대조적으로, 뇌터 스킴은 유한 개의 기약 성분만 갖는다.)
6. 1. 위상 공간으로서 동형이지만 스킴으로서 동형이 아닌 두 스킴
가장 간단한 예로, 서로 동형이 아닌 체 K, L을 생각할 수 있다. 모든 체의 스펙트럼은 한원소 공간이지만, 서로 동형이 아닌 체에 대응하는 아핀 스킴은 스킴으로서 서로 동형이 아니다.6. 2. 위상 공간으로서의 곱과 다른 스킴의 곱
스킴의 곱은 거의 항상 집합(또는 위상 공간)으로서의 곱과 일치하지 않으며, 후자보다 점이 더 많을 수도, 적을 수도 있다.예를 들어, 가 체인 경우 는 한원소 공간이며, 따라서 위상 공간으로서의 곱을 취하면 여전히 한원소 공간을 얻는다.
:
그러나
:
에서 는 체가 아닌 축소환이므로 2개 이상의 소 아이디얼을 가지며, 따라서 한원소 공간이 아니다. 이 스킴의 점들은 구체적으로 (또는 인 경우 ) 위의 갈루아 군 에 대응한다.[14]
다른 예로, 와 가 서로 다른 표수의 체 위에 정의된 스킴이라면, 는 아무 점을 갖지 않는다.[14]
체 위의 스킴의 경우, 체에 대한 올곱 역시 위상 공간으로서의 곱공간과 다르다. 예를 들어, 체 에 대한 아핀 스킴 을 생각하자.[13] 그렇다면
:
이다. 이 경우, 의 점들의 집합은 의 점들의 집합의 제곱과 일반적으로 다르다. 이는 아핀 평면 속에는 곱으로 나타낼 수 없는 대수 곡선들이 존재하기 때문이다. 다만, 닫힌 점들로 국한할 경우, 의 닫힌 점들은 와 표준적으로 대응하므로, 의 닫힌 점들은 의 닫힌 점들의 집합의 제곱과 같다.
7. 역사
대수기하학의 이탈리아 학파는 대수다양체의 일반점 개념을 도입하였으며, 바르털 레인더르트 판데르바르던은 1926년 책에서 일반점 개념을 엄밀히 정의하였다.[14] 이후 볼프강 크룰은 파리에서의 강의에서 임의의 가환환의 스펙트럼 및 그 위의 자리스키 위상을 정의하였으나, 청중들은 크룰의 정의를 비웃었고 크룰은 이 이론을 출판하지 않았다.[14]
피에르 카르티에 역시 박사 학위 논문을 집필하던 중 그로텐디크의 스킴과 동치인 개념을 독자적으로 제안하였으나, 논문이 서론부터 지나치게 길어지는 것을 피하기 위하여 논문에 수록하지 않았다.[14]
스킴 개념은 알렉산더 그로텐디크가 그의 저서 《대수기하학 원론》 1권[15]에서 처음으로 정의하였다. 원래 그로텐디크는 《대수기하학 원론》 초판[15]에서 오늘날 "스킴"이라고 불리는 개념을 "준스킴"(prescheme영어, préschéma프랑스어)라고 불렀고, 오직 분리 "준스킴"만을 "스킴"이라고 불렀다. 그러나 2판[16]에서는 제약 없이 모든 준스킴을 스킴이라고 불렀고, 현재는 이 용어가 통용되고 있다.
1950년대에 클로드 슈발레, 나가타 마사요시, 장-피에르 세르는 수론과 대수 기하학을 연결하는 베유 추측에 부분적으로 영감을 받아 대수 기하학의 대상을 더 확장했다. 예를 들어, 허용되는 기저 환을 일반화했다. '스킴'이라는 단어는 1956년 슈발레 세미나에서 처음 사용되었는데, 슈발레는 자리스키의 아이디어를 추구했다.[2] 피에르 카르티에에 따르면, 임의의 가환환의 스펙트럼을 대수 기하학의 기반으로 사용할 가능성을 세르에게 제안한 것은 앙드레 마르티노였다.
8. 발전
대수 기하학은 주로 실수에 대한 다항식 방정식 연구에서 시작되었다. 19세기 장-빅토르 퐁슬레와 베른하르트 리만의 연구를 통해, 대수적으로 닫힌 복소수 체에서 대수 기하학을 연구하는 것이 더 단순하다는 것이 밝혀졌다.[2] 20세기 초, 대수 기하학과 수론 사이의 유사성이 제기되었고, 양의 표수를 갖는 체와 같이 위상수학과 복소해석학의 도구를 적용할 수 없는 정수와 같은 수환 위에서 대수 기하학을 연구할 수 있는지에 대한 질문이 나왔다.
힐베르트 영점 정리는 임의의 대수적으로 닫힌 체 위에서 대수 기하학에 대한 접근법을 제시한다. 다항식환 의 극대 아이디얼은 의 원소의 -튜플 집합과 일대일 대응을 이루며, 소 아이디얼은 아핀 다양체로 알려진 의 기약 대수 집합에 해당한다. 1920년대와 1930년대에 에미 뇌터와 볼프강 크룰은 이러한 아이디어에 영감을 받아 가환대수를 발전시켰다.[2] 그들의 연구는 대수 기하학을 순수하게 대수적인 방향으로 일반화하여, 점(다항식환의 극대 아이디얼) 연구를 임의의 가환환의 소 아이디얼 연구로 일반화했다. 예를 들어, 크룰은 소 아이디얼을 통해 가환환의 차원을 정의했으며, 링이 뇌터 환일 때 이 정의가 기하학적 차원의 직관적인 속성을 만족함을 보였다.
뇌터와 크룰의 가환대수는 ''아핀'' 대수 다양체에 대한 대수적 접근법이었다. 그러나 대수 기하학의 많은 논증은 콤팩트 공간이기 때문에 사영 다양체에 더 적합하다. 1920년대부터 1940년대까지 바르텔 레언데르트 반 데르 바르덴, 앙드레 베유, 오스카 자리스키는 가환대수를 사영(또는 준사영) 다양체의 더 풍부한 설정에서 대수 기하학의 새로운 기반으로 적용했다.[2] 특히 자리스키 위상은 임의의 대수적으로 닫힌 체 위의 다양체에 대한 유용한 위상이며, 복소수 다양체의 고전적 위상(복소수의 거리 위상)을 어느 정도 대체한다.
수론에 적용하기 위해 반 데르 바르덴과 베유는 대수적으로 닫혀 있을 필요는 없는 임의의 체 위에서 대수 기하학을 공식화했다. 베유는 위상수학의 추상 다양체 모델에서 아핀 다양체를 열린 부분 집합을 따라 붙여서 ''추상 다양체''(사영 공간에 포함되지 않음)를 처음으로 정의했다. 그는 임의의 체 위의 곡선의 야코비 다양체를 구성하기 위해 이러한 일반성이 필요했다. (나중에 야코비는 베유, 차우, 마쓰사카에 의해 사영 다양체로 밝혀졌다.)
이탈리아 대수 기하학 학파의 대수 기하학자들은 종종 일반점을 사용했는데, 이는 다양체의 "대부분"의 점에 대해 참인 성질을 갖는 다소 모호한 개념이었다. 베유의 "대수 기하학의 기초"(1946)에서 일반점은 ''보편 영역''이라고 하는 매우 큰 대수적으로 닫힌 체의 점을 취함으로써 구성된다.[2] 이것은 같은 다양체에 대해 여러 개의 서로 다른 일반점이 존재하는 등 어색하게 작동했다. (나중에 스킴 이론에서 각 대수 다양체는 단일 일반점을 갖는다.)
1950년대에 클로드 슈발레, 나가타 마사요시, 장-피에르 세르는 수론과 대수 기하학을 연결하는 베유 추측에 부분적으로 영감을 받아 대수 기하학의 대상을 더 확장했다. 예를 들어, 허용되는 기저 환을 일반화했다. ''스킴''이라는 단어는 1956년 슈발레 세미나에서 처음 사용되었는데, 슈발레는 자리스키의 아이디어를 추구했다.[2] 피에르 카르티에에 따르면, 임의의 가환환의 스펙트럼을 대수 기하학의 기반으로 사용할 가능성을 세르에게 제안한 것은 앙드레 마르티노였다.[2]
9. 스킴의 기원
대수기하학의 이탈리아 학파는 대수다양체의 일반점 개념을 도입하였으며, 바르털 레인더르트 판데르바르던은 1926년 책에서 일반점 개념을 엄밀히 정의하였다.[14] 이후 볼프강 크룰은 파리에서의 강의에서 임의의 가환환의 스펙트럼 및 그 위의 자리스키 위상을 정의하였으나, 청중들은 크룰의 정의를 비웃었고 크룰은 이 이론을 출판하지 않았다.[14]
피에르 카르티에 역시 박사 학위 논문을 집필하던 중 그로텐디크의 스킴과 동치인 개념을 독자적으로 제안하였으나, 논문이 서론부터 지나치게 길어지는 것을 피하기 위하여 논문에 수록하지 않았다.[14]
스킴 개념은 알렉산더 그로텐디크가 그의 저서 《대수기하학 원론》 1권[15]에서 처음으로 정의하였다. 원래 그로텐디크는 《대수기하학 원론》 초판[15]에서 오늘날 "스킴"이라고 불리는 개념을 "준스킴"(prescheme영어, préschéma프랑스어)이라고 불렀고, 오직 분리 "준스킴"만을 "스킴"이라고 불렀다. 그러나 2판[16]에서는 제약 없이 모든 준스킴을 스킴이라고 불렀고, 현재는 이 용어가 통용되고 있다.
그로텐디크는 스킴 개념에 대하여 회고록에 다음과 같이 적었다.
10. 스킴의 동기
알렉산더 그로텐디크는 그의 저서 《대수기하학 원론》 1권[15]에서 처음으로 스킴의 개념을 정의하였다. 그로텐디크는 《대수기하학 원론》 초판[15]에서 오늘날 "스킴"이라고 불리는 개념을 "준스킴"(prescheme영어, préschéma프랑스어)라고 불렀고, 오직 분리 "준스킴"만을 "스킴"이라고 불렀다. 그러나 2판[16]에서는 제약 없이 모든 준스킴을 스킴이라고 불렀고, 현재는 이 용어가 통용되고 있다.
스킴은 이전의 대수적 다양성 개념을 다음과 같은 방식으로 확장한다.
- '''체 확대''': 체 ''k''에 대한 ''n''개의 변수를 갖는 몇 가지 다항식 방정식이 주어지면, 곱 집합 ''k''''n''에서 방정식의 해 집합 ''X''(''k'')를 연구할 수 있다. 체 ''k''가 대수적으로 닫혀 있으면(예: 복소수), ''X''(''k'')와 같은 집합을 기반으로 대수 기하학을 구축할 수 있다. 하지만 ''k''가 대수적으로 닫혀 있지 않으면 집합 ''X''(''k'')는 충분히 풍부하지 않다. 체 ''k''에 대한 스킴 ''X''는 ''k''의 모든 확대체 ''E''에 대해 ''E''-유리 점의 집합 ''X''(''E'')를 결정하기에 충분한 정보를 가지고 있다.
- '''일반점''': 스킴으로서의 아핀 선 A의 점은 복소수 점과 하나의 일반점을 갖는다. 일반점은 Spec('''C'''(''x'')) → A의 자연스러운 사상의 이미지이며, 여기서 '''C'''(''x'')는 1변수의 유리 함수의 체이다. ''X''를 복소수에 대한 평면 곡선 ''y''2 = ''x''(''x''−1)(''x''−5)라고 하면, 이것은 A의 닫힌 부분 스킴이다. 이것은 ''x''-좌표로 투영하여 아핀 선 A의 분기 덮개 이중 덮개로 볼 수 있다. 사상 ''X'' → A1의 올은 A1의 일반점을 따라 정확히 ''X''의 일반점이며, 이는 체 확대의 차수-2 확대와 동일하다.
- '''멱영원''': ''X''를 ''x''2 = 0으로 정의된 아핀 선 A의 닫힌 부분 스킴이라고 하자. ''X''에 대한 정칙 함수의 환은 '''C'''[''x'']/(''x''2)이다. 아핀 선에 대한 두 개의 정칙 함수는 원점에서 동일한 값과 첫 번째 도함수를 갖는 경우에만 ''X''로의 제한이 동일하다. 이러한 비-'''환원 스킴''' 스킴을 허용하면 미적분과 무한소의 개념이 대수 기하학에 도입된다. 멱영원은 교차 이론에서 자연스럽게 발생한다. 예를 들어, 체 에 대한 평면 에서 ''x-''축과 포물선 을 고려한다. 이들의 스킴론적 교차는 횡단하지 않으므로, 점 일 뿐만 아니라, 접선 방향을 포함하는 두꺼운 점이며, 교차 다중도 2를 갖는다. 매끄러운 스킴 복소 다양체 ''Y''에서 차수가 2인 모든 영차원 닫힌 부분 스킴은 ''Y''의 서로 다른 두 복소수 점 또는 ''X'' = Spec '''C'''[''x'']/(''x''2)와 동형인 부분 스킴으로 구성된다. 후자의 유형의 부분 스킴은 ''Y''의 복소수 점 ''y''와 접선 공간 T''y''''Y''의 선에 의해 결정된다.
11. 가환층
스킴 이론의 핵심 부분은 벡터 다발의 개념을 일반화한 가환층의 개념이다. 스킴 ''X''에 대해, 먼저 ''O''''X''-가군, 즉 정칙 함수 층 ''O''''X'' 위에 가군을 형성하는 ''X''상의 아벨 군 층인 '''''O''''X''-가군'''의 아벨 범주를 고려한다. 특히, 가환환 ''R'' 위의 가군 ''M''은 ''X'' = Spec(''R'') 상에서 연관된 ''O''''X''-가군을 결정한다. 스킴 ''X''상의 '''준가환층'''은 ''X''의 각 아핀 열린 부분 집합에 대한 가군에 연관된 층인 ''O''''X''-가군을 의미한다. 마지막으로, '''가환층''' (예를 들어, 노에터 스킴 ''X''에 대한)은 ''X''의 각 아핀 열린 부분 집합에서 유한 생성 가군에 연관된 층인 ''O''''X''-가군이다.
가환층은 유한 생성 자유 가군에서 국소적으로 오는 층인 '''벡터 다발'''의 중요한 부류를 포함한다. 한 예는 체 위의 매끄러운 다양체의 접다발이다. 그러나 가환층은 더 풍부하다. 예를 들어, ''X''의 닫힌 부분 스킴 ''Y'' 위의 벡터 다발은 (직상 구성에 의해) ''Y'' 외부에서는 0인 ''X''상의 가환층으로 볼 수 있다. 이런 방식으로, 스킴 ''X''상의 가환층은 ''X''의 모든 닫힌 부분 스킴에 대한 정보를 포함한다. 게다가, 층 코호몰로지는 가환 (및 준가환) 층에 대해 좋은 성질을 갖는다. 결과적인 가환층 코호몰로지 이론은 아마도 대수 기하학의 주요 기술적 도구일 것이다.[1][2]
12. 일반화
스킴은 여러 가지 방법으로 일반화될 수 있다. 한 가지 방법은 에탈 위상을 사용하는 것이다. 마이클 아르틴은 '''대수적 공간'''을 에탈 위상에서 층이며, 에탈 위상에서 국소적으로 아핀 스킴인 함자로 정의했다. 동치적으로, 대수적 공간은 에탈 동치 관계에 의한 스킴의 몫이다. 강력한 결과인 아르틴 표현 가능성 정리는 함자가 대수적 공간으로 표현되기 위한 간단한 조건을 제공한다.[5]
더 나아가 일반화된 것은 스택의 개념이다. 대략적으로 말하면, '''대수적 스택'''은 각 점에 부착된 대수적 군을 가지는 방식으로 대수적 공간을 일반화하며, 이는 해당 점의 자기 동형 군으로 간주된다. 예를 들어, 대수적 군 ''G''의 대수적 다양체 ''X''에 대한 모든 작용은 ''G''의 작용에 대한 고정 부분군을 기억하는 '''몫 스택''' [''X''/''G'']를 결정한다. 더 일반적으로, 대수 기하학의 모듈 공간은 종종 스택으로 가장 잘 볼 수 있으며, 이는 분류되는 객체의 자기 동형 군을 추적한다.
그로텐디크는 원래 강하 이론을 위한 도구로 스택을 도입했다. 그러한 공식에서 스택은 (비공식적으로 말하면) 범주의 층이다. 이러한 일반적인 개념에서 아르틴은 대수적 대상으로 간주될 수 있는 더 좁은 클래스의 대수적 스택 (또는 "아르틴 스택")을 정의했다. 여기에는 델린-멈포드 스택 (위상수학의 오비폴드와 유사)이 포함되며, 안정자 군이 유한하고, 안정자 군이 자명한 대수적 공간도 포함된다. 킬-모리 정리는 유한 안정자 군을 가진 대수적 스택이 대수적 공간인 조잡한 모듈 공간을 갖는다고 말한다.
또 다른 유형의 일반화는 구조 층을 풍부하게 하여 대수 기하학을 호모토피 이론에 더 가깝게 만드는 것이다. 유도 대수 기하학 또는 "스펙트럼 대수 기하학"으로 알려진 이 설정에서 구조 층은 가환환의 층의 호모토피적 유사체로 대체된다 (예: E-무한대 링 스펙트럼의 층). 이러한 층은 동치 관계까지 연관적이고 가환적인 대수적 연산을 허용한다. 이 동치 관계에 대한 몫을 취하면 일반 스킴의 구조 층이 생성된다. 그러나 몫을 취하지 않으면 유도 함자가 텐서 곱 및 모듈에 대한 Hom 함자와 같은 연산에 대한 더 높은 정보를 생성하는 것과 같은 방식으로 더 높은 정보를 기억할 수 있는 이론으로 이어진다.
참조
[1]
문서
Introduction of the first edition of "[[Éléments de géométrie algébrique]]"
[2]
간행물
Les schémas
http://www.numdam.or[...]
[3]
웹사이트
Stacks Project, Tag 020D
http://stacks.math.c[...]
[4]
웹사이트
Elliptic curves
https://homepages.wa[...]
[5]
웹사이트
Stacks Project, Tag 07Y1
http://stacks.math.c[...]
[6]
서적
Algebraic geometry and arithmetic curves
http://www.math.u-bo[...]
Oxford University Press
2013-07-16
[7]
서적
[8]
서적
The geometry of schemes
Springer-Verlag
[9]
저널
[10]
서적
2015-08-13
[11]
저널
[12]
서적
Current trends in arithmetical algebraic geometry. Proceedings of the AMS–IMS–SIAM joint summer research conference held August 18–24, 1985 with support from the National Science Foundation
American Mathematical Society
[13]
서적
[14]
서적
http://www.ams.org/b[...]
[15]
저널
http://www.numdam.or[...]
[16]
서적
[17]
서적
http://lipn.univ-par[...]
2016-08-23
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com
