맨위로가기

수학 교육

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

수학 교육은 시대, 문화, 국가에 따라 다양한 목표를 가지며, 수학적 지식과 기술을 가르치는 과정을 의미한다. 고대부터 현대에 이르기까지 수학 교육은 사회의 변화와 함께 발전해 왔으며, 학교 교육의 핵심 과목으로 자리 잡았다. 수학 교육의 목표는 기본적인 수리력, 실용 수학, 문제 해결 능력 등을 함양하는 것이며, 교수 방법은 고전 교육, 컴퓨터 기반 교육, 탐구 수학 등 다양하게 존재한다. 수학 교육은 연령대별로 내용과 수준이 다르며, 각 국가 및 지역의 교육 과정과 기준에 따라 운영된다. 또한, 수학교육 연구는 양적 연구와 질적 연구를 통해 이루어지며, 문화적 형평성, 수학교사 교육, 방법론 등에 대한 논쟁이 존재한다.

더 읽어볼만한 페이지

  • 수학 교육 - 받아올림
    받아올림은 덧셈에서 자릿수 합이 10을 넘을 때 윗자리로 1을 올리는 것이며, 뺄셈에서는 윗자리에서 10을 빌려오는 빌림이 발생하는 개념이다.
  • 수학 교육 - 구구단
    구구단은 곱셈을 간편하게 계산하도록 곱셈 결과를 표로 정리한 것이며, 1단부터 9단까지 외우는 곱셈 구구가 일반적이고, 덧셈, 뺄셈, 나눗셈 구구 등 다양한 형태가 존재하며, 수학적 개념 이해의 기초가 되고 실생활에도 응용된다.
수학 교육
개요
분야수학, 교육
목적수학적 지식, 기술, 태도 함양
대상유아 교육부터 고등 교육까지 모든 학습자
역사
기원고대 문명의 수학 교육
발전시대와 사회 변화에 따른 교육 방법 변화
내용 영역
초등 수학수와 연산, 도형, 측정, 확률과 통계, 규칙성
중등 수학대수, 기하, 미적분, 확률과 통계
교육 방법
강의식교사의 설명 중심 수업
탐구식학생 스스로 문제 해결 능력 향상
협동 학습모둠 활동을 통한 상호 학습
프로젝트 학습특정 주제에 대한 심층 연구 및 발표
토론식학생 간의 의견 교환 및 비판적 사고 능력 함양
ICT 활용 교육컴퓨터, 인터넷, 교육용 소프트웨어 활용
평가
평가 방법지필 평가, 수행 평가, 관찰 평가, 자기 평가, 동료 평가
평가 목적학생의 학업 성취도 측정, 학습 개선, 교육 과정 개선
교육 과정
국가 교육 과정국가 수준에서 제시되는 수학 교육 목표 및 내용 기준
교과서교육 과정에 기반하여 개발된 학습 자료
교사교육 과정 운영의 주체
교수 학습 자료
교구자, 컴퍼스, 각도기, 모형 등
소프트웨어GeoGebra, R, Python 등
웹사이트Khan Academy, Wolfram Alpha 등
연구 분야
수학 학습 심리수학 학습 과정에 대한 인지적, 정의적 요인 연구
수학교육 방법효과적인 교수 학습 방법 개발 및 적용 연구
수학교육 정책수학교육 관련 정책 결정 과정 및 효과 분석 연구
수학교육 평가타당하고 신뢰성 있는 평가 도구 개발 및 활용 연구
수학교육사수학교육의 역사적 변천 과정 연구
관련 단체
국내대한수학회, 한국수학교육학회, 전국수학교사모임
국제국제수학연맹(IMU), 국제수학교육위원회(ICMI)
영향 요인
사회 문화적 요인사회적 요구, 문화적 가치관, 교육 정책 등
기술 발달컴퓨터, 인터넷, 계산기 등
학습 이론행동주의, 인지주의, 구성주의 등
문제점 및 개선 방향
문제점수학에 대한 흥미 저하, 학습 부진, 사교육 의존 심화 등
개선 방향수학에 대한 흥미 유발, 자기 주도 학습 능력 함양, 공교육 강화 등

2. 역사

수학의 역사는 고대 그리스 시대까지 거슬러 올라가기 때문에 수학 교육의 역사도 거기서 비롯됐다고 볼 수 있다. 고대 그리스, 고대 로마, 고대 이집트 등 수많은 고대 문명에서 산술과 기하학(에우클레이데스의 《원론》에 기초)이 자리 잡았다. 이것은 당시 석공, 상인, 대금업과 같은 직업에서 중요시되었지만, 당시 교육 대상은 부유층 남성뿐이었으며 모든 사람이 배울 수 있는 것은 아니었다.

르네상스 시대에 수학의 학술적 위상은 크게 떨어졌다. 이 시기 수학은 무역 등의 경제 활동에서 중요시되었고, 학술적으로는 서양 대학교에서 자연 철학 및 도덕 철학 연구를 위한 수단에 머물렀다. 이러한 상황은 17세기 영국 애버딘 대학교, 옥스퍼드 대학교, 케임브리지 대학교 등에서 수학 교수직이 생기면서 호전되었지만, 여전히 대학교 밖에서 수학을 가르칠 수는 없었다.

18세기 산업 혁명을 계기로 유럽 각지 인구가 급증하면서 도시 생활도 변화했는데, 시각을 파악하거나 돈을 계산하거나 간단한 연산을 하는 능력 등의 기본적 기술이 모든 사람에게 필수적이었다. 새로 도입된 학교 교육 제도에서 수학은 일찍부터 교과 과정의 핵심이 되었다. 이러한 학교 교육 체계는 20세기까지 모든 선진국에서 도입되었다. 또한 마셜 맥루헌의 "전기의 시대"(Electric ages)라는 발언을 계기로 수학 교육은 이전의 지식 주입형에서 문제 해결형으로 변화하게 되었다.

2. 1. 고대

고대 이집트, 고대 바빌로니아, 고대 그리스, 고대 로마, 고대 인도 등 많은 고대 문명에서 초등 수학은 교육의 핵심 부분이었다. 대부분의 경우, 정규 교육은 충분히 높은 지위, 재산 또는 카스트를 가진 남성 아이들에게만 제공되었다. 가장 오래된 수학 교과서는 기원전 1650년경의 린드 파피루스이다.[1]

메소포타미아 역사가들은 피타고라스 법칙의 사용이 고(古) 바빌로니아 제국 (기원전 20-16세기)까지 거슬러 올라가며, 피타고라스가 태어나기 천 년도 더 전에 서기관 학교에서 가르쳐졌다는 것을 확인했다.[2][3][4][5][6]

플라톤은 자유 교양 과목을 트리비움과 쿼드리비움으로 나누었는데, 쿼드리비움에는 산수와 기하학과 같은 수학 분야가 포함되었다. 이 구조는 중세 유럽에서 발전된 고전 교육의 구조에서도 이어졌다. 기하학의 가르침은 거의 보편적으로 유클리드의 ''원론''에 기초했다. 석공, 상인, 돈을 빌려주는 사람과 같은 직업의 견습생들은 직업과 관련된 실용 수학을 배우기를 기대할 수 있었다.

수학의 역사는 고대 그리스 시대까지 거슬러 올라가기 때문에, 수학 교육의 역사도 거기에서 시작되었다고 생각할 수 있다. 실제로 고대 그리스, 로마 제국, 이집트 등 수많은 고대 문명에서 초등 교육 및 교양 과목의 한 분야로서 산술과 기하학(유클리드의 『원론』에 근거)이 자리 잡고 있었다. 이것들은 당시의 석공, 상인, 돈놀이꾼과 같은 직업에서 중요시되었지만, 당시 교육의 대상은 부유층에 속하는 남자뿐이었으며, 모든 사람이 배울 수 있는 것은 아니었다.

2. 2. 중세 및 근대 초기

르네상스 시대에는 수학의 학문적 지위가 하락했지만, 상업 활동의 필요성에 따라 실용 수학은 여전히 중요하게 여겨졌다.[7] 중세 시대 유럽 대학교에서는 자연 철학, 형이상학, 윤리학 연구에 수학이 활용되었다.[7] 1300년대 이탈리아의 주산 학교에서 현대적인 산술 교육 과정(덧셈, 뺄셈, 곱셈, 나눗셈)이 시작되었다.[8] 17세기 영국 애버딘 대학교, 옥스퍼드 대학교, 케임브리지 대학교 등에서 수학 교수직이 생기면서 수학 연구의 사회적 지위가 향상되었다.

2. 3. 근대

18세기 산업 혁명을 계기로 유럽 각지의 인구가 급증하면서 도시 생활도 변화했는데, 시각을 파악하거나 돈을 계산하거나 간단한 연산을 하는 능력 등의 기본적 기술이 모든 사람들에게 필수적이었다. 새로 도입된 학교 교육 제도에서 수학은 일찍부터 교과 과정의 핵심이 되었다.[56] 이러한 학교 교육 체계는 20세기까지 모든 선진국에서 도입되었다.

2. 4. 현대

20세기까지 모든 선진국에서 학교 교육 체계가 도입되면서 수학은 교과 과정의 핵심이 되었다. 또한 마셜 맥루헌의 "전기의 시대"(Electric ages)라는 발언을 계기로 수학 교육은 이전의 지식 주입형에서 문제 해결형으로 변화하게 되었다. 수학 교육에는 집합, 논리학을 시작으로 계산에는 대수학, 도형 문제에는 기하학 (특히 유클리드 기하학이 중심이 됨), 함수·미분·적분법에는 해석학, 그리고 확률론·통계학과 같이 기본이 되는 이론이 있다.

토야마 히로시의 수도 방식, 카게야마 히데오의 백칸 계산, 시미즈 히로시의 채점법 등이 저명한 실천 사례이다. 특히 백칸 계산은 수준별 교육이 추진되던 시기에 널리 퍼졌으며, 현대에도 초등학교를 중심으로 많은 학교에서 실천되고 있다. 한편, 계산기 등의 보급에 따라 계산 속도보다 대략적인 계산이나 연산 결정과 같은 다른 능력이 중요해지고 있다는 현실을 감안하여, 이러한 실천 방안을 재검토하려는 움직임도 보인다.

이론적인 측면에서는 최근 인지 심리학의 발전에 따라 수의 이해나 수학적 개념의 발달 단계별 이해 모델이 구축되고 있다.

2. 5. 한국의 역사

조선 시대에는 데라코야에서 상인이 되기 위한 지식으로 산술을 가르쳤고, 와산이 오락 및 학문 분야로 존재했다. 대한제국 시기, 학제 실시와 함께 서양식 수학(양산)이 도입되었다. 일제강점기에는 가쿠슈인 등에서 수학 교육이 이루어졌다. 해방 이후 미군정 시기, 교수요목 제정으로 교육과정이 정비되었다. 대한민국 정부 수립 이후, 교육과정 개정을 거치며 수학 교육 내용과 방법이 변화해 왔다. 최근에는 문이과 통합 교육과정, 소프트웨어 교육 도입 등 변화가 이루어지고 있다. 더불어민주당은 수학 교육과정 개선을 통해 창의융합형 인재 양성을 지원하고 있다.

3. 목표

다른 시기와 문화, 그리고 여러 나라에서 수학 교육은 다양한 목표를 달성하고자 노력해 왔다. 이러한 목표에는 다음이 포함된다.[13]

목표
모든 학생에게 기본적인 수리력 기술을 가르치고 배우게 하기
대부분의 학생에게 실용 수학(산수, 기초 대수학, 평면 및 입체 기하학, 삼각법, 확률, 통계)을 가르쳐 직업이나 기술을 습득하고, 뉴스나 인터넷에서 사용되는 수학(예: 백분율, 차트, 확률, 통계)을 이해하도록 돕기
어린 나이에 추상적인 수학 개념(예: 집합, 함수) 가르치기
공리계[15]의 예시이자 연역적 추론의 모델로서, 선택된 수학 분야(예: 유클리드 기하학) 가르치기[14]
현대 세계의 지적 업적의 예시로 선택된 수학 분야(예: 미적분학) 가르치기
과학, 기술, 공학, 수학 (STEM) 분야에서 경력을 쌓고 싶어하는 학생들에게 고급 수학 가르치기
발견법[16] 및 기타 문제 해결 전략을 가르쳐 비정형적인 문제 해결하기
사회 과학 및 보험 계리 과학에서 수학을 가르치고, 교양 교육을 받는 교양 대학 또는 대학교에서 일부 선택된 예술 분야에서 수학 가르치기



1974년 기니비사우에서 산수를 하는 소년

4. 교수 방법

어떤 특정한 맥락에서 사용되는 교육 방식은 관련 교육 시스템이 달성하려고 하는 목표에 의해 크게 결정된다. 수학을 가르치는 방식은 다음과 같다.


  • '''고전 교육(Classical education):''' 중세 시대의 고전적 교육 커리큘럼의 일부인 사과를 가르치는 방식인 수학 교육이다. 연역에 따른 추론의 패러다임으로 여겨진 《에우클레이데스의 원론》을 기반으로 한다.
  • '''컴퓨터 기반 수학(Computer-based math):''' 수학 소프트웨어를 계산의 주요 도구로서 사용하는 것에 기초하는 접근법이다.
  • '''컴퓨터 기반 수학 교육(Computer-based mathematics education):''' 컴퓨터를 사용하여 수학을 가르치는 교육 방식이다. 모바일 애플리케이션은 또한 학생들이 수학을 배우는 것을 돕기 위해 개발되었다.[17][18][19]
  • '''전통적인 접근법:''' 수학적 개념, 사상, 기술의 계층을 통한 점진적이고 체계적인 지도 방식이다. 산술로 시작해서 유클리드 기하학과 기초 대수학을 동시에 가르친다. 교육 과정과 교과 과정 결정은 교육학적 고려보다는 과목의 논리에 의해 좌우되는 경우가 많기 때문에 강사가 기초 수학에 대해 잘 알고 있어야 한다. 다른 방법들은 이 접근법의 일부 측면을 강조함으로써 나타난다.
  • '''탐색 수학(Discovery math):''' 개방형 질문 및 조작물 도구를 사용하여 문제 기반 또는 탐구 기반 학습을 중심으로 수학을 가르치는(발견 학습) 구성론적 방법이다.[23] 이러한 유형의 수학 교육은 2005년부터 캐나다의 여러 지역에서 시행되었다.[24] 직접 학습, 암기를 중시하는 전통적인 교수 모델에 비해 많은 사람들이 수학 점수 하락으로 인한 효과성을 비판하면서 캐나다 수학 전쟁 논쟁의 선두에 서 있다.
  • '''연습:''' 분수를 추가하거나 이차 방정식을 푸는 것과 같은 유사한 유형의 연습을 대량으로 완료함으로써 수학적 기술을 강화한다.
  • '''역사적 방법:''' 역사적, 사회적, 문화적 맥락에서 수학의 발전을 가르친다. 기존 접근 방식보다 더 많은 인간적 관심을 제공한다.[22]
  • '''숙달:''' 대부분의 학생들이 진보하기 이전에 높은 수준의 역량을 획득할 것으로 기대되는 접근 방식이다.
  • '''신수학(New Math):''' 집합론, 함수, 10 이외의 밑과 같은 추상적인 개념에 초점을 맞추는 수학을 가르치는 방법이다. 냉전 초기에 소련이 차지하고 있던 우주에서의 기술적 우위의 도전에 대한 대응 차원에서 미국에서 채택되었고 1960년대 후반부터 도전을 받기 시작했다. 신수학에 대한 가장 영향력 있는 평론 가운데 하나는 1973년 모리스 클라인(Morris Kline)의 책 《왜 조니는 덧셈을 못하는가(Why Johnny Can't Add)》였다. 신수학 방법은 톰 레러(Tom Lehrer)의 가장 인기 있는 패러디 노래 가운데 하나의 주제였다. 레어러는 이 노래를 통해 "... 알다시피 새로운 접근법에서 중요한 것은 올바른 답을 얻는 것보다 여러분이 무엇을 하고 있는지 이해하는 것이다."라고 지적했다.
  • '''문제 해결(Problem solving):''' 학생들을 개방적이고 특이하며 때로는 풀리지 않는 문제들로 설정함으로써 수학적 독창성, 창의성, 그리고 휴리스틱 이론에 따른 사고 방식을 키운다. 그 문제들은 간단한 단어 문제에서부터 국제수학올림피아드와 같은 국제 수학 대회의 문제까지 다양할 수 있다. 문제 해결은 새로운 수학적 지식을 쌓기 위한 수단으로 사용되며 일반적으로 학생들의 사전 이해를 바탕으로 한다.
  • '''레크리에이션 수학(Recreational mathematics):''' 재미있는 수학 문제는 학생들이 수학을 배우도록 동기를 부여하고 수학의 즐거움을 높일 수 있다.[25]
  • '''개혁 수학(Reform mathematics):''' 미국과 캐나다의 대학 수학 이전의 교육 비전, 수학 사상과 절차에 대한 학생 이해 심화에 초점을 맞춘 교육 방식이다. 전미수학교사협의회(National Council of Teachers of Mathematics)가 공식화했으며, 이는 학교 수학의 원칙 및 표준(Principles and Standards for School Mathematics)을 만들었다.
  • '''관계형 접근 방식:''' 수업 주제를 사용하여 일상적인 문제를 해결하고 이 주제를 현재 사건과 연관시킨다.[21] 이러한 접근법은 수학의 많은 사용에 초점을 맞추고 학생들이 왜 수학을 알아야 하는지 이해하는 데 도움을 줄 뿐만 아니라 학생들이 교실 밖의 실제 상황에 수학을 적용하는 데에 도움을 준다.
  • '''암기(Rote learning):''' 일반적으로 의미가 없거나 논리적 추론에 의해 뒷받침되는 반복과 암기에 의한 수학적 결과, 정의 및 개념을 가르치는 교육 방식이다. 파괴적인 용어는 "굴착하고 죽이기"(drill and kill)이다. 전통적인 교육에서 암기 학습은 구구단, 정의, 공식, 그리고 수학의 다른 측면을 가르치기 위해 사용된다.
  • '''수학 산책(Math walk):''' 인식된 객체와 장면의 경험을 수학적 언어로 번역하는 산책이다.


게임은 학생들이 암기식으로 배우는 기술을 향상하도록 동기를 부여할 수 있다. "넘버 빙고"에서 플레이어는 주사위 3개를 굴린 다음, 해당 숫자에 대한 기본적인 수학적 연산을 수행하여 새로운 숫자를 얻고, 보드에서 그 숫자를 덮어 행으로 4개의 사각형을 덮으려고 한다. 이 게임은 라오스에서 빅 브라더 마우스(Big Brother Mouse)가 주최한 "디스커버리 데이"에 진행되었다.


일본에서 중학교 및 고등학교 "수학" 교원 면허를 취득할 때에는, 교원 면허법 시행 규칙 제4조 및 제5조에 의거하여 다음 내용을 포함하는 과목을 규정 단위 수 이상 이수해야 한다.[58]

이수 과목내용
대수학방정식, 행렬, 군 등
기하학집합론, 비유클리드 기하학, 위상 공간 등
해석학함수, 편미분, 중적분, 미분 방정식 등
응용 수학주로 확률론, 통계학, 계산 과학 등



이 외에, 제6조 제4란에 규정되어 있는 "각 교과의 지도법"으로, "수학"의 지도법 (수학과 교육법 등으로 불림. 기본적으로는, 수학교육학을 포함)을 이수할 필요가 있다.

2010년 3월 현재, 일본에서 중학교·고등학교 "수학" 면허는 많은 교원 양성 계열·이공계열·정보 과학 계열의 대학·학부에서 취득 가능하다.[59] 통신 교육에 의해 취득 가능한 대학은 2020년도에 다마가와 대학, 부교 대학, 메이세이 대학, 홋카이도 정보 대학, 환태평양 대학의 5개교이며, 국어과의 7개교, 시민과의 9개교보다는 적지만, 이과 1개교보다 많아 현재는 극단적으로 적은 상태는 아니다.[60]

학교 교육 현장에서는 수준별 학습이나 팀 티칭을 실시할 필요성 때문에 모집 인원이 많지만, 그에 비해 면허 취득자가 적은 현상이 있다.

또한 현대 일본의 교원 면허 제도에서는, 수학과 관련이 깊은 학문 영역이 많이 존재하지만(물리학・화학을 비롯한 자연 과학, 철학・경제학・심리학・사회학 등), 이러한 학문 영역을 이수해도, 수학 교원 면허 취득을 위한 단위로 거의 고려되지 않는다. 또한 응용 수학의 컴퓨터는 정보에도 크게 관련된 내용이지만, 서로 단위의 호환성은 없다.

5. 내용 및 연령 수준

국가별로 수학의 수준과 순서는 다르게 구성된다.[26] 각기 다른 수준의 수학은 국가별로 서로 다른 연령대에서 다소 다른 순서로 가르쳐진다. 때때로 특별 또는 영재반과 같은 이유로 일반적인 연령보다 더 어린 나이에 수업을 가르치는 경우도 있다.

대부분의 국가에서 초등 수학은 유사하게 가르쳐지지만 차이점도 있다. 대부분의 국가에서는 미국보다 더 적은 주제를 더 깊이 다루는 경향이 있다.[26] 초등학교 시절에 아이들은 덧셈, 뺄셈, 곱셈 및 나눗셈을 포함한 정수와 산술에 대해 배운다.[27] 숫자 및 그림 형태의 비교 및 측정, 분수 및 비례, 패턴, 그리고 기하학과 관련된 다양한 주제를 가르친다.[28]

대부분의 미국 고등학교 수준에서는 대수, 기하학, 그리고 해석학(미적분학 예비 과정 및 미적분학)이 서로 다른 해에 별도의 과목으로 가르쳐진다. 반면에 대부분의 다른 국가(및 몇몇 미국 주)에서는 수학이 통합된 과목으로 가르쳐지며, 매년 수학의 모든 분야의 주제를 공부한다. 따라서 학생들은 미국에서처럼 ''à la carte'' 방식으로 과목을 선택하는 대신, 여러 주제를 포함하는 미리 정의된 과정을 수강한다. 이러한 경우에도 고등학교 졸업 후 학생의 예상 진로에 따라 여러 "수학" 선택 과목이 제공될 수 있다. (예를 들어, 남아프리카 공화국에서는 선택 과목으로 수학, 수학적 리터러시 및 기술 수학이 있다.) 따라서, 과학 중심 커리큘럼은 일반적으로 대학교 1학년 수학과 겹치며, 16~17세에 미분 미적분학과 삼각법을 포함하고, 고등학교 마지막 해에 적분 미적분학, 복소수, 해석 기하학, 지수 함수 및 로그 함수, 그리고 무한 급수를 포함한다. 확률과 통계도 마찬가지로 자주 가르쳐진다.

대학 수준에서는 이학사와 공학사 학생들이 다변수 미적분학, 미분 방정식, 그리고 선형대수를 수강해야 한다. 몇몇 미국 대학에서는 수학 부전공 또는 준학사가 이러한 과목들을 실질적으로 포함한다. 수학 학사 전공자들은 해석학과 현대 대수학의 지정된 고급 과목을 수강해야 하며, 순수 수학 내에서, 그리고 종종 응용 수학에서 다른 분야를 추가로 공부한다. 순수 수학의 다른 주제에는 미분 기하학, 집합론, 그리고 위상수학이 있다. 응용 수학은 편미분 방정식, 최적화, 그리고 수치 해석과 같이 자체적으로 전공 과목으로 선택할 수 있다. 특정 주제는 다른 과목 내에서 가르쳐진다. 예를 들어, 토목 기사는 유체 역학을 공부해야 할 수 있으며,[29] "컴퓨터 과학을 위한 수학"에는 그래프 이론, 순열, 확률, 그리고 형식적 증명과 같은 수학적 증명이 포함될 수 있다.[30] 순수 및 응용 수학 학위는 종종 확률론 또는 수리 통계학, 그리고 확률 과정에서 모듈을 포함한다. 이론 물리학은 수학 집약적이며, 종종 순수 또는 응용 수학 학위와 실질적으로 겹친다. 경영 수학은 일반적으로 소개 미적분학 및 (때때로) 행렬 계산으로 제한된다. 경제학 학사 프로그램은 추가로 수학적 최적화, 종종 미분 방정식 및 선형 대수학을 다루며, 때때로 해석학도 다룬다.

6. 표준

현대에 들어와서는 지역 또는 국가 표준으로 수학 교육 과정이 설정되는 추세이다. 예를 들어, 영국에서는 수학 교육에 대한 기준이 잉글랜드의 국가 교육 과정의 일부로 설정되어 있으며,[31] 스코틀랜드는 자체 교육 시스템을 유지하고 있다. 다른 많은 국가들은 국가 표준 또는 교육 과정을 설정하는 중앙 집중식 부처를 두고 있으며, 때로는 교과서까지 지정하기도 한다.

Ma (2000)의 연구에 따르면, 표준화된 수학 시험에서 높은 점수를 받은 학생들이 고등학교에서 더 많은 수학 과목을 수강했다. 이로 인해 일부 주에서는 2년 대신 3년의 수학 수강을 요구하게 되었다. 그러나 이 요구 사항은 종종 다른 하위 수준의 수학 과목을 수강함으로써 충족되었기 때문에, 추가 과목들은 성취 수준을 높이는 데 "희석된" 효과를 보였다.[32]

북미에서는 전미 수학교사 협의회(NCTM)가 2000년에 미국과 캐나다를 위해 ''학교 수학의 원리와 기준''을 발표하여 수학 개혁의 흐름을 가속화했다. 2006년, NCTM은 ''교육 과정 핵심 사항''을 발표하여 8학년까지 각 학년별로 가장 중요한 수학 주제를 권장했다. 그러나 이러한 기준은 미국의 주와 캐나다의 주(Province)가 선택하여 시행하는 지침이었다. 2010년, 전미 주지사 협회 모범 실천 센터와 주 교육감 협의회는 미국 주를 위한 공통 핵심 국가 표준을 발표했으며, 이후 대부분의 주에서 이를 채택했다. 수학에서의 공통 핵심 국가 표준 채택은 각 주의 재량에 달려 있으며, 연방 정부가 의무화하지는 않는다.[33] "주는 정기적으로 학업 기준을 검토하며, 학생들의 요구를 가장 잘 충족시키기 위해 기준을 변경하거나 추가할 수 있다."[34] NCTM에는 주 수준에서 서로 다른 교육 기준을 가진 주 협회가 있다. 예를 들어, 미주리주에는 미주리 수학교사 협의회(MCTM)가 있으며, 이 협회는 웹사이트에 교육의 기둥과 기준을 게시하고 있다. MCTM은 또한 교사와 미래의 교사에게 회원 자격을 제공하여 수학 교육 기준의 변화에 대한 최신 정보를 얻을 수 있도록 한다.[35]

경제 협력 개발 기구(OECD)가 만든 국제 학업 성취도 평가 프로그램(PISA)은 15세 학생들의 읽기, 과학, 수학 능력을 연구하는 글로벌 프로그램이다.[36] 첫 번째 평가는 2000년에 실시되었으며 43개국이 참여했다.[37] PISA는 3년마다 이 평가를 반복하여 비교 가능한 데이터를 제공하고, 미래 경제에 대비할 수 있도록 전 세계 교육을 안내하는 데 도움을 준다. 3년마다 실시되는 PISA 평가 결과에 따라 이해관계자들의 암묵적이고 명시적인 반응으로 인해 많은 파급 효과가 있었으며, 이는 교육 개혁 및 정책 변화로 이어졌다.[37][38][23]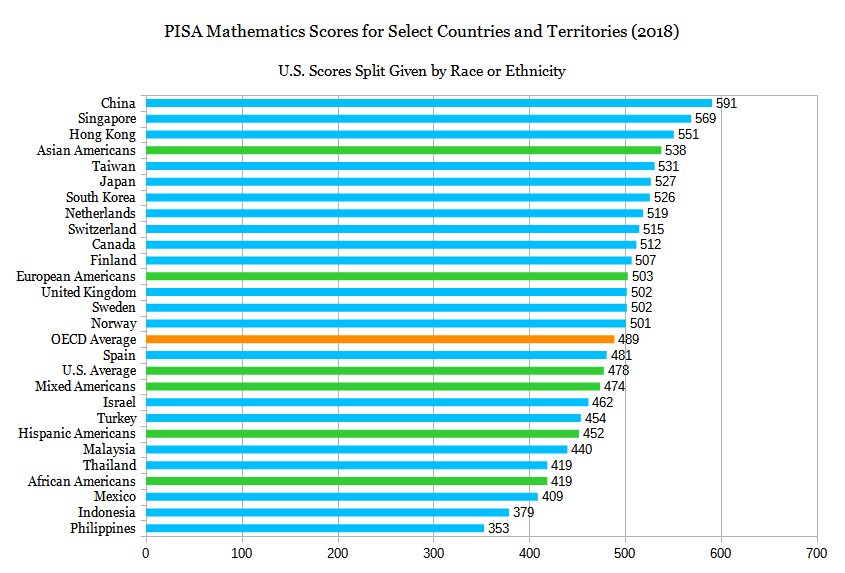

2018년 PISA 수학 점수

  • 일본
  • * 수학 교육 학회 [https://mes-j.or.jp/ 공식 페이지]
  • * 전국 수학 교육 학회 [https://www.jasme.jp/ 공식 페이지]
  • * 일본 수학 교육 학회 [https://www.sme.or.jp/ 공식 페이지]
  • * 일본 수학회 [https://www.mathsoc.jp/ 공식 페이지]
  • 해외
  • * 국제 수학 연합 [https://www.mathunion.org/ 공식 페이지]

7. 연구

Hiebert와 Grouws에 따르면, "강력하고 유용한 교실 수업 이론은 아직 존재하지 않는다."[39] 그러나 아이들이 수학을 배우는 방법에 대한 유용한 이론들이 있으며, 이러한 이론들을 어떻게 가르침에 적용할 수 있는지 탐구하기 위한 많은 연구가 최근 수십 년 동안 진행되어 왔다.

수학 교육 연구는 추론 통계를 사용하는 양적 연구와 사례 연구, 실천 연구, 담론 분석, 임상 인터뷰 등과 같은 질적 연구에 모두 의존한다. 양적 연구는 교수법 등의 효과를 검증하기 위해 학생이나 학급을 무작위로 배정하는 무작위 시험을 포함한다. 질적 연구는 작지만 집중된 표본을 통해 학생 학습을 이해하고 특정 방법의 효과와 그 원인을 파악한다.

다양한 유형의 연구 방법론에 대한 논쟁도 존재한다. 정책 입안자들은 "무엇이 효과가 있는가"에 대한 명확하고 객관적인 증거를 제공한다는 이유로 무작위 실험을 선호하는 경향이 있다. 그러나 일부 학자들은 철학적 반대, 윤리적 문제, 실제 학교 환경의 통제 어려움 등을 이유로 무작위 실험 확대에 비판적인 입장을 보인다. 전국 수학 자문 위원회(NMAP)는 2008년에 교실이나 학생 단위의 무작위 배정 연구를 선호하는 보고서를 발표했지만, 일부 학자들은 이에 대해 비판했다.[54] 2010년, What Works Clearinghouse는 이러한 논란에 대응하여 연구 기반을 회귀 불연속 설계 및 사례 연구와 같은 비실험 연구까지 확장했다.[55]

7. 1. 문화적 형평성

수학이 인종적으로 중립적이라는 일반적인 믿음에도 불구하고, 일부 연구[44]에 따르면 문화적으로 다양한 학생들을 위한 효과적인 수학 교육은 학생들의 문화적 배경과 경험을 고려하는 문화 관련 교수법을 필요로 한다. 문화 관련 교수법의 세 가지 기준은 학문적 성공, 문화적 역량, 비판적 의식이다. 보다 최근의 연구[45]에서는 학생들이 문화적 정체성을 유지하면서 학업적으로 성공할 수 있도록 지원하는 문화 유지 교수법이 교육 시스템 내에서 문화적, 언어적 다원주의를 명시적으로 영속화하고 육성한다고 제안한다.

7. 2. 수학교사 교육

교생 실습은 예비 교사가 교사가 되는 과정에서 중요한 부분이다. 수학 교사 교육 개혁 권고안은 교실 관리와 생존에 과도하게 중점을 둔 모델 대신, 학생들의 수학적 사고를 예측하고, 이끌어내고, 활용하는 것을 주요 목표로 삼는 데 중점을 둔다.[46]

일본에서 중학교 및 고등학교 "수학" 교원 면허를 취득할 때에는, 교원 면허법 시행 규칙 제4조 및 제5조에 의거하여 다음 내용을 포함하는 과목을 규정 단위 수 이상 이수해야 한다.[58]

분야내용
대수학방정식, 행렬, 군 등
기하학집합론, 비유클리드 기하학, 위상 공간 등
해석학함수, 편미분, 중적분, 미분 방정식 등
응용 수학주로 확률론, 통계학, 계산 과학 등



이 외에, 제6조 제4란에 규정되어 있는 "각 교과의 지도법"으로, "수학"의 지도법 (수학과 교육법 등으로 불림. 기본적으로는, 수학교육학을 포함)을 이수할 필요가 있다.

2010년 3월 현재, 일본에서 중학교·고등학교 "수학" 면허는 많은 교원 양성 계열·이공계열·정보 과학 계열의 대학·학부에서 취득 가능하다.[59] 통신 교육으로 취득 가능한 대학은 2020년도에 다마가와 대학, 부교 대학, 메이세이 대학, 홋카이도 정보 대학, 환태평양 대학의 5개교이며, 국어과의 7개교, 시민과의 9개교보다는 적지만, 이과 1개교보다 많아 현재는 극단적으로 적은 상태는 아니다.[60]

학교 교육 현장에서는 수준별 학습이나 팀 티칭을 실시할 필요성 때문에 모집 인원이 많지만, 그에 비해 면허 취득자가 적은 현상이 있다.

또한 현대 일본의 교원 면허 제도에서는, 수학과 관련이 깊은 학문 영역(물리학, 화학을 비롯한 자연 과학, 철학, 경제학, 심리학, 사회학 등)이 많이 존재하지만, 이러한 학문 영역을 이수해도 수학 교원 면허 취득을 위한 단위로 거의 고려되지 않는다. 또한 응용 수학의 컴퓨터는 정보에도 크게 관련된 내용이지만, 서로 단위의 호환성은 없다.

7. 3. 방법론 논쟁

수학 교육 연구는 양적 연구와 질적 연구 모두에 의존한다. 양적 연구는 추론 통계를 사용하며, 교수법 등의 효과를 검증하기 위해 학생이나 학급을 무작위로 배정하는 무작위 시험을 포함한다. 질적 연구는 사례 연구, 실천 연구, 담론 분석, 임상 인터뷰 등과 같이 작지만 집중된 표본을 통해 학생 학습을 이해하고 특정 방법의 효과와 그 원인을 파악한다.

다양한 유형의 연구 방법론에 대한 논쟁도 존재한다. 정책 입안자들은 "무엇이 효과가 있는가"에 대한 명확하고 객관적인 증거를 제공한다는 이유로 무작위 실험을 선호하는 경향이 있다. 그러나 일부 학자들은 철학적 반대, 윤리적 문제, 실제 학교 환경의 통제 어려움 등을 이유로 무작위 실험 확대에 비판적인 입장을 보인다.

전국 수학 자문 위원회(NMAP)는 2008년에 교실이나 학생 단위의 무작위 배정 연구를 선호하는 보고서를 발표했지만, 일부 학자들은 이에 대해 비판했다.[54] 2010년, What Works Clearinghouse는 이러한 논란에 대응하여 연구 기반을 회귀 불연속 설계 및 사례 연구와 같은 비실험 연구까지 확장했다.[55]

8. 관련 단체

국가/지역단체명링크
(전 세계)국제 수학 연합https://www.mathunion.org/ 공식 페이지
일본수학 교육 학회https://mes-j.or.jp/ 공식 페이지
전국 수학 교육 학회https://www.jasme.jp/ 공식 페이지
일본 수학 교육 학회https://www.sme.or.jp/ 공식 페이지
일본 수학회https://www.mathsoc.jp/ 공식 페이지
수학교육 자문위원회
미국 2년제 대학 수학 협회
수학교사 협회(Association of Teachers of Mathematics)
캐나다 수학회(Canadian Mathematical Society)
C.D. 하우 연구소(C.D. Howe Institute)
수학 협회(Mathematical Association)
전미 수학교사 협의회(National Council of Teachers of Mathematics)
OECD
국제 교육 성취도 평가 협회(International Association for the Evaluation of Educational Achievement)
수학교사 교육자 협회(Association of Mathematics Teacher Educators)https://amte.net/


참조

[1] 학술지 The World's First Mathematics Textbook Taylor & Francis, Ltd. 2002-04
[2] 서적 The exact sciences in antiquity https://archive.org/[...] Dover Publications
[3] 학술지 Methods and traditions of Babylonian mathematics: Plimpton 322, Pythagorean triples, and the Babylonian triangle parameter equations https://www.research[...]
[4] 학회자료 Babylon: Focus mesopotamischer Geschichte, Wiege früher Gelehrsamkeit, Mythos in der Moderne. 2. Internationales Colloquium der Deutschen Orient-Gesellschaft 24.–26. März 1998 in Berlin http://akira.ruc.dk/[...] Berlin: Deutsche Orient-Gesellschaft / Saarbrücken: SDV Saarbrücker Druckerei und Verlag 2022-11-15
[5] 서적 Mathematics in Ancient Iraq: A Social History Princeton University Press
[6] 서적 Pythagoras : His Lives and the Legacy of a Rational Universe Icon
[7] 웹사이트 Why We Learn Math Lessons That Date Back 500 Years https://www.npr.org/[...] National Public Radio 2016-07-23
[8] 웹사이트 Why We Learn Math Lessons That Date Back 500 Years https://www.npr.org/[...] 2018-04-10
[9] Webarchive A Bibliography of Mathematical Education http://babel.hathitr[...] Forest Hills, N.Y. : Stevinus Press 1941
[10] 웹사이트 McLuhan: Understanding Media http://www9.georgeto[...] 1964
[11] 서적 Teaching and learning discrete mathematics worldwide: Curriculum and research 2018
[12] 학술지 Mathematical modelling and discrete mathematics: opportunities for modern mathematics teaching 2022
[13] 웹사이트 5 Approaches to Teaching PreK-12 Numeracy https://medium.com/i[...] 2017-10-20
[14] 웹사이트 Euclidean Geometry https://www.pitt.edu[...] 2019-02-12
[15] 웹사이트 Axiomatic Systems http://web.mnstate.e[...] 2019-02-12
[16] 웹사이트 Heuristics http://theory.stanfo[...] 2019-02-12
[17] 뉴스 Passing Mathematics Just Got Easier For Students With This New Platform: Mathematica - Techzim https://www.techzim.[...] 2018-06-16
[18] 뉴스 5 Apps to Help All Students with Math https://edtechmagazi[...] 2017-10-13
[19] 뉴스 This Free App Will Solve Math Problems For You https://www.huffingt[...] 2014-10-22
[20] 웹사이트 Classical Education and STEM: a Common Misconception http://claphamschool[...] 2018-01-25
[21] 웹사이트 Mathematical Current Events http://www.math.unl.[...] 2011-11-29
[22] 서적 Crossroads in the History of Mathematics and Mathematics Education https://books.google[...] IAP
[23] 학술지 No More Math Wars 2016-03
[24] 서적 What to Do About Canada's Declining Math Scores C.D. Howe Institute
[25] 웹사이트 The Unreasonable Utility of Recreational Mathematics http://anduin.eldar.[...] 2012-09-17
[26] 웹사이트 Foundations for Success: The Final Report of the National Mathematics Advisory Panel http://www2.ed.gov/a[...] U.S. Department of Education
[27] Citation Teaching and Learning About Whole Numbers in Primary School Springer International Publishing 2016
[28] 학술지 Mathematics Achievement in the Primary School Years. IEA's Third International Mathematics and Science Study (TIMSS). International Association for the Evaluation of Educational Achievement; Boston College Center for the Study of Testing, Evaluation, and Educational Policy. 1997-06
[29] 웹사이트 MIT - S.B. In 1-C Civil Engineering Curriculum | Department of Civil & Environmental Engineering, MIT https://cee.mit.edu/[...] 2014-06-18
[30] 웹사이트 Mathematics for Computer Science https://ocw.mit.edu/[...] 2019-01-02
[31] 웹사이트 Mathematics curriculum http://www.education[...] UK Department of Education 2013-01-17
[32] 학술지 A longitudinal assessment of antecedent course work in mathematics and subsequent mathematical attainment
[33] 웹사이트 Myths vs. Facts - Common Core State Standards Initiative http://www.corestand[...] 2017-07-28
[34] 웹사이트 Standards in Your State - Common Core State Standards Initiative http://www.corestand[...] 2017-07-28
[35] 웹사이트 MoCTM - Home https://www.moctm.or[...] 2018-02-11
[36] 웹사이트 What is PISA? http://www.oecd.org/[...] 2018
[37] 서적 The Experience of Middle-Income Countries Participating in PISA 2000. PISA OECD Publishing
[38] 논문 International large-scale assessments, affective worlds and policy impacts in education https://e-space.mmu.[...] 2018-04
[39] 간행물 The Effects of Classroom Mathematics Teaching on Students' Learning National Council of Teachers of Mathematics
[40] 간행물 Trends in International Mathematics and Science Study (TIMSS) - Overview http://nces.ed.gov/t[...] U.S. Department of Education 2012-05-08
[41] 논문 Assessment and Classroom Learning https://www.gla.ac.u[...] 2018-07-25
[42] 웹사이트 Research clips and briefs http://www.nctm.org/[...] 2009-11-15
[43] 논문 Calling for Research Collaborations and the Use of Dis/ability Studies in Mathematics Education https://jume-ojs-tam[...] 2017-12-29
[44] 논문 But that's just good teaching! The case for culturally relevant pedagogy http://www.tandfonli[...] 1995-06
[45] 논문 Culturally Sustaining Pedagogy: A Needed Change in Stance, Terminology, and Practice https://journals.sag[...] 2012-04
[46] 논문 Purposefully Designing Student Teaching to Focus on Students' Mathematical Thinking 2010
[47] 논문 Learning from Attempts to Improve Schooling: The Contribution of Methodological Diversity
[48] 논문 Randomized Experiments in Educational Policy Research: A Critical Examination of the Reasons the Educational Evaluation Community has Offered for Not Doing Them
[49] 웹사이트 Using Statistics Effectively in Mathematics Education Research: A report from a series of workshops organized by the American Statistical Association with funding from the National Science Foundation http://www.amstat.or[...] The American Statistical Association 2013-03-25
[50] 서적 Experimental and quasi-experimental designs for generalized causal inference Houghton Mifflin
[51] 문서 See articles on [[No Child Left Behind|NCLB]], [[National Mathematics Advisory Panel]], [[Scientifically based research]] and [[What Works Clearinghouse]]
[52] 간행물 Evidence Matters: Randomized Trials in Education Research Brookings Institution Press
[53] 논문 Evidence on "What Works": An Argument for Extended-Term Mixed-Method (ETMM) Evaluation Designs 2004-12
[54] 논문 Reflections on the National Mathematics Advisory Panel Final Report
[55] 뉴스 Federal Criteria For Studies Grow 2010-10-20
[56] 문서 但しこの傾向は、程度の差はあれ[[フィンランド]]や[[韓国]]などの好成績を残した他国でも見られる。
[57] 문서 比較的著名な人物として、前者では[[三浦朱門]]や[[曽野綾子]]、後者では[[藤原正彦]]や[[ゴッドフレイ・ハロルド・ハーディ|G.H.ハーディ]]が挙げられる。なお、上記の傾向については、[[チャールズ・パーシー・スノー|C.P.スノー]]の『二つの文化と科学革命』において興味深い言及がなされている。
[58] 문서 '{{Egov law| 329M50000080026 |教育職員免許法施行規則}}を参照'
[59] 웹사이트 文部科学省「中学校・高等学校教員（数学）の免許資格を取得することのできる大学」 https://www.mext.go.[...]
[60] 웹사이트 私立大学通信教育協会「取得できる教員免許状一覧」 http://www.uce.or.jp[...]


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com