행렬

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

행렬은 숫자, 기호 또는 표현식을 직사각형 형태로 배열한 것으로, 수학과 과학의 다양한 분야에서 널리 활용되는 개념이다. 환 위의 행렬은 행과 열로 구성되며, 각 위치의 성분은 환의 원소이다. 행렬은 덧셈, 스칼라배, 곱셈 등의 연산을 수행할 수 있으며, 행렬의 크기, 종류, 그리고 행렬식, 전치 행렬, 대각합과 같은 특징에 따라 다양한 종류로 분류된다. 행렬은 선형 변환 표현, 연립 일차 방정식 해법, 그래프 이론, 양자 역학, 기하 광학 등 다양한 분야에 응용되며, LU 분해, 특이값 분해, 고유값 분해와 같은 행렬 분해 기법을 통해 계산을 단순화하고 효율성을 높일 수 있다.

더 읽어볼만한 페이지

행렬 - 스핀 (물리학)
스핀은 양자역학적 각운동량으로, 양자화된 값을 가지며 자기 쌍극자 모멘트를 유발하여 다양한 분야에 응용되고 스핀트로닉스 기술 발전에 기여하지만, 전자의 스핀 기원은 아직 완전히 밝혀지지 않았다.
행렬 - 파울리 행렬
파울리 행렬은 양자역학에서 스핀을 나타내는 데 사용되는 에르미트 행렬이자 유니타리 행렬로, 행렬식은 -1이고 대각합은 0이며, 리 대수의 생성원이자 파울리 벡터로 정의되어 다양한 물리학 분야에서 활용된다.

행렬
지도
기본 정보
정의	수 또는 다른 수학적 대상의 직사각형 배열
분류	수학적 대상
로마자 표기	haengnyeol
수학적 속성
크기	m × n (m개의 행과 n개의 열)
원소	a_ij (i번째 행과 j번째 열에 위치)
연산	행렬 덧셈, 행렬 곱셈, 스칼라 곱셈, 전치, 역행렬 등
관련 개념
벡터	열 또는 행이 하나인 행렬
선형 변환	행렬로 표현 가능
행렬식	정방 행렬에 대해 정의되는 스칼라 값
고윳값과 고유벡터	행렬의 중요한 속성
활용
응용 분야	선형 방정식 시스템 해법 컴퓨터 그래픽스 물리학 통계학 공학 인공지능 암호학
역사
기원	선형 방정식 시스템 연구에서 비롯됨
발전	19세기 후반 아서 케일리와 다른 수학자들에 의해 체계화됨
표기법
행렬 표기	대문자 (예: A, B)
원소 표기	소문자 (예: a_ij)
특수 행렬	영행렬 단위 행렬 대각 행렬 전치 행렬 역행렬

2. 정의

환 $R$ 위의 $m\times n$ '''행렬'''은 각 행 $i\in\{1,\dotsc,m\}$ 및 열 $j\in\{1,\dotsc,n\}$ 의 순서쌍 $(i,j)$ 에 환의 원소 $A_{ij}\in R$ 를 대응시키는 함수 $A=(A_{ij})_{i,j}$ 이다.^[139]

행렬 $A$ 는 모든 성분을 직사각형으로 배열한 다음 소괄호 또는 대괄호를 추가하여 다음과 같이 표기한다.

: $\begin{pmatrix}A_{11} & A_{12} & A_{13} &\cdots & A_{1n} \\A_{21} & A_{22} & A_{23} &\cdots & A_{2n} \\A_{31} & A_{32} & A_{33} &\cdots & A_{3n} \\\vdots & \vdots & \vdots & \ddots & \vdots \\A_{m1} & A_{m2} & A_{m3} &\cdots & A_{mn}\end{pmatrix}$

또는

: $\begin{bmatrix}A_{11} & A_{12} & A_{13} &\cdots & A_{1n} \\A_{21} & A_{22} & A_{23} &\cdots & A_{2n} \\A_{31} & A_{32} & A_{33} &\cdots & A_{3n} \\\vdots & \vdots & \vdots & \ddots & \vdots \\A_{m1} & A_{m2} & A_{m3} &\cdots & A_{mn}\end{bmatrix}$

각 $A_{ij}$ 를 $A$ 의 $i$ 번째 행 $j$ 번째 열의 '''성분'''(成分, entry^영어) 또는 '''원소'''(元素, element^영어)라고 한다. 행렬 $A$ 의 각 성분은 행과 열의 번째수를 첨수로 사용하여 $A_{ij}$ , $A_{i,j}$ , $a_{ij}$ , $a_{i,j}$ , $A(i,j)$ , $A[i,j]$ 등과 같이 나타낸다. 행과 열의 번째수가 같은 성분 $A_{ii}$ ( $i\in\{1,\dotsc,\min\{m,n\}\}$ )을 $A$ 의 '''대각 성분'''(對角成分, diagonal entry^영어)이라고 한다.^[139]

환 $R$ 위의 $m\times n$ 행렬의 집합은 $\operatorname{Mat}(m,n;R)$ 또는 $\operatorname M_{m,n}(R)$ 로 표기한다.

2. 1. 크기

행렬의 크기는 행과 열의 수의 순서쌍

(m,n)

또는

m\times n

으로 나타낸다.^[139] 예를 들어, 아래와 같은 행렬은 두 개의 행과 세 개의 열로 구성되어 있으므로, (2, 3)형 또는 2×3형 행렬이라고 한다.

:

\begin{bmatrix}1 & 9 & -13 \\20 & 5 & -6 \end{bmatrix}

일부 특수한 크기의 행렬들은 특별한 이름으로 불린다.^[139]

행렬 크기 개요^[2]^[5]^[121]
이름	크기	예시	설명
행 벡터	1×n	$\begin{bmatrix}3 & 7 & 2 \end{bmatrix}$	하나의 행을 가진 행렬
열 벡터	n×1	$\begin{bmatrix}4 \\ 1 \\ 8 \end{bmatrix}$	하나의 열을 가진 행렬
정방 행렬	n×n	$\begin{bmatrix}$	행과 열의 개수가 같은 행렬

3. 연산

행렬에는 덧셈, 스칼라배, 곱셈, 전치 행렬 등의 연산이 정의된다.^[139] 정사각 행렬의 경우 역행렬, 대각합, 행렬식 등의 추가 연산이 가능하다.

덧셈: 같은 크기의 두 행렬에 대해서만 정의되며, 각 성분별로 더한다.
스칼라배: 행렬의 각 성분에 스칼라 값을 곱한다.
뺄셈: 행렬 덧셈과 -1에 대한 스칼라 곱을 결합하여 정의한다.
곱셈: 첫 번째 행렬의 열의 수와 두 번째 행렬의 행의 수가 같을 때만 정의되며, 각 행렬의 해당 행과 열의 내적으로 계산된다.^[10] 행렬 곱셈은 교환 법칙이 성립하지 않는다.^[10]
전치: 행렬의 행과 열을 바꾼다. 전치는 덧셈 및 스칼라 곱과 호환된다.^[9]

3. 1. 덧셈과 스칼라배

환 ''R'' 위의 두 ''m'' × ''n'' 행렬 '''A''', '''B''' ∈ Mat(''m'',''n'';''R'')의 덧셈 '''A''' + '''B''' ∈ Mat(''m'',''n'';''R'')은 두 행렬을 성분별로 합한 ''m'' × ''n'' 행렬이다. 즉, 각 행과 열 ''i'', ''j''에 대하여 다음과 같이 정의된다.:(A+B)_ij = A_ij + B_ij실수 행렬의 덧셈 예시는 다음과 같다.:

\begin{pmatrix}1 & 3 & 7 \\1 & 0 & 0\end{pmatrix}+\begin{pmatrix}0 & 0 & 5 \\7 & 5 & 0\end{pmatrix}=\begin{pmatrix}1+0 & 3+0 & 7+5 \\1+7 & 0+5 & 0+0\end{pmatrix}=\begin{pmatrix}1 & 3 & 12 \\8 & 5 & 0\end{pmatrix}

환 ''R'' 위의 ''m'' × ''n'' 행렬 '''A''' ∈ Mat(''m'',''n'';''R'') 및 환의 원소 ''r'' ∈ ''R''에 대하여, 왼쪽·오른쪽 스칼라배 ''r'''''A''', '''A'''r ∈ Mat(''m'',''n'';''R'')는 각각 행렬의 각 성분의 왼쪽·오른쪽에 스칼라를 곱한 ''m'' × ''n'' 행렬이다.

:(rA)_ij = rA_ij

:(Ar)_ij = A_ijr

만약 ''R''가 가환환일 경우, 이 두 연산은 일치하며, 이를 스칼라배라고 부른다.

실수 행렬의 스칼라배 예시는 다음과 같다.

:

2\begin{pmatrix}1 & 8 & -3 \\4 & -2 & 5\end{pmatrix}=\begin{pmatrix}2\cdot 1 & 2\cdot 8 & 2\cdot -3 \\2\cdot 4 & 2\cdot -2 & 2\cdot 5\end{pmatrix}=\begin{pmatrix}2 & 16 & -6 \\8 & -4 & 10\end{pmatrix}

환 ''R'' 위의 ''m'' × ''n'' 행렬의 집합 Mat(''m'',''n'';''R'')은 위 덧셈과 왼쪽·오른쪽 스칼라배에 따라 (''R'',''R'')-쌍가군을 이룬다. 만약 ''R''가 가환환일 경우, 이는 (덧셈과 스칼라배에 따른) ''R''-가군이 되며, 특히 만약 ''R''가 체일 경우 ''R''-벡터 공간이다. 이 쌍가군의 덧셈 항등원은 '''영행렬'''(즉, 모든 성분이 0인 행렬)이다.

:

0_{m\times n}=\begin{pmatrix}0 & 0 & \cdots & 0 \\0 & 0 & \cdots & 0 \\\vdots & \vdots & \ddots & \vdots \\0 & 0 & \cdots & 0\end{pmatrix}\in\operatorname{Mat}(m,n;R)

각 행렬 '''A''' ∈ Mat(''m'',''n'';''R'')의 덧셈 역원은 성분별 덧셈 역원이다.

: -'''A''' ∈ Mat(''m'',''n'';''R'')

: (-A)_ij = -A_ij

특히, 두 행렬 '''A''', '''B''' ∈ Mat(''m'',''n'';''R'')의 차는 다음과 같이 정의할 수 있다.

: '''A''' - '''B''' = '''A''' + (-'''B''') ∈ Mat(''m'',''n'';''R'')

3. 2. 곱셈

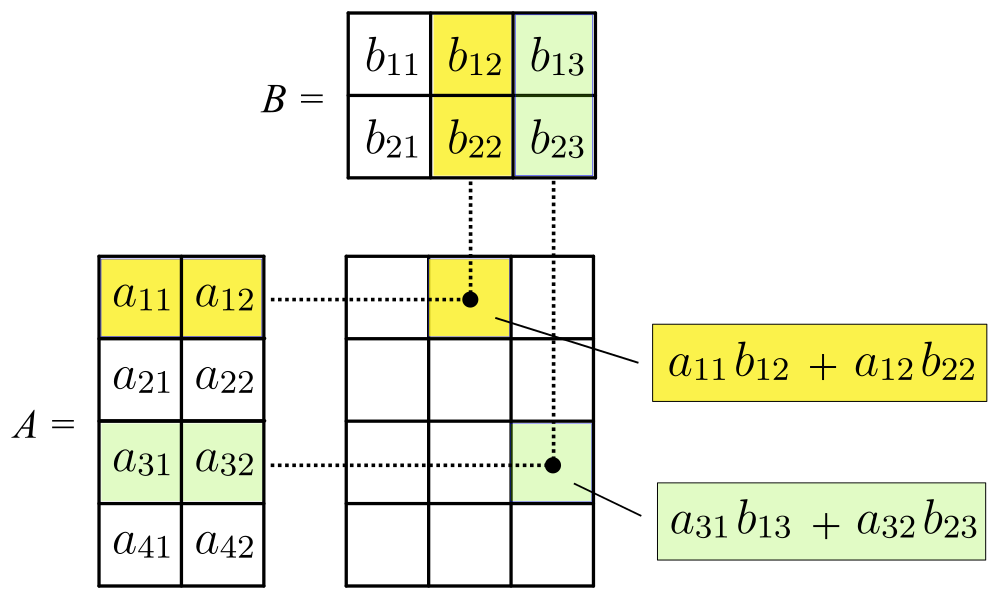
환

R

위의

m\times n

행렬

A

와

n\times p

행렬

B

의 곱

AB

는

m\times p

행렬이며, 그

i

번째 행

j

번째 열 성분은

A

의

i

번째 행벡터와

B

의

j

번째 열벡터의 스칼라곱이다.

:

(AB)_{ij}=\sum_{k=1}^nA_{ik}B_{kj}=A_{i1}B_{1j}+A_{i2}B_{2j}+\cdots A_{in}B_{nj}

다음은 실수 행렬의 예이다.

:

\begin{pmatrix}1 & 0 & 2 \\

1 & 3 & 1 \\

\end{pmatrix}\begin{pmatrix}3 & 1 \\2 & 1 \\1 & 0\end{pmatrix}=\begin{pmatrix}1\cdot 3+0\cdot 2+2\cdot 1 & 1\cdot 1+0\cdot 1+2\cdot 0 \\

1\cdot 3+3\cdot 2+1\cdot 1 & -1\cdot 1+3\cdot 1+1\cdot 0

\end{pmatrix}=\begin{pmatrix}5 & 1 \\4 & 2\end{pmatrix}

행렬 곱셈은 결합 법칙을 만족시킨다. 즉, 임의의

m\times n

행렬

A

,

n\times p

행렬

B

,

p\times q

행렬

C

에 대하여,

:

(AB)C=A(BC)

가 성립한다.

행렬 곱셈은

:

\operatorname{Mat}(m,n;R)\oplus\operatorname{Mat}(n,p;R)\to\operatorname{Mat}(m,p;R)

에서

(R,R)

-쌍선형 함수를 이룬다.

특히, 환

R

위의 정사각 행렬들의

(R,R)

-쌍가군

\operatorname{Mat}(n;R)

는 행렬 곱셈에 따라

R

-결합 대수를 이루며, 행렬환이라고 한다. 행렬환의 곱셈 항등원은 단위 행렬이다.

:

1_{n\times n}=\begin{pmatrix}1 & 0 & \cdots & 0 \\0 & 1 & \cdots & 0 \\\vdots & \vdots & \ddots & \vdots \\0 & 0 & \cdots & 1\end{pmatrix}\in\operatorname{Mat}(n;R)

3. 2. 1. 교환 법칙과 소거 법칙의 실패

행렬환은 일반적으로 가환환이 아니다. 즉, 행렬 곱셈의 교환 법칙은 (체의 경우에도) 일반적으로 성립하지 않는다. 예를 들어, 실수 2×2 행렬의 경우 다음과 같다.

:

\begin{pmatrix}1 & 0 \\0 & 0\end{pmatrix}\begin{pmatrix}1 & 2 \\0 & 3\end{pmatrix}=\begin{pmatrix}1 & 2 \\0 & 0\end{pmatrix}

:

\begin{pmatrix}1 & 2 \\0 & 3\end{pmatrix}\begin{pmatrix}1 & 0 \\0 & 0\end{pmatrix}=\begin{pmatrix}1 & 0 \\0 & 0\end{pmatrix}

물론 가환하는 두 행렬도 존재한다. 예를 들어, 가환환 위의 스칼라 행렬은 (같은 크기의) 모든 행렬과 가환한다.

행렬환은 일반적으로 0이 아닌 왼쪽·오른쪽 영인자를 갖는다. 즉, 0이 아닌 두 행렬의 곱은 0일 수 있으며, 소거 법칙이 일반적으로 성립하지 않는다. 예를 들어, 실수 행렬에서 다음과 같다.

:

\begin{pmatrix}2 & -1 \\

2 & 1

\end{pmatrix}\begin{pmatrix}1 & 3 \\2 & 6\end{pmatrix}=\begin{pmatrix}0 & 0 \\0 & 0\end{pmatrix}

3. 2. 2. 역행렬

행렬환

\operatorname{Mat}(n;R)

의 가역원은 '''가역 행렬'''이라고 하며, 그 곱셈 역원은 '''역행렬'''이라고 한다. 일반적으로 행렬환은 (체 위에서도) 0이 아닌 비가역 행렬을 갖는다. 예를 들어, 실수 2×2 정사각 행렬

:

\begin{pmatrix}0 & 5 \\0 & 3\end{pmatrix}

은 가역 행렬이 아니다.

만약

R

가 가환환일 경우, 가역 행렬은 행렬식이 환의 가역원인 것과 동치이며, 특히 체의 경우 행렬식이 0이 아닌 것과 동치이다. 또한, 가역 행렬

A\in\operatorname{Unit}(\operatorname{Mat}(n;R))

의 역행렬은 행렬식과 수반 행렬을 통하여 다음과 같이 나타낼 수 있다.

:

A^{-1}=\frac 1{\det A}\operatorname{adj}A

정방 행렬 A는 행렬 B가 존재하여^[28]^[29]

\bold{AB} = \bold{BA} = \bold I_n,

을 만족할 때 ''가역'' 또는 ''비특이''라고 한다. 여기서 I_n은 주대각선에 1이 있고 다른 곳에는 0이 있는 ''n×n'' 단위행렬이다. B가 존재한다면, 그것은 유일하며 A의 ''역행렬''이라고 부르고 A⁻¹로 나타낸다.

정방 행렬이 가역인지 여부를 검사하고 가역인 경우 역행렬을 계산하는 알고리즘은 많이 있다. 여전히 널리 사용되는 가장 오래된 알고리즘 중 하나는 가우스 소거법이다.

3. 3. 전치 행렬

환

R

위의

m\times n

행렬

A\in\operatorname{Mat}(m,n;R)

의 '''전치 행렬'''

A^\top\in\operatorname{Mat}(n,m;R)

는 행과 열을 교환한

n\times m

행렬이다. 즉, 각

i\in\{1,\dotsc,n\}

및

j\in\{1,\dotsc,m\}

에 대하여,

:

(A^\top)_{ij}=A_{ji}

이다.^[139]

다음은 실수 행렬의 예다.

:

\begin{pmatrix}9 & 8 & 7 \\

1 & 3 & 4

\end{pmatrix}^\top=\begin{pmatrix}9 & -1 \\8 & 3 \\7 & 4\end{pmatrix}

이다.

전치 행렬은 함수

:

^\top\colon\operatorname{Mat}(m,n;R)\to\operatorname{Mat}(n,m;R)

로서

(R,R)

-쌍가군 동형을 이루며, 그 역함수 또한 (정의역과 공역이 뒤바뀐) 전치 행렬이다.

또한, 임의의

m\times n

행렬

A\in\operatorname{Mat}(m,n;R)

및

n\times p

행렬

B\in\operatorname{Mat}(n,p;R)

에 대하여,

:

(AB)^\top=B^\top A^\top

이다.

특히, 환

R

위의 정사각 행렬의

R

-결합 대수

\operatorname{Mat}(n;R)

위에서, 전치 행렬은

\operatorname{Mat}(n;R)

와 그 반대환

\operatorname{Mat}(n;R)^{\operatorname{op}}

사이의 대합

R

-결합 대수 동형이며, 만약

R

가 가환환일 경우

\operatorname{Mat}(n;R)

는 전치 행렬에 따라

R

-대합 대수를 이룬다.

3. 4. 대각합

환

R

위의

n\times n

정사각 행렬

A\in\operatorname{Mat}(n;R)

의 '''대각합'''은 모든 대각 성분들의 합이다.

:

\operatorname{tr}A=\sum_{i=1}^nA_{ii}=A_{11}+A_{22}+\cdots+A_{nn}\in R

대각합

:

\operatorname{tr}\colon\operatorname{Mat}(n;R)\to R

는

(R,R)

-선형 변환을 이룬다. 또한, 임의의

A\in\operatorname{Mat}(n;R)

에 대하여, 그 대각합은 그 전치 행렬의 대각합과 같다.

:

\operatorname{tr}(A^\top)=\operatorname{tr}A

만약

R

가 가환환일 경우, 임의의 두 행렬

A,B\in\operatorname{Mat}(n;R)

에 대하여, 두 행렬의 곱의 대각합은 곱하는 순서와 무관하게 같다.

:

\operatorname{tr}(AB)=\operatorname{tr}(BA)

이는 행렬 곱셈의 정의에서 바로 유도된다.

:

\operatorname{tr}(\mathbf{AB}) = \sum_{i=1}^m \sum_{j=1}^n a_{ij} b_{ji} = \operatorname{tr}(\mathbf{BA}).

3. 5. 행렬식

가환환

R

위의

n\times n

정사각 행렬

A\in\operatorname{Mat}(n;R)

의 '''행렬식'''은 다음과 같다.

:

\det A=\sum_{\sigma\in\operatorname{Sym}(n)}\sgn\sigma\prod_{i=1}^nA_{i,\sigma(i)}\in R

여기서

\operatorname{Sym}(n)

은 대칭군이며,

\sgn\sigma

는 순열의 부호이다. 행렬

A

의 행렬식은

\det A

,

|A|

,

\operatorname D(A)

등으로 표기한다. 특히, 2×2 행렬

A\in\operatorname{Mat}(2;R)

의 행렬식은 다음과 같다.

:

\det A=\begin{vmatrix}A_{11} & A_{12} \\A_{21} & A_{22}\end{vmatrix}=A_{11}A_{22}-A_{12}A_{21}

^[33]

행렬식은

n

개의 행벡터(또는 열벡터)의 함수

:

\det\colon\operatorname{Mat}(n;R)=\underbrace{\operatorname{Mat}(1,n;R)\oplus\cdots\oplus\operatorname{Mat}(1,n;R)}_n\to R

로서, 단위 행렬의 상이 1인 유일한

R

-교대 다중 선형 형식이다. 또한, 행렬식은 두 환의 곱셈 모노이드 사이의 준동형이며, 전치 행렬에 대하여 불변이다. 즉, 임의의

A,B\in\operatorname{Mat}(n;R)

에 대하여, 다음이 성립한다.

:

\det(AB)=\det A\det B

:

\det A^\top=\det A

행렬식은 크라메르 공식에서 사용된다.^[38]

주어진 행렬로 나타낸 선형 변환. 이 행렬의 행렬식은 -1이다. 오른쪽의 녹색 평행사변형의 면적은 1이지만, 이 사상은 벡터의 반시계 방향 배향을 시계 방향으로 바꾸므로 방향을 반전시키기 때문이다.

정방 행렬의 ''행렬식''(det(A) 또는 로 표기)은 행렬의 특정 속성을 나타내는 숫자이다. 행렬이 가역인 것은 행렬식이 0이 아닌 것과 필요충분조건이다. 행렬식의 절댓값은 단위 정사각형(또는 정육면체)의 영상의 면적() 또는 부피()와 같고, 그 부호는 해당 선형 사상의 방향에 해당한다. 행렬식이 양수인 것은 방향이 보존되는 것과 동치이다.

3×3 행렬의 행렬식은 6개의 항을 포함하며(사루스의 규칙), 더 복잡한 라이프니츠 공식은 이 두 공식을 모든 차원으로 일반화한다.^[34]

정방 행렬의 곱의 행렬식은 각 행렬의 행렬식의 곱과 같다.

:

|\bold{AB}| = |\bold A| \cdot |\bold B|.

^[35]

어떤 행에 다른 행의 배수를 더하거나 어떤 열에 다른 열의 배수를 더해도 행렬식은 변하지 않는다. 두 행 또는 두 열을 바꾸면 행렬식에 -1을 곱한 것과 같은 영향을 미친다.^[36] 이러한 연산을 사용하여 모든 행렬을 하삼각형(또는 상삼각형) 행렬로 변환할 수 있으며, 이러한 행렬의 경우 행렬식은 주대각선의 요소의 곱과 같다. 이것은 모든 행렬의 행렬식을 계산하는 방법을 제공한다. 마지막으로, 라플라스 전개는 소행렬식(더 작은 행렬의 행렬식) 측면에서 행렬식을 표현한다.^[37]

크기가 ''n'' × ''n''인 행렬 ''A'' = [''a''_{''i j''}]의 '''행렬식'''은 다음과 같이 정의되는 수이다.^[130]

:

\det(A) = \sum_{\sigma \in \mathfrak{S}_n} \operatorname{sgn} (\sigma) \prod_{i = 1}^n a_{i \sigma (i)}

이는 행렬의 고유값의 곱과 일치하며, , 등의 성질이 성립한다.

3. 6. 부분 행렬과 소행렬식

환

R

위의

m\times n

행렬

A\in\operatorname{Mat}(m,n;R)

의 행 집합

I=\{i_1,i_2,\dotsc,i_

\}\subseteq\{1,\dotsc,m\}\qquad(i_1

)와 열 집합

J=\{j_1,j_2,\dotsc,j_

\}\subseteq\{1,\dotsc,n\}\qquad(j_1

)에 속하는 행과 열을 취한 '''부분 행렬'''은 다음과 같다.

:

A_{I,J}=\begin{pmatrix}A_{i_1,j_1} & A_{i_1,j_2} & \cdots & A_{i_1,j_

} \\A_{i_2,j_1} & A_{i_2,j_2} & \cdots & A_{i_2,j_

} \\\vdots & \vdots & \ddots & \vdots \\A_{i_

,j_1} & A_{i_

,j_2} & \cdots & A_{i_

,j_

}\end{pmatrix}\in\operatorname{Mat}(|I|,|J|;R)

여기서,

$A$ 의 $I$ 에 대한 '''주부분 행렬'''은 부분 행렬 $A_{I,I}$ 이다.^[140]
$A$ 의 $k\times k$ '''선행 주부분 행렬'''은 부분 행렬 $A_{\{1,\dotsc,k\},\{1,\dotsc,k\}}$ 이다.^[140]
$A$ 의 $i$ 번째 '''행벡터'''는 $A_{i,\{1,\dotsc,n\}}$ 이다.
$A$ 의 $j$ 번째 '''열벡터'''는 $A_{\{1,\dotsc,m\},j}$ 이다.

가환환 위의 행렬에서 부분 정사각 행렬의 행렬식을 '''소행렬식'''이라고 한다.

'''부분행렬'''(submatrix)은 어떤 행렬에서 일부 행과 열을 제거하여 얻은 행렬이다.^[14]^[15]^[16] 예를 들어, 다음과 같은 3×4 행렬에서 3행과 2열을 제거하면 2×3 부분행렬을 얻을 수 있다.

:

\mathbf{A}=\begin{bmatrix}1 & \color{red}{2} & 3 & 4 \\5 & \color{red}{6} & 7 & 8 \\\color{red}{9} & \color{red}{10} & \color{red}{11} & \color{red}{12}\end{bmatrix} \rightarrow \begin{bmatrix}1 & 3 & 4 \\5 & 7 & 8\end{bmatrix}.

소행렬식과 여인자는 특정 부분행렬의 행렬식을 계산하여 구한다.^[16]^[17]

'''주요 부분행렬'''(principal submatrix)은 특정 행과 같은 열을 제거하여 얻은 정방 부분행렬이다. 정의는 저자에 따라 다른데, 일부는 남은 행과 열의 인덱스 집합이 같은 부분행렬을 주요 부분행렬로 정의한다.^[18]^[19] 다른 저자는 처음

k

개의 행과 열이 남아 있는 부분행렬을 주요 부분행렬로 정의하며,.^[20] 이를 '''주요 선행 부분행렬'''(leading principal submatrix)이라고도 한다.^[21]

4. 종류

다음은 여러 종류의 행렬이다.

영행렬
단위 행렬
스칼라 행렬
대각 행렬
삼각 행렬
대칭 행렬
반대칭 행렬
직교 행렬
에르미트 행렬
반에르미트 행렬
유니터리 행렬
정규 행렬
정부호 행렬

행렬의 성분 는 주대각선을 이룬다. 이 성분들은 행렬의 왼쪽 위 모서리에서 오른쪽 아래 모서리까지 이어지는 가상의 선 위에 놓여 있다.

이름	을 사용한 예시
대각행렬
하삼각행렬
상삼각행렬

크기 의 ''단위 행렬'' 는 주대각선의 모든 원소가 1이고 다른 모든 원소가 0인 × 행렬이다.

\begin{align}\mathbf{I}_1 &= \begin{bmatrix} 1 \end{bmatrix}, \\[4pt]\mathbf{I}_2 &= \begin{bmatrix}1 & 0 \\0 & 1\end{bmatrix}, \\[4pt]\vdots& \\[4pt]\mathbf{I}_n &= \begin{bmatrix}1 &      0 & \cdots & 0 \\0 &      1 & \cdots & 0 \\\vdots & \vdots & \ddots & \vdots \\0 &      0 & \cdots & 1\end{bmatrix}\end{align}

단위 행렬은 임의의 행렬과의 곱셈에서 그 행렬을 변화시키지 않기 때문에 단위 행렬이라고 부르며, 특수한 형태의 대각행렬이다.

\bold{AI}_n = \bold I_m \bold A = \bold A

여기서 는 임의의 × 행렬이다. 단위 행렬의 0이 아닌 스칼라 배수를 ''스칼라'' 행렬이라고 한다.

자기 전치행렬과 같은 정방행렬 , 즉 는 대칭행렬이다. 반대로, 가 자기 전치행렬의 음수와 같다면, 즉 이면 는 반대칭행렬이다. 복소행렬에서는 대칭성이 종종 를 만족하는 에르미트 행렬의 개념으로 대체되는데, 여기서 별표는 행렬의 켤레 전치, 즉 의 켤레복소수의 전치를 나타낸다.

스펙트럼 정리에 따르면, 실수 대칭행렬과 복소 에르미트 행렬은 고유기저를 갖는다. 즉, 모든 벡터는 고유벡터의 일차결합으로 표현될 수 있다. 두 경우 모두 모든 고유값은 실수이다.^[27]

정방 행렬 A는 행렬 B가 존재하여^[28]^[29]

\bold{AB} = \bold{BA} = \bold I_n,

을 만족할 때 ''가역'' 또는 ''비특이''라고 한다. 여기서 I_n은 주대각선에 1이 있고 다른 곳에는 0이 있는 ''n×n'' 단위행렬이다. B가 존재한다면, 그것은 유일하며 A의 ''역행렬''이라고 부르고 A⁻¹로 나타낸다.

양정부호 행렬	부정부호 행렬
$\begin{bmatrix}$	$\begin{bmatrix}$
$Q(x,y)= \frac{1}{4}x^2+y^2$	$Q(x,y)= \frac{1}{4}x^2-\frac{1}{4}y^2$
타원	쌍곡선

대칭 실수 행렬 는 관련된 이차 형식 가 의 영벡터가 아닌 모든 벡터 에 대해 양의 값을 갖는 경우 ''양정부호''라고 한다. 만약 가 음의 값만 생성하는 경우 는 ''음정부호''이고, 가 음의 값과 양의 값을 모두 생성하는 경우 는 ''부정부호''이다.^[30]

대칭 행렬은 모든 고유값이 양수일 경우에만 양정부호이며, 즉 행렬이 양반정부호이고 가역적이다.^[31]

두 개의 서로 다른 벡터를 입력으로 허용하면 와 관련된 쌍선형 형식이 생성된다.^[32]

$B_{\bold A} (\bold x, \bold y) = \bold x^{\rm T} \bold{Ay}.$

복소 행렬의 경우, 동일한 용어와 결과가 적용되며, ''대칭 행렬'', ''이차 형식'', ''쌍선형 형식'', ''전치'' 는 각각 에르미트 행렬, 에르미트 형식, 세스킬리니어 형식, 켤레 전치 로 대체된다.
직교 행렬은 열 벡터와 행 벡터가 모두 직교 단위 벡터(즉, 직교 정규 벡터)인 실수 성분의 정방 행렬이다. 행렬 가 직교 행렬이라는 것은 그 전치 행렬이 그 역행렬과 같다는 것을 의미한다.

: $\mathbf{A}^\mathrm{T}=\mathbf{A}^{-1}, \,$

이는 다음을 의미한다.

: $\mathbf{A}^\mathrm{T} \mathbf{A} = \mathbf{A} \mathbf{A}^\mathrm{T} = \mathbf{I}_n,$

여기서 은 크기 의 단위 행렬이다.

직교 행렬 는 반드시 가역이며, 유니터리이고, 정규이다. 어떤 직교 행렬의 행렬식은 또는 이다. 특수 직교 행렬은 행렬식이 +1인 직교 행렬이다. 선형 변환으로서, 행렬식이 인 모든 직교 행렬은 반사가 없는 순수한 회전이며, 즉 변환된 구조의 방향을 유지한다. 반면에 행렬식이 인 모든 직교 행렬은 방향을 반전시키며, 즉 순수한 반사와 (아마도 영인) 회전의 합성이다. 단위 행렬은 행렬식이 이고 각도 0으로 순수한 회전이다.

복소수의 직교 행렬에 대한 아날로그는 유니터리 행렬이다.

5. 응용

행렬은 수학뿐만 아니라 여러 과학 분야에서 널리 사용된다. 예를 들어, 게임 이론과 경제학에서는 지불 행렬을 사용하여 플레이어의 선택에 따른 보상을 나타낸다.^[75] 텍스트 마이닝에서는 문서-단어 행렬을 사용하여 문서 내 단어 빈도를 분석한다.^[76]

복소수는 2×2 실수 행렬로 표현할 수 있으며, 이는 사원수^[77]나 클리포드 대수와 같이 확장될 수 있다. 초기 암호화 기법인 힐 암호는 행렬을 사용했지만, 선형적인 특성 때문에 쉽게 해독된다.^[78]

컴퓨터 그래픽스에서는 아핀 회전 행렬을 사용하여 객체의 변환을 계산하고, 3차원 객체를 2차원 화면에 투영한다.^[79] 이미지 처리에도 활용된다. 다항식 환 위의 행렬은 제어 이론에서 중요하게 다루어진다.

화학에서는 양자 이론을 바탕으로 분자 결합과 분광학을 설명하는 데 행렬이 사용된다. 겹침 행렬과 포크 행렬은 분자 궤도함수 계산에 활용된다.

물리학에서는 고전역학, 광학, 전자기학, 양자역학 등에서 물리 현상을 모델링하고 연구하는 데 행렬이 사용된다.

확률론 및 통계학에서 확률 행렬은 확률 집합을 나타내며, 구글 검색의 페이지랭크 알고리즘 등에 사용된다. 행렬 미적분학은 미분이나 지수 함수와 같은 개념을 고차원으로 일반화한다.

경제학에서는 경제적 관계를 나타내는 데 행렬이 사용된다. 행렬 계산 알고리즘 연구는 수치 해석의 중요한 분야이며, 행렬 분해는 계산을 단순화하는 데 사용된다.

운동학이나 로봇공학에서는 좌표 변환이나 자세 제어에 행렬이 사용되며, 컴퓨터 그래픽스에도 응용된다.

5. 1. 선형 변환

행렬은 선형 변환(선형 사상)을 나타내는 데 사용될 수 있다. 실수 m×n 행렬 A는 각 벡터 '''x'''를 Rⁿ에서 (행렬) 곱 '''Ax'''로 매핑하는 선형 변환

\R^n \to \R^m

를 생성하며, 이는 R^m의 벡터이다.

예를 들어, 다음과 같은 2×2 행렬

:

\mathbf{A} = \begin{bmatrix} a & c\\b & d \end{bmatrix}

은 (0, 0), (a, b), (a + c, b + d), 및 (c, d)에 꼭짓점이 있는 평행사변형으로 단위 정사각형을 변환하는 것으로 볼 수 있다.

다음 표는 R²의 연관된 선형 사상을 가진 여러 2×2 실수 행렬을 보여준다. 파란색 원본은 녹색 격자 및 도형으로 매핑된다. 원점 (0, 0)은 검은 점으로 표시된다.

수평 전단 m = 1.25.	수직축에 대한 반사	압축 사상 r = 3/2	스케일링 3/2의 비율	회전 π/6 = 30°
$\begin{bmatrix}$	$\begin{bmatrix}$	$\begin{bmatrix}$	$\begin{bmatrix}$	$\begin{bmatrix}$

5. 2. 연립 일차 방정식

행렬은 여러 개의 연립 일차 방정식을 간결하게 작성하고 처리하는 데 사용될 수 있다. 예를 들어, 가 행렬이고, 가 개의 변수 의 열 벡터(즉, -행렬)이고, 가 -열 벡터이면, 행렬 방정식:

\mathbf{Ax} = \mathbf{b}

은 다음 연립 일차 방정식과 같다.^[22]

:

\begin{align}a_{1,1}x_1 + a_{1,2}x_2 + &\cdots + a_{1,n}x_n = b_1 \\&\ \ \vdots \\a_{m,1}x_1 + a_{m,2}x_2 + &\cdots + a_{m,n}x_n = b_m\end{align}

행렬을 사용하면 모든 방정식을 개별적으로 작성하는 것보다 더 간결하게 풀 수 있다. 이고 방정식이 일차 독립이면, 다음과 같이 쓸 수 있다.

:

\mathbf{x} = \mathbf{A}^{-1} \mathbf{b}

여기서 은 의 역행렬이다. 에 역행렬이 없으면, 해가 존재하는 경우 일반화된 역행렬을 사용하여 구할 수 있다.

5. 3. 그래프 이론

유한 그래프의 인접 행렬은 그래프 이론의 기본적인 개념이다.^[80] 이 행렬은 그래프의 어떤 정점들이 간선으로 연결되어 있는지를 기록한다. 단 두 가지 값(예를 들어 "예"와 "아니오"를 의미하는 1과 0)만 포함하는 행렬을 논리 행렬이라고 한다. 거리 행렬(또는 비용 행렬)은 간선의 거리에 대한 정보를 포함한다.^[81] 이러한 개념은 하이퍼링크로 연결된 웹사이트나 도로로 연결된 도시 등에 적용될 수 있으며, 이 경우 (연결 네트워크가 매우 조밀하지 않다면) 행렬은 대부분 희소 행렬이 된다. 즉, 0이 아닌 항목이 거의 없다. 따라서, 네트워크 이론에서는 특별히 고안된 행렬 알고리즘을 사용할 수 있다.

5. 4. 양자 역학

양자장론에서 소립자는 특수 상대성이론의 로렌츠 군의 표현으로 분류되며, 더 구체적으로는 스핀 군에 대한 그들의 거동에 의해 분류된다. 파울리 행렬과 더 일반적인 감마 행렬을 포함하는 구체적인 표현은 스피너로 작용하는 페르미온의 물리적 설명에 필수적이다.^[95] 세 가지 가장 가벼운 쿼크의 경우, 특수 유니터리 군 SU(3)을 포함하는 군론적 표현이 존재한다. 물리학자들은 강한 핵 상호 작용의 현대적 설명의 기초를 형성하는 SU(3) 게이지 군에도 사용되는 편리한 행렬 표현인 겔만 행렬을 계산에 사용한다. 카비보-코바야시-마스카와 행렬은 약한 상호 작용에 중요한 기본 쿼크 상태가 특정하고 구별되는 질량을 갖는 입자를 정의하는 기본 쿼크 상태와 동일하지 않지만 선형적으로 관련되어 있다는 사실을 나타낸다.^[96]

최초의 양자역학 모델(베르너 하이젠베르크(Werner Heisenberg), 1925)은 양자 상태에 작용하는 무한 차원 행렬로 이론의 연산자를 나타냈다.^[97] 이것은 또한 행렬역학으로 불린다. 특정한 예로, 양자계의 "혼합" 상태를 기본적인 "순수" 고유상태의 선형 결합으로 특징짓는 밀도 행렬이 있다.^[98]

또 다른 행렬은 실험 입자 물리학의 초석을 이루는 산란 실험을 설명하는 핵심 도구 역할을 한다. 입자가속기에서 발생하는 것과 같은 충돌 반응은 나가는 입자 상태의 스칼라 곱과 들어오는 입자 상태의 선형 결합으로 설명될 수 있다. 선형 결합은 S-행렬이라는 행렬로 주어지며, 이것은 입자 간의 가능한 모든 상호 작용에 대한 정보를 담고 있다.^[99]

5. 5. 기하 광학

기하광학은 행렬이 응용되는 한 분야이다. 기하광학은 빛의 파동성을 무시하고, 광선을 기하학적 광선으로 간주하는 근사 이론을 사용한다. 광학 요소에 의한 광선의 굴절이 작다면, 렌즈나 반사 요소가 광선에 작용하는 것을 2x2 행렬과 두 성분 벡터의 곱으로 나타낼 수 있다. 이를 레이 전달 행렬 분석이라고 한다. 여기서 벡터는 광선의 기울기와 광축으로부터의 거리를 나타내는 성분으로 구성되고, 행렬은 광학 요소의 특성을 나타낸다.^[102]

이때 사용되는 행렬에는 두 가지 종류가 있다. 하나는 렌즈 표면에서 굴절을 나타내는 ''굴절 행렬''이고, 다른 하나는 다음 굴절 표면으로의 기준면 이동을 설명하는 ''변환 행렬''이다. 광학계는 렌즈나 반사 요소의 조합으로 구성되는데, 이는 각 구성 요소 행렬을 곱하여 얻어지는 행렬로 간단하게 표현할 수 있다.^[102]

5. 6. 전자 공학

5. 7. 기타 응용

확률 행렬은 행이 확률 벡터인, 즉 항목이 음이 아니고 합계가 1인 정방 행렬로, 유한한 상태를 가진 마르코프 체인을 정의하는 데 사용된다.^[88] 확률 행렬의 행은 현재 해당 행에 해당하는 상태에 있는 어떤 입자의 다음 위치에 대한 확률 분포를 제공하며, 흡수 상태와 같은 마르코프 체인의 속성은 전이 행렬의 고유 벡터에서 확인할 수 있다.^[89]

두 개의 서로 다른 마르코프 체인. 이 차트는 상태 "2"에 있는 입자의 수(총 1000개 중)를 나타낸다. 두 가지 모두의 한계값은 다음과 같이 주어진 전이 행렬에서 결정할 수 있다.

\begin{bmatrix}0.7 & 0\\0.3 & 1\end{bmatrix}(빨간색) 및

\begin{bmatrix}0.7 & 0.2\\0.3 & 0.8\end{bmatrix}

(검정색).]]

통계학에서는 여러 가지 형태로 행렬을 사용한다.^[90] 기술 통계학은 데이터 집합을 설명하는 데 사용되며, 종종 데이터 행렬로 나타내어 차원 축소 기법을 적용할 수 있다. 공분산 행렬은 여러 확률 변수의 상호 분산을 나타낸다.^[91]

확률론이나 통계학에서 행렬은 확률의 집합을 표현하는 데 사용되며, 예를 들어 구글 검색의 페이지랭크 알고리즘에 사용된다.

경제학에서는 경제적 관계의 시스템을 설명하는 데 행렬이 사용된다.

운동학이나 로봇공학에서는 좌표변환이나 자세 제어 등에 행렬이 사용된다. 특히 2차원 좌표 변환에서는 3×3 행렬이, 3차원 좌표 변환에서는 4×4 행렬이 자주 사용된다. 컴퓨터 그래픽스에도 응용되고 있다.

6. 역사

실베스터가 1848년에 처음으로 사용한 '행렬(matrix)'이라는 단어는 해부학에서 자궁(子宮)을 뜻하며, 행렬식에 대한 행렬의 의미를 표현한 것으로 알려져 있다.^[141]

행렬은 연립 일차 방정식을 푸는 데 오랫동안 사용되었지만, 1800년대까지는 배열(array)로 알려졌다. 기원전 10세기에서 2세기 사이에 쓰인 중국 수학 서적 구장산술은 연립 방정식을 풀기 위해 배열 방법을 사용한 최초의 사례이며, 행렬식의 개념도 포함하고 있다.^[103] 1545년 이탈리아 수학자 제롤라모 카르다노는 그의 저서 ''Ars Magna''에서 이 방법을 유럽에 소개하였다.^[104] 일본 수학자 세키 다카카즈는 1683년에 동일한 배열 방법을 사용하여 연립 방정식을 풀었다.^[105] 네덜란드 수학자 얀 더 위트는 그의 1659년 저서 ''Elements of Curves''에서 배열을 이용하여 변환을 나타내었다.^[106] 1700년에서 1710년 사이에 고트프리트 빌헬름 라이프니츠는 정보 또는 해를 기록하기 위해 배열의 사용을 알리고 50가지가 넘는 배열 시스템을 실험하였다.^[104] 가브리엘 크라메르는 1750년에 크라머의 법칙을 제시하였다.

제임스 조셉 실베스터가 1850년에 "matrix"라는 용어를 만들었는데,^[108] 그는 행렬을 오늘날 소행렬식이라고 불리는 여러 행렬식을 생성하는 객체로 이해했다. 즉, 원래 행렬에서 열과 행을 제거하여 얻은 더 작은 행렬의 행렬식을 말한다. 1851년 논문에서 실베스터는 다음과 같이 설명하였다.^[109]

아서 케일리는 행렬을 사용하여 기하 변환에 대한 논문을 발표했는데, 그는 덧셈, 뺄셈, 곱셈, 나눗셈과 같은 연산을 해당 행렬의 변환으로 정의하고 결합 법칙과 분배 법칙이 성립함을 보였다. 케일리는 행렬 곱셈의 비가환성과 행렬 덧셈의 가환성을 조사하고 증명했다.^[104] 초기 행렬 이론은 배열의 사용을 거의 전적으로 행렬식에 국한했고 아서 케일리의 추상적인 행렬 연산은 혁명적이었다. 그는 방정식 시스템과 독립적인 행렬 개념을 제안하는 데 중요한 역할을 했다. 1858년 아서 케일리는 그의 저서 ''A memoir on the theory of matrices''에서^[110]^[111] 케일리-해밀턴 정리를 제안하고 증명하였다.^[104]

영국의 수학자 커스버트 에드먼드 컬리스는 1913년에 행렬에 대한 현대적인 괄호 표기법을 처음으로 사용했으며, 동시에 행렬을 나타내는 최초의 중요한 사용법을 보여주었다.^[104]

행렬식의 현대적인 연구는 여러 출처에서 비롯되었다.^[112] 정수론 문제는 가우스가 이차 형식의 계수와 3차원 선형 사상을 행렬과 관련짓도록 이끌었다. 고틀로브 아이젠슈타인은 현대 용어로 행렬 곱이 비가환적이라는 언급을 포함하여 이러한 개념을 더욱 발전시켰다. 오귀스탱 루이 코시는 행렬식에 대한 일반적인 명제를 최초로 증명했다. 그는 또한 1829년에 대칭 행렬의 고유값이 실수임을 보였다.^[113] 카를 구스타프 야코프 야코비는 야코비 행렬식을 연구했는데, 이것은 국소적(또는 무한소) 수준에서 기하 변환을 설명하는 데 사용될 수 있다. 레오폴트 크로네커의 ''Vorlesungen über die Theorie der Determinanten''^[114]과 카를 바이어슈트라스의 ''Zur Determinantentheorie''^[115]는 모두 1903년에 출판되었으며, 행렬식을 처음으로 공리적으로 다루었다.

케일리-해밀턴 정리는 처음에 작은 행렬에 대해서만 확립되었는데, 예를 들어 케일리에 의해 2×2 행렬에 대해, 윌리엄 로완 해밀턴에 의해 4×4 행렬에 대해 증명되었다. 게오르크 프로베니우스는 이차 형식에 대해 작업하면서 모든 차원으로 정리를 일반화했다(1898). 19세기 말에 가우스-조르단 소거법(현재 가우스 소거법으로 알려진 특수한 경우를 일반화)이 빌헬름 조르단에 의해 확립되었다. 20세기 초에 행렬은 선형 대수에서 중심적인 역할을 하게 되었는데,^[116] 부분적으로는 이전 세기의 초복소수 시스템의 분류에 사용되었기 때문이다.

베르너 하이젠베르크, 막스 보른, 파스쿠알 요르단에 의한 행렬 역학의 시작은 무한히 많은 행과 열을 가진 행렬을 연구하게 되었다.^[117] 나중에 존 폰 노이만은 함수 해석학적 개념을 발전시킴으로써 양자 역학의 수학적 공식화를 수행하였다.

7. 추상대수학적 측면과 일반화

추상대수학에서 행렬은 체뿐만 아니라 환의 원소를 가질 수 있도록 일반화된다.^[56] 선형대수학에서는 선형 사상의 개념을 통해 행렬의 성질을 체계화한다. 무한히 많은 행과 열을 갖는 행렬이나, 텐서와 같이 수의 고차원 배열로 행렬을 확장할 수도 있다.^[56]

특정 조건을 만족하는 행렬들은 군이나 환을 형성하기도 한다. 예를 들어, 행렬군은 행렬 곱셈을 군 연산으로 하는 군이며,^[65]^[66] 행렬환은 특정 조건에서 행렬들이 환을 형성하는 것이다. 그러나 행렬의 곱은 일반적으로 교환법칙이 성립하지 않는다.^[56]

7. 1. 일반적인 성분을 갖는 행렬

체나 환의 원소를 성분으로 갖는 행렬은 수학에서 널리 사용된다.^[57] 특히, 부호 이론에서는 유한체 위의 행렬을 사용한다. 환은 나눗셈 연산이 존재할 필요가 없다는 점에서 체보다 더 일반적인 개념이다. 행렬의 덧셈과 곱셈 연산은 환의 성분을 갖는 경우에도 동일하게 적용된다. ''R'' 위의 모든 ''n''×''n'' 정방 행렬의 집합 M(''n'', ''R'') (로도 표기됨)^[7]은 행렬환이라고 불리는 환이며, 왼쪽 ''R''-가군 ''R''^''n''의 자동사상환과 동형이다.^[58]

가환환 ''R'' 위의 정방 행렬의 행렬식은 라이프니츠 공식을 사용하여 정의할 수 있다. 이러한 행렬은 행렬식이 ''R''에서 가역적일 때만 가역적이다.^[59]

블록 행렬은 성분 자체가 행렬인 행렬로, 성분 행렬들의 크기는 특정 조건을 만족해야 한다.

7. 2. 선형 사상과의 관계

행렬은 선형 사상을 표현하는 도구로 볼 수 있다.

; 선형사상의 행렬 표현

: 행렬 로부터 선형 사상 이 각 벡터 을 행렬로서의 곱 으로 사상하는 것으로 정의된다. 반대로, 각 선형사상 을 생성하는 행렬 는 유일하게 결정된다. 명시적으로 쓰면, 의 -성분은 의 제 ''i''-성분이다. 단, 는 제 -성분만이 이고 다른 것이 모두 인 단위 벡터이다.

이때, 행렬 는 선형사상 를 표현한다고 말하며, 를 의 '''변환행렬''' 또는 '''표현행렬'''이라고 부른다.

예를 들어 행렬

:

A = \begin{bmatrix} a & c\\b & d \end{bmatrix}

은 단위 정사각형을 를 꼭짓점으로 하는 평행사변형으로 사상하는 것으로 간주할 수 있다. 이 평행사변형은 단위 정사각형의 꼭짓점을 이루는 네 개의 (열) 벡터 각각에 를 곱하는 것에 의해 얻어진다.

이 행렬과 선형사상 사이의 일대일 대응하에서, 행렬의 곱셈은 사상의 합성에 대응한다^[61]: 위의 와 에 더하여, 행렬 가 다른 선형사상 을 표현하는 것이라면, 합성 는 행렬의 곱 로 표현된다. 실제로,

:

이다. 마지막 등호는 행렬의 곱의 결합성에 의한 것이다.

선형사상 는 이미 설명했듯이 × 행렬과 동일하다. 일반적으로 유한차원 벡터 공간 사이의 선형사상 는 (의 차원을 , 의 차원을 으로 하여) 의 기저 과 의 기저 를 선택하면

:

f(\mathbf{v}_j) = \sum_{i=1}^m a_{i,j} \mathbf{w}_i\qquad\mbox{for}\ j=1,\ldots,n.

을 만족하는 행렬 에 의해 기술할 수 있다. 다시 말해,

의 제 -열은 기저 벡터 의 상을 의 기저 로 나타낸 것이다. 따라서 이러한 관계는 행렬 의 성분으로부터 유일하게 결정된다. 주의해야 할 것은 선형사상을 나타내는 행렬은 기저의 선택에 의존한다는 것이다. 기저의 선택을 바꾸면 다른 행렬이 생기지만, 그것은 원래 행렬과 동치가 된다.^[61]

전치 행렬 는 가 정의하는 선형사상의 전치사상을 쌍대 기저에 관해 기술하는 것이다.^[62]

7. 3. 행렬군

군은 특정 조건을 만족하는 이항 연산과 객체의 집합으로 구성된 수학적 구조이다.^[64] 행렬을 객체로, 행렬 곱셈을 군 연산으로 하는 군을 ''행렬군''이라고 한다.^[65]^[66] 모든 원소가 가역적이어야 하므로, 가장 일반적인 행렬군은 주어진 크기의 모든 가역 행렬의 군으로, 일반 선형군이라고 한다.

행렬 곱과 역행렬에서 보존되는 행렬의 속성은 추가 행렬군을 정의하는 데 사용될 수 있다. 예를 들어, 주어진 크기의 행렬 중 행렬식이 1인 행렬은 일반 선형군의 부분군을 형성하며, 특수 선형군이라고 한다.^[67] 다음 조건

\bold M^{\rm T} \bold M = \bold I,

을 만족하는 직교 행렬은 직교군을 형성한다.^[68] 모든 직교 행렬은 행렬식이 1 또는 −1이다. 행렬식이 1인 직교 행렬은 ''특수 직교군''이라는 부분군을 형성한다.

모든 유한군은 대칭군의 정칙 표현을 고려하면 행렬군과 동형임을 알 수 있다.^[69] 일반적인 군은 비교적 잘 이해되는 행렬군을 사용하여 표현론을 통해 연구할 수 있다.^[70]

7. 4. 무한 행렬

무한히 많은 행과/또는 열을 갖는 행렬을 고려할 수 있다.^[71] 무한한 객체이므로 이러한 행렬을 명시적으로 적어낼 수는 없다. 행을 색인하는 집합의 모든 원소와 열을 색인하는 집합의 모든 원소에 대해 잘 정의된 항이 존재해야 한다 (이러한 색인 집합은 자연수의 부분집합일 필요조차 없다). 덧셈, 뺄셈, 스칼라 곱셈, 전치 연산과 같은 기본 연산은 여전히 문제없이 정의될 수 있다. 하지만 행렬 곱셈은 결과 항을 정의하기 위해 무한 합을 포함할 수 있으며, 이는 일반적으로 정의되지 않는다.

단위원을 갖는 임의의 환이 주어지면, 오른쪽 모듈로서

M=\bigoplus_{i\in I}R

의 준동형 사상 환은

I\times I

에 의해 색인되고 각 열에 유한 개의 영이 아닌 항만 포함하는 '''열 유한 행렬'''

\mathrm{CFM}_I(R)

의 환과 동형이다. 왼쪽 모듈로서 고려되는 의 준동형 사상은 각 행에 유한 개의 영이 아닌 항만 갖는 '''행 유한 행렬'''

\mathrm{RFM}_I(R)

이라는 유사한 객체를 생성한다.

무한 행렬을 선형 사상을 설명하는 데 사용하는 경우, 모든 열에 유한 개의 영이 아닌 항만 있는 행렬만 사용할 수 있다. 행렬 A가 선형 사상 f': V → W를 설명하려면, 두 공간 모두에 대한 기저를 선택해야 한다. 정의에 따라 이는 공간의 모든 벡터가 기저 벡터의 (유한한) 선형 결합으로 유일하게 표현될 수 있음을 의미하며, 따라서 (열) 벡터의 계수로 작성될 때 유한 개의 항만 영이 아니다. A의 열은 V의 개별 기저 벡터의 f에 의한 영상을 W의 기저에서 설명하며, 이는 이러한 열에 유한 개의 영이 아닌 항만 있는 경우에만 의미가 있다. 그러나 A의 행에는 제한이 없다. 곱 A · v에는 유한 개의 영이 아닌 v의 계수만 포함되므로, 무한한 곱의 합으로 주어지더라도 그 항 각각은 유한 개의 영이 아닌 항만 포함하므로 잘 정의된다. 또한 이는 A의 열의 선형 결합을 형성하는 것과 같으며, 효과적으로 그 중 유한 개만 포함하므로, 결과는 그 열 각각이 그러하기 때문에 유한 개의 영이 아닌 항만 갖는다. 주어진 유형의 두 행렬의 곱은 (열 색인 집합과 행 색인 집합이 일치하는 경우) 잘 정의되고, 같은 유형이며, 선형 사상의 합성에 해당한다.

R이 노름 환이라면, 행 또는 열 유한 조건을 완화할 수 있다. 노름이 있으면, 유한 합 대신 절대 수렴 급수를 사용할 수 있다. 예를 들어, 열 합이 수렴 수열인 행렬은 환을 형성한다. 마찬가지로, 행 합이 수렴 급수인 행렬도 환을 형성한다.

무한 행렬은 힐베르트 공간 위의 연산자를 설명하는 데에도 사용할 수 있으며, 여기서 수렴과 연속성 문제가 발생하며, 이는 다시 부과해야 하는 특정 제약 조건을 초래한다.^[72]

7. 5. 공행렬

'''공행렬'''(empty matrix)은 행 또는 열(혹은 둘 다)의 개수가 0인 행렬이다.^[73]^[74] 공행렬은 영벡터 공간을 포함하는 사상을 다루는 데 도움이 된다. 예를 들어, '''A'''가 3×0 행렬이고 '''B'''가 0×3 행렬이라면, '''AB'''는 3차원 공간 ''V''에서 자신으로 가는 영사상에 해당하는 3×3 영행렬이 되는 반면, '''BA'''는 0×0 행렬이 된다. 공행렬에 대한 일반적인 표기법은 없지만, 대부분의 컴퓨터 대수 시스템에서는 공행렬을 생성하고 계산할 수 있다. 0×0 행렬의 행렬식은 1이며, 이는 행렬식의 라이프니츠 공식에서 나타나는 공곱을 1로 간주하는 것과 관련이 있다. 이 값은 또한 유한 차원 공간에서 자신으로 가는 항등 사상의 행렬식이 1이라는 사실과 일치하며, 이 사실은 종종 행렬식의 특징을 나타내는 데 사용된다.

8. 행렬 분해

행렬 분해는 행렬을 여러 행렬의 곱으로 나타내는 방법이다. 이는 행렬을 더 다루기 쉬운 형태로 변환하여 계산을 용이하게 하거나, 특정 문제 해결에 유리한 형태로 만들기 위해 사용된다.

행렬 분해는 다양한 방법이 있으며, 각각의 방법은 고유한 특징과 장점을 가진다. 주요 분해 방법은 다음과 같다.

분해 방법	설명	주요 특징
LU 분해	정방 행렬을 하삼각 행렬(Lower triangular matrix)과 상삼각 행렬(Upper triangular matrix)의 곱으로 분해한다.	선형 시스템을 효율적으로 풀거나 삼각 행렬의 역행렬을 쉽게 계산할 때 유용하다.
콜레스키 분해	양의 정부호 대칭 행렬(또는 에르미트 행렬)을 하삼각 행렬과 그 전치 행렬(또는 켤레 전치 행렬)의 곱으로 분해한다.	양의 정부호 행렬에 특화된 분해 방법으로, 계산 효율성이 높다.
QR 분해	임의의 행렬을 직교 행렬(Orthogonal matrix) 또는 유니터리 행렬(Unitary matrix)과 상삼각 행렬의 곱으로 분해한다.	선형 최소 제곱 문제(Linear least squares problem)나 고유값 문제를 해결하는 데 사용된다.
고유값 분해	대각화 가능한 행렬을 고유 벡터(eigenvector) 행렬과 고유값(eigenvalue) 대각 행렬의 곱으로 분해한다.	행렬의 거듭제곱 계산, 선형 미분 방정식 해결 등에 활용된다.
특이값 분해	임의의 행렬을 두 개의 유니터리 행렬과 특이값(singular value) 대각 행렬의 곱으로 분해한다.	차원 축소, 데이터 압축, 노이즈 제거 등 다양한 응용 분야에 사용된다.

이러한 행렬 분해 기법들은 선형대수학의 다양한 문제를 해결하는 데 핵심적인 역할을 하며, 수치선형대수학 분야에서 알고리즘의 효율성과 안정성을 높이는 데 기여한다.

9. 행렬과 관련된 한국 인물

행렬과 관련된 연구나 교육 활동을 한 한국인 수학자는 다음과 같다.

이름	주요 내용
이광연	1968년생 수학자로, 한서대학교 교수를 역임했다. 행렬과 선형대수학 분야에서 다수의 저서를 출간하고 교육에 기여했다.
김홍종	서울대학교 명예교수로, 선형대수학을 비롯한 다양한 수학 분야에서 연구 및 교육 활동을 수행했다.
계승혁	서울대학교 명예교수로, 행렬 이론과 관련된 연구를 수행했다.

참조

_[1] 문서
_[2] 논문
_[3] 논문
_[4] 논문
_[5] 웹사이트 Matrix https://mathworld.wo[...] 2020-08-19
_[6] 논문
_[7] 서적 Square Matrices of Order 2 Springer International Publishing
_[8] 논문
_[9] 논문
_[10] 웹사이트 How to Multiply Matrices https://mathsisfun.c[...] 2020-08-19
_[11] 논문
_[12] 논문
_[13] 논문
_[14] 논문
_[15] 논문
_[16] 논문
_[17] 논문
_[18] 서적 Matrices and Linear Algebra https://books.google[...] Courier Dover Corporation
_[19] 서적 Theory of Matrices https://books.google[...] Courier Dover Corporation
_[20] 서적 Elementary Linear Algebra https://books.google[...] John Wiley & Sons
_[21] 서적 Matrix Analysis https://books.google[...] Cambridge University Press
_[22] 논문
_[23] 논문
_[24] 논문
_[25] 논문
_[26] 논문
_[27] 논문
_[28] 논문
_[29] 논문
_[30] 논문
_[31] 논문
_[32] 논문
_[33] 웹사이트 Matrix mathematics https://britannica.c[...] 2020-08-19
_[34] 논문
_[35] 논문
_[36] 논문
_[37] 논문
_[38] 논문
_[39] 문서 Eigen means "own" in German and Dutch
_[40] 논문
_[41] 논문
_[42] 논문
_[43] 논문
_[44] 논문
_[45] 논문
_[46] 논문
_[47] 논문
_[48] 학술지 John von Neumann's Analysis of Gaussian Elimination and the Origins of Modern Numerical Analysis https://epubs.siam.o[...] 2011-01-01
_[49] 논문
_[50] 논문
_[51] 논문
_[52] 논문
_[53] 논문
_[54] 논문
_[55] 논문
_[56] 논문
_[57] 논문
_[58] 논문
_[59] 논문
_[60] 논문
_[61] 논문
_[62] 논문
_[63] 논문
_[64] 문서 See any standard reference in a group.
_[65] 문서 Additionally, the group must be closed in the general linear group.
_[66] 논문
_[67] 논문
_[68] 논문
_[69] 논문
_[70] 문서 See any reference in representation theory or group representation.
_[71] 서적 Matrix
_[72] 서적 Not much of matrix theory carries over to infinite-dimensional spaces, and what does is not so useful, but it sometimes helps.
_[73] 웹사이트 Glossary https://omatrix.com/[...] O-Matrix v6 User Guide
_[74] 웹사이트 MATLAB Data Structures https://system.nada.[...]
_[75] 서적
_[76] 서적
_[77] 서적
_[78] 서적
_[79] 서적
_[80] 서적
_[81] 서적
_[82] 서적
_[83] 서적
_[84] 서적
_[85] 서적
_[85] 서적
_[86] 서적
_[87] 서적
_[88] 서적
_[89] 서적
_[90] 서적 Matrices for Statistics Oxford University Press
_[91] 서적
_[92] 서적
_[93] 서적
_[94] 서적
_[95] 서적
_[96] 서적
_[97] 서적
_[98] 서적
_[99] 서적
_[100] 서적
_[101] 서적
_[102] 서적
_[103] 서적
_[103] 서적
_[104] 서적 Discrete Mathematics Addison Wesley 2001-10-10
_[105] 서적 Science and Civilisation in China https://books.google[...] Cambridge University Press
_[106] 서적 Discrete Mathematics Addison Wesley 2001-10-10
_[107] 웹사이트 Merriam-Webster dictionary https://merriam-webs[...] Merriam-Webster 2009-04-20
_[108] 문서 Additions to the articles in the September number of this journal, "On a new class of theorems," and on Pascal's theorem https://books.google[...] 1850
_[109] 서적 The Collected Mathematical Papers of James Joseph Sylvester: 1837–1853 https://books.google[...]
_[110] 간행물 Phil.Trans. 1858
_[111] 논문 1978
_[112] 논문 1994
_[113] 논문 1975
_[114] 논문 1897
_[115] 논문 1915
_[116] 논문 2004
_[117] 논문 1987
_[118] 서적 Principia Mathematica to *56* Cambridge at the University Press 1913
_[119] 서적 Introduction to Logic and the Methodology of Deductive Sciences Dover Publications, Inc 1946
_[120] 웹사이트 https://raksul.com/d[...]
_[121] 문서 斎藤2017
_[122] 논문 1999
_[123] 서적 Science and Civilisation in China https://books.google[...] Cambridge University Press 1959
_[124] 웹사이트 Merriam–Webster dictionary http://www.merriam-w[...] Merriam–Webster 2009-04-20
_[125] 서적 The Collected Mathematical Papers of James Joseph Sylvester: 1837–1853 https://books.google[...]
_[126] 문서 斎藤2017
_[127] 문서 斎藤2017
_[128] 문서 斎藤2017
_[129] 문서 斎藤2017
_[130] 문서 斎藤2017
_[131] 문서 斎藤2017
_[132] 문서 斎藤2017
_[133] 웹사이트 http://www2.math.kyu[...]
_[134] 웹사이트 Crimes against Matrices http://see.stanford.[...] 2013-03-02
_[135] 서적 矩形行列の行列式 http://pub.maruzen.c[...] 丸善 2012
_[136] 웹사이트 Glossary http://www.omatrix.c[...]
_[137] 웹사이트 MATLAB Data Structures http://www.system.na[...]
_[138] 서적 Algebra Springer 2002
_[139] 서적 An Introduction to Numerical Methods A MATLAB Approach 학산미디어 2013
_[140] 서적 Matrix computations https://archive.org/[...] The Johns Hopkins University Press 2013
_[141] 서적 고등기하와 벡터 ( $\mathbf{I}$ 일차변환과 행렬) 성지출판

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com