원 (기하학)
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
원(Circle)은 평면 위의 한 점에서 같은 거리에 있는 점들의 집합으로 정의되는 2차원 도형이다. 원은 기하학의 기본 도형 중 하나로, 다양한 용어와 성질을 가진다. 주요 용어로는 반지름, 지름, 원주, 중심각, 원주각 등이 있으며, 원의 구성 요소로는 현, 접선, 호, 부채꼴, 활꼴 등이 있다. 원은 둘레와 넓이를 가지며, 원의 둘레는 2πr 또는 πd로, 넓이는 πr²로 계산된다. 원은 데카르트 좌표계, 극좌표계, 복소평면 등 다양한 좌표계에서 방정식으로 표현될 수 있으며, 기하학적 성질로는 대칭성, 닮음, 현의 성질, 접선의 성질 등이 있다. 원은 작도를 통해 그릴 수 있으며, 아폴로니우스 원, 내접원, 외접원 등 다양한 관련 주제가 존재한다.
더 읽어볼만한 페이지
- 원 (기하학) - 대원
구면기하학에서 대원은 구의 중심을 지나는 평면과 구의 교선으로, 유클리드 공간의 직선에 대응하며, 서로 대극점이 아닌 두 점을 잇는 최단 거리인 대원 거리를 정의하고, 자오선이나 적도처럼 항해, 천문학 등 다양한 분야에서 응용된다. - 원 (기하학) - 반지름
반지름은 원의 중심에서 원 위의 점까지의 거리로, 원의 지름과 둘레, 넓이 계산에 사용될 뿐 아니라 정다각형 외접원, 그래프 이론, 극좌표계 등 다양한 분야에서 활용되며, 여러 도형의 반지름을 구하는 공식이 존재하고 한국의 교육, 건축, 디자인 분야에서도 널리 쓰인다. - 원뿔 곡선 - 이심률
이심률은 원뿔곡선의 형태를 결정하는 값으로, 초점과 준선으로부터의 거리 비율로 정의되며, 값에 따라 원, 타원, 포물선, 쌍곡선으로 구분되고, 타원과 쌍곡선의 경우 중심과 초점 사이의 거리와 반장축의 비율로 나타낼 수 있으며, 이심률이 같은 원뿔곡선은 서로 닮음이다. - 원뿔 곡선 - 포물선
포물선은 원뿔 곡선의 일종으로, 메나이크모스에 의해 처음 연구되었으며, 아르키메데스와 아폴로니오스에 의해 성질이 연구되었고, 고전역학, 광학 등 다양한 분야에 응용되며, 초점과 준선, 이차 함수의 그래프 등의 기하학적 성질을 가진다. - 기하학 - 밀러 지수
밀러 지수는 결정학에서 결정 면과 방향을 나타내기 위해 사용되는 지수이며, 역격자 벡터 또는 격자 벡터 절편의 역수를 통해 정의되며, 물질의 물리적, 화학적 성질 및 기술적 응용에 중요한 역할을 한다. - 기하학 - 반지름
반지름은 원의 중심에서 원 위의 점까지의 거리로, 원의 지름과 둘레, 넓이 계산에 사용될 뿐 아니라 정다각형 외접원, 그래프 이론, 극좌표계 등 다양한 분야에서 활용되며, 여러 도형의 반지름을 구하는 공식이 존재하고 한국의 교육, 건축, 디자인 분야에서도 널리 쓰인다.
2. 용어
원과 관련된 기본적인 용어는 다음과 같다.[1]
- '''할선''': 원과 두 점에서 만나는 직선이다.
- '''현''': 할선이 원에 의해 잘려나가는 선분 (선분 AB)
- '''중심선''': 원의 중심을 지나는 할선. 원의 대칭축이며, 원의 넓이를 이등분한다.
- '''지름''': 중심선이 원에 의해 잘려나가는 현 또는 그 길이. 반지름의 2배이다.
- '''원주율''': 원주의 길이와 지름의 비. 모든 원에서 일정하며, 보통 π로 나타낸다.
- 원의 반지름을 ''r''이라 하면, 원주는 2π''r'', 원의 넓이는 π''r''2이다. 같은 둘레를 가진 닫힌 도형 중 넓이가 가장 크다. (등주 문제)
- '''호''' (원호): 할선에 의해 나뉜 원주의 두 부분.
- '''우호''' (major arc): 두 호 중 긴 쪽.
- '''열호''' (minor arc): 두 호 중 짧은 쪽.
- '''반원''': 두 호의 길이가 같을 때. 이때 할선은 중심선이다.
- 호 AB: 원주상의 두 점 A, B를 양 끝으로 하는 호 (기호: A͡B, ⌒는 AB 위에 덮어 씀). 우호와 열호를 구분하기 위해 호 위의 점 P를 사용하여 호 APB와 같이 표기하기도 한다.
- '''부채꼴''' (sector) O-A͡B: 반지름 OA, OB와 호 AB로 둘러싸인 도형.
- '''중심각''': 부채꼴에 포함되는 쪽의 ∠BOA. 중심각과 호의 길이, 부채꼴의 넓이는 비례한다.
- '''활꼴''' (segment): 현 AB와 호 AB로 둘러싸인 도형.
- '''원주각''': 호 AB 위에 없는 점 P에 대한 ∠APB. 원주각은 점 P의 위치와 관계없이 일정하며, 중심각의 절반이다. (원주각의 정리)
- 특히 호 AB가 반원이면 원주각은 직각이다. (지름을 낀 원주각: 탈레스의 정리)
thumb
- '''내접한다''': 원 O의 원주상에 4점 A, B, C, D가 있을 때, 사각형 ABCD는 원 O에 내접한다. (내접 사각형)
- '''외접원''': 내접 사각형 ABCD의 원 O. 사각형이 원에 내접하면, 마주보는 각의 합은 평각이다. (내접 사각형의 정리) 원에 내접하는 사각형의 외각은 그 내대각과 크기가 같다. 이 명제들의 역도 성립한다. (네 점 공원 정리, 내접 사각형의 정리)
thumb
- '''접선''' (tangent): 원과 한 점에서 만나는 직선.
- '''접점''': 접선과 원의 교점. 접점과 원의 중심을 잇는 반지름(접점 반지름)은 접선과 직교한다.
- '''접선의 길이''': 원 외부의 점에서 원에 그은 두 접선의 길이 (선분 AS, AT). 접선의 길이는 서로 같다. 접선과 접점을 지나는 현이 이루는 각은 그 각 안의 호에 대한 원주각과 같다. ('''접현 정리''') (AT가 접선이면, ∠BAT = ∠APB). 접현 정리의 역도 성립한다.
- 원의 키스수는 6이다.
2. 1. 원의 구성 요소
원과 관련된 기본적인 용어는 다음과 같다.
- '''단위원''': 반지름이 1인 원
- '''동심원''': 중심이 같은 두 원
- '''반원''': 중심각이 평각인 부채꼴 또는 활꼴
- '''반지름''': 원의 중심과 그 원 위의 점을 잇는 선분 또는 그 선분의 길이. 반지름의 길이는 지름의 1/2이다.
- '''부채꼴''': 두 개의 반지름과 하나의 호로 둘러싸인 영역
- '''사분원''': 중심각이 직각인 부채꼴
- '''원주''': 원의 둘레
- '''원주각''': 한 끝점을 공유하는 두 현이 원 내부에서 이루는 각. 크기는 이에 대응하는 중심각의 1/2이다.
- '''원판''': 원으로 둘러싸인 도형
- '''원환''': 두 동심원으로 둘러싸인 도형
- '''접선''': 원과 한 점에서 만나는 직선
- '''접현각''': 원의 현과 현의 한 끝점에서의 접선이 이루는 각
- '''중심''': 원 위의 임의의 점에 이르는 거리가 일정한, 그 원을 포함하는 평면 위의 점
- '''중심각''': 호의 두 끝점을 지나는 반지름이 호와 같은 쪽에서 이루는 각. 크기는 이에 대응하는 원주각의 2배이다.
- '''지름''': 원의 중심을 지나는 현 또는 그 길이. 길이는 반지름의 2배이다.
- '''켤레호''': 원주 전체를 이루는 두 호
- '''할선''': 원과 두 점에서 만나는 직선
- '''현''': 원 위의 두 점을 잇는 선분
- '''호''': 원의 일부가 되는 곡선
- '''활꼴''': 같은 끝점을 갖는 호와 현으로 둘러싸인 영역
- '''시''': 할선의 중점을 수선의 발로 하는 선
- '''환상''': 두 개의 동심원으로 둘러싸인 고리 모양 물체
- '''원호''': 원의 모든 연결된 부분
- '''원반''': 원으로 둘러싸인 평면의 영역
- '''렌즈''': 두 개의 겹치는 원반의 공통 영역(교차 부분)
3. 역사
20세기 초 추상 미술의 등장과 함께 기하학적 대상은 그 자체로 예술적 주제가 되었다. 특히 바실리 칸딘스키는 자신의 작품에서 원을 자주 사용했다.[8][9]
3. 1. 고대
기원전 5세기경 안티폰은 정다각형의 변 수를 계속 늘려가면 결국엔 원이 된다고 생각했다. 이에 15세기 독일의 신학자 니콜라우스는 아무리 변을 늘려도 원이 될 수는 없다는 사상으로 반박했다.단어 ''circle''(원)은 그리스어 κίρκος/κύκλος (''kirkos/kuklos'')에서 유래되었으며, 이는 "고리" 또는 "반지"를 의미하는 호메로스 그리스어 κρίκος (''krikos'')의 전위이다.[1] 단어 ''서커스''와 ''회로''의 기원은 밀접하게 관련되어 있다.

선사 시대 사람들은 석원과 목원을 만들었고, 원형 요소는 암각화와 동굴 벽화에서 흔히 발견된다.[2] 원반 모양의 선사 시대 유물에는 네브라 천문반과 벽옥이라고 불리는 옥 디스크가 포함된다.
기원전 1700년으로 거슬러 올라가는 이집트의 린드 파피루스는 원의 면적을 찾는 방법을 제시한다. 결과는 파이(π)의 근사값인 256/81 (3.16049...)에 해당한다.[3]
유클리드의 ''원론'' 제3권은 원의 속성을 다룬다. 유클리드가 정의한 원은 다음과 같다.
플라톤의 일곱 번째 편지에는 원에 대한 상세한 정의와 설명이 나와 있다. 플라톤은 완벽한 원에 대해 설명하고, 그것이 그림, 단어, 정의 또는 설명과 어떻게 다른지 설명한다. 초기 과학, 특히 기하학과 점성술과 천문학은 대부분의 중세 학자들에게 신성한 것과 연결되었으며, 많은 사람들이 원에서 본질적으로 "신성"하거나 "완벽"한 무언가를 찾을 수 있다고 믿었다.[5][6]
1880년, 페르디난트 폰 린데만은 파이(π)가 초월수임을 증명하여, 수천 년 된 원적 문제가 자와 컴퍼스로는 해결될 수 없음을 증명했다.[7]
원적 문제는 주어진 원과 면적이 같은 정사각형을 컴퍼스와 자만 사용하여 유한 번의 단계로 작도하는 문제로, 고대 기하학자들이 제시했다. 1882년, 이 문제는 린데만-바이어슈트라스 정리의 결과로 불가능함이 증명되었는데, 이 정리는 원주율(π)이 초월수이며 대수적 수가 아님을 증명한다. 즉, 원주율은 유리수 계수를 갖는 어떤 다항식의 근이 아니다. 불가능함에도 불구하고, 이 주제는 유사수학 애호가들에게 지속적인 관심을 받고 있다.
3. 2. 중세 및 근대
기원전 5세기경 안티폰은 정다각형의 변 수를 계속 늘려가면 결국엔 원이 된다고 생각했다. 이에 15세기 독일의 신학자 니콜라우스는 아무리 변을 늘려도 원이 될 수는 없다는 사상으로 반박했다.플라톤의 일곱 번째 편지에는 원에 대한 상세한 정의와 설명이 나와 있다. 플라톤은 완벽한 원에 대해 설명하고, 그것이 그림, 단어, 정의 또는 설명과 어떻게 다른지 설명한다. 초기 과학, 특히 기하학과 점성술과 천문학은 대부분의 중세 학자들에게 신성한 것과 연결되었으며, 많은 사람들이 원에서 본질적으로 "신성"하거나 "완벽"한 무언가를 찾을 수 있다고 믿었다.[5][6]
1880년, 페르디난트 폰 린데만은 π(파이)가 초월수임을 증명하여, 수천 년 된 원적 문제가 자와 컴퍼스로는 해결될 수 없음을 증명했다.[7]
4. 해석적 성질
원의 해석적 성질에 대해 설명한다.
- '''원의 방정식'''
- * 데카르트 좌표계에서 중심이 이고 반지름이 인 원의 방정식은 다음과 같다.
:
:이는 피타고라스 정리를 통해 유도된다.[28]
- * 일반적인 형태는 다음과 같다.
:
:(단, 는 실수이며, 이어야 한다.)[28] 좌변은 반지름의 4배에 해당하며, '=0'일 경우 한원소 집합이 되고, '<0'일 경우 공집합이 된다.[28]
- * 평면 위의 모든 원은 적절한 데카르트 좌표계를 설정하면 다음과 같은 표준 방정식으로 표현할 수 있다.
:
:(단, ). 원의 중심을 좌표계의 원점으로 설정하면 된다.
- * 매개변수 방정식은 다음과 같다.
:
:(은 각각 코사인 함수와 사인 함수, 는 매개 변수)[28]
- '''극좌표계에서의 원의 방정식'''
극좌표계 위의 중심이 이고 반지름이 인 원의 방정식은 다음과 같다.
:
- '''복소평면에서의 원의 방정식'''
복소평면 위에서, 중심이 이고 반지름이 인 원의 방정식은 다음과 같다.
:
:(는 복소수의 절댓값)
- * 일반적인 형태는 다음과 같다.
:
:(는 켤레 복소수. 는 실수, 는 복소수, , )
:이면 복소평면 위 직선 방정식의 일반적인 형태를 얻는다. 즉, 조건을 제거하면 일반화 원 방정식의 일반적인 형태가 된다.
- '''접선의 방정식'''
- * 2차원 데카르트 좌표계 위에서, 다음 원의 을 접점으로 하는 접선의 방정식은 다음과 같다.
:
:
- * 기울기가 인 접선의 방정식은 다음과 같다.
:
4. 1. 둘레와 넓이
어떤 원의 반지름의 길이를 이라고 하고, 지름의 길이를 라고 하면, 원의 둘레는 다음과 같다.:
여기서 는 원주율이다. 이는 약 3.1415…를 값으로 하는 초월수이다.
어떤 원의 반지름의 길이를 , 지름의 길이를 , 둘레를 라고 하면, 원(으로 둘러싸인 도형)의 넓이는 다음과 같다.
:}}
등주 부등식에 따르면, 이는 둘레가 인 닫힌 곡선으로 둘러싸인 도형이 가질 수 있는 최대 넓이이다.
아르키메데스는 저서 《원 측정》에서 원 내부의 면적은 밑변이 원의 둘레와 같고 높이가 원의 반지름과 같은 삼각형의 면적과 같으며,[11] 이는 에 반지름의 제곱을 곱한 것과 같음을 증명하였다.
:
지름을 로 표기하면 다음과 같다.
:
이는 외접하는 사각형(변의 길이가 )의 약 79%이다.
원은 주어진 호의 길이에서 최대 면적을 둘러싸는 평면 곡선이다. 이는 원을 등주 부등식이라는 변분법 문제와 관련시킨다.


반지름 의 원호 상의 시작점에서 폭 }}, 종점에서 폭 }}인 확폭 원호의 길이 계산은 다음과 같다.
- }
로 하면,
:
:{{math|1=\begin{array}{rcl}
Lw &= &\displaystyle (R+w_1 )\theta +\frac{1}{2} kR\theta^2 \\
&= &\displaystyle L\left\{1+\frac{w_1}{R} +\frac{kL}{2R} \right\} \\
&= &\displaystyle L\left\{1+\frac{1}{R} ( w_1 +\frac{1}{2}kL)\right\} \\
&= &\displaystyle L\left\{1+\frac{1}{R} \left( w_1 +\frac{1}{2} (w_2 -w_1 )\right) \right\} \\
&= &\displaystyle L\left\{1+\frac{1}{R} \frac{w_1 + w_2}{2} \right\} \\
&= &\displaystyle \left( R+\frac{w_1 +w_2}{2} \right) \theta
\end{array}}}
따라서 확폭 원의 길이는 평균 반지름에 중심각을 곱한 값이 된다.
4. 2. 방정식
데카르트 좌표계나 극좌표계를 복소수 로 대신하면, 원과 직선의 통일된 방정식을 얻을 수 있다.복소평면에서 중심이 이고 반지름이 인 원의 방정식은 복소수의 절댓값을 사용하여 다음과 같이 나타낼 수 있다.
:
이는 복소 평면에서의 복소수 덧셈 및 실수배가 성분 표시된 평면 벡터의 덧셈 및 실수배와 동일하고, 복소수의 절댓값이 유클리드 노름과 같다는 점에서 원의 벡터 방정식과 본질적으로 같다.
복소평면 위 원의 방정식의 일반적인 형태는 다음과 같다.
:
여기서 는 켤레 복소수이다. 단, 는 실수이고, 는 복소수이며, 이고 이어야 한다. 이고 다른 조건이 같으면 복소평면 위 직선 방정식의 일반적인 형태가 된다. 즉, 조건을 제거하고 다른 조건을 그대로 두면 일반화 원 방정식의 일반적인 형태를 얻는다.
극형식을 고려하면, 조건은 (는 임의)와 동치임을 알 수 있다. 이는 매개변수 표시에 해당한다.
복소수 곱셈에서 가 성립하므로, 이 방정식은 실수 및 복소수 를 사용하여 다음과 같이 나타낼 수 있다.
: ()
이 형태의 방정식은 원뿐만 아니라 일반화된 원(일반화된 원은 통상적인 원이거나 직선이다)을 나타낸다.
4. 2. 1. 데카르트 좌표계

2차원 데카르트 좌표계에서 중심이 이고 반지름이 인 원의 방정식은 다음과 같다.
:
이 식은 피타고라스 정리를 통해 유도된다.[28]
2차원 데카르트 좌표계에서 원의 방정식의 일반적인 형태는 다음과 같다.
:
(단, 는 실수이며, 이어야 한다.)[28]
이때 좌변은 반지름의 4배에 해당하며, '=0'이면 한원소 집합이 되고, '<0'이면 공집합이 된다.[28]
평면 위의 모든 원은 적절한 데카르트 좌표계를 설정하면 다음과 같은 표준 방정식으로 표현할 수 있다.
:
(단, )
이 방정식은 원의 중심을 좌표계의 원점으로 설정하면 얻을 수 있다.
2차원 데카르트 좌표계에서 중심이 이고 반지름이 인 원은 다음과 같은 매개변수 방정식으로도 나타낼 수 있다.[28]
:
여기서 은 각각 코사인 함수와 사인 함수이며, 는 매개 변수이다.
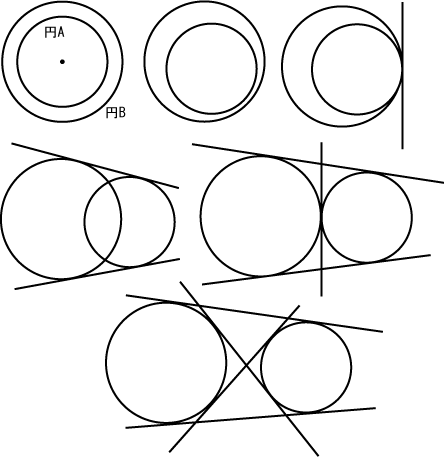
두 원에 공통으로 접하는 접선을 '''공통 접선'''이라고 한다.
특히, 두 원이 공통 접선에 대해 같은 쪽에 있으면 '''공통 외접선''', 다른 쪽에 있으면 '''공통 내접선'''이라고 한다.
두 원의 위치 관계에 따라 그릴 수 있는 공통 접선의 개수는 다음과 같다.
# 없음
# 공통 외접선 1개
# 공통 외접선 2개
# 공통 내접선 1개, 공통 외접선 2개 (총 3개)
# 공통 내접선 2개, 공통 외접선 2개 (총 4개)
4. 2. 2. 극좌표계
극좌표계에서 원의 방정식은 다음과 같다.:
여기서 ''a''는 원의 반지름이고, 는 원 위의 임의의 점의 극좌표이며, 는 원의 중심의 극좌표이다. ''r''0는 원점에서 원의 중심까지의 거리이고, ''φ''는 양의 ''x''축에서 원점을 원의 중심과 연결하는 선까지의 반시계 방향 각도이다. 원점이 중심인 원(즉, )의 경우, 로 단순화된다. 이거나 원점이 원 위에 있는 경우, 방정식은 다음과 같다.
:
일반적인 경우, 방정식을 ''r''에 대해 풀면 다음과 같다.
:
± 기호가 없으면 방정식은 경우에 따라 원의 절반만 나타낼 수 있다.
4. 2. 3. 복소평면
데카르트 좌표나 극좌표를 복소수 로 대신하면, 원과 직선의 통일된 방정식을 얻을 수 있다.복소평면 위에서, 중심이 이고 반지름이 인 원의 방정식은
:
이다. 여기서 는 복소수의 절댓값이다.
또한 복소평면 위의 원의 방정식의 일반적인 꼴은
:
이다. 여기서 는 켤레 복소수이다. 단, 는 실수이고, 는 복소수이며,
:
:
이어야 한다. 대신 을 취하고 다른 조건을 그대로 두면 복소평면 위의 직선의 방정식의 일반적인 꼴을 얻는다. 즉, 이라는 조건을 제거하고 다른 조건을 그대로 두면 일반화 원의 방정식의 일반적인 꼴을 얻는다.
복소 평면에서 중심이 ''c''이고 반지름이 ''r''인 원은 다음 방정식을 갖는다.
매개변수 형식으로, 이것은 다음과 같이 쓸 수 있다.
실수 ''p'', ''q''와 복소수 ''g''에 대해, 약간 일반화된 방정식
은 때때로 일반화된 원이라고 불린다. 이것은 일 때 위의 원의 방정식이 되는데, 이기 때문이다. 모든 일반화된 원이 실제로 원인 것은 아니다. 일반화된 원은 (진정한) 원 또는 선이다.
복소수 평면을 사용하면 평면 위의 원은 복소수를 사용하여 기술할 수 있다. 중심이 이고 반지름이 인 원의 방정식은 복소수의 절댓값을 사용하여 로 쓸 수 있다. 이것은 본질적으로 원의 벡터 방정식과 같은 것이다(복소수 평면에서의 복소수의 덧셈 및 실수배는, 성분 표시된 평면 벡터의 덧셈 및 실수배와 동일하며, 복소수의 절댓값은 유클리드 노름과 동일시할 수 있다). 극형식을 생각하면, 라는 조건은 (는 임의) 와 동치임을 알 수 있다(이것은 매개변수 표시에 대응한다).
복소수의 곱셈에 관하여 가 성립한다는 점에 주의하면, 이 방정식은 실수 및 복소수 를 사용하여 형태로 쓸 수 있다(). 이 형태의 방정식은 원뿐만 아니라 일반적으로 일반화된 원을 나타낸다(일반화된 원이란, 통상의 원이 되거나, 그렇지 않으면 직선이다).
극방정식도 극형식을 사용하면 복소수로 기술할 수 있다.
4. 3. 접선의 방정식
2차원 데카르트 좌표계에서, 중심이 (a, b)이고 반지름이 r인 원의 방정식은 다음과 같다.:()
이 원 위의 점 (, )에서의 접선의 방정식은 다음과 같다.
:()
또한, 기울기가 m인 접선의 방정식은 다음과 같이 표현할 수 있다.
:()
원 위의 점 P를 지나는 접선은 P를 지나는 지름에 수직이다. P = (, )이고 원의 중심이 (a, b)이며, 반지름이 r이라면, 접선은 (a, b)에서 (, )까지의 선에 수직이므로 ( − a)x + ( – b)y = c 형태를 갖는다. (, )에서 이 식을 계산하면 c의 값을 구할 수 있으며, 접선의 방정식은 다음과 같다.
:
또는
:
만약 ≠ b 이면, 이 접선의 기울기는 다음과 같다.
:
이는 음함수 미분법으로도 구할 수 있다.
원의 중심이 원점에 있을 때, 접선의 방정식은 다음과 같다.
:
이때 기울기는 다음과 같다.
:
원점을 중심으로 하는 원에서 각 점의 위치 벡터 (, )와 접벡터 (, )는 항상 직교한다. 즉, 내적이 0이므로 다음 식이 성립한다.
:
5. 기하적 성질
- 임의의 두 원은 서로 중심 닮음이며, 동심원이 아닐 경우 두 원의 중심을 잇는 선분의 반지름의 비에 따른 내분점 및 외분점을 닮음 중심으로 갖는다.[29]
- 반지름의 길이가 같은 모든 원은 서로 합동이다.[31]
- 공선점이 아닌 세 점을 지나는 원은 항상 유일하게 존재한다.[31]
- 원은 주어진 둘레의 길이에서 가장 넓은 면적을 가진 도형이다. (등주 부등식 참조)
- 모든 원은 닮음이다.[12]
- * 원의 둘레와 반지름은 비례한다.
- * 닫힌 면적과 반지름의 제곱은 비례한다.
- * 비례 상수 값은 각각 2π와 π이다.
- 원점을 중심으로 하고 반지름이 1인 원을 단위 원이라고 한다.
- * 단위 구의 대원으로 생각하면, 리만 원이 된다.
- 동일 직선상에 있지 않은 임의의 세 점을 지나는 유일한 원이 존재한다. 데카르트 좌표계에서는 세 점의 좌표를 사용하여 원의 중심 좌표와 반지름에 대한 명시적인 공식을 제공할 수 있다. 외접원을 참조하라.
- 삼각형이나 원에 관한 사항을 다루는 기하학 (닮음이나 면적을 사용하지 않음)은 '''원론'''이라고 불리며, 예로부터 매우 깊이 연구되어 왔다. 가장 평면 기하학다운 기하학이라고도 불린다.
5. 1. 대칭
- 원은 지름에 대한 반사와 원의 중심에 대한 회전에 대하여 대칭이다.[30] 즉, 원의 대칭군은 2차원 직교군 이다.
- 원은 매우 대칭적인 도형으로, 중심을 지나는 모든 선은 반사 대칭을 이루고, 모든 각도에 대해 중심을 기준으로 회전 대칭을 갖는다. 원의 대칭군은 직교군 O(2, ''R'')이다. 회전만의 군은 원군 '''T'''이다.
5. 2. 호와 현
- 현의 수직 이등분선은 원의 중심을 지난다.[30]
- * 즉, 현에 수직인 지름은 현을 이등분한다.[30]
- * 즉, 지름이 아닌 현을 이등분하는 지름은 현에 수직이다.[30]
- 지름은 원의 가장 긴 현이다.[31]
- (방멱 정리) 원 위에 있지 않은 점 를 지나는 두 직선 가운데 하나는 원과 점 와 에서 만나고, 다른 하나는 원과 점 와 에서 만난다고 하면, 이다.[31]
- 원 위의 점과 현 사이의 거리와 지름의 곱은 점과 현의 양 끝점 사이의 거리의 곱과 같다.[29]
- 현의 길이는 원의 중심으로부터 같은 거리에 있을 때에만 서로 같다.
- 원의 중심에서 현에 수직인 선은 현을 이등분한다.
- 중심을 통과하고 현을 이등분하는 선분은 현에 수직이다.
- 원의 중심각과 원주각이 같은 현에 의해 만들어지고 현의 같은 쪽에 있으면, 중심각은 원주각의 두 배이다.
- 두 각이 같은 현과 같은 쪽에 내접하면, 그 각은 같다.
- 두 각이 같은 현과 현의 반대쪽에 내접하면, 그 각은 보충각이다.
- * 원내접사각형의 외각은 내대각과 같다.
- 지름에 의해 만들어진 원주각은 직각이다 (탈레스의 정리 참조).
- 공통 현 AB를 가진 모든 원 중에서, 반지름이 가장 작은 원은 지름이 AB인 원이다.
- 두 현의 교점이 한 현을 길이 ''a''와 ''b''로 나누고 다른 현을 길이 ''c''와 ''d''로 나누면, ''ab'' = ''cd'' 이다.
- 두 수직인 현의 교점이 한 현을 길이 ''a''와 ''b''로 나누고 다른 현을 길이 ''c''와 ''d''로 나누면, ''a''2 + ''b''2 + ''c''2 + ''d''2 는 지름의 제곱과 같다.[13]
- 주어진 점에서 직각으로 교차하는 두 현의 제곱 길이의 합은 동일한 점에서 교차하는 다른 두 수직 현의 제곱 길이의 합과 같으며, 8''r''2 − 4''p''2로 주어진다. 여기서 ''r''은 원의 반지름이고, ''p''는 중심점과 교차점 사이의 거리이다.[14]
- 원 위의 한 점에서 주어진 현까지의 거리에 원의 지름을 곱한 값은 점에서 현의 끝점까지의 거리의 곱과 같다.[15]
- 현의 정리는 두 현 ''CD''와 ''EB''가 점 ''A''에서 교차하면 ''AC'' × ''AD'' = ''AB'' × ''AE'' 가 성립한다고 말한다.
- 현과 그 끝점에서의 접선 사이의 각은 현의 반대쪽에서 원의 중심에서 이루는 각의 절반과 같다(접선-현 각).
- 현이 중심에서 이루는 각이 90°이면 ''ℓ'' = ''r'' √2 가 성립하며, 여기서 ''ℓ''은 현의 길이이고, ''r''은 원의 반지름이다.
- 원과 두 점에서 만나는 직선을 '''할선'''이라고 한다. 이때의 교점을 두 점 A, B라고 할 때, 원주에 의해 할선에서 잘려나가는 선분 AB를 '''현'''이라고 하며, 현 AB라고 부른다.
- 원주는 할선에 의해 두 부분으로 나뉜다. 이 각각의 부분을 '''원호''' (arc) 또는 단순히 '''호'''라고 한다.
- * 두 호의 길이가 같지 않을 때, 긴 쪽의 호를 '''우호''' (major arc), 짧은 쪽의 호를 '''열호''' (minor arc)라고 한다.
- * 두 호의 길이가 같을 때, 이 호들을 '''반원'''이라고 한다. 이때, 할선은 원의 중심을 지나는 중심선이다.
- 원주상의 두 점 A, B를 양 끝으로 하는 호를 호 AB라고 부른다. 기호로는, A͡B로 표기한다 (기호 ⌒는 AB 위에 덮어 쓰는 것이 옳다). 이것으로는 우호와 열호 중 어느 것인지 지정할 수 없는 단점이 있어, 한 쪽을 특정하고 싶을 때는, 그 호 위의 점 P를 사용하여 호APB와 같이 표기한다.
- 현 AB와 호 AB로 둘러싸인 도형을 '''활꼴''' (segment)이라고 한다.
5. 3. 원과 직선의 위치 관계
평면 위의 원과 직선의 위치 관계는 원의 중심에서 직선까지의 거리 와 원의 반지름 의 대소 관계에 따라 다음과 같이 나뉜다.- 라면, 원과 직선은 만나지 않는다.
- 라면, 원과 직선은 한 점에서 만난다. 이때 직선은 원의 접선이다.
원 위의 점 ''P''를 지나는 접선은 ''P''를 지나는 지름에 수직이다. 원의 중심이 (''a'', ''b'')이고 반지름이 ''r''인 원에서 점 P (''x''1, ''y''1)를 지나는 접선의 방정식은 다음과 같다.
만약 이면, 이 접선의 기울기는 다음과 같다.
이것은 음함수 미분법을 사용하여 구할 수도 있다.
원의 중심이 원점에 있을 때, 접선의 방정식은 다음과 같다.
그리고 그 기울기는 다음과 같다.
- 원의 반지름의 끝점을 지나고 반지름에 수직으로 그려진 선은 원의 접선이다.
- 원과 접하는 접점을 지나 접선에 수직으로 그려진 선은 원의 중심을 지난다.
- 원 밖의 임의의 점에서 항상 두 개의 접선을 그릴 수 있으며, 이 접선들의 길이는 같다.
- 점 ''A''에서의 접선과 점 ''B''에서의 접선이 외부 점 ''P''에서 교차하는 경우, 중심을 ''O''라고 표시하면, 각 ∠''BOA''와 ∠''BPA''는 보각 관계이다.
- 만약 ''AD''가 원에 접선이고 점 ''A''에서 접하며 ''AQ''가 원의 현이라면, 이다.
- 현의 정리는 두 현 ''CD''와 ''EB''가 점 ''A''에서 교차하면 가 성립한다고 말한다.
- 두 할선 ''AE''와 ''AD''가 원과 각각 ''B''와 ''C''에서 교차하면 가 성립한다 (현의 정리의 따름 정리).
- 접선은 끝점이 일치하는 할선의 극한 경우로 간주할 수 있다. 외부 점 ''A''에서 그은 접선이 원과 점 ''F''에서 만나고, 외부 점 ''A''에서 그은 할선이 원과 각각 점 ''C''와 ''D''에서 만나면 가 성립한다 (접선-할선 정리).
- 현과 그 끝점에서의 접선 사이의 각은 현의 반대쪽에서 원의 중심에서 이루는 각의 절반과 같다(접선-현 각).
- 현이 중심에서 이루는 각이 90°이면 가 성립하며, 여기서 ''ℓ''은 현의 길이이고, ''r''은 원의 반지름이다.
- 오른쪽 그림과 같이 두 할선이 원에 내접하면 각 ''A''의 크기는 갇힌 호(와 )의 크기 차이의 절반과 같다. 즉, 이며, 여기서 ''O''는 원의 중심이다(할선-할선 정리).
5. 4. 두 원의 위치 관계
두 원의 위치 관계는 두 원의 반지름 와 두 중심 사이의 거리 에 따라 다음과 같이 나뉜다.- 이거나 이면, 두 원은 만나지 않는다.
- * 이면, 두 원은 서로의 외부에 있으며 교점을 가지지 않는다.
- * 이면, 작은 원은 큰 원의 내부에 있으며 교점을 가지지 않는다.
- 이거나 이면, 두 원은 한 점에서 만난다. 즉, 두 원은 서로 접한다.
- * 이면, 두 원은 서로의 외부에서 접한다. 즉, 두 원은 외접한다.
- * 이면, 작은 원이 큰 원의 내부에서 큰 원에 접한다. 즉, 두 원은 내접한다.
- 이면, 두 원은 두 점에서 만난다.
5. 5. 중심각과 원주각
- 주어진 호에 대한 원주각의 크기는 그 호에 대한 중심각의 1/2이다.[31]
- 같은 호에 대한 두 원주각의 크기는 서로 같다.[31]
- 켤레호에 대한 두 중심각은 서로 보각이다.
- * 내접 사각형의 두 대각은 서로 보각이다.[31]
- * 내접 사각형의 외각의 크기는 내대각과 같다.
- (탈레스 정리) 지름에 대한 원주각은 직각이다.
- * 삼각형의 외심이 변 위에 있을 필요충분조건은 직각 삼각형이다.[31]
- 원의 두 현이 원 내부에서 이루는 각의 크기는 이 각과 맞꼭지각의 내부에 포함되는 두 호에 대한 중심각의 합의 1/2이다.[31]
- 원의 두 할선이 원 외부에서 이루는 각의 크기는 이 각의 내부에 포함되는 두 호에 대한 중심각의 차의 1/2이다.[31]
원주각(그림에서 파란색과 녹색 각도가 예시)은 해당 중심각(빨간색)의 정확히 절반이다. 따라서 같은 호(분홍색)에 대한 모든 원주각은 같다. 호(갈색)에 내접하는 각은 보충 관계에 있다. 특히, 지름에 대한 모든 원주각은 직각이다(중심각이 180°이기 때문에).
호 AB에 대하여, 호 AB 위에 없는 원 O의 원주상의 점 P를 잡을 때, ∠APB를 호 AB에 대한 '''원주각'''이라고 한다. 호 AB에 대한 원주각은 점 P의 위치에 관계없이 일정하며, 중심각 AOB의 절반과 같다 ('''원주각의 정리'''). 특히 호 AB가 반원주일 때는, 호 AB에 대한 원주각은 직각이다 ('''지름을 낀 원주각''': 탈레스의 정리).
5. 6. 접선
- 원 위의 한 점을 지나는 원의 접선은 유일하게 존재하고, 이는 이 점을 지나는 반지름에 수직이다.[30][31]
- * 즉, 반지름의 끝점에서의 수선은 원에 접한다.[30]
- * 즉, 원의 접선의 접점에서의 수선은 원의 중심을 지난다.
- 원 외부의 한 점을 지나는 원의 접선은 정확히 2개이고, 이 점과 두 접점 사이의 거리는 같으며, 두 접선이 이루는 각과 두 접점을 지나는 반지름이 이루는 각은 서로 보각이다.
- 원의 접현각의 크기는 현을 기준으로 이와 같은 쪽에 있는 호에 대한 중심각의 1/2이다.[31]
- 원의 접선과 할선이 원 외부에서 이루는 각은 각의 내부에 포함된 두 호의 중심각의 차의 1/2이다.[31]
- 외접하는 두 원의 교점을 지나는 두 공통 할선 사이의 두 현은 서로 평행하다.[31]
- (접선에 대한 방멱 정리) 원 외부의 점 를 지나는 두 직선 가운데 하나는 원과 와 에서 만나고, 하나는 원에 점 에서 접한다고 하면, 이다.
- 원 위의 점 ''P''를 지나는 접선은 ''P''를 지나는 지름에 수직이다. 원의 중심이 원점에 있을 때, 접선의 방정식은 다음과 같다.
그리고 그 기울기는 다음과 같다.
- 원의 반지름의 끝점을 지나고 반지름에 수직으로 그려진 선은 원의 접선이다.
- 원과 접하는 접점을 지나 접선에 수직으로 그려진 선은 원의 중심을 지난다.
- 원 밖의 임의의 점에서 항상 두 개의 접선을 그릴 수 있으며, 이 접선들의 길이는 같다.
- 점 ''A''에서의 접선과 점 ''B''에서의 접선이 외부 점 ''P''에서 교차하는 경우, 중심을 ''O''라고 표시하면, 각 ∠''BOA''와 ∠''BPA''는 보각 관계이다.
- 만약 ''AD''가 원에 접선이고 점 ''A''에서 접하며 ''AQ''가 원의 현이라면, 이다.
- 원주와 직선이 하나의 공통점을 가질 때, 그 직선을 원의 '''접선''' (tangent)이라고 하며, 공통점을 '''접점'''이라고 한다. 원의 중심과 접점을 잇는 반지름 ('''접점 반지름''')은 접선과 접점에서 직교한다.
- 원의 외부의 점 A에서 원 O에 두 개의 접선을 그릴 수 있다. 이 접점을 S, T라고 하면, 선분 AS, AT의 길이를 '''접선의 길이'''라고 한다. 접선의 길이는 같다. 원의 접선과 그 접점을 지나는 현이 이루는 각은, 그 각 안에 있는 호에 대한 원주각과 같다 ('''접현 정리'''). 즉, 아래 그림에서 AT가 접선이라면, ∠BAT = ∠APB이다. 접현 정리는 역도 성립한다.
5. 7. 원의 직교
두 원의 교점에서의 두 접선이 서로 수직일 경우 두 원이 서로 직교한다고 한다.[29]- 두 원의 반지름이 이고, 두 중심 사이의 거리가 라고 할 때, 두 원이 서로 직교할 필요충분조건은 이다.[29]
- 주어진 원에 직교하고 중심이 원 외부의 주어진 점인 원은 유일하게 존재한다.[29]
- 주어진 원에 직교하고 원의 지름이 아닌 현의 두 끝점을 지나는 원은 유일하게 존재한다.[29]
6. 작도
컴퍼스와 자를 사용하여 작도할 수 있는 방법은 다음과 같다.
- 공선점이 아닌 세 점 를 지나는 원
:# 선분 의 수직 이등분선을 그린다.
:# 선분 의 수직 이등분선을 그린다.
:# 선분 와 의 교점 를 취한다.
:# 점 를 중심으로 하고 선분 를 반지름으로 하는 원을 그린다. 이 경우 원은 점 를 지난다.

- 주어진 원의 중심
:# 원 위의 두 점 을 취한다.
:# 선분 의 점 에서의 수선 를 그린다.
:# 직선 와 원의 교점 를 취한다. 이 경우 선분 는 원의 지름이다.
:# 또 다른 지름 을 작도한다.
:# 선분 와 의 교점 를 취한다. 이 경우 점 는 원의 중심이다.
자(도구)와 컴퍼스 작도법들을 이용하여 원(기하학)을 그릴 수 있다.
가장 간단하고 기본적인 방법은 원의 중심과 원 위의 한 점이 주어졌을 때 작도하는 것이다. 컴퍼스의 고정 다리를 원의 중심에 놓고, 움직이는 다리를 원 위의 점에 놓은 다음 컴퍼스를 회전시킨다.
7. 기타 관련 주제
모든 삼각형은 유일한 내접원 및 외접원과 정확히 3개의 방접원을 갖는다. 그러나 일반적으로 다각형은 내접원이나 외접원을 가질 필요가 없다. 어떤 다각형이 모든 변에 접하는 원을 가질 경우, 이 다각형을 외접 다각형이라고 한다. 어떤 다각형이 모든 꼭짓점을 지나는 원을 가질 경우, 이 다각형을 내접 다각형이라고 한다. 동시에 외접 다각형이며 내접 다각형인 다각형을 이중중심 다각형이라고 한다. 예를 들어, 모든 삼각형과 모든 정다각형은 이중중심 다각형이다.[31]
페르가의 아폴로니우스는 원이 평면 상의 한 점의 집합으로 정의될 수 있으며, 두 개의 고정된 초점 ''A''와 ''B''까지의 거리가 상수 ''비율'' (1이 아닌)을 가진다는 것을 보였다.[16][17] (거리가 같은 점들의 집합은 선분 ''AB''의 수직 이등분선이다.)
만약 ''C''가 선분 ''AB''의 중점이라면, 아폴로니우스 조건을 만족하는 점 ''P''의 집합은 원이 아니라 직선이다. 따라서 ''A'', ''B'', ''C''가 평면 위의 서로 다른 점으로 주어지면, 위의 방정식을 만족하는 점 ''P''의 자취를 "일반화된 원"이라고 한다. 이것은 진정한 원이거나 직선일 수 있다. 이러한 의미에서 직선은 무한 반지름을 가진 일반화된 원이다.
모든 삼각형에는 세 변 각각에 접하도록 하는 고유한 원, 즉 내접원을 내접시킬 수 있다.[19]
모든 삼각형에 대해, 삼각형의 세 꼭짓점을 모두 지나는 유일한 원, 즉 외접원을 외접시킬 수 있다.[20]
접선 다각형, 예를 들어 접선 사각형은 다각형의 각 변에 접하는 내접원을 내접시킬 수 있는 모든 볼록 다각형을 말한다.[21] 모든 정다각형과 모든 삼각형은 접선 다각형이다.
원내 다각형은 각 꼭짓점을 지나는 외접원을 외접시킬 수 있는 모든 볼록 다각형이다. 잘 연구된 예는 원내 사각형이다. 모든 정다각형과 모든 삼각형은 원내 다각형이다. 원내 다각형이면서 접선 다각형인 다각형을 이중중심 다각형이라고 한다.
하이포사이클로이드는 주어진 원 안에 구르는 더 작은 원 위의 고정된 점의 자취를 추적하여 주어진 원에 내접하는 곡선이다.
원은 다양한 다른 도형의 극한으로 볼 수 있다.
- ''n''개의 변을 가진 일련의 정다각형은 ''n''이 무한대로 접근함에 따라 원을 극한으로 갖는다. 이 사실은 아르키메데스가 π 근사에 적용했다.
- 데카르트의 난형선은 임의의 점에서 두 개의 고정된 점(초점)까지의 거리의 가중 합이 상수인 점들의 집합이다. 타원은 가중치가 같은 경우이다. 원은 이심률이 0인 타원이며, 이는 두 초점이 원의 중심과 일치한다는 의미이다. 원은 또한 가중치 중 하나가 0인 데카르트의 난형선의 또 다른 특수한 경우이다.
- 초타원은 양수 ''a'', ''b'', ''n''에 대해 형태의 방정식을 갖는다. 초원(supercircle)은 를 갖는다. 원은 인 초원의 특수한 경우이다.
- 카시니 타원은 임의의 점에서 두 개의 고정된 점까지의 거리의 곱이 상수인 점들의 집합이다. 두 고정점이 일치하면 원이 생성된다.
- 정폭 도형은 경계와 한 점에서 만나는 서로 다른 두 개의 평행선 사이의 수직 거리로 정의되는 폭이 두 평행선의 방향에 관계없이 동일한 도형이다. 원은 이러한 유형의 도형의 가장 간단한 예이다.
평면 상의 유한한 개의 점을 고려해 보자. 주어진 점까지의 거리의 제곱의 합이 일정한 점들의 자취는 원이며, 그 중심은 주어진 점들의 무게중심이다.[22]
정삼각형의 경우, 거리의 2제곱과 4제곱의 합이 일정한 점들의 자취는 원이 되며, 정사각형의 경우, 2제곱, 4제곱, 6제곱의 합이 일정한 점들의 자취가 원이 된다. 정오각형의 경우, 거리의 8제곱의 합이 일정한 점들의 자취가 원으로 추가될 것이다.
원을 한 점에서 고정된 거리에 있는 점들의 집합으로 정의할 때, 거리의 다른 정의 하에서 다양한 모양을 원으로 간주할 수 있다. ''p''-노름에서 거리는 다음과 같이 결정된다.
유클리드 기하학에서 ''p'' = 2이며, 이는 다음과 같이 익숙한 형태를 가진다.
택시 기하학에서 ''p'' = 1이다. 택시 원은 좌표축과 45° 각도를 이루는 면을 가진 정사각형이다.
평면에서 체비쇼프 거리 (''L''∞ 메트릭)에 대한 반지름 ''r''의 원은 또한 좌표축에 평행한 변의 길이가 2''r''인 정사각형이므로 평면 체비쇼프 거리는 평면 택시 거리로 회전 및 스케일링을 통해 등가로 볼 수 있다. 그러나 ''L''1 및 ''L''∞ 메트릭 간의 이러한 등가는 더 높은 차원으로 일반화되지 않는다.
원은 1차원 초구 (1-구)이다.
위상수학에서 원은 기하학적 개념에만 국한되지 않고 모든 위상동형에 해당한다. 두 위상 원은 하나를 '''R'''3 자체의 변형(주위 등위로 알려짐)을 통해 다른 것으로 변환할 수 있다면 동일하다.[24]
8. 같이 보기
- 아폴로니우스 원
- 아르키메데스 원
- 아르키메데스의 쌍둥이 원
- 뱅코프 원
- 카라일 원
- 색상환
- 반사상 원
- 포드 원
- 측지 원
- 존슨 원
- 쇼크 원
- 우 원
참조
[1]
웹사이트
krikos
https://www.perseus.[...]
2013-11-06
[2]
논문
Sacred landscapes of the south-eastern USA: prehistoric rock and cave art in Tennessee
https://www.cambridg[...]
2013-06-01
[3]
웹사이트
Chronology for 30000 BC to 500 BC
http://www-history.m[...]
2008-03-22
[4]
간행물
'7227282M'
[5]
서적
The Sleepwalkers: A History of Man's Changing Vision of the Universe
1959
[6]
서적
The Six Books of Proclus, the Platonic Successor, on the Theology of Plato
https://books.google[...]
2017-01-23
[7]
웹사이트
Squaring the circle
http://www-history.m[...]
2008-06-24
[8]
웹사이트
Circles in a Circle
https://philamuseum.[...]
2023-12-28
[9]
웹사이트
Why Did Wassily Kandinsky Paint Circles?
https://www.thecolle[...]
2022-06-15
[10]
간행물
The Circle from East to West
Rizzoli International Publications, Incorporated
2019-10-29
[11]
서적
A History of Mathematics / An Introduction
https://archive.org/[...]
Addison Wesley Longman
[12]
논문
Circular reasoning: who first proved that {{mvar|C}} divided by {{var|d}} is a constant?
[13]
서적
Challenging Problems in Geometry
Dover
[14]
간행물
College Mathematics Journal
1998-09
[15]
서적
Advanced Euclidean Geometry
Dover Publ.
[16]
논문
Introduction to the theory of analytic functions
http://dlxs2.library[...]
[17]
서적
Excursions in Geometry
Dover
[18]
서적
College Geometry
Dover
[19]
웹사이트
Incircle – from Wolfram MathWorld
http://mathworld.wol[...]
2012-01-21
[20]
웹사이트
Circumcircle – from Wolfram MathWorld
http://mathworld.wol[...]
2012-01-20
[21]
웹사이트
Tangential Polygon – from Wolfram MathWorld
http://mathworld.wol[...]
2013-09-03
[22]
논문
Sums of squares of distances in m-space
2003
[23]
논문
Cyclic Averages of Regular Polygons and Platonic Solids
https://www.rgnpubli[...]
2020
[24]
서적
Introduction to topology
https://archive.org/[...]
Dover Publications
[25]
웹사이트
半径
https://kotobank.jp/[...]
デジタル大辞泉
[26]
웹사이트
半径
https://kotobank.jp/[...]
精選版 日本国語大辞典
[27]
웹사이트
もっと数学の世界、「原点はオー!」
https://www.kyo-kai.[...]
[28]
서적
[29]
서적
[30]
서적
[31]
서적
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com


